온도에 따른 시선 안정화 시스템의 마찰 변수 추정
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
The objective of this study was to address the parameter estimation of the line-of-sight stabilization system on temperature variation, which is a significant element in regulating the control performance of mobile platform with visual targeting system. To this end, the LuGre friction model in this study was used both to represent the characteristic of the friction behavior and to design a control algorithm for the friction compensation. Results from both simulation and experimental tests helps to identify the friction parameters on LuGre friction model. Based on LuGre with parameter estimation, PI-LEAD control algorithm is designed to compensate nonlinear characteristic of the line-of-sight stabilization system on the variation of temperature. Finally, through simulation, the good control performance of line-of-sight stabilization system was evaluated according to the temperature variation.
Keywords:
Line-of-sight stabilization system, Stabilization gimbal, LuGre friction model키워드:
시선 안정화 시스템, 안정화 짐벌, LuGre 마찰 모델1. 서론
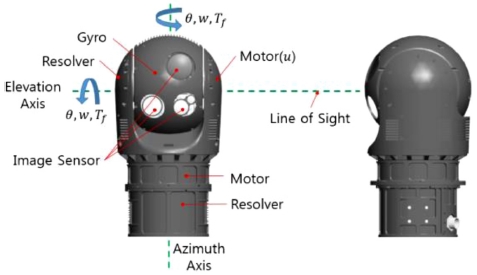
군수 분야에서 주로 사용되는 시선 안정화 시스템은 이동형 플랫폼에 탑재되어 표적의 탐지, 추적, 조준 등의 목적으로 사용되며, 영상 센서를 포함하는 안정화 짐벌(Gimbal) 형태로 주로 구현된다. 특히, 원하는 목표물이나 방향으로 영상 센서의 시선(Line of Sight)을 일정하게 유지할 수 있는 높은 안정화 성능이 요구되므로, 불특정한 외란에 대한 강인성이 보장되어야 한다.1,2
그러나 시선 안정화 시스템은 베어링, 회전씰(Rotary Seal), 슬립링(Slip Ring) 등에 의한 비선형 마찰 성분이 발생하기 때문에 마찰이 가지는 복잡한 형태의 동적 특성에 취약하다. 또한 마찰은 시선 안정화 시스템의 정밀 제어 성능을 저하시키는 요인으로써, 정상상태 오차, 리밋 사이클 진동(Limit Cycle Oscillation)을 발생시키고, 시스템 불안정성을 초래한다.3,4 따라서, 시선 안정화 시스템의 효과적인 제어를 위해서는 마찰 현상에 대한 명확한 이해와 해석이 요구된다.
마찰의 정적 및 동적 거동 특성에 관한 이론적 모델은 지속적으로 연구되었다.5 그 중, LuGre 마찰 모델은 정지마찰 영역, 다양한 속도 영역을 포함한 하나의 함수로 표현하다. 또한 마찰의 동적 특성, 즉, 스틱-슬립(Stick-Slip), 마찰 지연(Friction Lag), 히스테리시스(Hysteresis), 외부 작용력에 따른 항복력(Break-Away Force) 변화, 스트라이벡 효과(Stribeck Effect), 제어시스템과 결부하여 리밋 사이클(Limit Cycle) 발생 등도 표현 가능하기 때문에 시선 안정화 시스템의 마찰 특성을 규명하는데 적합한 모델이다.3,5
그러나 LuGre 마찰 모델의 적용을 위해서는 마찰 모델의 정적 및 동적 변수 값을 추정하는 과정이 필요하다. 최근 다양한 마찰 추정 방법들이 연구되고 있으며,6-8 이를 통해 마찰을 보상할 수 있는 제어기법들도 활발히 연구되고 있다.9,10 하지만, 현재 연구되는 방법으로는 시선 안정화 시스템 적용에 한계가 있다. 우선, 적응 제어기법을 이용하는 방법은 입력 신호가 미분 가능한 주기적 함수 형태가 아니라서, 시선 안정화 시스템처럼 외란이 불규칙할 경우에 추정 정확도 및 안정성이 부정확하다. 또한, 마찰은 부하, 온도, 윤활 상태, 베어링의 예압 등의 다양한 요인에 민감하기 때문에, 특정한 조건에서 식별된 마찰 변수의 활용은 제한적이다. 특히 외부 온도 변화는 단일 시스템에서 마찰 특성을 변화시키는 큰 요인이다. 따라서, 시선 안정화 시스템은 제어기의 설계나 검증 과정에서 온도에 따른 마찰 변동성이 반드시 고려되어야 한다.
2. 시스템 모델링
2.1 플랜트 모델
시선 안정화 시스템은 Fig. 1과 같이 각각 선회 방향 및 고저 방향으로 직류 전동기에 의해 구동되는 2축 안정화 짐벌구조로써, 리졸버(Resolver)와 자이로(Gyro) 센서를 포함하고 있어 위치 및 속도 신호 제어가 가능하다. 각 구동 축에 대한 평형 방정식은 식(1)과 같이 유도된다.
| (1) |
일반적인 시선 안정화 시스템은 선회 방향의 짐벌이 고저 방향의 짐벌을 포함하므로, 본 논문에서는 선회 방향 짐벌의 마찰에 대한 부분만이 고려되었으며, 실제 시스템의 선회 방향 관성 모멘트는 0.342 kg·m2이다.
2.2 제어기 모델
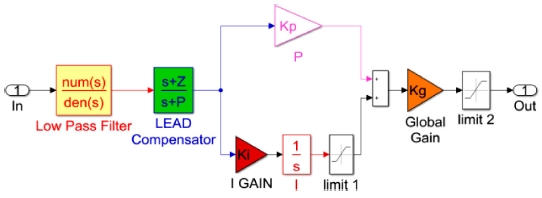
시선 안정화 시스템의 제어기는 저역통과 필터(Low Pass Filter) - PI 제어기 - 진상 보상기(Lead Compensator)로 구성하였다. PI-LEAD 알고리즘은 전통적인 PID 제어방식에 고주파 잡음에 의한 발산 현상을 제거하고, 진상 보상기를 통해 시간 지연 현상을 보상하여 시스템의 강인성 및 안정성을 높여준다.1
2.3 마찰 모델
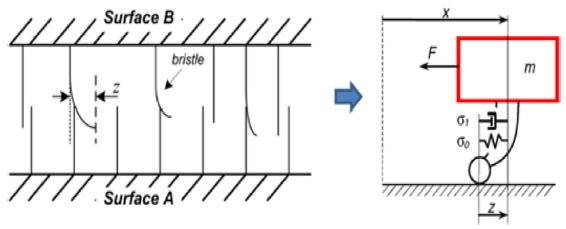
정지된 두 물체의 접촉 표면은 미시적인 관점에서 매우 거친 상태로 서로 결합되어 있다고 볼 수 있다. LuGre 마찰 모델은 접촉면의 특성을 강모(Bristle)의 굽힘에 의한 강성과 댐핑으로 표현하였다.
강모들의 평균 굽힘 변위를 의미하는 상태변수(z)와 전체 마찰 토크(Tf)를 나타내는 식은 아래와 같다.
| (2) |
| (3) |
| (4) |
g(w)는 스트라이벡 효과를 나타내며, 시스템의 속도가 일정한 상태에서 내부 상태 변수(zss)와 마찰 토크(Tfss)는 각각 다음과 같이 수렴하게 된다.
| (5) |
| (6) |
스틱션(Stiction) 구간의 상태변수는 식(7)처럼 근사화 가능하며, 이 때, 시스템의 평형 방정식 식(1)은 식(8)과 같이 선형화 할 수 있다.
| (7) |
| (8) |
3. 마찰 변수의 추정 기법
3.1 정적 마찰 변수
정상상태에서의 마찰 토크는 식(6)처럼 정적 마찰 변수(fs, fc, ωs, σ2)와 속도의 함수로써 속도와 마찰 토크의 상관 관계 분석을 통해 마찰 변수 추정이 가능하다. 또한, 일정 속도에서의 입력 토크는 식(1)의 u = Tf 처럼, 직류 전동기로부터의 전달 토크는 식(9)처럼 나타낼 수 있다.
| (9) |
km은 직류전동기의 특성에 따라 결정되는 상수이며, 직류 전동기의 입력 전압(V)에 대한 시스템의 속도 측정 시험 정보 기반으로 식(6)를 근사화하여 마찰 변수 fc, fs, ωs, σ2 추정이 가능하다.
3.2 동적 마찰 변수
선-미끄러짐(Pre-Sliding) 영역, 즉 입력 토크가 정지 마찰보다 작은 구간(u ≤ fs, ω ≈ 0)에서 마찰 토크는 식(4)에 의해 동적 마찰 변수 σ0, σ1과 내부 상태 변수 z의 함수로 나타낼 수 있다. 내부 상태 변수는 측정이 어렵기 때문에 마찰 변수 추정을 위한 다음 가정이 필요하다.
(1) 모터의 입력 토크를 시간에 비례하여 증가시킨다면 로 근사화할 수 있다.
(2) 선-미끄러짐(Pre-Sliding) 영역에서 변위-마찰 히스테리시스 루프 면적은 선-미끄러짐 거리 제곱에 따라 선형 비례하며, 정규화된 변위 ξ∈[0, 1]와 토크 h∈[0, 1]의 식은 식(10)과 같다.11,12
| (10) |
kc는 시간에 따른 입력 토크의 비례 상수이며, 가정 1에 의해 식(1)과 식(3)은 다음과 같이 정리할 수 있다.
| (11) |
| (12) |
식(11)과 식(12)를 식(2)에 대입하여 식(13)을 구할 수 있다.
| (13) |
ω ≈ +0일 때, 식(13)을 적분하면 다음과 같다.
| (14) |
입력 토크 u = fs가 되는 순간의 시간은 fs/kc이며, 각도 변위를 θs라고 하면, 가정 2에 의해 식(10)을 아래처럼 나타낼 수 있다.
| (15) |
식(15)의 양변을 시간에 관해 미분하면 식(16)과 같다.
| (16) |
식(16)을 식(14)에 대입하여 시간 t = fs/kc일 때, 상태 변수를 zs라고 하면, 식(17)을 얻을 수 있다.
| (17) |
따라서, u = fs이 되었을 때, 식(17)의 결과를 식(11)에 대입하면 식(18)을 얻을 수 있다.
| (18) |
입력 토크 u ≅ 0 일 때, 시스템의 선형화된 평형 방정식(8)에서 σ1 + σ2는 스프링-댐퍼 시스템의 댐핑 계수와 같으며, σ1은 다음과 같이 구할 수 있다.
| (19) |
ζ는 스프링-댐퍼 시스템의 감쇠비(Damping Ratio)이며, 상기식에서 σ1을 바로 추정하기 어렵다. 따라서, 시선 안정화 시스템의 동적 안정화 시험 결과와 시뮬레이션 결과의 비교를 통해 σ1값을 추정하는 방안을 다음 절에서 제시하고자 한다.
4. 시험 및 해석
4.1 마찰 변수 추정
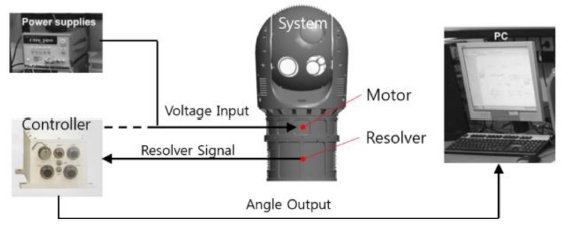
제안된 마찰 변수 추정 검증을 위한 시스템을 Fig. 4와 같이 구성하였다.
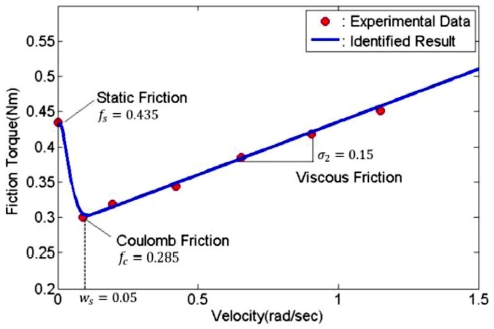
정적 마찰 변수 추정을 위해 시스템의 구동 시작 순간의 정지 마찰 토크를 산출하였다. 스틱션(Stiction) 구간에서는 시스템의 속도가 불안정하므로 전압이 높은 구간에서 서서히 전압을 감소시키는 방법으로 점성 마찰 구간과 쿨롱 마찰 구간의 데이터를 획득하였다. Fig. 5는 식(6)에 측정된 데이터를 입력하여 보간 결과를 보여준다.
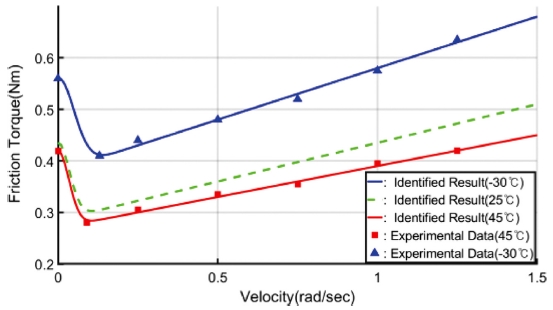
온도에 따른 마찰 특성을 추정하기 위해, 온도 챔버 내에 시스템을 설치한 후 챔버 온도가 -30oC와 +45oC인 조건에서 각각 동일한 마찰 측정 시험을 수행하였다. Fig. 6과 같이 마찰 토크는 외부 온도가 내려갈수록 높아지는 경향을 보였으며, 각각의 마찰 변수가 정지 마찰 변수에 대해 일정한 비율을 유지하면서 변화하는 특성을 보였다. 하지만, 마찰 변수의 불확실성이 온도 변화량에 비례하는 것은 아니며, 상대적으로 저온 영역에서 고온 영역에 비해 변동성이 크게 나타나는 것이 확인되었다. 정적 마찰 변수의 변동성은 상온을 기준으로 -30oC에서는 약 28.7-40%이고, 45oC에서는 3.7-6.7% 수준으로 나타났다.
식(18)을 이용하여 동적 마찰 변수인 σ0를 추정하기 위해 직류전동기 입력 전압을 0에서부터 초당 0.05 V씩 서서히 증가시켜 정지 마찰 토크에 도달하는 순간의 회전 변위를 측정하는 시험을 수행하였다. 시험 오차를 줄이기 위해 회전변위는 시스템 위치를 10°간격으로 변경하면서 총 36회의 반복 평균 값을 사용하였으며, 온도에 따른 변동성을 확인하기 위해 –30oC 및 45oC의 온도 조건에서 반복 시험하였다. 시험 결과인 σ0 값은 Table 1과 같다.
σ1 값을 추정하기 위해 시스템의 동적 안정화 시험 결과를 활용한다. 동적 안정화 시험이란 외란이 인가되었을 때 LOS 각도의 오차를 산출하여 시선 안정화 시스템의 안정화 성능을 평가하는 것이다. 일반적인 지상 플랫폼을 가진 시스템에서 동적 안정화 시험 규격은 회전축 방향으로 83 il/sec RMS 이상의 각속도 외란을 인가하였을 때, LOS 각도 오차를 100 μrad RMS이하로 규정하며, 외란의 입력 함수는 다음과 같이 정의한다.
| (20) |
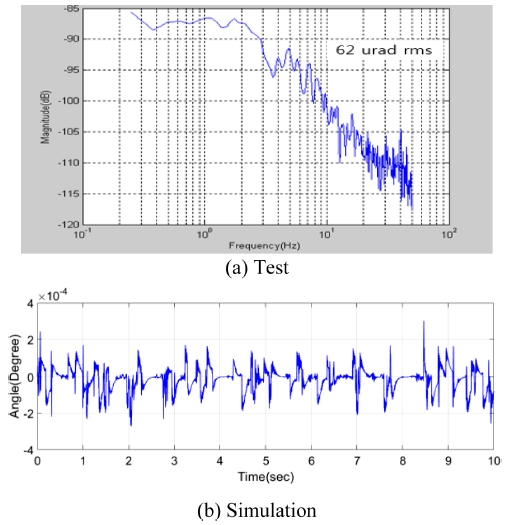
동적 마찰 변수는 속도의 방향이 전환되거나, 변하는 구간에서의 마찰 거동과 밀접한 관련이 있다. 따라서 동적 안정화 시험은 랜덤한 각속도 외란 인가를 통해 시스템의 속도 전환을 수시로하여 응답특성을 확인하는 시험이다. 이 때, 입력되는 외란이 랜덤함수의 형태이기 때문에, 시험 결과와 해석 결과의 절대적인 비교 대신 시선 오차의 RMS 값을 비교하여 마찰 변수를 추정하였다. 실제 시스템의 시험결과에서 LOS 오차는 62 μrad RMS이며, 해석 모델의 시뮬레이션 결과가 동일한 LOS 오차 RMS 값을 가지도록 σ1 값을 조정하며 해석을 반복하였다.
해석을 통해 추정된 최종 값은 σ1 = 192.5 Nm/(rad/s)이며, 식(19)에 의해 ζ = 0.6임을 알 수 있다. 온도에 따른 안정화 성능 시험 데이터가 없기 때문에 σ1의 변동성은 저온 및 고온 구간에서 추정된 마찰 변수 값을 식(19)에 입력하여 계산하였다. 이와 같이 시험 및 시뮬레이션을 통해 전체 마찰 변수를 추정할 수 있으며, 그 결과는 Table 2와 같다.
4.2 안정화 성능 예측
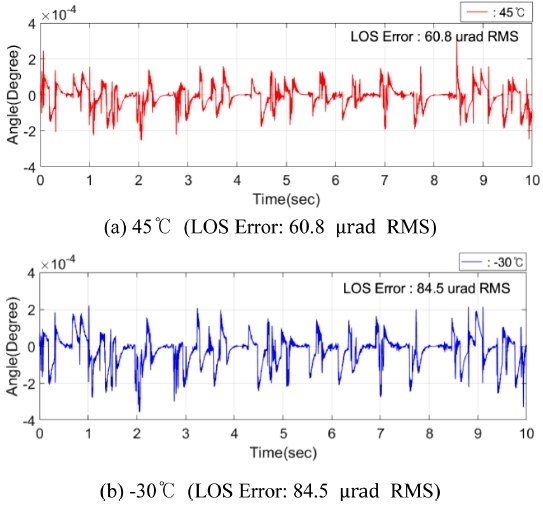
시선 안정화 시스템의 안정화 성능 시험은 시험기가 설치된 장소에서만 수행할 수 있는 공간적 제약 때문에 온도에 따른 영향성을 파악하기 어렵다. 하지만, 온도에 따라 추정된 마찰 변수를 이용한 모의실험을 통해 시스템의 안정화 성능에 따른 온도변화가 예측 가능하다. Table 2에서 -30oC와 45oC에서 추정된 마찰 변수를 통해 안정화 성능 해석을 수행한 결과는 Fig. 9와 같다.
마찰이 커지는 저온의 환경에서 LOS 오차가 상온의 결과값을 기준으로 22.5 μrad RMS정도 증가하였지만, 100 μrad RMS 이하의 요구성능을 충족하는 수준으로 나타나, PI-LEAD 제어기가 온도에 의한 마찰 토크 변화에도 안정화 성능에 있어 강인성이 확보되어 있음을 알 수 있다.
하지만, 시스템의 마찰 특성 변화는 온도변화 이외의 요인으로 추가적으로 발생할 수 있으며, 마찰 변수 추정 과정에서의 발생하는 오차까지 고려한다면, 실제 LOS 오차는 더욱 증가할 수 있다. 따라서, 추정된 마찰 변수 데이터를 기준으로 각 변수값을 일정 비율로 증가시켰을 때, 안정화 성능 해석 결과를 분석하여, 요구 성능에 대한 여유 마진을 확인하였다.
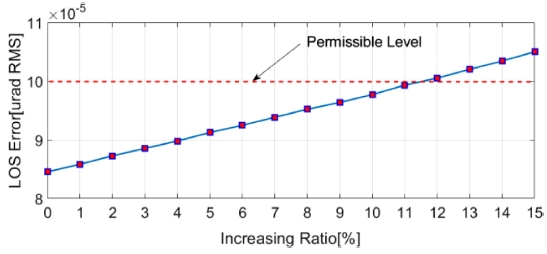
Fig. 10은 -30oC에서 추정된 마찰 변수 데이터를 초기값으로 설정하고, 각 변수 값을 1%씩 증가시켰을 때, LOS 오차가 변화하는 추이를 보여준다. 마찰 변수 값의 증가에 따라 LOS 오차가 거의 선형적으로 증가하는 것을 확인할 수 있었으며, -30oC에서 추정된 마찰 변수 값보다 12% 이상인 경우 시스템의 LOS 오차가 100 μrad RMS 를 초과하였다. 따라서, 추정된 마찰 변수의 변동성을 기준으로 시스템의 안정화 성능에 대해 마찰은 약 11%의 여유 마진을 가지고 있는 것으로 볼 수 있다.
5. 결론
군사적 목적을 가진 시선 안정화 시스템의 마찰을 LuGre 마찰 모델로 수식화하여, 시험과 시뮬레이션을 통해 LuGre 마찰 모델을 구성하는 6개의 변수들을 추정하고 검증하였으며, 시스템의 운용 온도 범위에서 발생할 수 있는 마찰 변수의 변동성을 분석하였다. 추정된 마찰 변수 데이터를 이용한 시뮬레이션 결과 PI-LEAD 제어가 온도에 따른 마찰의 변동성에 강인함을 확인하였으며, 추가적인 마찰 특성 변화에 대한 시스템의 마진을 분석하였다. 향후 온도 이외에 마찰 변화를 초래할 수 있는 영향 요소들을 분석하여 마찰의 변동 범위를 더욱 구체적으로 추정하고, 이러한 마찰 변동성에 강인한 제어기 및 토크 제어기 설계 방안 등에 대한 연구를 진행할 예정이다.
NOMENCLATURE
| J : | Moment of inertia |
| ω : | Angular velocity |
| Tf : | Frictoin Torque |
| fs : | Static friction |
| fc : | Coulomb friction |
| ωs : | Stribeck velocity |
| σ0 : | Stiffness coefficient of the bristle |
| σ1 : | Damping coefficient of the bristle |
| σ2 : | Viscous friction coefficient |
REFERENCES
- Lee, J. B. and Choi, H. G., “The Control for the 2-Axis Stabilized Gimbal Using the PI-LEAD Algorithm,” The Korea Institute of Convergence Signal Processing, Vol. 14, No. 2, pp. 117-123, 2013.
- Kang, M. S., “Precision Stabilization Control of Servo-System by Using Friction Compensation,” Journal of the Korean Society for Precision Engineering, Vol. 16, No. 3, pp. 109-115, 1999.
-
De Wit, C. C., Olsson, H., Astrom, K. J., and Lischinsky, P., “A New Model for Control of Systems with Friction,” IEEE Transactions on Automatic Control, Vol. 40, No. 3, pp. 419-425, 1995.
[https://doi.org/10.1109/9.376053]

-
Dupont, P. E. and Dunlap, E. P., “Friction Modeling and PD Compensation at Very Low Velocities,” Journal of Dynamic Systems Measurement and Control, Vol. 117, No. 1, pp. 8-14, 1995.
[https://doi.org/10.1115/1.2798527]

- Olsson, H., “Control Systems with Friction,” Department of Automatic Control, Lund Institute of Technology, pp. 9-169, 1996.
- Madi, M. S., Khayati, K., and Bigras, P., “Parameter Estimation for the LuGre Friction Model Using Interval Analysis and Set Inversion,” Proc. of IEEE International Conference on Systems, Man and Cybernetics, pp. 428-433, 2004.
-
Lu, Y., Yan, D., and Levy, D., “Friction Coefficient Estimation in Servo Systems Using Neural Dynamic Programming Inspired Particle Swarm Search,” Applied Intelligence, Vol. 43, No. 1, pp. 1-14, 2015.
[https://doi.org/10.1007/s10489-014-0621-2]

-
Wang, X., Lin, S., and Wang. S., “Dynamic Friction Parameter Identification Method with LuGre Model for Direct-Drive Rotary Torque Motor,” Mathematical Problems in Engineering, Vol. 2016, Article No. 6929457, pp. 1-8, 2016.
[https://doi.org/10.1155/2016/6929457]

-
Xie, W. F. and Zhao, Z.-Y. “Sliding-Mode-Observer-Based Adaptive Control for Servo Actuator with Friction,” Proc. of International Conference on Mechatronics and Automation, pp. 1196-1201, 2007.
[https://doi.org/10.1109/ICMA.2007.4303718]

-
Lee, T. H., Tan, K. K., and Huang, S., “Adaptive Friction Compensation with a Dynamical Friction Model,” IEEE/ASME Transactions on Mechatronics, Vol. 16, No. 1, pp 133-140, 2011.
[https://doi.org/10.1109/TMECH.2009.2036994]

-
Ruderman, M. and Iwasaki, M., “Control of Pre-Sliding Friction Using Nonlinear State Observer,” Proc. of IEEE 13th International Workshop on Advanced Motion Control, pp. 592-597, 2014.
[https://doi.org/10.1109/AMC.2014.6823348]

-
Koizumi, T. and Shibazaki, H., “A Study of the Relationships Governing Starting Rolling Friction,” Wear, Vol. 93, No. 3, pp. 281-290, 1984.
[https://doi.org/10.1016/0043-1648(84)90202-3]


Senior Engineer in the Mechanical Eng. Team, Hanwha Systems Co. His research interests are design and control of the sight stabilization system.
E-mail: kyungsoo04.kim@hanwha.com

Assistant professor in the Department of Mechanical Engineering, Kyungpook National University. His research interests are design and control of robotic system.
E-mail: yihak@knu.ac.kr

Professor in the Department of Mechanical Engineering, Kyungpook National University. His research interests are design and control of mobile robots, intelligent systems and automation.
E-mail: srlee@knu.ac.kr