구속 운동을 고려한 병렬기구 기계의 기상측정 정확도 개선

1. 서론

로봇, 공작기계와 같이 다축 제조 기계의 활용분야가 다양해지면서, 일반적인 직렬형태의 구조가 아닌 병렬 또는 직렬/병렬하이브리드 구조의 메커니즘을 채택한 기계가 개발되고 있으며, 일부 구조는 가공용으로 출시되고 있다.^1-5 병렬 메커니즘은 이동질량(Moving Mass)이 각 액추에이터에 분산되어 민첩한 구동이 가능하고, 유연한 공구 자세를 취할 수 있는 장점이 있다.⁶ Exechon^7-10 메커니즘을 활용한 병렬기구 기계(The Parallel Kinematic Machine, PKM)는 병렬, 하이브리드 공작기계 중 성공적으로 상용화된 형태로, Neumann¹¹이 Tricept 구조에서 볼 조인트를 대체하는 구조를 개발하여 가공에 충분한 강성과 정밀도를 확보하였다. 또한, 공구측에 상대 운동에 대한 자유도가 모두 있기 때문에, 갠트리 시스템 등의 확장 축과 연계하여 항공기 날개와 같은 대형 부품 가공에도 활용되고 있다. PKM은 가 공목적에 따라 복합기능이 요구되며, 기상측정(On-Machine Measurement, OMM) 기능은 중요하게 사용된다.

OMM은 가공기계에 측정 기능을 부여하여 가공과 검사를 통합함으로써 생산비용 및 시간을 저감하고 있다.¹² 최근에는 측정 프로브(Probe)와 마스터(Mater)를 이용하여 공작기계 및 3차원 측정기 자체의 오차를 측정하는 용도로도 OMM이 활용되고 있다.^13-16 OMM에 사용되는 센서로는 터치 프로브(Touch-Trigger Probe), 스캐닝 프로브(Scanning Probe) 및 레이저 변위 센서(Laser Displacement Sensor) 등이 활용되고 있다.¹⁷ 특히, 터치프로브는 비교적 저렴하고 유지보수가 용이하여 산업용으로 널리 사용되고 있다.

프로브 방식의 OMM은 프로빙 오차(Probing Error), 프로브의 오프셋, 스타일러스(Stylus) 반경 오차 등과 같은 계통 오차(Systematic Error)에 의해 측정 정확도가 저하되며, 이러한 오차들을 분석하고 최소화하기 위한 다양한 연구가 있어 왔다.^18-20 OMM의 정확도는 기계 자체의 위치 정확도, 반복정밀도 등 이송 성능에 종속적이기 때문에, CMM에 준하는 측정 성능을 위해서는 충분한 기계 이송 정확도를 확보해야 한다.

Exechon 메커니즘이 적용된 병렬기구 공작기계는 5자유도로 구동하며, 스핀들 회전 축 방향의 자유도는 기구적인 구속으로 인해 종속적으로 움직인다. 즉, PKM은 기상측정에서 일반 직선축으로 구성된 기계와는 달리 프로브의 오프셋 오차가 종속적인 회전 운동(Dependent Rotational Motion, DRM)에 의해 변하게 된다. 즉, 프로브의 오프셋 오차가 위치에 따라서 변화하기 때문에 측정 데이터로부터 오프셋 오차 계산이 어렵다.

본 연구에서는 PKM의 DRM을 분석한 후 이를 고려하여 터치프로브의 오프셋 오차를 정확하게 측정하는 방법을 제안하고, 기상측정에서 오프셋 오차 영향을 제거하는 측정 절차를 소개한다. DRM은 일반적인 밀링 등의 가공 시에 문제가 되지 않지만, 말단장치(End-Effector)의 일정한 방향이 필요한 작업에는 필수적으로 고려해야 한다. 2장에서는 Exechon 메커니즘의 DRM을 역기구학 모델을 수립하여 분석한다. 3장에서는 DRM을 고려한 오프셋 측정 방법 및 정확한 기상측정을 위한 절차를 소개한다. 4장에서는 병렬기구 공작기계에서 원형 마스터를 이용하여 기상측정 한 결과를 마스터의 원호 크기 및 진원도 값과 비교하여 제안한 방법의 타당성을 검증한다.

2. 병렬기구 기계의 구속 운동 분석

2.1 병렬기구 기계 구조

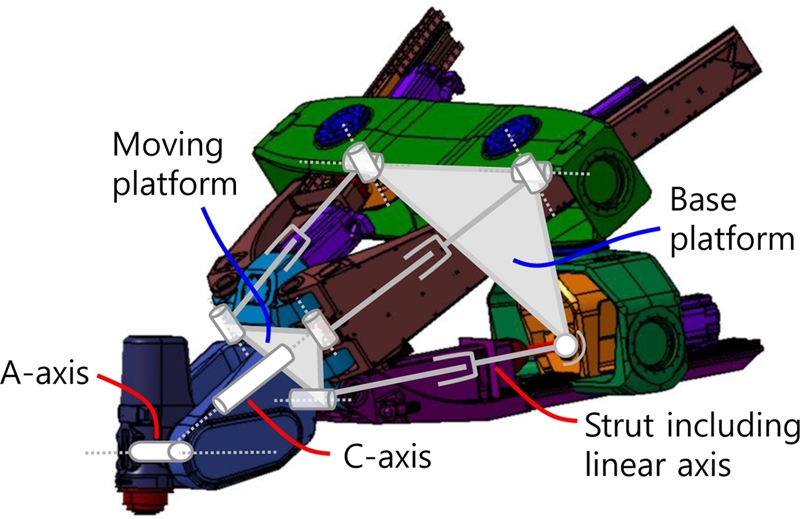
Exechon 메커니즘을 사용한 병렬기구 기계는 병렬과 직렬이 혼합되어 있는 구조로, 3개의 직선축이 포함된 지주(Struts)가 기저 플랫폼(Base Platform) 및 구동 플랫폼(Moving Platform)과 연결된 병렬부와 2개의 회전 축이 스핀들과 직렬로 연결된 직렬부로 Fig. 1과 같이 구성되어 있다. 첫 번째와 세 번째 지주는 기저 플랫폼과 유니버설 조인트로 연결되어 있고, 두 번째 지주는 직선축 방향 회전이 허용된 짐벌(Gimbal) 형태로 연결되어 있다. 구동 플랫폼은 과구속 되어 3자유도 구동을 하며, 회전축 C, A축과 직렬로 결합하여 PKM은 최종적으로 5자유도 구동을 하게 된다.

Fig. 1

Structural configuration of the parallel kinematic machine

2.2 역기구학 분석

PKM은 정기구학과 역기구학 모두 해석적인 해(Analytic Solution)를 얻기 어렵다.⁷ 지령 위치에 도달하기 위해서는 회전축 구동 각도와 직선축의 길이를 결정하는 구동 플랫폼의 위치 및 방향을 계산해야 하며, 해를 구하기 위해서 수치해석적 방법이 활용된다.

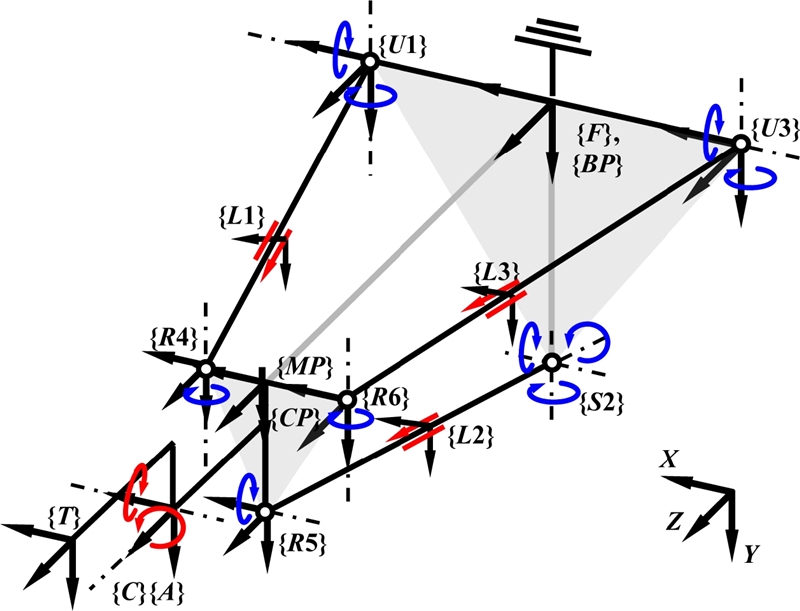
먼저, 기구학 모델을 수립하기 위해서 Fig. 2와 같이 좌표계를 설정하였다. 기준 좌표계인 기저 플랫폼 좌표계 (Base Platform Coordinate System, BP-CS)를 기저 플랫폼 상의 외부짐벌(Outer Gimbal)의 중간위치, 즉 조인트 U1과 U3의 중간지점에 설정하고, 구동 플랫폼 좌표계(Moving Platform Coordinate System, MP-CS)를 회전 조인트 R4와 R6의 중간 위치에 설정한다. C축의 좌표계 C-CS와 A축의 좌표계 A-CS를 두 회전축의 교차점에 있다고 가정하고, C축이 MP-CS의 xy평면에 투영된 좌표계를 Cp-CS로 설정하였다. 직선축 구동에 의한 각 지주의 길이(l₁, l₂, l₃)는 구동 플랫폼 위치 및 방향으로부터 다음 식(1)-식(3)과 같이 계산된다.

$\[ l_1=\begin{array}{l}sqrt\left\{{\left(x_{MP}+r_{11}{x}_{R4}+x_{U1}\right)}^2+{\left(y_{MP}+r_{21}{x}_{R4}\right)}^2\right.\\ \left.+{\left(z_{MP}+r_{31}{x}_{R4}\right)}^2\right\}\end{array} \]$

(1)

$\[ l_2=\begin{array}{l}\mathrm{s}\mathrm{q}\mathrm{r}\mathrm{t}\left\{{\left(x_{MP}+r_{12}{x}_{R5}\right)}^2+{\left(y_{MP}+r_{22}{x}_{R5}-y_{S2}\right)}^2\right.\\ \left.+{\left(z_{MP}+r_{32}{x}_{R5}\right)}^2\right\}\end{array} \]$

(2)

$\[ l_3=\begin{array}{l}\mathrm{s}\mathrm{q}\mathrm{r}\mathrm{t}\left\{{\left(x_{MP}+r_{13}{x}_{R6}+x_{U3}\right)}^2+{\left(y_{MP}+r_{23}{x}_{R6}\right)}^2\right.\\ \left.+{\left(z_{MP}+r_{33}{x}_{R6}\right)}^2\right\}\end{array} \]$

(3)

Fig. 2

Coordinate systems in the parallel kinematic machine

여기서, 기준좌표계를 기저 플랫폼 좌표계와 동일하게 설정하면, x_k, y_k, z_k는 기준좌표계에 대한 조인트 k(=U1, S2, U3)의 각 방향 위치이고, x_n, y_n, z_n (n= R4, R5, R6)은 구동 플랫폼 좌표계에 대한 조인트 n의 위치를 나타낸다. x_MP, y_MP, z_MP는 기준좌표계에 대한 구동 플랫폼 좌표계의 위치벡터 ^BPp_MP의 각 방향 성분이다. r_ij(i = 1, 2, 3, j = 1, 2, 3)는 기준좌표계에 대한 구동 플랫폼 회전행렬 ^BPR_MP의 성분이며, 위치에 의해 다음 식(4)와 같이 결정된다.

$\[ \begin{array}{l}{r}_{11}=\frac{y_{MP}^2-y_{S2}{y}_{MP}+z_{MP}^2}{K_1},r_{12}=\frac{x_{MP}{y}_{MP}}{K_1},r_{13}=\frac{x_{MP}{z}_{MP}}{K_1},\\ r_{21}=0, r_{22}=\frac{z_{MP}}{\sqrt{y_{MP}^2+z_{MP}^2}},r_{23}=-\frac{y_{MP}}{\sqrt{y_{MP}^2+z_{MP}^2}},\\ r_{31}=\frac{x_{MP}\left(y_{MP}^2+z_{MP}^2\right)}{K_1\sqrt{y_{MP}^2+z_{MP}^2}},r_{32}=\frac{y_{MP}\left(y_{MP}^2-y_{S2}{y}_{MP}+z_{MP}^2\right)}{K_1\sqrt{y_{MP}^2+z_{MP}^2}},\\ r_{33}=-\frac{z_{MP}\left(y_{MP}^2-y_{S2}{y}_{MP}+z_{MP}^2\right)}{K_1\sqrt{y_{MP}^2+z_{MP}^2}},\\ \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}, K_1=\sqrt{{\left(y_{MP}^2-y_{S2}{y}_{MP}+z_{MP}^2\right)}^2+x_{MP}^2\left(y_{MP}^2+z_{MP}^2\right)}\end{array} \]$

(4)

공구의 위치 ^BPp_t와 방향벡터 t가 결정되면, 구속 조건에 의해서 구동 플랫폼 위치, 방향, 상수로 구성된 식(5)와 같은 관계식이 유도된다. 즉, PKM의 역기구학은 회전축의 각도와 구동 플랫폼 위치에 대한 비선형 방정식을 구하는 문제로 귀결되고, 구동 플랫폼의 위치는 Newton-Raphson 방법과 같은 수치해석적 방법을 통해 계산한다.

$\[ \begin{array}{l}-y_{\mathrm{t}}\cdot \frac{{}^{BP}{\mathbf{p}}_S-{}^{BP}{\mathbf{p}}_{MP}-{}^{BP}{R}_{MP}{\left[\begin{array}{ccc}0& {}^{MP}{y}_{Cp}& {}^{Cp}{z}_C\end{array}\right]}^T-k_2\mathbf{t}}{‖{}^{BP}{\mathbf{p}}_S-{}^{BP}{\mathbf{p}}_{MP}-{}^{BP}{R}_{MP}{\left[\begin{array}{ccc}0& {}^{MP}{y}_{Cp}& {}^{Cp}{z}_C\end{array}\right]}^T-k_2\mathbf{t}‖}\\ +{}^{BP}{\mathbf{p}}_S-{}^{BP}{\mathbf{p}}_{MP}-{}^{BP}{R}_{MP}{\left[\begin{array}{ccc}0& {}^{MP}{y}_{Cp}& {}^{Cp}{z}_C\end{array}\right]}^T=0\\ \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}, k_2=\mathbf{t}\cdot \left({}^{BP}{\mathbf{p}}_S-{}^{BP}{R}_{MP}{}^{MP}{\mathbf{p}}_{Cp}\right),{}^{BP}{\mathbf{p}}_S={}^{BP}{\mathbf{p}}_t-t\cdot {}^A{z}_t.\end{array} \]$

(5)

여기서 y_t는 A-CS에 대한 공구의 Y방향 위치를 의미한다. ^BPp_S는 회전축 A와 스핀들 축이 직교로 만나는 점을 의미하고, ^BPy_Cp, ^Cpz_C, ^Az_t는 설계치로 상수 값이다. 수치해석적 방법을 통해 구동플랫폼의 위치 벡터와 회전행렬이 계산되면, A축과 C축의 회전각도는 구동 플랫폼의 회전행렬과 공구 벡터 관계로부터 계산된다.

3. 종속적 회전 운동을 고려한 터치프로브 오프셋 측정 및 보정

3.1 터치프로브의 오프셋

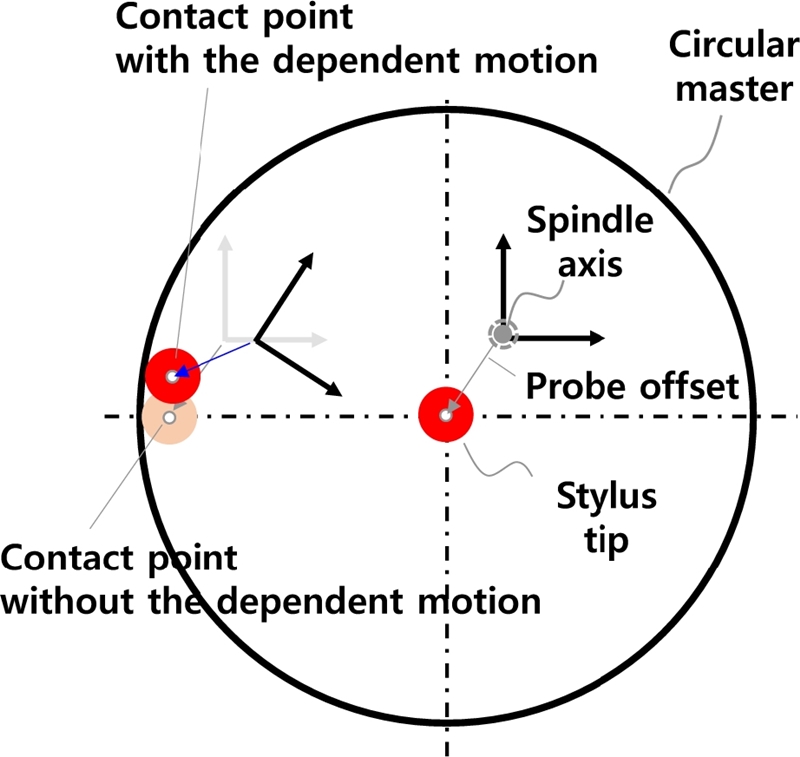
일반적으로 프로브 기반 측정 시스템의 교정을 위해서 정밀구(Precision Ball) 또는 원형 마스터(Circular Master)가 사용된다.¹⁹ 기계좌표계에 대한 프로브의 길이방향에 직교한 두 방향 X, Y의 오프셋은 스핀들 회전 축에 대해서 스타일러스(Stylus) 볼 중심이 벗어나며 발생된다. 공구의 방향이 일정하게 유지되면 이 오프셋은 위치에 관계없이 일정하며 원형 마스터를 이용하여 간단하게 측정할 수 있다. 하지만, PKM과 같이 DRM으로 인해 공구의 방향이 일정하게 유지될 수 없는 경우 Fig. 3과 같이 PKM 말단장치의 위치에 따라서 각 방향의 오프셋이 변하기 때문에 정확한 측정이 어렵다. 또한, 공작물 형상 측정 시에 DRM으로 인해서 측정 데이터로부터 오프셋에 의한 오차를 일정하게 고려할 수 없기 때문에, 측정 정확도 개선을 위해서는 DRM 각도를 보상하여 일정한 터치프로브 방향으로 측정이 필요하다.

Fig. 3

Contact point of stylus tip (ball) w/wo the dependent rotational motion

3.2 종속적 회전 운동을 고려한 오프셋 측정

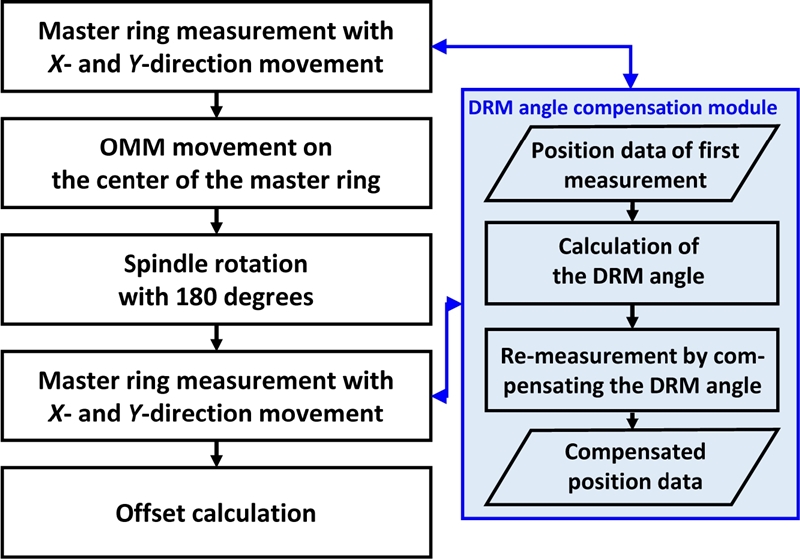
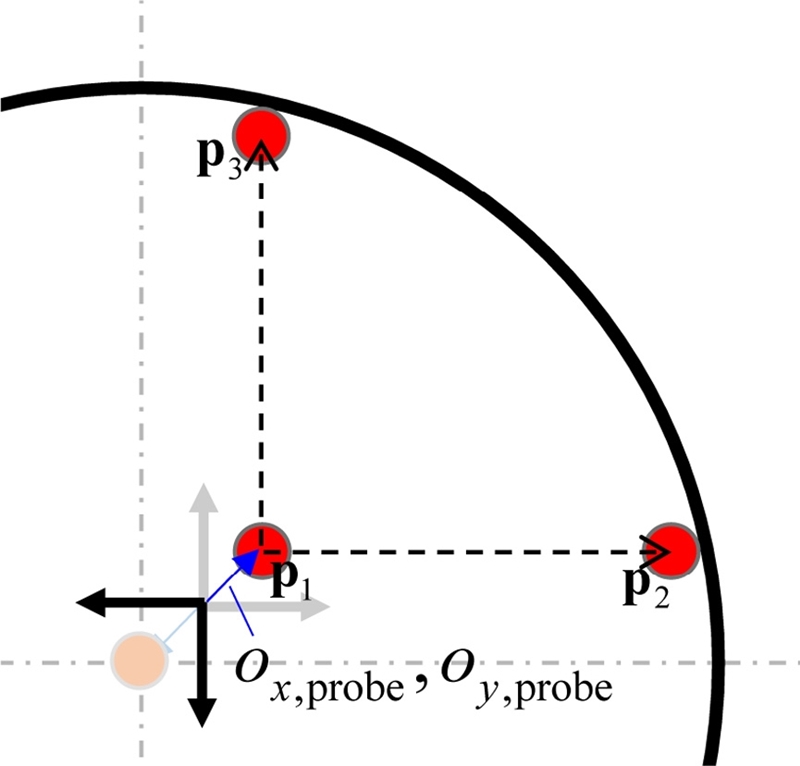
PKM의 OMM을 위해 장착된 터치프로브의 오프셋은 Fig. 4와 같은 절차를 통해 측정한다. 먼저, 스타일러스 볼 중심을 원형 마스터의 중심에 위치시킨다. 오프셋 오차는 평면상 두 방향에 대한 이송을 통한 기상측정으로 간단하게 측정한다. 하지만, DRM으로 인해 오프셋이 기계좌표계에 대해서 변하기 때문에, DRM 각도를 보상해주어야 한다. DRM 각도 보상은 스핀들 위치 제어를 통해 가능하다. 보상 각도는 마스터 링의 중심 위치를 기준으로 터치프로브 접촉 위치에서의 DRM 각도 차이로 계산하고 측정 코드에 각도 보상 값을 적용하여 오프셋을 측정한다. DRM 각도 보상을 통해 터치프로브 방향을 일정하게 유지하면 마스터 링 중심을 기준으로 X, Y 방향으로 양방향 측정을 통해 스타일러스의 중심이 원형 마스터 중심에 정확하게 위치시킬 수 있다. 마스터 링 중심에 위치시킨 스핀들을 반전시키면 Fig. 5와 같이 스핀들 회전축에 대한 터치프로브의 오프셋 영향은 두 배로 나타나게 된다. 동일하게 DRM을 고려하여 X, Y 방향으로 측정하면 위치는 식(8)과 같은 관계를 가진다.

Fig. 4

Measurement procedure for the touch probe offset considering the dependent rotational motion

$\[ \begin{array}{l}{x}_2-x_1=\left(R_{\mathrm{m}\mathrm{a}\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{r}}-r_{\mathrm{s}\mathrm{t}\mathrm{y}\mathrm{l}\mathrm{u}\mathrm{s}}\right)\cos \left({\theta }_2\right)-2o_{x,\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{b}\mathrm{e}}\\ y_3-y_1=\left(R_{\mathrm{m}\mathrm{a}\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{r}}-r_{\mathrm{s}\mathrm{t}\mathrm{y}\mathrm{l}\mathrm{u}\mathrm{s}}\right)\sin \left({\theta }_3\right)-2o_{y,\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{b}\mathrm{e}}\end{array} \]$

(8)

Fig. 5

Measurement points for finding the touch probe offset

여기서, o_x,probe와 o_y,probe는 터치프로브의 오프셋 오차를 의미하고, R_master와 r_stylus는 마스터 링과 스타일러스 볼의 반경이다. θ₂와 θ₃은 마스터 링의 중심에서 접촉점 p₂, p₃까지의 원호 각으로, 터치프로브 오프셋은 미소각 근사(Small Angle Approximation)를 하면 식(9)와 같이 간단하게 계산할 수 있다.

$\[ \begin{array}{l}{o}_{x,\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{b}\mathrm{e}}=\left(-x_2+x_1+R_{\mathrm{m}\mathrm{a}\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{r}}-r_{\mathrm{s}\mathrm{t}\mathrm{y}\mathrm{l}\mathrm{u}\mathrm{s}}\right)∕2,\\ o_{y,\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{b}\mathrm{e}}=\left({-y}_3+y_1+R_{\mathrm{m}\mathrm{a}\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{r}}-r_{\mathrm{s}\mathrm{t}\mathrm{y}\mathrm{l}\mathrm{u}\mathrm{s}}\right)∕2\end{array} \]$

(9)

3.3 오프셋 보정을 위한 기상측정 절차

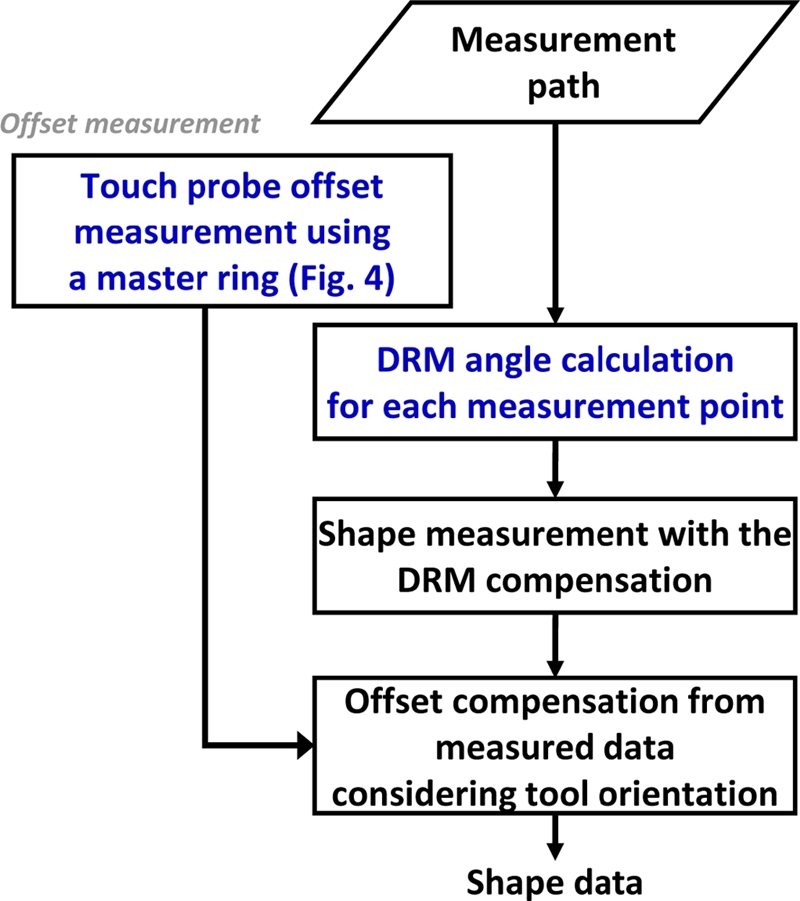
PKM에 장착된 터치프로브의 오프셋 영향을 최소화 하기 위해서 Fig. 6과 같이 일반적인 기상측정 절차에 오프셋 측정 및 DRM 각도를 보상하는 절차가 추가적으로 필요하다. 측정 형상이 결정되면 작업공간 내에서 DRM에 의한 회전 각도가 계산되고 측정 시에 이 각도를 보상하여 일정한 오프셋 오차를 가지고 측정하도록 한다. 측정하는 형상에 따라 터치프로브의 방향(공구 벡터 방향)이 바뀌는 경우, 기 측정한 오프셋을 고려하여 OMM 데이터로부터 오프셋에 따른 측정 오차를 제거하여 정확한 형상 측정 데이터를 얻을 수 있다.

Fig. 6

Measurement procedure for improving measurement accuracy of the OMM of the PKM

4. 실험

제안한 터치프로브 오프셋 오차 측정 및 보정 방법은 머시닝센터로 사용하고 있는 PKM을 대상으로 Fig. 7과 같이 마스터링을 이용한 원호 테스트 실험을 통해 검증하였다. PKM은 Table 1과 같이 구동플랫폼에 연결된 스트럿에 포함된 직선축의 이송범위가 0-700 mm이며, 스핀들 위치제어가 가능하다. PKM의 기본 좌표계는 1) l₁, l₃가 1438 mm이고, 2) 구동 플랫폼이 기저 플랫폼과 평행, 3) C축은 원점, A축은 -4 5° 회전했을 때의 BP-CS에 대한 공구의 위치와 방향으로 설정한다. 터치프로브는 Renishaw Plc 社의 RMP600 모델을 사용하였고, 마스터는 ± 1.0mm의 형상 정확도인 세팅 링(Setting Ring)을 사용하였으며, 사양은 Table 2와 같다.

Fig. 7

Experimental setup for measuring the touch probe offset

Table 1

Specification of the PKM

Table 2

Specification of the touch probe and the circular master

먼저, 작업공간 내의 지정된 위치{-0.625 mm, 200.914 mm, -168 mm}에 세팅 링의 중심이 위치하도록 설치하고 제안한 절차에 따라 터치프로브의 오프셋을 측정하였다. DRM 각도는 마스터 링의 중심위치를 기준으로 측정 위치에서의 DRM 각도를 역기구학 모델을 활용하여 미리 계산하였다. 제어기에서 스핀들 회전을 통한 DRM 각도 보상을 위해 스핀들 회전 각은 5차 다항식 모델로 식(10)과 같이 고려하였다.

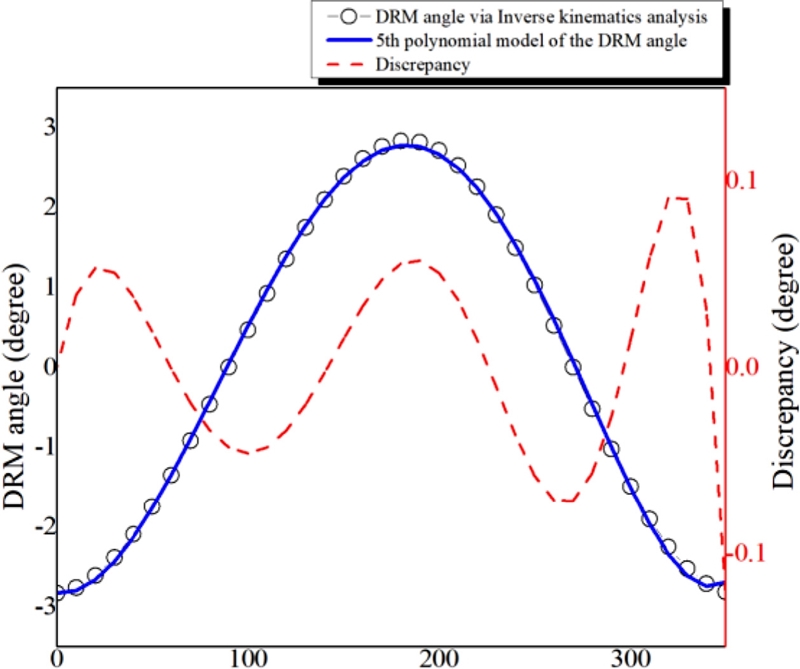
여기서, c_n (n = 1-5)은 다항식의 계수이며, q는 원호 테스트의 측정 각도를 의미한다. 5차 다항식 모델로 계산된 DRM 각도와 역기구학으로 계산된 DRM 각도의 차이는 Fig. 8과 같이 0.1° 이내로 오프셋 측정에는 큰 영향을 주지 않는다.

Fig. 8

Discrepancy between inverse kinematics result and 5th polynomial model of the DRM angle

DRM 각도 보상을 통해 측정한 터치프로브 오프셋 o_x,probe, o_y,probe는 Table 3과 같이 각 0.210 mm, 0.160 mm로 계산되었다. 세팅 링을 다른 위치{-319.135 mm, 198.236 mm, -168.0 mm}에 설치하고 DRM 각도를 보정했을 때, 각 방향 터치프로브의 오프셋은 0.212 mm, 0.163 mm으로 유사하게 측정되었다. 하지만, DRM 각도 보정을 하지 않고 측정했을 때, 각 방향으로 0.253mm, 0.097 mm의 오프셋이 측정되어 최대 66 μm의 편차가 있었다.

Table 3

Offset measurement w/wo compensating the DRM angle

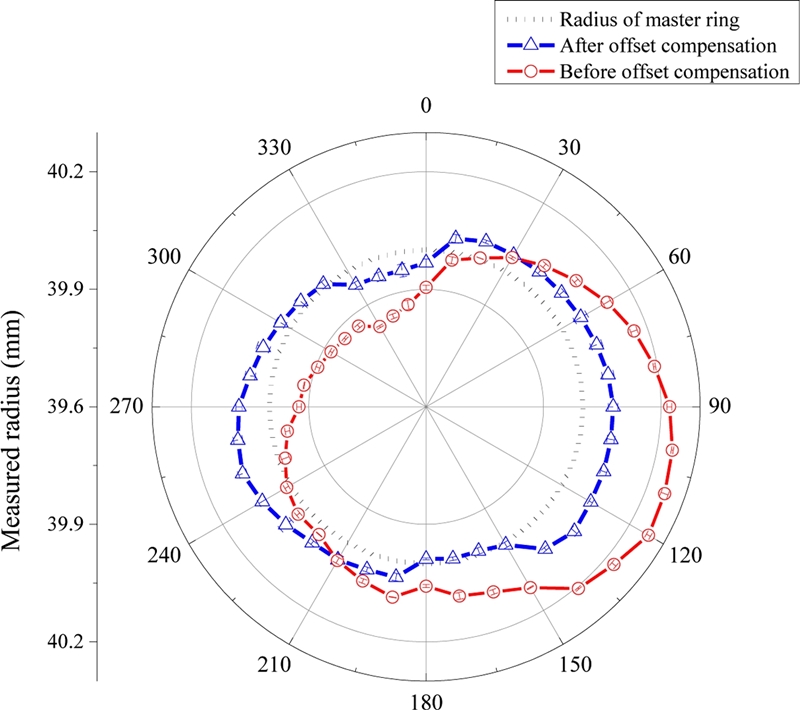
제안한 기상측정 방법을 활용하여 원호 형상 측정 정확도 확인 실험을 실시하였다. Fig. 9와 같이 DRM 보상 없이 측정한 결과와 DRM을 보상한 측정 결과를 비교하였으며, 측정은 10° 간격으로 5회 반복하였다. 측정 대상인 원호 마스터는 기계좌표계{-316.081 mm, 247.037 mm, -166.817 mm}에 중심이 오도록 설치하였고 내경을 측정하였다. DRM 각도를 보상하여 측정한 결과는 Table 4와 같고, 최적원의 크기는 두 경우 모두 유사하게 실제 내경에 비해 크게 계산되었지만, 진원도에서 274 μm의 큰차이가 있었다. DRM을 보상하고 측정 했을 때, PKM 자체의 오차가 보정되지 않고 측정되어 왜곡된 원호 형상을 보였지만, 보상하지 않은 결과에 비해 진원도 편차가 65% 가량 줄어든 것을 확인하였다.

Fig. 9

Circular deviation measurement considering the touch probe offset w/wo compensating the DRM angle

Table 4

Circular deviation measurement w/wo compensating the DRM angle

5. 결론

본 논문에서는 높은 자유도, 속도 및 충분한 강성으로 가공등에 활용되고 있는 PKM에서 터치프로브 기반 기상측정의 정확도를 개선하기 위한 오프셋 측정 및 보정 기술을 제안하였다. PKM의 종속적인 회전 운동을 고려하여 기상측정 시 위치에 따라 변하는 터치 프로브의 오프셋을 정확하게 측정하였고, 보정을 통해 측정 정확도가 개선되었다. 정확한 기상측정을 위해서 터치프로브의 초기 설치 및 공구 교환 시 원형 마스터 등을 이용하여 오프셋 측정이 필요하고, DRM 각도 보상을 하면 정확하게 공작물 형상 측정이 가능하다. OMM 정확도는 터치프로브의 오프셋뿐만 아니라 PKM 자체의 위치 오차에 직접적인 영향을 받기 때문에, 장비 자체의 정확도 확보가 요구된다. PKM의 종속적인 회전 운동을 보상하거나, 추가적인 회전축을 활용하면 일반적인 절삭 공정 외에도 다양한 제조 공정에서 PKM활용이 가능하다.

Acknowledgments

이 논문은 2019년도 정부(과기정통부, 산통부)의 재원으로 한국연구재단의 중견연구(2017R1A2B2009475)와 한국산업기술평가관리원(10053878)의 지원을 받아 수행된 연구임.

REFERENCES

• Karimi, D. and Nategh, M. J., “Kinematic Nonlinearity Analysis in Hexapod Machine Tools: Symmetry and Regional Accuracy of Workspace,” Mechanism and Machine Theory, Vol. 77, pp. 115-125, 2014. [https://doi.org/10.1016/j.mechmachtheory.2013.09.007]
• Gao, F., Peng, B., Zhao, H., and Li, W., “A Novel 5-DOF Fully Parallel Kinematic Machine Tool,” International Journal of Advanced Manufacturing Technology, Vol. 31, pp. 201-207, 2006. [https://doi.org/10.1007/s00170-005-0171-1]
• Neugebauer, R., Drossel, W. G., Harzbecker, C., Ihlenfeldt, S., and Hensel, S., “Method for the Optimization of Kinematic and Dynamic Properties of Parallel Kinematic Machines,” CIRP Annals-Manufacturing Technology, Vol. 55, No. 1, pp. 403-406, 2006. [https://doi.org/10.1016/S0007-8506(07)60445-4]
• Kanaan, D., Wenger, P., and Chablat, D., “Kinematic Analysis of a Serial-Parallel Machine Tool: The VERNE Machine,” Mechanism and Machine Theory, Vol. 44, No. 2, pp. 487-498, 2009. [https://doi.org/10.1016/j.mechmachtheory.2008.03.002]
• Son, S., Kim, T., Sarma, S. E., and Slocum A., “A Hybrid 5-Axis CNC Milling Machine,” Precision Engineering, Vol. 33, No. 4 pp. 430-446, 2009. [https://doi.org/10.1016/j.precisioneng.2008.12.001]
• Weck, M. and Staimer, D., “Parallel Kinematic Machine Tools – Current State and Future Potentials,” CIRP Annals, Vol. 51, No. 2, pp. 671-683, 2002. [https://doi.org/10.1016/S0007-8506(07)61706-5]
• Bi, Z. M. and Jin, Y., “Kinematic Modeling of Exechon Parallel Kinematic Machine,” Robotics and Computer-Integrated Manufacturing, Vol. 27, No. 1 pp. 186-193, 2011. [https://doi.org/10.1016/j.rcim.2010.07.006]
• Bi, Z. M. and Wang, L., “Optimization of Machining Processes from the Perspective of Energy Consumption: A Case Study,” Journal of Manufacturing Systems, No. 31, No. 4 pp. 420-428, 2012. [https://doi.org/10.1016/j.jmsy.2012.07.002]
• Jin, Y., Bi, Z. M., Liu, H. T., Higgins, C., Price, M., et al., “Kinematic Analysis and Dimensional Synthesis of Exechon Parallel Kinematic Machine for Large Volume Machining,” Journal of Mechanisms and Robotics, Vol. 7, No. 4, Article No. 041004, 2015. [https://doi.org/10.1115/1.4029499]
• Shang, M. and Butterfield, J., “The Experimental Test and FEA of a PKM (Exechon) in a Flexible Fixture Application for Aircraft Wing Assembly,” Proc. of the IEEE International Conference on Mechatronics and Automation, pp. 1225-1230, 2011. [https://doi.org/10.1109/ICMA.2011.5985836]
• Neumann, K., “Parallel-Kinematical Machine,” US patent, No. 20090205457A1, 2009.
• Choi, J., Min, B., and Lee, S., “Machining Accuracy Improvement by on Machine Part Measurement and Error Compensation,” Journal of the Korean Society for Precision Engineering, Vol. 20, No. 12, pp. 34-41, 2003.
• Kim, S., Kim, O., Lee, E., Oh, C., and Lee, C., “A Study of an OMM System for Machined Spherical Form using the Volumetric Error Calibration of Machining Center,” Journal of the Korean Society for Precision Engineering, Vol. 18, No. 7, pp. 98-105, 2001.
• Lee, K. I., Lee, J. C., and Yang, S. H., “Optimal On-Machine Measurement of Position Independent Geometric Errors for Rotary Axes in Five-Axis Machine with a Universal Head,” International Journal of Precision Engineering and Manufacturing, Vol. 19, No. 4, pp. 545-551, 2018. [https://doi.org/10.1007/s12541-018-0066-3]
• Ibaraki, S., Iritani, T., and Matsushita, T., “Calibration of Location Errors of Rotary Axes on Five-axis Machine Tools by On-the-Machine Measurement using a Touch-Trigger Probe,” International Journal of Machine Tools and Manufacture, Vol. 58, pp. 44-53, 2012. [https://doi.org/10.1016/j.ijmachtools.2012.03.002]
• Givi, M. and Mayer, J., “Validation of Volumetric Error Compensation for a Five-Axis Machine Using Surface Mismatch Producing Tests and On-Machine Touch Probing,” International Journal of Machine Tools and Manufacture, Vol. 87, pp. 89-95, 2014. [https://doi.org/10.1016/j.ijmachtools.2014.08.001]
• Kim, S. H. and Kim, D. H, “On-the-Machine Measurement System,” Journal of the Korean Society for Precision Engineering, Vol. 18, No. 6, pp. 9-18, 2001.
• Lee, S. J., Kim, S. H., and Kim, O. H., “The Analysis of Measuring Error in OMM System,” Journal of the Korean Society for Precision Engineering, Vol. 15, No. 5, pp. 34-42, 1998.
• Zhao, B., Gao, F., and Li, Y., “Study on Pre-Travel Behaviour of Touch Trigger Probe under Actual Measuring Conditions,” Procedia CIRP, Vol. 27, pp. 53-58, 2015. [https://doi.org/10.1016/j.procir.2015.04.043]
• Yang, Q., Butler, C., and Baird, P., “Error Compensation of Touch Trigger Probes,” Measurement: Journal of the International Measurement Confederation, Vol. 18, No. 1, pp. 47-57, 1996. [https://doi.org/10.1016/0263-2241(96)00044-9]