Study on Mobility of Planetary Rovers and the Development of a Lunar Rover Prototype with Minimized Redundancy of Actuators
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
This paper reviews design elements and presents a mobile platform that has full access of wheel actuation for explicit steering with a minimized number of actuators. For the purpose of exploring lunar surfaces, there are two main design perspectives to be considered. First, the mobile system should guarantee traversability on rough terrain in microgravity condition. Secondly, the system should be sustainable in the extreme environment of the lunar surface including cosmic rays and excessive temperature changes. One of the potential solutions to improve the reliability of the rover system is to reduce the chance of failure by minimizing the number of electronic components including actuators and their following components and installing them in the rover’s warm-box. We approached the design of the mobile system in the aspect of its kinematics with assumptions of pure-rolling and non-lateral slip. We found a relation that a pair of front and rear wheels on the same side is coupled so that their alignment and rotational speed can be coupled by a mechanism. This allows advantages of explicit steering, minimizing redundancy of actuators and isolating all the electronic components from the effects of external environments. To demonstrate the feasibility of the system, we developed a rover testbed and presented its mobility of explicit steering by experiments of open-loop trajectory traveling.
Keywords:
Planetary rover, Lunar exploration, Wheeled mobile robot, Robotic mechanism키워드:
행성 로버, 달탐사, 차량형 이동 로봇, 로봇 메커니즘1. Introduction
The Korean government announced the lunar exploration mission and multiple Korean national institutes are participating in the project. Especially, during the second phase of the exploration mission, a ground probe, also called “rover”, will be sent to the lunar surface to explore and collect scientific data.1 An unmanned rover, a ground vehicle specialized for space exploration has been used in multiple space missions to explore the surface of a celestial body that is nearly impossible to reach by humans, perform experiments, and collect scientific data. At the Korea Institute of Science and Technology, we are developing a lunar rover prototype and the core technologies, prior to the development of a flight model for the real mission.2
In a rover system, mobility is a key element for a successful exploration mission due to rough terrain in the target environment. There are many methods studied to ensure mobility in the fields of robotics and space engineering. Thueer et al. proposed defined metrics to evaluate the mobile performance of rover platforms and evaluated three different mobile systems based on the metrics.3 Patel et al. analyzed multiple suspension types of six-wheel configuration and searched tradeoffs regarding a rover’s locomotion.4 Ghotbi et al. found that reducing normal force distribution improves drawbar pull of a ground robot and suggested the variance of each wheel’s normal force to be a critical parameter to search mobility efficiency of the chassis.5
Focusing on lunar exploration missions, a target area that a rover traverses on is potentially more challenging. On the lunar surface, a ground vehicle experiences microgravity and soft lunar regolith, which causes slippage between the rover’s wheels and the terrain. In the aspect of terramechanics, multiple research groups searched effect of wheels on a rover’s mobility through both simulations and experiments.6-10 Yoshida et al. reflected the terramechanic properties of lunar environments in the design of their four-wheel skid-steering rover.11
On the other hand, due to the absence of atmosphere, the failure rate of electronic components, especially, are easily affected by cosmic rays, excessive temperature changes and lunar dust.12 In the aspect of mechanical elements, it is possible to deal with thermal expansion problems by limiting the rover’s operation corresponding to the surrounding temperature, and utilize seals to decrease the failure rate of gears by isolating mechanical components from external lunar dust.13 However, the failure rates of electronic components, especially, are easily affected by the harsh environments since they are required to operate consistently and more sensitive to temperature and radiation.12
One of the potential solutions is to reduce the chance of failure by minimizing the electronic components installed outside the warm-box of the rover. In the warm-box, the temperature can be controlled and sun rays are blocked. By minimizing the exposure of electronic parts, it increases the components’ reliability and robustness. Another solution is to increase the reliability of the rover system by assignment of electronic components. Assigning redundancy, such as marginal actuation components, improves the robustness of the system against failure.14 However, in a hostile environment, such the Moon’s surface, adding a part means its following components are also required to be installed as well and then the reliability of the entire system would decrease due to the fragility of the added components. In addition, the rover hardware must satisfy the specified volume and mass limits, and secure capacity for scientific equipment to guarantee its economic feasibility. For these reasons, it is important to simplify the system and the consisting elements.
Thus, the main contributions of the paper are the following; First, researches related to planetary rovers are reviewed to draw a micro lunar rover design. Second, by minimizing the actuator redundancy and increasing the complexity of the hardware in the rover system, it is proposed that the chance of electronic component failure can be minimized with achieving explicit active steering, which is based on 2-dimensional kinematic analysis of the rover's locomotion. Finally, the design approach is demonstrated and it is validated by the hardware implementation and evaluation of its steering performance. We expect this not only contributes to the development of planetary rovers but also ordinary wheeled ground robots.
2. Design Elements for the Mobile Platform
To satisfy the volume and mass requirements, a 20 kg-class light-weight rover is under development for the mission. The mobile platform of the rover must secure capacity for scientific equipment and guarantee fine traversability and stability in lunar environments, which is strictly defined, compared with previous and ongoing planetary rovers.
2.1 Consideration of Design
First, uneven terrain and microgravity of the Moon cause different dynamics environment from one of the Earth surfaces. Therefore, the mobile platform needs to be developed to guarantee its mobility in the target environment. Traversability over obstacles and rough terrain, and enough drawbar pull on the soft terrain are often used to analyze the performance of the mobile platform.4,15 Moreover, slip between the rover’s wheel and the soft terrain of the Moon causes issues of state estimation errors. Even if the state estimation would be corrected by equipped sensors, reduction of uncertainty caused by slip important to further improve the estimation.16
In addition, due to the absence of atmosphere, the rover would be exposed to an excessive change of temperature and radiation. Electronic components are extremely sensitive to working temperature and fragile on radioactive rays. In mechanical aspects, such environment compromises the durability of machine parts and the actuation of the mobile platform can be critically affected by temperature expansion and contraction. One of the solutions regarding the issue is to install the electronic components inside the warm-box of the body, which blocks radiation and protects electronic components from excessive temperature changes more effectively. At the same time, it is necessary to use as fewer electronic components as possible to reduce the complexity of the system and the chance of failure.12
Based on the issues stated above, we selected four representative design elements: wheel configuration, suspension, steering method, and actuator placement. In the following subsections, previous and ongoing researches on the development of planetary rovers would be reviewed based on the chosen design elements and compare the mechanism candidates of each element.
2.2 Wheel Configuration
The rocker-bogie mechanism with 6-wheel configuration developed by NASA is known to have great traverseability and terrain adaptation on rough terrain without actuation of the chassis. For this reason, 6-wheel configuration with the rocker-bogie mechanism has been applied in many planetary and lunar exploration missions. However, in a lunar surface exploration mission, the rover would traverse soft terrain covered by the lunar regolith so these advantages are less effective and the slip caused by the lunar regolith is a rather more challenging issue.11 Moreover, in the aspect of the cost, 6-wheel configuration requires not only great volume and weight but also increases the complexity of the electronic systems to drive and steer wheels.
Instead, 4-wheel configuration is applied in the mobile platform. It is known that bigger wheel size is more advantage to slip on loose regolith and 4-wheel configuration allows bigger wheel size given with the same volume and payload capacity.11 In addition, by reducing the number of wheels, it requires a smaller number of actuators, and therefore, the overall system of the mobile platform is simplified.
2.3 Suspension
The rover would traverse rough terrain, and therefore, a suspension system takes a critical role to stabilize roll and pitch orientation and to minimize the damage of the system. On the other hand, as the complexity of suspension depends on the stability of the rover system, choice of suspension system must be decided carefully by analyzing the lunar environment where the rover traverses. In general, there are three types of suspension; passive, semi-passive, and active suspensions. The main difference between these three types is the method of damping. The mobility of the rover controlled by sequence-based commands from the ground station would be slow, approximately 1 cm/sec, due to the time delay occurring at its communication and data processing so the dynamics is approximated as to be a quasi-static model,17 which the advantage of semi-passive suspension is not effective. In the case of active suspension, it may not react to external shock effectively with limited communication and computing power.
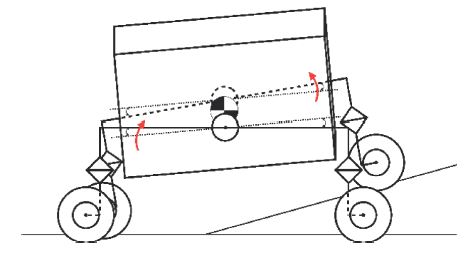
Another role of suspension is to ensure all wheels to contact with the ground of uneven terrain. To ensure all wheels to contact with the ground, we selected a passive suspension mechanism that has been applied in many 4-wheeled platforms as shown in Fig. 1: the mechanism consists of a pair of differencing rockers with wheels at their ends.11,18 In the suspension system, four wheels are installed at the end of the rockers, and the suspension allows each wheel to passively contact with uneven terrain. In terms of geometry, the four wheels consist of up to two contact planes. On uneven terrain, three contact points of wheels define a contact plane and the other wheel passively lie on the terrain defining another contact plane with the adjacent two wheels, which offers good stability with a simple mechanism.
2.4 Steering Method
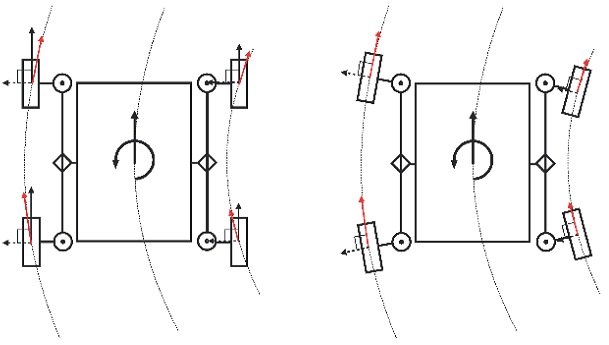
In a lunar exploration mission, we can consider two methods to change the direction of the rover; spot-turning motion and making a curve. A spot-turning motion allows the rover to change the direction without moving long distance, which optimizes a trajectory in a limited area. On the other hand, making a curve is an effective method to follow a smooth trajectory or to correct the direction. Both methods are essential for the rover to traverse robustly against high uncertainties of the lunar environment.
The skid-steering mechanism performs both steering methods without changing the alignments of the wheels. In skid-steering, each wheel has a fixed rolling direction with respect to the body. Then, by controlling the revolution of each wheel, steering torque can be generated from contact friction and slips with respect to the terrain. A skid-steering mechanism has an advantage of not requiring additional actuators for the wheel alignment but the rover’s motion depends on slips,19 which causes severe odometry error to affects the position determination of the rover. Considering uncertainties of nonlinear dynamics of rough terrain, sensor error, and communication delay, skid-steering runs risks of control or estimation failure of the rover's state.
On the other hand, to minimize the lateral slip of wheels, the active explicit-steering mechanism aligns every wheel to the tangential direction of the wheel's desired trajectory by using actuators.20 However, as motors for aligning the wheels are added, the system becomes more complex. In addition, considering the cost and limit of payload capacity, the explicit-steering mechanism is less economic than the skid-steering mechanism.
There is a tradeoff between skid-steering and explicit-steering systems: skid-steering more relies on the slip of the wheels while the explicit-steering requires a more complex system. In the present research, we aimed to develop an explicit-steering mechanism that uses a minimized number of actuators to increase stability against the slip of wheels and to reduce the systematic costs of motors at once.
2.5 Actuator Placement
Conventionally, motors to drive wheels are installed directly on the wheels. It implies that the motors and following electronic components are exposed to hostile environments. Subsequently, the system would run a high failure risk due to external effects on electronic components. Hence, it is suggested that every motor is installed inside the body, which requires a more complex mechanical mechanism but protects the motors and the following components from excessive radiation and temperature changes. The thermal expansion problems on mechanical components can be solved by limiting the rover’s operation to the daytime of the Moon and the failure rate of gears caused by external lunar dust can be prevented by utilizing seals.13 For this reason, although the design has a tradeoff between the complexity of the actuation system and the reliability of the electronic components, we consider the reliability of electronic components more critical, and the design is expected to improve the stability of the mobility systems. This approach is the main difference between the rover design of the present research and ones of previous and on-going previous or ongoing planetary rovers, such as Opportunity rover, that have motors for their wheel actuation installed on the wheel module.21
3. Design of Mobile Platform
It is known that an explicit steering system has an advantage of minimizing slip over other steering systems20 so we aimed to modify explicit steering system by minimizing the number of actuators to increase the reliability of the entire system. We considered the case that the rover's mobility follows the conditions of non-lateral-slip and pure-rolling to simplify the kinematic model. Under the non-lateral-slip condition, each wheel is aligned with the tangential direction of its trajectory and slip in the lateral direction by rolling is minimized. In the analysis, only second-dimensional trajectories are considered: third-dimensional analysis will be studied in future works by extending the studies of second-dimensional analysis. The error in the pure-rolling assumption due to slip can be compensated by various methods and will not be dealt with in this research.
3.1 2D Kinematic Analysis
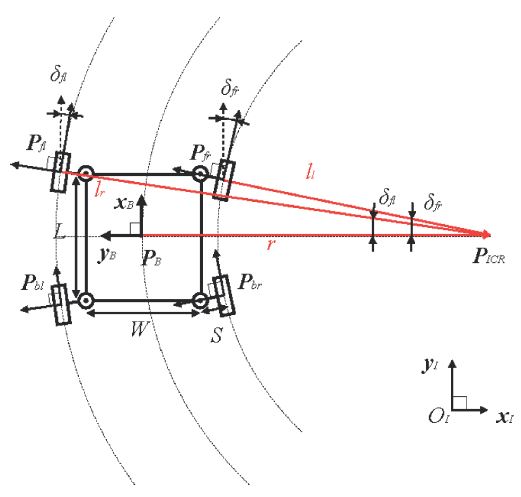
Let the rover’s state configuration in the inertial frame be (x, y, θ) where x and y are second-dimensional coordinates and θ is the orientation. Define the body frame of the rover such that the origin is the center of gravity (CG) PB of the rover and the positive x-axis direction is the rover's forward direction. Assume the rover’s CG only moves with the linear velocity v on the x-axis of the body frame. Then, the rover’s state in the inertial frame can be written with respect to the rover’s linear velocity v and angular velocity w in the body frame.
| (1) |
Here, the differential of the rover’s orientation in the inertial frame is equivalent to the angular velocity w on the flat terrain. The instant center of rotation (ICR) is always on the y-axis of the body frame and we can define the coordinate of ICR in the body frame to be PICR = (0, r). Then, we can obtain the following equation.
| (2) |
Under the assumption of the non-lateral-slip condition, the ICR is equivalent to one of each wheel. Define the wheel frames such that the ICR is on the y-axis of the wheel frames and the origins of the frames are on the wheels’ CG Pmn, where m = f (forward) or b (backward), n = l (left) or r (right). The indexes of the wheels as shown in Fig. 3. Let δmn be the direction of the wheel regarding the body frame. Then, δmn is given as the following equation, where L and W are the length and width of the rover’s body, respectively.
| (3) |
If the wheels’ radius is large, inward alignments of the wheels cause physical interference between the chassis and the wheels. In addition, it is known that enough surface of the wheels’ contact points should be secured for the rover’s stability on its tipover.22 Therefore, we limit the wheels’ alignment to be outward from the body as δmn = (-π/2, π/2). Then, we can find the following relations from Eq. 3.
| (4) |
Note that the rover’s trajectory shows spot-turning with zero linear velocity v = 0 when r = 0.
Define the y-axis coordinate of the ICR in the wheel frame to be lmn, where m and n are the indexes of the wheel. The symmetry of the rover model allows lfl = lbl and lfr = lbr. Then, lmn is given with respect to r, as shown in the below equations, where S is the length of the steering offset.
| (5) |
The sign functions are multiplied due to the defined range of δmn in Eq. 4. In order to satisfy the pure-rolling condition, a wheel's rolling speed equals to the translation velocity in the rolling direction. Let ωmn be the angular speed of each wheel and R be the radius of the wheels. Then, from the relation of Eq. 4 of the steering angles δmn, the angular velocities are given by the below equation.
| (6) |
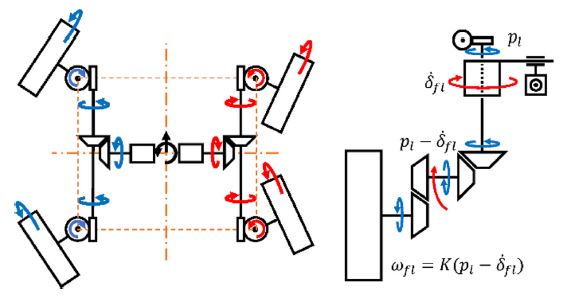
Here, the first term on the right side denotes the wheels’ trajectories according to the ICR and the second term denotes the effect of the steering angles’ changes. Since the 4 × 2 matrixes of Eq. 6 are not identical, it is required to realize each term independently. The first term is coupled with respect to wlfl/R and wlfr/R and they can be easily controlled by two actuators. The second term depends only on the wheels' alignment rate and and it can be manipulated passively corresponding to the change of wheels’ alignments, which will be described in Subsection 3.2.
From Eq. 3 and 6, the effect of the offsets’ rotation on the wheels' rolling is passively canceled by the rolling compensation and the actuation of the rover's driving is decoupled from the one of the steering’s. Therefore, driving of each wheel can be controlled to its trajectory regardless of the rotational velocity of the wheel's alignment, which simplifies the model of the mobile system. We can find a relation such that driving wlfl/R and wlfr/R of the mobile system is similar to the differential wheeled mobile system in terms of DOF but additional 2 actuators for the wheels’ alignments, δfl and δfr, and mechanical compensation, , and , of driving for explicit steering are added.
3.2 Mechanism Design
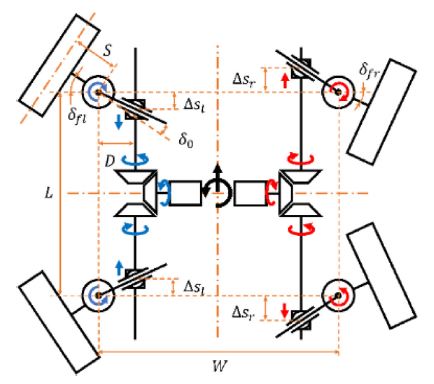
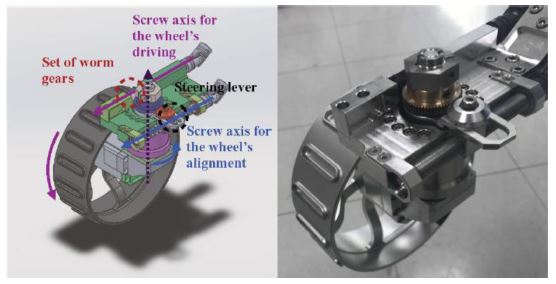
In Subsection 3.1, it is presented that a pair of front and rear wheels on the same side is coupled and it can be controlled by two actuators. To demonstrate the issues, we developed a mechanism of the rover’s mobile system. There are two pairs of motors are installed in the rover system: a pair of motors are used for steering and driving of each side of wheels. Due to the fragility of electronic components, all the motors are placed in the rover's body. In particular, each pair of motors are installed on the rotational axis of the rocker. Then, each motor can convey power through the revolution of its bevel gear in the direction of the axis.
Firstly, a motor for aligning wheels, a steering motor, rotates two screw axes through bevel gears as shown in Fig. 4. Note that the screws revolute in the opposite direction of each other to realize Eq. 4. Then, the screws push or pull levers that are installed on the wheel modules in the opposite direction of each other. Define the displacements of the screws to be Δsl and Δsr and their positive direction to be outward from the body. The housing of gears and a wheel rotates corresponding to the lever’s revolution as the equations below.
| (7) |
| (8) |
These equations yield the following equations from the kinematic relation in Eq. 3 so the required displacement of the steering angle is expressed with respect to the desired angle of the wheels.
| (8) |
Since the linear displacement is proportional to the revolution of the bevel gear, the rover’s steering can be easily controlled by computing Δsl and Δsr. This steering system has an advantage of large maximum torques working on the lever. In addition, if the angle offset of the lever is negligible, i.e. δ0 = 0, computation of Δsl and Δsr are simplified as .
Secondly, a motor for driving rotates a screw axis through bevel gears, as shown in Fig. 5. Unlike the case of the steering system, only one screw is used and it conveys rolling of the same direction to each wheel. At the end of the screw, a set of worm gears are placed and driving power is conveyed through the revolution of them. However, the gear is designed to rotate independently from the rotation of the wheel's housing. It allows a relative rotation between the axis of the worm gear and the axis of the wheel's driving, which mechanically realizes passive compensation of the wheel’s rolling term caused by the change of the wheel's steering mentioned in Eq. 6. Therefore, the wheel speed is represented in the below equation, where pn, n = l, r is the motor’s rotation and K is the composite gear ratio for mapping rotational velocity of steering into wheel speed compensation.
| (9) |
Here, the ratio K is chosen corresponding to the ratio s/R. Then, Eqs. 6 and 9 become identical. The proportional relation between the wheels’ rolling ωmn and the motors' rotation pn are set depending on the requirement of wheel torque.
| (10) |
Note that Δsl and Δsr of Eq. 8 and pl and pr of Eq. 10 represent the four motor inputs used in the mobile system. Δsl,r is an input to align a pair of wheels on either left or right side in the tangential directions of the trajectory and pl,r is for the wheels’ trajectory following corresponding to the rover’s velocity. Δsl,r depends only on r and, with the given r, w only affects the input for driving, pl,r.
4. Hardware Implementation
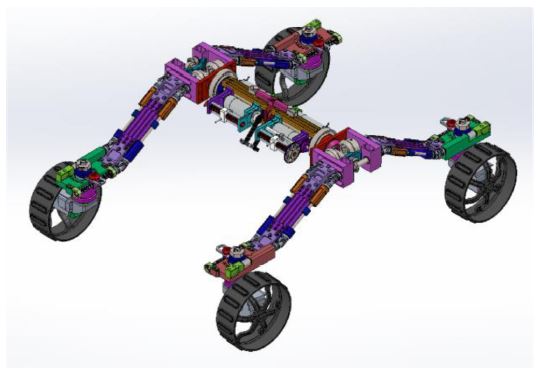
A rover testbed was designed and built to validate the feasibility of the mechanism presented in Subsection 3.2 as shown in Fig. 6. The hardware specification of the rover testbed, shown in Table 1, satisfies the requirements of the mission; the geometry of the chassis is W × L = 140 mm × 580 mm and the offset length of the wheel’s module is S = 65 mm. The wheel dimension is ∅140 mm × 50 mm (R = 70 mm). The total mass of the rover is 12.85 kg.
The 3D model of the hardware is presented in Fig. 7. At the center of the chassis, a seesaw-like mechanism is applied for the passive differential mechanism. In order to secure enough height of the body from the ground, the rocker is designed to be V-shaped and universal joints are used at the rockers’ curved edges for power transmission of the screws. The actuation systems of the rover are implemented based on Subsection 3.2. Four DC motors with planetary gearboxes are installed and fixed on the axes of the rockers. Power of each motor is conveyed to the wheel module through the screw's revolution along the rocker. Details about driving and steering mechanism used in the testbed are described in Figs. 8, 9. The rocker is designed to allow independent rotations of the bevel gears for steering and driving by layering their axes. The housing of the wheel module that has a lever on it rotates with the revolution of the screw axis for the wheel’s steering. Power is transmitted by the other independent screw axis. However, power transmission for driving is affected by actuation of the steering system when the rover is changing the wheels’ alignment as described in Section 3.
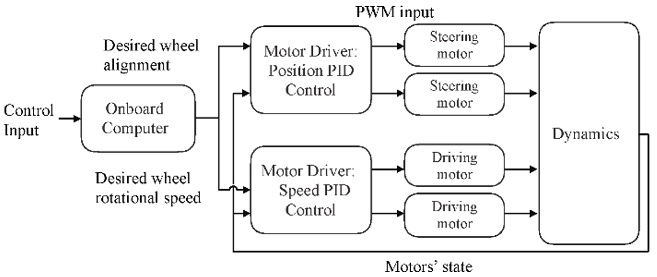
The control system overview of the rover testbed is shown in Fig. 10. The onboard computer receives control via Wi-Fi and computes desired alignments and rotational speeds of the wheels based on the kinematic model presented in Subsection 3.1. Since the present research aimed to demonstrate the mechanism, we did not consider feedback control and the rover solves open-loop kinematics to compute motor inputs. In the low-level control for the motors, PID controllers for DC motors are used for the wheels’ alignment and driving. The controllers are implemented on two motor drivers based on digital signal processors of Texas Instruments. The state of the motors is measured by the built-in incremental encoders and the data are sent to each motor driver.
5. Experiment
For the validation of the mobile system, a series of experiments were conducted with focusing on the steering performance. In the present research, we excluded the effect of potential soft terrain on the lunar surface: for the rover’s locomotion on soft terrains of the lunar surface, a terramechanic model of the rover and a control scheme to compensate the wheel’s slip are required, which is out of the main focus of the present research and will be studied in future works. Therefore, the rover was tested in the indoor environment on a rigid marble floor. The rover’s state was taken approximately 4m above the floor every 10 seconds and its time-lapse pictures ware used for discussion. Firstly, the rover’s steering performance was tested with circle trajectories. Considering the speed requirement of sequence-based mission scenario as stated in Subsection 2.1, the desired velocity of the rover’s CG in the experiments was set as v = 1.33 cm/sec so the rover's velocity and the radius of trajectories were set as r = 1 m and r = 2 m, respectively, as control inputs. The spent time for the rover to make one rotation was measured and the radius of the actual trajectories was estimated by projecting the pixel coordinates of the circles' left and right ends. In the case of testing the spot-turning performance, the rover’s angular velocity was set to w = 3.17 × 10-2 rad/sec so that velocity of each wheel is v = 1.33 cm/sec. Likewise, the spent time for the rover’s 180° of spot-turning was measured and the changes in the center of turning were estimated.
The results are shown in Fig. 11 and Table 2. We found that there are about 3% of errors of the radius in both cases of r = 1.00m and r = 2.00 m. The errors of time spent for 1 circulation for the control inputs r = 1.00 m and 2.00 m are 8.06% and 7.41%, respectively, and one of the spot-turning case is 4.76%. These results imply that pure-rolling is not satisfied in practical environments.
6. Conclusion and Future Works
We presented a 4-wheel mechanism taking advantage of complex a hardware system to minimize the wheels’ slip by explicit steering and to maximize the reliability of a potential electronic system in the lunar environments. Due to slow motion of the rover, a passive adaptive differencing suspension consisting of two differencing rockers on the sides of the rover was used. The kinematics of a 4-wheel mobile robot's explicit steering was analyzed under the assumption of non-lateral-slip and pure-rolling. Based on the analysis, we presented a mobile system that minimizes the redundancy of actuators by increasing the complexity of the rover’s hardware. The developed mobile system cancels the effect of the wheel offsets’ rotation by the passive rolling compensation and decouples motor inputs for driving and steering. Finally, we developed a rover testbed and validated the feasibility of the mobile system by experiments of the rover’s open-loop course traveling.
In this work, we assumed ideal environments of terrain to analyze kinematics of the rover but, in practice, the rover is suffered from wheels’ slip and terramechanic uncertainty. Thus, experiments regarding terramechanic property will be carried out on lunar regolith simulant to further discuss the mobility of the system designed in this work. Finally, in the steering system, there is a tradeoff in reducing the number of actuators because the system loses marginal DOFs controlling the rover's locomotion. Also, the rover’s mobility can be compromised in case of failure of an actuator. Therefore, future works are needed to study the failure configurations and develop a novel control scheme to enhance the robustness of the system.
Acknowledgments
This authors gratefully acknowledge funding for this research through MSIP under the space technology development program NRF-2016M1A3A9005563 supervised by the NRF.
REFERENCES
- Ju G., Roh, W.-R., Choe, N., and Lee S. R., “A Feasibility Study on Korean Lunar Exploration Mission,” Proc. of the KSAS-JSASS Joint International Symposium, 2008.
-
Seo M. and Lee W., “Approaches for the Design of Mobile Platforms with Mobility, Economic Feasibility, and Robustness in Lunar Environments”, Proc. of the 14th International Conference on Ubiquitous Robots and Ambient Intelligence, 2017.
[https://doi.org/10.1109/URAI.2017.7992804]

-
Thueer T. and Siegwart R., “Mobility Evaluation of Wheeled All-Terrain Robots,” Robotics and Autonomous Systems, Vol. 58, No. 5, pp. 508-519, 2010.
[https://doi.org/10.1016/j.robot.2010.01.007]

-
Patel N., Slade R., and Clemmet J., “The ExoMars Rover Locomotion Subsystem,” Journal of Terramechanics, Vol. 47, No. 4, pp. 227-242, 2010.
[https://doi.org/10.1016/j.jterra.2010.02.004]

-
Ghotbi B., Gonz´alez F., K¨ovecses J., and Angeles J., “Mobility Evaluation of Wheeled Robots on Soft Terrain: Effect of Internal Force Distribution,” Mechanism and Machine Theory, Vol. 100, pp. 259-282, 2016.
[https://doi.org/10.1016/j.mechmachtheory.2016.02.005]

-
Ishigami G., Miwa A., Nagatani K., and Yoshida K., “Terramechanicsbased Model for Steering Maneuver of Planetary Exploration Rovers on Loose Soil,” Journal of Field Robotics, Vol. 24, No. 3, pp. 233-250, 2007.
[https://doi.org/10.1002/rob.20187]

-
Ding L., Gao H., Deng Z., Nagatani K., and Yoshida K., “Experimental Study and Analysis on Driving Wheels’ Performance for Planetary Exploration Rovers Moving in Deformable Soil,” Journal of Terramechanics, Vol. 48, No. 1, pp. 27-45, 2011.
[https://doi.org/10.1016/j.jterra.2010.08.001]

-
Sutoh M., Nagaoka K., Nagatani K., and Yoshida K., “Evaluation of Influence of Surface Shape of Locomotion Mechanism on Traveling Performance of Planetary Rovers,” Proc. of Robotics and Automation International Conference, 2012.
[https://doi.org/10.1109/ICRA.2012.6225024]

-
Zhou, F., Arvidson, R. E., Bennett, K., Trease, B., Lindemann, R., et al., “Simulations of Mars Rover Traverses,” Journal of Field Robotics, Vol. 31, No. 1, pp. 141-160, 2014
[https://doi.org/10.1002/rob.21483]

-
Ding L., Deng Z., Gao H., Tao J., Iagnemma K. D., et al., “Interaction Mechanics Model for Rigid Driving Wheels of Planetary Rovers Moving on Sandy Terrain with Consideration of Multiple Physical Effects,” Journal of Field Robotics, Vol. 32, No. 6, pp. 827-859, 2015.
[https://doi.org/10.1002/rob.21533]

- Yoshida K., Britton N., and Walker J., “Development and Field Testing of MoonRaker: a Four-Wheel Rover in Minimal Design,” Proc. of Robotics and Automation International Conference, 2013.
- Wertz J. R., Everett D. F., and Puschell J. J., “Risk and Reliability,” Microcosm Press, No. 24, pp. 753-780, 2011.
- Delgado, I. R. and Handschuh, M. J., “Preliminary Assessment of Seals for Dust Mitigation of Mechanical Components for Lunar Surface Systems,” Document No. 20100025844, 2010.
- O’Connor, P. and Kleyner, A., “Practical Reliability Engineering,” John Wiley & Sons, pp. 1-512, 2012.
-
Ghotbi B., Gonz´alez F., K¨ovecses J., and Angeles J., “A Novel Concept for Analysis and Performance Evaluation of Wheeled Rovers,” Mechanism and Machine Theory, Vol. 83, pp. 137–151, 2015.
[https://doi.org/10.1016/j.mechmachtheory.2014.08.017]

-
Helmick D. M., Cheng Y., Clouse D. S., Bajracharya M., Matthies L. H., et al., “Slip Compensation for a Mars Rover,” Proc. of Intelligent Robots and Systems International Conference, 2005.
[https://doi.org/10.1109/IROS.2005.1545178]

-
Krebs A., Thueer T., Michaud S., and Siegwart R., “Performance Optimization of All-Terrain Robots: A 2D Quasi-Static Tool,” Proc. of Intelligent Robots and Systems International Conference, 2006.
[https://doi.org/10.1109/IROS.2006.281955]

- Bartlett P., Wettergreen D., and Whittaker W., “Design of the Scarab Rover for Mobility & Drilling in the Lunar Cold Traps,” Proc. of Artificial Intelligence, Robotics and Automation International Symposium, 2008.
-
Yi J., Wang H., Zhang J., Song D., Jayasuriya S., et al., “Kinematic Modeling and Analysis of Skid-Steered Mobile Robots with Applications to Low-Cost Inertial-Measurement-Unit-Based Motion Estimation,” IEEE Transactions on Robotics, Vol. 25, No. 5, pp. 1087-1097, 2009.
[https://doi.org/10.1109/TRO.2009.2026506]

- Shamah B., “Experimental Comparison of Skid Steering vs. Explicit Steering for Wheeled Mobile Robot,” M. S Thesis, Robotics Institute, Carnegie Mellon University, 1999.
-
Lindemann, R. A., Bickler, D. B., Harrington, B. D., Ortiz, G. M., and Voothees, C. J., “Mars Exploration Rover Mobility Development,” IEEE Robotics & Automation Magazine, Vol. 13, No. 2, pp. 19-26, 2006.
[https://doi.org/10.1109/MRA.2006.1638012]

- Papadopoulos E. and Rey D. A., “A New Measure of Tipover Stability Margin for Mobile Manipulators,” Proc. of Robotics and Automation International Conference, 1996.

Mingyo Seo is a researcher in the Korea Institute of Science and Technology. He received his B.Eng. degree in aerospace engineering from Tohoku University, Sendai, Japan, in 2014, and his M.S. degree in mechanical engineering from the University of Illinois at Urbana-Champaign, Urbana, IL, USA, in 2016. His research interests include control of mobile robots and aerial vehicles.
E-mail: mingyo@kist.re.kr

Woosub Lee received the B.S. degree in mechanical engineering from Sogang University, Seoul, Korea, in 1999, the M.S. degree in electronic engineering from Yonsei University, Seoul, Korea in 2004, and the Ph.D. degree in mechanical and aerospace engineering from Tokyo Institute of Technology, Tokyo, Japan in 2013. Since 2004, he has been with Korea Institute of Science and Technology, Seoul, Korea, where he is currently a Principle Research Scientist. His current research interests include creative robot mechanism design, reliable motion control systems, and field robot systems for hazardous duty.
E-mail: robot@kist.re.kr