해저 케이블 매설 로봇의 수중 매니퓰레이션을 위한 터치스크린 기반 원격 조종 어시스턴스 기술 개발
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
URI-T can perform various underwater construction tasks such as cable burial and maintenance. Successful sea trial results show that URI-T could be used in underwater construction fields. To improve the efficiency of URI-T, an assisted teleoperation scheme for underwater manipulations was also proposed. For the proposed scheme, by touching several points on the touch screen, one can move the manipulator to the target; it can reduce the burden of teleoperation of every degree-of-freedom (DOF) of the manipulators. The scheme also has a position estimation technique that can estimate six DOF position of the objects using 2D positions on the two images from cameras deployed in stereo. Via touch screen, the 2D positions are fed to guarantee reliability of the estimated results, which is one of the most important points in the underwater interventions. A control structure for the assisted teleoperation was investigated using the position estimation technique. The structure involved an inverse kinematics scheme based on the weighted damped least squares, which can resolve the kinematical limitations: workspace limit and singularity, and joint limits on position and velocity. This study established that the proposed assistance technique could significantly reduce operation time in comparison with the conventional teleoperation.
Keywords:
Remotely operated vehicle, Underwater cable burial, Underwater manipulation, Teleoperation assistance, Touch screen키워드:
원격무인잠수정, 해저 케이블 매설, 수중 매니퓰레이션, 원격조작 어시스턴스, 터치스크린1. 서론
해양은 사람의 직접적인 접근이 제한되는 공간이며, 수중 로봇을 활용하여 다양한 작업들이 수행되고 있다.1,2 한 예로 해저케이블 매설 분야를 들 수 있는데, 이 분야에는 육지와 도서 간의 전력 공급을 위한 HVDC 케이블 설치,3 해상 풍력 단지와 육지 간의 해저케이블 연결,4 해저 통신 케이블의 설치5 등이 포함된다. 해저케이블 매설 분야는 사람이 접근하기 어려운 심해 작업을 포함할 뿐만 아니라, 작업 수행 시 매우 큰 힘이 필요하기 때문에 중작업 수행이 가능한 대형 수중 로봇이 활용된다.
해저케이블 매설을 위한 중작업용 수중 로봇은 해외 소수 기업이 독과점하고 있는 상황이다. 따라서, 관련 공사를 진행하기 위해서는 해외의 로봇을 구매하여 사용하거나 해외 공사 업체에 의뢰하여 왔다. 따라서, 로봇 및 부대 장비를 마련하기 위해 고가의 비용을 지출해야 하며, 로봇의 정비에 상당한 시간과 비용이 소요 되는 등 경제적 비효율성이 상당히 큰 상황이다.
최근, 해저케이블 매설 작업을 위한 중작업용 ROV인 URI-T가 개발되고 있다.6 URI-T는 수심 2,500 m급의 해저에서 해저케이블 및 소구경 파이프의 매설 작업과 유지보수 작업을 수행하는 로봇이다. URI-T는 국내 기술로 개발되고 있으며, 국외 소수 기업이 독과점하고 있는 수중 로봇 분야에서 국내 기술 경쟁력을 향상시킬 수 있을 것으로 기대된다.
해저 케이블 매설 분야는 케이블을 매설하는 작업과 케이블을 유지보수하는 작업을 포함한다. 해저 케이블 매설 작업은 수중 로봇 등을 이용하여 해저 면에 놓인 케이블을 지하로 매설하는 작업을 말한다. 해저케이블 유지보수 작업은, 손상된 해저케이블의 유지보수를 위해 해저케이블을 커팅하는 작업과 케이블을 수상의 선박으로 끌어올리기 위한 그리핑 작업 등을 포함한다. 이러한 작업은 수중 로봇에 장착된 매니퓰레이터를 이용하여 커팅 장치 및 그리핑 장치를 조작함으로써 수행된다.
해저케이블 매설 작업은 수중 로봇을 원격조작함으로써 수행되고 있다. 특히, 매니퓰레이션 작업은 로봇 팔의 모든 자유도를 오퍼레이터가 원격조작을 통해 조종한다. 이 경우, 오퍼레이터는 카메라 영상 정보와 각종 센서 정보 등 한정된 정보만으로 수중 공간의 작업 상황을 인지해야 한다. 더욱이, 오퍼레이터는 입력장치를 이용하여 매니퓰레이터의 모든 자유도에 대한 조작 명령을 인가해야 한다.2,7,8 결과적으로, 수중에서 원격 조작하는 작업들은 많은 작업시간이 소모될 뿐만 아니라, 숙련된 오퍼레이터를 필요로 하며, 이에 따라 작업을 수행하는데 많은 비용이 발생한다.
수중 작업의 효율을 높이기 위해, 자율 제어를 이용한 연구들이 일부 보고되었다. 기존에 보고된 연구들은, 소나 센서 기반 기술9,10 및 영상 기반의 접근 방식11,12을 이용하여 객체의 위치를 자동으로 인식하는 것에 초점을 맞추고 있다. 이 기법들은 운용자에게 편안함을 제공할 수 있으나, 물체의 자동 인식 과정의 신뢰도 이슈로 인해 실제 작업현장에는 잘 활용되지 못하는 실정이다. Oceaneering사에서 10년간 ROV 오퍼레이터로 근무한 전문가의 의견에 따르면, ROV에는 많은 자동 기능이 있지만, 오퍼레이터는 오작동의 위험을 방지하기 위해 자동기능들을 잘 사용하지 않는다고 한다.
이 논문에서는, 국내 기술로 개발 중인 케이블 매설 수중 로봇 URI-T에 대해 소개한다. 그리고, URI-T에 포함된 매니퓰레이터의 원격조작 효율을 향상시키기 위한 어시스턴스 기술을 제안하고자 한다. 어시스턴스 기법은 운용 중 오퍼레이터의 개입이 가능하기 때문에 기존에 제안된 자율제어기법에 비해 신뢰성을 확보하는데 용이하다. 제안하고자 하는 어시스턴스 기법의 기본 개념은 단순한데, 카메라 영상에 대해 오퍼레이터가 터치스크린을 이용하여 목표물의 위치를 지정해 주면, 매니퓰레이터가 목표물의 위치를 추정하여 이동하게 하는 것이다. 이 개념은 섬세한 조작이 필요한 작업 보다는 작업물로의 이동 등 거시적 조작(Gross Motion)을 보조하는데 초점을 맞추고 있다. 제안된 어시스턴스 기법의 주요 이슈는 다음과 같다.
- 터치스크린 입력을 이용한 목표물 위치 및 자세 추정
- 위치/자세 추정 결과를 활용하여 원격조작을 보조하는 제어 구조
위치 추정 이슈와 관련하여, 스테레오로 배치된 카메라 영상에 대해 수 회의 터치 입력 값을 이용함으로써 목표물의 6자유도 위치 추정 기술을 제안한다. 여기서 터치 입력은 오퍼레이터가 터치스크린의 영상에서 작업물을 직접 터치하는 것으로 입력 받게 된다. 이를 통해, 오퍼레이터가 매니퓰레이터의 각 자유도를 직접 원격 조작하기 위한 작업 부담을 줄일 수 있다. 더 나아가, 목표물의 위치를 파악하기 위한 기초 정보는 오퍼레이터에 의해 주어지기 때문에, 목표물의 위치 추정 결과에 대한 신뢰성을 쉽게 확보 가능하며, 따라서 기존의 자율제어기법에 비해 오류를 줄일 수 있다. 본 연구에서는 또한, 원격조작 어시스턴스를 위한 적절한 제어 구조 또한 제안한다. 이 구조는 목표물 위치가 매니퓰레이터의 작업 영역, 특이점 및 위치와 속도, 조인트 등의 운동학적 한계를 초과하는 상황에도 적절하게 대응할 수 있는 역기구학을 포함한다. 직교공간상에서 주어진 매니퓰레이터의 목표 위치는 매니퓰레이터의 운동학적 한계들을 초과할 위험이 다분히 존재한다. 이 문제를 해결하기 위해, WDLS (Weighted Damped Least Squares)13-15를 활용하여 역기구학 이슈를 해결하고자 한다. 특히, 작업 영역의 제약과 특이점 문제는 DLS (Damped Least Squares)16,17를 적용하여 해결하였으며, 매니퓰레이터 조인트의 위치 및 속도 한계 이슈는 WLS(Weighted Least Squares)20 기법을 적용하였다. DLS는 특이점 문제를 극복하는 효과적인 기법 중 하나로 산업용 로봇,18 여유 자유도 매니퓰레이터 등,19 다양한 어플리케이션을 통해 검증되었다. WLS는 에너지 최소화,20 토크 최소화,21 조인트 위치 한계 회피22 등 물리적 의미에서 운동학적 솔루션을 최적화하기 위해 적용되었다. 특히, 조인트의 위치 한계를 해결함에 있어서, WLS가 영 공간(Null Space) 기반 접근법에 비해 효과적이다.22 제안된 원격조작 보조 기법의 성능은 수중 케이블 유지보수에 대한 실험적 연구를 통해 검증하였다. 실험에는 KnR Systems에서 개발한 수중 매니퓰레이터, UW3가 이용하였으며, 실험 결과의 통계적 분석을 통해 제안한 어시스턴스 기법의 성능을 기존 원격조작 방법과 비교하였다.
2. URI-T, 해저 케이블 매설 로봇
URI-T는 해저 케이블 및 소구경 파이프의 매설 작업 및 유지보수 작업을 수행하기 위해 개발 중인 중작업용 수중로봇이다. URI-T의 모습을 Fig. 1에 도시하였으며, 대략적인 사양을 Table 1에 나타냈었다. URI-T는 수심 2,500 m의 해저에서도 작업이 가능하도록 설계되어 있으며, 워터젯 시스템을 이용하여 케이블을 매설하는 작업과 매니퓰레이터 및 작업 공구를 이용하여 케이블 유지보수 작업을 수행할 수 있다. 또한, URI-T는 작업 공구 및 장치를 추가하거나 변경함으로써, 다양한 수중 작업에 활용 가능하다.
2.1. URI-T의 구성 및 주요 특징
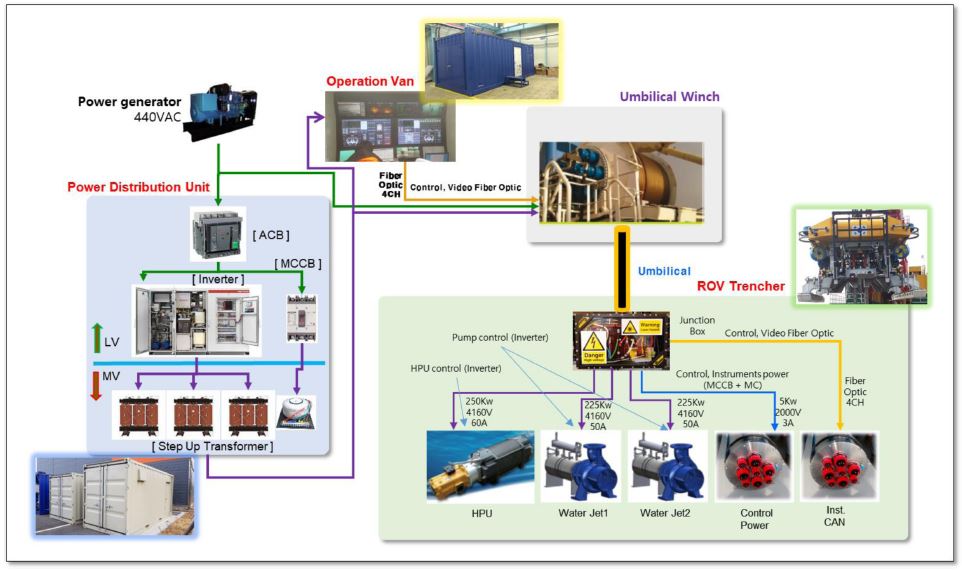
URI-T의 구성도를 Fig. 2에 도시하였다. Fig. 2에서 알 수 있듯이, URI-T는 운영시스템과 전원공급시스템, 엄빌리컬 케이블 및 윈치, 그리고 ROV 본체로 구성된다. 운영 시스템은 ROV를 운용하는 선박에 배치되며, ROV를 조작을 위한 운영 콘솔을 포함한다. 운영 콘솔은 두 개가 배치되어 있으며, 두명의 오퍼레이터가 협업하여 ROV를 조작할 수 있다. 전원 시스템 역시 운용 선박에 배치되어 ROV가 동작하는데 필요한 전원을 공급한다. 선상 운용 시스템과 전원 공급 시스템은 각각 컨테이너 형태로 개발되었으며, 선박에 쉽게 탑재할 수 있다. 엄빌리컬 케이블은 ROV 운용에 필요한 통신 및 전력을 ROV에 공급하는 역할을 한다. 현재, 수심 500 m급까지 활용할 수 있는 엄빌리컬 케이블 및 윈치가 개발된 상태로, 향후 2,500 m급까지 운용 가능한 엄빌리컬 윈치를 개발할 예정이다. ROV 본체는 엄빌리컬 케이블을 통해 전원 및 통신을 공급받아서 해저 면에서 작업을 수행하는 역할을 한다. ROV에는 이동 및 작업 수행을 위한 장비들을 포함하고 있다. 주요 특징을 조금 더 상세히 설명하면 다음과 같다.
HPU: HPU (Hydraulic Power Unit)는 전기 동력을 유압 동력으로 변환하여 각종 유압구동기를 구동하기 위한 구동력을 생성하는 역할을 한다. URI-T는 333마력의 HPU를 탑재하고 있으며, 이를 통해 각종 유압장비들을 구동한다. URI-T에 탑재된 유압 장비를 예를 들면, 추진기, 워터젯 모션베이스, TSS 핸들러, 매니퓰레이터, 작업공구(케이블커팅장치 및 케이블그리핑장치) 등을 들 수 있다. 각 유압 장비는 아래에서 조금 더 상세히 설명하도록 한다.
로봇 이동을 위한 시스템: URI-T의 이동 동작은 로봇에 포함된 추진기를 이용하여 수행된다. URI-T는 수평 추진기 4기 및 수직 추진기 4기 등, 총 8기의 추진기를 장착하고 있다. 각 추진기는 유압으로 구동되며, 기당 약 1 tonf의 추진력을 발생시킬 수 있다. Fig. 3은 수직 추진기를 작동 시키는 모습을 도시한 그림이며, 이를 통해 각 추진기의 추력 수준을 예상해 볼 수 있다. 추진기의 조합을 통해 전후, 좌우, 상하의 이동 모션과, 헤딩, 피칭 등의 회전 모션 등을 인가할 수 있다. 이러한 모션을 조작하기 위해 선상 운용 시스템에서는 기본적으로 조이스틱으로 지령을 내릴 수 있으며, 그 외에도 지정된 방향으로 일정한 추진력을 발생시키는 트림 기능과, 자동헤딩제어, 자동수심제어 등이 구현되어 있다. 또한, 수중에서의 ROV의 위치를 파악하기 위해, USBL (Ultra Short Base Line), DVL (Doppler Velocity Log), IMU (Inertial Measurement Unit), 수심 센서를 포함한 다양한 항법 센서와 항법 알고리즘이 구축되어 있다.
요약하면, URI-T는 수중에서 운용 시, 항법 센서를 통해 로봇의 위치를 파악하여, 추진기 시스템을 이용하여 원하는 위치로 이동시키게 된다.
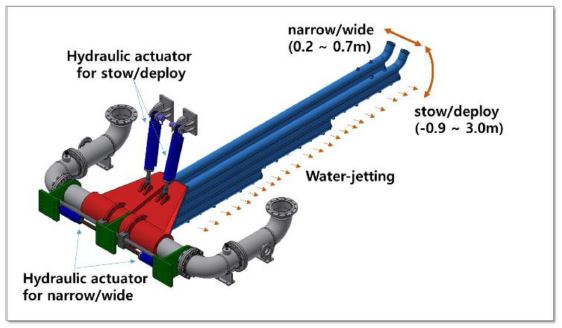
해저 케이블 매설 작업을 위한 시스템: 해저케이블 매설 작업을 위해서는 케이블의 위치를 파악할 필요가 있다. URI-T는 해저 케이블의 위치를 파악하기 위한 센서를 포함하고 있는데, TSS350과 TSS440 등 두 종류를 탑재하고 있다. TSS350은 해저 케이블에 인위적으로 인가된 신호를 탐지하는 방식이며, TSS440은 자성을 감지하는 방식이다. Fig. 1에서 확인할 수 있듯이, TSS350은 ROV 본체에 고정되어 있으며, TSS440은 TSS 핸들러에 장착되어 사용할 때 펼치거나 사용하지 않을 때 접을 수 있다(Fig. 1은 TSS 핸들러를 접은 모습임). URI-T는 해저케이블 매설 작업을 수행하는 장비인 워터젯 시스템을 장착하고 있다. 워터젯 시스템은 고압을 물을 분사함으로써 해저 면을 파는 역할을 수행하며 이를 통해 케이블을 매설하게 된다. 워터젯 시스템은 두 기의 워터 펌프를 포함하며, 각각의 워터 펌프는 300마력의 출력으로 시간당 986 m3의 물을 9 bar의 압력으로 분사할 수 있다. 워터 펌프를 통해 공급되는 물은 제팅암의 노즐을 통해 고압으로 분사된다. Fig. 1에서 워터펌프 및 제팅암의 모습을 확인할 수 있다. 또한, 워터젯 시스템은 제팅암의 배치 및 조작을 위한 모션베이스를 포함하고 있다. 오퍼레이터는 모션베이스를 이용하여 제팅암의 폭과 펼침 수준을 조절할 수 있다. Fig. 4에 워터젯 시스템 도시하였으며, 제팅암, 모션베이스의 구성 및 동작 방식을 확인할 수 있다.
해저케이블 유지보수를 위한 시스템: URI-T에는 해저케이블 유지보수를 위한 기능을 포함하고 있다. 이를 위한 장비로는 유압 매니퓰레이터와 케이블 커팅 장치, 케이블 그리핑 장치 등이 있으며, 각 장치의 모습을 Fig. 5에 도시하였다. Fig. 5에는 케이블커팅장치를 이용하여 절단 실험을 수행한 케이블의 모습도 함께 도시되어 있는데, 직경 약 40 m의 전선이 깔끔하게 절단된 모습을 확인할 수 있다.
2.2 URI-T의 개발 현황
URI-T는 시스템 개발 및 기능 구현이 거의 마무리되고 있는 상태이며, 연근해 시험 및 실해역 시험을 통해 작업 성능을 검증하는 과정을 마쳤다. 특히, 최대 매설 심도와 최대 매설 속도, 최대 전진 속도 등이 Table 1의 사양을 만족하는지 중점적으로 검증되었다. 작업 수심의 경우, 수심 500 m수준의 실해역 시험을 통해 검증되었으며, 추후 수심 2,500 m급의 엄빌리컬 윈치를 개발한 후에 더 깊은 심해에서의 작업 성능을 검증할 예정이다. Fig. 6과 Fig. 7은 각각 연근해 시험과 실해역 시험의 결과를 나타낸 그림이다. Fig. 6에서는 연근해 시험 시 1 m 깊이로 매설한 결과와 로봇팔을 이용한 케이블 유지보수 작업을 도시하였으며, Fig. 7에서는 수심 500 m실해역 시험에서 3 m 깊이의 매설 작업 후 그 결과를 탐사하는 모습을 나타낸다. 연근해 시험과 실해역 시험에서는 목표로 하는 작업 성능의 검증 외에도 케이블 유지보수 작업에 대한 검증 및 장거리 매설 작업을 통한 매설 작업성의 검증 등 다양한 검증 실험이 이루어졌다.
연근해 시험과 실해역 시험을 통한 성능 검증 결과는 URI-T가 기존의 해외 상용 수중 로봇과 유사한 수준의 작업 성능을 확보했음을 의미한다. URI-T는 앞으로 추가 실해역 시험을 통한 성능 검증과 작업 현장 투입을 통한 트랙 레코드 확보를 목표로 계속해서 연구개발을 진행할 예정이다.
URI-T의 개발은 작업 수행 능력의 확보 및 검증과 실용화를 위한 개발 외에도, 작업 효율 향상을 위한 연구도 병행되고 있다. 예를 들어, 로봇 매니퓰레이터를 이용한 케이블 유지보수 작업의 효율성 향상을 위해 원격조작 어시스턴스 기술을 개발하고 있다. 이 기법은 오퍼레이터가 카메라 영상의 목표물 위치를 터치스크린을 이용하여 입력하면 목표물의 위치를 추정하여 매니퓰레이터를 목표물로 이동시켜 주는 기술로서, 매니퓰레이터 작업 효율을 증대에 도움이 될 것으로 기대된다. 3 - 4장에서는 원격조작 어시스턴스 기술에 대한 알고리즘 및 시험 결과를 상세히 다루도록 한다.
3. 터치스크린 입력을 사용한 위치 추정
이 장에서는 터치스크린 입력을 이용하여 목표물의 위치를 추정하는 기술에 대해 서술한다. 이를 위해, 먼저 ROV에 두 대의 카메라가 설치되어 서로 다른 각도에서 목표물을 바라보는 영상을 확보할 수 있다고 가정한다. 또한, 운영 룸에는 터치스크린이 설치되어 오퍼레이터가 조작 명령을 입력할 때 활용할 수 있다고 가정한다. 통상적으로, ROV 시스템에는 매니퓰레이션 작업을 위해 다수의 카메라가 장착되어 있으며, 조작 편의성을 향상 시키기 위해 터치스크린이 많이 활용되고 있는 추세이다. 따라서, 위의 가정은 현실적이라고 할 수 있다.
3.1 터치스크린 입력 설정
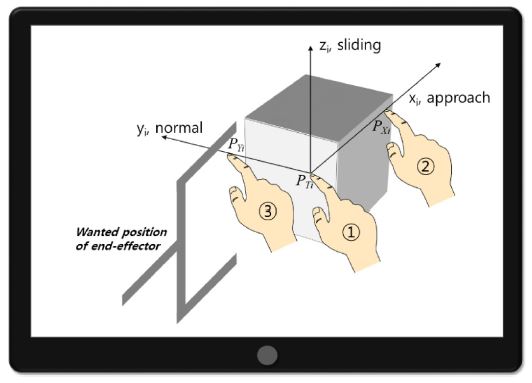
제안하는 위치 추정 기법은 각 카메라의 영상에서 세 개의 점 정보(두 대의 카메라 영상에서 총 여섯 개의 점 정보)를 활용한다. Fig. 8은 제안된 기법에서 사용하는 터치 입력 정보를 나타내며, 다음과 같다.
- ①, 목표물의 중심점,PTi
- ②, 접근 방향 위의 점,PXi
- ③, 법선 방향 위의 점,PYi
여기서, i (= 1, 2)는 카메라 번호를 의미한다. 각각의 터치 입력 정보들은 카메라 영상 좌표계 상의 이차원 위치 정보를 포함한다.
3.2 목표물의 위치 추정
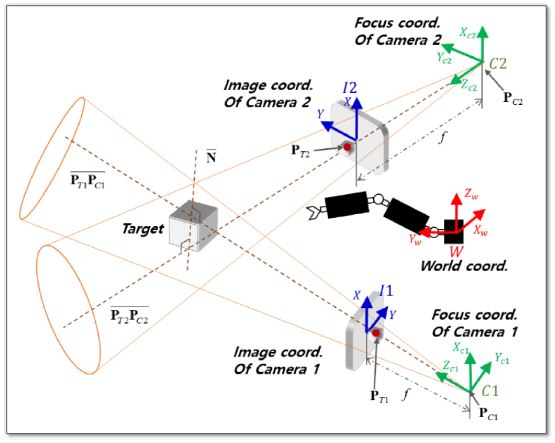
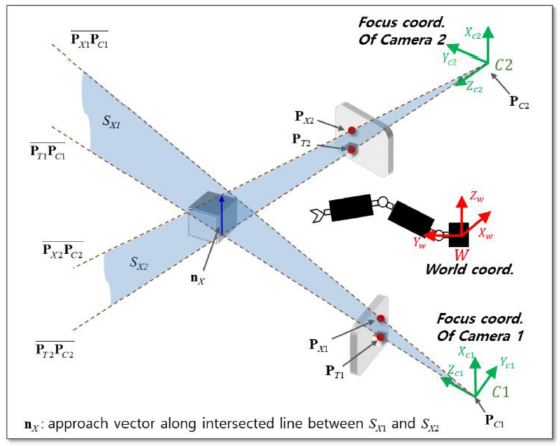
Fig. 9에 목표물의 위치 추정을 위한 개념도를 나타내었다. Fig. 9에는 목표물 위치 추정에 사용된 좌표계도 함께 도시되어있다. 월드 좌표계 W와 영상 좌표계 Ii 간의 상대 위치는 매니퓰레이터와 카메라의 배치 위치에 따른 기하학적 관계에 의해 주어진다. 카메라 초점 좌표계 Ci의 위치는 각 카메라의 위치 Ii 와 카메라의 초점거리 f에 의해 결정된다. 카메라의 초점거리는 캘리브레이션 툴을 활용하여 쉽게 확인할 수 있다. 이 연구에서는 Microsoft 사의 웹캠 HD_3000모델을 사용하였으며, 이 카메라의 초점 거리는 fx = 617.88 mm, fy = 625.32 mm이다.
좌표계 사이의 관계를 사용하여 월드 좌표계에 대한 초점 좌표의 PCi원점 을 구할 수 있다(표현의 편의를 위해, 벡터 표현시 월드 좌표계에 대한 표식은 생략한다: •가 임의의 벡터일 때,• ≡W •). 또한, 영상 좌표계 상의 목표물 중심점 정보(Fig. 8에서 ①번 정보) 는 카메라 초점 좌표계에 대해 다음과 같이 나타낼 수 있다.24
| (1) |
식(1)의 목표물 위치는 좌표 변환을 통해 월드좌표계에 대해 표현할 수 있으며, 식(2)와 같다.23,24
| (2) |
여기서, 은 월드 좌표계 W에 대한 카메라 초점 좌표계 Ci의 회전 행렬을 나타낸다. 목표물의 위치 PTi와 카메라 초점 위치 PCi가 파악 되었으므로, 두 점을 연결하는 직선의 방정식을 식(3)과 같이 구할 수 있다.
| (3) |
여기서, t = [x, y, z]T는 위치 벡터, αi는 독립 변수를 나타낸다. i = 1, 2임을 고려할 때, 식(3)은 두 개의 독립적인 직선을 나타내며, Fig. 9에 도시된 바와 같다.
식(3)의 두 직선에 대해 근접점(Nearest Point)를 구함으로써, 목표물의 3차원 위치를 구할 수 있다. 근접점은 식(3)의 선들과 수직으로 접하는 직선을 파악하고 서로간의 교점을 이용하여 구할 수 있다. 식(3)의 두 직선에 대해 수직인 벡터는 식(4)와 같다.25
| (4) |
따라서, 식(4)의 벡터에 평행한 직선방정식은 식(5)와 같이 얻을 수 있다.
| (5) |
여기서, β는 독립 변수이고 D는 오프셋 벡터이다. 식(3)과 식(5)로 주어진 직선 간의 교점을 구하기 위한 제약 조건은 식(6)과 식(7)과 같이 주어진다.
| (6) |
| (7) |
여기서, 는 각각 교점에서의 αi와 βi의 값을 나타낸다. 식(7)에서 식(6)을 뺀 방정식을 재구성하면 식(8)과 같이 를 구할 수 있다.
| (8) |
여기서, U ≡ [PT1 − PC1, PC2 − PT2, N]이다. 식(3)에 식(8)의 를 대입함으로써, 식(3)과 식(5)에 나타낸 직선 간의 교점들을 구할 수 있다. 또한, 교점들의 평균값을 이용하여 목표물의 위치를 추정할 수 있으며, 식(9)와 같다.
| (9) |
3.3 목표물의 자세 추정
Fig. 8에서 설명한 세 개의 터치 입력 정보(두 개 카메라 영상에 대해 전체 여섯 개 정보)를 이용하여 목표물의 자세를 추정할 수 있다. 회전 행렬의 접근 벡터(nX)는 PTi와 PXi, 법선 벡터(nY)는 PTi와 PYi를 이용하여 추정할 수 있다.
제안하는 접근 벡터 추정 기법의 개념도를 Fig. 10에 도시하였다. 그 방법을 요약하여 설명하면, i) i = 1,2에 대해, 직선 를 구하는 단계, ii) i = 1,2에 대해, 앞서 구한 직선을 포함하는 평면 SXi를 구하는 단계, iii) 앞서 구한 평면 (i = 1, 2에 대해 두 개의 평면)의 교직선의 방향을 얻는 단계로 구분된다.
의 직선방정식은 식(3)으로 주어진다. 또한, 식(3)을 유도한 방법과 유사한 방법을 사용하여, PXi와 PCi를 지나는 직선을 식(10)과 같이 얻을 수 있다.
| (10) |
여기서, γi는 독립 변수를 나타낸다.
이제, 를 포함하는 평면의 방정식을 구해보도록 하자. 먼저, 두 직선에 수직인 벡터를 식(11)과 같이 계산할 수 있다.
| (11) |
따라서, 직선 를 포함하는 평면의 방정식은 식(12)와 같이 구할 수 있다.
| (12) |
여기서 이다.
식(12)의 평면에 대해 수직인 벡터의 외적을 취함으로써, 두 평면이 교차하는 직선의 방향을 구할 수 있으며, 그 결과는 식(13)과 같다.
| (13) |
식(13)을 정규화함으로써 접근 벡터를 구할 수 있으며, 그 결과는 식(14)와 같다.
| (14) |
식(14)에는 부호 함수(sgn())가 사용되었는데, 이것은 접근 벡터가 (PX1 − PT1)와 반대 방향을 가리키는 것을 방지하기 위함이다.
법선 벡터(nY)는, PXi 대신에 PYi를 이용하고 식(10)부터 식(14)까지의 절차를 반복함으로써 추정할 수 있다. 그리고, 접근 벡터와 법선 벡터를 이용함으로써, 목표물의 자세를 나타내는 회전 행렬을 식(15)와 같이 구할 수 있다.
| (15) |
3.4 목표물 접근 시 안전 거리 확보 방안
목표물의 위치 및 자세가 정확히 추정되었을 때, 목표물 위치로 매니퓰레이터가 움직인다면, 매니퓰레이터의 말단 장치는 목표물과 충돌하게 된다. 따라서, 매니퓰레이터가 목표물로 접근할 때, 목표물과 말단 장치 사이에는 적절한 이격 거리가 고려되어야 한다. 이격 거리가 고려된 목표물의 위치는 식(16)과 같이 표현할 수 있다.
| (16) |
여기서, TL은 말단 장치 좌표계에 대한 이격 거리 벡터를 나타낸다. 예를 들어서, 이격 거리의 방향은 Fig. 8에서 접근 방향의 반대 방향으로 설정하는 것을 고려할 수 있는데, 이 경우, L = [−l, 0, 0]로 설정할 수 있다. 여기서, l은 접근 방향으로의 이격 거리를 나타낸다.
4. 수중 매니퓰레이션을 위한 원격조작 보조 기술
4.1 제어 구조
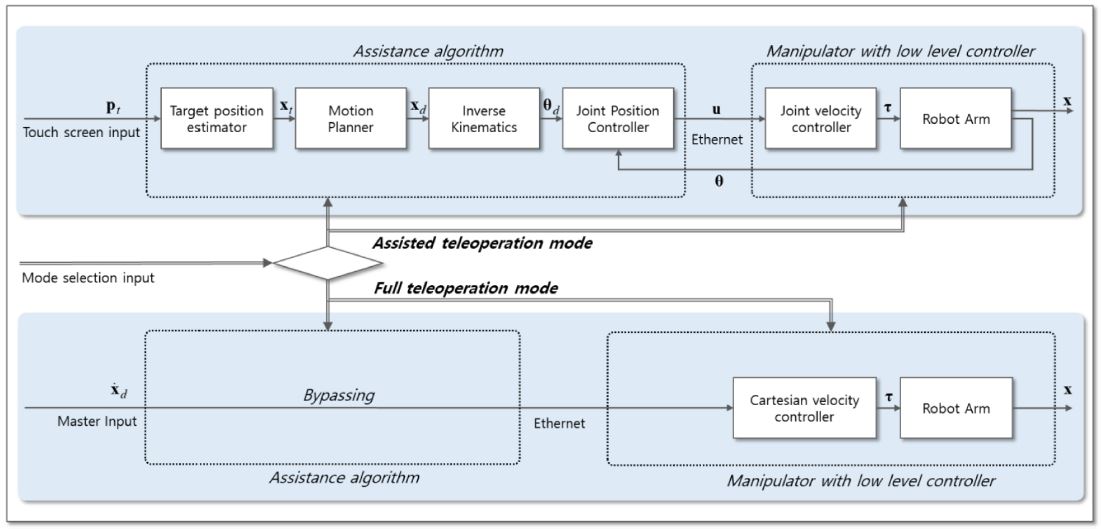
제안된 원격조작을 위한 전반적인 제어 구조는 Fig. 11에서 표현한 바와 같다. Fig. 11에 도시한 바와 같이 오퍼레이터는 모드 선택 입력을 통해 완전 원격조작 모드(Full Teleoperation Mode)와 원격조작 어시스턴스 모드를 선택하여 운용할 수 있다. 완전 원격조작 모드는 통상적인 조작 방법으로, 오퍼레이터가 매니퓰레이터의 모든 조인트를 원격조작하는 모드를 말한다. 원격조작 어시스턴스 모드는 본 연구에서 제안된 어시스턴스 기법을 적용한 모드이며, 오퍼레이터가 카메라 영상에 수 회의 터치 입력함으로써 매니퓰레이터를 조종할 수 있는 모드이다.
Fig. 11에 나타낸 두 모드에서, 제어 구조는 어시스턴스 알고리즘과 저수준 제어기를 가진 매니퓰레이터 등 두 파트로 분리할 수 있다. 원격조작 어시스턴스 모드에서 어시스턴스 알고리즘은 논문에서 제안된 구조로 구성된다. 반면, 완전 원격조작 모드는 오퍼레이터의 조종 신호가 어시스턴스 알고리즘을 거치지 않고 직접 저수준 제어기를 가진 매니퓰레이터로 입력된다. 통상적으로, 수중 매니퓰레이터에는 저수준 제어기가 포함되어 있으며, 이 연구에 사용 된 KnR Systems의 UW3는 조인트 속도 제어와 카테시안 속도 제어를 제공하는 저수준 제어기가 포함되어 있다.
Fig. 11에서 도시된 바와 같이, 원격조작 어시스턴스 알고리즘은 몇 가지 블록으로 구성되어있다. ‘Target Position Estimator’는 오퍼레이터에 의한 터치스크린 입력을 이용하여 목표물의 6 자유도 위치 정보를 추정하는 블록으로, 알고리즘은 3장에서 제안된 바와 같다. ‘Motion Planner’는 직교좌표계상에서 매니퓰레이터의 현재 위치부터 목표물 위치까지 실시간 경로를 생성 및 계산한다. ‘Inverse Kinematics’는 조인트 직교좌표계의 경로를 조인트 공간 경로로 변환한다. ‘Joint Position Controller’는 매니퓰레이터가 포함하는 조인트 속도 제어기에 피드백을 추가함으로써, 조인트 위치제어기를 구현한다.
4.2 경로 계획
Fig. 11에서 나타낸 것처럼, ‘Motion Planner’ 블록은 직교 좌표계 상의 매니퓰레이터의 현재 위치 x에서 목표물 위치 xt까지의 부드러운 경로를 생성한다. 경로 생성 알고리즘으로서 5차 다항식 기법23을 사용하였으며, 이 기법은 궤적의 2차 미분치(가속도)까지 연속성을 보장하는 방법이다. 5차 다항식 기법의 궤적은 식(17)과 같이 주어진다.
| (17) |
여기서,aj(j = 0,...,5)는 궤적의 계수를 나타내며, t는 진행 시간을 나타낸다. 계수 aj는 경계 조건(), 시작 시간(t0), 종료시간(tf) 등이 주어지면 결정할 수 있다.23 경계 조건의 경우, 현재 위치 x는 로봇의 자세를 측정함으로써 알 수 있으며, 그 미분치는 수치 미분을 통해 계산할 수 있다. 목표물의 위치 xt는 Fig. 11에 도시된 ‘Target Position Estimator’에 의해 추정되며, 그 미분치는 로 설정함으로써 목표물 위치에서 부드럽게 정지하도록 했다. 시작 시간(t0)은 xt가 주어지는 시간으로 설정할 수 있다. 마지막으로, 궤적 이동 소요 시간 dt가 결정되면, tf = t0+ dt 와 같이 종료 시간을 설정할 수 있으며, 식(17)에서의 기준 궤적을 결정할 수 있게 된다. 궤적 이동 소요 시간은 식(18)과 같이 설계했다.
| (18) |
여기서, 는 평균 속도 한계 값을 나타내며, 사용자가 설계하는 값이다. 궤적 이동 소요 시간을 식(18)과 같이 설정할 경우, x의 각각 요소에 대한 평균 속도가 이하로 제한된다. 여기서, 는 로봇 각 조인트의 속도 한계 값을 고려하여 설계되어야 한다. 그러나, 모든 경우에 대해 를 조정하여 조인트 속도가 한계 값을 넘지 않도록 설계하는 것은 어렵다. 그 이유는, 을 통해 평균 속도 한계를 설계할 수 있을 뿐, 최대 속도 한계를 설정 할 수 없기 때문이다. 더욱이, 직교좌표계상에서 속도와 조인트 속도의 관계는 자코비안에 의해 결정되는 비선형관계를 가진다. 따라서, 직교좌표계상의 속도 한계 값을 설정함으로써 조인트 공간의 속도 한계를 제한하는 것은 어려움이 따른다. 조인트 속도가 한계 값을 넘는 것을 막기 위해서는 추가적인 방법이 마련되어야 하며, 다음절에서 설명할 역기구학에서 고려되었다.
4.3 WDLS (Weighted Damped Least Square) 기반 역기구학
추정 알고리즘에 의해 목표물의 위치가 주어질 때, 추정된 위치는 기구학적 한계를 벗어날 수 있다. 따라서, 역기구학은 이러한 경우에도 안정적으로 동작할 수 있어야 한다. 본 논문에서는 매니퓰레이터가 갖는 작업 영역 한계 및 특이성 이슈와 조인트 위치 및 속도 제한 등을 고려한다
본 연구에서는 WDLS13-15를 활용하여 앞서 언급한 한계 상황을 해결하였다. 즉, DLS 를 통해 작업 영역과 특이성 문제를 해결하였으며, WLS를 적용하여 조인트 위치 및 속도 제한 값을 넘지 않는 역기구학 해를 도출할 수 있다.
WDLS는 가중치가 고려된 자코비안을 이용하여 수치적으로 역기구학을 구하는 기법이다. 직교 좌표 공간 위치 x∈ℜn 및 조인트 공간 위치 θ∈ℜm 사이의 관계는 식(19)와 같이 주어진다.23
| (19) |
여기서, 은 직교 좌표계 상의 말단 장치의 속도 벡터를 나타낸다. 는 조인트 공간상의 속도 벡터이며, J∈ℜn×m는 자코비안 행렬이다. 양의 정치 행렬 W∈ℜm×m를 도입하면, 식(19)를 식(20)과 식(21)과 같이 표현할 수 있다.22
| (20) |
| (21) |
기구학 문제에 대한 비용 함수를 식(22)와 같이 결정할 수 있다.10
| (22) |
여기서, 은 최소화하고자 하는 추가 비용 함수 h(θ)의 음의 경사 벡터로 식(23)과 같이 표현된다.
| (23) |
식(22)를 최소화하는 해는 식(24)와 같이 구해진다.
| (24) |
여기서, 는 JW의 감쇠 역행렬을 나타낸다. 의 정의는 식(25)와 같이 주어진다.
| (25) |
식(24)와 식(21)로부터 식(26)과 같이 WDLS 해를 얻을 수 있다.
| (26) |
식(26) 및 식(24)의 WDLS 해는 λ, W, h(θ)등, 세 개의 설계 인자를 포함하고 있으며, 이 설계 인자를 적절히 결정함으로써, 역기구학을 설계할 수 있다.
감쇠 설계 인자 λ를 적절히 설계함으로써, 특이점 이슈를 해결할 수 있다. 의 역은 J가 특이점일 때 정의되지 않는다. 이때, λ를 0이 아닌 값으로 설계하면 식(25)의 유사역행렬을 계산할 수 있다. 단, 상수 λ를 사용하면 사이에 정확한 역관계가 성립하지 않기 때문에 기구학 해가 왜곡될 수 있다. 역기구학의 정확성을 위해, λ는 식(27)과 같은 특이점 부근에서만 사용해야 한다.15
| (27) |
여기서, σmin은 JW의 최소 특이값을 나타내며, λmax는 λ의 최대값, η는 특이 영역의 경계 값을 나타낸다. λmax와 η를 적절하게 설계함으로써, JW의 특이점 이슈를 해결할 수 있으며, 또한 특이 영영이 아닐 때의 역기구학의 정밀도를 유지할 수 있다.
가중치 행렬 W은 매니퓰레이터의 각 조인트 상태가 한계 값을 넘어가는 것을 방지하는데 이용될 수 있다.18 본 논문에서는, 위치 한계와 각 조인트의 속도 한계를 고려하였으며, W는 식(28)과 같이 설계하였다.
| (28) |
여기서, WPL ∈ℜm×m은 조인트 위치 한계를 위한 가중 행렬을 나타내며, WVL ∈ℜm×m는 조인트 속도 한계를 위한 가중 행렬을 나타낸다. WPL 및 WVL의 각 요소를 설계하기 위해, 식(29)와 같이 비용 함수를 설계 한다.
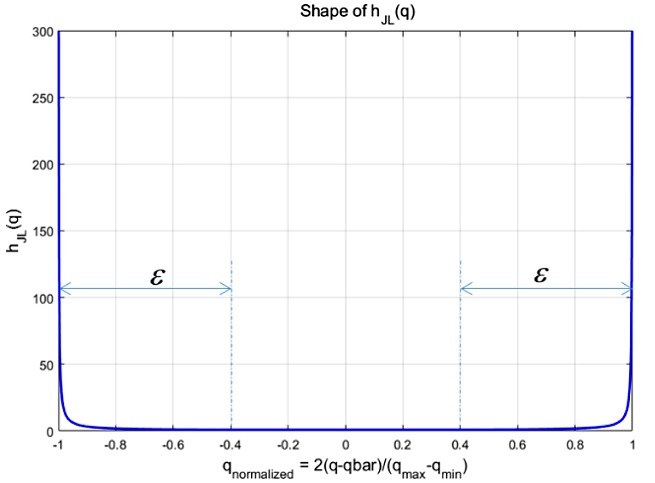
| (29) |
여기서, q는 입력 변수, qmin 및 qmax는 각각 q의 최소값과 최대값, ε은 한계 지역의 경계 값을 나타낸다. Fig. 12에 도시된 바와 같이, 식(29)는 q가 한계 지역에 있지 않을 경우 일정한 값을 유지하다가, 한계 지역에 있을 경우 급격하게 증가하는 함수이다. 식(29)를 이용하여, WPL과 WVL를 설계할 수 있으며, 식(30)과 같다.
| (30) |
가중 행렬의 대각 요소값은 식(29)를 이용하여 식(31)과 같이 설계할 수 있다.
| (31) |
h(θ)를 설계함으로써, JW의 영 공간을 사용하여 추가 비용 함수를 최적화 할 수 있다. n = m 및 λ = 0일 때, 가 되어 영 공간이 존재하지 않기 때문에, h(θ)는 기구학적 솔루션에 영향을 줄 수 없다. 그러나, λ ≠ 0인 경우, (25)의 의 정확한 역수가 될 수 없기 때문에 영 공간이 존재한다. 따라서 n = m일 경우에도 h(θ)를 이용하여 특이점 근처에서의 역기구학 해를 조정할 수 있다. h(θ)는 매니퓰레이터가 선호되는 자세에 가까운 자세를 갖도록 설계할 수 있으며, 예를 들어, 선호하는 자세를 조인트 위치 제한과 거리가 먼 자세로 설정할 수 있는데, 식(32)와 같다.
| (32) |
여기서, i = 1,...,m이며, θi는 θ의 요소 값을 나타내며, θi,max와 θi,min는 각각 θi의 최대값과 최소값, 는 θi,max와 θi,min의 중간 값을 나타낸다.
4.4 조인트 위치 제어기
로봇의 말단 장치를 추정된 목표물의 위치로 이동 시키려면 위치 제어기가 필요하다. 만약, 매니퓰레이터의 저수준 제어기가 속도 제어만 제공한다면, 적절한 피드백을 추가하여 위치 제어가 적절히 구현되도록 할 필요가 있다. 이런 경우를 대비하여, 어시스턴스 알고리즘에는 조인트 위치 제어기가 포함되어 있다. 위치 제어기는 피드포워드 속도 명령과 P타입 피드백 제어를 사용하여 식(33)과 같이 간단한 구조로 설계하였다.
| (33) |
여기서, u는 저수준 제어기에 입력되는 가공된 속도 명령을 의미하며, KP는 게인 행렬이다. 많은 경우, 매니퓰레이터에 포함된 저수준 속도 제어기는 PI 타입 제어로 설계되며 식(34)와 같이 표현된다.
| (34) |
여기서, QP와 QI는 각각 비례 게인 행렬과 적분 게인 행렬을 나타낸다. 식(35)을 식(34)에 대입하여 정리하면, 두 제어기의 조합이 식(35)와 같은 PID 제어기로 동작함을 확인할 수 있다.
| (35) |
여기서, e ≡ θd − θ이다.
5. 실험을 통한 어시스턴스 알고리즘의 성능 검증
이 장에서는 수중 매니퓰레이터 UW3를 이용한 원격 조작 시험을 통해, 제안한 어시스턴스 알고리즘의 성능을 검증하였다. 검증 방법은 URI-T를 이용하여 해저케이블을 유지보수하는 작업을 수행하는 상황을 설정하였으며, 이를 모사한 환경을 구축하여 실험하였다.
5.1 작업
해저케이블의 유지보수를 위해 케이블에 그리핑 장치를 배치하는 작업을 모사하여 실험을 수행하였다. Fig. 5에 도시된 바와 같이, 그리핑 장치는 ROV 본체의 버켓에 장착되어 있으며, 필요시 매니퓰레이터를 이용해 케이블 위에 배치한 후 그리핑 작업을 수행하게 된다. 그리핑을 위한 매니퓰레이션 과정을 조금 더 상세히 설명하면 다음과 같이 구분된다.
- Approaching: 버켓에 있는 그리핑 장치에 접근
- Seizing: 로봇팔로 그리핑 장치 손잡이 잡기
- Moving: 그리핑 장치를 케이블 위로 옮긴 후 배치하기
Table 2에서 그리핑 장치 배치 작업들을 상세하게 설명하였다. 각 단계는 매니퓰레터 말단 장치의 상태를 이용하여 구분하였다. 예를 들면, 말단 장치가 닫힌 상태에서 ‘Approaching’ 단계를 진행한 후 오퍼레이터가 말단 장치를 열어서 그리핑 장치의 손잡이를 잡기 위한 단계를 시작하면, ‘Approaching’ 단계가 끝나고, ‘Seizing’ 단계를 시작한 것으로 판단한 것이다. 말단 장치의 개폐 여부는 토글스위치에 의해 간단하게 조작되기 때문에, 개폐를 위한 조작 시간은 무시할 수 있다. Table 2에서 설명되어있는 것과 같이, 어시스턴스 알고리즘은 매니퓰레이터를 크게 움직이는 동작(Gross Motion)에만 적용하였다. 그리핑 장치를 잡기 위한 정교한 매니퓰레이터 조작은 작업 대상물과 매우 근접하여 진행되기 때문에 충돌 등 위험한 상황이 발생할 수 있으며, 따라서 완전 원격조작을 통해 진행하였다.
5.2 실험 환경
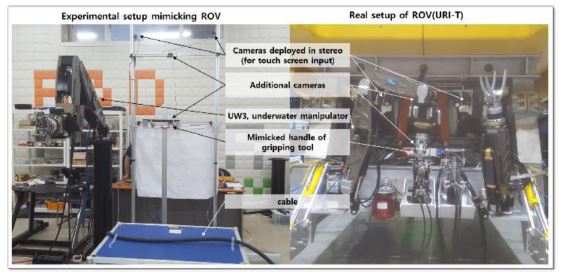
어시스턴스 알고리즘의 성능 검증을 위한 실험 환경을 Fig. 13에 도시하였다. Fig. 1에 도시된 URI-T의 구성을 모사하여 실험 환경을 구축하였으며, 안전 이슈를 고려하여 그리핑 장치는 손잡이 부분을 모사한 장치로 대체하였다.
5.3 실험 방법
임상 평가를 통해, 제안된 어시스턴스 알고리즘의 성능 검증을 진행하였다. 그리고, 그 결과를 기존의 완전 원격조작의 결과와 비교하였다. 성능 지표는 작업 수행에 소요된 시간으로 설정했다.
다섯 명의 피실험자(나이: 27 - 40세)가 이 연구에서 참가했다. 각 실험자는 각각 2회의 실험을 수행하였으며, 총 10개의 실험 결과를 확보하여 통계적인 방법을 통해 분석하였다. 통계적 분석은 Paired-T 기법26을 적용하여 작업 소요 시간 비교에서 유효한 차이가 발생했는지 여부를 판단하였으며, 유의성 판단을 위한 P-Value 기준은 0.05를 적용했다.
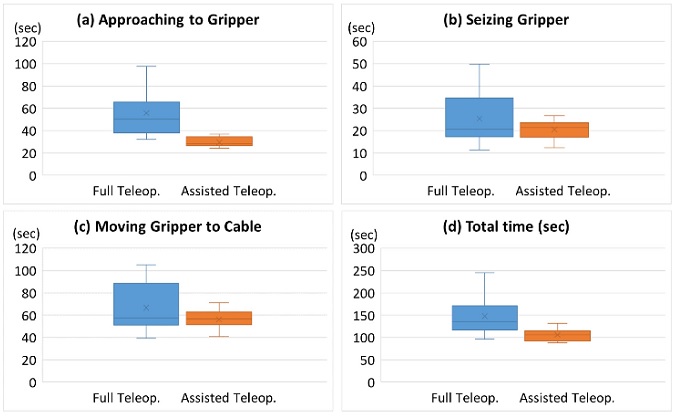
5.4 실험 결과
Fig. 14와 Table 3에 실험 결과를 정리하였다. Table 3으로부터, ‘Approaching’ 단계의 경우, 어시스턴스 알고리즘을 적용한 경우가 기존 원격조작에 비해 작업 시간이 평균 47.0% 감소한 것을 알 수 있다. 이 때의 P-Value는 0.0013으로 0.05 이하이며, 따라서, 작업시간의 차이는 통계적으로 유효함을 알 수 있다. 이 결과는 어시스턴스 알고리즘이 작업 시간을 단축시키는데 효과가 있음을 의미한다. ‘Seizing’ 단계의 경우, 어시스턴스 알고리즘의 평균 작업 시간은 19.3%로 감소하는 것으로 나타났으나, 통계적으로는 유의미한 차이를 보이지 않았다(p > 0.05). 이 결과는, 두 방법(기존의 완전 원격조작 방법과, 원격조작 어시스턴스 방법) 모두 ‘Seizing’ 단계는 완전 원격조작을 통해 이루어지기 때문이다. Table 2에서 설명한 바와 같이 어시스턴스 알고리즘은 정밀 조작이 필요한 ‘Seizing’ 단계에는 적용하지 않았다. ‘Moving’ 단계의 경우, 어시스턴스 알고리즘을 적용한 경우의 작업 시간이 평균 15.8% 감소하였으며, 이 결과는 통계적으로도 유의함을 보였다(p < 0.05). Table 2에서 설명한 바와 같이, ‘Moving’ 단계에서는 제안한 기법이 어시스턴스 알고리즘을 적용한 부분과 그렇지 않은 부분이 혼합되어 있으며, 따라서 작업 시간이 감소한 수준은 상대적으로 낮게 나타났다. 마지막으로, 전체 작업 소요 시간은 어시스턴스 알고리즘을 적용했을 경우 28.2% 감소하였으며, 이 결과는 통계적으로 유의미한 것으로 나타났다(p < 0.05). 이상의 결과를 통해, 제안한 어시스턴스 기법이 작업 시간을 효과적으로 감소시킬 수 있음을 알 수 있다.
6. 결론
본 논문에서는 해저케이블 매설 작업을 위해 국내에서 개발중인 중작업용 수중 로봇 URI-T의 특징과 개발 현황을 소개하였다. URI-T는 순수 국내 기술로 개발되는 중작업 수중로봇으로 실해역 시험을 통한 작업 성능 검증을 마쳤다. URI-T의 개발을 통해, 해외 소수 기업이 독과점하고 있는 시장에서 국내 기술을 향상 시킬 수 있을 것으로 기대된다.
본 논문에서는 또한, URI-T의 매니퓰레이션 작업 효율성 향상을 위해, 원격조작 어시스턴스 기술을 제안하였다. 특히, 터치스크린 입력을 통한 목표물의 위치 및 자세 추정 기법을 제안하였다. 이 방법은 오퍼레이터로부터 입력 받은 터치 정보를 활용하는 방법으로 기존의 자율 기법에 비해 추정 결과의 신뢰도를 향상시킬 수 있다. 또한, 어시스턴스 기술의 제어 구조를 연구하였다. 제어 구조는 WDLS에 기반한 역기구학을 포함하며, 작업 공간의 제한 및 특이점 이슈, 조인트 위치 및 속도 제한과 같은 기구학적 한계에 대해 적절히 대처할 수 있도록 설계하였다. 이를 통해, 추정된 목표물의 위치가 매니퓰레이터의 한계를 벗어 나더라도 큰 문제 없이 적절한 해를 도출할 수 있도록 설계하였다. 어시스턴스 기법의 성능 검증을 위한 실험 결과는 제안한 기법을 통해 작업 시간 효율을 상당히 개선할 수 있음을 보여준다.
Acknowledgments
이 논문은 해양수산부 재원으로 해양수산과학기술진흥원의 지원을 받아 수행된 연구임(해양개발용 수중건설로봇 사업단, PJT200539).
REFERENCES
- Christ, R. D. and Wernli, R. L., “The ROV Manual: A User Guide for Remotely Operated Vehicles,” Elsevier, 2nd Edition, 2014.
-
Yuh, J., “Design and Control of Autonomous Underwater Robots: A Survey,” Autonomous Robots, Vol. 8, pp. 7-24, 2000.
[https://doi.org/10.1023/A:1008984701078]

- Kwon T. W., Kim, W. K., Yoo, S. H., Lim, H. E., and Jeong, H. W., “Study for Maintenance of HVDC Submarine Cable,” Proc. of Korean Institute of Electrical Engineers Summer Conference, pp. 557-559, 2002.
- Kim, K.-H., Song, Y.-U., Kim, M.-Y., and Kim, M.-E., “Trend of Industry and Standard Related to Offshore Cable for Offshore Wind Farm,” Journal of Wind Energy, Vol. 3, No. 2, pp. 11-17, 2012.
- Choi, K. T., Kim, M. J., “A Study on the Submarine Optical Cable Construction,” Proc. of Communication Science Conference, pp. 246-252, 1997.
- Kang, H. J., Lee, M.–J., Ki, H., Kim, M.–G., Cho, G.R., et al., “URI-T, A ROV for Underwater Cable Burying Tasks: Development and Performance Evaluation through Sea Trial,” Proc. of Korean Marine Robot Technology Society Fall Conference, pp. 63-65, 2018.
-
Dhanak, M. R. and Xiros, N. I., “Springer Handbook of Ocean Engineering,” Springer, 2016.
[https://doi.org/10.1007/978-3-319-16649-0]

-
Hildebrandt, M., Albiez, J., and Kirchner, F., “Computer-Based Control of Deep-Sea Manipulators,” Oceans - MTS/IEEE Kobe Techno-Ocean, pp. 1-6, 2008.
[https://doi.org/10.1109/OCEANSKOBE.2008.4531026]

-
Marani, G., Choi, S. K., and Yuh, J., “Underwater Autonomous Manipulation for Intervention Missions AUVs,” Ocean Engineering, Vol. 36, No. 1, pp. 15-23, 2009.
[https://doi.org/10.1016/j.oceaneng.2008.08.007]

-
Marani, G. and Choi, S. K., “Underwater Target Localization,” IEEE Robotics & Automation Magazine, Vol.17, No. 1, pp. 64-70, 2010.
[https://doi.org/10.1109/MRA.2010.935793]

-
Prats, M., Garcia, J. C., Wirth, S., Ribas, D., Sanz, P. J., et al. “Multipurpose Autonomous Underwater Intervention: A Systems Integration Perspective,” Proc. of Control & Automation 20th Mediterranean Conference, pp. 1379-1384, 2012.
[https://doi.org/10.1109/MED.2012.6265831]

-
Garcia, J. C., Fernandez, J. J., Sanz, P. J., and Martin, R., “Increasing Autonomy Within Underwater Intervention Scenarios: The User Interface Approach,” IEEE International Systems Conference, Vol. 4, pp. 71-75, 2010.
[https://doi.org/10.1109/SYSTEMS.2010.5482454]

-
Cho, G. R., Lee, M.-J., Kim, M.-G., and Li, J.-H., “Inverse Kinematics for Autonomous Underwater Manipulations Using Weighted Damped Least Squares,” Proc. of Ubiquitous Robots and Ambient Intelligence 14th International Conference, pp. 765-770, 2017.
[https://doi.org/10.1109/URAI.2017.7992822]

-
Deo, A. S. and Walker, I. D., “Overview of Damped Least-Squares Methods for Inverse Kinematics of Robot Manipulators,” Journal of Intelligent and Robotic Systems, Vol. 14, No. 1, pp. 43-68, 1995.
[https://doi.org/10.1007/BF01254007]

- Buss, S. R., “Introduction to Inverse Kinematics with Jacobian Transpose, Pseudoinverse and Damped Least Squares Methods,” http://web.cse.ohio-state.edu/parent/classes/694A/Lectures/Material/IKsurvey.pdf (Accessed 14 MAR 2019)
-
Wampler, C. W., “Manipulator Inverse Kinematic Solutions Based on Vector Formulations and Damped Least-Squares Methods,” IEEE Transactions on Systems, Man, and Cybernetics, Vol.16, No. 1, pp. 93-101, 1986.
[https://doi.org/10.1109/TSMC.1986.289285]

-
Nakamura, Y. and Hanafusa, H., “Inverse Kinematics Solutions with Singularity Robustness for Robot Manipulator Control,” Journal of Dynamic Systems, Measurement, and Control, Vol. 108, No. 3 pp. 163-171, 1986.
[https://doi.org/10.1115/1.3143764]

-
Chiaverini, S., Siciliano, B. and Egeland, O., “Review of the Damped Least-Squares Inverse Kinematics with Experiments on an Industrial Robot Manipulator,” IEEE Transactions on Control Systems Technology, Vol. 2, No. 2, pp. 123-134, 1994.
[https://doi.org/10.1109/87.294335]

-
Chiaverini, S., “Singularity-Robust Task-Priority Redundancy Resolution for Real-Time Kinematic Control of Robot Manipulators,” IEEE Transactions on Robotics and Automation, Vol. 13, No. 3, pp. 398-410, 1997.
[https://doi.org/10.1109/70.585902]

-
Whitney, D. E., “The Mathematics of Coordinated Control of Prosthetic Arms and Manipulators,” Journal of Dynamic Systems, Measurement, and Control, Vol. 94, No. 4, pp. 303-309, 1972.
[https://doi.org/10.1115/1.3426611]

-
Hollerbach, J. M. and Suh, K., “Redundancy Resolution of Manipulators Through Torque Optimization,” IEEE Journal of Robotics and Automation, Vol. 3, No. 4, pp. 308-316, 1987.
[https://doi.org/10.1109/JRA.1987.1087111]

-
Chan, T. F. and Dubey, R. V., “A Weighted Least-Norm Solution Based Scheme for Avoiding Joint Limits for Redundant Joint Manipulators,” IEEE Transactions Robotics and Automation, Vol. 11, No. 2, pp. 286-292, 1995.
[https://doi.org/10.1109/70.370511]

- Craig, J. J., “Introduction to Robotics: Mechanics and Control,” Addison-Wesley, 2nd Edition, 1989.
- David, A. F. and Ponce, J., “Computer Vision A Modern Approach,” Pearson Education International, 2nd Edition, 2003.
-
Hartley, R. and Zisseman, A., “Multiple View Geometry in Computer Vision,” Cambridge, 2nd Edition, 2003.
[https://doi.org/10.1017/CBO9780511811685]

- Smith, M. J., “Statistical Analysis Handbook,” The Winchelsea Press, 2018.

Principal Researcher in Marine Robotics R&D Division, Korea Institute of Robot and Convergence. His research interests include underwater robotics; underwater manipulation and control; robust control; nonlinear control, etc.
E-mail: sandman@kiro.re.kr.

Assistant Researcher in Marine Robotics R&D Division, Korea Institute of Robot and Convergence. His research interest is robot vision.
E-mail: hyeonski@kiro.re.kr

Chief Researcher in Marine Robotics R&D Division, Korea Institute of Robot and Convergence. His research interests include underwater robotics; underwater navigation, guidance, and control; nonlinear control, etc.
E-mail: jhli5@kiro.re.kr.