CMP에서 패드 돌기와 산화막 패턴의 접촉 모드에 따른 평탄화 모델링

1. 서론

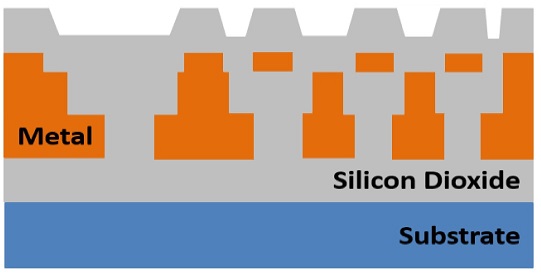
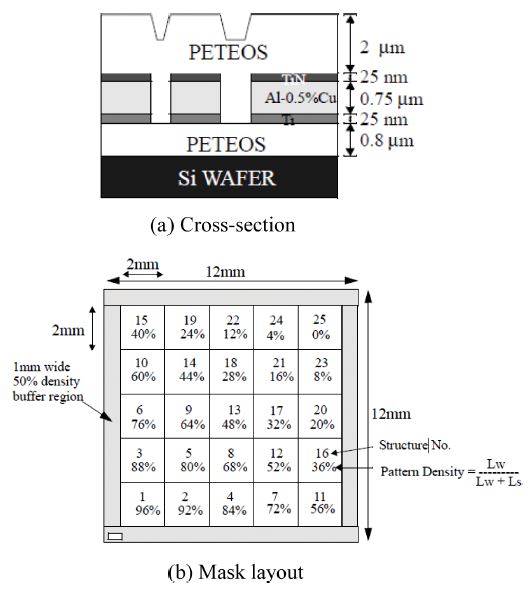
반도체의 기술동향은 고집적화를 위해 2차원적 회로 설계 및 칩 사이즈 증대 방향에서 3차원 다층배선화 구현으로 발전하였다. 반도체 구조변화에 대응하기 위한 핵심 기술 중 화학적 기계적 평탄화(Chemical Mechanical Planarization, CMP) 공정은 웨이퍼 표면의 요철을 제거하여 광역평탄화를 실현하고 고성능 고집적 반도체 제조의 핵심기술로 자리잡았다.¹ CMP 공정은 패턴이 형성된 디바이스 칩과 폴리우레탄 재질 연마패드의 상대 회전에 의한 마찰과 슬러리(Slurry)의 화학적 반응 및 마멸로 연마가 이루어진다. 특히, Fig. 1과 같이 소자 및 배선 형성 공정 후 발생하는 패턴의 단차는 다층배선화를 위해 제거되어야 하며, 패턴구조에서 CMP 공정의 연마거동을 이해하는 것이 필수적이다.

Fig. 1

Cross section of multi-layer wiring with step height

이상적인 제거메커니즘은 요철의 상부부터 점진적으로 제거되어 웨이퍼 전면의 광역 평탄화를 이루는 것이다. 하지만 실제 CMP 공정에서 패턴의 상대 단차가 특정 높이에 도달하면 상부층과 하부 층의 연마가 동시에 이루어지며, 재료제거율(Material Removal Rate, MRR)은 하부 층 대비 상부 층의 길이인 패턴 밀도와 패턴의 크기에 따라 달라진다. 이러한 MRR 차이는 국부적인 불균일을 야기시킨다. 따라서 광역평탄화를 실현하기 위해 패턴의 크기 및 밀도에 따른 MRR을 예측하는 것이 요구된다.

Stine B.²는 산화막 패턴의 밀도에 따른 재료제거율 모델을 제시하였다. 패턴 밀도는 전체 길이 대비 단차 상부 층의 길이 비를 의미한다. 최종 모델 식은 패턴 밀도와 박막 제거율의 항으로 나타내었다. Ouma D.³는 패드 변형에 의한 인접 패턴 사이 영향을 고려하여 유효 패턴 밀도(Effective Pattern Density)개념을 도입하였다. 실제 국부적인 평탄화가 이루어짐에 따라 다양한 패턴 밀도를 갖는 칩에서 인접한 패턴 사이 평탄화 길이(Planarization-Length)가 발생한다. 평탄화 길이를 이용한 가중치 함수(Weighting Function)와 패턴 밀도의 퓨리에 변환으로 유효 패턴 밀도를 도출하였다. Tang B.⁴는 가중치 함수로 정규분포를 사용하였으며, 평탄화 길이를 함수의 크기로 정의하여 유효 패턴 밀도를 계산하였다. 최종적으로 폴리실리콘 패턴의 MEMS 구조를 대상으로 실험값과 모델링 적합성을 검토하였다.

그러나 앞서 언급된 패턴 밀도 이론은 패드의 기계적 특성 및 표면의 변화에 대응할 수 없다. 실제 연마 패드의 표면은 공정 중 발생하는 마멸과 컨디셔닝을 통한 돌기 생성 및 분포의 변화가 발생한다. 패드 표면의 거칠기, 돌기의 직경과 분포의 변화는 재료제거율에 영향을 미친다.^5,6 따라서 본 연구에서는 디바이스 패턴의 형상정보 뿐만 아니라 연마 패드의 표면 특성까지 고려하여 돌기와 웨이퍼 접촉에 초점을 맞춘 평탄화 모델링을 제시하였다.

2. 이론적 배경

CMP 공정의 재료제거율은 프레스톤 지배방정식으로 나타낼 수 있다. 프레스톤 식은 압력, 웨이퍼-정반의 상대 회전 속도 그리고 프레스톤 계수의 곱으로 표현된다.⁷ CMP 공정은 슬러리의 화학적 반응과 연마 패드와 웨이퍼의 접촉면에서 하중이 연마입자에 전달되어 기계적 제거가 발생한다. 이때 연마입자에 발생하는 압력은 패턴의 구조에 따라 달라지며 패드와 웨이퍼의실 접촉면적에 따라 달라진다. 실 접촉면적은 패드의 약 1%이며 이는 패드의 미세 돌기가 웨이퍼와 접촉함을 의미한다.⁸ 따라서 본 연구에서는 미세 돌기와 디바이스 패턴의 접촉에 따른 압력분포를 정의하고 재료제거율을 도출하였다.

2.1 접촉 이론

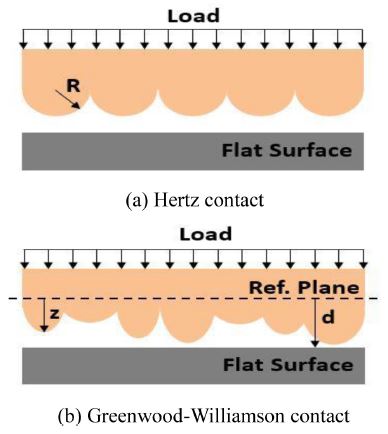
Hertz, H.⁹는 탄성고체의 접촉이론을 제시하였다. 그는 Fig. 2(a)와 같이 계면에서 요철의 동일한 직경 및 높이를 가정하였다. 요철이 평평한 면과 접촉할 때, 돌기의 탄성변형에 따른 하중과 접촉 면적을 다음과 같이 나타내었다.

$\[ F_a=\frac{4E_a}{3\sqrt{k_{asp}}}\cdot {\delta }^{\frac{3}{2}} \]$

(1)

$\[ A_a=\frac{\mathrm{\pi }}{k_{asp}}\cdot \delta \]$

(2)

Fig. 2

Schematics of the contact between asperity and flat surface

k_asp는 돌기의 곡률, E_a는 돌기의 탄성계수, δ는 돌기의 변형량이다. 하중과 접촉 면적은 돌기의 압입량에 따라 증가함을 알 수 있다. 돌기의 압입량은 계면에서 접촉할 때 하중에 의해 발생하는 요철의 탄성변형을 의미 한다.¹⁰ 그러나 자연계에서 동일한 직경과 높이의 요철을 갖는 표면은 볼 수 없으며 무작위 분포를 갖는다. Greenwood와 Willamson은 Fig. 2(b)와 같이 무작위 돌기 높이를 고려했다. 실험적 결과에 따르면 패드의 돌기분포는 정규분포를 따른다.¹¹ 그러나 지수분포로 나타낼 경우 연산상의 장점이 있고 오차를 무시할 수 있기 때문에 본 연구에서는 불규칙한 돌기의 분포를 지수분포로 나타내었다.^9,10

$\[ \begin{array}{cc}\mathrm{\varphi }\left(\mathrm{z}\right)=\frac{1}{\sigma }\cdot e^{\left(-\frac{z}{\sigma }\right)}& z\ge 0\end{array} \]$

(3)

여기서 σ는 지수분포의 편차를 의미한다. 주어진 돌기높이 지수분포를 압입량 δ에 대입하면 식(1)에서 식(2)는 다음과 같다.

$\[ F_a=\frac{4E_a}{3\sqrt{k_{asp}}}\cdot N{\int }_d^{\infty }{\left(z-d\right)}^{\frac{3}{2}}\varphi \left(z\right)dz \]$

(4)

$\[ A_a=\frac{\mathrm{\pi }}{k_{asp}}\cdot N{\int }_d^{\infty }\left(z-d\right)\varphi \left(z\right)dz \]$

(5)

$\[ n_a= \mathrm{N}{\int }_d^{\infty }\varphi \left(z\right)dz \]$

(6)

N은 전체 돌기의 수를 의미하며 d는 유효 돌기 높이를 의미한다. 돌기가 하중에 의해 변형이 발생하게 된다. 이때 변형량을 정의하기 위해 유효 돌기 높이 개념을 도입하였다.¹¹ 참조면(Reference Plane)으로부터 접촉 대상 표면까지 거리를 유효 돌기 높이라고 정의한다. 접촉에 따른 하중, 면적, 접촉하는 돌기 개수를 나타내기 위해서는 유효 돌기 높이(d)의 값을 도출해야한다. 이는 3.1장에서 자세히 다루었다.

Vasilev B.^12,13는 Greenwood-Williamson 이론을 바탕으로 단차가 존재하는 패턴 웨이퍼에서 패드-웨이퍼 접촉에 따른 재료 제거율 모델을 제시하였다. 단차의 상부 층과 하부 층에서 돌기의 곡률이 달라지며 이는 패턴의 크기에 의존한다. 따라서 서로 다른 곡률과 단차를 고려하여 식(4)에서 식(6)을 다음과 같이 세분화 하였다. 아래첨자의 Up은 상부 층을 나타내며 Down은 하부 층을 의미한다. 3장의 수학적 모델링에서 유효 돌기 곡률과 접촉 하중 및 접촉 면적, 접촉하는 돌기의 개수 그리고 최종 재료제거율 모델에도 적용된다.

그러나 Greenwood-Williamson 접촉이론은 요철의 탄성변형만 가정한다. 폴리우레탄 재질 CMP 연마 패드의 돌기는 하중 조건에 따라 탄성에서부터 소성까지 변형한다.¹⁴ 따라서 평탄화 모델에서 상부 층과 하부 층뿐만 아니라 접촉 모드에 따른 접촉하중, 접촉면적 그리고 접촉개수를 정의한다면 공정 중 발생하는 패드 돌기 변화까지 대응할 수 있다.

$\[ F_{a,up}=\frac{4E_a}{3\sqrt{k_{eff,up}}}\cdot N\cdot {\rho }_{eff}{\int }_d^{\infty }{\left(z-d\right)}^{\frac{3}{2}}\varphi \left(z\right)dz \]$

(7)

$\[ F_{a,down}=\frac{4E_a}{3\sqrt{k_{eff,down}}}\cdot N\cdot \left(1-{\rho }_{eff}\right){\int }_{d+h}^{\infty }{\left(z-d-h\right)}^{\frac{3}{2}}\varphi \left(z\right)dz \]$

(8)

$\[ A_{a,up}=\frac{\mathrm{\pi }}{k_{eff,up}}\cdot N\cdot {\rho }_{eff}{\int }_d^{\infty }\left(z-d\right)\varphi \left(z\right)dz \]$

(9)

$\[ A_{a,down}=\frac{\mathrm{\pi }}{k_{eff,down}}\cdot N\left(1-{\rho }_{eff}\right){\int }_{d+h}^{\infty }\left(z-d-h\right)\varphi \left(z\right)dz \]$

(10)

$\[ n_{a,up}= \mathrm{N}\cdot {\rho }_{eff}{\int }_d^{\infty }\varphi \left(z\right)dz \]$

(11)

$\[ n_{a,down}=\mathrm{N}\cdot \left(1-{\rho }_{eff}\right){\int }_{d+h}^{\infty }\varphi \left(z\right)dz \]$

(12)

2.2 패드 돌기 변형

공정 중 웨이퍼에 하중이 가해지면서 폴리우레탄 재질의 연마패드는 국부적으로 변형이 발생한다. 웨이퍼의 이탈을 방지하는 리테이닝 링(Retaining Ring)에는 더 큰 하중이 가해진다. 이때, 리테이닝 링 주변에서 패드의 리바운딩(Rebounding) 현상이 발생되어 웨이퍼 가장자리에서 과연마가 발생한다.¹⁵ 또한 중심부에서는 국부적인 패드변형 뿐만 아니라 미세 돌기의 압축 및 회복이 반복되면서 압력분포가 달라진다. 특히 돌기의 소성변형은 패드의 거칠기를 변화시키고 재료제거율에 직접적인 영향을 미친다.¹⁴ 탄성부터 소성까지 접촉 모드에 따라 실 접촉면적을 정의한다면 압력분포를 해석할 수 있으며 최종적으로 재료제거율을 얻을 수 있다.

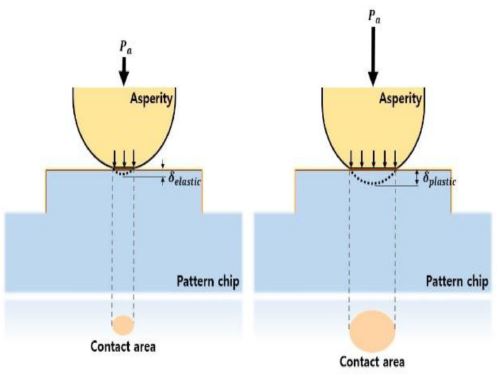
Zhao¹⁵ 등은 계면의 접촉에서 탄성-소성변형 구간 사이 천이 구간을 수식적으로 풀어내었다. 최종적으로 탄성과 탄·소성 천이영역 그리고 완전소성 영역까지 돌기의 변형량에 따라 접촉압력과 접촉면적을 나타내었다. 돌기들의 반지름(R_a)은 평균값으로 동일하다고 가정하였으며 무작위한 높이 분포를 반영하였다. Fig. 3은 접촉모드에 따른 돌기의 압입 및 접촉면적의 모식도이다.

Fig. 3

Schematics of contact areas according to pressure in single asperity

돌기 접촉면적은 압입량에 정비례하여 증가한다. 압입량은 하중에 비례하여 증가하며 특정 하중 이상에 도달하면 단일돌기에서의 압력이 더 이상 증가하지 않는다. 그 시점을 완전소성 변형이 시작되는 구간으로 판단할 수 있다. 등방성 재료의 돌기에서 접촉압력과 접촉면적 식은 다음과 같이 나타낼 수 있다.^16,17

(13)

(14)

이때 Hertz 접촉의 초기 항복은 다음과 같은 조건에서 발생한다.¹⁶

$\[ P_a=\mathrm{K}\cdot H_a \]$

(15)

이때 Hertz 접촉 계수 K값은 약 1/3으로 식(13)의 탄성영역의 평균 접촉 압력에 식(15)를 대입하면 초기 항복 압입량(δ_Y)을 다음과 같이 정의할 수 있다.⁹

$\[ {\delta }_Y=\frac{{\pi }^2}{16}\cdot R_a\cdot \frac{{H_a}^2}{{E_a}^2} \]$

(16)

돌기의 초기 항복 압입량(δ_Y)은 연마 패드의 기계적 특성인 경도와 탄성계수 그리고 돌기의 반지름에 의존한다.

본 연구에서는 패드 돌기의 탄성 변형만 가정한 GW 접촉 이론을 기초로 하여 소성 변형까지 고려한 평탄화 모델을 제시하기 위해 접촉모드에 따라 돌기에 작용하는 접촉 하중과 접촉 면적 그리고 접촉하는 돌기의 개수를 나타내었다. 이때 탄성-소성천이 구간은 무시하였으며, 돌기의 초기 항복 압입량 이후 완전소성에 도달하는 것으로 가정하였다. 따라서 초기 항복 압입량 δ_Y을 기점으로 식(7)에서 식(12)를 다음과 같이 표현하였다.

$\[ F_{e,up}=\frac{4E_a}{3\sqrt{k_{eff,up}}}\cdot N\cdot {\rho }_{eff}{\int }_d^{\mathrm{d}+{\delta }_Y}{\left(z-d\right)}^{\frac{3}{2}}\varphi \left(z\right)dz \]$

(17)

$\[ F_{e,down}=\frac{4E_a}{3\sqrt{k_{eff,down}}}N\left(1-{\rho }_{eff}\right){\int }_{d+h}^{d+h+{\delta }_Y}{\left(z-d-h\right)}^{\frac{3}{2}}\varphi \left(z\right)dz \]$

(18)

$\[ F_{p,up}=\frac{2\pi H_a}{k_{eff,up}}\cdot N{\rho }_{eff}{\int }_{d+{\delta }_Y}^{\infty }\left(z-d\right)\varphi \left(z\right)dz \]$

(19)

$\[ F_{p,down}=\frac{2\pi H_a}{k_{eff,down}}\cdot N\cdot \left(1-{\rho }_{eff}\right){\int }_{d+{h+\delta }_Y}^{\infty }\left(z-d-h\right)\varphi \left(z\right)dz \]$

(20)

$\[ A_{e,up}=\frac{\mathrm{\pi }}{k_{eff,up}}\cdot N\cdot {\rho }_{eff}{\int }_d^{\mathrm{d}+{\delta }_Y}\left(z-d\right)\varphi \left(z\right)dz \]$

(21)

$\[ A_{e,down}=\frac{\mathrm{\pi }}{k_{eff,down}} N\left(1-{\rho }_{eff}\right){\int }_{d+h}^{d+{h+\delta }_Y}\left(z-d-h\right)\varphi \left(z\right)dz \]$

(22)

$\[ A_{p,up}=\frac{2\mathrm{\pi }}{k_{eff,up}}\cdot N\cdot {\rho }_{eff}{\int }_{d+{\delta }_Y}^{\infty }\left(z-d\right)\varphi \left(z\right)dz \]$

(23)

$\[ A_{p,down}=\frac{2\mathrm{\pi }}{k_{eff,down}}N\left(1-{\rho }_{eff}\right){\int }_{d+{h+\delta }_Y}^{\infty }\left(z-d-h\right)\varphi \left(z\right)dz \]$

(24)

$\[ n_{e,up}= \mathrm{N}\cdot {\rho }_{eff}{\int }_d^{\mathrm{d}+{\delta }_Y}\varphi \left(z\right)dz \]$

(25)

$\[ n_{e,down}=\mathrm{N}\cdot \left(1-{\rho }_{eff}\right){\int }_{d+h}^{\mathrm{d}+{\mathrm{h}+\delta }_Y}\varphi \left(z\right)dz \]$

(26)

$\[ n_{p,up}= \mathrm{N}\cdot {\rho }_{eff}{\int }_{d+{\delta }_Y}^{\infty }\varphi \left(z\right)dz \]$

(27)

$\[ n_{p,down}=\mathrm{N}\cdot \left(1-{\rho }_{eff}\right){\int }_{d+{h+\delta }_Y}^{\infty }\varphi \left(z\right)dz \]$

(28)

접촉모드에 따라 돌기 압입량의 적분구간이 달라지며 초기 항복 압입량 δ_Y와 유효 돌기 높이 d에 의존한다.

3. 수학적 모델링

연마 패드의 돌기와 디바이스 패턴 사이 탄성 및 소성 접촉에 의해 발생하는 압력분포를 수식으로 나타내었으며 최종적으로 재료제거율을 도출하였다. 앞서 나타낸 접촉 하중, 접촉 면적 그리고 접촉 개수에 대한 수식들은 측정을 통해 구해낼 수 없으며, 적분 항을 풀어내야 한다.

따라서 본 장에서는 유효 돌기 높이를 정의한 후 각 수식들을 전체 하중(F_Total)의 식으로 나타내었다. 이론적 모델을 도출하고 적용함에 있어 다음과 같이 가정하였다.

1. 돌기는 초기 항복 압입량(δ_Y) 이후 탄·소성 천이구간을 무시하며 완전소성변형을 한다.
2. 무작위 돌기 반경은 평균값으로 대표한다.
3. 접촉 시 압입된 돌기는 원형의 모양을 갖는다.

이러한 가정으로 다음과 같은 제약이 발생한다.

1. 실제 탄·소성 천이변형에 의한 압입 조건을 설명할 수 없다.
2. 돌기의 반경이 패턴 사이 폭보다 작은 경우 하부 층의 이론적 모델이 수정되어야 한다.

3.1 유효 돌기 높이(d)

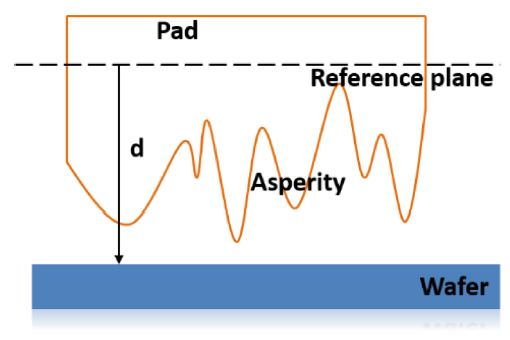
Fig. 4는 유효 돌기 높이 개념을 표현한다. 패드 돌기의 높이는 무작위 분포를 보이며 시작점을 정의할 수 없다. 또한 공정 중 돌기 높이 분포의 변화에 따라 유효 돌기 높이가 달라지므로 계수로 나타낼 수 없다. 본 연구에서는 공초점 현미경을 사용하여 돌기 높이와 분포를 측정하였으며 힘의 평형방정식을 이용하여 d값을 정의하였다. 뉴턴의 제3법칙에 따라 연마헤드에서 웨이퍼로 인가되는 하중은 돌기 전체에 발생하는 하중과 동일하다고 표현할 수 있다.

$\[ F_{Total}=F_{e,up}+F_{e,down}+F_{p,up}+F_{p,down} \]$

(29)

Fig. 4

Schematics of asperity distribution and concept of the effective asperity height

2장에서 정의한 하중에 대한 식(17)에서 식(20)의 합을 수치적으로 풀어내면 식(30)과 같이 유효 돌기 높이를 구할 수 있다. 이때 탄성변형에 의한 하중(F_e)에서 적분 항을 풀어내면 돌기 높이(z)와 유효 돌기 높이(d) 그리고 돌기 높이 분포(σ)로 이루어진 무한급수로 표현된다. 이러한 무한급수 항을 J로 치환하였다. 수식의 간결함을 위해 A, B, ξ 등으로 치환하였다.

$\[ \mathrm{d}=\mathrm{\sigma }\cdot \text{In}\left[\frac{N\cdot \xi }{F_{Total}\cdot k_{eff,up}\cdot k_{eff,down}}\right]-{\delta }_Y \]$

(30)

$\[ \begin{array}{l}\mathrm{\xi }=\frac{4}{3}{E}_a\sqrt{k_{eff,up}\cdot k_{eff,down}}\cdot \left(A+B\right)\cdot J +\\ 2\pi H_a\cdot \left({\delta }_Y+\sigma \right)\cdot \left(\sqrt{k_{eff,down}}\cdot A+\sqrt{k_{eff,up}}\cdot B\right)\end{array} \]$

(31)

$\[ A=\sqrt{k_{eff,down}}\cdot {\rho }_{eff}, B=\sqrt{k_{eff,up}}\cdot \left(1-{\rho }_{eff}\right)\cdot e^{-\frac{h}{\sigma }} \]$

(32)

유효 돌기 높이(d)를 전체 하중(F_Total)의 함수로 나타내었다. 이때 연마 공정 및 컨디셔닝 공정 중 돌기 높이 분포(σ)가 변화하며 그에 따라 유효 돌기 높이 역시 변하는 것을 알 수 있다.

4. 모델 검증

본 연구에서 제시한 재료 제거율 모델과 실험을 통해 얻은 재료 제거율 및 패턴의 단차를 비교하였다. 실험은 G&P Technology사의 POLI-500 연마기를 사용하였으며 SKW사의 SKW1-1 (150 mm) 테스트 패턴 웨이퍼를 연마하였다. Fig. 5에 사용된 패턴 웨이퍼의 단면 정보 및 패턴 배치 정보를 나타내었으며,¹⁹ 다이의 크기는 12 mm로 축소되었다. 패턴 밀도는 96%부터 0%까지 배치되어 있으며 초기 단차는 880 nm이다. CMP 소모품인 패드와 슬러리는 KPX사의 KONI 연마패드와 상용 퓸드 실리카(Fumed Silica) 슬러리를 사용하였다. 공정 조건은 Table 1과 같다.

Fig. 5

Structural information on test pattern wafer19 (Adapted from Ref. 19 on the basis of open access)

Table 1

Experimental conditions

패드 안정화를 위해 5분 동안 더미 웨이퍼를 연마하였으며 패턴 웨이퍼 연마는 1분 간격으로 실시하였다.

패드 돌기의 높이 분포 변화를 최소화 하기 위해 공정 중 컨디셔닝을 실시간으로 진행하였다. KMAC사의 ST5030-SL 박막두께 측정기를 사용하여 재료 제거율을 비교하였으며, Nanosystem사의 NV-2400 광학식 표면 프로파일러를 사용하여 단차를 측정하였다.

패드의 기계적 특성 및 돌기의 평균 반지름과 높이 분포는 Table 2에 나타내었다. 돌기의 강도 및 탄성계수는 CSM Instruments SA사의 Nano Indentation Tester를 통해 측정되었으며 돌기의 평균 반지름과 높이 편차는 Nanoscope사의 NS-3000 공초점현미경을 사용하여 측정하였다. 실험을 통해 얻은 산화막 박막의 평균 재료제거율은 141 nm/min이다.

Table 2

Mechanical properties of polishing pad asperity

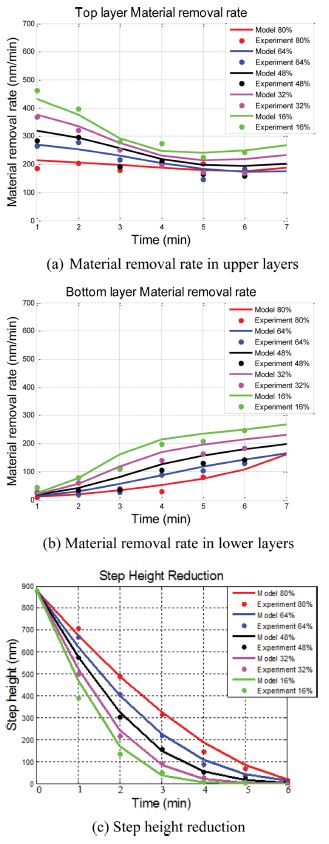
Fig. 6에서 연마실험을 통해 얻은 측정값과 평탄화 모델에서 얻은 재료제거율 및 단차를 비교하였다. 실선은 모델 식으로 도출한 결과 값이며 각 %는 패턴밀도를 나타낸다. 실험을 통해 얻은 분당 재료제거율과 단차는 점으로 나타내었다. 패턴 밀도가 낮을수록 높은 재료제거율과 높은 단차 감소율을 볼 수 있다. 연마 시작 초기에서 하부 층의 제거가 거의 발생하지 않는다. 그러나 단차가 감소함에 따라 상-하부 층의 재료제거율이 비슷해진다. 이는 일정 단차 이하에서 패드의 변형에 의해 상-하부층에서 동시 연마가 진행됨을 의미한다. 약 5분부터 국부적인 평탄화가 달성되었다고 판단할 수 있으며 공정이 진행 됨에 따라 상-하부 층의 재료제거율이 수렴한다.

Fig. 6

Graph of planarization model and measured values according to pattern density

상부 층 재료제거율의 평균제곱근 오차는 약 24.59 nm/min이다. 하부 층 재료제거율의 평균제곱근 오차는 약 22.03 nm/min을 가지며 단차의 오차는 약 22.66 nm를 보였다. 오차의 원인으로 공정 중 발생하는 외부환경의 변화에 의한 오차가 가장 클 것으로 판단된다. 서로 다른 웨이퍼 7장을 1분씩 증가시키며 연마하였기 때문에 외부요인에 의한 오차가 발생할 수 있다. 특히 공정 시간이 길수록 공정 온도가 증가하게 되며 그에 따라 재료 제거율이 다소 증가할 것으로 판단된다. 또한 돌기의 탄-소성천이 변형구간을 무시하였기 때문에 그에 따른 오차 발생도 판단할 수 있다.

공정 중 패드 돌기 표면의 마모에 의해 돌기 높이 분포가 달라진다. Fig. 7은 실시간 컨디셔닝 유무에 따른 연마결과를 나타낸다. 패턴의 밀도가 80%, 64%, 48%에서 단차 및 상-하부 층 재료제거율을 비교하였다. 실선은 공정 중 컨디셔닝을 실시한 조건에서 모델 식으로 도출한 결과 값이며 실선은 컨디셔닝을 수행하지 않고 얻은 모델 식 결과 값이다. 또한 점과 정사각형 데이터는 실험 및 측정을 통해 얻은 값이다. 각 공정 조건은 Table 1과 동일하며 패드 물성은 Table 3에 나타내었다.

Fig. 7

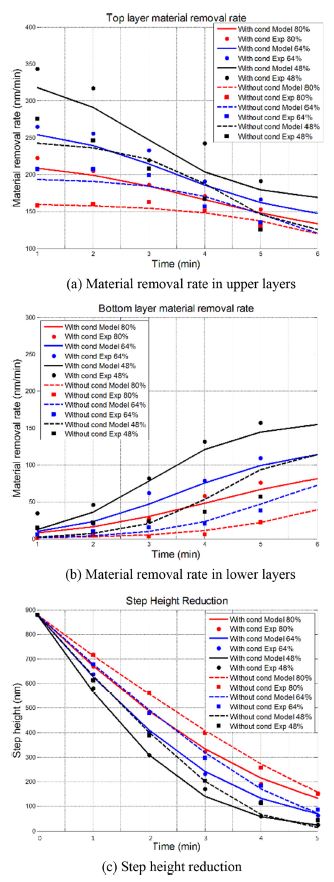
Graph of planarization model and measured values according to pattern density and in situ conditioning

Table 3

Mechanical properties of polishing pad asperity

실시간 컨디셔닝을 수행한 경우 돌기 높이 편차의 변화가 거의 없으며 박막 제거율은 162 nm/min이다. 컨디셔닝을 수행하지 않은 경우 분당 약 10 nm의 편차감소가 발생했으며 박막 제거율은 121 nm/min이다. 이는 공정 중 감소하는 패드 돌기 높이의 편차가 컨디셔닝을 통해 유지됨을 의미한다. 편차가 클수록 상-하부 층의 재료제거율이 증가하며 단차가 빠르게 감소한다. 그러나 연마 5분 경과 시 단차가 거의 일치함을 볼 수 있다. 따라서 패드 돌기의 높이 편차는 재료제거율에 영향을 미치지만 단차 제거 측면에서 큰 영향력이 없는 것으로 판단된다. 하지만 높이 편차에 따라 평탄화가 이루어질 때 제거된 상-하부 층의 두께를 예측할 수 있다.

5. 결론

본 연구에서는 연마 패드의 돌기가 웨이퍼와 접촉하는 계면에서 하중에 의한 압입과 실 접촉면적을 고려한 압력 분포를 확률적 접근법으로 식(3)과 같이 나타내어 실 접촉하중 및 실 접촉면적을 수식화하였다. 이를 통해 단일 돌기에 작용하는 압력을 나타낼 수 있으며 접촉하는 돌기의 개수를 통해 최종적인 재료제거율을 도출할 수 있다. 돌기의 접촉 모드와 상하부 층에 따른 평탄화 모델을 박막 재료제거율에 대한 비례식으로 수식화 하였다. 제시된 수식 모델은 실험을 통해 얻은 값과 비교하여 검증하였다. 재료제거율은 패턴 밀도에 반비례하여 증가하는것을 확인하였으며 돌기 분포의 편차가 클수록 증가하는 경향을 보였다. 기존 패턴 밀도에 의존한 모델과 비교하였을 때, 패드의 기계적 특성이 모델에 반영되었고 그에 따른 컨디셔닝 효과를 고려할 수 있게 되었다. 이러한 결과를 바탕으로 패드 물성에 따른 재료제거율의 시뮬레이션을 기대할 수 있다.

상부 층과 하부 층의 재료제거율과 단차의 평균제곱근 오차는 각각 24.59 nm/min, 22.03 nm/min, 22.66 nm/min를 보였다. 오차의 원인으로는 온도변화 등 외부 환경에 의한 요소와 공정 중 발생하는 돌기 높이 편차의 변화가 가장 클 것으로 판단되며 탄-소성 변형 구간에서 발생하는 오차가 예상된다. 또한 동일한 크기의 연마입자(Abrasive Particle)가 고르게 분포한다고 가정하였으나 공정 중 응집이 발생할 수 있으며 크기의 편차가 존재하기 때문에 실제 연마율에서 오차가 발생할 수 있다.

컨디셔닝 공정 유무에 따른 돌기 높이의 편차를 확인하였으며 단차 제거에 미치는 영향을 고찰하였다. 패드의 물성에 따라 평탄화 시 제거된 두께를 예측할 수 있으며, 연마 종점(End Point)을 예측할 수 있을 것으로 판단된다. 추가적으로 공정 중 발생하는 패드의 거칠기 변화를 수식화하여 나타낸다면 패턴 밀도에 따른 개선된 재료제거율 예측이 가능 할 것으로 판단된다.

Acknowledgments

이 논문은 2017년도 정부(미래창조과학부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(No.2016R1A2B4011466).

REFERENCES

• Takeno, Y. and Okamoto, K., “New Market Trend in CMP Equipment/Material for the “More Than Moore” Era,” Proc. of the International Conference on Electronics Packaging and iMAPS All Asia Conference, pp. 423-425, 2018. [https://doi.org/10.23919/ICEP.2018.8374338]
• Stine, B., Ouma, D., Divecha, R., Boning, D., and Chung, J., “A Closed-Form Analytic Model for ILD Thickness Variation in CMP Processes,” Proc. of CMP-MIC, Vol. 1, pp. 1-8, 1997.
• Ouma, D., Boning, D., Chung, J., Shin, G., Olsen, L., et al., “An Integrated Characterization and Modeling Methodology for CMP Dielectric Planarization,” Proc. of International Interconnect Technology Conference, pp. 67-69, 1998.
• Tang, B. D., “Characterization and Modeling of Polysilicon MEMS Chemical-Mechanical Polishing,” Massachusetts Institute of Technology, Paper No. 17983, 2004.
• Hooper, B., Byrne, G., and Galligan, S., “Pad Conditioning in Chemical Mechanical Polishing,” Journal of Materials Processing Technology, Vol. 123, No. 1, pp. 107-113, 2002. [https://doi.org/10.1016/S0924-0136(01)01137-2]
• Suzuki, N., Oshika, S., Misono, H., Hashimoto, Y., Yasuda, H., et al., “Improvement of Material Removal Efficiency by Optimization of Anisotropic Contact of Pad Asperities,” Proc. of International Conference on Planarization/CMP Technology Conference, pp. 1-5, 2017.
• Preston, F., “The Theory and Design of Plate Glass Polishing Machines,” Journal of Glass Technology, Vol. 11, No. 44, pp. 214-256, 1927.
• Elmufdi, C. L. and Muldowney, G. P., “A Novel Optical Technique to Measure Pad-Wafer Contact Area in Chemical Mechanical Planarization,” Proc. of MRS Online Proceedings Library Archive, Vol. 914, 2006. [https://doi.org/10.1557/PROC-0914-F12-06]
• Johnson, K. L., “Contact Mechanics,” Cambridge University Press, pp.90-106, 1987.
• Vlassak, J., “A Model for Chemical–Mechanical Polishing of a Material Surface Based on Contact Mechanics,” Journal of the Mechanics and Physics of Solids, Vol. 52, No. 4, pp. 847-873, 2004. [https://doi.org/10.1016/j.jmps.2003.07.007]
• Greenwood, J. and Williamson, J. P., “Contact of Nominally Flat Surfaces,” Proc. of the Royal Society of London. SERIES A. Mathematical and Physical Sciences, Vol. 295, No. 1442, pp. 300-319, 1966. [https://doi.org/10.1098/rspa.1966.0242]
• Vasilev, B., Rzehak, R., Bott, S., Kucher, P., and Bartha, J.W., “Greenwood–Williamson Model Combining Pattern-Density and Pattern-Size Effects in CMP,” IEEE Transactions on Semiconductor Manufacturing, Vol. 24, No. 2, pp. 338-347, 2011. [https://doi.org/10.1109/TSM.2011.2107756]
• Vasilev, B., Bott, S., Rzehak, R., Liske, R., and Bartha, J. W., “A Method for Characterizing the Pad Surface Texture and Modeling Its Impact on the Planarization in CMP,” Microelectronic Engineering, Vol. 104, pp. 48-57, 2013. [https://doi.org/10.1016/j.mee.2012.10.007]
• Borucki, L., “Mathematical Modeling of Polish-Rate Decay in Chemical-Mechanical Polishing,” Journal of Engineering Mathematics, Vol. 43, Nos. 2-4, pp. 105-114, 2002. [https://doi.org/10.1023/A:1020305108358]
• Babu, S., “Advances in Chemical Mechanical Planarization (CMP),” Woodhead Publishing, pp.417-432, 2016.
• Zhao, Y., Maietta, D. M. and Chang, L., “An Asperity Microcontact Model Incorporating the Transition from Elastic Deformation to Fully Plastic Flow,” Journal of Tribology, Vol. 122, No. 1, pp. 86-93, 2000. [https://doi.org/10.1115/1.555332]
• Kim, S. H., Saka, N. and Chun, J. H., “The Role of Pad Topography in Chemical-Mechanical Polishing,” IEEE Transactions on Semiconductor Manufacturing, Vol. 27, No. 3, pp. 431-442, 2014. [https://doi.org/10.1109/TSM.2014.2335156]
• Yang, Z., Xu, Q. and Chen, L., “A Chemical Mechanical Planarization Model Including Global Pressure Distribution and Feature Size Effects,” IEEE Transactions on Components, Packaging and Manufacturing Technology, Vol. 6, No. 2, pp. 177-184, 2016. [https://doi.org/10.1109/TCPMT.2016.2514707]
• SKW Associates, Inc., “Patterned Test Wafters for CMP Process Characterization,” SKW Associates, http://www.testwafer.com/testwafers.htm, (Accessed 11 MAR 2019)