볼스크류 성능 향상을 위한 볼 순환구조 최적화에 관한 연구
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
The ball screw can be included in steering systems, the brake system, seat moving devices, and transmission systems of vehicles. Performance of the ball screw in these systems plays a key role in delivering agile and accurate power transmission. The purpose of this study is to improve performance by focusing on performance of the ball screw, by applying various conditions based on a design factor in the circulation system. The selected single design factor is to apply the cycloid curve to a circulation area. The circulation part to obtain a cycloid curve with highest performance, can have the smoothest ball flow. In addition, based on results, we intend to reduce failure cost that may be incurred in developing future ball screws for automobiles, and to establish databases that can be applied to developed products by deriving optimal shape.
Keywords:
Ball screw, Circulation system, End-cap, Cycloid curve키워드:
볼스크류, 순환구조, 앤드캡, 사이클로이드 곡선1. 서론
최근 공작기계 분야에서부터 차량, 항공 등 다양한 분야에 고성능(High Performance), 고정밀(High Precision)의 볼스크류(Ball Screw)에 대한 요구가 증가하고 있다. 이에 따라 볼스크류는 각종 분야에서 적용되고 있으며, 각종 적용 분야에 따라 볼스크류의 차별화된 기술이 요구되고 있다. 특히 차량에 적용되는 볼스크류는 조향 장치, 제동 장치, 변속 장치 등에 적용되는 추세이다. 이러한 장치 내에서 볼스크류의 성능은 빠르고 정확한 동력을 전달하는데 중요한 역할을 하며, 볼스크류의 성능에 따른 자체 강성, 구동 소음 등은 운전자가 느끼는 승차감과 운전자의 안전에 큰 영향을 미칠 수 있다.
고성능, 고정도의 볼스크류를 제작하기 위해서는 구동 효율과 관련된 설계인자를 선택하고, 선택된 설계 인자가 볼스크류의 구동 성능에 어떠한 영향을 미치는지 면밀히 분석할 필요가 있으며, 이와 관련된 연구는 다양한 분야에서 진행 중이다.
Park1은 볼스크류의 소음을 최소화하기 위해 볼 순환 구조의 최적화에 초점을 맞추어 튜브 타입 순환 구조와 앤드캡 타입 순환 구조에 대한 비교 시험을 수행하였으며, 튜브 타입에 비해 앤드캡 타입에서 약 6 dB의 소음이 개선된 결과를 확인하였다. Park2은 볼스크류의 최대 효율을 얻기 위해 Hertzian의 접촉 이론을 응용하여 볼스크류의 볼 순환로 설계에서 상사비 결정 방법을 제안하였다. 하지만 순환 구조가 가지는 곡률의 변경에 따른 볼스크류 구동 성능 개선에 관한 연구는 미흡한 상태이다.
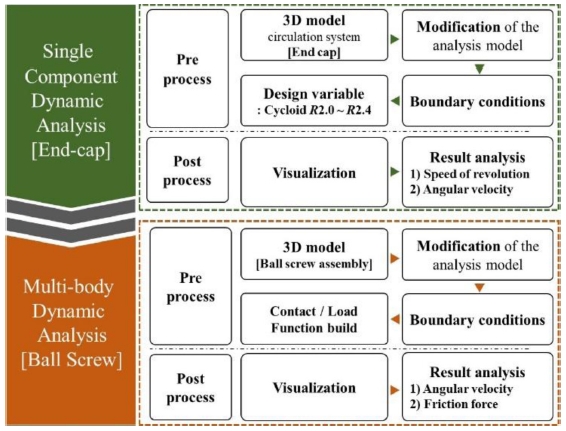
따라서 본 논문에서는 다물체 동역학 해석 소프트웨어인 DAFUL의 전처리기(Pre-Processor)와 후처리기(Post-Processor)을 이용하였으며 동역학 해석 프로세스는 Fig. 1과 같다. 볼스크류의 순환 구조 내 곡률 변경에 따른 동역학 해석을 수행하여 각 조건에 따른 순환 구조에 대한 성능을 확인하고자 한다. 이후 다물체 동역학 해석(Multi-Body Dynamic Analysis)을 활용하여 각 순환 구조를 볼스크류에 적용하여 전체적인 시스템에 대한 구동 성능을 개선할 수 있는 방안에 대해 논하고자 한다.
2. 볼스크류 이론
2.1 볼스크류 원리 및 구조
볼스크류의 구조는 체결용 삼각나사의 수나사와 암나사의 골에 상당하는 부분이 아치형을 이루고 그 가운데에 다수의 볼과 조립되어 축을 회전시키고, 볼이 아치형의 골을 따라 자전과 공전하며 순차적으로 순환로를 따라 무한 순환하는 구조이다. 즉 볼스크류는 볼스크류 축과 너트(Nut) 사이의 볼을 이용하여 정확하게 힘과 움직임을 전달하는 역할을 하는 것이다.
2.2 볼스크류 메커니즘
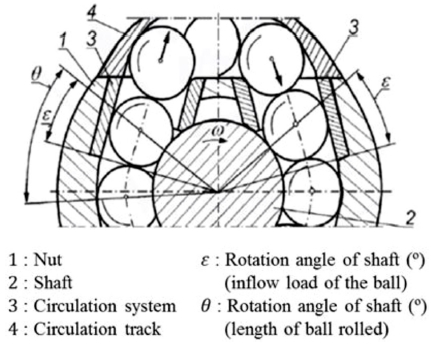
Fig. 2는 튜브 타입 순환 구조 볼스크류의 수직 단면을 나타내었으며, 작동중인 볼스크류 시스템 내에서 볼은 축(2)와 너트(1) 사이에서 아치형 골을 따라 움직이며 순환 시스템(3, 4)를 통해 시작점과 도착점을 반복하는 순환이 이루어진다.3,4
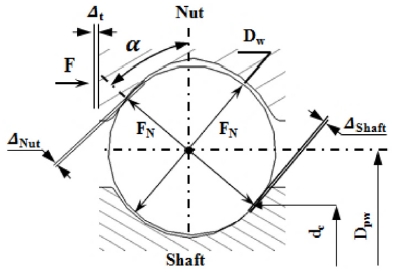
Fig. 3은 볼스크류의 볼 하나와 축, 너트 간 접촉에 관한 기하학적 변수와 발생하는 힘에 대해 나타내고 있다. Fig. 3의 계수 Dpw는 볼 피치 원 직경, Dw는 볼 직경, dc는 볼스크류 축의 부하 응력에 대한 직경, FN'은 볼에 작용하는 보통 힘, ΔNut는 너트에서 볼과 볼 궤도면의 변형량, ΔShaft는 축에서 볼과 볼 궤도면의 변형량, 축 변형량 Δt는 식 (1) 과 같이 Δt는 외부 힘 F에서 볼과 볼 궤도면의 축 변형량으로 정의된다. 여기서 α는 접촉각(Contact Angle)이고, Ф는 리드각(Lead Angle)이다.3,4
| (1) |
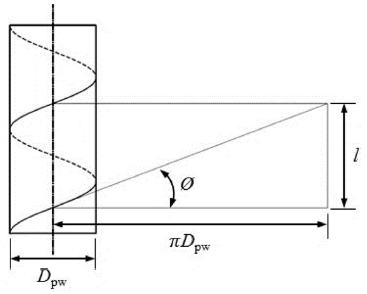
리드각은 원통면에 새겨진 나사산의 나선의 임의의 한 점과 그 점에서 나사축에 직각으로 그은 유효 원통면의 접선이 이루는 각을 말하며, 식(2)와 같이 리드와 볼 피치 원 직격으로 정의된다. 리드(Lead)는 볼 스크류 축 또는 너트를 1회전시켰을 때, 너트 또는 볼 스크류 축이 진행한 거리를 말한다.
| (2) |
3. 볼 순환트랙 곡률에 따른 동역학 해석
3.1 설계변수 선정
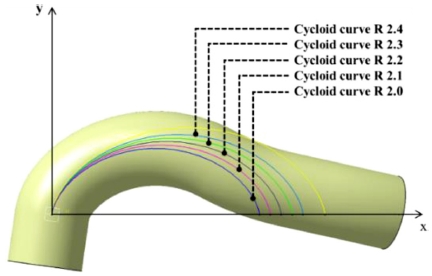
볼 순환트랙은 볼과 직접적으로 접촉하는 부분으로 볼 순환트랙 내부에서 발생하는 볼의 움직임은 볼스크류의 성능 및 내구적인 측면에 중대한 영향을 미칠 수 있다. 따라서 볼이 접촉하는 내부 순환로의 최적의 곡률을 도출하고자 한다. 본 연구에서 최적의 곡률을 도출하기 위해 적용한 곡선은 사이클로이드 곡선으로 Fig. 5와 같이 앤드캡 내부 볼 순환로가 형성되는 xy 평면을 기준으로 곡선을 생성하고자 하였으므로 평판 위를 구르는 원에 대한 사이클로이드 곡선을 적용하였다. Park1의 연구 결과에 따라 순환구조는 소음에 유리한 볼 순환구조인 앤드캡 타입의 볼 순환구조를 선정하였으며, 이를 바탕으로 앤드캡 내부 볼의 진행경로에 대한 곡률 반경에 사이클로이드 곡선을 적용하여 설계변수를 선정하였다.
사이클로이드 곡선은 기계요소 내외부적인 마찰요소를 최소화하여 효율 및 흐름을 극대화하기 위해 여러 기계요소 설계에 적용된다. Ham5은 사이클로이드 치형을 적용한 기어를 설계하여 핀과 피니언 기어의 백래쉬(Backlash) 및 물림 특성이 가장 적합하고, 정밀제어가 가능한 치형을 설계하였다. 또한, Lee6은 전기차(EV, Electrical Vehicles)의 휠 모터용 감속기를 사이클로이드(Cycloid) 곡선을 적용하여 설계하여 요구 성능에 대한 형상 변수값 및 공차 할당의 최적화를 수행하였다. Yun7은 사이클로이드 형상이 적용된 블레이드 시스템(CBS)을 설계, 제작하여 정지 비행 상태에서 다양한 파라미터에 대한 추력 및 파워 등 성능 특성을 연구하였다. 이 외에도 사이클로이드 곡선은 각종 다양한 분야에서 모델의 최적화를 위해 지속적으로 연구개발 중에 있으며 다양한 제품에 적용되고 있다. 따라서 본 연구에서는 최적의 볼 움직임을 얻기 위해 사이클로이드 곡선을 앤드캡 내 순환로에 적용하였으며, 이를 통해 볼과 앤드캡 사이의 마찰을 최소화하고 효율 및 흐름을 극대화하여 최적의 앤드캡 모델을 도출하고자 한다.
순환로의 형상은 현재까지 볼 순환 곡률에 대한 선행 연구된 사례가 없으며, 볼의 크기가 다른 볼 스크류 사양에서도 쉽게 적용하기 위해 사용하는 볼 반지름을 기준으로 해석 범위를 선정하였다. 따라서 볼의 반지름 2 mm를 기준으로 -5% (R1.9), +0% (R2.0), +5% (R2.1), +10% (R2.2), + 15% (R2.3), +20% (R2.4), +25% (R2.5), 전체 7가지 경우를 초기 조건으로 설정하였으며, 결과는 Fig. 5와 같다.
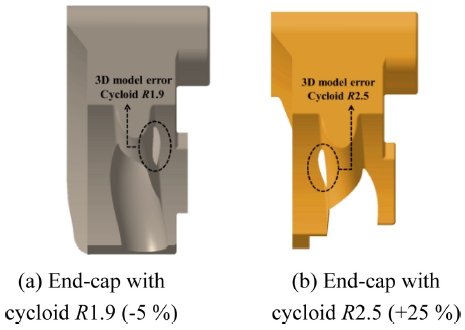
하지만 사이클로이드 R1.9, R2.5모델 경우 Fig. 6과 같이 3D 모델링이 구현되지 않는 현상이 발생하여 설계 변수에서 제외하였으며, 최종적으로 사이클로이드 R2.0, R2.1, R2.2, R2.3, R2.4의 전체 5가지의 경우에 대해 앤드캡의 3D 모델링을 수행하였다.
이후 각 경우에 대해 사이클로이드 곡선을 지나며 발생하는 볼의 자전속도 값과, 앤드캡 내 발생하는 볼의 공전속도에 대한 값을 얻고자 한다. 본 연구의 전체적인 프로세스는 단품에 대한 동역학 해석 수행 후, 볼스크류 조립체에 적용된 앤드캡간 상관관계를 분석하고자 한다.
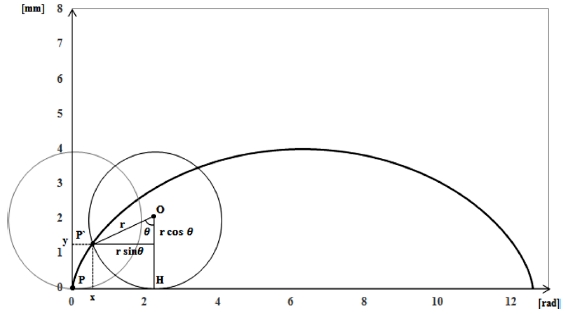
사이클로이드 곡선은 좌표평면에서 반지름이 r인 원의 원점에서 한 점이 x축의 양의 방향으로 2 π rad 만큼 이동할 때 한 점이 그리는 곡선을 말한다. 흔히 사이클로이드 곡선은 두 점 사이를 이동할 때 최단 시간을 가지는 최단 강하곡선(Brachistochrone)으로 정의되기도 하며, 사이클로이드 상의 어느 한 점에서 시작하여도 끝 점까지 도달하는 시간이 일정한 곡선, 등시곡선(Isochrone)이라 정의된다.
3.2 앤드캡 동역학 해석
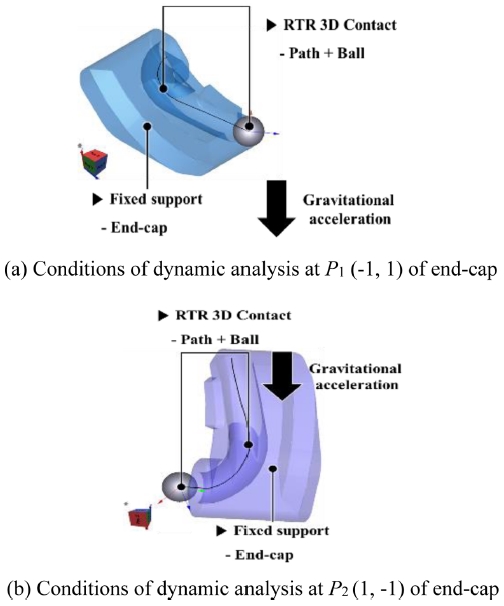
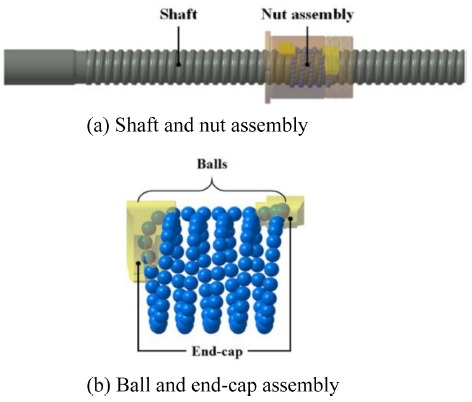
본 연구에서 수행하는 앤드캡 타입의 볼스크류의 구조는 Fig. 8(a)와 같으며, 앤드캡의 위치는 Fig. 8(b)와 같이 B.C.D (Ball Center Diameter)을 나타내는 원을 기준으로 볼스크류 조립체 내 점 P1 (-1, 1), 점 P2 (1, -1)의 위치에서 전체 2개의 앤드캡이 위치한다.
따라서 두 점 P1, P2에서 사이클로이드 R2.0에서 R2.4까지 적용된 앤드캡에 대해 동역학 해석을 수행하였다. Table 1은 앤드캡 단일 모델에 대한 동역학 해석의 전체 10가지 경우에 대해 나타내었다.
앤드캡의 동역학 해석을 통해 앤드캡의 순환로에 적용된 각 사이클로이드 모델에 따라 볼이 순환하며 발생하는 자전속도를 얻고자 하며, 자전속도와 볼스크류 내 볼의 공전속도 간에 상관관계를 분석하고자 한다.
두 강체에 대한 동역학 해석을 수행하기 위해 볼과 앤드캡 접촉면에 대해 강체-강체 접촉(Rigid-to-Tigid 3D Contact)를 수행하였다. RTR 접촉 조건은 접촉점에서 두 강체 사이 접촉력을 나타낼 수 있으며, 행동면(Action Surface)과 기준면(Base Surface) 간 관통 및 상대 속도에 기반을 둔다. 행동면은 움직이는 접촉점에 적용되며, 반력은 기준 강체의 동일 위치에 적용된다.
볼스크류 너트에 결합되는 앤드캡은 구동 중 분리를 방지하기 위해 스냅링 및 각종 이탈 방지를 위한 구성품으로 결합된 상태로, 앤드캡에 대한 구속조건은 6자유도 구속조건인 고정지지(Fixed Support) 조건을 부여하였으며, 앤드캡의 위치와 사이클로이드 R 값에 따른 앤드캡 내 볼의 흐름을 알고자 하므로 볼은 중력에 의해 볼 순환트랙을 지날 수 있도록 설정하였다. 앤드캡 타입 볼 순환구조에 대한 해석 모델은 Figs. 9(a)와 9(b)와 같다.
3.3 앤드캡 동역학 해석 결과
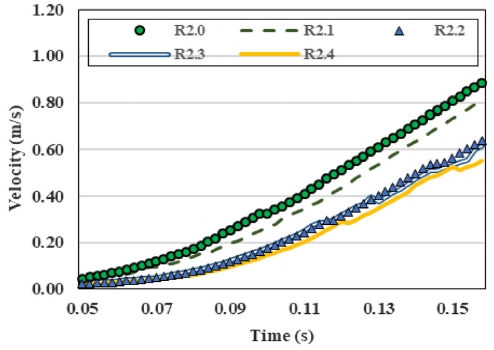
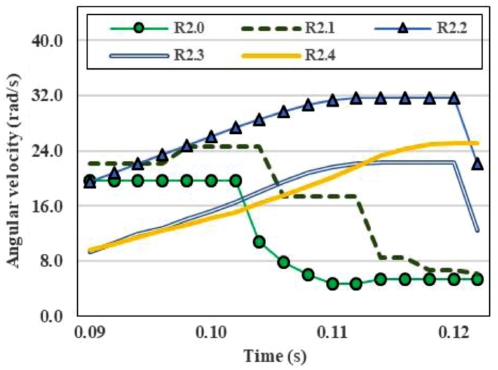
앤드캡이 P1 (-1, 1)에 위치할 경우 볼의 공전속도 및 자전속도에 대한 결과는 Table 2, Figs. 10에서 11과 같이 나타내었다. 사이클로이드 R 값이 증가함에 따라 앤드캡 내부 볼의 공전속도는 감소하지만, 볼의 자전속도는 R2.2까지 증가 이후 감소하는 경향을 확인할 수 있다.
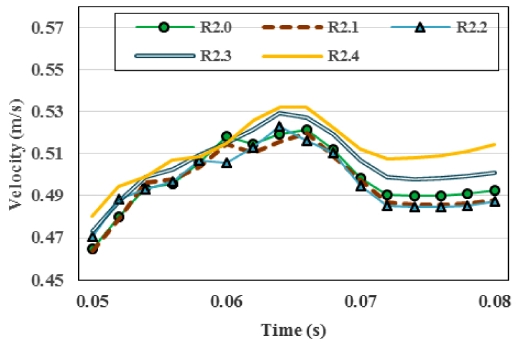
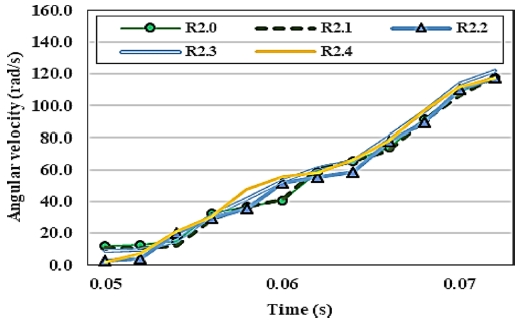
P2 (1, -1)에 위치할 경우 볼의 공전속도 및 자전속도에 대한 결과는 Table 3, Figs. 12에서 13와 같이 나타내었다. P1 (-1, 1)의 결과와 반대로 사이클로이드 R값이 증가함에 따라 앤드캡 내부 볼의 공전속도는 증가하였으며 이는 앤드캡 위치에 따라 볼이 중력의 영향을 받는 정도에 차이가 발생하여 반대의 결과를 보여준 것으로 사료된다. 볼의 자전속도는 P1 (-1, 1)의 결과 경향과 달리, 모든 경우에 대해 뚜렷한 자전속도의 경향은 나타나지 않으며 유사한 값들이 나타나는 결과를 확인할 수 있다. 또한 P1 (-1, 1) 대비 전반적으로 높은 자전속도가 나타나는 것을 확인 할 수 있다.
볼의 공전 및 자전속도에 대한 인자 중, 자전속도는 앤드캡 내부 순환로 내에서 볼의 자전 능력을 나타내고 볼간 원활한 순환을 보여주는 척도로 볼스크류 조립체에서는 단일 볼에 대한 공전 속도 보다 볼 구름성에 직접적인 영향을 가진 인자이다. 따라서 볼스크류 조립체의 다물체 동역학 해석에서는 앤드캡 단일 부품에서 얻은 자전속도 값에 초점을 맞추어 각 경우에 대해 비교 분석하여 볼스크류 조립체 내 앤드캡과의 비교분석을 수행하였다.
4. 볼스크류 다물체 동역학 해석
4.1 다물체 동역학 해석 목적 및 모델
5가지 경우의 앤드캡을 적용한 각 볼스크류 모델에 대한 마찰력을 분석하여 앤드캡 단일모델에 대한 결과와 앤드캡이 볼스크류에 조립되었을 경우에 대한 결과를 비교하여 사이클로이드 곡선이 적용된 앤드캡이 볼스크류 조립체에 미치는 영향도를 확인하고 분석하고자 한다.
볼스크류 시스템의 다물체 동역학 해석을 수행하기 위해 3D 모델링을 수행하였으며 결과는 Fig. 14와 같다.
4.2 다물체 동역학 해석 조건
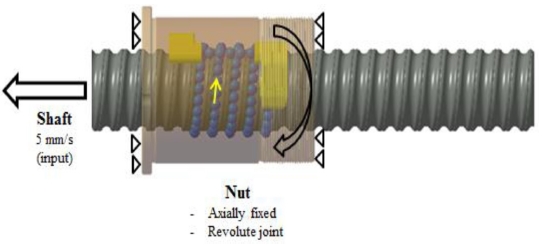
본 연구에 적용된 볼스크류 시스템에 대한 동역학 해석 구동 조건은 Fig. 15와 같으며, 너트의 회전운동을 통해 축의 직선운동을 원활히 수행할 수 있도록 하는 정전회전 구동 방식으로 구성되어 있다. 본 조건은 볼스크류 구동 시 너트 – 볼 – 샤프트 축에 발생하는 마찰력을 알고자 샤프트 축의 한 쪽 끝 단에 5 mm/s의 속도 조건을 적용하였으며, 이 때 너트는 제자리에서 회전할 수 있도록 조건을 적용하였다.
4.3 다물체 동역학 해석 결과
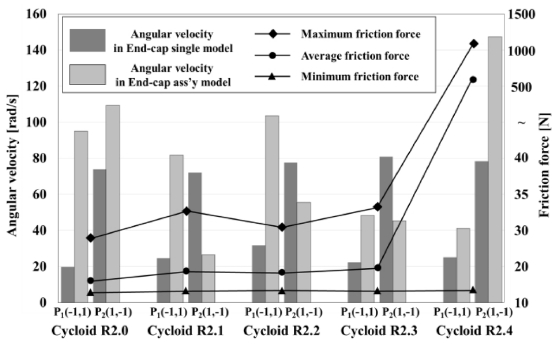
볼스크류 시스템에 대한 구동 성능평가는 5가지 항목에 대해 마찰력 평균값 비교를 통해 구동 성능의 우위를 판단하였다. 마찰력의 최소(min), 최대(max) 값은 작동 구간 중 각각 한 점에 대한 특정 값을 나타내고, 평균값(avg)은 전 구간에 대한 값을 나타내며, 볼스크류 시스템 성능을 판단할 수 있는 지표이다.
본 연구의 전체 결과는 Table 4, Fig. 16과 같으며, 사이클로이드 R2.0 앤드캡이 적용된 볼스크류의 P1, P2 두 점 모두 볼의 자전속도가 증가하였으며, 이 때 가장 적은 마찰력 값이 도출되어 에너지 손실이 적고, 가장 높은 볼스크류 구동 성능을 가지는 것을 확인할 수 있었다. 또한 사이클로이드 R2.0 앤드캡의 동역학 해석 결과에서 P1, P2 두 점 모두에서 자전속도가 낮은 축에 속하였다. 하지만 볼스크류에 조립된 앤드캡의 경우에는 가장 우수한 결과를 확인할 수 있다. 따라서 앤드캡에 대한 자전속도의 결과를 이용하여 볼스크류 전체 모델에 대한 성능을 판단하는 것은 어려울 것으로 판단하였지만, 조립체에 적용된 앤드캡에 대한 자전속도를 분석함으로써 볼스크류 전체 모델에 대한 성능 예측은 가능할 것으로 판단하였다. 따라서 사이클로이드 R2.0이 적용된 앤드캡을 볼스크류 조립체에 적용한다면 향후 설계 시 소요되는 시간 단축을 통해 경제적으로 이익을 얻을 수 있을 것으로 예상되며, 볼스크류의 구동 성능 측면에서도 유리할 것으로 판단하였다.
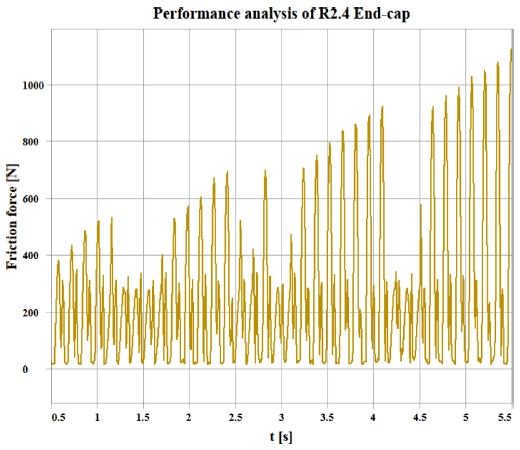
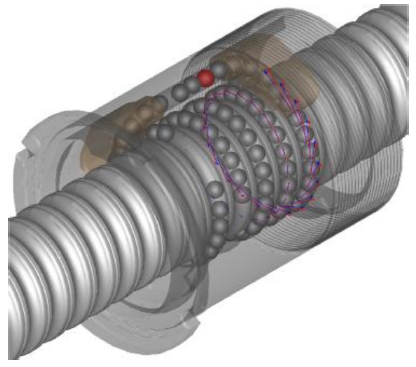
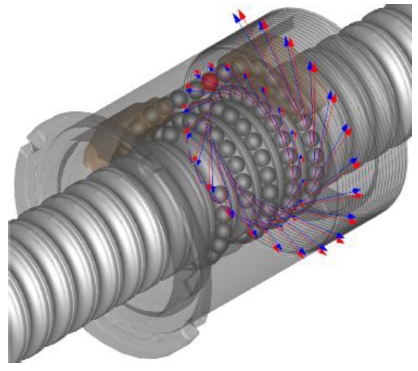
사이클로이드 R2.4 앤드캡이 조립된 볼스크류 내 앤드캡 P1, P2의 볼의 자전속도 결과는 단일 앤드캡 모델 내 볼의 자전속도 결과 보다 높게 나타났다. 하지만 볼스크류 조립체에서 발생하는 마찰력은 Fig. 17과 같이 볼스크류 작동구간 내에서 계속해서 증가되는 경향을 확인할 수 있다. Figs. 18과 19에서 화살표는 볼스크류 내 볼에서 발생하는 반력의 크기를 나타내며, 앤드캡 내 볼이 완전히 채워지면서 급격히 반력이 증가하는 결과를 확인 할 수 있다. 이는 볼의 구름성에 악영향을 미치는 과도한 사이클로이드 R 값이 적용되었기 때문인 것으로 판단되며 사이클로이드 R2.4 앤드캡은 볼스크류의 구동 성능에 악영향을 미칠 것으로 사료된다.
5. 결론
본 연구에서는 볼스크류의 성능 향상을 위해 볼스크류 구성품 중 앤드캡 타입의 볼 순환구조에 사이클로이드 곡선을 적용한 다섯 가지 디자인을 제시하였다. 설계된 다섯 가지 디자인에 대해 동역학적 특성을 예측하기 위해 앤드캡 단품 및 볼스크류 조립체에 적용된 앤드캡에 대해 점 P1, P2에서 각 5가지, 전체 10가지 경우에 대해 다물체 동역학 해석을 진행하였으며, 앤드캡 단품과 볼스크류 조립체 내 앤드캡 간에 볼 흐름과 관련된 구동 성능을 비교하였다. 본 연구를 통해 도출한 내용은 다음과 같다.
(1) 볼의 자전속도 값은 볼스크류 내 볼의 자전 능력을 나타내는 값으로, 값이 클 경우 볼의 순환이 원활하여 볼스크류의 내구 및 성능에 유리한 것으로 판단된다.
(2) 사이클로이드 R2.0(볼 반지름 대비 100%) 앤드캡이 적용된 볼스크류에서 P1, P2 두 점 대한 가장 높은 자전속도 상승폭을 얻을 수 있었으며, 이때 가장 적은 마찰력을 가지며 가장 높은 구동 성능을 가지는 것을 확인할 수 있었다.
(3) 사이클로이드 R2.4(볼 반지름 대비 120%) 앤드캡이 적용된 볼스크류에서 두 개의 앤드캡 내 볼이 가득 차있을 경우에는 과도한 사이클로이드 R 값으로 인해 볼의 흐름이 원활하지 못하게 되는 현상을 확인할 수 있었다.
본 연구를 통하여 더 높은 성능을 얻을 수 있는 앤드캡 타입 볼 순환구조에 대한 적절한 사이클로이드 R 값을 얻을 수 있었으며, 추후 너트 구동방식, 앤드캡 타입 볼 순환구조 이외에도 다양한 구동 방식 및 순환 구조에 대해 다양하게 고려하여 최적화된 볼 순환구조를 도출할 수 있을 것으로 사료된다.
NOMENCLATURE
| Dpw : | Pitch circle diameter |
| Dw : | Ball diameter |
| Ф : | Lead angle |
| l : | Lead |
| α : | Contact angle |
| dc : | Diameter of axial pressure |
| FN' : | Normal force on the ball |
| ΔNut : | Deformation of the ball and ball raceway in the nut |
| ΔShaft : | Deformation of the ball and ball raceway in the shaft |
| Δt : | Axial strain |
Acknowledgments
본 연구는 2016년도 정부(미래창조과학부)의 재원으로 한국연구재단의 지원을 받아 수행된 지역 신산업선도 인력 양성사업 성과임(NRF-2016H1D5A1910421).
REFERENCES
- Park, D. K., Kim, H. K., and Lee, C. M., “A Study of Endcap Type on Ball Screw,” Journal of the Korean Society for Precision Engineering, Vol. 25, No. 12, pp. 13-19, 2008.
- Park, C. W., Kim, D. E., and Lee, S. J., “A Study on the Groove Design in Ball Screws,” Journal of the Korean Society of Mechanical Engineering, Vol. 20, No. 1, pp. 154-162, 1996.
- Choi, C., “A Study on Performance Improvement of Feed System in a High-Precision Ball Screw,” Ph.D. thesis, Mechanical and Aerospace Engineering, Gyeongsang National University, 2015.
-
Sobolewski, J. Z., “Vibration of the Ball Screw Drive,” Engineering Failure Analysis, Vol. 24, pp. 1-8, 2012.
[https://doi.org/10.1016/j.engfailanal.2012.03.002]

-
Ham, S.-H. and Youm, K.-W., “A Study of Pin-Pinion Tooth Profile Applied with Cycloid Tooth Profile,” Journal of the Korean Institute of Gas, Vol. 18, No. 6, pp. 45-50, 2014.
[https://doi.org/10.7842/kigas.2014.18.6.45]

- Lee, C. S. and Park, K. S., “Development of Surface Creation Program for Cycloid Reducer of In-Wheel Motor,” Proc. of the Korean Society of Automotive Engineering Autumn Conference, pp. 1359-1363, 2010.
- Yun, C. Y., Yun, Y. H., Kim, D. S., Park, I. G., and Kim, S. J., “Design and Performance Tests of Cycloidal Blades System (CBS),” Proc. of the Korean Society Aeronautical and Space Sciences Conference, pp. 151-154, 2003.

Research Engineer in the Advanced Research Team of Central Motek, Korea. His research interest are machine and dynamics.
E-mail: Chaeyoon.yang@ctr.co.kr

Ph.D. candidate in the Department of Mechanical and Aerospace Engineering, Gyeongsang National University. His research interests are automotive power train, mechanical structure and vibration.
E-mail: sghan7589@gnu.ac.kr

Associate Research Engineer in the Advanced Research Team of Central Motek, Korea. His research interest are machine and dynamics.
E-mail: Bokyun.kim@ctr.co.kr

Director in the Advanced Research Team of Central Motek, Korea. His research interest are machine and dynamics.
E-mail: jongheun.park@ctr.co.kr

Professor in the School of Mechanical Engineering and Engineering Research Institute, Gyeongsang National University. His research interests are vibration control, system dynamics, and automotive power train.
E-mail: cksong@gnu.ac.kr