3면 지지 철근 콘크리트 복합 구조 방폭문의 최대탄성변위 산정 방법
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Displacement ductility and rotational ductility are used, to verify the performance of blast doors subjected to explosive loads. The values of these performance items are calculated by measuring the maximum elastic displacement in the laboratory, and the maximum displacement during the explosion test. To attain the maximum elastic displacement, the finite element analysis and the load distribution method are applied. In applying the load distribution method, the behavior of a blast door along a width direction is converted to a cantilever beam and along a height direction to a simply supported beam. The results by the load distribution method are verified by a finite element analysis and compared with those by a plate theory.
Keywords:
Blast door, Displacement ductility ratio, Maximum elastic displacement, Load distribution, Finite element analysis키워드:
방폭문, 변위연성도, 최대탄성변위, 하중분배, 유한요소해석1. 서론
방호구조물의 성능은 정부에서 제정한 민방위 시설의 경우 방호도를 7등급으로 구분하고 있으며 1등급은 유사시 군 본부로 활용할 수 있는 시설로 핵 공격을 제외한 모든 공격에 대한 방호가 가능하고 2등급은 GP550 폭탄의 직접 폭발에 방호가 가능하도록 규정되어 있다. 이런 방호구조물에 대한 연구는 주로 방호구조물의 설계 방법과 방호구조물의 신뢰성 검증에 대하여 이루어지고 있다.
근래에 철근 콘크리트 방호구조물의 설계와 신뢰성 검증에 대해 공학해석 프로그램을 사용한 연구성과들이 다수 발표되었다. 콘크리트 기둥이 폭발하중을 받을 때 Autodyn 프로그램에 의하여 설계변수의 변화에 따라 저항 성능을 예측하는 연구결과들1,2이 보고되었으며, 콘크리트 패널에 폭발하중이 작용하였을 때 부재의 최대변형을 평가하고 콘크리트의 강도와 프리캐스트 적용여부 및 프리스트레싱 적용유무에 따른 거동과 손상강도를 평가하는 연구가 유한요소해석 프로그램을 사용하여 발표된 바 있다.3 Kim은 방폭문의 실증시험 데이터와 ANSYS-Autodyn을 이용한 수치해석결과를 분석하여 슬라이딩 방폭문의 설계안정성을 검토하였다.4
정부는 2012년에 한국가스안전공사를 화생방 방호 설비 시험 인증분야의 국제 공인시험기관으로 지정하였고 한국가스안전공사는 방폭문 체계의 공인 인증을 위하여 화생방 방호 시설과 방폭문 폭발실증시험의 세부 절차 및 방법을 제시하였다.5
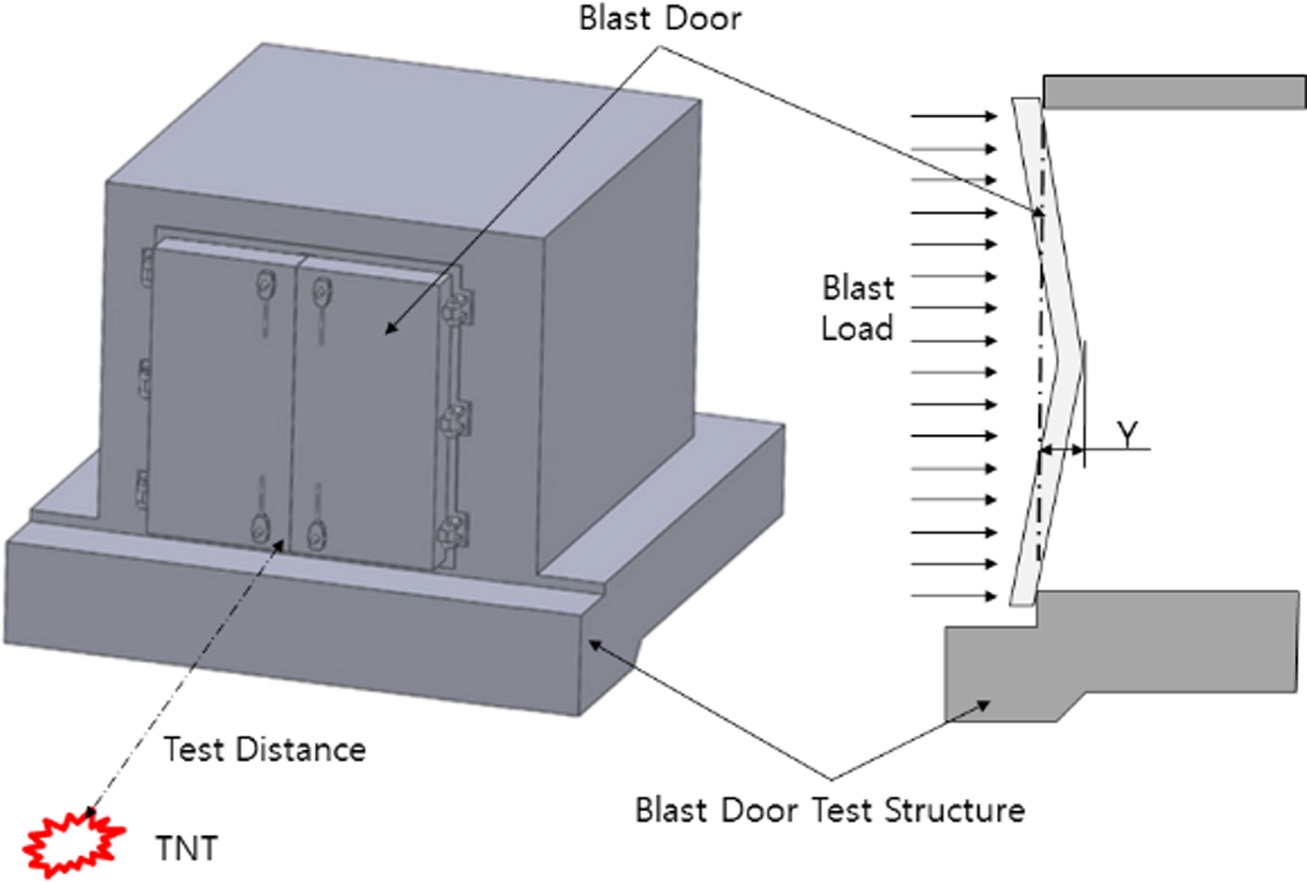
폭발실증시험은 방폭문이 설치되는 콘크리트 구조체와 폭발물이 동일한 수평면 상에 위치하며 지표면 폭발을 원칙으로 한다. 반사 압력 효과를 차단하기 위하여 폭발 원점을 기준으로 구조체의 정 반대편에 인공 구조물의 설치가 없어야 하며 폭발물은 콘크리트 포장 면 위에 설치되어야 한다. 방폭문의 성능등급기준은 폭발 하중을 받은 후 방폭문이 사용상에 문제가 없어야하며, Table 1에 제시한 성능 지표의 값의 수준에 따라서 등급이 결정된다.
표에서 회전연성도(Rotational Ductility Ratio)는 방폭문이 폭발압력을 받은 후 부재의 지지 점에서 발생하는 최대 회전각도(θ)로 정의되며, 폭발 시험 중 발생한 최대 변위(Ym)와 최대 변위가 발생한 지점과 문의 지지점 사이의 거리(S/2)를 측정하여 구한다. 변위연성도(μ)는 폭발에 의해 발생한 최대 변위(Ym)와 방폭문의 최대탄성변위(Ye)의 비율로 μ = Ym/Ye로 정의된다.
폭발실증시험을 할 때 한국가스안전공사는 성능 등급을 판정하기 위하여 최대탄성변위(Ye)를 업체에서 산정하여 제출하도록 요구한다. 국내 방폭문 제조업체는 전문 기관에 최대탄성변위 산정을 위탁하여 제출하고 있으나 이에 대한 신뢰도 향상이 필요한 실정이다. 본 연구에서는 양개형 방폭문에 대하여 성능 지표 판정의 기준이 되는 최대탄성변위를 유한요소해석에 의하여 구하였고 하중분배이론(Load Distribution Theory)을 사용하여 설계 현장에서 실용적으로 근사 값을 구하는 방법을 제시하였으며 판이론(Plate Theory)으로 부터 구한 결과와 비교하였다.
2. 양개형 방폭문의 구조 및 거동
2.1 철근 콘크리트 양개형 방폭문의 구조
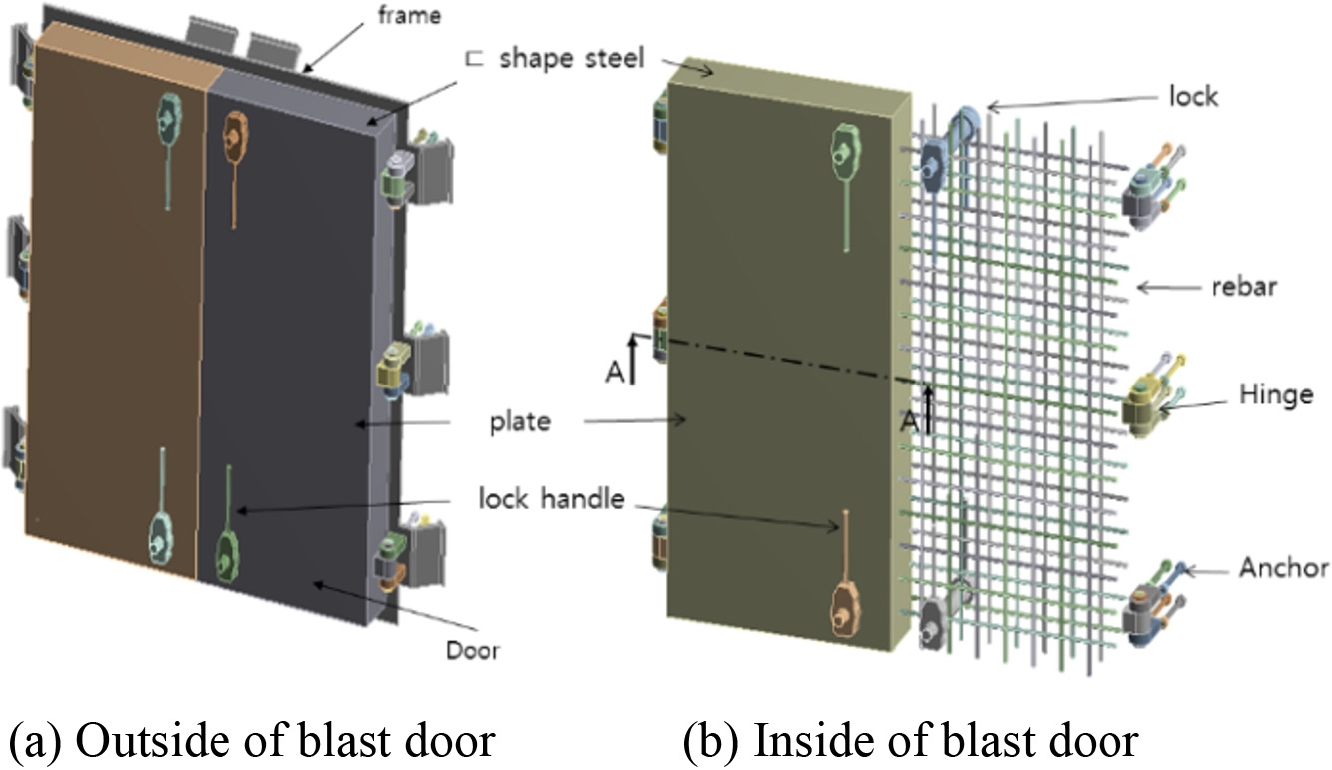
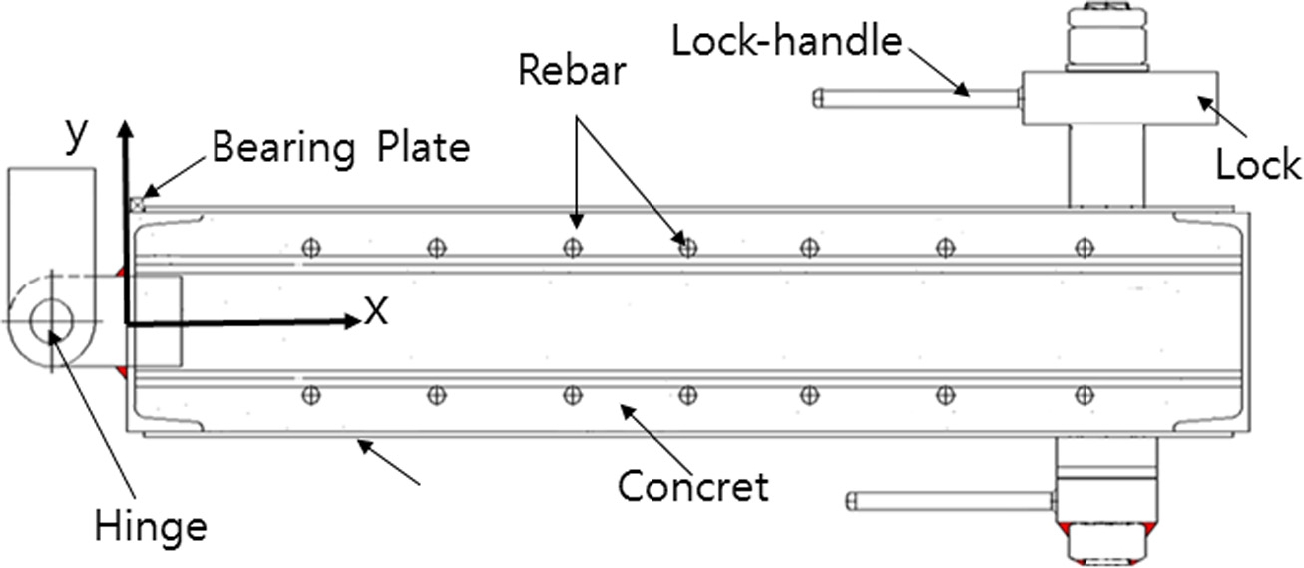
철근 콘크리트로 구성된 양개형 방폭문은 방호구조물의 입구에 2개의 여닫이 문으로 설치된다. 본 연구의 대상인 문의 한쪽 치수는 높이 2540 mm, 폭 1263 mm, 두께 318 mm이며 방폭문 골조는 전면 철판 12 mm와 후면 철판 6 mm로 구성되어 있고 전면과 후면 철판을 연결하며 콘크리트를 가두어 두는 역할을 하는 ㄷ-형강이 양 옆과 위아래에 설치되어 있으며 4개의 ㄷ-형강은 용접으로 접합되어 있다. 방폭문 내부에는 이형 철근(Deformed Bar) 22개가 일정간격으로 격자 형식으로 배치되어 방폭문과 용접되어 있으며 내부 공간은 콘크리트로 충진 되어 있다(Fig. 2).
문이 설치되는 방호구조체(콘크리트)와 연결되는 부분은 2700 × 2700 mm의 강 프레임(Steel Frame)이며 앵커 볼트에 의해 구조체에 고정되며 방폭문과 프레임이 접촉하는 부분에 각띠(Bearing Plate)가 있어 방폭문과 방호구조체가 완전히 밀착되며, 고무패킹을 사용하여 방호구조체 내부로 폭발에 의해 오염된 가스가 유입되지 않는 구조로 되어있다. 방폭문은 프레임에 6개의 힌지로 연결되어 회전성을 확보하고 각 방폭문에 2개씩 총 4개의 잠금 장치가 설치되어 있다.
2.2 철골 콘크리트 양개형 방폭문의 거동
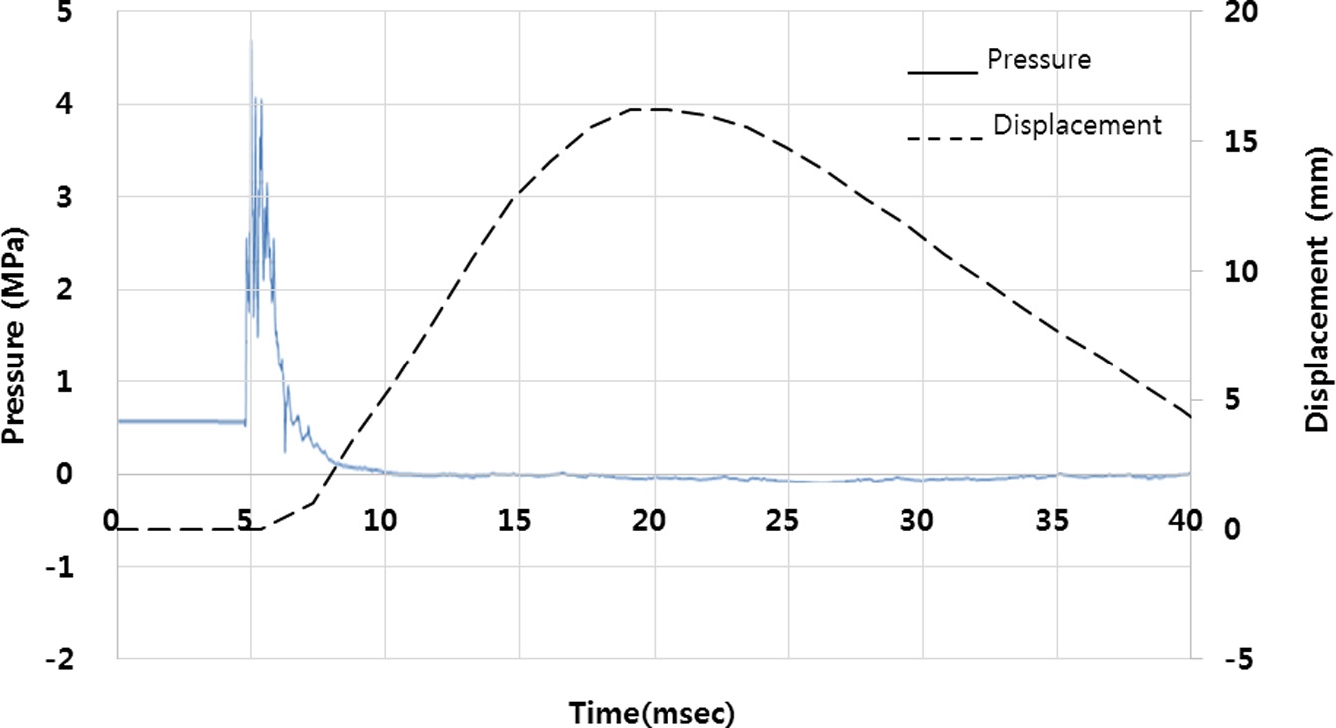
Fig. 3은 본 연구의 대상인 양개형 방폭문을 이격거리 5.66 m에서 TNT 125 kg을 폭발시킨 실험의 수행 전∙후의 형상이다. 이 실험결과 방폭문에는 최대 4.84 MPa의 충격 하중이 가해졌고, 이로 인해 방폭문은 16.7 mm의 최대 변위(Ym)가 발생되었다(Fig. 4). 본 실험에서는 방폭문에 48.4 bar의 폭발 압력이 발생하였으며 이는 방폭문 설계기준압력 40 bar를 넘어서는 것이며 방폭문의 방호 등급을 검증할 수 있는 크기이다.
방폭문은 폭발 하중이 작용하는 방향으로 볼 때 방호구조체에 지지된 슬래브(Slab)와 같은 거동을 한다. 슬라브는 지지하는 양변의 길이 비에 따라서 1방향 슬라브와 2방향 슬래브로 분류되며 하중이 작용하면 휨 파괴 모드를 갖는다.6
3. 유한요소해석에 의한 처짐과 응력 계산
철근 콘크리트 양개형 방폭문의 최대탄성변위를 산정하기 위하여 유한요소해석(Finite Element Analysis)을 수행하였으며 해석에 사용된 소프트웨어는 ANSYS이다.
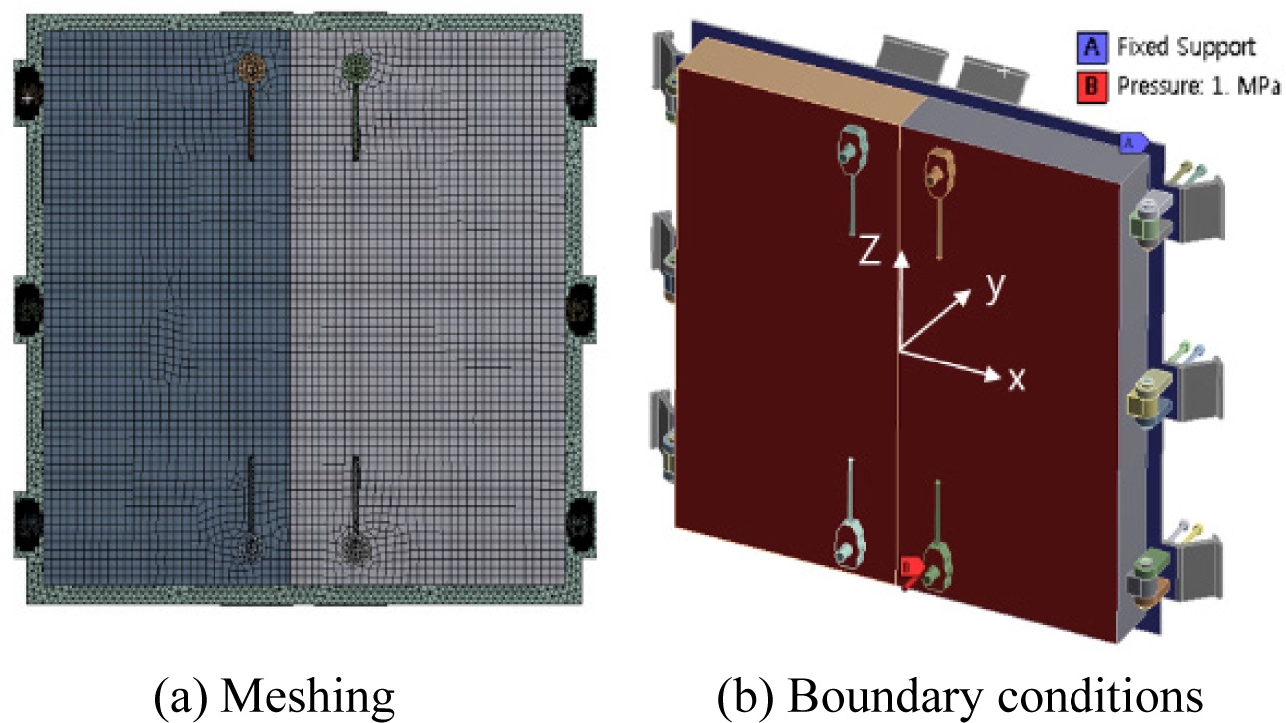
Fig. 5(a)와 같이 방폭문에 사용되는 모든 부재는 실 형상의 기하 모델로 구성하였고 유한요소모델은 Fig. 5(a)와 같이 약 10만개의 요소로 구성하였다. 경계 조건은 방폭문이 잠김 상태에 있을 때에 폭압이 작용한 상태에 대하여 부여하였으며 이 때 방폭문 뒷면의 바깥테두리에 용접된 각띠가 방호구조체상에 앵커로 고정되어 있는 강프레임에 압착하여 접촉되므로 각띠와 방폭문이 접촉하는 부분의 방폭문의 y축 방향 변위는 고정하였고 방폭문의 잠금 손잡이가 있는 앞면 철판에 Fig. 5(a)와 같이 균일한 압력을 가하여 구조해석을 수행하였으며 방폭문에서 발생하는 변위와 응력을 계산하였다.
4. 하중분배법에 의한 처짐 및 응력 계산
4.1 슬래브에 작용하는 하중의 배분 방법
일반적으로 슬래브 설계는 건설구조기준에서는 등가 골조 설계법이나 직접법으로 설계하도록 규정하고 있으나 이런 방법은 소성 응력을 고려한 방법이므로 방폭실증 시험에서 요구하는 최대탄성변위를 산정하기 어렵다.7
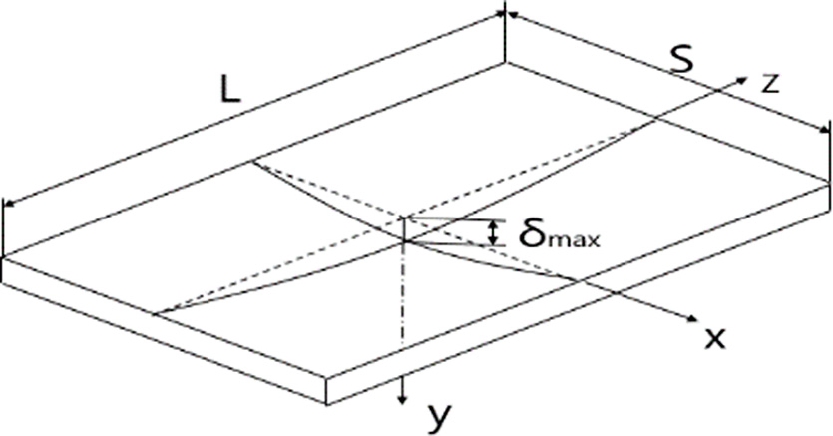
하중분배법(Load Distribution Method, LDM)에서는 사변 단순 지지의 슬래브인 경우(Fig. 6) 거동을 단순화하기 위해 슬래브의 긴 변(L)과 짧은 변(S)의 비(L/S)가 2를 넘는 경우 1방향 단순지지보로 해석하고, 비가 2를 넘지 않는 경우 슬래브의 하중을 2방향으로 분배하여 거동을 해석한다. 2방향 슬래브에 작용하는 균일분포하중(W)은 x-방향 하중(Wx)과 z-방향 하중(Wz)으로 분리하며 식(1)과 같이 두 하중의 합은 작용 하중과 같고, 슬래브의 중앙에 위치한 단위 폭의 대(Strip)가 단순 지지 상태에서 균일분포하중을 받아 처지는 변위량이 두 방향(x, z방향)의 대에 대하여 같다고 보아 두 방향으로 하중을 분배한다.8 분배된 하중은 식(2)와 식(3)과 같고 L > S이므로 슬래브의 하중은 짧은 변 방향으로 더 큰 하중이 작용한다.
| (1) |
| (2) |
| (3) |
4.2 양개형 방폭문에 작용하는 분포 압력의 배분
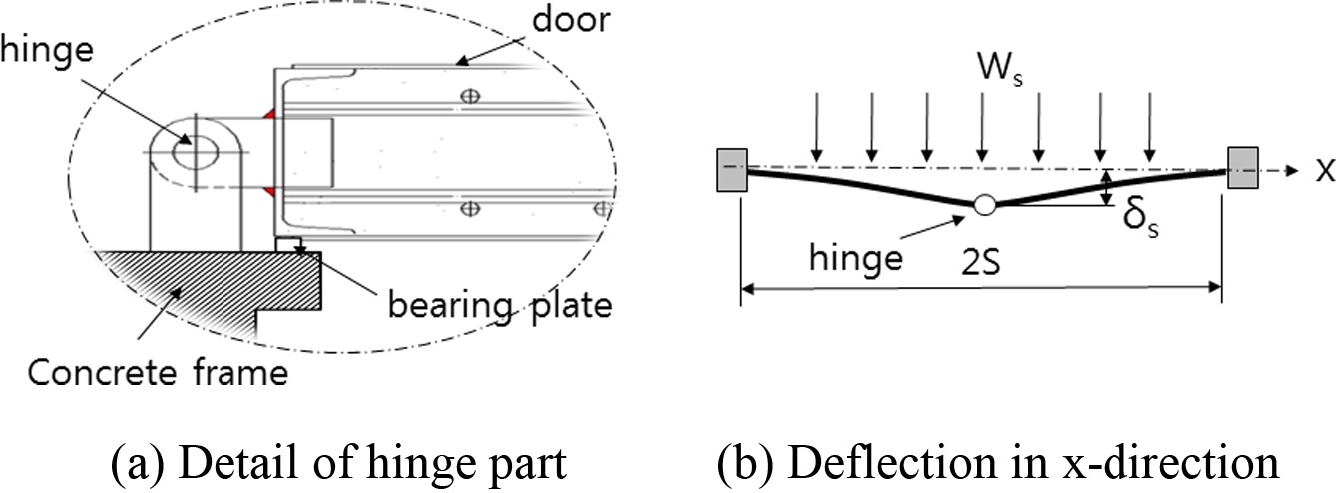
폭발압력을 받는 양개형 방폭문의 변위는 Fig. 7과 같이 나타낼 수 있다. 2방향 슬래브에서 Fig. 6의 사변 지지 슬래브에 적용한 하중분배원리를 양개형 방폭문에 적용하여 하중을 분배할 수 있다. 방폭문의 힌지가 설치된 쪽의 가장자리는 힌지와 각띠의 영향으로 내민보 구조이며 Fig. 7(a)와 같이 힌지와 각띠(Bearing Plate)의 간격이 좁기 때문에 방폭문의 각띠와 콘크리트 구조체가 접촉하는 부분에서는 처짐각을 0으로 가정할 수 있다. 양쪽 방폭문의 중앙에서 최대 변위가 발생하고 양쪽 방폭문이 접촉하는 부분은 자유단으로 모멘트가 0이다. 따라서 방폭문에서 폭 방향(x축 방향)으로는 Fig. 7(a)와 같은 부정정 구조물로 모델링할 수 있다. 높이 방향(z축 방향)은 균일 분포 압력을 받는 단순지지보로 모델링하였다.
그리고 방폭문의 중앙에서 각 방향의 단위 폭의 대(Strip)에 작용하는 분포 하중에 의해 발생하는 높이 방향의 최대 변위(δL)와 폭 방향의 최대 변위(δS)가 기하학적으로 같다고 하여 분배 하중(WL, WS)을 계산 하였다.
| (4) |
그리고 방폭문 전면 철판과 후면 철판의 두께가 다르므로 방폭문의 중립축은 다음과 같이 계산하며 A는 방폭문 부재의 면적이다.
| (5) |
방폭문 부자재의 단면 2차 모멘트(IX)는 중립축에서 부재중심까지의 거리 (y0)를 반영하여 다음 식(6)과 같이 산정한다.
| (6) |
철골, 철판과 철근 콘크리트 구조물은 변형률이 같고 탄성변형을 한다고 가정하고 부자재를 콘크리트로 단면 치환하여 콘크리트에 상당하는 방폭문의 단면 2차 모멘트를 다음 식(7)과 같이 구하였다.9
| (7) |
위 식에서 ni = Ei / Ec (Ec =콘크리트 탄성계수, Ei =콘크리트·철근∙철판의 탄성계수)이다. 폭 방향에 작용하는 분포 압력(Ws)에 의한 부정정 구조물(=외팔보)의 최대 변위는 다음 식(8)과 같다.
| (8) |
높이 방향의 분포 하중(Wl)이 작용하는 단순지지보의 최대변위는 다음 식(9)와 같다.
| (9) |
식(8)과 식(9)를 식(4)에 적용하면 다음 식(10)과 같다.
| (10) |
식(10)을 정리하여 식(1)에 대입하여 다음과 같이 각 방향으로 분배된 하중을 구하였다.
| (11) |
| (12) |
4.3 양개형 방폭문의 단면 2차 모멘트
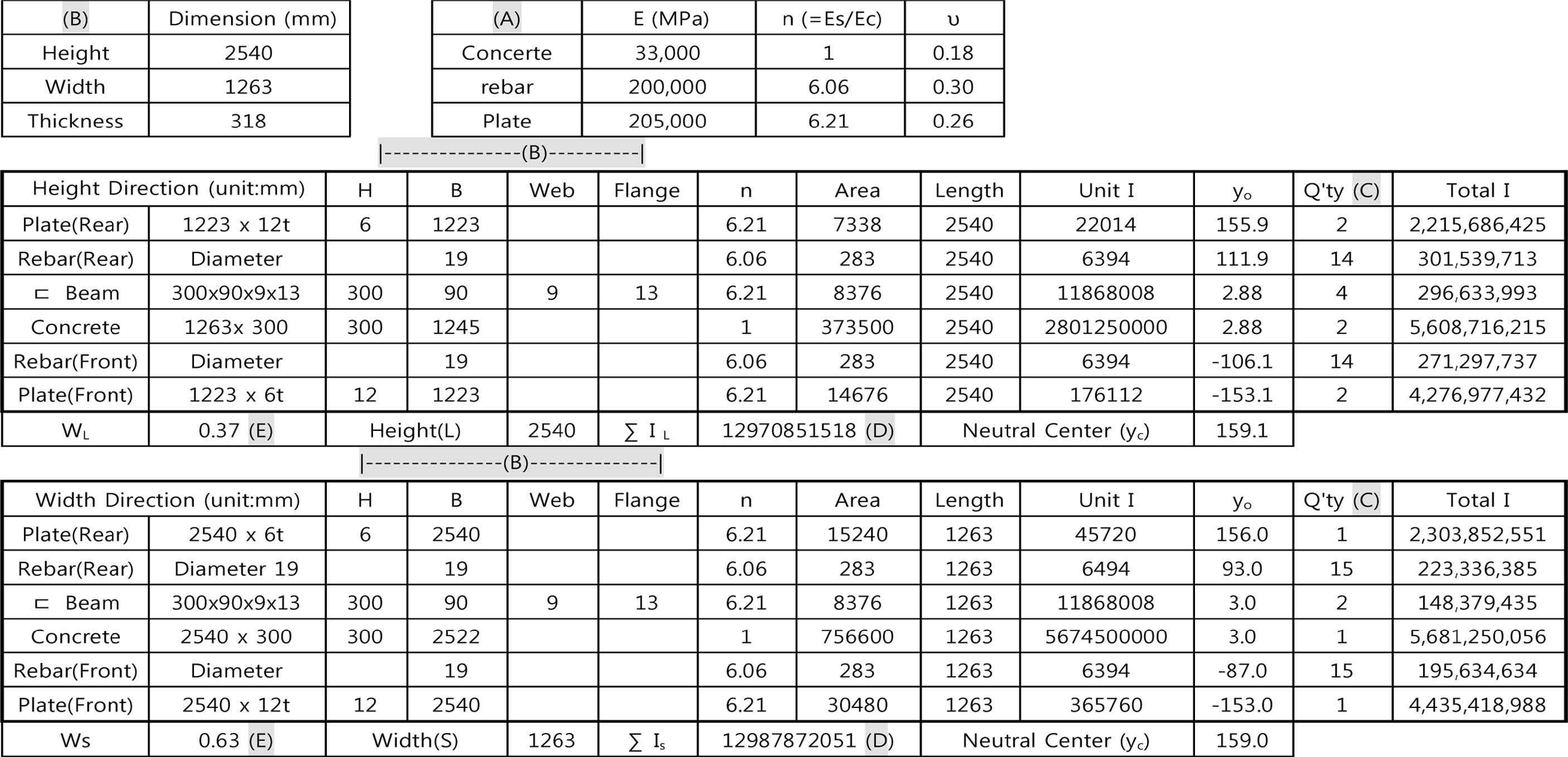
Fig. 8은 양개형 방폭문의 높이 방향의 휨에 영향을 주는 단면 2차 모멘트(IL)를 산정하는데 영향을 주는 부재의 단면을 도시한 것이다. 철근의 길이를 폭(x축) 방향으로 배근한 철근은 높이 방향의 휨에 영향을 주지 않으므로 단면 2차 모멘트 계산에서 제외한다. 콘크리트 부재의 단면을 간편하게 계산하기 위하여 콘크리트 속 철근의 면적에 해당하는 콘크리트 면적은 제외하지 않고 계산하였다. 방폭문 전면 철판과 후면 철판의 두께가 다르기 때문에 식(5)를 사용하여 중립축을 계산하였다.
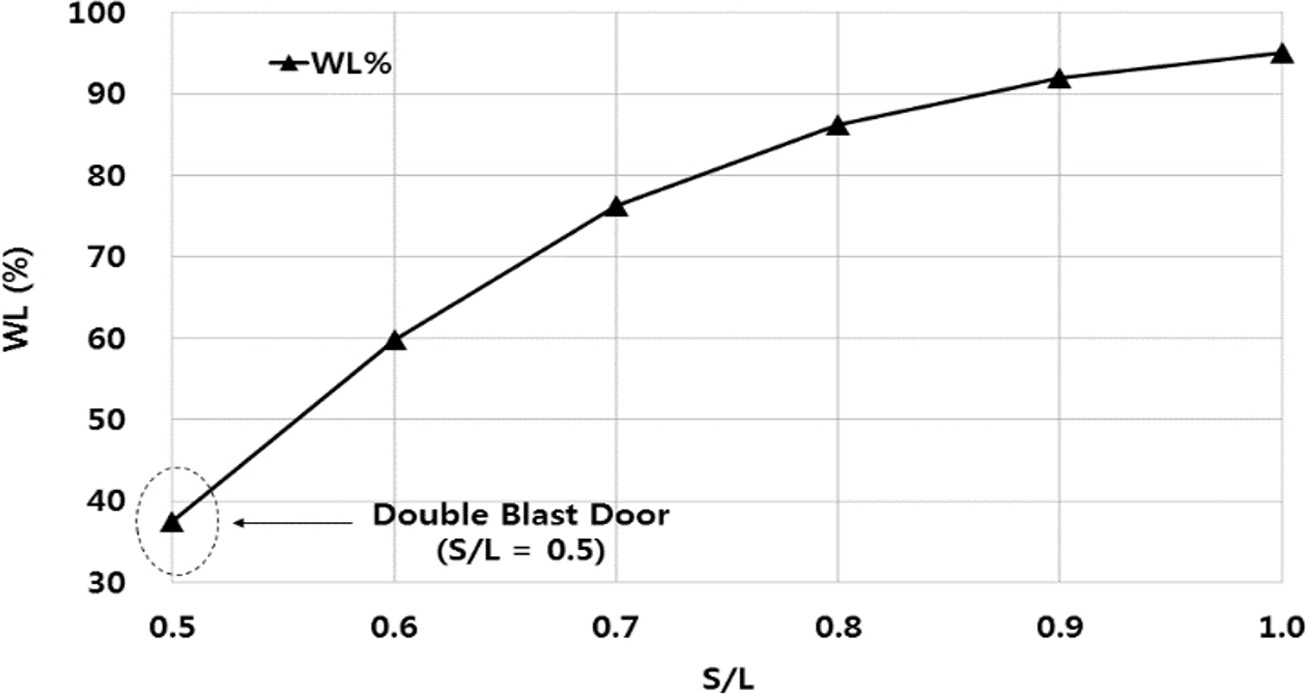
Table 2는 부재의 형상과 배치에 따라서 단면 2차 모멘트와 분배된 하중을 구하는 방법을 엑셀로 논리화한 것이다. 방폭문부재에 대하여 Table 2의 회색 박스에 부재의 물성(A)과 부재의 치수(B), 부재의 개수(C)를 입력하면 단면 2차 모멘트(D)를 구하고 폭 방향과 높이 방향의 하중이 분배된다(E). 본 연구의 방폭문의 경우 W의 압력이 작용할 때 폭 방향에 작용하는 압력은 Ws= 0.63 w로 분배되고 높이 방향에 작용하는 압력은 Wl= 0.37 w로 분배되었다. 양개형 방폭문의 폭과 높이의 비(S/L)가 달라질 때 방폭문에 작용하는 분포 하중 중에서 높이 방향으로 작용하는 분포 하중(Wl)의 비율을 Fig. 9에 도시하였다. 양개형 방폭문의 폭이 길어질수록 방폭문의 높이 방향으로 휘게 하는 분포하중의 분담률은 증가 하는 것을 알 수 있다. 방폭문이 정사각형(S/L = 1)이며 상하면은 단순 접촉되고 좌측면의 처짐각이 0이며 우측면은 자유단인 경우 방폭문의 높이방향으로 휨을 유발시키는 분배 압력은 전체 압력의 95%가 된다.
4.4 양개형 방폭문의 처짐과 응력 계산
양개형 방폭문을 하중분배법으로 하중을 배분하고 높이 방향으로 분배된 압력(Wl)을 받는 단순지지보의 변위와 응력을 계산하면 다음 식(13), 식(14)와 같다.
| (13) |
| (14) |
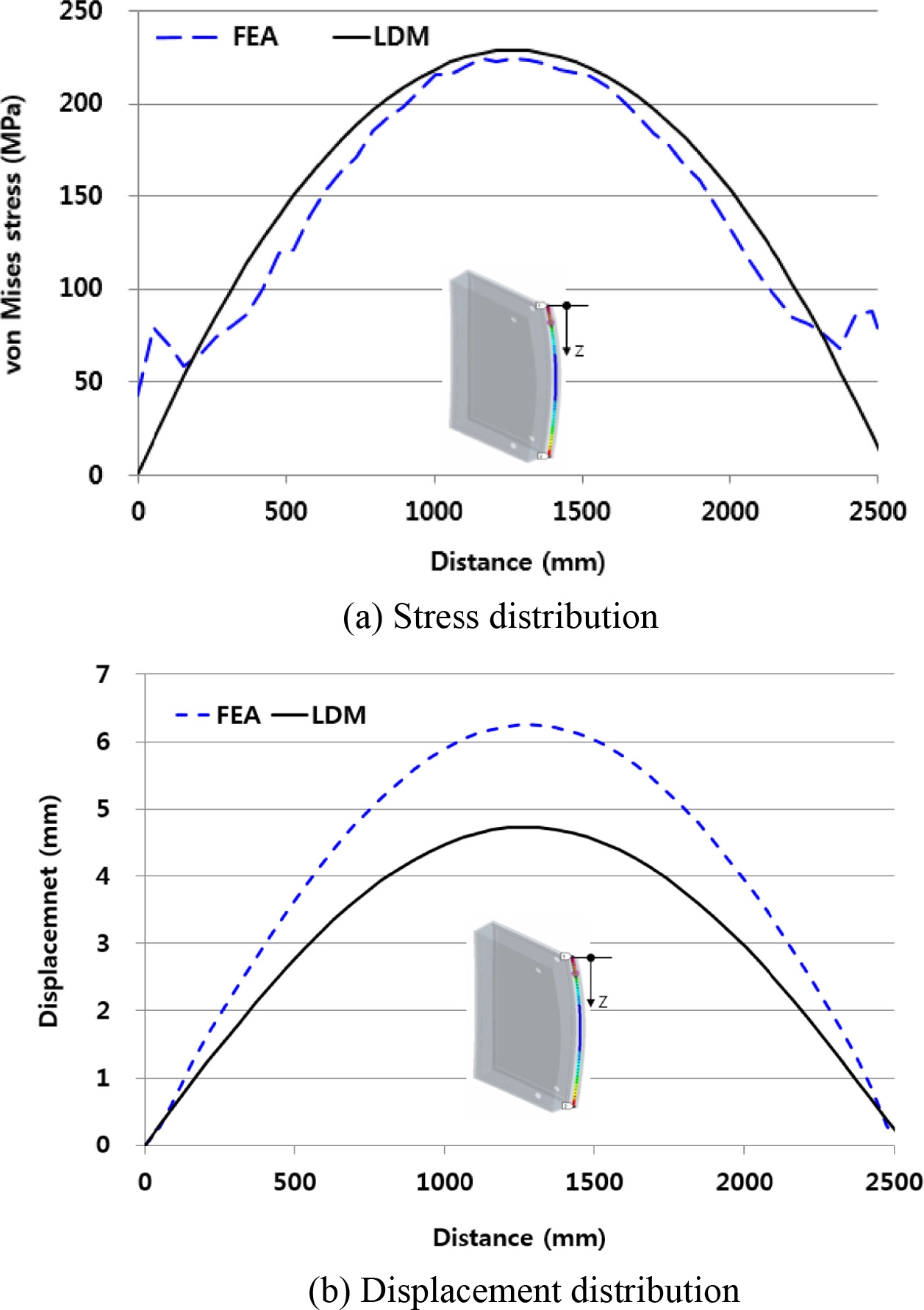
여기서 z는 방폭문 높이 방향의 위치이며 y는 방폭문 두께의 중립면에서 후면 철판의 외측 면까지의 위치이다. 하중분배법과 유한요소해석으로 4 MPa의 폭발압력을 받은 방폭문의 변위와 응력 분포를 Fig. 10에 나타내었다.
Fig. 10(a)는 방폭문이 4 MPa의 폭발압력을 받을 때 높이 방향에 따른 Von Mises 응력 분포를 도시한 것이다. 방폭문은 양쪽 끝에는 형강으로 구성되어 있어 강성이 크고 가운데는 철골과 콘크리트만으로 구성되어 있어 상대적으로 강성이 작다. FEA에서는 방폭문의 위치에 따라 강성의 불균형이 반영되어 계산되므로 콘크리트를 가두기 위한 상측 ㄷ-형강 부분에 응력이 집중되며 아래쪽에는 하측 ㄷ-형강 부분에 응력이 집중되는 것으로 나타났다. 하중분배법에서는 방폭문의 높이 방향의 중앙에서 구한 방폭문의 강성을 방폭문 높이에 따라 동일하게 적용하므로 방폭문 상하부에 있는 ㄷ-형강의 영향을 반영하지 못하여 응력집중 현상이 계산되지 않았다. 따라서 단면 2차 모멘트가 작게 되어 방폭문에 작용하는 응력이 FEA 결과보다 크게 계산되었다.
변위 분포는 문의 상부와 하부 끝에는 변위가 없고 가운데가 최대가 되는 2차 함수의 형상을 보인다(Fig. 10(b)).
하중분배법으로 구한 양개형 방폭문의 최대 변위와 최대 응력은 양쪽 방폭문이 접촉하는 중앙의 후면철판에서 발생한다. 방폭문 중앙부에서 최대 모멘트는 wLL2/8이므로 최대 변위와 최대 응력은 다음 식(15), 식(16)으로 계산된다.
| (15) |
| (16) |
하중분배법에 의해 방폭문의 높이 방향으로 분배된 하중이 높이 방향의 단순지지보에 작용할 때 구한 변위(식(15))의 타당성을 검증하기 위하여, 방폭문과 동일한 조건(2변 = 단순지지, 1변 = 고정지지, 1변 = 자유단)이고 등방성 물성을 갖는 슬래브를 대상으로 장∙단변의 길이 비(S/L)를 변화시키면서 판이론(Plate Theory)을 적용하여 구한 변위와 비교하였다.10 판 이론으로 계산한 최대 변위는 다음 식(17)과 같다.
| (17) |
위 식(17)에서,
| (18) |
| (19) |
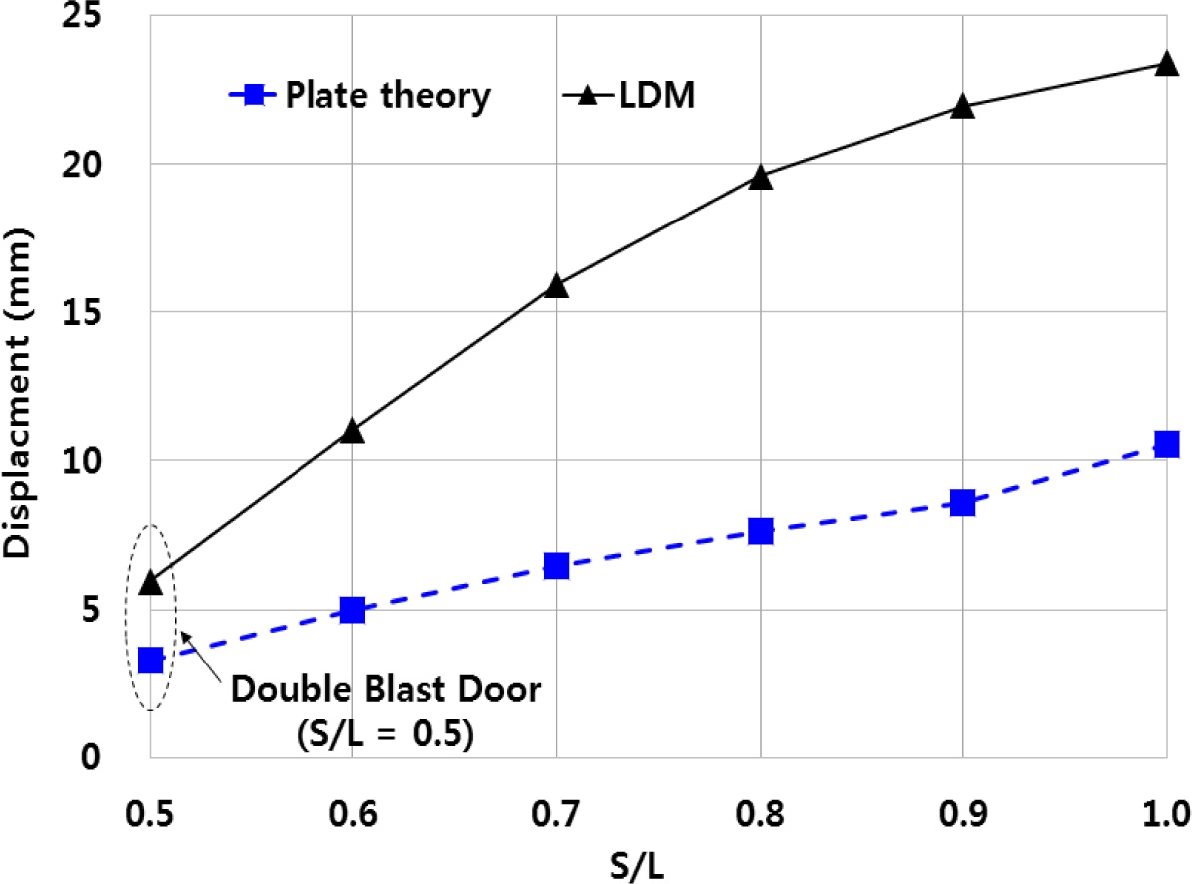
이며, 장변의 길이(L)는 2540 mm, 두께(h)는 318 mm, 등가 탄성계수(Ecm)는 62.7 GPa, Poisson’s Ratio (v)는 0.3인 판에 균일분포압력(W) 4 MPa이 작용할 때, S/L 비율에 따른 최대 변위를 판이론으로 구한 식(17)과 하중분배법으로 구한 식(15)에 의해 계산하여 그 결과를 Fig. 11에서 비교하였다.
S/L이 증가하면 변위가 증가하는 경향은 유사하나, 하중분배법의 처짐량은 판 이론에 비하여 2배 정도 크게 산정된다. 따라서 하중분배법을 사용하여 방폭문의 처짐을 산정하여 설계하면 보수적으로 설계되는 것으로 보인다.
4.5 양개형 최대탄성변위 산정 방법
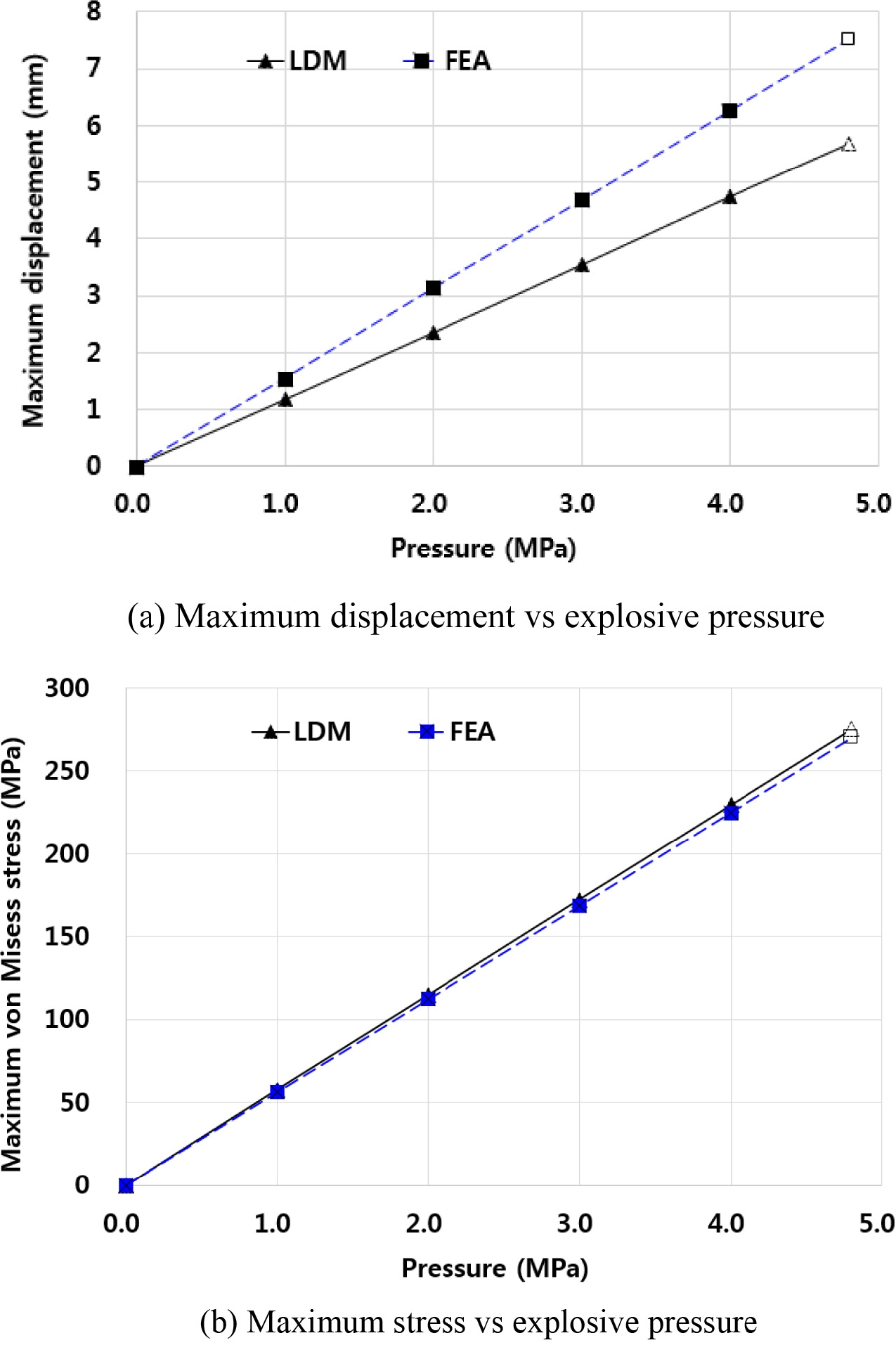
방폭문에 작용하는 폭발압력을 1 MPa로부터 증가시키면서 식(15)을 사용하여 유한요소법과 하중 분배법으로 최대 변위를 구한다. 식(16)으로 최대 응력을 구하여 방폭문 철판의 항복 강도인 275 MPa와 비교하여 철판의 소성 여부를 판단하였다. 철근 콘크리트 구조물의 최대탄성변위는 연구에 의하면 철근의 영향을 주로 받으므로 철근에서 발생하는 최대 응력이 항복 강도에 도달할 때의 변위로 하였다.11
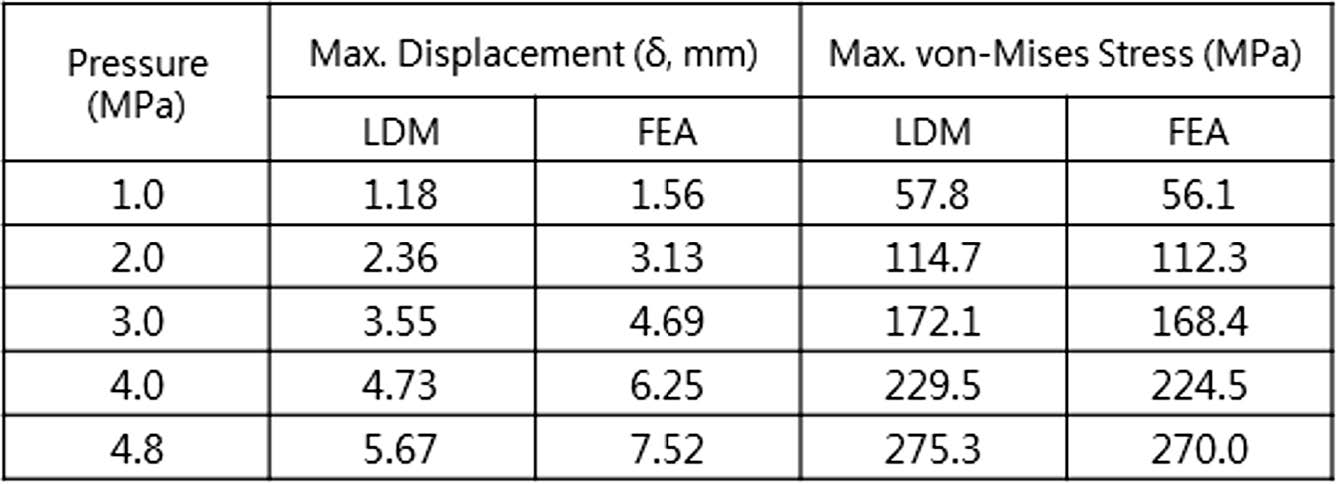
Table 3은 4 MPa까지 하중을 증가시킨 양개형 방폭문의 최대변위와 최대응력을 하중분배법과 유한 요소법으로 구한 후 그 결과를 비교한 것이다. Table 3과 Fig 10(b)와 같이 하중분배법으로 계산한 폭압 방향의 최대 변위는 유한요소해석으로 계산한 값의 76.7% 정도가 된다. 방폭문에 발생한 응력이 방폭문 철판의 재질(SS275)의 항복강도인 275 MPa에 이를 때 방폭문이 항복에 이르므로 Fig 12(b)와 같이 FEA 기준으로 폭발 압력이 4.8 MPa일 때 항복 강도에 도달한다. 이 때 방폭문의 후면 철판이 소성변형을 시작하게 되어 최대 탄성 변위(Ye)는 7.52 mm로 산정할 수 있다.
이로부터 본 연구에서 실증 실험한 방폭문은 최대 변위(Ym)가 16.7 mm이므로 변위연성도(μ)는 2.22, 회전연성도(θ)는 0.75°로 산정된다. 따라서 Table 1의 판정기준에 의하여 본 연구 대상인 양개형 방폭문은 방호 2등급 A수준으로 판정할 수 있다.
5. 결론
본 연구에서는 철근, 철판, 콘크리트로 만들어진 양개형 방폭문의 성능평가 등급의 기준이 되는 최대탄성변위를 유한요소해석에 의하여 구하였고 이를 하중분배이론에 의해 간단히 계산하여 실용적으로 사용할 수 있는 방법을 제시하였다. 하중분배법에서는 분포 압력을 받는 방폭문을 2방향 슬래브와 같이 장축과 단축으로 하중을 분배하여 분배된 하중을 받는 1방향 슬래브로 치환하고 1방향 슬래브를 외팔보 및 단순지지보로 보아 변위 및 응력을 계산하였으며 철근, 철판 및 형강을 콘크리트를 기준으로 단면을 환산하여 철강과 철근의 응력을 산정하였다.
유한요소해석에서는 철근 콘크리트 양개형 방폭문을 구성하는 모든 부품이 3차원 실제 형상일 때의 변위와 응력을 구하였으며 하중분배법에 의한 계산 결과와 비교하였다. 그리고 하중분배법에 의해 최대탄성변위를 문의 가로와 세로의 비가 변화 할 때에 대하여 구하고 그 결과 값을 판 이론에 의해 얻은 결과와 비교하여 타당성을 검토하였으며 본 연구로부터 다음과 같은 결론을 얻었다.
(1) 폭발 실증시험에서 인증 평가의 기준이 되는 최대탄성변위를 유한요소해석과 하중분배법으로 산정할 수 있음을 보였다.
(2) 하중분배법으로 구한 변위량은 판 이론으로 얻은 값보다 커서 보수적인 설계가 된다.
(3) 본 연구 대상의 양개형 방폭문은 폭발 압력이 4.8 MPa일때 최대탄성변위가 7.52 mm이 되어 방호 2등급 A수준으로 판정할 수 있다.
(4) 방폭문의 설계 변경 시 유한요소해석의 사용은 3D 모델링을 수정하기 위한 시간이 필요한데 비하여 하중분배법은 간단히 수치 변경으로 최대 변위와 최대 응력을 실용적으로 계산할 수 있다.
REFERENCES
- Kim, H. S. and Park, J. P., “Evaluation of Blast Resistance Performance for CFT Columns by Using Computational Analysis,” Journal of the Architectural Institute of Korea Structure & Construction, Vol. 27, No. 3, pp. 65-72, 2011.
-
Choi, H., Shin, D. H., Kim, M. S., Kim, D. J., Kim, H., et al., “A Study on the Proposal of Residual Strength Equation of Reinforced Concrete Columns Under Blast Load,” Journal of the Korean Society of Hazard Mitigation, Vol. 13, No. 1, pp. 17-24, 2013.
[https://doi.org/10.9798/KOSHAM.2013.13.1.017]

-
Kang, J. W., Jo, E., Kim, M. S., and Lee, Y. H., “Behavior of Precast Prestressed Concrete Panels Subjected to Blast Loading,” Journal of the Korean Association for Spatial Structures, Vol. 15, No. 1, pp. 95-102, 2015.
[https://doi.org/10.9712/KASS.2015.15.1.095]

- Kim, N. H., “A Study on the Structural Stability of the Sliding Blast Door under Blast Load,” M.Sc. Thesis, Seoul National University of Science and Technology, 2015.
- Gas Safety Corporation, “Explosion Proof Door Explosion Test Execution Guide,” Performance Criterion, p. 24, 2014.
- Byun, K. J., Kim, H. J., and Nam, J. W., “Blast Load and Design of Protective Structures,” Magazine of the Korea Concrete Institute, Vol. 23, No. 2, pp. 16-22, 2011.
- Ministry of Land, Infrastructure and Transport, “Korea Building Code,” http://law.go.kr/LSW//admRulLsInfoP.do?admRulSeq=2100000109291, (Accessed 25 NOV 2019)
- Shin, H. M. and Lee, J. H., “Reinforced Concrete,” Dong Myeong Publisher, 2016. (in Korean)
- Barry, J. G. and James, M. G., “Mechanics of Material,” Cengage Learning, 8th Ed., 2017.
- Timoshenko, S. and Woinowsky-Krieger, S., “Theory of Plates and Shells,” McGraw-Hill, 2nd Ed., 1989.
- Goltermann, P., “Reinforced Concrete Slabs – Analysis and Design,” http://www.betonkonstruktioner.byg.dtu.dk//-/media/Subsites/Betonkonstruktioner/Nye_pdfer/Reinforced-Concrete-Slabs.ashx, (Accessed 28 NOV 2019)

Assistant Professor in the Department of Smart Mechanical Engineering, Korea Polytechnic University. His research interest is Fracture Mechanics.
E-mail: kbshim@kpu.ac.kr

Professor in the Department of Mechanical Design Engineering, Korea Polytechnic University. His research interest is Applied Mechanics.
E-mail: lts724@kpu.ac.kr