너클크레인 링크의 형상 최적화
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Due to urbanization, it is difficult to secure a large knuckle crane workspace. To solve this problem, we developed a small knuckle crane combined with a one-ton truck. In this study, the safety of small knuckle cranes is evaluated through Finite Element Analysis. Shape optimization was performed using the Design of Experiment for parts speculated to have failed from fatigue. As a result, maximum equivalent stress of a plate in link speculated to have failed from fatigue was reduced by approximately 84.2%.
Keywords:
Knuckle crane, Special vehicle, Finite element analysis, Optimal design, Design of experiment키워드:
너클 크레인, 특장차, 유한요소해석, 최적설계, 실험계획법1. 서론
산업용 차량은 고하중의 물체를 들어올리거나 회전을 통해 다양한 방향으로 화물을 이송하는 크레인과 결합하여 발전해 왔다. 그 중 너클크레인은 중량물의 이송과정에서 관절을 이용하여 중량물을 들어올리는 동시에 붐(Boom)의 길이를 자유롭게 조절할 수 있는 특징이 있으며, 스크랩 및 폐지 등을 상·하차할 때 사용된다.
도시화로 인해 특정디자인의 건물, 비좁은 도로, 주차공간의 부족으로 인해 9.5톤 또는 5톤 트럭과 결합되는 대형 너클크레인은 작업공간으로의 진입 및 작업공간을 확보하는데 많은 어려움을 겪고 있다. 이러한 문제에 대응하기 위해 작업거리 3.5 m에서 인양하중 250 kg의 사양을 가지며, 1톤 트럭과 결합하는 소형 너클크레인의 개발을 통하여 협소한 작업현장의 원활한 진입과 효율성 있는 작업을 수행할 수 있다. 이를 위해서는 다양한 작업을 수행하는 소형 너클크레인의 안전성이 요구된다. 이동식 크레인의 안전성을 확보하기 위하여 상용유한요소해석 S/W를 이용하여 안전성을 확보하려는 노력을 하고 있다.1-10
Lim1은 트럭장착용 너클크레인을 모델링하여 Optistruct 9.0을 이용하여 안전성을 확인하였으며, 두께 최적화 기법을 통해 약 5%의 경량화 모델을 얻었다. Lee2는 너클크레인에 대하여 등가정 하중법을 이용하여 비선형동적 상태를 고려한 두께 최적화 기법을 수행하였고, 이를 통해 약 1.68%의 경량화 모델을 얻었다. Choi등3은 특장차용 텔레스코픽 붐의 단면 형상에 따른 등가응력 및 모서리 증가에 따른 변형량 등의 구조적 특성을 분석하였다. Park4은 텔레스코픽 붐의 각도와 형상에 따라 구조해석을 진행하여 붐의 단에서의 응력 및 변형을 비교 분석하였다. Hong5은 고소작업차의 붐대에 형상최적화기법 중 실험계획법을 적용하여 형상최적설계를 진행하여, 정적·동적 강성을 증가시킨 경량화 모델을 얻었다. Lee6는 고소작업차 붐의 최적화를 위해 극한상황의 작업조건을 가정하기 위하여 작업 각도를 조정한 후 Ansys Workbench를 이용하여 해석을 진행하였고, 이를 통해 실험계획법을 적용하여 엔드 붐(End Boom)의 최적화된 설계값을 제시하였다. Savkovic 등7은 텔레스코픽 붐의 접촉영역 사이에서의 응력과 변형을 유한요소해석을 통해 분석하였고, 최적화 방안을 제시하였다. So8는 붐 사이에 탄성물체인 패드를 고려하여 구조해석을 진행하였으며, 패드의 두께 및 접촉면적에 따른 응력을 분석하였다. Lee9는 실험계획법을 통하여 붐의 높이 및 두께를 변수로 설정하여 구조해석을 수행하여, 붐의 높이와 두께를 제시하였다. Han10은 고소작업차 붐의 안전성을 확인하기 위하여 붐의 각도에 따른 구조해석을 수행하였으며, 고유진동수 해석을 통해 엔진에서 발생 가능한 진동수와 비교하여 공진에 따른 붐의 안전성을 확인하였다.
본 논문은 이러한 노력의 일환으로 소형 너클크레인의 안전성을 확보하기 위하여 유한요소해석을 통한 응력을 분석하여 파손을 예측하였으며, 파손이 예측되는 부품에 대하여 형상최적설계를 진행하였다. 이는 추후 너클크레인을 설계 및 형상최적화하는 과정에 도움이 될 것이라 판단된다.
2. 유한요소해석
2.1 크레인 모델
소형 너클크레인의 실제 사진은 Fig. 1(a)와 같고, 1톤 트럭과 결합하여 협소한 공간에서 효율적인 작업을 할 수 있다. Fig. 1(b)와 같이 아우트리거(Outrigger), 베이스(Base), 칼럼(Column), 이너붐(Inner Boom), 아우터 붐(Outer Boom), 익스텐션 붐(Extension Boom) 링크 1(Link1), 링크 2(Link2), 너클(Knuckle)로 구성되어있다. SolidWorks를 통하여 3D 모델링 하였고, Ansys Workbench(Version 17)를 이용하여 유한요소해석을 수행하였다.
2.2 요소분할 및 경계조건
요소분할을 위하여 형상이 복잡하여 요소의 수를 증가시키는 너클(Knuckle) 및 아우트리거는 모델에서 제외하였다. 요소분할시 사용된 요소는 Tetra Mesh이고, 전체 요소크기는 10 mm, 링크 2의 요소크기는 4 mm, 유압 실린더의 핀과 결합되는 부분의 붐은 1 mm로 나누었다. 요소분할의 결과 요소 수는 748,759개이며, 절점 수는 1,316,525개 이다. 붐의 재질은 ATOS8011이고, 링크 2의 재질은 ATOS6011, 핀의 재질은 S45C이다.
국제표준 ‘크레인-하중 및 조합 하중에 관한 설계원리’(ISO 8686-212)에 따르면 눈, 얼음 및 풍속 등과 같이 기후효과에 따른 간헐적 하중을 고려하지 않고, 크레인의 질량 및 정격하중의 중량 등과 같이 일상적 하중만 고려하는 경우 설계시 안전율 1.48을 고려하도록 제시하고 있다. 따라서 본 논문에서는 크레인의 질량 및 정격하중인 인양하중의 무게만을 고려하여 해석을 진행하였다.
구조해석을 위한 경계조건은 Fig. 2와 같으며, 아우트리거를 제외한 베이스의 양 끝단에 고정조건을 부가하였으며, 붐이 3.5 m로 신장된 상태에서 익스텐션 붐 끝단에 너클의 무게 100 kg 및 인양하중 250 kg을 고려하여 3.5 kN을 적용하였다.
2.3 구조해석 결과
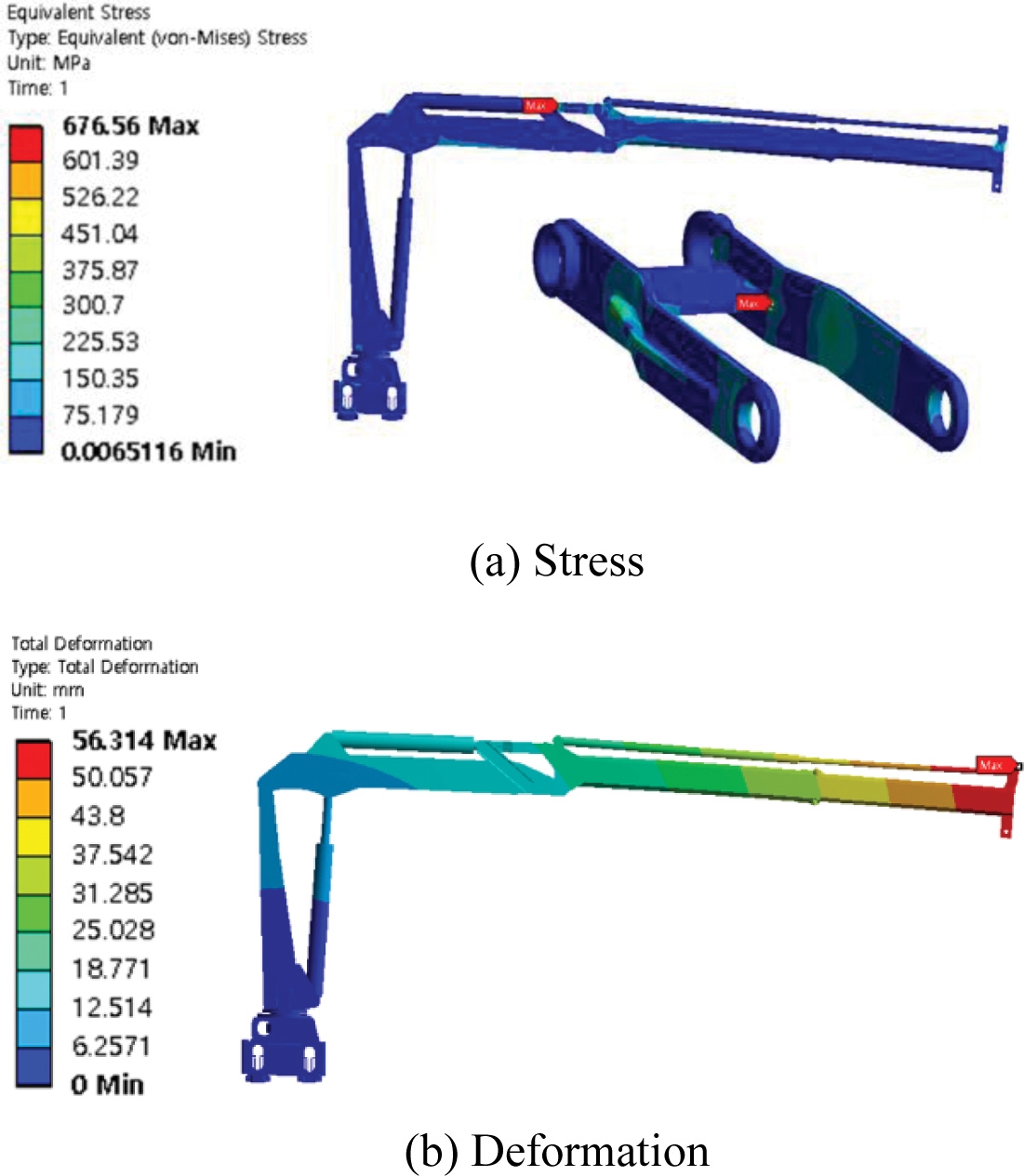
구조해석 결과는 Fig. 3과 같으며 최대등가응력(Maximum Von-Mises Stress)은 Fig. 3(a)와 같이 링크2의 플레이트에서 발생하였으며 그 값은 676.56 MPa이고, Fig. 3(b)와 같이 익스텐션 붐 끝단에서 56.31 mm의 처짐이 발생하였다. 붐에 발생하는 최대등 가응력은 아우터 붐에서 발생하였으며 그 값은 438.34 MPa이다. 붐의 재질인 ATOS 80의 항복강도는 700 MPa이며, 링크 2의 재질인 ATOS 60의 항복강도는 440 MPa이다. ATOS80과 ATOS60의 항복강도에 ‘크레인-하중 및 조합 하중에 관한 설계원리’(ISO 8686-2)에 명시된 안전율 1.48을 고려하게 되면 ATOS80과 ATOS60의 허용응력은 각각 472 MPa, 297 MPa 이다. 따라서 붐은 파손이 없을 것이라 예측되며, 링크2는 파손이 있을 것이라 예상된다.
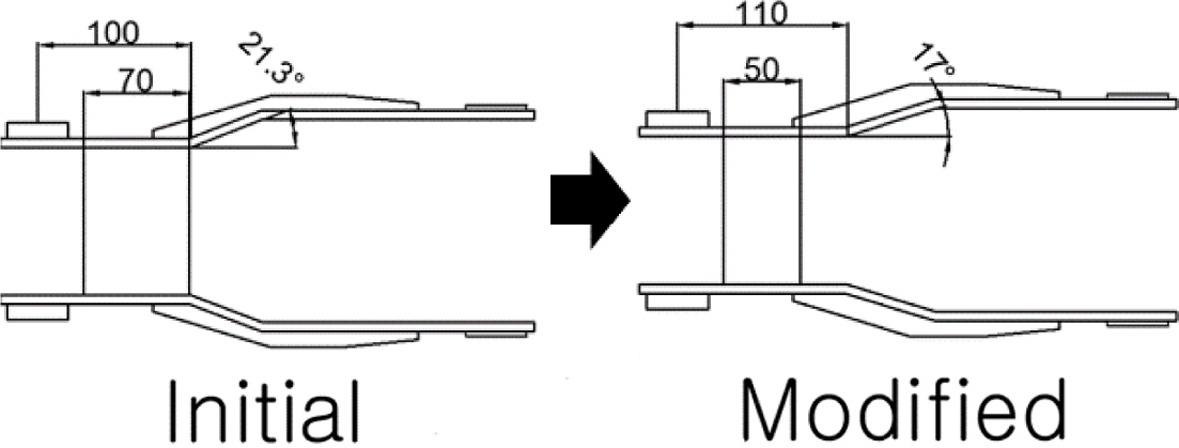
파손의 위험이 있을 것이라 판단되는 링크 2의 플레이트에 대한 응력개선을 위하여 설계변경시 간섭이 발생하지 않는 설계요소를 선택하여 Fig. 4와 같이 플레이트의 폭을 70 mm에서 50 mm로, 핀홀에서 절곡부까지의 거리를 100 mm에서 110 mm로, 절곡부의 각도를 21.3°에서 17°로 보강하여 구조해석을 수행하였다.
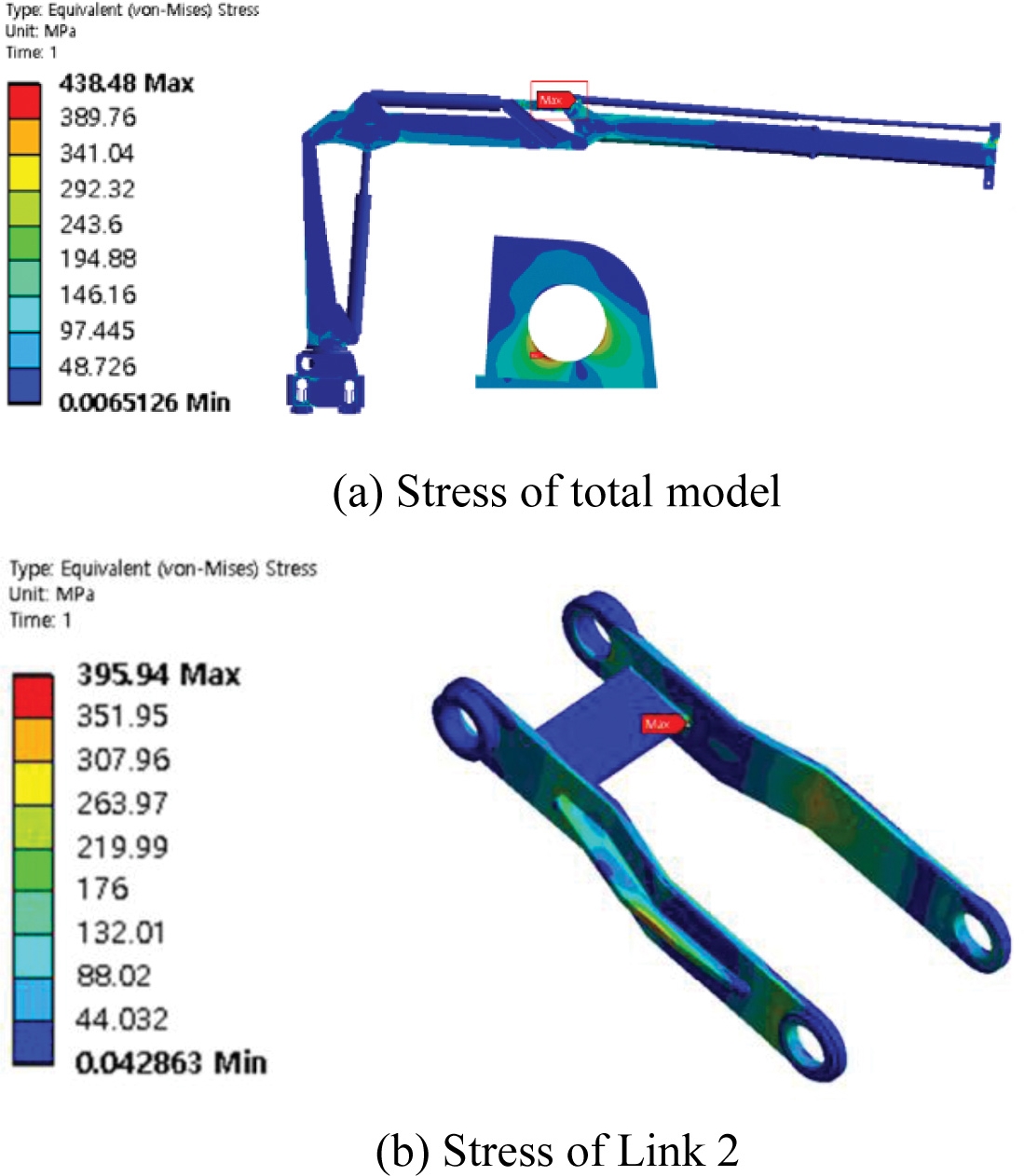
해석결과 Fig. 5(a)와 같이 최대등가응력은 아우터 붐에서 438.48 MPa이 발생하였고, Fig. 5(b)와 같이 최대응력이 발생하였던 링크 2의 플레이트에서는 최대 395.94 MPa 이 발생하였다.
3. 실험계획법
링크 2에 대하여 설계를 수정한 후 링크 2의 플레이트에 발생하는 최대응력은 395.94 MPa로 초기 모델의 응력인 676.56 MPa 보다 약 41.48% 감소하였지만 허용응력인 297 MPa보다 높게 발생하여 파손의 위험이 있을 것으로 판단된다. 따라서 링크2의 플레이트에서 발생하는 응력을 감소시키기 위하여 수치해석 통계프로그램인 MINITAB을 이용하여 실험계획법을 수행하였다.
3.1 실험계획법 인자와 수준선정
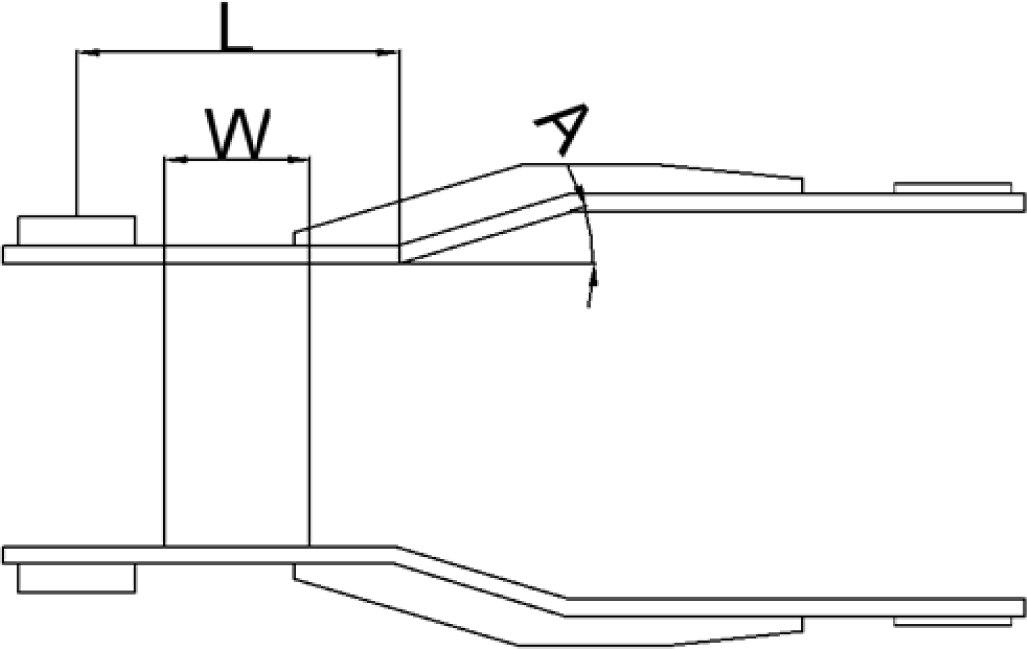
실험인자는 Fig. 6과 같이 플레이트의 너비 W, 절곡부의 각도 A, 핀홀로부터 절곡부의 거리 L을 선정하였다. 실험인자의 선정 이유는 실험인자의 수정을 통하여 링크 2의 플레이트에 발생하는 응력의 감소효과를 확인하였기 때문이다. 인자의 수준은 작업시에 붐과 링크 2와의 간섭을 피하기 위하여 A의 각도는 13°에서 21°로, L의 거리는 105 mm에서 115 mm로, W의 너비는 45 mm에서 55 mm로 선정하였다.
3.2 완전요인배치법
반응 값 Y (MPa)는 유한요소 해석을 통해 얻은 값으로써 링크 2의 플레이트에서 발생하는 최대등가응력을 측정하였다. 반응 값 Y가 요인의 수준에 따라 어떻게 반응하는지 알아보기 위하여 Table 1과 같이 각 인자 수준의 중앙점을 포함한 3인자 2수준의 실험을 계획하였고, 반응 값 Y는 구조해석을 통하여 얻었다. 중앙점은 각 인자의 제일 높은 수준과 제일 낮은 수준의 평균값을 나타낸다.
인자의 수준이 2수준일 때, 인자가 반응 값에 미치는 영향은 선형적으로만 나타난다. 하지만 인자가 반응 값에 미치는 영향이 비선형적인 경우도 존재할 수 있다. 비선형적인 경우가 존재한다면 즉, 곡률 효과(Curvature Effect)가 있다고 판단되면, 기존의 완전요인배치법보다 더 높은 차수의 실험을 수행하여 얻은 반응값을 통해 인자에 따른 정확한 반응을 확인할 수 있다. 따라서 인자가 반응 값에 미치는 영향이 선형 또는 비선형인지를 파악하기 위하여 중앙점을 포함하여 실험을 계획하였다.
MINITAB을 이용한 Table 1에 대한 분산분석 결과는 Table 2와 같다. 여기서 DF는 자유도를 나타내며, Adj SS는 제곱합(Sum of Square)으로, 이는 인자 수준에 따른 변동성을 나타내며, Adj MS는 평균 제곱(Mean Square)으로 각항의 제곱합을 자유도로 나눈 값이다. Error는 인자들의 효과만으로는 설명이 되지 않는 변동성을 뜻한다. F-Value는 각항의 평균 제곱을 Error의 평균 제곱으로 나눈 값으로써 F-Value의 값이 클수록 P-Value의 값이 작아지게 되고 P-Value의 값이 유의 수준인 0.05를 넘게 되면, 그 인자는 반응에 영향을 미치지 못한다고 판단한다.13
P-Value를 분석하면 A, L, W는 각각 0.011, 0.025, 0.016이며, 인자들의 교호작용인 A*L, A*W, L*W는 각각 0.061, 0.221, 0.808이다.
P-Value의 값이 큰 L*W, A*W항에 대하여 오차항에 포함시킨 후 검정하는 풀링(Pooling)작업을 수행한 결과는 Table 3과 같고, L*W, A*W항을 제외한 모든 인자가 유의하다고 해석되었다.
MINITAB을 이용하여 구한 반응 값 Y에 대한 회귀방정식은 식(1)과 같이 표현할 수 있다.
| (1) |
회귀방정식이 모형을 나타내는 정도를 결정계수R2이라하고, 100%에 가까울수록 모형을 잘 설명한다고 할 수 있으며, 식(1)에 대한 R2 값은 99.85%로써 모형을 잘 설명한다고 할 수 있다.13
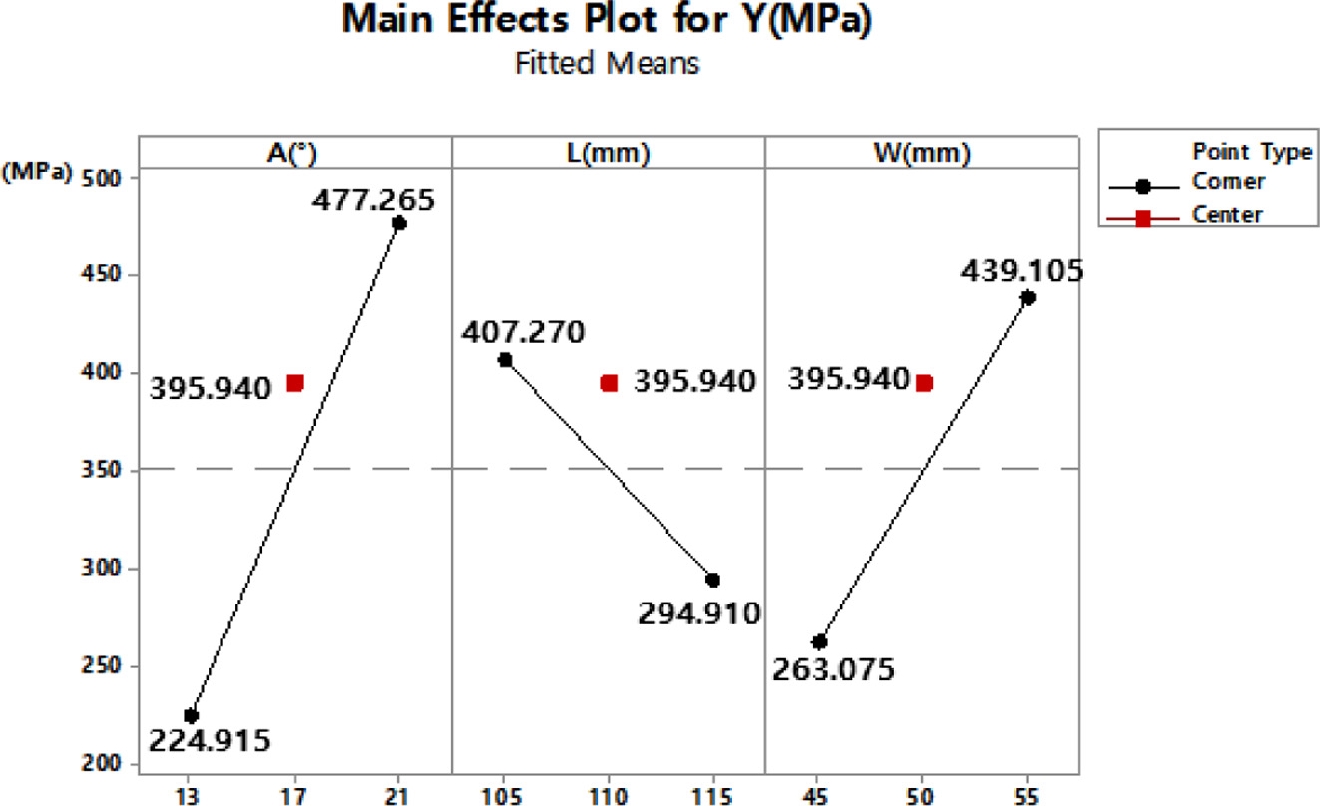
인자가 반응 값 Y에 영향을 미치는 정도를 나타내는 주효과도는 Fig. 7과 같으며, y축은 각 인자 수준에 따른 반응 값 Y를 나타내고, x축은 각 인자의 수준을 나타낸다. 주효과도의 기울기가 클수록 반응 값 Y에 큰 영향을 준다고 판단할 수 있으며, A, W, L 순으로 반응 값에 큰 영향을 준다 해석할 수 있다.
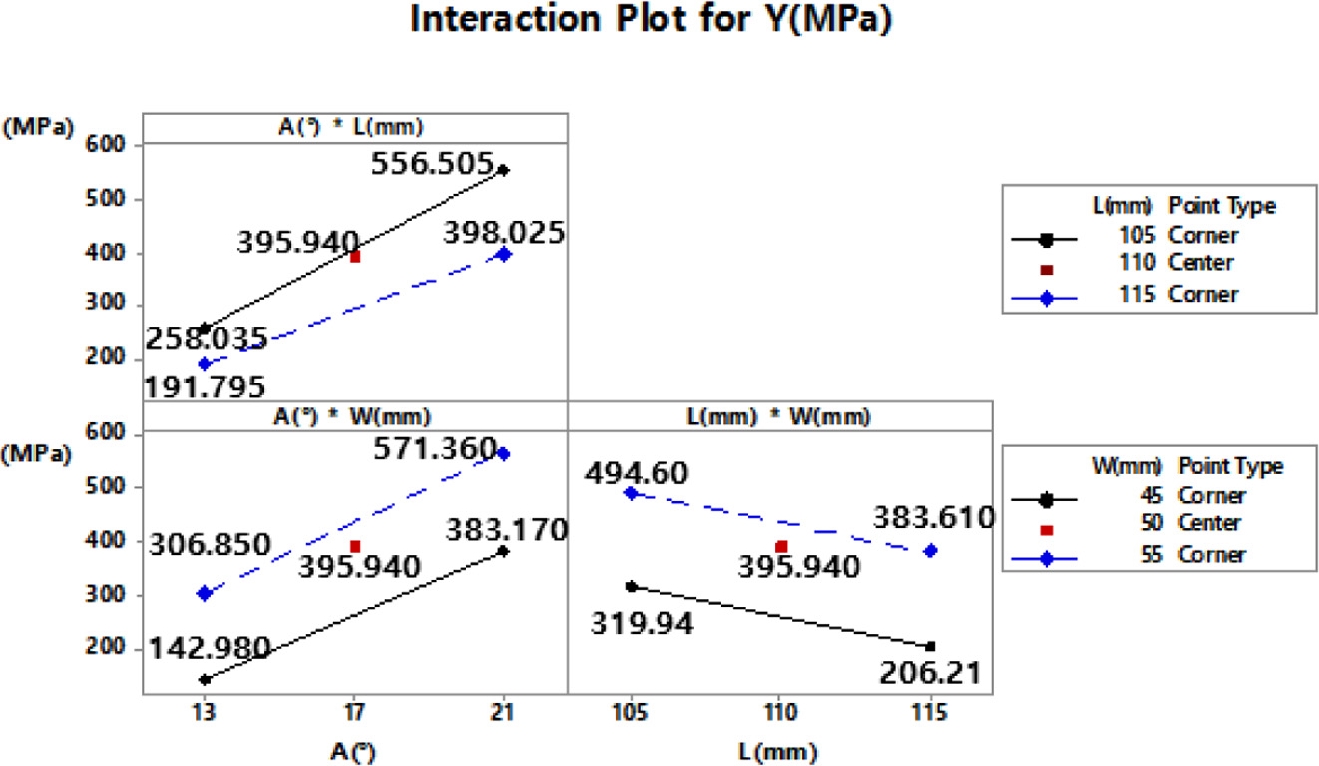
인자간 상호작용을 나타내는 교호작용도는 Fig. 8과 같으며, y축은 각 인자 수준에 따른 반응 값 Y를 나타내고, x축은 각 인자의 수준을 나타낸다. 교호작용도는 각 인자의 기울기가 엇갈릴수록 상호작용이 크다고 할 수 있으며 A*L의 기울기가 엇갈려 상호작용이 크다는 것을 확인하였다.
Fig. 7의 주효과도를 보면 각 인자 수준의 중앙점에서의 반응값이 비선형이므로 곡률 효과를 예측할 수 있다. 주효과도의 분석결과뿐 만 아니라 Table 3의 통계분석 결과도 곡률 효과를 의미하는 P-Value가 0.028으로 나타나 유의수준인 0.05보다 작으므로 비선형성을 가지고 있음을 예상할 수 있다.
Fig. 7에 따르면 인자는 수준에 따라 반응 값이 감소 또는 증가하는 경향을 보이고 있다. 이를 통해 최소 응력을 보이는 인자를 유추할 수 있지만 더 높은 차수의 실험계획법을 진행한다면 설계 인자에 따른 반응 값을 정확히 예측할 수 있다. 따라서 더 높은 차수의 실험을 계획하기 위하여 반응표면분석법을 이용한 추가적인 실험이 필요하다.
3.3 반응표면분석법
반응표면을 생성하기 위한 실험계획은 Table 4와 같다. 반응표면을 생성하기 위하여 면중심의 중심합성법을 통해 실험을 계획하였다. 면중심의 중심합성법을 통해 실험을 계획한 이유는 수준에 제한이 있을 경우 수준의 범위를 초과하지 않고 실험을 계획할 수 있기 때문이다. 반응 값 Y는 구조해석을 통하여 얻었다.
MINITAB을 이용한 Table 4에 대한 분산분석 결과는 Table 5와 같으며 A*A, A*W, L*W항의 P-Value는 각각 0.083, 0.092, 0.838로 유의수준인 0.05를 초과하여 유의하지 않은 것으로 판단했다. 이를 통해 풀링을 수행한 결과는 Table 6과 같다.
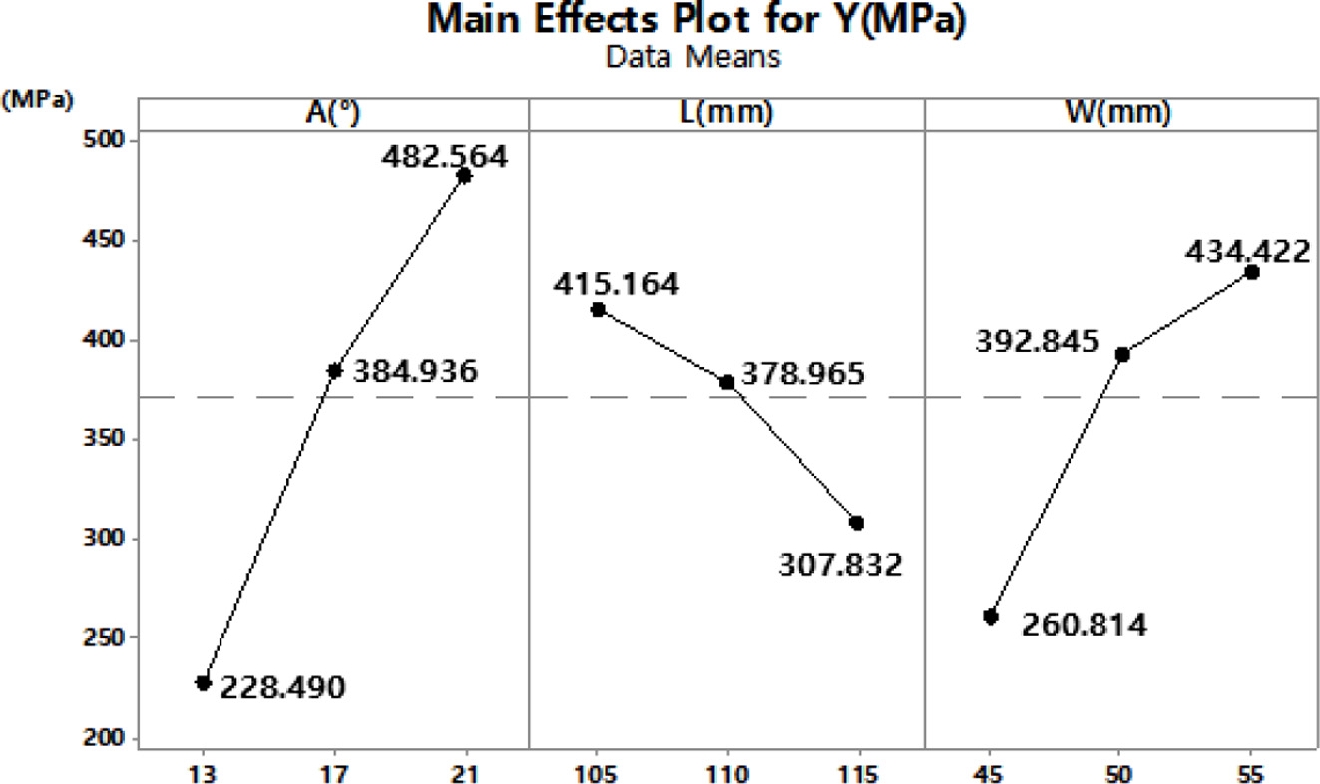
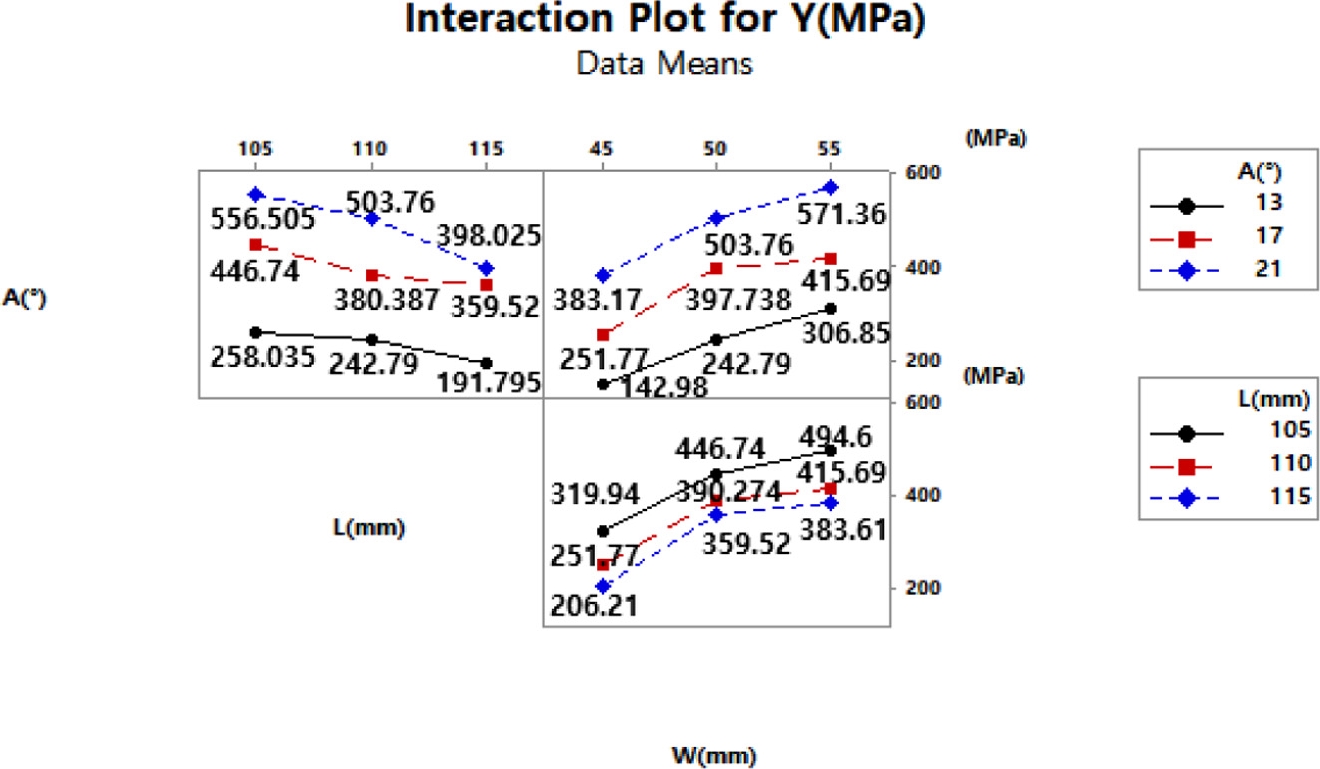
인자가 반응 값 Y에 미치는 영향을 나타내는 주효과도 및 교호작용도는 Figs. 9와 10과 같이 나타났다. 인자 A와 W는 인자수준이 낮을수록 반응 값 Y가 작아졌으며, 인자 L은 인자수준이 높을수록 반응 값 Y가 작아지는 효과를 보였다. 교호작용도에서는 A*L의 기울기가 크게 엇갈려 교호효과가 크게 나타난 것을 확인하였다.
분산분석을 통해 확인한 유의한 인자는 A, L, W, L*L, W*W, A*L 이며 이를 통하여 반응 값 Y에 대한 회귀방적식을 표현하면 식(2)와 같이 표현할 수 있다.
| (2) |
식(2)에 대한 R2 값은 99.48%로써 모형을 잘 설명한다고 할 수 있다.
4. 결론
본 논문에서는 1톤 트럭과 결합되는 소형 너클크레인에 대한 유한요소해석 결과와 재질의 항복강도를 비교하였으며, 국제표준 ISO 8686-2에 따른 안전율을 고려하였을 때 붐에서는 파손이 예측되지 않았으나 링크 2의 플레이트에서는 파손이 예측되었다. 안전성을 확보하기 위하여 A(링크의 굽힘 각도), L(핀홀부터 절곡부까지의 거리), W(플레이트의 너비) 인자를 선정하여 실험계획법을 통한 링크의 최적화를 진행하였고, 그 결과는 아래와 같다.
(1) 소형 너클크레인에서 발생하는 최대등가응력은 링크 2의 플레이트에서 발생하였으며, 그 값은 676.56 MPa이다. 안전율 1.48을 고려하였을 때, 재료의 허용응력인 297 MPa을 초과하여 파손이 위험이 있다. 링크2의 설계인자 A, L, W를 각각 21.3°에서 17°로, 100 mm에서 110 mm로, 70 mm에서 50 mm로 변경하여 재해석한 결과, 링크 2의 플레이트에서 발생한 최대등가응력은 395.94 MPa로 약 41.48% 감소하였다.
(2) 설계인자 변경에 따른 링크 2의 플레이트 응력은 감소하였지만 허용응력은 초과하였다. 따라서 플레이트의 안전성을 확보하기 위하여 중간점을 포함한 3인자 2수준의 완전요인배치 실험을 수행하였고, 그 결과 A, W는 인자의 수준이 낮을수록, L은 인자의 수준이 높을수록 반응 값이 낮아지는 경향을 나타냈다.
(3) 반응표면분석법을 통하여 A = 13°, L = 115 mm, W = 45mm일 때, 링크 2의 플레이트에서 발생한 최대등가응력은 106.97 MPa이다. 실험계획법을 통하여 링크 2의 플레이트에 발생한 최대등가응력은 약 84.2% 감소하였다.
NOMENCLATURE
| W : | Width of plate |
| L : | Distance from pin hole to bending point |
| A : | Angle of bending |
| Y : | Response value (Equivalent stress, MPa) |
Acknowledgments
본 연구는 케이에이치특장㈜의 지원으로 수행 되었음.
References
-
Lim, H.-B., Shin, M.-K., and Yang, H.-I., “Structural Optimization of the Knuckle Crane Installed in Truck,” Journal of the Korean Society of Manufacturing Technology Engineers, Vol. 21, No. 2, pp. 344-348, 2012.
[https://doi.org/10.7735/ksmte.2012.21.2.344]

- Lee, D. K., “Structural Optimization of The knuckle Crane using Equivalent Static Loads Method,” M.Sc. Thesis, Department of Mechanical Design and Mechatronics, Hanyang University, 2013.
- Choi, Y., Lee, S., Park, S., and Ryu, Y., “Structural Analysis of Telescopic Boom in a Special Vehicle,” Proc. of the Korean Society of Mechanical Engineering Autumn Conference, pp. 451-455, 2009.
- Park, K. S., “Structural Analysis according to Changed Shape of the Telescopic Boom of High Place Operation Car,” M.Sc. Thesis, Department of Carbon and Nano Component Materials Engineering, Jeonju University, 2015.
- Hong, S.-K., Henty, P., Chung, T. J., Hong, Y., and Yoo, S., “Structural Optimum Design for the Lightweight of an Aerial Work Platform Truck's Telescopic Boom and Frame System,” Proc. of the Korean Society of Mechanical Engineering Autumn Conference, pp. 344-345, 2011.
- Lee, B. K., “Optimization of the Insulation Telescopic Aerial Boom using the Finite Element Method,” M.Sc. Thesis, Department of Mechanical System Engineering, Chonbuk National University, 2012.
-
Savković, M., Gašić, M., Pavlović, G., Bulatović, R., and Zdravković, N., “Stress Analysis in Contact Zone Between the Segments of Telescopic Booms of Hydraulic Truck Cranes,” Thin-Walled Structures, Vol. 85, pp. 332-340, 2014.
[https://doi.org/10.1016/j.tws.2014.09.009]

- So, J. U., “Finite Element Analysis of Boom Structure of an Aerial Lift Truck Considering Friction and Contact Condition Between the Elastic Bodies,” Proc. of the KSPE Autumn Conference, pp. 514-515, 2014.
- Lee, J. J., “A Stduy on Optimization of the Aerial Lift Boom Through the Finite-Element Analysis(FEA),” M.Sc. Thesis, Department of Precision Mechanical Engineering, Chonbuk National University, 2012.
- Han, S. H., “A Study on Safety Analysis Solution of Aerial Platform Truck,” M.Sc. Thesis, Department of Mechanical Design, Chonbuk National University, 2007.
- POSCO, “Automobile Structural Steel,” 2014.
- ISO 8686-2:2004, “Cranes - Design Principles for Loads and Load Combinations - Part 2: Mobile Cranes,” 2004
- Yoo, S. M. and Park, H. J., “Minitab with Basic Statistics,” Eretec, 2006.

M.S. in the Department of Mechanical Design Engineering, Korea Polytechnic University. His research interest is Solid Mechanics and Optimal Design.
E-mail: xoghkthd3000@naver.com

Professor in the Department of Mechanical Design Engineering, Korea Polytechnic University. His research interest is Solid Mechanics and Optimal Design.
E-mail: jhlee@kpu.ac.kr