외부 하중을 받는 선형 롤러베어링의 가이드 레일 변형에 관한 연구

1. 서론

기계 장비의 고속/정밀화를 위해서는 회전과 직선 이송계의 핵심 요소인 베어링에 대한 보다 정확한 특성 예측이 요구된다.¹ 선형 베어링은 공작기계를 비롯하여 반도체 장비, 정밀 측정기기 등 직선 이송계를 필요로 하는 기계 장비에서 폭넓게 사용되고 있으며, 기계 장비 전체의 성능과 정밀도에 직접적인 영향을 미치게 된다.

선형 베어링은 하중을 직접 지지하는 캐리지와 캐리지가 이동하는 가이드 레일 그리고 캐리지로부터 전달되는 하중을 지지함과 동시에 적은 마찰로 레일 위를 움직일 수 있게 하는 구름 요소의 조합으로 구성되며, 가이드 레일은 볼트를 이용하여 바닥면에 견고하게 고정된다. 선형 베어링은 베어링 내부의 구름 요소 종류에 따라 선형 볼베어링(Linear Ball Bearing)과 선형 롤러베어링(Linear Roller Bearing)으로 구분되며 그 중 선형 롤러베어링은 선형 볼베어링에 비해 큰 하중을 지지할 수 있어 큰 하중 지지를 필요로 하는 대형 공작기계 등에 널리 사용되고 있다.

직선 운동의 핵심 부품인 선형 베어링도 기계 장비 전체에 미치는 영향으로 인해 그 특성을 정확히 파악하는 것이 중요하다. 특히 베어링 강성과 마찰 특성 등은 이송정밀도에 큰 영향을 미치므로 정확한 예측을 위해 많은 연구가 진행되어 왔다. 아래에 근래 수행된 주요 연구를 간단히 요약한다.

베어링이 하중을 받을 때의 변위와 강성은 특히 많은 관심을 모아왔다. Kwon 등^2,3은 베어링의 변위를 롤러 접촉면의 변형으로 인해 발생하는 변위와 캐리지가 변형하면서 발생하는 변위의합으로 정의하여 계산하는 방법을 제안하였다. 그리고, 제안된 베어링 모델을 이용하여 베어링에 인가되는 수직, 수평방향과 비틀림방향 하중에 대한 변위를 계산하고 검증하였다. Li 등⁴도 선형 볼베어링에 대하여 캐리지의 변형을 고려한 수직 강성의 이론적 모델을 제안하였으며 실험 결과와 비교하여 캐리지 변형의 중요성을 확인하였다.

Choi 등⁵은 Hertz 접촉 이론을 이용하여 선형 볼베어링의 강성과 고유진동수를 계산하고, 베어링 예하중과 가이드웨이의 곡률, 접촉각 등 여러 설계 변수에 의해 변하는 특성에 대해 연구하였다. Shaw와 Su⁶ 그리고 Sun 등⁷은 유한요소 모델을 이용하여 선형 볼베어링의 수직방향 압축 하중에 대한 강성을 계산하고 실험과 비교하였다. Ohta와 Tanaka⁸는 선형 볼베어링의 수직방향 강성에 대한 연구를 수행하였다. 특히, 캐리지와 가이드 레일의 변형을 고려했으며 실험을 통하여 제안한 연구의 유효성을 보였다. Rahmani와 Bleicher⁹는 예하중에 의한 선형 볼베어링의 수직, 수평방향과 회전방향 강성의 변화를 실험적으로 연구하였다. Pawelko 등¹⁰은 유한요소를 이용한 선형 볼베어링 모델링 방법을 제안하고 예하중과 외부 하중에 대한 변위를 시뮬레이션 하여 베어링업체 제공 데이터와 비교 검증하였다.

한편 베어링의 운동오차나 마찰열, 고유진동수 등 베어링 사용시의 여러 특성들에 대해서도 활발하게 연구가 진행되어 왔다. Khim 등¹¹은 선형 볼베어링에서 볼에 대한 반력을 계산하여 수직방향 강성을 예측하였으며 실험을 통해 검증하였다. 또한 베어링 강성 예측 모델을 발전시켜 베어링의 전달함수를 계산하였고, 이를 통해 선형 볼베어링으로 지지된 테이블의 운동오차를 예측하고 보정하는 실험을 수행하였다. Kim 등¹²은 선형 볼베어링의 볼을 8개의 스프링으로 대체할 수 있는 수치 모델을 제안하였고 각각의 강성을 분배하여 선형 볼베어링의 정/동적 특성을 반영할 수 있도록 하였다.

Li 등¹³은 유한요소 해석을 이용하여 선형 볼베어링의 변위와 강성을 계산하고, 스프링-댐퍼-관성모멘트 모델을 구성하여 고유진동수를 계산하였다. Yi 등¹⁴은 선형 볼베어링의 동적 특성을 나타내는 실험을 수행하고 이를 예측할 수 있는 모델을 개발하였다. 또한, 캐리지가 낮은 속도로 움직일 때 미세 스케일의 마찰로 인한 히스테리시스 현상을 토의하였으며 LuGre 모델을 사용하여 첫번째 고유진동수를 계산하고 실험과 비교하였다.

선형 베어링에서 발생되는 마찰열에 대한 연구도 다양하게 수행되어 왔다. Oh 등¹⁵은 선형 볼베어링의 마찰력을 모델링하고 실험 결과와 비교하였다. 선형 볼베어링의 마찰력은 베어링의 형상, 물성치, 조립 조건 및 운전 조건에 대한 함수로 나타낼 수 있으며 예하중과 외부 하중에 대해 비선형적 관계를 가지는 것을 확인하였다. Zou 등¹⁶은 마찰에 의해 발생하는 열과 마모를 고려한 베어링 강성 해석 모델을 개발하였으며 주행 중에 블록의 열변형과 마모 증가로 인해 강성이 감소함을 확인하였다. Jang 등¹⁷은 마찰력으로 인해 발생한 열 해석을 수행하였다. 또한 계산된 마찰력을 실험 결과와 비교하였다. 최근 Cheng 등¹⁸은 개선된 마찰력 공식을 제안하고 기존의 문헌결과와의 비교를 통해 검증하였다. Tao 등²⁰은 선형 롤러베어링의 롤러 접촉면에 발생하는 마찰로 인한 마모를 고려했으며 베어링의 이동거리에 따른 수직 변위를 계산하였다.

그 밖에도 해석적 모델이나 실험을 통한 오차해석이 관심을 모아왔는데, Jastrzębski 등¹⁹은 볼 직경 오차와 레일의 평행 오차 그리고 진직도 오차가 있을 때 수직 하중에 따른 베어링의 변위와 강성 변화를 분석하였다.

이상과 같은 문헌조사를 통해 선형 베어링에 관한 많은 연구가 선형 볼베어링을 중심으로 진행되어 왔으며, 선형 롤러베어링에 대한 연구는 극히 제한적임을 알 수 있었다. 또한 볼 또는 롤러와 레이스의 접촉면에서 발생하는 변형에 대한 연구에 집중되어 왔으며 가이드 레일이나 가이드 레일이 결합되는 베이스의 변형에 대한 연구는 많이 이루어지지 않았다.

본 논문에서는 선형 롤러베어링에 수직 및 수평 하중을 인가하였을 때 발생하는 가이드 레일의 변형에 대해 기술하였다. 이를 위해 외부 하중에 의한 가이드 레일의 변위를 결정하는 방법을 제안하였다. 즉, 외부 접근이 불가한 캐리지 내부의 가이드 레일 변위는 캐리지에서의 변위 측정과 상용프로그램²¹의 계산결과를 활용하여 추정하고, 다른 부분에서의 가이드 레일 변형은 직접 측정하여 가이드 레일의 전체적인 변형 양상을 예측하였다. 이를 통해 가이드 레일 부분의 변형이 베어링 전체의 변형에 미치는 효과를 분석하였다. 마지막으로 대형 공작기계에서 사용되는 다수의 선형 롤러베어링으로 지지된 테이블에 대해 동일한 과정을 통해 유사한 수준의 가이드 레일 변형 효과가 발생함을 확인하였다.

2. 선형 롤러베어링 변위 측정 실험 장치

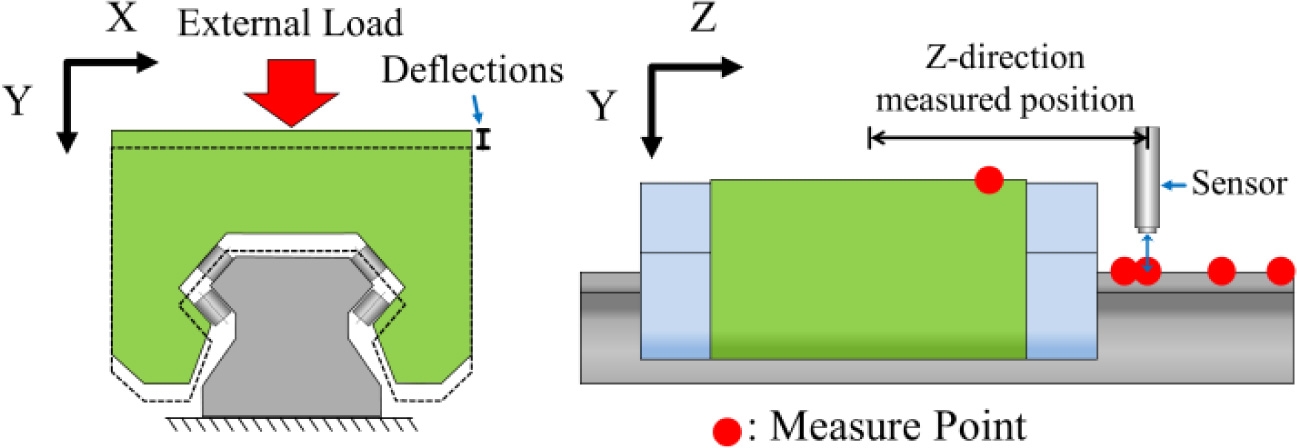
본 연구를 위하여 제작한 실험 장치를 Fig. 1에서 보여주고 있다. 그림에서 볼 수 있는 바와 같이 실험 장치는 하판에 가이드 레일과 갠트리(Gantry)를 함께 고정하여 베어링과 갠트리의 상대적인 위치가 변하지 않도록 제작되었다. 또한 갠트리가 캐리지의 중앙에 위치하도록 제작하여 수직 하중과 수평 하중을 캐리지 중앙에서 전달할 수 있도록 하였다. 스크류를 사용하여 하중을 전달하였으며 스러스트 베어링을 중간에 위치시켜 하중인가 부위가 회전운동 없이 캐리지에 하중을 전달하도록 제작하였다. 그림에서 볼 수 있는 바와 같이 캐리지와 가이드 레일 사이의 상대 변위를 측정할 수 있도록 정전용량형 변위센서를 배치하였다. 변위 특성을 살펴보기 위해 캐리지에 1 kN단위로 5 kN까지 하중을 인가하였다.

Fig. 1

Experimental setup and external loading system

실험에서 사용한 대상 선형 롤러베어링은 RUE35-E-H 모델이다. 인가한 하중을 측정하기 위해 OMEGA사의 LCMWD로드셀을 사용하였으며 최대 10 kN까지 측정이 가능하다. 또한 변위를 측정하기 위해 분해능이 1.58 nm인 AED사의 정전 용량형 변위센서를 사용하였다. 변위를 측정하기 위해 사용한 정전 용량형 변위센서는 매우 우수한 분해능을 가지고 있으나 측정 환경에 매우 민감하므로 측정 환경 변화를 고려하여 반복 실험을 진행하였다.

3. 수직 방향 하중에 의한 변위 측정

3.1 실험 구성

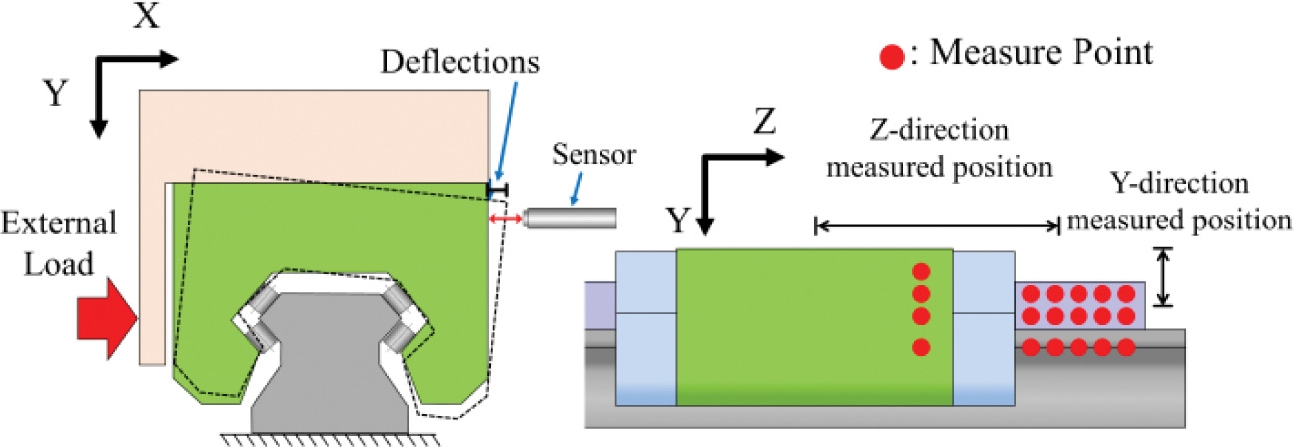
Fig. 2는 수직방향 하중에 의한 변위를 측정하기 위해 하중을 인가한 위치와 변위를 측정한 위치를 나타낸다. 베어링 상판의 중심에서 y축 방향으로 하중을 인가하였으며 캐리지 윗면과 가이드 레일 윗면의 변위를 측정하였다.

Fig. 2

Locations of vertical load and measured positions

3.2 실험 결과

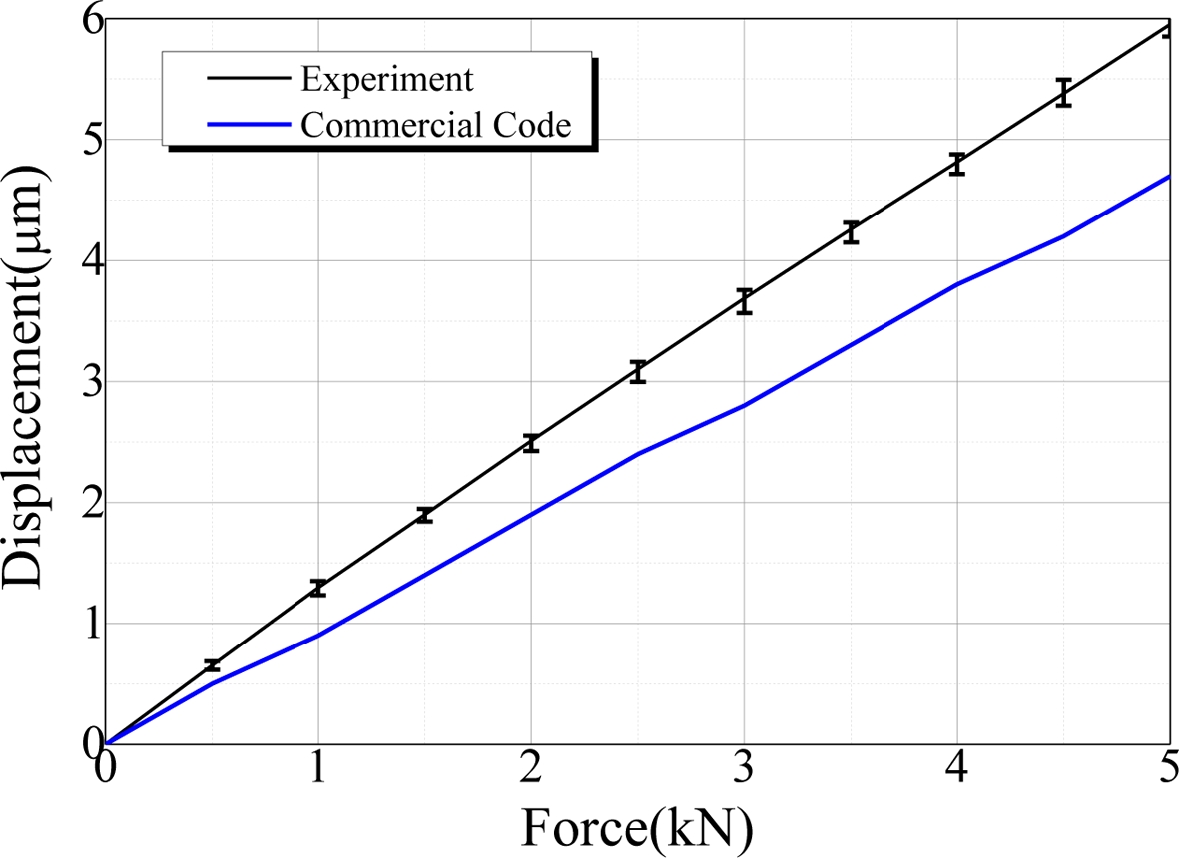
Fig. 3은 캐리지의 변위를 상용 프로그램의 결과와 비교하여 나타낸 결과이다. 상용 프로그램의 결과와 비교하여 실험 결과가 평균 22% 정도 크게 발생한 것을 확인할 수 있다. 사용한 상용 프로그램²¹은 캐리지 변형 효과는 고려하나 가이드 레일의 변형을 고려하지 않고 있으므로 실험 결과와 상용 프로그램의 계산결과의 차이는 가이드 레일 변형으로 인해 발생한 변위로 추정할 수 있다.

Fig. 3

Comparison of carriage displacements subject to vertical load

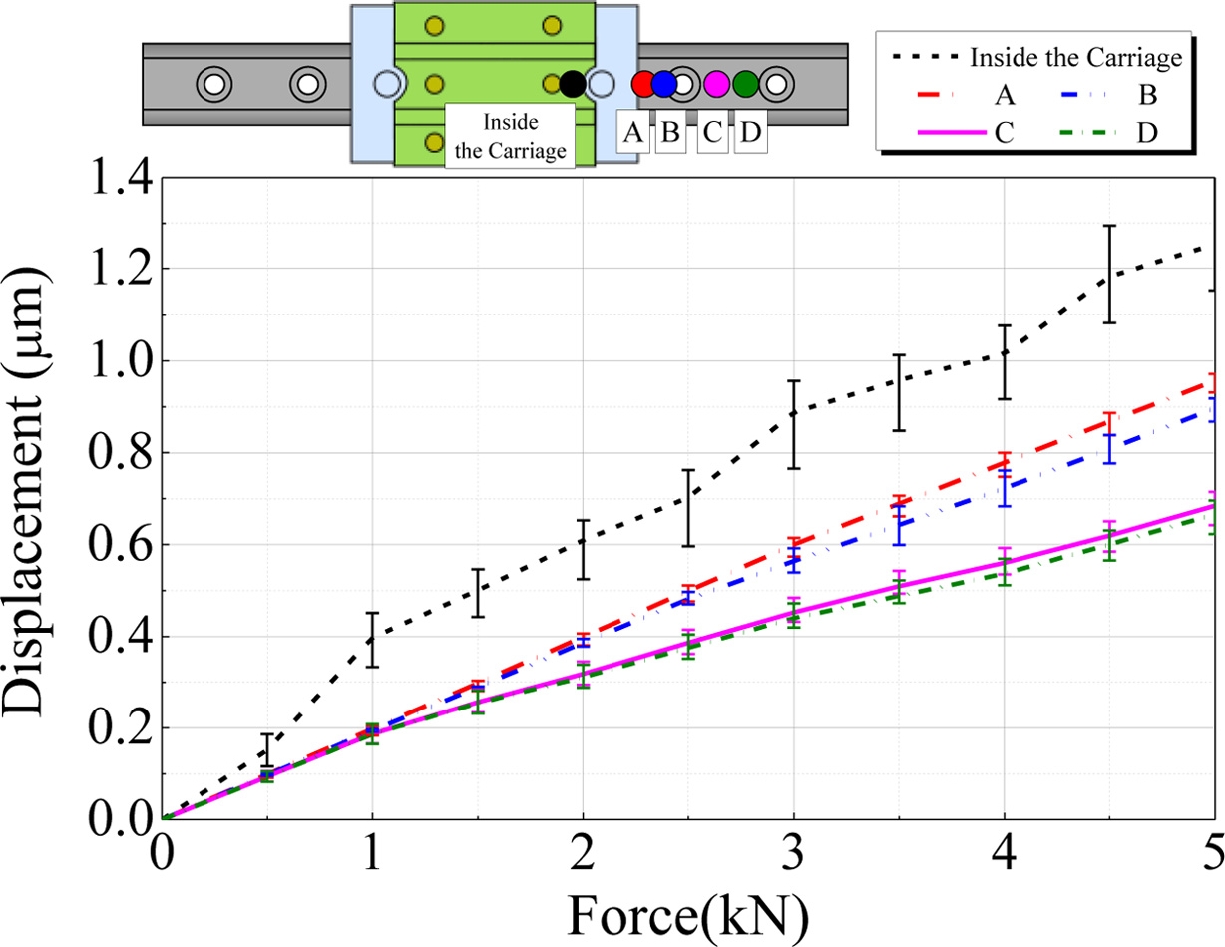
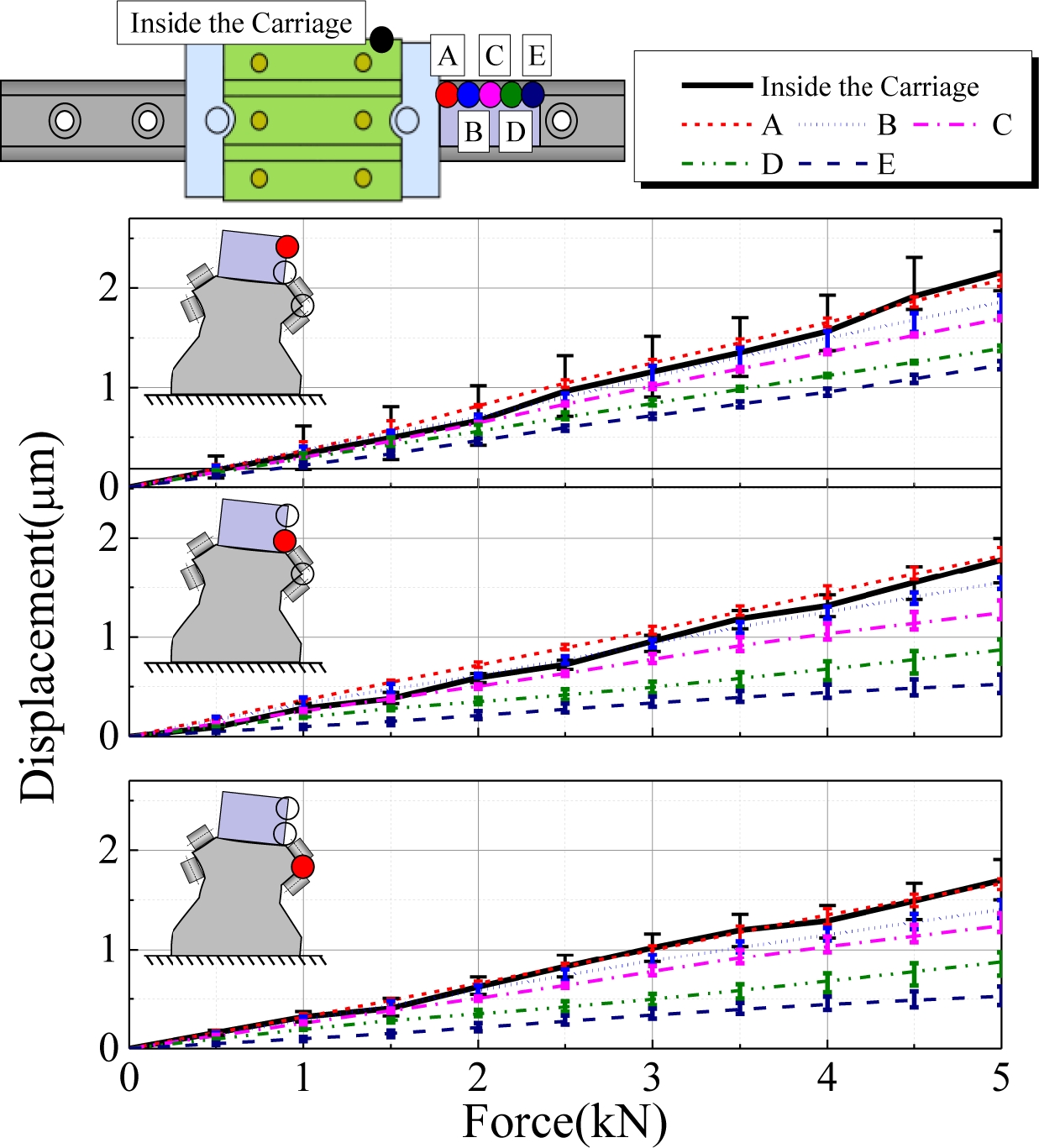
Fig. 4에 수직 하중에 의한 가이드 레일의 변위를 나타내었다. 앞서 설명한 것과 같이 캐리지 내부의 가이드 레일 변위는 측정된 캐리지 변위와 상용프로그램에서의 캐리지 변위 차이로 계산하였다. 상용프로그램의 결과는 가이드 레일 및 바닥면의 변형을 고려하지 않으므로 이 차이는 가이드 레일 및 바닥면의 변형에 의한 것으로 추정할 수 있다. 직접 측정한 가이드 레일 변형과 달리 캐리지 변형을 통해 간접 추정한 캐리지 내부 가이드 레일의 변형은 다소 변화폭이 크게 나타나고 있다.

Fig. 4

Guide rail deflections due to vertical load

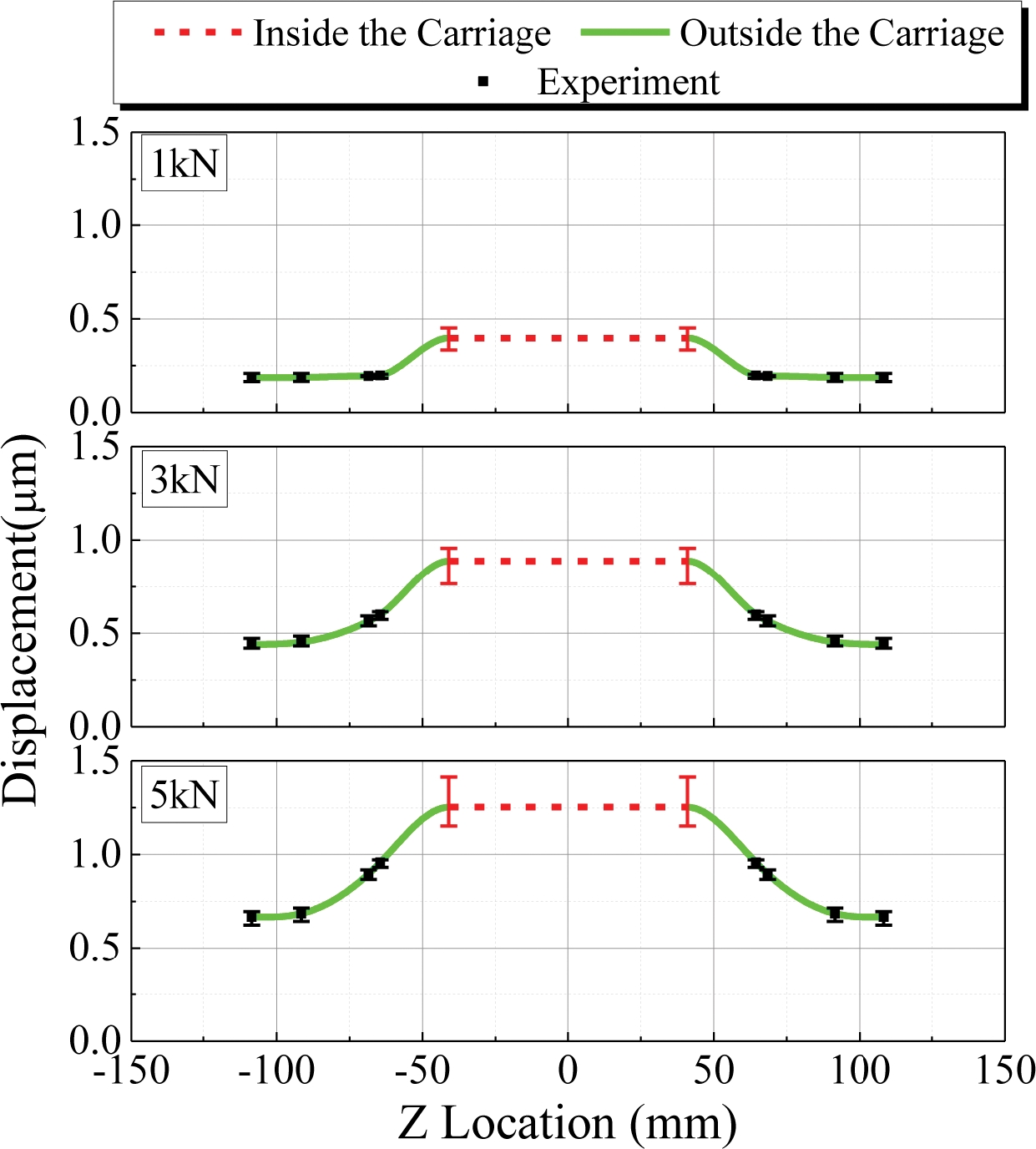
Fig. 5은 수직 하중이 각각 1 kN, 3 kN, 5 kN 인가될 때 가이드 레일의 변형 양상을 나타낸 것이다. 측정된 가이드 레일의 변위를 기반으로 Spline 곡선을 이용하여 변형 곡선을 구현하였고, 중앙 부분은 캐리지의 내부 위치이며, 앞서 언급한 방식으로 추정된 값을 나타내었다.

Fig. 5

Deformed shape of guide rail due to vertical load

변형된 가이드 레일의 형상이 수직으로 옵셋되는 것을 확인할 수 있는데 그 양이 하중 크기에 따라 증가하는 것을 볼 수 있다. 이는 가이드 레일을 고정한 바닥면이 하중을 받아 변형하기 때문에 발생하는 것으로 파악된다.

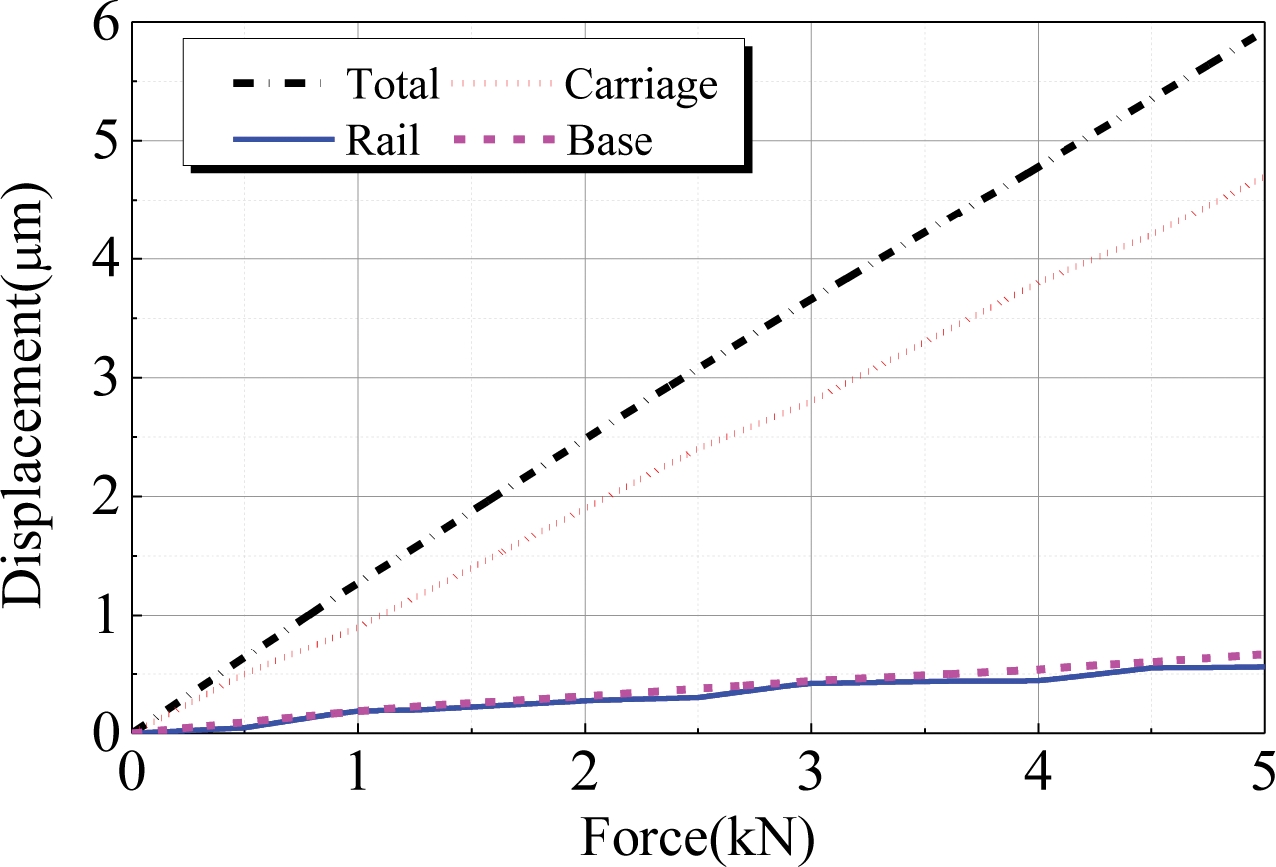
Fig. 6은 수직 하중에 의해 발생한 캐리지의 변위에서 캐리지의 직접 변위와 가이드 레일 변형, 바닥면의 변형이 미치는 영향을 비교하여 나타낸 것이다. 평균적으로 캐리지 자체의 변위가 전체 변위의 약 78%를, 가이드 레일과 베이스의 변형이 각각 전체 변위의 약 10%, 12%를 차지하고 있는 것으로 계산된다. 따라서 실험에 사용된 베어링의 경우, 가이드 레일과 베이스의 변형을 종합하면 하중에 따른 베어링 변위의 약 22% 정도가 되며, 베어링 전체의 변위나 강성을 고려함에 있어 무시할 수 없는 기여를 하고 있음을 알 수 있다.

Fig. 6

Deflections of individual elements due to vertical load

4. 수평 방향 하중에 의한 변위 측정

4.1 실험 구성

Fig. 7에 수평 방향 하중을 인가한 위치와 변위 측정 위치를 나타내었다. 캐리지 옆면에서 2열로 구성된 롤러열의 중심에 x축 방향으로 수평 하중을 인가하였다. 이는 실제 캐리지가 견고한 테이블에 결합되면 캐리지 상면의 각변위가 억제되므로 상면에 미치는 모멘트 하중을 최소화할 수 있도록 한 것이다. 실제로는 이를 구현하기 위해 Fig. 8과 같은 고정구를 이용하였다. 캐리지에 직접 하중을 인가하게 되면 캐리지 변형이 억제되는 효과가 나타나게 되어 캐리지 측면(Swing) 부위의 변화를 적절히 고려할 수 없게 된다. 따라서 베어링 상면에 수평 하중을 가하면서 수평 하중에 의해 발생되는 모멘트 하중은 상쇄하도록 하였다. 계산과정에서는 캐리지 상면에 수평 하중과 모멘트 하중을 인가하였다. 실험에서 고려한 하중 범위 내에서 고정구가 캐리지에 접촉하지 않음을 확인하였고, 하중을 인가하는 반대 위치에서 변위를 측정하였다.

Fig. 7

Locations of horizontal load and measured points

Fig. 8

Fixture for horizontal loading

가이드 레일 측정 시 캐리지 중심을 기준으로 측정하였으며 캐리지와의 비교를 위해 측정용 지그를 설치하였다. 캐리지를 측정한 위치와 동일한 높이에서 변위를 측정하였고 이를 위해 센서를 Fig. 9와 같이 배치하였다.

Fig. 9

Locations of measured positions on carriage and guide rail

4.2 캐리지 변형 계산에 의한 오차 보상

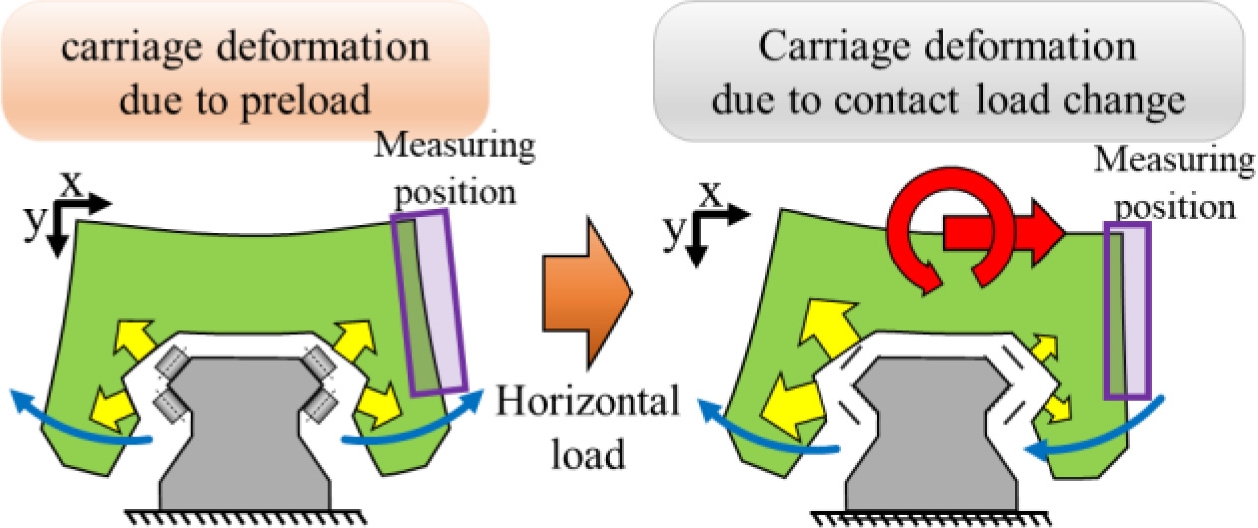
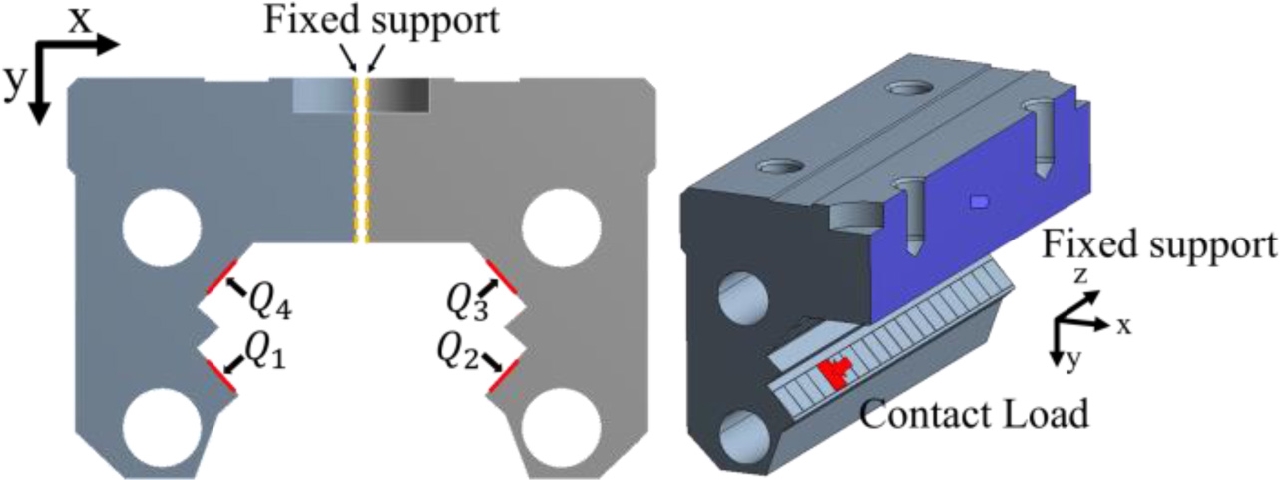
Fig. 10은 외부 하중이 캐리지의 변형에 미치는 영향을 개념적으로 나타낸 것이다. 앞서 설명한 바와 같이 수평 하중을 인가할 때 실제로는 그림에서와 같이 모멘트 하중이 같이 가해지게 된다. 그리고 선형 롤러베어링에 외부 하중이 인가되지 않았을 때에도 예하중으로 인해 캐리지에는 초기 변형이 발생하며 외부 하중이 작용할 때 추가적인 변형이 발생하게 된다. 이러한 현상은 캐리지 변위 측정 결과에 직접 영향을 미치게 된다. 특히 상용 프로그램21의 계산 결과는 캐리지가 변형될 때 캐리지 표면 변형 형상을 고려하지 않으므로 본 논문에서는 외부 하중에 의해 발생하는 캐리지의 변형을 유한요소 해석을 통하여 계산하여 보상하였다. Fig. 11에 캐리지 변형을 계산하기 위한 유한요소 모델(ANSYS)과 구속 및 하중 조건을 나타내었다. 효율적인 계산을 위해 캐리지의 변형에 영향을 미치는 부분으로 국한하여 모델링 하였으며, 베어링 제조업체에서 제공하는 도면을 기반으로 모델을 구축하였다. 구조의 대칭성을 고려하여 모델을 좌우측으로 분할하여 대칭면을 고정하였으며 각 롤러에서의 접촉 하중을 그림과 같이 인가하여 베어링의 변형을 계산하였다.

Fig. 10

Carriage deformation process due to horizontal load

Fig. 11

Finite element model with constraints and loading conditions

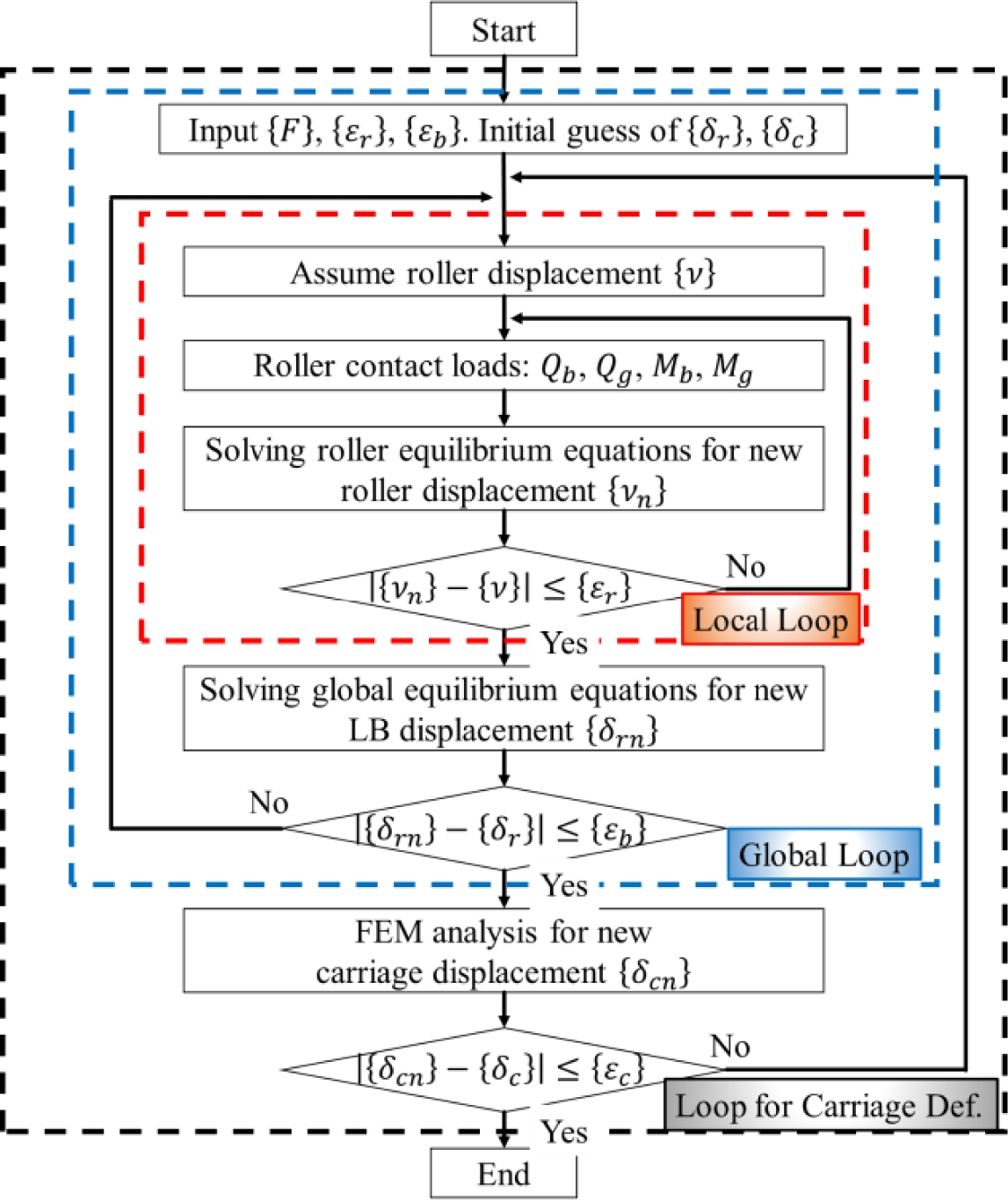
외부 하중에 의한 캐리지 변형 계산 알고리즘을 Fig. 12에 나타내었다. 먼저 캐리지에 인가되는 접촉 하중을 계산하기 위해 Kwon 등^2,3에 의해 제안된 해석적 모델을 사용하였으며 계산된 접촉 하중을 유한요소 모델에 적용하여 캐리지와 롤러 간 접촉면의 변위를 계산하였다.

Fig. 12

Calculation procedure of carriage deformation

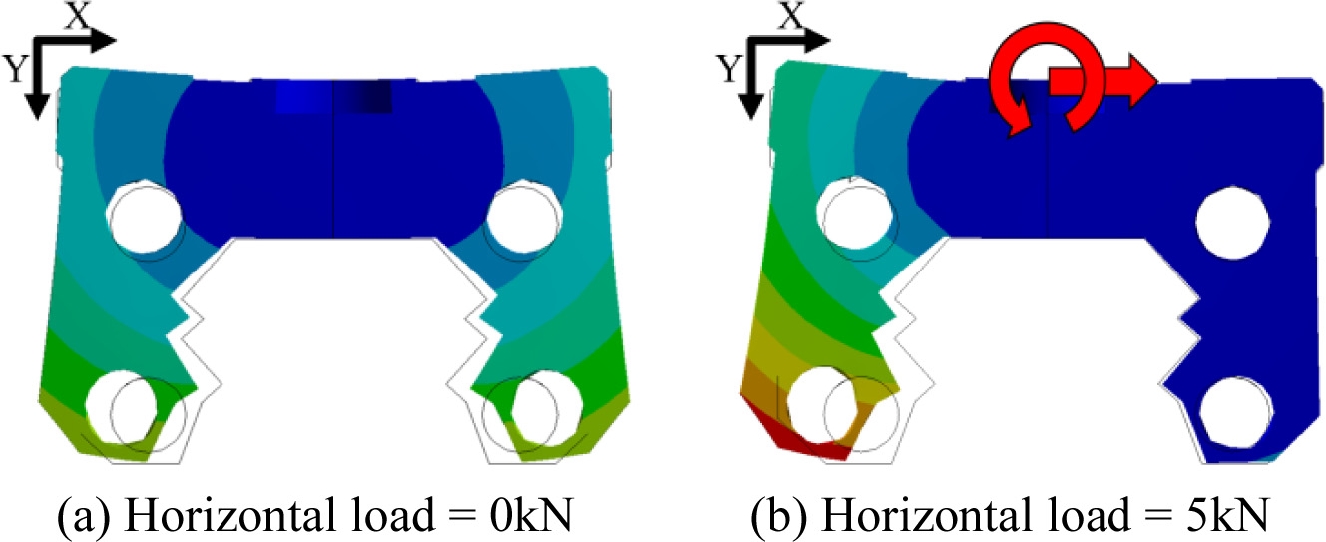
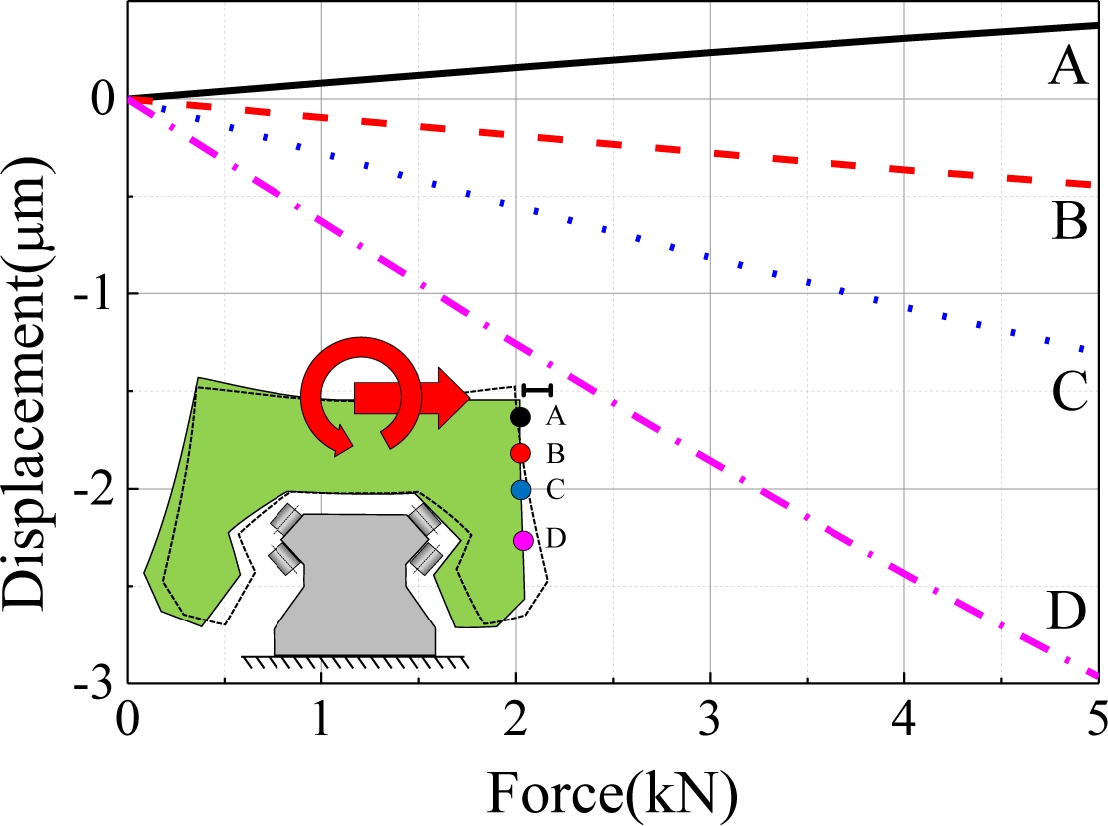
하중을 인가할 때 캐리지와 롤러 간의 상대변위는 캐리지의 접촉 하중을 결정하는 중요한 요소이므로 캐리지와 롤러 간 접촉면의 변위를 고려하여 접촉 하중을 계산하였다. 특히 캐리지가 변형하게 되면 이 같은 접촉 조건이 변경될 수 있어 계산 과정을 반복적으로 실행하여 접촉 하중과 캐리지 변형을 수렴시켜 결정하였다. Fig. 13은 ANSYS 유한요소 모델에서 얻어진 캐리지의 변형을 보여주고 있으며 Fig. 14에는 이를 통해 얻어지는 센서 위치에서의 변위를 보여주고 있다. Fig. 13에서 볼 수 있는 바와 같이 하중이 가해지지 않았을 때에도 예하중으로 인해 캐리지가 변형됨을 확인할 수 있으며 수평 하중이 인가되면 측정 위치에 따라서 변위 값이 달라질 수 있음을 보여주고 있다. 본 연구에서 사용한 상용 프로그램²¹에서는 이와 같은 캐리지의 변형 효과를 반영하고 있지 않으므로 계산 결과에 측정위치에 따른 오차를 보상하였다.

Fig. 13

Carriage deformation due to horizontal load

Fig. 14

Horizontal displacements of the measure positions on the carriage

4.3 실험 결과

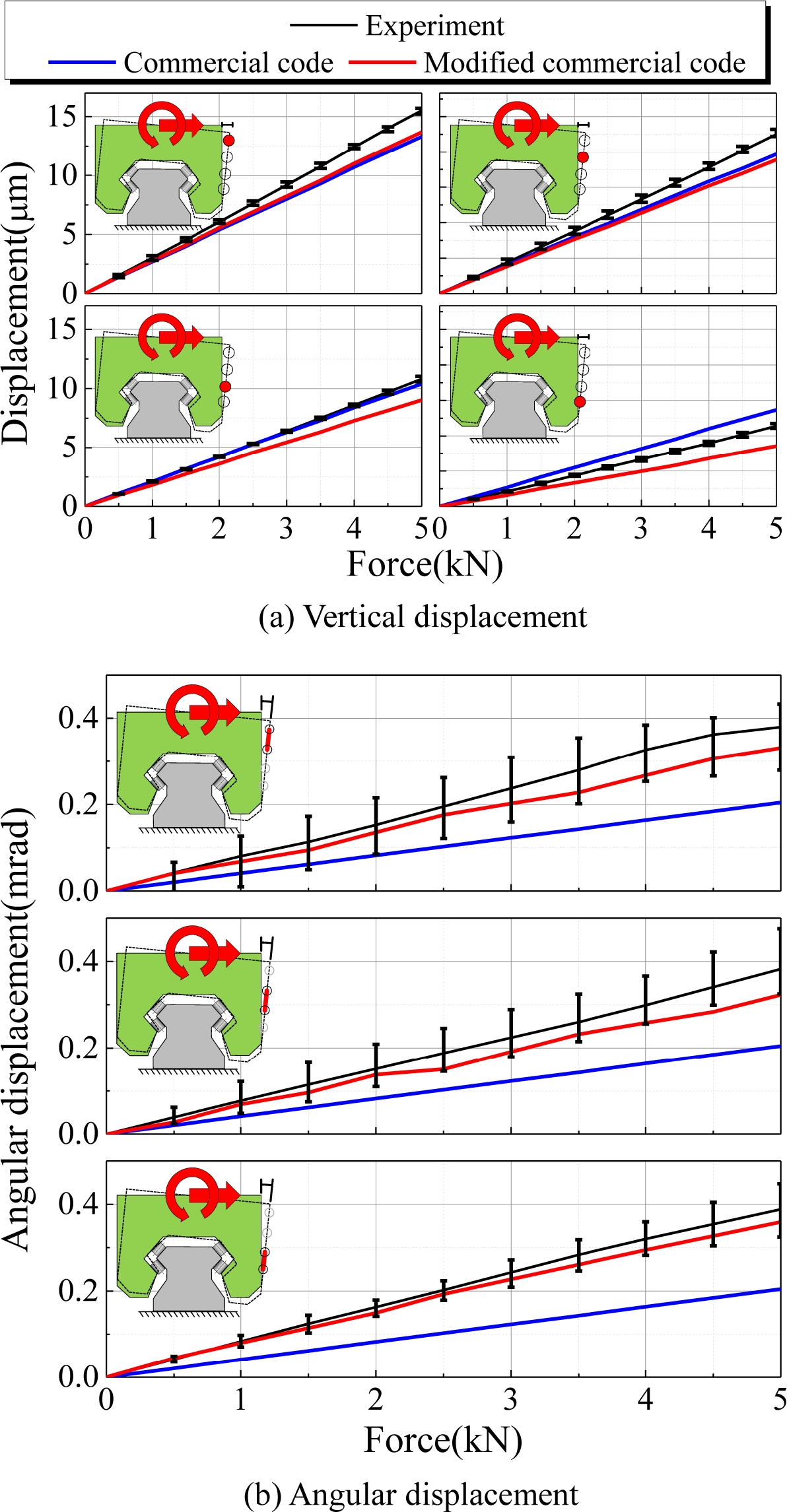
Fig. 15는 캐리지의 수평 방향 변위와 각변위를 상용 프로그램의 결과와 비교하여 나타낸 것이다. 이 때 상용 프로그램의 결과는 캐리지의 변형을 고려하기 전, 후와 함께 비교하였고 인접한 두 측정 위치에서의 변위를 통해 각변위를 계산하였다. 모든 위치에서 측정 결과가 상용 프로그램의 결과보다 크게 발생하였으며, 측정 위치에 따라 수평방향 변위의 14 - 21%, 각변위의 5 - 13%의 차이가 발생하고 있음을 볼 수 있다. 이는 가이드 레일, 바닥면 및 바닥면과 가이드 레일 결합부 등에서 발생한 변형으로 추정할 수 있다.

Fig. 15

Carriage deflection due to horizontal load

Fig. 16은 수평 하중에 의해 발생한 가이드 레일의 위치 별 변위를 나타낸 것이다. 수직 하중에서와 마찬가지로 캐리지 내부에서의 가이드 레일 변위는 캐리지 변위 측정치와 상용 프로그램의 변위 계산치의 차이로 추정하였다. 모든 측정 위치에서 캐리지 내부의 가이드 레일 변위가 가이드 레일에서 직접 측정한 변위에서 예상되는 값과 유사하게 나타남을 확인할 수 있다.

Fig. 16

Guide rail deflections due to horizontal load

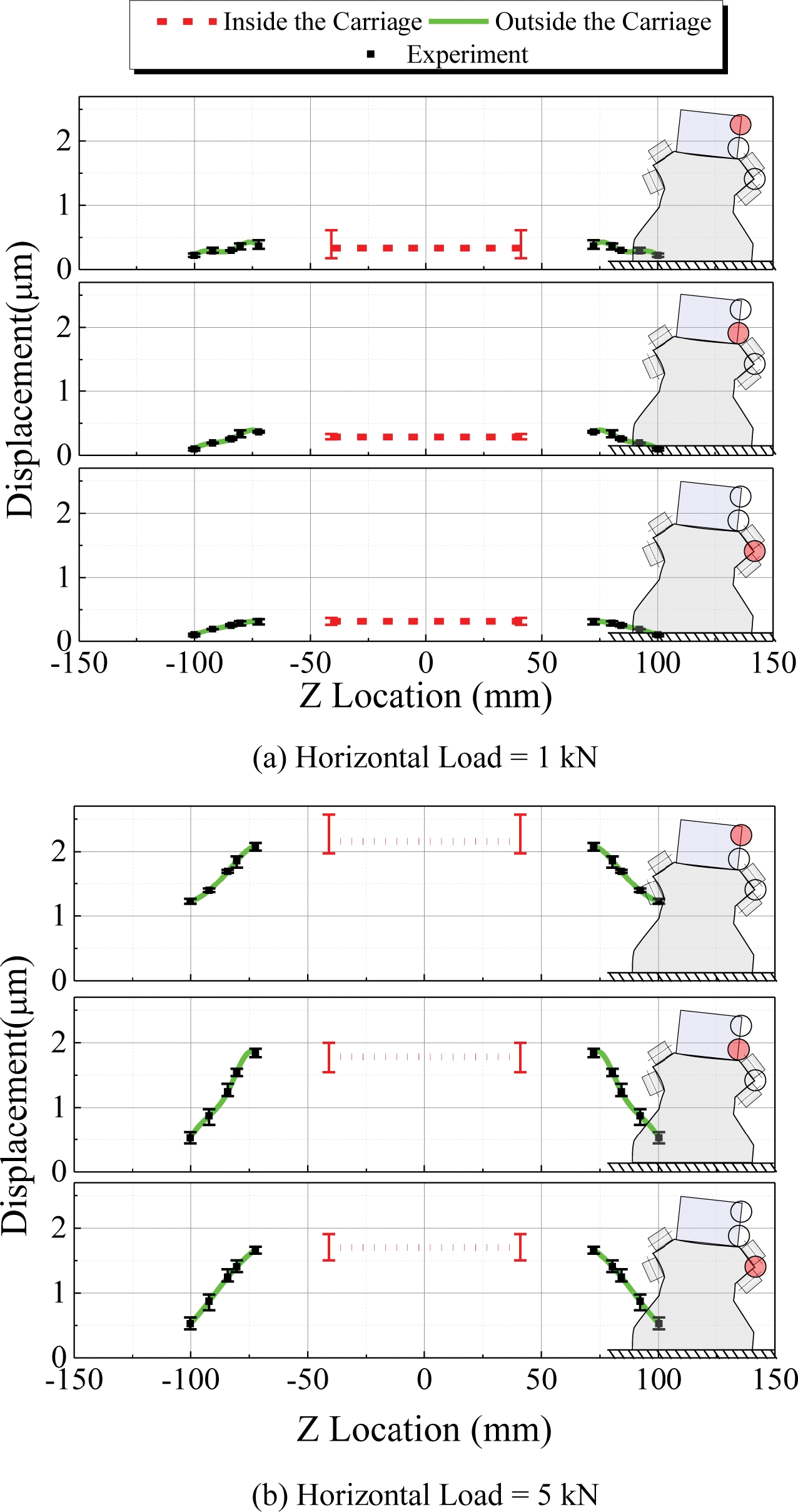
Fig. 17은 각 측정 위치에서 수평 하중이 각각 1, 5 kN 인가될 때 가이드 레일의 변형 양상을 나타낸 것이다. 측정된 가이드 레일의 변위를 이용하여 캐리지 주변의 가이드 레일 변형을 Spline곡선으로 예측하였다. 가이드 레일의 상단에서 변위가 상대적으로 크게 발생하고 있으며 이는 캔틸레버 구조를 갖는 가이드 레일의 휨 현상이 발생함을 보여준다. 수직 방향 하중에서 나타난 현상과 마찬가지로 하중에 따른 약간의 옵셋이 관측되고 있으며 이는 바닥면의 변형에 의한 것으로 추정된다.

Fig. 17

Deformed shape of guide rail due to horizontal load

이상의 실험 결과에 따라 롤러열 중심을 기준으로 평가하면 수평 하중에 의한 베어링 변위의 평균 약 19% 정도가 가이드 레일 및 바닥면 변형에 의한 것으로 추정된다.

5. 선형 롤러베어링으로 지지된 테이블의 변위 측정 실험

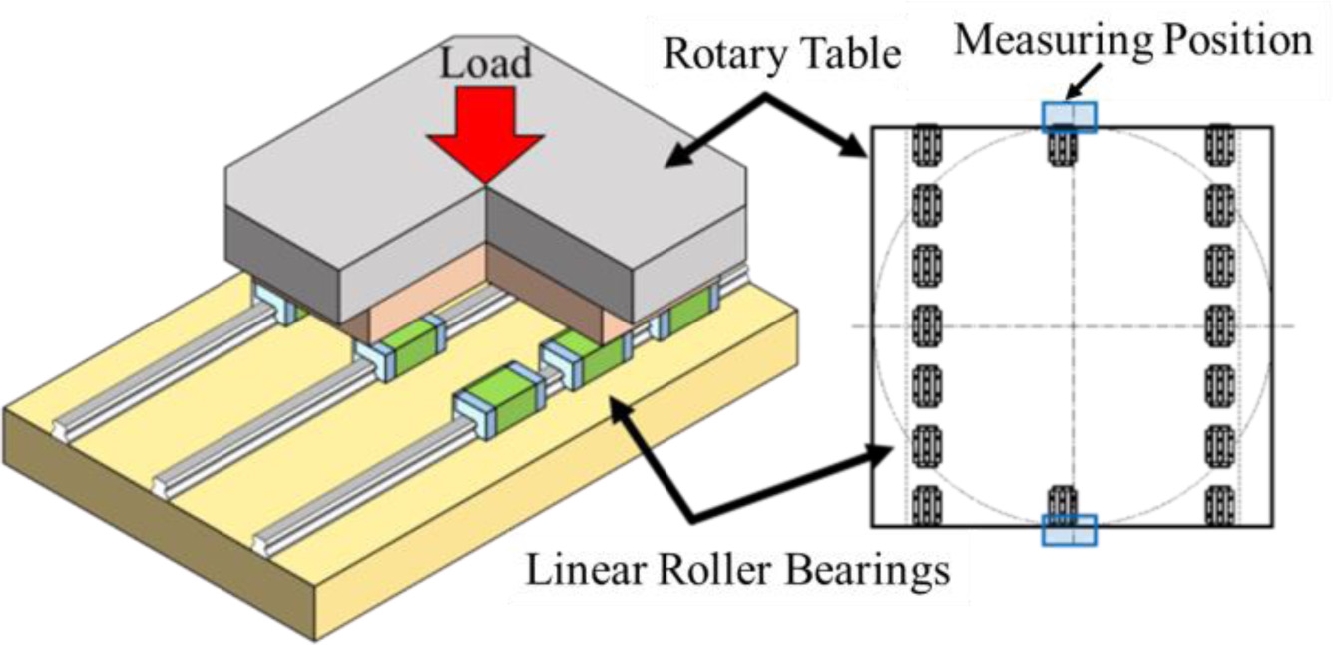
대형 가공물을 지지하기 위해 Fig. 18과 같이 다수의 선형 롤러베어링을 사용하고 있는 로터리 테이블을 고려하였다. 실험에 사용된 로터리 테이블은 대형 가공물을 지지하고 회전시킴은 물론 직선 이송도 가능하게 할 목적으로 제작된 것이다.²² 테이블의 회전축에는 복열 롤러베어링²³을, 테이블의 수직 하중 지지를 위해 스러스트 원통롤러베어링을 사용하였으며 직선 이송을 위해 선형 롤러베어링을 사용하였다. 로터리 테이블 자체의 질량과 가공물의 질량 등에 의해 직선 이송 중 처짐이 발생하게 되고 이는 가공 정밀도에 영향을 미치게 된다. 따라서 이에 대한 보다 정확한 예측을 필요로 하게 된다.²²

Fig. 18

Table supported by multiple linear roller bearings

스러스트 원통롤러베어링의 처짐 효과는 참고문헌²⁴에서 제시한 시뮬레이션 방법과 실험을 통해 분석이 완료된 바 있다. ²² 여기서는 선형 롤러베어링에 의한 테이블 하판의 변위를 측정하기 위해 1 ton의 질량체를 차례로 테이블에 얹어 총 10 ton의 하중을 인가하였으며 테이블 하판의 전면 및 후면에 정전용량형 변위센서를 설치하여 변위를 측정하였다. Fig. 19에 실험장치 셋업 상태를 보여주고 있다. 본 실험장치에 사용된 선형 롤러 베어링은 RUE65-E-H 모델로서 앞서 사용한 롤러베어링과 동일한 형식에 대형인 모델이다. ²⁵ 변위 측정을 위한 정전용량형 변위센서도 앞서 사용한 센서와 동일한 모델을 이용하였다.

Fig. 19

Experimental system for measuring table deflection subjected to vertical load

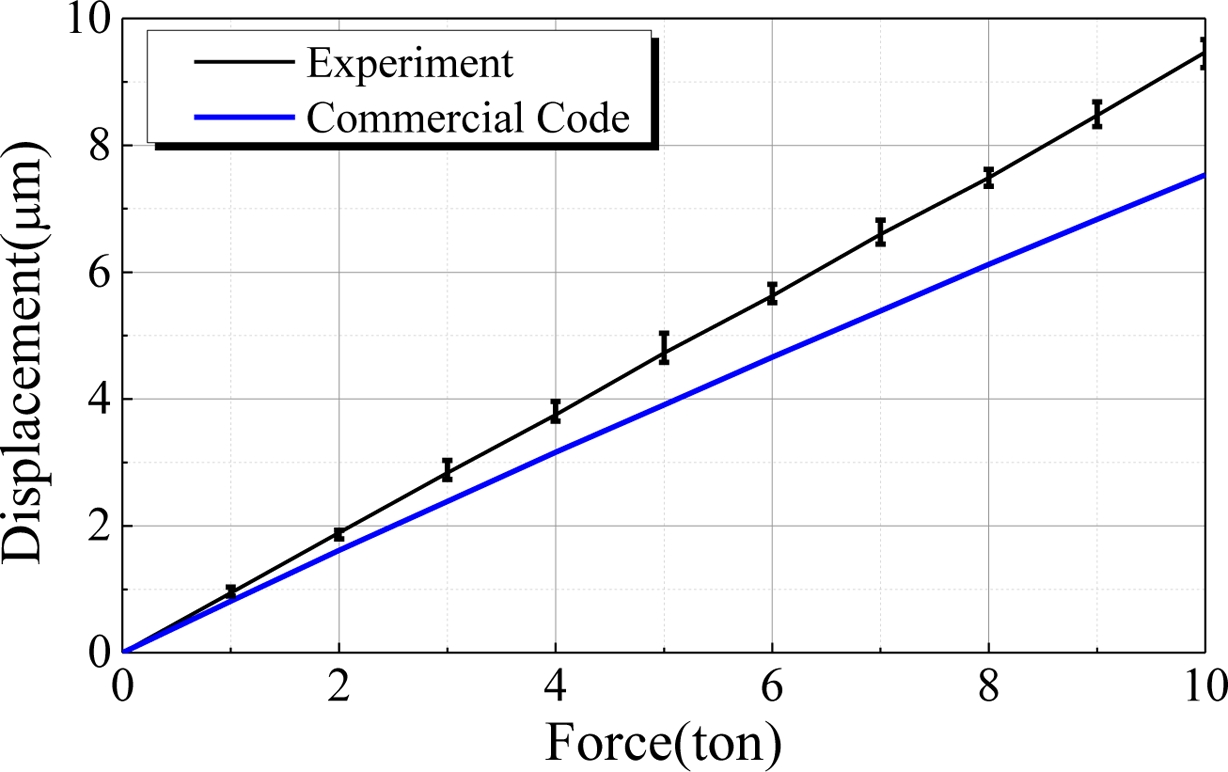
Fig. 20은 하중에 의해 발생한 테이블의 처짐을 나타내고 있다. 상용 프로그램의 결과와 비교하여 평균적으로 약 25%의 변위가 추가로 발생하였으며 이는 본 논문에서 확인한 바와 같이 가이드 레일 및 바닥면에서의 변형으로 인해 발생한 것으로 추정된다. 특히 앞선 실험에서 약 22% 정도의 가이드 레일 및 바닥면 변형 효과와 비교할 때 유사한 특성을 나타내고 있음을 볼 수 있다.

Fig. 20

Comparison of measured and simulated table deflections due to vertical load

6. 결론

본 논문에서는 선형 롤러베어링에 수직 및 수평 하중이 인가될때 발생하는 가이드 레일의 변형을 실험적으로 연구하였다. 이를 위하여 선형 롤러베어링에 하중을 가하면서 가이드 레일의 변위를 측정하기 위한 실험장치를 제작하고 실험을 수행하였다. 외부에서 접근이 불가한 캐리지 내부 가이드 레일 변위는 캐리지 변위의 측정과 유한요소 모델을 통한 계산결과를 활용하여 추정하는 방법을 제시하였다. 실험결과, 본 연구에서 사용된 베어링의 경우, 수직과 수평 하중 인가 시 각각 베어링 전체 변위 중 약 22%와 19% 정도가 가이드 레일 및 바닥면의 변형에 의해 발생하였다. 본 연구에서는 한 가지 종류의 단일 베어링을 중심으로 실험이 수행되었으나 다수의 베어링에 의해 지지되는 실제 테이블에서의 수직 하중 실험을 통해서도 유사한 특성을 확인할 수 있었다.

본 연구를 통해 외부 하중에 의한 선형 롤러베어링의 변위를 보다 정확히 예측하기 위해서는 가이드 레일 및 바닥면의 변형을 적절히 고려해야 할 필요가 있음을 확인하였다. 임의의 일반 베어링에 대해 이 같은 효과를 예측하기 위해서는 가이드 레일 및 바닥면, 그리고 바닥면과의 접촉부 등에 대한 모델링 및 해석 기술에 관한 후속적인 연구가 필요할 것으로 사료된다.

Acknowledgments

본 연구는 한국기계연구원의 연구비 지원에 의해 수행된 연구 결과의 일부이며 관계자 여러분에게 감사드립니다.

References

• Hong, S.-W. and Tong, V.-C., “Rolling-Element Bearing Modeling: A Review,” International Journal of Precision Engineering and Manufacturing, Vol. 17, No. 12, pp. 1729-1749, 2016. [https://doi.org/10.1007/s12541-016-0200-z]
• Kwon, S.-W., Tong, V.-C., and Hong, S.-W., “Modeling of Displacement of Linear Roller Bearing Subjected to External Forces Considering LM Block Deformation,” Transactions of The Korean Society of Mechanical Engineers A, Vol. 40, No. 12, pp. 1077-1085, 2016. [https://doi.org/10.3795/KSME-A.2016.40.12.1077]
• Kwon, S.-W., Tong, V.-C., and Hong, S.-W., “Five-Degrees-of-Freedom Model for Static Analysis of Linear Roller Bearing Subjected to External Loading,” Proc. of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, Article No. 0954406218792573, 2018. [https://doi.org/10.1177/0954406218792573]
• Jinfeng, L., Liping, W., and Liwen, G., “Analysis of the Vertical Stiffness of Rolling Guide that Involves the Elastic Deformation of Carriage Skirt,” Open Mechanical Engineering Journal, Vol. 9, pp. 726-732, 2015. [https://doi.org/10.2174/1874155X01509010726]
• Choi, J. S., Yi, Y.-s., Kim, Y. Y., Lee, D. J., Lee, S. J., et al., “Vibration Analysis and Its Application of a Linear Motion Guide Supported by Rolling Ball Bearings,” Transactions of the Korean Society of Mechanical Engineers A, Vol. 29, No. 7, pp. 955-963, 2005. [https://doi.org/10.3795/KSME-A.2005.29.7.955]
• Shaw, D. and Su, W., “Study of Stiffness of a Linear Guideway by Fea and Experiment,” Structural Longevity, Vol. 5, No. 3, pp. 129-138, 2011.
• Sun, W., Kong, X., Wang, B., and Li, X., “Statics Modeling and Analysis of Linear Rolling Guideway Considering Rolling Balls Contact,” Proc. of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, Vol. 229, No. 1, pp. 168-179, 2015. [https://doi.org/10.1177/0954406214531943]
• Ohta, H. and Tanaka, K., “Vertical Stiffnesses of Preloaded Linear Guideway Type Ball Bearings Incorporating the Flexibility of the Carriage and Rail,” Journal of Tribology, Vol. 132, No. 1, Paper No. 011102, 2010. [https://doi.org/10.1115/1.4000277]
• Rahmani, M. and Bleicher, F., “Experimental and Analytical Investigations on Normal and Angular Stiffness of Linear Guides in Manufacturing Systems,” Procedia CIRP, Vol. 41, No. pp. 795-800, 2016. [https://doi.org/10.1016/j.procir.2015.12.033]
• Pawełko, P., Berczyński, S., and Grządziel, Z., “Modeling Roller Guides with Preload,” Archives of Civil and Mechanical Engineering, Vol. 14, No. 4, pp. 691-699, 2014. [https://doi.org/10.1016/j.acme.2013.12.002]
• Khim, G., Park, C. H., Shamoto, E., and Kim, S. W., “Prediction and Compensation of Motion Accuracy in a Linear Motion Bearing Table,” Precision Engineering, Vol. 35, No. 3, pp. 393-399, 2011. [https://doi.org/10.1016/j.precisioneng.2010.12.006]
• Kim, H.-Y., Jeong, J.-K., Won, J.-J., and Jeong, J.-I., “A Computational Modeling Reflecting Static and Dynamic Characteristics of LM Bearings for Machine Tools,” Journal of the Korean Society for Precision Engineering, Vol. 29, No. 10, pp. 1062-1069, 2012. [https://doi.org/10.7736/KSPE.2012.29.10.1062]
• Li, X., Liu, Y., Liu, J., and Guo, H., “Theory and Experimental Research on Static Stiffness of Linear Rolling Guide,” Proc. Computer Science and Automation Engineering International Conference, Vol. 2, pp. 85-87, 2012. [https://doi.org/10.1109/CSAE.2012.6272733]
• Yi, Y.-S., Kim, Y. Y., Choi, J. S., Yoo, J., Lee, D. J., et al., “Dynamic Analysis of a Linear Motion Guide Having Rolling Elements for Precision Positioning Devices,” Journal of Mechanical Science and Technology, Vol. 22, No. 1, pp. 50-60, 2008. [https://doi.org/10.1007/s12206-007-1006-9]
• Oh, K.-J., Khim, G., Park, C.-H., and Chung, S.-C., “Mathematical Modeling of Friction Force in LM Ball Guides,” Journal of the Korean Society for Precision Engineering, Vol. 32, No. 5, pp. 423-429, 2015. [https://doi.org/10.7736/KSPE.2015.32.5.423]
• Zou, H. and Wang, B., “Investigation of the Contact Stiffness Variation of Linear Rolling Guides Due to the Effects of Friction and Wear During Operation,” Tribology International, Vol. 92, No. pp. 472-484, 2015. [https://doi.org/10.1016/j.triboint.2015.07.005]
• Jang, S. H., Khim, G. and Park, C. H., “Heat Transfer Characteristics of the LM Guide Considering Friction Force,” Proc. of the KSPE Spring Conference, No. 5, p. 744, 2014.
• Cheng, D.-J., Park, T.-J., and Kim, S.-J., “Improved Friction Model for the Roller LM Guide Considering Mechanics Analysis,” Journal of Mechanical Science and Technology, Vol. 32, No. 6, pp. 2723-2734, 2018. [https://doi.org/10.1007/s12206-018-0529-6]
• Jastrzębski, D., Pawełko, P., and Szwengier, G., “Modeling the Effect of Geometric Errors on the Static Characteristics of Guide Rail Systems,” Advances in Manufacturing Science and Technology, Vol. 36, No. 2, pp. 31-41, 2012.
• Tao, W., Zhong, Y., Feng, H., and Wang, Y., “Model for Wear Prediction of Roller Linear Guides,” Wear, Vol. 305, Nos. 1-2, pp. 260-266, 2013. [https://doi.org/10.1016/j.wear.2013.01.047]
• Schaeffler Technologies, BEARINX®-online Linear System Calculation, https://bearinx-online.ina.de, , 2015.
• Oh, H.-I., Tong, V.-C., Park, W.-S. and Hong, S.-W., “Modeling of Displacements in a Large-Size Rotary Table Subjected to Loads,” Journal of the Korean Society for Precision Engineering, Vol. 35, No. 4, pp. 443-450, 2018. [https://doi.org/10.7736/KSPE.2018.35.4.443]
• Tong, V.-C. and Hong, S.-W., “Modeling and Analysis of Double-Row Cylindrical Roller Bearings,” Journal of Mechanical Science and Technology, Vol. 31, No. 7, pp. 3379-3388, 2017. [https://doi.org/10.1007/s12206-017-0627-x]
• Tong, V.-C., Bae, G.-H., and Hong, S.-W., “Dynamic Analysis of Spindle Supported by Multiple Bearings of Different Types,” Journal of the Korean Society for Precision Engineering, Vol. 32, No. 2, pp. 117-125, 2015. [https://doi.org/10.7736/KSPE.2015.32.2.117]
• Schaeffler, “Monorail Guidance Systems - Linear Recirculating Roller Bearing and Guideway Assemblies Linear Recirculating Ball Bearing and Guideway Assemblies Linear Guidance Systems with Linear Recirculating Ball Bearing Units Accessories,” https://www.schaeffler.us/content.schaeffler.us/en/mediathek/library/library-detail-language.jsp?id=2774255, (Accessed 21 November 2018)