미세 홈 구조 폴리머 표면의 발수성과 비등방 젖음성

1. 서론

식물의 잎과 같이 복잡한 표면 구조를 지닌 생체 표면은 독특한 젖음성(Wettability)으로 인해 지금까지 활발히 모사되고 연구되어오고 있다.^1,2 가장 특징적인 젖음성은 발수성(Water-Repellency)으로서 표면 위의 미세한 돌기 구조에 의해 발현되며, 이러한 미세 구조를 지닌 표면 위에서 액적은 서로 다른 두 젖음 상태(Wetting State)를 보인다.³ 두 가지 젖음 상태 중 하나는 Cassie-Baxter (Cassie) 젖음 상태인데 액적이 표면 구조체 위에 놓여 액적 아래의 접촉면(Contact Area)이 표면과 공기의 이질(Heterogeneous) 상태에 해당한다.⁴ 또 다른 젖음 상태인 Wenzel 젖음 상태는 이와 달리 표면의 형태를 액체가 모두 따라가 젖어있는 상태이다.⁵ 이 중 Cassie 젖음 상태는 높은 접촉각(Contact Angle)과 낮은 접촉각 이력(Contact Angle Hysteresis)을 지녀 자가세정(Self-Cleaning)에 유리한 초소수성(Superhydrophobicity)을 가지는 것으로 알려져 있다. 따라서, 높은 발수 성능을 가진 미세 결 표면(Micro Textured Surface)은 Cassie 젖음 상태가 안정적으로 유지되는 표면이라 할 수 있다.

생체 표면이 지니는 또 다른 젖음성은 비등방 젖음성(Anisotropic Wettability)이다.⁶ 비등방 젖음성이란 방향성을 지닌 젖음 현상으로 표면 위 미세 구조의 비등방 형태나 배열로부터 기인한다.⁷ 간단한 형태인 평행하게 배열된 미세 홈(Micro-Groove) 구조에서도 비등방 젖음성이 관찰된다. 이러한 표면 위에선 미세 구조의 방향을 기준으로 표면에 놓인 액적의 접촉선(Contact Line) 움직임이 향상되거나 제한을 받게 된다. 그 결과, 측정 방향에 따라 서로 다른 액적의 접촉각이 관찰되고 기울임 방향에 따라 흐름각(Sliding Angle)이 큰 차이를 보이게 된다.⁸ 실제로 표면 위 액적의 홈 방향 흐름각은 동일한 소수성(Hydrophobicity)을 나타내는 균일 배열 구조물 표면에 비해 낮은 각도임이 실험적으로 보고되었다.^9,10 이러한 비등방 젖음성을 이용하면 지정된 방향으로 표면 위 액적을 보다 쉽게 이동시킴으로써 발수성 향상 등 다양한 기능성을 기대할 수 있다.

미세 홈 구조 표면은 단순한 형태임에도 불구하고 초소수성과 비등방 젖음성을 동시에 나타내는 장점을 지닌다. 따라서 미세 홈 구조가 가지는 기하학적 특성과 이에 따른 젖음성에 대한 이해는 앞으로 요구될 다양한 기능성 표면 제작에 큰 도움을 줄 수 있다. 또한 이러한 연구는 여러 표면 재료들로 확장되어야 하는데 재료에 따라 고유 젖음성(Intrinsic Wettability)이 다르며, 제작 방법도 달라져 미세 구조가 가질 수 있는 치수의 한계가 달라지기 때문이다. 하지만, 현재까지 보고된 미세 홈 구조의 젖음성 연구들은 대부분 금속 표면의 미세밀링(Micro-Milling)이나 습식 에칭(Wet Etching)된 표면으로 이뤄져 있다.⁹ 반면 폴리머 미세 홈 표면에 대한 연구는 그 수가 많지 않다. 그마저도 표면 위 액적이 Wenzel 젖음 상태이거나¹¹ 홈 구조가 단 하나일 뿐이어서⁷ 홈 패턴에 따른 발수성과 비등방성을 알아보기에는 부족하다고 판단된다. 따라서 본 연구에서는 서로 다른 패턴의 폴리머 미세 홈 표면들을 제작하고, 이들의 초소수성과 비등방 젖음성을 알아보고자 한다.

2. 미세 홈 표면 제작 및 젖음성 측정

본 연구에 사용된 미세 홈 표면은 대량 반복 생산이 가능한 레플리카 몰딩(Replica Molding)^12,13 방식으로 제작되었다. 틀 역할을 할 몰드 마스터(Mold Master)는 Si 웨이퍼(Wafer)에 포토리소그래피(Photolithography) 공정을 통해 제작되고, 이 위에 경화성 수지인 Polydimethylsiloxane (PDMS)를 부은 뒤 경화 후 떼어내어 사용하게 된다. 본 실험에 사용된 몰드 마스터와 PDMS 미세 홈 표면 이미지를 Fig. 1에서 확인할 수 있다. 미세 홈 표면은 홈 간의 간격(w)이 서로 다르도록 설계되었다. 구체적으로 모든 표면의 b와 h를 각각 10, 5 μm가 되도록 설계하였고, w는 표면에 따라 10, 20, 40, 그리고 80 μm가 되도록 디자인하였다. 이 홈 간의 거리를 기준으로 표면의 명칭을 G₁₀, G₂₀, G₄₀, 그리고 G₈₀으로 지정하였다.

Fig. 1

Scanning electron microscope (SEM) images of negative Si mold masters (Left) and optical images of the resulting replica micro-grooved surfaces (Right) for (a) G10, (b) G20, (c) G40, and (d) G80

각 미세 홈 표면들의 형상 치수는 삼차원 공초점 레이저 현미경(VK-9700, KEYENCE Corporation)으로 측정되었고 상세한 수치를 Table 1에 기재하였다.

Table 1

Geometric parameters of the micro-grooved surfaces and the water contact angle (CA) values estimated and measured on the micro-grooved surfaces

물에 대한 젖음성 및 비등방 젖음성을 관찰하기 위해 홈 길이 방향을 기준으로 두 가지 방향을 지정하여 접촉각 및 흐름각이 측정되었다. Fig. 2(a)에 나타낸 바와 같이 홈을 따라 평행한 방향과 수직한 방향으로 두 가지 방향을 지정하였다. 정확한 측정 방향 구분을 위해 Fig. 2(b)에 측정 방향에 따른 측정값 표기를 도식화하였다. 접촉각(θ) 및 흐름각(α)이 홈의 길이 방향과 수직하게 측정될 경우 아래 첨자에 ⊥를 수평할 경우엔 ‖를 사용하여 측정 방향을 구분하였다.

Fig. 2

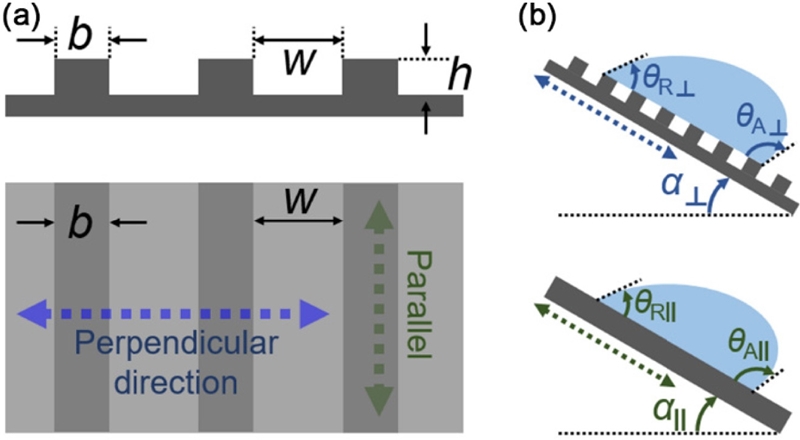
Schematic diagrams of the micro-grooved surfaces showing (a) Geometric parameters and (b) Dynamic contact angles. The quantities measured perpendicular (Parallel) to grooves are denoted with the subscript ⊥ (‖)

실험은 증류수(Distilled Water)를 사용하여 진행되었고, 밀도(ρ)와 표면장력(γ)은 각 995 kg/m³과 72 mN/m로 측정되었다. 정적 접촉각(Static Contact Angle, SCA)과 흐름각의 측정은 액적 이미지 기반의 접촉각 측정기(SmartDrop, FEMTOBIOMED)를 통해 수행되었다. 모든 측정은 동일한 크기(5 μL)의 액적을 분주하여 진행되었고 실제 측정 영상의 일부를 Fig. 3에서 확인할 수 있다. SCA 측정은 액적을 표면 위에 충격이 없도록 얹은 후 측정하는 앉은 액적 측정법(Sessile Drop Method)이 사용되었다.

Fig. 3

Sessile droplets on the G40 for the measurements of (a) The static contact angle perpendicular to grooves θ⊥, (b) Parallel to grooves θ‖, and (c) The sliding angle perpendicular to grooves α⊥. The volume of a droplet is 5.0 μL. The base lines between droplets and surfaces are indicated in blue solid lines

흐름각은 접촉각 측정기에서 표면을 일정한 속도로 기울이며 액적을 관찰하는데, 중력에 의해 액적이 움직이기 시작할 때 표면의 기울여진 각도를 흐름각으로 판단하였다(Fig. 3(c)). 이때 액적이 흐르는 방향에 놓인 접촉선과 표면이 이루는 접촉각인 전진 접촉각(Advancing Contact Angle, ACA)과 반대편 접촉선의 후진 접촉각(Receding Contact Angle, RCA) 역시 같이 측정하였다. 이들을 동적 접촉각(Dynamic Contact Angle)이라 하고 이 두 값들의 차이가 접촉각 이력(Contact Angle Hysteresis, CAH)이다. 또한 ACA와 RCA 각각은 액적의 표면 위 머무름 힘(Retention Force)을 결정하는 중요한 인자이기도 하다.¹⁴ 모든 접촉각들은 측정 정확도 및 산포를 고려하여 각 조건별로 최소 7회 이상 반복 측정되었다.

3. 미세 홈 표면의 젖음성 분석

3.1 정적 접촉각 분석

정적 접촉각은 표면의 젖음성을 대표하는 대표적인 물성 값이다. 소수성 표면의 기준으로 90°라는 정적 접촉각 수치가 널리 쓰이고 있듯이 초소수성 역시 150° 이상의 높은 정적 접촉각 수치로 대변된다. 하지만, 미세 구조를 지닌 표면의 경우 높은 정적 접촉각이 항상 높은 발수 성능을 보장하는 것은 아님이 실험적으로 보고된 바 있다.^15-17 이는 앞서 언급한 바와 같이 액적의 젖음 상태와 밀접하게 연관되어 있다. 또한 각 젖음 상태별 정적 접촉각인 겉보기 접촉각(Apparent Contact Angle)은 표면의 구조에 의해서도 그 값이 변하며 이를 예측하는 이론적인 수식이 존재한다. 우선, Wenzel 젖음 상태의 겉보기 접촉각(θ_W)은 표면의 거칠기 계수(Roughness Factor, r)에 의해 다음 식(1)과 같이 예측된다.⁵

$\[ \cos {\theta }_W=r\cos {\theta }_e \]$

(1)

여기서 거칠기 계수란 실제 표면적과 거칠기가 없는 투영 면적(Projection Area)의 비율이며 θ_e는 미세 구조 또는 거칠기가 없는 표면의 고유 접촉각(Intrinsic Contact Angle)을 의미한다. 그리고 Cassie 젖음 상태의 겉보기 접촉각(θ_C)은 다음 식(2)와 같이 예측할 수 있다.⁴

$\[ \cos {\theta }_C=\varphi \cos {\theta }_e+\varphi -1 \]$

(2)

여기서 ϕ는 결 면적 비율(Texture Area Fraction)로 Cassie 상태의 액적이 표면과 접촉하는 면적과 그렇지 않은 면적의 비율이다. 본 실험에 사용된 PDMS는 미세 홈 구조는 r = 1 + 2h/(w + b) 그리고 ϕ = b/(w + b)의 관계식을 가지며 각 표면별 수치와 겉보기 접촉각 예측치는 Table 1에서 확인할 수 있다.

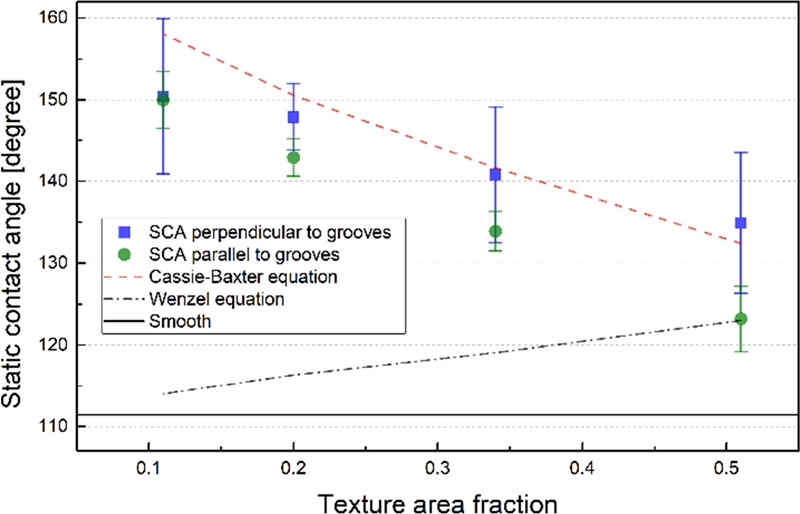
미세 구조와 정적 접촉각의 상관관계를 파악하기 위해 Fig. 4에 실제 측정치와 예측치, 그리고 홈이 없는 매끄러운 표면 위 측정값(θ_e)을 함께 표시하였다. 우선 파악되는 것으로는 측정 방향에 상관없이 미세 홈 구조 위 접촉각이 θ_e 값인 111.4 ± 2.4°보다 크다는 점과 Cassie 젖음 상태의 예측치와 유사한 값을 지닌다는 점이다. 더 나아가 미세 홈 간 거리가 멀어질수록, 즉 ϕ가 작을수록 접촉각이 커지는 경향성도 동일하다. 이는 Wenzel 상태의 예측치와 정반대의 추세이다. 따라서, 미세 홈 표면 위 액적의 젖음 상태는 Cassie 상태일 것이라 판단된다. 미세 홈 구조가 가지는 비등방 젖음성은 정적 접촉각에서도 나타나는데, 수평 방향에서 측정된 값(θ_‖)이 수직 방향의 그것(θ_⊥)보다 모든 경우 작은 값을 나타낸다. 이러한 점은 기존 연구들에서도 확인되었는데, 액적의 접촉선이 홈의 수직 방향으로 접촉선 고정(Contact Line Pinning)에 의해 전진이 힘들기 때문으로 파악되었다.^7,18-20 이 영향으로 인해 측정의 산포 역시 θ_‖의 경우가 θ_⊥에 비해 항상 작은 것을 확인할 수 있다.

Fig. 4

Apparent contact angles measured on the micro-grooved surfaces in this study. Theoretical values of contact angles according to the Cassie (Ref. 4) and Wenzel (Ref. 5) state are also depicted as red and black dashed lines, respectively

3.2 동적 접촉각 분석

발수성의 측면에서 높은 접촉각보다 중요한 것은 액적이 표면에서 쉽게 다른 위치로 이동되어야 한다는 점이다. 이는 낮은 액적의 고정력(Retention Force)이 요구되는 것이며, 고정력(F)은 다음 식(3)과 같이 표현된다.²¹

$\[ F=w\gamma \left(\cos {\theta }_R-\cos {\theta }_A\right) \]$

(3)

여기서 w는 액적 접촉면의 너비이며, θ_R과 θ_A는 각각 후진 접촉각(RCA)과 전진 접촉각(ACA)을 의미한다. 따라서 낮은 접촉각 이력(CAH)은 낮은 고정력 및 흐름각, 그리고 결과적으로 높은 발수성에 필수적임을 알 수 있다. 본 연구에 사용된 미세 홈 표면의 흐름각은 Fig. 5에 표시된 것처럼 흐르는 방향에 따라 큰 차이를 보였다.

Fig. 5

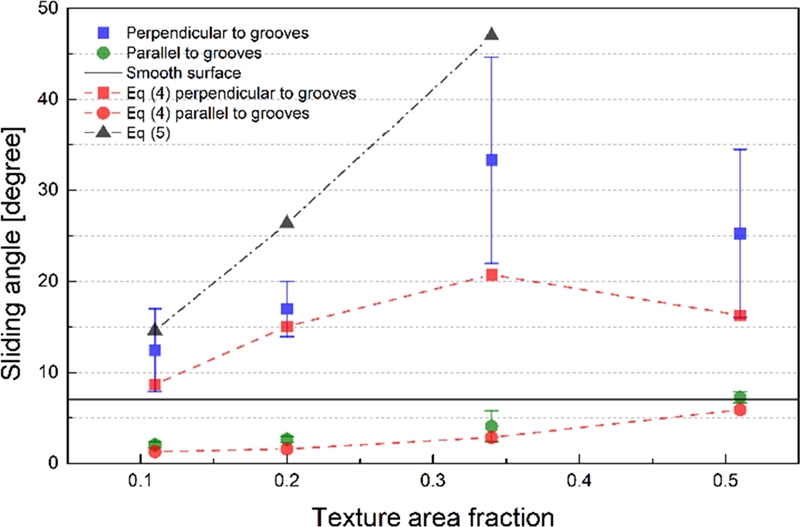
Sliding angles corresponding to the texture area fractions of the micro-grooved surfaces. Estimation derived by Lv et al. (Ref. 22) and Extrand and Gent (Ref. 21) are also indicated with black and red dashed lines, respectively

미세 홈 구조가 없는 표면의 흐름각에 비해 홈의 수직 방향으로 흐를 때 훨씬 더 많은 힘이 요구됨을 알 수 있다. 이와 반대로 홈과 같은 방향으로 흐를 때 매우 낮은 각도부터 액적이 흐르기 시작함을 알 수 있다.

미세 홈 표면에서 정적 접촉각이 미세 홈이 없는 표면보다 매우 높았기 때문에 발수성이 향상되었다고 판단할 여지가 있다. 하지만, 홈의 수직 방향으로의 흐름각(α_⊥)이 미세 구조가 없는 PDMS 표면 위 흐름각보다 크다. 따라서 정적 접촉각만으로 표면의 발수 성능을 논하는 것은 정확하지 못하다는 것을 알 수 있다. 여기서 주목할 점은 미세 홈 구조가 표면 위 흐름성에 큰 비등방성을 제공한다는 점이다. 그리고 미세 홈 방향으로의 효과적인 흐름성 증가 또는 발수성 증가를 위해선 0.5 미만의 결 면적 비율을 지녀야 함을 알 수 있다.

흐름각은 기울여진 표면에서 중력에 의한 힘과 고정력 사이의 평형을 기반으로 다음 식(4)와 같이 표현된다.²¹

$\[ \sin \alpha =\frac{2w\gamma }{\pi mg}\left(\cos {\theta }_R-\cos {\theta }_A\right) \]$

(4)

여기서 m은 액적의 질량 그리고 g는 중력가속도를 의미한다. 위 식(4)의 경우 표면의 미세 구조를 반영하지 않은 식인데, 결 면적 비율을 반영한 흐름각의 경우 다음 식(5)와 같이 나타낼 수 있다.²²

$\[ \sin \alpha =\frac{2^3\sqrt{3}\gamma \sqrt{2\left(1+\cos {\theta }_e\right)-{\left(1+\cos {\theta }_e\right)}^2\varphi }}{\rho g^3\sqrt{{\pi V^2}^3}\sqrt{4-3{\left(1+\cos {\theta }_e\right)}^2{\varphi }^2+{\left(1+\cos {\theta }_e\right)}^3{\varphi }^3}}\left(1+\cos {\theta }_e\right)\varphi \]$

(5)

여기서 V는 액적의 부피를 의미한다. Fig. 4에서 확인되듯이 접촉각 이력(CAH)만 반영된 식(4)가 측정값과 유사하며, 미세 구조가 반영되었지만 CAH가 반영되지 않은 식(5)는 ϕ가 커질수록 실제 측정값과 큰 차이를 보이며 0.5 이상일 경우 아예 식이 성립하지 않게 된다.

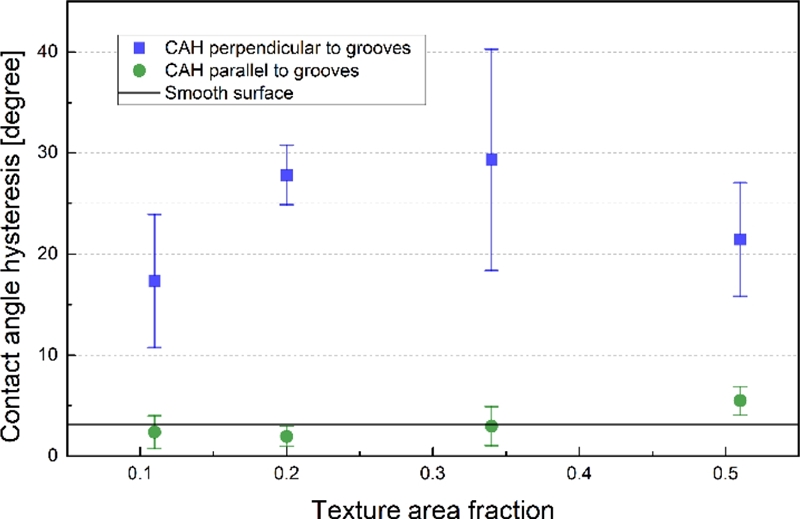
앞서 살펴본 바와 같이 미세 홈 표면의 흐름성 및 발수성은 접촉각 이력과 밀접한 관계를 가지고 있다. Fig. 6에 접촉각 이력의 실제 측정값을 나타내었는데, 흐름각과 유사한 경향을 확인할 수 있다. 하지만 홈과 평행한 방향으로의 측정값과 미세 구조가 없는 PDMS 표면의 값과의 상관관계는 흐름각의 그것과 상이하다.

Fig. 6

Contact angle hystereses with respect to the texture area fractions of the micro-grooved surfaces

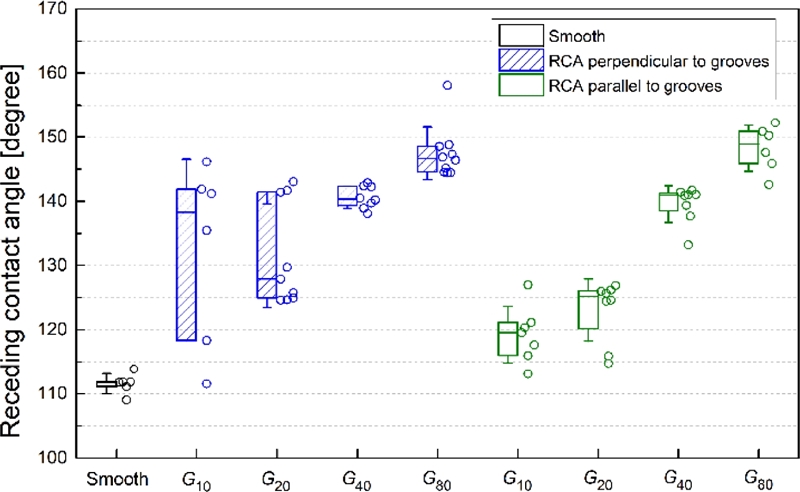
접촉각 이력의 경우 평행 방향 측정값이 평평한 표면의 값과 거의 유사하다. 또다른 특징은 수직 방향 측정값의 넓은 산포이다. 이는 ACA (Fig. 7)와 RCA (Fig. 8) 각각 수직 방향 측정값들(θ_A⊥, θ_R⊥)이 산포가 크기 때문이다. 미세 홈과 같은 방향성이 존재하는 미세 구조는 길이 방향의 수직으로 접촉선이 움직일 때, 홈 구조를 건너뛰어야 하는 불연속성(Discontinuity)으로 인해 전진과 후진 모두 Stick-Slip 움직임이 발생한다고 알려져있다.²³ 본 연구에서 나타난 수직 방향 측정값의 큰 산포 역시 이러한 접촉선 움직임의 불연속성 때문이라고 판단된다.

Fig. 7

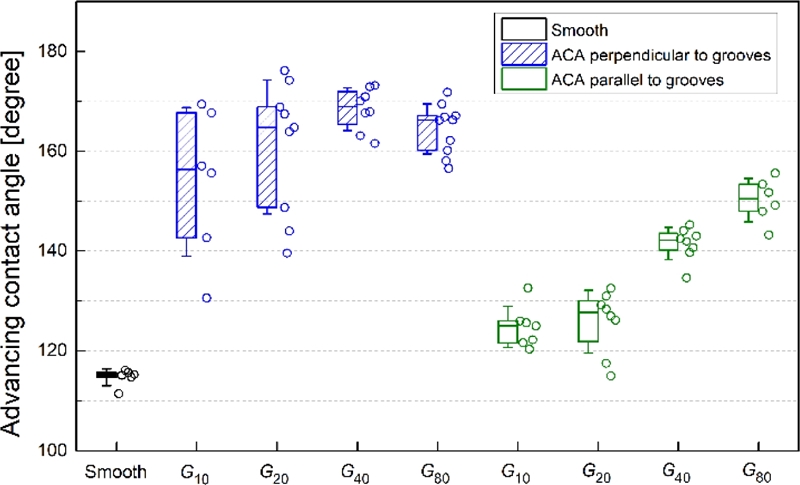
Advancing contact angles measured on the micro-grooved surfaces. Actual measurement points are shown right next to the box plots

Fig. 8

Receding contact angles measured on the micro-grooved surfaces

4. 결론

본 연구에서는 PDMS 재질의 표면에 미세 홈 구조가 가져온 젖음성과 이의 방향성에 대해 살펴보았다. 이번 연구에서 파악한 결과를 바탕으로 우선, 미세 홈 구조를 지니는 PDMS 재질의 표면에 대한 젖음성을 실험적으로 확인해보았다. 미세 구조가 없는 표면에 비해 높은 접촉각을 보여 미세 홈 구조가 소수성을 증가시킨 것으로 판단할 수 있다. 하지만 발수성의 측면에서 살펴본 흐름각은 그 크기가 액적의 흐름 방향에 따라 큰 차이를 지님을 알 수 있었다. 이러한 비등방 젖음성은 미세 홈의 길이 방향으로의 흐름성 및 발수성을 증가시키며 동시에 수직 방향으로의 흐름성은 감소시킴을 확인하였다. 그리고 그 정도는 홈 간의 간격이 클수록 즉, 결 면적 비율이 작을수록 증가하였다. 본 실험에서 측정된 모든 접촉각 및 흐름각은 홈의 수직 방향으로 측정된 값의 경우 큰 산포를 지닌다. 이는 수직 방향 측정값의 비등방성 특징인 보다 높은 정적 접촉각 및 흐름각과 동일한 유래를 가지고 있다. 바로 접촉선의 고정(Pinning)이 수직 방향으로 계속 발생하는 것이다. 이는 접촉선이 움직일 경우 불연속적인 움직임을 유발한다.

본 연구에서는 PDMS 재료의 미세 홈 구조에서 홈 간 거리를 조절하며 미세 홈 구조와 비등방 젖음성에 대한 연관성을 이론적인 분석과 함께 체계적으로 확인하였다. 본 연구를 통해 표면 미세 구조와 젖음성 및 방향성에 대한 이해가 다양한 소수성 폴리머인 재료들로 확대 적용될 수 있기를 기대한다. 하지만, 표면의 발수성 및 흐름성을 나타내는 흐름각의 이론적인 예측은 현재까지 등방성(Isotropic) 구조에 국한되어 있다. 이마저도 본 실험 결과와는 큰 차이를 보임에 따라 이를 보완하는 추가 연구가 필요하다고 판단된다. 발수성과 흐름성을 잘 대변하는 접촉각 이력을 기본으로 하고, 미세 홈 구조가 가지는 비등방성을 접촉선의 연속성을 바탕으로 예측하는 이론적인 정립이 향후 진행되어야 할 것이다.

Acknowledgments

이 성과는 2018년도 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(No. NRF-2017R1C1B5076710).

REFERENCES

• Barthlott, W. and Neinhuis, C., “Purity of the Sacred Lotus, or Escape from Contamination in Biological Surfaces,” Planta, Vol. 202, No. 1, pp. 1-8, 1997. [https://doi.org/10.1007/s004250050096]
• Koch, K., Bhushan, B., and Barthlott, W., “Diversity of Structure, Morphology and Wetting of Plant Surfaces,” Soft Matter, Vol. 4, No. 10, pp. 1943-1963, 2008. [https://doi.org/10.1039/b804854a]
• Feng, L., Li, S., Li, Y., Li, H., Zhang, L., et al., “Super-Hydrophobic Surfaces: from Natural to Artificial,” Advanced Materials, Vol. 14, No. 24, pp. 1857-1860, 2002. [https://doi.org/10.1002/adma.200290020]
• Cassie, A. and Baxter, S., “Wettability of Porous Surfaces,” Transactiions of the Faraday Society, Vol. 40, pp. 546-551, 1944. [https://doi.org/10.1039/tf9444000546]
• Wenzel, R. N., “Resistance of Solid Surfaces to Wetting by Water,” Industrial & Engineering Chemistry, Vol. 28, No. 8, pp. 988-994, 1936. [https://doi.org/10.1021/ie50320a024]
• Bixler, G. D. and Bhushan, B., “Bioinspired Rice Leaf and Butterfly Wing Surface Structures Combining Shark Skin and Lotus Effects,” Soft Matter, Vol. 8, No. 44, pp. 11271-11284, 2012. [https://doi.org/10.1039/c2sm26655e]
• Long, C. J., Schumacher, J. F., and Brennan, A. B., “Potential for Tunable Static and Dynamic Contact Angle Anisotropy on Gradient Microscale Patterned Topographies,” Langmuir, Vol. 25, No. 22, pp. 12982-12989, 2009. [https://doi.org/10.1021/la901836w]
• Rahman, M. A. and Jacobi, A. M., “Wetting Behavior and Drainage of Water Droplets on Microgrooved Brass Surfaces,” Langmuir, Vol. 28, No. 37, pp. 13441-13451, 2012. [https://doi.org/10.1021/la302669g]
• Sommers, A. D. and Jacobi, A. M., “Creating Micro-Scale Surface Topology to Achieve Anisotropic Wettability on an Aluminum Surface,” Journal of Micromechanics and Microengineering, Vol. 16, No. 8, pp. 1571-1578, 2006. [https://doi.org/10.1088/0960-1317/16/8/018]
• Yoshimitsu, Z., Nakajima, A., Watanabe, T., and Hashimoto, K., “Effects of Surface Structure on the Hydrophobicity and Sliding Behavior of Water Droplets,” Langmuir, Vol. 18, No. 15, pp. 5818-5822, 2002. [https://doi.org/10.1021/la020088p]
• Kusumaatmaja, H., Vrancken, R., Bastiaansen, C. W., and Yeomans, J., “Anisotropic Drop Morphologies on Corrugated Surfaces,” Langmuir, Vol. 24, No. 14, pp. 7299-7308, 2008. [https://doi.org/10.1021/la800649a]
• Xia, Y. and Whitesides, G. M., “Soft Lithography,” Annual Review of Materials Science, Vol. 28, No. 1, pp. 153-184, 1998. [https://doi.org/10.1146/annurev.matsci.28.1.153]
• Yang, M. T., Fu, J., Wang, Y. K., Desai, R. A., and Chen, C. S., “Assaying Stem Cell Mechanobiology on Microfabricated Elastomeric Substrates with Geometrically Modulated Rigidity,” Nature Protocols, Vol. 6, No. 2, pp. 187-213, 2011. [https://doi.org/10.1038/nprot.2010.189]
• Gao, N., Geyer, F., Pilat, D. W., Wooh, S., Vollmer, D., et al., “How Drops Start Sliding over Solid Surfaces,” Nature Physics, Vol. 14, No. 2, pp. 191-196, 2018. [https://doi.org/10.1038/nphys4305]
• Murase, H., Nanishi, K., Kogure, H., Fujibayashi, T., Tamura, K., et al., “Interactions between Heterogeneous Surfaces of Polymers and Water,” Journal Applied Polymer Science, Vol. 54, No. 13, pp. 2051-2062, 1994. [https://doi.org/10.1002/app.1994.070541307]
• Oner, D. and McCarthy, T. J., “Ultrahydrophobic Surfaces. Effects of Topography Length Scales on Wettability,” Langmuir, Vol. 16, No. 20, pp. 7777-7782, 2000. [https://doi.org/10.1021/la000598o]
• Yeh, K. Y., Chen, L. J., and Chang, J. Y., “Contact Angle Hysteresis on Regular Pillar-Like Hydrophobic Surfaces,” Langmuir, Vol. 24, No. 1, pp. 245-251, 2008. [https://doi.org/10.1021/la7020337]
• Chen, Y., He, B., Lee, J., and Patankar, N. A., “Anisotropy in the Wetting of Rough Surfaces,” Journal of Colloid and Interface Science, Vol. 281, No. 2, pp. 458-464, 2005. [https://doi.org/10.1016/j.jcis.2004.07.038]
• Kannan, R. and Sivakumar, D., “Drop Impact Process on a Hydrophobic Grooved Surface,” Colloids and Surfaces A: Physicochemical and Engineering Aspects, Vol. 317, Nos. 1-3, pp. 694-704, 2008. [https://doi.org/10.1016/j.colsurfa.2007.12.005]
• Liu, L., Jacobi, A. M., and Chvedov, D., “A Surface Embossing Technique to Create Micro-Grooves on an Aluminum Fin Stock for Drainage Enhancement,” Journal of Micromechanics and Microengineering, Vol. 19, No. 3, Paper No. 035026, 2009. [https://doi.org/10.1088/0960-1317/19/3/035026]
• Extrand, C. and Gent, A., “Retention of Liquid Drops by Solid Surfaces,” Journal of Colloid and Interface Science, Vol. 138, No. 2, pp. 431-442, 1990. [https://doi.org/10.1016/0021-9797(90)90225-D]
• Lv, C., Yang, C., Hao, P., He, F., and Zheng, Q., “Sliding of Water Droplets on Microstructured Hydrophobic Surfaces,” Langmuir, Vol. 26, No. 11, pp. 8704-8708, 2010. [https://doi.org/10.1021/la9044495]
• Liu, M. and Chen, X. P., “Numerical Study on the Stick-Slip Motion of Contact Line Moving on Heterogeneous Surfaces,” Physics of Fluids, Vol. 29, No. 8, Paper No. 082102, 2017. [https://doi.org/10.1063/1.4996189]