유전 알고리즘을 이용한 로봇의 최적 경로 탐색 방법 연구

1.1 연구 배경 및 동기

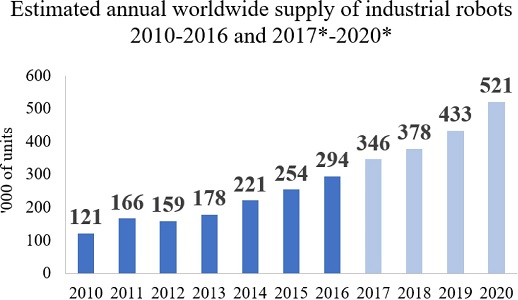
최근, 생산 및 제조 분야에서는 물건의 이송, 용접 및 조립, 도색 작업, 그리고 제품 검사 등 제품 생산 전반에 대한 효율성 향상과 노동력 절감을 위해 산업용 로봇을 적극적으로 생산 라인에 적용하고 있다. 뿐만 아니라, Fig. 1에서 보이는 바와 같이 2017년 이후의 전세계 산업용 로봇 공급이 연평균 15% 이상 증가할 것으로 예측되고 있다.¹ 이러한 산업 트랜드에 발맞추어, 산업용 로봇의 효율적인 이동 및 작업을 위한, 최적 경로 탐색 문제에 관한 연구 필요성과 그 중요성이 크게 대두되고 있다.

Fig. 1

Worldwide supply of industrial robots1 (Adapted from Ref. 1 with permission)

1.2 연구 목적 및 필요성

본 논문에서 다루고자 하는 로봇의 경로 탐색 문제는 로봇이 작업을 수행하고자 하는 다수의 작업점들에 대하여 최적의 작업 순서를 결정하는 문제이다. 즉, 이는 로봇이 작업을 수행할 때, 방문하는 모든 작업점들에 대하여 그 최적 순서를 탐색하는 것이다.

로봇의 경로 탐색 문제에 대한 중요성이 강조되면서, 이와 관련된 다양한 연구가 이미 진행되어 왔다. 그러나 로봇의 경로 탐색 문제에 관한 대부분의 기존 연구들은 실제 생산 라인에 적용될 때, 다음과 같은 두 가지 필수적인 사항이 고려되지 못한다는 한계점을 보이고 있다. 먼저, 첫 번째는 작업 종류에 따른 특성으로, 로봇에 부착되는 작업 도구 또는 작업에 필요한 기타 장비의 특징이 로봇의 경로 탐색에 크게 영향을 미칠 수 있다는 것이다. 즉, 로봇 자체의 공구중심점(Tool Center Point, TCP)이 특정 작업점의 위치에 도달할 수 있다 하더라도, 작업 도구와 기타 장비의 특징에 의해 해당 작업점에서 작업을 완벽히 수행할 수 없다면, 이는 로봇의 경로 탐색 문제에 있어서 유효하지 않은 작업점으로 볼 수 있다. 두 번째는, 로봇 및 작업 도구와 작업 대상 물체 사이의 충돌 회피가 제약 조건 및 요구사항으로 제대로 반영되지 못하고 있다는 사실이다.^2,3 뿐만 아니라, 탐색한 경로가 위와 같은 고려 사항과 제약 조건을 만족하더라도 항상 작업의 효율성을 고려한 최적 경로로써 보장할 수 없다는 한계가 존재한다. 이에 따라, 기존 연구 결과를 토대로 최적의 작업 순서를 결정하더라도 위와 같은 한계점을 극복하지 못하고 있기 때문에, 실제 작업 현장에서 로봇의 이동 및 작업 수행 경로 결정은 최종적으로 전문가의 경험에 의존한 결정을 따르고 있다. 그러나 매번 사람이 로봇 경로 생성 방법을 익히고 실제 경로를 생성하는 데에는 오랜 시간이 소요되며, 사람의 의사결정이 개입된 로봇 경로는 작업의 효율성을 보장할 수 없다. 이는, 사람의 실수나 오판으로 인해 위의 고려 사항이나 제약 조건을 만족시키지 못하는 경로가 생성될 수 있다는 가능성이 존재할 수밖에 없기 때문이며, 이로 인해 작업의 완성도가 떨어질 뿐만 아니라 충돌로 인한 사고 발생의 위험을 야기할 수 있다.

1.3 관련 연구

로봇의 최적 경로 탐색 문제에 대하여, 관련 연구에서는 유전 알고리즘을 이용하여 여러 대의 로봇에 작업을 분배하고 최적의 작업 순서를 결정하는 문제를 해결하였다.⁴ 그러나 로봇 및 작업 도구와 작업 대상 물체 사이의 충돌을 고려하지 않았으며, 작업 도구나 기타 장비가 최적의 작업 순서 탐색에 영향을 미치지 않는다고 가정하였으므로, 연구 결과를 실제 다양한 생산 라인에 적용하는 데에는 한계점이 존재한다.

다른 관련 연구에서는 유전 알고리즘을 이용하여 작업의 특성을 고려한 최적 경로 탐색 문제를 해결하려고 하였으나, 이 연구에서도 마찬가지로 로봇의 경로 탐색에 있어서 충돌 회피 문제를 고려하지 않았다.⁵

2.1 최적 경로 탐색 문제

본 연구에서 해결하고자 하는 로봇의 최적 경로 탐색 문제는, 로봇 자체와 로봇에 부착되는 작업 도구가 작업 대상 물체와 충돌을 일으키지 않으면서, 초기 위치(Home Position)에서 시작하여 n개의 모든 작업점에 한 번씩 방문하여 작업을 수행하고 초기 위치로 다시 돌아오는 최적의 경로를 찾는 문제이다. 이 때, 최적 경로는 로봇의 총 이동 시간 T_travel과 총 작업 시간 T_work의 합인 T가 최소가 되는 경로로 수식을 정립할 수 있다.

그러나 사실상 n개의 작업점에 방문하는 로봇 경로의 순서가 달라진다고 하더라도, 각 작업점에서 소요되는 실질적 작업 시간에는 영향을 주지 않으므로, 해당 수식의 값인 T_work는 고정된 상수 값이라고 할 수 있다. 이에 따라, 본 연구에서는 최종적으로 로봇의 총 이동 시간 T_travel 값이 최소가 되는 최적 경로를 탐색하는 것으로 문제를 정의하고 이를 해결하고자 한다.

2.2 순환 외판원 문제

순환 외판원 문제(Traveling Salesman Problem, TSP)는 판매원이 현재 위치(Starting City)에서 출발하여, 해당 도시를 제외한 나머지 n개의 도시에 한 번씩 방문하고 현재 위치로 다시 돌아오는 최적의 방문 순서를 찾는 문제이다. 이 문제에서는 판매원이 모든 도시를 방문하고 돌아오는 데에 필요한 비용 C_travel이 최소가 되는 방문 순서를 탐색한다.

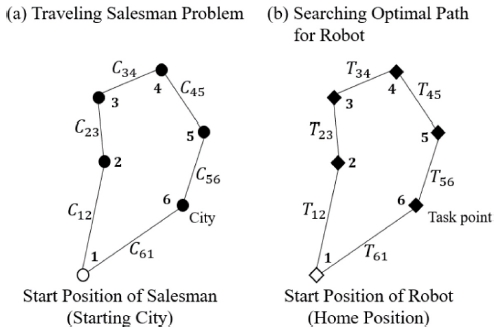
순환 외판원 문제와 본 연구에서 해결하고자 하는 로봇의 최적 경로 탐색 문제의 특성을 비교해보면, Fig. 2에서 보이는 바와 같이 이 두 문제를 연결시킬 수 있다. Fig. 2에서 C_ij는 판매원이 I번 도시에서 j번 도시로 이동하는 데에 필요한 비용을 나타내고, T_ij는 로봇이 i번 작업점에서 j번 작업점으로 이동하는 데에 걸리는 시간을 나타낸다. 즉, 순환 외판원 문제에서 탐색하고자 하는 최적의 도시 방문 순서는 그림에서 표현된 C_ij의 합이 최소가 되는 순서이며, 본 연구에서 탐색하고자 하는 최적의 로봇 경로는 그림에서 표현된 T_ij의 합이 최소가 되는 경로이다. 이와 같은 두 문제의 유사성을 바탕으로, 순환 외판원 문제의 해결 방식을 로봇의 최적 경로 탐색 문제에 적용하고자 한다.

Fig. 2

Mapping problem of searching optimal path for robot onto TSP

2.3 유전 알고리즘

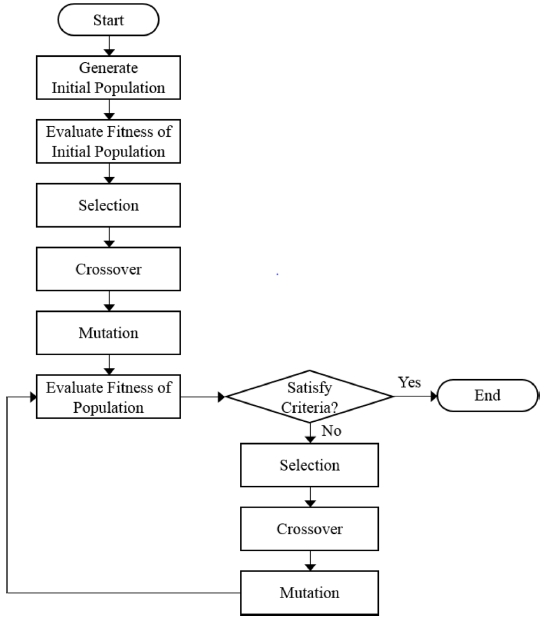
유전 알고리즘은 자연계의 진화 과정을 모델링한 최적화 기법으로, 이 알고리즘이 순환 외판원 문제를 해결하는 데에 좋은 성능을 발휘한다는 많은 연구 결과가 존재한다.^6-8 Fig. 3은 유전 알고리즘의 순서도를 나타낸 것이다.

Fig. 3

Flow chart of genetic algorithm

다음, 유전 알고리즘에 대하여 염색체를 예로 들어 설명한다. 먼저, 다양한 초기 집단(Initial Population)을 생성하여 초기 세대(Generation)를 구성하고 해당 초기 세대의 적합도(Fitness)를 평가한다. 평가한 적합도를 기준으로, 비교적 우수한 염색체를 선택(Selection)하고, 선택된 염색체에 교배(Crossover) 및 변이(Mutation) 과정을 수행하여, 자손 염색체를 생성한다. 자손 염색체가 생성되고 이를 포함하는 다음 세대가 구성되면, 초기 세대와 마찬가지로 다음 세대의 적합도를 평가한다. 이후, 설정한 세대의 수만큼 선택, 교배 및 변이 연산을 다시 수행하여 다음 세대를 생성하고 적합도를 평가하는 과정을 반복한다. 만약, 적합도가 미리 설정한 출현 중복 기준을 지속적으로 만족하거나, 학습의 최대 반복 횟수에 도달하게 되면, 유전 알고리즘 학습을 종료한다.⁹

2.4 유전 알고리즘을 적용한 최적 경로 탐색

순환 외판원 문제를 완전 탐색 방식(Exhaustive Search Method)을 이용하여 해결하는 경우, 외판원이 방문하고자 하는 도시의 개수가 증가함에 따라 계산 복잡도가 기하 급수적으로 증가한다.

그런데 유전 알고리즘은 그 특성 상 다양한 초기 집단을 생성하여 먼저 초기 세대를 구성하고, 이전 세대의 정보를 염색체에 저장하여 다음 세대로 전달하되 교배, 변이 등의 진화 연산을 거치면서 보다 우월한 염색체를 전달한다. 즉, 이전 세대 중 일부 염색체가 다음 세대에 유전 정보를 남길 확률은 적합도에 따라 선정되기 때문에, 적합도 평가를 통한 비교적 우수한 염색체가 다음 세대에 유전 정보를 전달하게 된다. 따라서 여러 세대를 거치고 나면 가장 우수한 염색체가 생존하게 되며, 이렇게 마지막까지 생존한 가장 우수한 염색체는 전역 최적해에 근접한 최적해가 된다. 따라서, 순환 외판원 문제에 유전 알고리즘을 적용하면 모든 해를 탐색하지 않고도 전역 최적해에 가까운 해를 찾을 수 있다.

본 연구에서 해결하고자 하는 로봇의 최적 경로 탐색 문제도 순환 외판원 문제와 마찬가지로 작업점의 개수가 많아지면 완전 탐색을 이용하여 문제를 해결하기 쉽지 않다. 또한, 실제 생산 라인에서 로봇의 작업점의 개수는 얼마든지 증가할 수 있기 때문에, 그 확장성을 고려하여 유전 알고리즘을 적용하여 문제를 해결하고자 한다.

3.1 시뮬레이션 환경

3.1.1 작업 공간의 구성

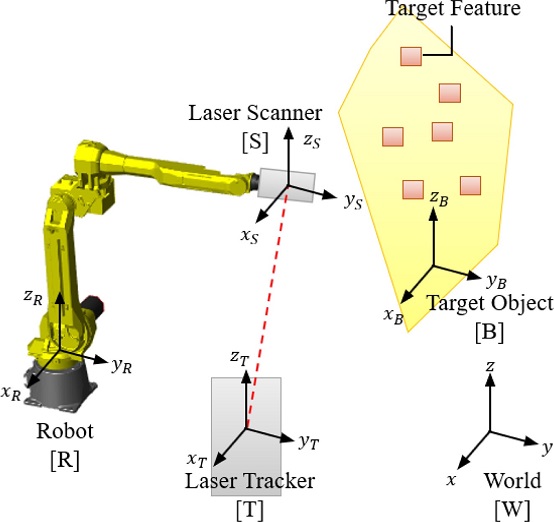
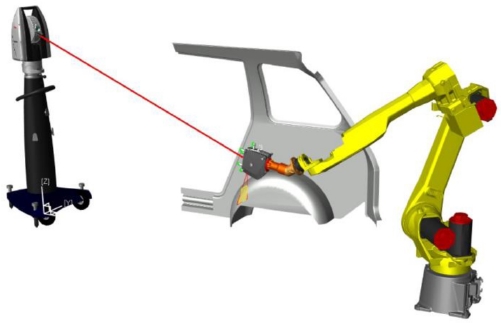
본 논문에서는 산업용 로봇을 이용하는 생산 라인 중, 제품 검사 작업에 대한 실험 및 시뮬레이션을 진행하였다. Fig. 4와 같이 시뮬레이션 환경은 임의의 작업 공간에 레이저 스캐너(Laser Scanner)가 부착된 6 자유도 산업용 로봇 한 개와 로봇의 작업 대상 물체(Target Object), 그리고 레이저 트레커(Laser Tracker)가 존재한다. 여기에서 로봇에 부착된 레이저 스캐너는 제품 검사 작업을 수행하는 작업 도구이며, 레이저 트레커는 이 레이저 스캐너의 제품 검사 작업을 위해 필요한 장비이다.

Fig. 4

Components of workspace in simulation environment

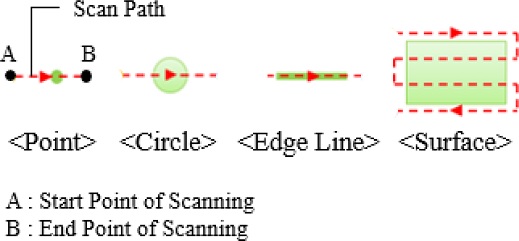
작업 대상 물체에는 레이저 스캐너가 스캔하고자 하는 서로 다른 네 종류의 스캔 대상 형상(Target Feature; Point, Circle, Edge Line, Surface)이 부착되어 있으며, 레이저 스캐너는 Fig. 5와 같이 각 형상에 따라 주어진 스캔 경로에 맞게 스캔을 진행한다. 이때, 스캔 경로는 스캔 시작 지점과 스캔 종료 지점이 주어지면 그에 따라 결정되고, 스캔 도중 로봇의 보간법(Interpolation Type)은 로봇 공구중심점의 이동 경로를 직선으로 제어하는 직선 보간법(Linear Interpolation)을 따른다.¹⁰

Fig. 5

Scan paths depending on types of target features

레이저 트레커는 레이저 스캐너 기준 좌표계[S]의 위치 및 방향을 측정한다. 로봇의 기준 좌표계[R]과 레이저 트레커 기준 좌표계[T], 작업 대상 물체의 기준 좌표계[B]는 작업 공간의 기준 좌표계[W]에 대하여 고정되어 있으므로, 다음과 같은 좌표 변환 행렬이 주어진다.

$\[ \begin{array}{c}{}_{ }{}^W{T}_T=\left[\begin{array}{cc}\overrightarrow{n_T}& \overrightarrow{o_T}\\ 0& 0\end{array} \begin{array}{cc}\overrightarrow{a_T}& \overrightarrow{p_T}\\ 0& 1\end{array}\right]\\ {}_{ }{}^W{T}_R=\left[\begin{array}{cc}\overrightarrow{n_R}& \overrightarrow{o_R}\\ 0& 0\end{array} \begin{array}{cc}\overrightarrow{a_R}& \overrightarrow{p_R}\\ 0& 1\end{array}\right]\\ {}_{ }{}^W{T}_B=\left[\begin{array}{cc}\overrightarrow{n_B}& \overrightarrow{o_B}\\ 0& 0\end{array} \begin{array}{cc}\overrightarrow{a_B}& \overrightarrow{p_B}\\ 0& 1\end{array}\right]\end{array} \]$

(2)

로봇의 움직임에 따라 로봇에 부착된 레이저 스캐너가 이동하면, 레이저 트레커가 레이저 스캐너 기준 좌표계의 위치 및 방향을 측정한다. 이를 통해, 레이저 트레커와 레이저 스캐너 사이의 좌표 변환 행렬 ^TT_S를 구할 수 있으며, 작업 공간의 기준 좌표계[W]에 대한 레이저 스캐너 기준 좌표계[S]의 좌표 변환 행렬을 다음과 같이 구할 수 있다.

$\[ {}_{ }{}^W{T}_S={}_{ }{}^W{T}_T{}_{ }{}^T{T}_S \]$

(3)

이와 같이 ^WT_S를 연산하여, 레이저 스캐너가 특정 스캔 대상 형상을 스캔하면 ^WT_S를 이용하여 최종적으로 작업 공간의 기준 좌표계[W]에 대한 스캔 대상 형상의 정보를 파악할 수 있다.

3.1.2 시뮬레이션 환경 구성

본 연구에서는 실험을 위한 데이터 수집 및 실험 진행을 위하여, 가상 생산 시뮬레이션 소프트웨어인 DMWorks (Digital Manufacturing Works)를 사용하였다.¹¹ Fig. 6은 Fig. 4에서 제시한 작업 공간의 구성 요소를 DMWorks의 3D View 상에 배치한 모습이다.

Fig. 6

Components of workspace in 3D view of DMWorks

3.1.4 가정

본 연구에서는 문제 해결을 위하여 다음과 같은 사항을 가정한다. 첫 번째로, 하나의 스캔 대상 형상에 대하여 여러 개의 스캔 경로 후보가 존재할 수 있다. 이는 레이저 스캐너가 스캔 대상 형상에 다양한 방향으로 접근할 수 있도록 함으로써, 한 개의 스캔 경로가 존재할 때보다 다양한 후보 해집합에서 최적해를 찾기 위함이다. 구체적으로, 스캔 대상 형상 중 점(Point)과 원형(Circle)의 경우에는 각각 점과 원형의 중심을 지나는 스캔 경로 후보가 36° 간격으로 총 10개 존재하며, 선형(Edge Line)의 경우에는 방향이 서로 반대인 총 두 개의 스캔 경로 후보가, 그리고 면(Surface)의 경우에는 면을 포함하는 사각형의 스캔 범위(Scan Box) 각 모서리에서 시작하여 좌/우로 진행하는 총 여덟 개의 스캔 경로 후보가 존재한다고 가정한다.

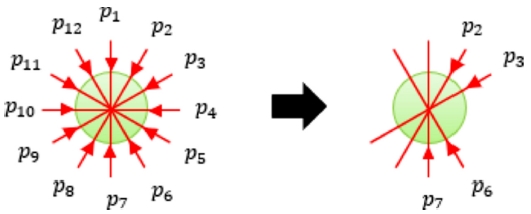
두 번째로, 모든 스캔 대상 형상에 대하여 앞서 가정한 스캔 경로 후보 중 한 개 이상의 스캔 경로를 따라 스캔을 진행할 수 있는 로봇의 위치 및 레이저 트레커의 위치가 존재한다. 여기에서 주어진 스캔 경로를 따라 스캔이 이루어지기 위해서는 로봇의 공구중심점이 해당 스캔 경로를 따라 이동할 수 있는지, 스캔 도중에 레이저 트레커의 트레킹이 중단되지 않는지, 그리고 스캔 도중에 로봇의 자세가 안정적인지와 같은 제약 조건을 만족시켜야 한다. 두 번째 가정을 통해 앞서 가정했던 스캔 경로 후보 중 최종 스캔 경로 후보를 결정할 수 있다. Fig. 7은 스캔 대상 형상 중 원형에 대하여 첫 번째 가정에 따라 스캔 경로 후보를 생성하고, 두 번째 가정을 통해 최종 스캔 경로 후보를 결정하는 과정이다.

Fig. 7

Determining final candidates for scan paths

세 번째로, 하나의 스캔 대상 형상을 스캔하는 데에 걸리는 시간은 어떤 스캔 경로 후보를 선택하는지에 상관 없이 일정하다고 가정한다. 즉, Fig. 7에서 p₂ 경로를 통해 스캔이 이루어 질 때와 p₃ 경로를 통해 스캔이 이루어 질 때에 걸리는 시간이 동일하다.

3.2 실험 내용

3.2.1 데이터 수집

모든 스캔 대상 형상에 대하여 최종 스캔 경로 후보가 결정되면, 각각의 스캔 경로에 따라 다음과 같이 두 가지의 필요한 정보를 파악할 수 있다. 첫 번째는 레이저 스캐너가 임의의 스캔 경로의 스캔 시작 지점에 위치했을 때 로봇의 여섯 개의 조인트(Joint)가 가지는 각각의 조인트 앵글(Joint Angle)과 해당 스캔 경로의 스캔 종료 지점에 위치했을 때 로봇의 여섯 개의 조인트가 가지는 각각의 조인트 앵글을 알 수 있다. 두 번째로, 각 스캔 경로에서의 프리즘(Prism) ID를 알 수 있다.

위의 두 가지 정보 이외에, 실험을 위하여 다음과 같은 정보가 추가적으로 필요하다. 우선, 임의의 스캔 경로가 총 n개의 스캔 대상 형상 중 몇 번째 스캔 대상 형상에 해당하는 경로인지를 파악하기 위해 각 형상(Feature)에 ID를 부여한다. 다음 두 번째로, 특정 스캔 경로가 스캔 대상 형상을 스캔하기 위한 여러 개의 스캔 경로 후보 중 몇 번째 스캔 경로인지 파악하기 위한 정보이다. 따라서 하나의 스캔 대상에 대한 다수의 스캔 경로에 각각 스캔 경로(Scan Path) ID를 부여하여 이를 파악한다.

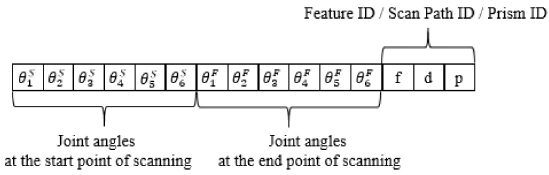
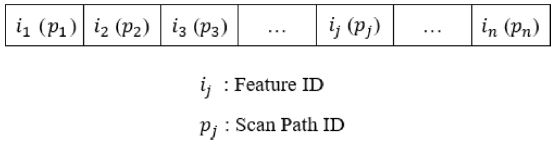
앞에서 제시한 모든 데이터를 수집하여, 하나의 스캔 경로에 대해 Fig. 8과 같이 15개의 필요한 정보들을 저장한다.

Fig. 8

Elements of an instance

3.2.2 염색체의 구성

데이터의 수집 및 준비 과정 이후, 유전 알고리즘을 위한 염색체를 구성하였다. 하나의 염색체는 Fig. 9와 같이 n개의 주어진 모든 스캔 대상 형상의 형상 ID를 임의로 나열한 경로이다. 이 때, i_j는 n개의 스캔 대상 형상 중 j번째에 해당하는 형상을 나타내는 형상 ID이며, p_j는 j번째 스캔 대상 형상을 스캔하기 위한 스캔 경로를 나타내는 스캔 경로 ID이다. 여기에서 염색체 즉, 로봇의 경로를 구성하는 하나의 유전자에 형상 ID와 스캔 경로 ID를 함께 나타낸 것은, 하나의 스캔 대상 형상을 스캔하기 위한 다수의 스캔 경로 후보들이 존재하기 때문이다. 염색체를 구성하는 하나의 유전자는 형상 ID와 스캔 경로 ID 이외에도 앞서 데이터 수집 및 준비 과정을 통해 파악한 총 12개의 조인트 앵글과 프리즘 ID의 정보를 담고 있다.

Fig. 9

Chromosome of genetic algorithm

3.2.3 모델링

3.2.3.1 충돌 회피를 고려한 적합도 평가

염색체의 적합도는 로봇이 경로를 구성하는 스캔 대상 형상에 순서대로 접근하는 동안 소요되는 시간의 역수 형태로 표현하여 정의한다.

$\[ \begin{array}{c}{T}_{total}=\sum T_j\\ \mathbf{F}\mathbf{i}\mathbf{t}\mathbf{n}\mathbf{e}\mathbf{s}\mathbf{s}=1/{\mathit{T}}_{\mathit{t}\mathit{o}\mathit{t}\mathit{a}\mathit{l}}\end{array} \]$

(4)

위 식에서 T_j은 로봇이 하나의 염색체를 구성하는 j번째 스캔 대상 형상에서 j + 1번째 스캔 대상 형상으로 이동하는 동안 걸리는 시간을 나타내며, 그 계산 방법은 다음과 같다.

$\[ \begin{array}{c}\mathrm{F}\mathrm{o}\mathrm{r}\mathrm{ }\mathrm{i}=\mathrm{ }1,\mathrm{ }\dots ,6\mathrm{ }\left(\mathrm{N}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r}\mathrm{ }\mathrm{o}\mathrm{f}\mathrm{ }\mathrm{J}\mathrm{o}\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{s}\right)\\ t_i=\frac{\Delta {\theta }_i}{{\omega }_i}\mathrm{ },\mathrm{ }\mathrm{ }\mathrm{ }t=\max \left(t_i\right) (\Delta {\theta }_i={\theta }_i^F-{\theta }_i^S)\\ {\omega }_i=\frac{\Delta {\theta }_i}{t}\\ {tacc}_i=\frac{{\omega }_i}{{\alpha }_i}\mathrm{ },\mathrm{ }\mathrm{ } tacc=\mathrm{m}\mathrm{a}\mathrm{x}\left({tacc}_i\right)\\ T_j=t+tacc\end{array} \]$

(5)

위의 수식에서 t는 로봇이 j번째 스캔 대상 형상의 스캔 종료 지점에서 j + 1번째 스캔 대상 형상의 스캔 시작 지점으로 이동하는 동안 로봇의 6개 조인트 앵글이 각각 정속으로 변화하는 시간 중 최대값이다. 또한 tacc는 동일한 상황에서 로봇의 여섯 개 조인트 앵글이 가속도 운동을 하며 변화하는 시간 중 최대값이다. 이 때, j번째 스캔 대상 형상의 스캔 경로와 j + 1번째 스캔 대상 형상의 스캔 경로가 가지는 프리즘 ID가 서로 다르면 T_d의 시간 지연이 발생하므로, T_j = T_j + T_d가 된다.

이와 같이 적합도를 평가하는 과정에서 DMWorks를 이용한 로봇 시뮬레이션을 통해 충돌 검사를 실시할 수 있다. 즉, 로봇이 조인트 보간(Joint Interpolation)방법을 이용하여 j번째 스캔 대상 형상에서 j + 1번째 스캔 대상 형상으로 이동하는 모션 시뮬레이션을 실시하고, 도중에 로봇 및 작업 도구와 작업 대상 물체 사이에 충돌이 발생하는 경우를 파악한다. 만약 충돌이 발생하였다면 적합도 평가 과정에서 충돌 회피를 위한 시간 지연을 고려해야 하므로, T_j를 최종적으로 아래와 같이 나타낼 수 있다. 아래의 수식에서 $$ T_j^{origin}$$은 위의 식(5)에서 계산한 T_j를 나타낸다.

$\[ T_j=T_j^{origin}+1/T_j^{origin} \]$

(6)

3.2.3.2 유전 알고리즘 기반 진화 연산

유전 알고리즘의 시작과 동시에 Fig. 9와 같은 염색체 N개로 구성된 초기 세대를 생성한다. 이 때, 초기 세대의 염색체는 N개의 스캔 대상 형상에 대한 형상 ID를 임의로 나열함으로써 생성한다. 이후에, 초기 세대를 구성하는 염색체들의 선택, 교배, 변이 연산을 통해 다음 세대를 구성한다. 여기에서, 다음 세대를 구성하기 위하여 중간 세대를 먼저 구성하였다. 다음은 중간 세대를 구성하는 방법이다.

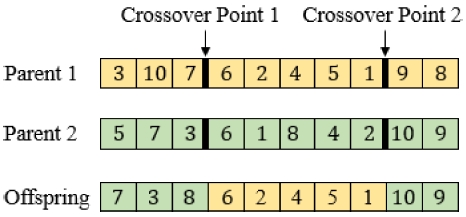
먼저, 초기 세대를 구성하는 염색체 중 적합도가 높은 상위 α%의 염색체를 선택하여 중간 세대에 전달한다. 그리고 N개의 염색체 중 선택 및 교배연산을 통해 한 세대를 구성하는 염색체의 개수 N의 β%만큼의 자손 염색체를 생성하여 중간 세대에 전달한다. 이 때 선택 연산은 N개의 염색체 중 임의의 p개 염색체를 선택하고, 최종적으로 그 중 적합도가 가장 높은 염색체를 선택하는 방법으로 수행한다. 그리고 이러한 선택 연산을 통해 두 개의 부모 염색체를 선택하여 Fig. 10과 같은 방법으로 교배 연산을 수행한다. Fig. 10은 스캔 대상 형상이 10개인 경우에 두 단계를 거쳐 부모 염색체를 교배하는 과정이다. 먼저 첫 번째 단계에서, 2 개의 교배 지점을 랜덤함수를 이용하여 결정한다. 교배 지점이 결정되면, 그림의 부모 1 염색체에서 두 교배 지점 사이에 존재하는 형상 ID를 추출하여 자손 염색체 내에 저장한다. 그리고 두 번째 단계에서, 부모 2 염색체의 첫 번째 형상 ID에서부터 순서대로 탐색하여 해당 형상 ID가 자손 염색체에 존재하지 않으면, 자손 염색체의 왼쪽 빈 공간부터 순서대로 해당 형상 ID를 추가하여 저장한다.

Fig. 10

Generation of offspring by crossover

다음으로, 선택 및 교배 연산으로 생성되어 중간 세대에 전달된 자손 염색체들 중에서 N의 γ%만큼의 염색체에 변이 연산을 수행하여 이를 중간 세대에 전달한다. 마지막으로, 초기 세대를 생성할 때와 같이 n개의 형상 ID를 랜덤하게 나열한 염색체를 N의 δ%만큼 생성하여 중간 세대에 전달한다.

이와 같이 생성된 총 M개(M > N)의 염색체로 구성된 중간 세대를 생성하였다면, 이 중간 세대 중에서 적합도가 높은 상위 N개의 염색체만을 선정하여 다음 세대를 구성한다.

이렇게 진화 연산을 반복하여 새로운 세대를 계속 만들어 나가면서, 새로운 세대의 적합도가 목표 적합도에 도달하면 유전 알고리즘을 종료한다.

본 연구에서 목표 적합도의 개념은, 50 세대의 진화가 이루어질 동안 각 세대에서 계산된 가장 높은 적합도의 동일 여부를 판단하는 것으로 정의하였다. 만약, 50 세대 동안 가장 높은 적합도가 반복하여 일치한다면, 이는 유전 알고리즘의 최적해가 수렴한다는 것을 의미하기 때문이다.

3.3 실험 결과

본 연구를 통해 탐색한 로봇의 경로가 사람이 생성하는 경로에 비해 효율적인지를 확인하기 위해, 사람이 생성한 경로를 하나의 염색체로 구성하고 그 적합도를 계산하여 유전 알고리즘을 통해 구한 최적 경로의 적합도와 비교 및 분석하였다. 여기에서, 사람이 생성한 경로는 6개월간 현장에서 로봇 경로 생성 경험을 쌓은 숙련자에 의해 생성된 경로이고, 로봇의 현재 위치에서 가장 가깝다고 판단되는 스캔 대상 형상을 찾아 첫 번째 작업 순서로 배치하며, 해당 형상에서 가장 가깝다고 판단되는 형상을 찾아 다음 작업 순서로 배치하는 과정을 반복하여 생성하였다. 다음은 두 가지 시나리오에 대해 실험을 진행하여 얻을 실험 결과이다.

첫 번째 실험은 총 28개의 스캔 대상 형상이 존재하는 차량 Door를 대상으로 진행하였으며, 두 번째 실험은 34개의 스캔 대상 형상이 존재하는 차량 Door를 대상으로 진행하였다. 이 때, 한 세대를 구성하는 염색체의 수 N은 스캔 대상 형상의 개수의 50배로 설정하였으며, 앞서 중간 세대를 구성하기 위해 정의했던 α, β, γ, δ 중 α의 값을 2로 고정하였다. 또한 다양한 실험 조건에서의 실험 결과를 확인하기 위하여 β, γ, δ 값의 변화에 따라 실험을 진행하였다.

Table 1은 28개의 스캔 대상 형상이 존재하는 첫 번째 시나리오에 대하여, 100 ≤ β + γ + δ ≤ 130의 범위 내에서 β의 값을 50, 60, 70, 80으로 변화시켜 구한 최적 경로의 적합도와 사람이 직접 생성한 경로의 적합도를 나타낸 것이다. 이 때, β, γ, δ의 값이 증가할수록 중간 세대를 구성하는 염색체의 개수가 증가하여 연산 시간이 많이 소요되므로, β + γ + δ의 값에 대한 범위를 제한하였다.

Table 1

Experiment result of first scenario

Table 2는 34개의 스캔 대상 형상이 존재하는 두 번째 시나리오에 대하여, 100 ≤ β + γ + δ ≤ 130의 범위 내에서 β의 값을 50, 60, 70, 80으로 변화시켜 구한 최적 경로의 적합도와 사람이 직접 생성한 경로의 적합도를 나타낸 것이다.

Table 2

Experiment result of second scenario

3.4 실험 결과 분석

첫 번째 시나리오에 대하여, 실험 결과를 통해 유전 알고리즘을 이용하여 구한 최적 경로의 적합도 평균이 사람이 직접 생성한 경로의 적합도보다 6.2% 높은 것을 확인하였다. 또한 두 번째 시나리오에 대하여, 실험 결과를 통해 유전 알고리즘을 이용하여 구한 최적 경로의 적합도 평균이 사람이 직접 생성한 경로의 적합도보다 15.7% 높은 것을 확인하였다. 이러한 실험 결과에 따르면, 본 연구에서 유전 알고리즘을 이용하여 구한 최적 경로가 사람이 직접 생성한 경로에 비해 로봇의 이동 시간 측면에서 효율적인 경로라는 것을 알 수 있다.

또한 첫 번째 시나리오에 대한 유전 알고리즘의 평균 연산 시간은 18.34초, 두 번째 시나리오에 대한 유전 알고리즘의 평균 연산 시간은 23.674초임을 확인하였다. 이는 사람이 실제 산업 현장에서 로봇의 경로를 직접 생성하는 행위와 비교하였을 때, 노동시간 측면에서도 효율적이라는 것을 알 수 있다.

뿐만 아니라 첫 번째 시나리오에 대한 실험 결과와 두 번째 시나리오에 대한 실험 결과를 비교하였을 때, 스캔 대상 형상의 개수가 많은 경우에 유전 알고리즘을 이용하여 구한 최적 경로의 효율성이 스캔 대상 형상의 개수가 적은 경우에 비해 더 높은 것을 확인하였다. 이를 통해, 로봇을 이용하여 작업을 수행하고자 하는 작업 대상의 개수가 많아질수록 사람이 효율적인 경로를 생성하기 어렵다는 것을 알 수 있다. 그 이유는, 작업 대상의 개수가 많아질수록 사람이 효율적인 로봇의 경로를 직관적으로 판단하기 어렵기 때문이다.

마지막으로, 본 연구에서의 제시한 유전 알고리즘을 위한 네 가지 파라미터 α, β, γ, δ 중 β, γ, δ의 변화에 따른 실험 결과를 분석하였다. 먼저 β의 값이 고정되고 나면, γ, δ의 변화는 실험 결과에 주목할 만한 영향을 미치지 않는 것을 확인하였다. 그런데 첫 번째 시나리오와 두 번째 시나리오 모두에 대하여, β의 값이 70일 때의 로봇 경로가 다른 경우에 비해 적합도가 높은 것을 확인하였다. 즉, 한 세대를 구성하는 염색체 전체에 대하여 선택 및 교배 연산을 통해 생성된 자손 염색체의 비율이 유전 알고리즘의 성능에 영향을 미칠 수 있다는 사실을 알 수 있다.

4.1 연구 결론 및 의의

본 연구에서는 자연 세계의 진화과정을 기초로 한 유전 알고리즘을 이용하여 로봇의 이동 및 작업 수행을 위한 최적 경로 탐색 방법을 제안하였다.

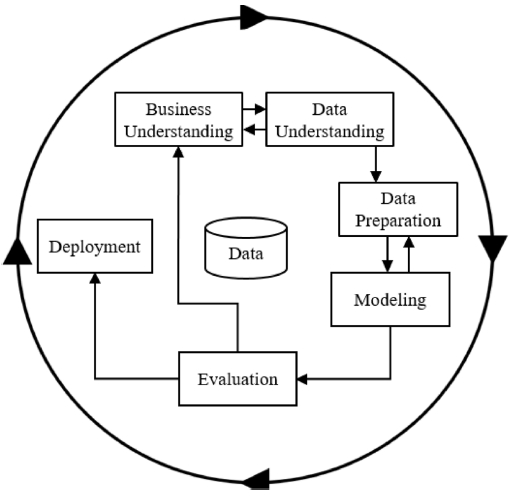
유전 알고리즘은 데이터 마이닝의 주된 기법 중 하나이므로, 데이터 마이닝 분야에서 검증된 방법론인 데이터 마이닝, 교차 산업 표준 절차(Cross-Industry Standard Process for Data Mining, CRISP-DM) 모델을 따라, 각 단계 순으로 연구를 진행하였다.

Fig. 11

Cross-industry standard process for data mining12 (Adapted from Ref. 12 with permission)

교차 산업 표준 절차 내, 첫 번째 단계인 비즈니스의 이해(Business Understanding)에서는 본 연구의 목적 및 해결하고자 하는 문제를 정확히 이해하고, 그에 따라 작업 공간에 필요한 구성 요소를 결정하고 작업의 특성을 파악하였다. 또한, 문제 해결에 필요한 제약 조건 및 요구 사항을 수집하여 정리하였다. 이 과정에서 로봇의 최적 경로 탐색에 대한 문제를 순환 외판원 문제에 연결(Mapping)하여 생산 및 제조 분야에서 해결하고자 하는 문제를 데이터 마이닝 문제로 전환하고, 그에 따른 문제 해결 계획을 준비하였다. 결과적으로 유전 알고리즘을 문제 해결 방법으로 결정하고, 문제 이해를 바탕으로 시뮬레이션 환경을 구성하였다. 두 번째 단계인 데이터 이해(Data Understanding)에서는 앞서 구성한 시뮬레이션 환경으로부터 알아낼 수 있는 데이터를 수집하고, 이 데이터가 전체적인 문제 해결 과정 중 어느 단계에서 필요한 데이터인지를 분석하였다. 또한, 문제를 해결하기 위하여 어떤 데이터가 추가적으로 필요한지에 대해 정리하고 수집하여 데이터 세트를 구성하였다. 세 번째 단계인 데이터 준비(Data Preparation) 단계에서는 이전 단계에서 구성한 데이터 세트를 바탕으로 유전 알고리즘 수행을 위한 입력 데이터 즉, 염색체를 구성하는 방법에 대해 계획하였다. 다음, 네 번째 단계인 모델링(Modeling)에서는 로봇의 최적 경로 탐색 문제에 알맞은 유전 알고리즘의 적합도 계산 방법에 대해 계획하였으며, 일반적인 유전 알고리즘의 진화 연산을 기반으로 중간 세대의 생성과 같이 본 연구에 적용시킬 진화적 연산 방법을 결정하였다. 다섯 번째 단계인 평가(Evaluation)에서는 유전 알고리즘을 이용하여 탐색한 로봇의 최적 경로의 적합도와 사람이 직접 생성한 로봇의 경로의 적합도를 비교함으로써, 본 연구 결과의 타당성을 판단하였다. 향후, 본 연구를 실제 생산 라인에 적용하며, 마지막 단계인 전개(Deployment)로 끝맺는다.

본 연구는 제조 분야의 산업 현장에서 해결하고자 하는 문제를 바탕으로 데이터 마이닝 프로젝트를 구성하고, 교차 산업 표준 절차 모델의 각 단계에 따라 연구를 진행하였으며, 이를 통해 타당한 연구 결과를 산출하였다는 것으로 그 의의가 있다.

4.2 연구 성과

본 연구를 통해, 충돌 회피와 작업 특성을 고려한 로봇의 최적 경로를 탐색하였으며, 탐색된 경로가 사람이 직접 생성한 로봇 경로에 비해 효율성 측면에서 우수하다는 사실을 입증하였다.

4.3 연구 한계점

본 연구에서는 로봇 및 작업 도구와 작업 대상 물체 사이의 충돌 회피 시간만을 고려한 로봇의 최적 경로를 결정하였다. 향후에는 충돌이 발생하였을 경우에 어떤 과정에 의해 충돌을 회피할 것인지에 대한 연구가 진행되어, 실제 충돌 회피 방법이 고려된 로봇의 최적 경로 탐색 방법 제안이 필요하다.