Vibration Analysis of Flexible Rotor with Angular Contact Ball Bearings Using a General Bearing Stiffness Model
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
The vibration analysis of flexible rotor systems supported by angular contact ball bearings is presented. Vibration analysis of rotor-ball bearing systems has often been performed via simplification of supporting bearings as linear springs with constant stiffness. In this study, an improved model of rotor-ball bearing systems was proposed. It utilizes a general bearing model based on response and time-dependent bearing characteristics. The system equations of motion were established using the finite-element method and numerically solved using the Newmark-β method. The method was used to recalculate the bearing stiffness matrices at every interval of numerical integration as a function of the instantaneous bearing displacements using a separated five-degrees-of-freedom bearing model. The method was verified via comparison with experimental data available in the literature. The extended simulations were conducted to investigate the unbalanced responses of a rotor-ball bearing system using the proposed and conventional methods. Numerical results showed a meaningful discrepancy between the vibrational responses obtained by the proposed model using the response and time-dependent bearing stiffness model and the traditional constant-stiffness model.
Keywords:
Angular contact ball bearing, Vibration analysis, Flexible rotor system, General bearing stiffness model키워드:
각접촉 볼베어링, 진동해석, 탄성 회전체 시스템, 일반적인 베어링 강성 모델1. Introduction
The vibration occurring in rotor-bearing systems is a crucial problem, because it has a significant contribution to the overall performance of the machine. Minimizing the vibration of rolling bearings has the benefit of reducing premature failure in components caused by oscillating loads. Therefore, great attention has been given for monitoring and controlling the vibration of rotor-bearing systems. Indeed, accurate prediction of vibration is becoming important because of the increasing demand for quieter operation, higher efficiency, and longer service life. The aim of this study is to develop an improved model for estimation of the vibration in rotor-bearing systems.
Among the vibration sources in rotor systems, unbalance is one of the most commonly observed sources.1,2 Vibration excitation of the unbalance in a rotor system often raises nonlinearities of the system in supporting bearings and mechanical coupling, or geometric nonlinearities of motion.3 Synchronous vibration caused by unbalance in the rotors was well studied. However, relatively few studies were concerned with the vibration attributed to the rolling element bearings. In practice, the bearing stiffness varies, even in one revolution of the orbital motion, which in turn affects the vibration of the rotor system. However, bearings have been usually considered as rigid supports or constant-stiffness coefficients.4-6 These assumptions are less accurate in some cases, because the dynamic loads and associated bearing compliance lead to time-varying and/or response-dependent bearing stiffness. To this end, several bearing stiffness models have been developed that include the time-varying stiffness.
Liew and Lim7 have modified the time-invariant stiffness model developed by Lim and Singh8 to consider the time-varying effect of raceway rotation. The effect of the dynamic load on the bearing stiffness was not considered in their model. Chu et al.9 introduced a model for determining the time-varying bearing stiffness caused by the finite number of balls and unbalance force. They showed that the spectrum of the bearing stiffness element comprises two major components corresponding to unbalance force and ball-passing frequencies. The stiffness model for multiple harmonic excitations, such as coupling misalignment10 was not addressed in Ref. 9. Recently, Li et al.11 proposed a new method to predict rotor-bearing vibration without the information of explicit bearing stiffness. Their model consists of a bearing model used for determining the rigid body motion of the system. The finite-element method (FEM) was then used for determining the elastic deformation of the rotor. The total response of the system is the summation of responses from the rigid and elastic models. This model seems difficult to implement because of its complexity.
In this paper, an improved model was proposed for rotor-bearing systems to consider the bearing characteristics precisely. This study employed a response-dependent, time-varying bearing stiffness model, in which the instantaneous bearing stiffness is determined with the instantaneous vibration responses at the bearing locations. The method was verified by means of comparison with experimental data available in the literature.11 Then, extended simulations were performed to investigate the unbalance responses of a rotor-bearing system by using the proposed and conventional methods. To show the difference caused by the inclusion of the proposed exact bearing stiffness, the vibration responses of a rotor system obtained by using the current model were compared with those of the conventional, time-invariant bearing stiffness model. Through numerical simulations, the proposed exact bearing stiffness model manifested its importance in the accurate estimation of vibration responses and their higher harmonic components.
This study is organized as follows. In Section 2, the modeling method for the system vibration computation is described. An overview of the finite-element model and ball-bearing models is presented. A flowchart for the computation of rotor system vibration is also described, which focuses on how the time-varying bearing stiffness is determined. In Section 3, the validation of the method is presented. An experimental comparison is also presented using existing measured data of a sample rotor angular contact ball-bearing (ACBB) system. In Section 4, a comprehensive analysis of the system vibration under various operating conditions is made. A model comparison was performed by means of the traditional time-invariant bearing stiffness model. Finally, in Section 5, conclusions are provided.
2. Rotor-bearing System Modeling
In this section, the modeling method for rotor-bearing systems is presented. The system consists of a flexible shaft supported by ACBBs and rigid disks. The FEM is used to model the elastic shaft, and a five-degree-of-freedom bearing model is adopted to calculate the ACBB stiffness matrix.
2.1 Finite Element Model of Rotor System
To make the system equations of motion of rotor-bearing systems, the FEM has been effectively used in many studies.1,12,13 The equations of motion for shaft elements, disk, and bearings are constructed and assembled to make the equations of motion for the whole rotor system, which are detailed in Ref. 1. Combining the shaft element and bearing equations, the assembled equation of motion of the rotor-bearing system is obtained as
| (1) |
where {q} is the displacement vector, which represents the displacements of all nodes along the shaft. The force vector on the right-hand side of Eq. (1) contains the external forces acting the rotor system. [M] and [G] are the mass and gyroscopic matrices, respectively. [K] is the stiffness matrix, which comprises the stiffness matrix of the shaft element and supporting bearings. [C] is the damping matrix. In this study, the unbalance excitation force resulting from the disk eccentricity is considered.
2.2 Bearing Stiffness Computation
There exist several analytical models for calculation of bearing stiffness in the literature. The quasi-static model of ball bearings outlined by de Mul et al.14 is used in this study. A great advantage of this model is that it can be organized in modules based on the effective use of vector and matrix methods. Unlike the original model proposed by de Mul et al.,14 the present model takes into account the ball gyroscopic moment, as in Refs. 15 and 16.
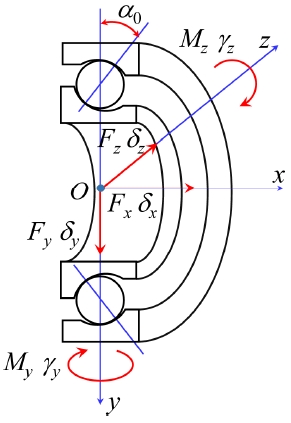
Fig. 1 shows the ACBB global coordinate system, loading, and corresponding displacements of the inner ring. The loads acting on the inner ring of the ACBB are described by
| (2) |
and the corresponding displacements of the inner ring are
| (3) |
The stiffness matrix of the bearing defines the relationship between the bearing load and displacement, written as
| (4) |
which is a fully occupied (5 × 5) stiffness matrix of the form
| (5) |
There are two kinds of bearing boundary condition for stiffness matrix computation. The first kind is that the load vector {F} is given, and the stiffness matrix is unknown. In this case, to find the bearing stiffness matrix, the equilibrium of all the balls needs to be obtained first. Thereafter, the equilibrium equations of the inner ring can be obtained, and then the unknown {δ} and the stiffness matrix are solved. However, it is often very difficult to find the exact bearing loading, especially when the rotor system is subjected to various excitation loads. Another kind of boundary condition can be adopted, such that the displacement vector {δ} is given, and the stiffness matrix is unknown. This study is mainly concerned with this type of bearing boundary condition, in which the displacements of the bearing are extracted from the vibration response of the system obtained in each iteration. Using this model, the corresponding loads {F} can be found directly without the global iteration. This means that only a local iteration loop is required for each ball to find the ball equilibrium. Thus, the global equilibrium of the bearing can be computed by taking the summation of the inner ring contact loads attributed to all rolling elements.
Because all equations are nonlinear, an iterative method is employed to solve the equilibrium equations. Detailed descriptions of ball and inner ring equilibrium equations and stiffness matrix computation are provided in Appendices A1-A6.
Note here that the axes of bearing local coordinate system (xyz) may be different from those of the global coordinate system (XYZ). The bearing direction can be defined as either positive or negative, depending on the direction of the bearing x-axis with respect to the rotor X-axis. Therefore, a right mapping for the stiffness matrix from the negative bearing local coordinate into the positive global coordinate should be considered. The mapping procedure for the stiffness matrix of a negative bearing can be found in Li and Shin.17
2.3 Calculation Procedure
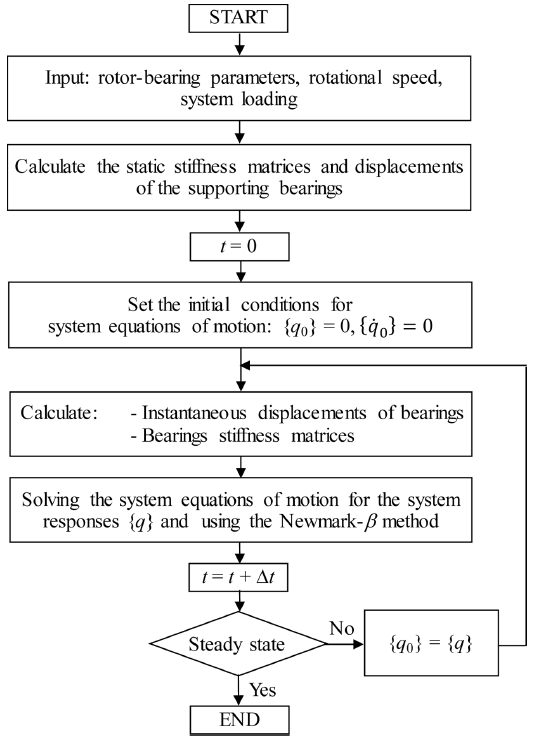
The calculation procedure for the vibration response of a rotor system using the proposed model is exhibited in Fig. 2. At first, the stiffness matrix and static displacements of each ACBB are estimated using the ACBB model.15,16,18 Input values for this calculation are the axial preload and the radial load caused by the rotor mass.
The rotor system is assumed to start rotating from its static position. Therefore, at t = 0, the initial conditions of system displacements and velocities are set to zero: i.e., {q0} = 0 and . At an arbitrary time t, the absolute displacements of each bearing {δ} are determined by summation of its static displacements and instantaneous displacements obtained from the previous step. Then, new stiffness matrices of the bearings are determined, with the inputs {δ} and the current time t. Subsequently, the equations of motion are solved using the Newmark-β method with a constant time step of Δt = 10-5(s). The incremental time Δt is added at the end of the iteration loop, and the current values of rotor displacements and velocities are set to initial values for the next time step. The process is repeated until the steady-state vibration is achieved. Finally, the fast Fourier transform is performed for the resultant rotor displacements to obtain the frequency domain response.
3. Model Validation
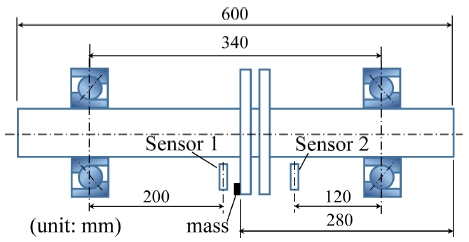
The vibration responses using the proposed model were compared with existing experimental data in the literature. Fig. 3 shows the geometry of the test rig used in Li et al.11 The rotor system consisted of a uniform shaft supported by a pair of identical ACBBs in back-to-back arrangement and two identical disks. The radial clearances between the ball and bearing rings were 7.5 μm. An additional eccentric mass was added to the disk on the left to generate an unbalance force and, thus, cause vibration of the rotor. The product of the eccentric mass and its radial position is 120 g.cm. The vibration responses of the rotor at two positions were measured using displacement sensors.
Details of the experimental setup can be found in Ref. 11. Because the bearing preloading conditions were not discussed by Li et al.,11 a bearing displacement preload of 20 μm was assumed for the two ACBBs.
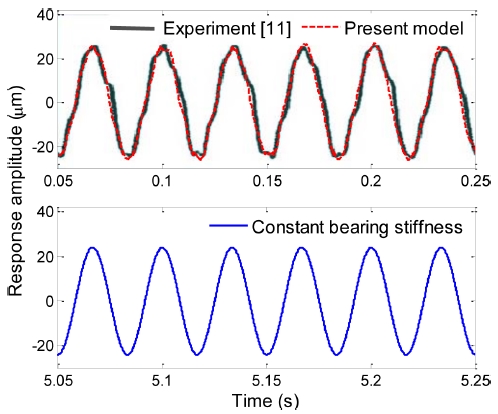
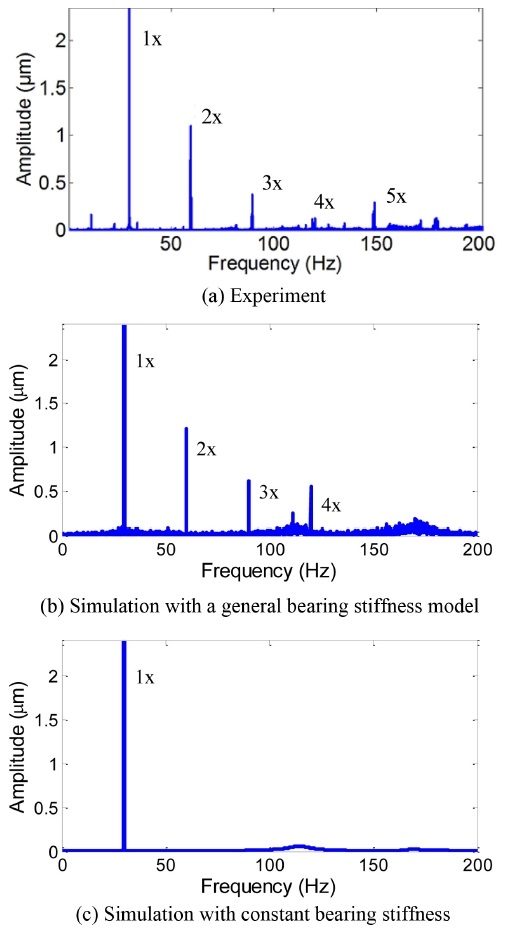
Fig. 4 shows the measured vibration response when the rotating speed was 1800 rpm. Fig. 4 also illustrates the simulated vibration response using the invariant and constant-bearing-stiffness models. Fig. 5 compares the measured and calculated frequency spectra of the vibrations, which are illustrated in zoomed plots of the response amplitude from 0 to 2.4 μm. Figs. 4 and 5 demonstrate that the simulated results using the proposed general bearing stiffness model agree well with those from the experiment. Although the response is mainly a synchronous behavior, higher harmonics (up to 5X) are visible. Such high harmonics are caused by the engagement of the bearing clearance.11 The constant-stiffness bearing model fails to predict the high-frequency components. Instead, only 1X synchronous frequency is found, as shown in Fig. 5(c). The predicted amplitudes show an overall good match with those from measurements.
4. Simulation and Discussion
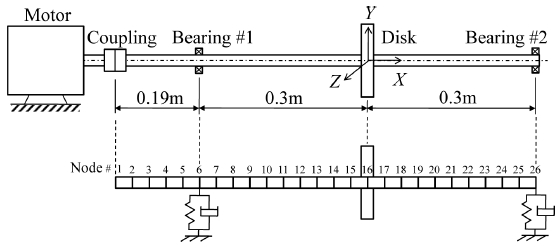
Fig. 6 shows the investigated rotor system and its FE model. The rotor system consists of a shaft, a rigid disk, and a pair of identical ACBBs. The rotor shaft is connected to the driving motor via a flexible coupling. The ACBBs are preloaded by the displacement preload method. Simulations were performed with MATLAB subjected to various operating conditions in terms of speed n, disk eccentricity e, ACBB clearance ε, and axial preload δa. Tables 1 and 2 show the parameters of the rotor system.
Fig. 7 shows the vibration amplitudes at the disk and bearings excited by unbalance force as a function of rotor speed. The disk eccentricity was set to 5 μm, and the rotational speed is varied from 1,000 to 100,000 rpm. The radial clearance and axial preload on the bearings were set to zero and 1.5 μm, respectively. For comparison, the vibration amplitudes were estimated with the proposed model and the conventional, constant-bearing-stiffness model. The vibration responses by the two methods are similar in the low-speed range. The first two modes are dominated by the shaft deflections, while the third mode around 70,000 rpm experiences significant displacements at the bearings. A large difference is observed near the third critical speed region. The peaks estimated by the proposed model are shifted from those of the conventional constant-stiffness model. This difference is caused by the nonlinearity in the bearing model.
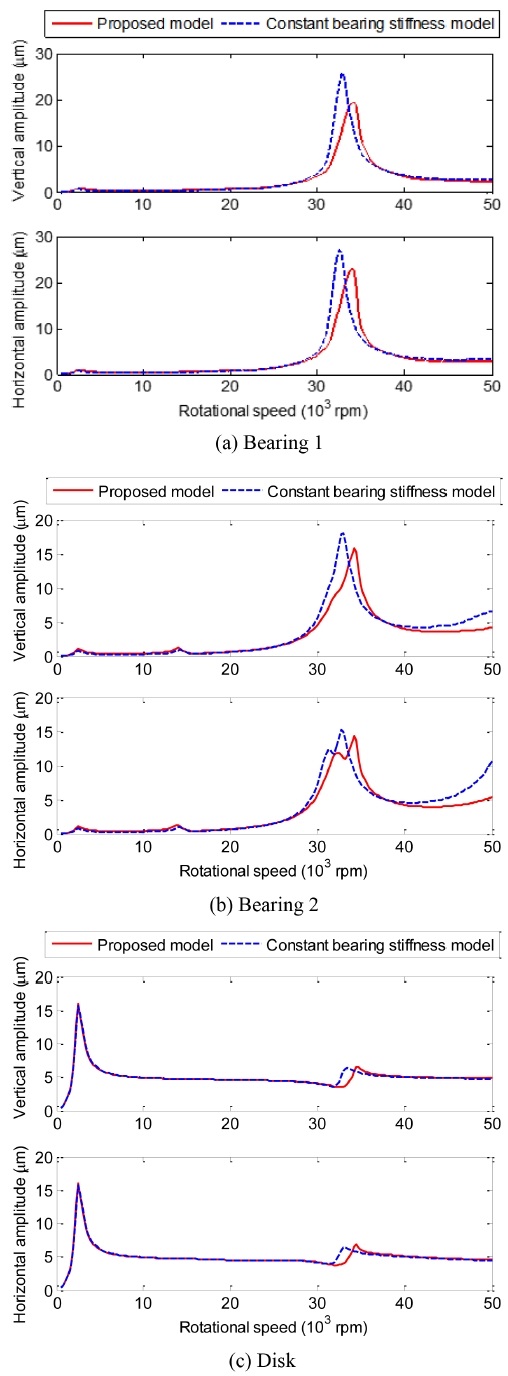
Vibration amplitudes at the disk and bearings without bearing radial clearance (e = 5 μm, ε = 0 μm, δa = 1.5 μm)
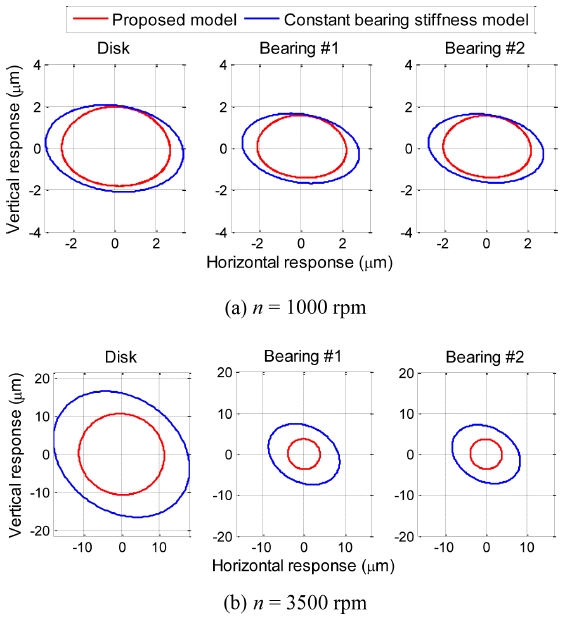
Fig. 8 shows the vibration amplitudes at the disk and bearings when applying 5-μm radial clearance to ACBBs. By introducing bearing clearance, the vibration amplitudes are altered, even in the low-critical-speed region. Fig. 9(a) illustrates the orbital trajectories of the disk and bearing centers. As already shown in Fig. 9, the constant-stiffness model is likely to make some discrepancies in the trajectories with those of the proposed time-varying stiffness model in the low-speed region. The trajectories are all elliptical because of the anisotropic bearing characteristics caused by the effect of rotor weight.
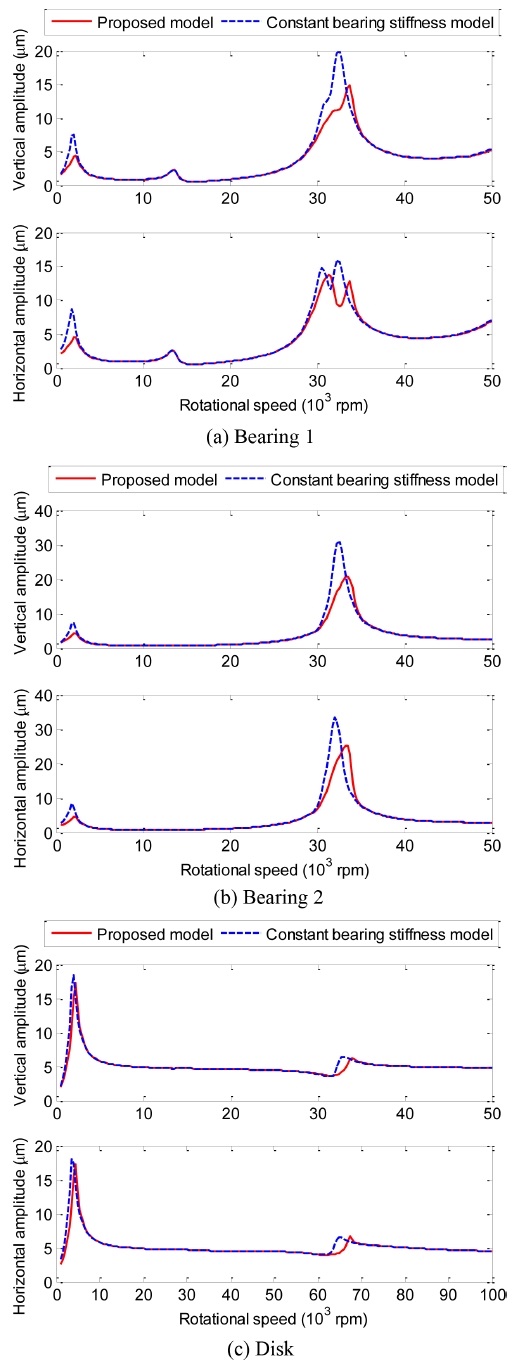
Vibration amplitudes at the disk and bearings with bearing radial clearance (e = 5 μm, ε = 5 μm, δa = 1.5 μm)
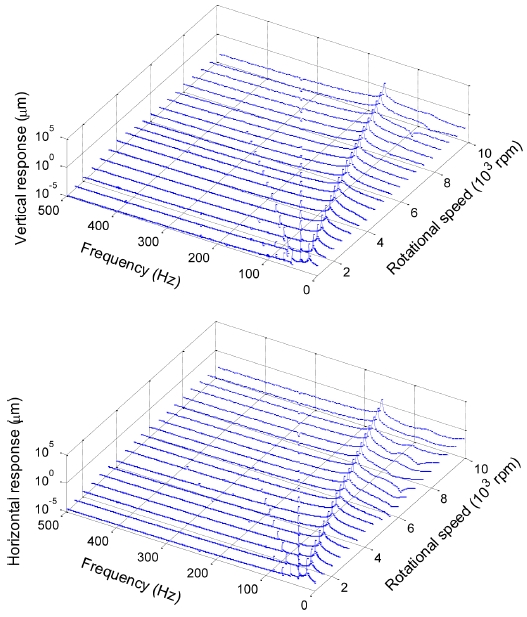
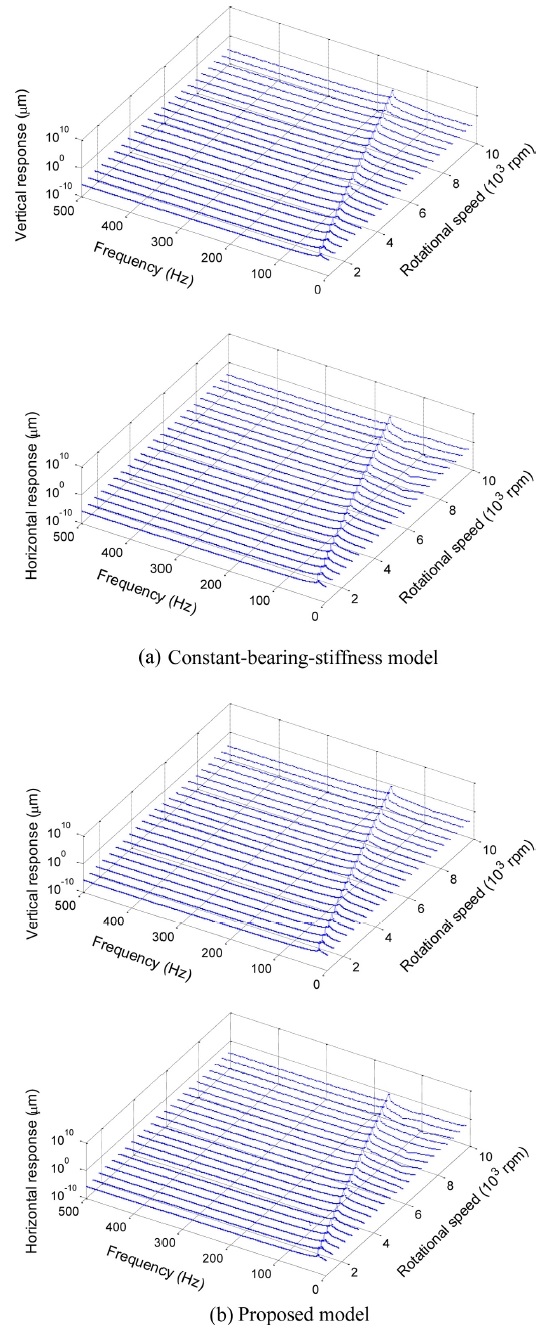
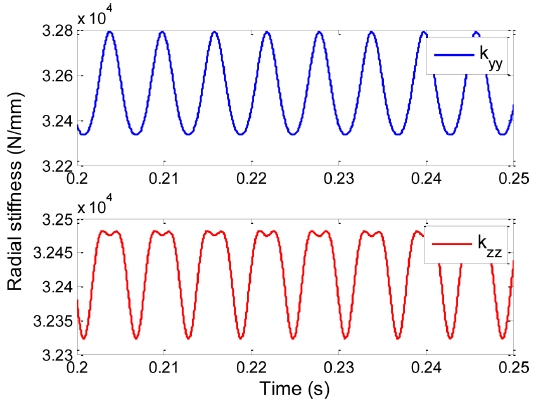
The waterfall plots at the disk using the two models are shown in Figs. 10 and 11. The disk eccentricity, bearing radial clearance, and preload were selected as e = 5 μm, ε = 5 μm, and δa = 1.5 μm, respectively. Fig. 10 shows only a 1X component that is synchronous to unbalance frequency, whereas Fig. 11 exhibits multiple harmonics. The occurrence of high-order harmonics, as shown in Fig. 11, is attributed to the effect of the time-varying and nonlinear nature of ACBB stiffness. Fig. 12 shows the variation in the time domain for the radial stiffness of ACBB No. 1. Under unbalance excitation, the multiple harmonic frequencies in the stiffness are observed; the 2X component is significant. This further shows that the constant-bearing-stiffness model, as well as the pre-described stiffness model with 1X and band-pass filter frequencies,9 may reduce the accurate prediction for vibration of the unbalanced rotor with rolling-element bearings.
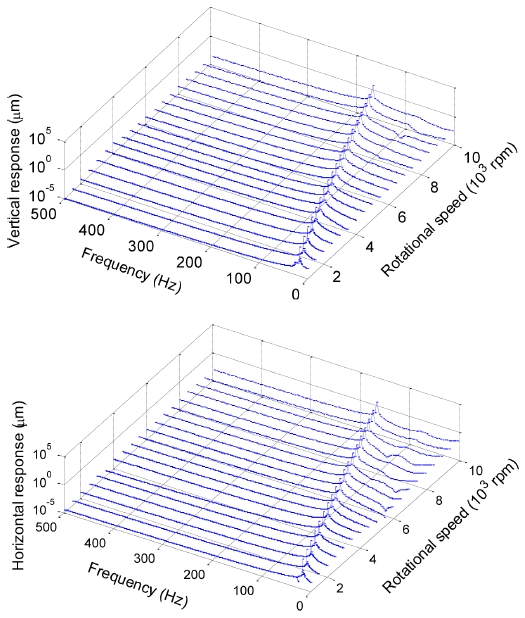
Waterfall plots at the disk using the constant-bearing-stiffness model (e = 5 μm, ε = 5 μm, δa = 1.5 μm)
Fig. 13 shows the waterfall plots at the disk when an axial preload of δa = 10 μm is applied to the ACBBs. The disk eccentricity and bearing clearance were kept the same as above, i.e., e = 5 μm and ε = 5 μm, respectively. In this case, the waterfall plot shows that only the synchronous response is dominant for both models. Fig. 14 illustrates the radial stiffness of ACBB No. 1. The stiffness variations are relatively small compared with the average values (below 0.7%).
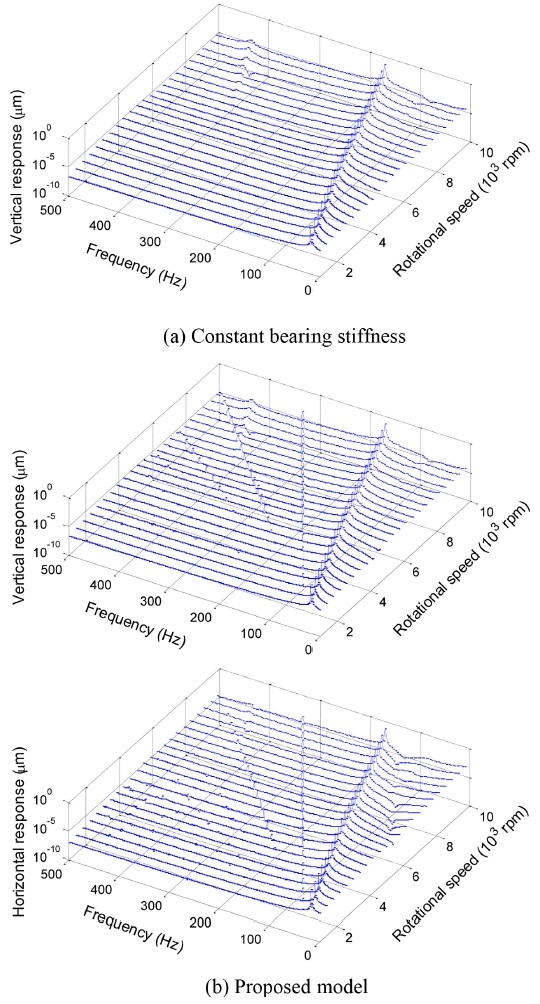
Fig. 15 shows the waterfall plot at ACBB No. 1. The proposed model gives multiple harmonics in the ACBB vibration, whereas the constant-stiffness model can predict only synchronous components. The constant bearing stiffness model is less precise in terms of vibration frequencies of supporting bearings, regardless of preload conditions.
5. Conclusions
An analysis of the vibration response of the rotor system supported by ACBBs was performed. A time-varying, response-dependent bearing stiffness approach was proposed to replace the traditional, time-invariant bearing stiffness model. The vibration responses of the rotor system caused by unbalance were considered. The model was validated with experimental data available in the literature. Extended simulations were conducted to investigate the effect of time-varying, response-dependent bearing characteristics on the rotor vibration. The computational results showed that the model could predict high-order harmonics in the rotor vibration because of the time-varying, response-dependent nature attributed to the radial clearance of ACBBs. The method can be further applied to investigate the vibration response of flexible rotor systems subjected to various excitation sources.
Acknowledgments
This research was supported by the Korea Institute of Machinery and Materials.
REFERENCES
-
Lee, C.-W., “Vibration Analysis of Rotors,” Kluwer Academic Publishers, 1993.
[https://doi.org/10.1007/978-94-015-8173-8]

-
Patel, T. H. and Darpe, A. K., “Vibration Response of Misaligned Rotors,” Journal of Sound and Vibration, Vol. 325, No. 3, pp. 609-628, 2009.
[https://doi.org/10.1016/j.jsv.2009.03.024]

-
Lees, A., “Misalignment in Rigidly Coupled Rotors,” Journal of Sound and Vibration, Vol. 305, Nos. 1-2, pp. 261-271, 2007.
[https://doi.org/10.1016/j.jsv.2007.04.008]

-
Sudhakar, G. and Sekhar, A., “Identification of Unbalance in a Rotor Bearing System,” Journal of Sound and Vibration, Vol. 330, No. 10, pp. 2299-2313, 2011.
[https://doi.org/10.1016/j.jsv.2010.11.028]

-
Jalan, A. K. and Mohanty, A., “Model Based Fault Diagnosis of a Rotor–Bearing System for Misalignment and Unbalance Under Steady-State Condition,” Journal of Sound and Vibration, Vol. 327, Nos. 3-5, pp. 604-622, 2009.
[https://doi.org/10.1016/j.jsv.2009.07.014]

-
Xul, J., Zheng, X., Zhang, J., and Liu, X., “Vibration Characteristics of Unbalance Response for Motorized Spindle System,” Procedia Engineering, Vol. 174, pp. 331-340, 2017.
[https://doi.org/10.1016/j.proeng.2017.01.148]

-
Liew, H.-V. and Lim, T. C., “Analysis of Time-Varying Rolling Element Bearing Characteristics,” Journal of Sound and Vibration, Vol. 3, No. 283, pp. 1163-1179, 2005.
[https://doi.org/10.1016/j.jsv.2004.06.022]

-
Lim, T. and Singh, R., “Vibration Transmission Through Rolling Element Bearings, Part I: Bearing Stiffness Formulation,” Journal of Sound and Vibration, Vol. 139, No. 2, pp. 179-199, 1990.
[https://doi.org/10.1016/0022-460X(90)90882-Z]

-
Zhang, X., Han, Q., Peng, Z., and Chu, F., “Stability Analysis of a Rotor–Bearing System with Time - Varying Bearing Stiffness Due to Finite Number of Balls and Unbalanced Force,” Journal of Sound and Vibration, Vol. 332, No. 25, pp. 6768-6784, 2013.
[https://doi.org/10.1016/j.jsv.2013.08.002]

-
Patel, T. H. and Darpe, A. K., “Experimental Investigations on Vibration Response of Misaligned Rotors,” Mechanical Systems and Signal Processing, Vol. 23, No. 7, pp. 2236-2252, 2009.
[https://doi.org/10.1016/j.ymssp.2009.04.004]

-
Li, Y., Cao, H., Niu, L., and Jin, X., “A General Method for the Dynamic Modeling of Ball Bearing - Rotor Systems,” Journal of Manufacturing Science and Engineering, Vol. 137, No. 2, pp. 1-11, 2015.
[https://doi.org/10.1115/1.4029312]

-
Nelson, H. and McVaugh, J., “The Dynamics of Rotor-Bearing Systems Using Finite Elements,” Journal of Engineering for Industry, Vol. 98, No. 2, pp. 593-600, 1976.
[https://doi.org/10.1115/1.3438942]

-
Hong, S.-W. and Park, J.-H., “An Efficient Method for the Unbalance Response Analysis of Rotor-Bearing Systems,” Journal of Sound and Vibration, Vol. 200, No. 4, pp. 491-504, 1997.
[https://doi.org/10.1006/jsvi.1996.0773]

-
de Mul, J. M., Vree, J. M. and Maas, D. A., “Equilibrium and Associated Load Distribution in Ball and Roller Bearings Loaded in Five Degrees of Freedom While Neglecting Friction - Part I,” Journal of Tribology, Vol.111, pp. 149-155, 1989.
[https://doi.org/10.1115/1.3261865]

-
Tong, V.-C. and Hong, S.-W., “Study on the Running Torque of Angular Contact Ball Bearings Subjected to Angular Misalignment,” Proc. of the Institution of Mechanical Engineers,” Part J: Journal of Engineering Tribology, Vol. 232, No. 7, pp. 890-909, 2018.
[https://doi.org/10.1177/1350650117732921]

-
Bae, G.-H., Tong, V.-C., and Hong, S.-W., “Fatigue Life Analysis for Angular Contact Ball Bearing with Angular Misalignment,” Journal of the Korean Society for Precision Engineering, Vol. 33, No. 1, pp. 53-61, 2016.
[https://doi.org/10.7736/KSPE.2016.33.1.53]

-
Li, H. and Shin, Y. C., “Analysis of Bearing Configuration Effects on High Speed Spindles Using an Integrated Dynamic Thermo-Mechanical Spindle Model,” International Journal of Machine Tools and Manufacture, Vol. 44, No. 4, pp. 347-364, 2004.
[https://doi.org/10.1016/j.ijmachtools.2003.10.011]

-
Hong, S.-W. and Tong, V.-C., “Rolling-Element Bearing Modeling: A Review,” International Journal of Precision Engineering and Manufacturing, Vol. 17, No. 12, pp. 1729-1749, 2016.
[https://doi.org/10.1007/s12541-016-0200-z]

-
Harris, T. A., and Kotzalas, M. N., “Advanced Concept of Bearing Technology,” 5th Edition, Taylor & Francis, 2006.
[https://doi.org/10.1201/9781420006582]

APPENDIX: ACBB Equilibrium and Stiffness Matrix Calculation
A1. Ball Equilibrium Equations
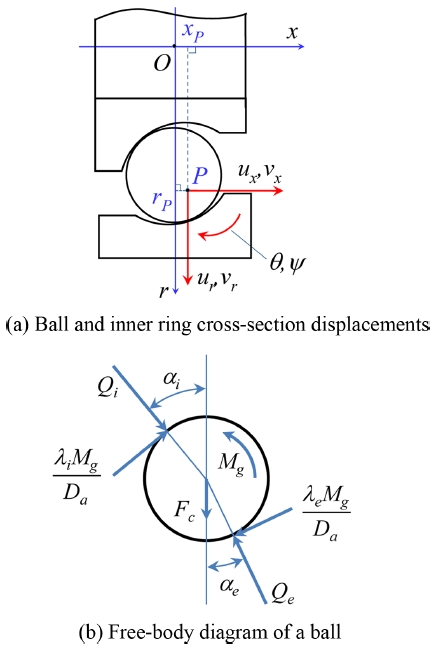
Modeling of rolling-element bearings was well summarized in Ref. [17]. Fig. A1(a) shows the cross-section of the bearing at a location angle ϕ. The inner ring and ball displacements are {u} = {ur, ux, θ}T and {v} = {vr, vx, ψ}T, respectively. Fig. A1(b) shows the free-body diagram of a ball. The equilibrium equations of a ball shown in Eq. (A1) can be solved to give {v}.
| (A1) |
A2. Global Equilibrium Equations of Inner Ring
The equilibrium equations of the inner ring can be written as
| (A2) |
where the inner ring contact load at a particular ball {Q} is defined as
| (A3) |
where [Rϕ] is the transformation matrix given by
| (A4) |
where ϕ is the time-varying angle depending on the instantaneous orbital position angles of the ball and rotating race, as calculated in Ref. 7.
A3. Contact Load Calculation
The contact loads between balls and races are calculated using the Hertzian theory,
| (A5), (A6) |
where the contact coefficients between the ball and raceways k can be determined using Harris.19 The contact compressions between the ball and raceways are calculated by
| (A7), (A8) |
where li and le can be derived based on a geometric relationship. The clearances between ball and races Δi and Δe become zero when a sufficient axial preload is applied.
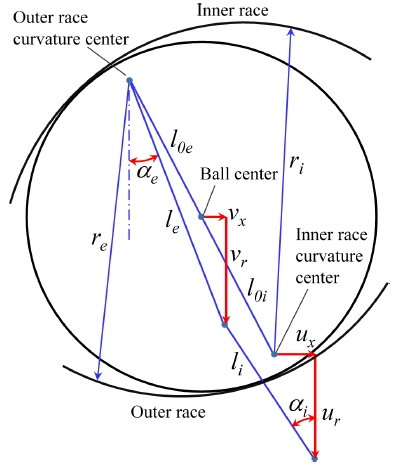
A4. Geometric Relationship
Fig. A2 shows the position of the ball center, inner, and outer race curvature center before and after loading. From Fig. A2, the following geometric relationships are derived for the ACBB considering inertial effects:
| (A9), (A10) |
| (A11), (A12) |
A5. Centrifugal Force and Gyroscopic Moment
The centrifugal force and gyroscopic moment acting on a ball can be calculated by
| (A13) |
| (A14) |
where the pitch angle β is defined as the angle between the bearing axis and rolling axis of the ball. There are several methods to determine β.18 This study calculates β using the outer race control theory as Ref. 18.
| (A15) |
The other parameters in Eqs. (A13, A14) can be calculated by
| (A16), (A17) |
| (A18) |
| (A19) |
| (A20) |
A6. Bearing Stiffness Matrix
The bearing stiffness matrix (5×5) is obtained from the Jacobian matrix as Ref. 14.
| (A21) |
where the contact stiffness matrix of a ball j is defined as
| (A22) |

He received his M.S Degree in Mechanical Engineering from Hanoi University of Science and Technology, Vietnam in 2011. He earned his Ph.D degree in Mechatronics from Kumoh National Institute of Technology, Korea in 2017. He is currently a Postdoctoral researcher at Korea Institute of Machinery & Materials.
E-mail: canhtong@kimm.re.kr

He is a professor in the Department of Mechanical System Engineering of Kumoh National Institute of Technology. His current research interests include spindle and bearings modeling and analysis, command shaping for positioning systems, and structural vibration analysis for mechanical system.
E-mail: swhong@kumoh.ac.kr