고증폭용 다단 지렛대형 유연 힌지의 최적 설계

1. 서론

최근 높은 정밀도를 요구하는 산업분야가 발달함에 따라 정밀 위치 결정 기구에 대한 연구가 활발히 이루어지고 있으며, 특히 압전(PZT) 구동기는 빠른 응답속도, 큰 구동력, 높은 분해능 등의 장점을 가지고 있어 많이 사용되고 있다. 그러나 발생시킬 수 있는 최대변위는 압전 구동기 길이의 1/1000정도에 불과하여 변위를 확대하는 기구인 유연힌지(Flexure Hinge)와 결합하지 않고는 실제 적용할 수가 없다.^1,2 유연힌지의 장점은 백래시나 마찰 없이 매끄럽고 연속적인 움직임을 얻을 수 있다는 것이고, 단점은 유연힌지 구조의 크기 때문에 증폭비가 제한되고 축과 축 운동 사이에 기생운동이 생길 수 있다는 점이다.^3-5 PZT의 변위를 증폭하기 위해서 지렛대 메커니즘, 브릿지 메커니즘, 무니 메커니즘등이 있다. 여기서 지렛대 힌지는 증폭비가 크고, 인가된 힘과 평행한 방향으로 안전된 변위를 증폭하는 장점들이 있다.⁶

보통 PZT 구동기의 변위는 10 - 20 μm 정도 이하로 작은데 이를 50 - 100배로 증폭하여 큰 변위를 출력 하려면 지렛대형 유연힌지의 길이가 커져야 한다. 그러나 유연 힌지의 크기가 제한될 때는 길이를 줄이기 위해 지렛대를 다단(Multi-Layer) 기구로 하여 증폭을 배가시키는 기구가 필요하다. 이때 몇 단으로 하는 게 최적인가에 대한 연구가 거의 없다. 따라서 본 연구에서는 고증폭용 다단 지렛대형 유연 힌지의 단 수에 따라 입력변위, 출력변위, 입력하중 등이 어떻게 변하는지 그 특성을 조사하고자 한다. 지렛대 힌지의 주요 설계 변수가 지렛대의 입력점 위치, 회전강성과 깊은 관련이 있는 노치 두께인데, 입력점 위치는 고정하고 회전강성의 영향을 비교분석하여 최적의 단과 최적의 노치 두께를 구하고자 한다. 각 지렛대 힌지의 자유물체도를 이용하여 각 단의 변위와 입력하중식을 유도하고, 이를 바탕으로 각 단의 입력변위, 출력변위, 입력하중 등을 계산하였다. 또는 힌지구조 제작에 앞서 힌지구조 해석을 통하여 각 단의 형상을 확인하였다.

2. 증폭비에 대한 노치 형상의 영향

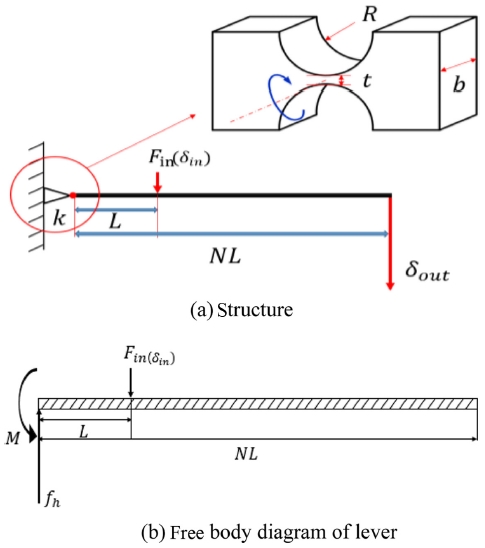
2.1 지렛대형 유연 힌지의 기본 구조

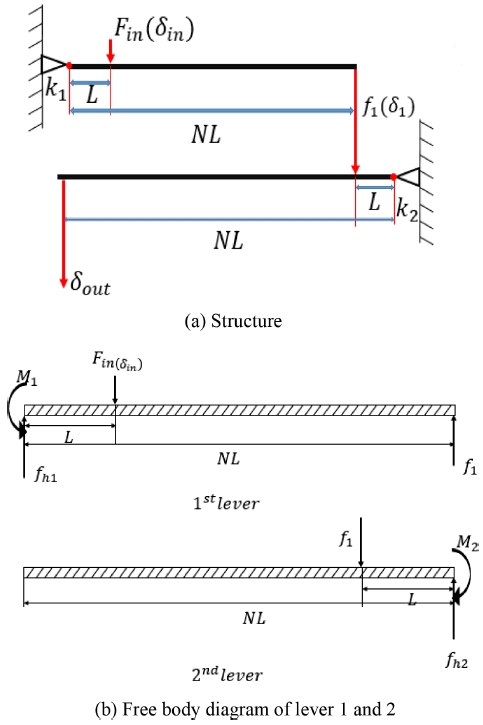
지렛대형 유연 힌지의 기본 구조는 Fig. 1에 보이는 것처럼 강체 구조물에 회전 스프링 역할을 하는 노치를 만들어 넣은 형태이고 동작원리는 강체의 입력점에 변위가 생기면 지렛대의 원리에 의해 강체의 출력점에 변위가 증폭되는 것이다. 즉, 입력점(L)의 변위가 δ_in 만큼 생기도록 작용점에 힘 F_in을 입력하면 회전강성 k_θ인 노치에서 θ 만큼 회전이 일어나고 강체 지렛대의 출력점의 변위(δ)가 Nδ_in 만큼 발생한다. 강체 지렛대의 자유물체도를 해석하면 다음과 같다.

Fig. 1

A lever type flexure hinge

$\[ F_{in}=\frac{M}{L}=\frac{k_{\theta }}{L^2}{\delta }_{in}\left(\theta =\frac{{\delta }_{in}}{L},M=k_{\theta }·\theta =\frac{k_{\theta }}{L}{\delta }_{in}\right) \]$

(1)

$\[ MR=\frac{{\delta }_{out}}{{\delta }_{in}}\left(\mathrm{M}\mathrm{R}:\mathrm{ }\mathrm{M}\mathrm{a}\mathrm{g}\mathrm{n}\mathrm{i}\mathrm{f}\mathrm{i}\mathrm{c}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{ }\mathrm{R}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\right) \]$

(2)

2.2 노치의 형상과 강성

힌지의 회전강성(k_θ)은 식(3)과 같이 노치의 폭(b), 반경(R), 두께(t)와 깊은 관련성이 있고 그중에서 노치 두께의 영향이 가장 큼을 알 수 있다.^7-9 여기서는 노치 반경을 3 mm, 두께를 다섯 가지(0.8, 1.0, 1.2, 1.4, 1.6 mm), 재료를 두 가지(AL6061, SUS3043)로 하여 노치 두께와 회전강성의 관계를 실험적으로 조사하여 최적의 노치 두께를 구하고 본 연구에 활용하고자 한다. 노치는 와이어 방전가공기로 가공하여 제작하였다.

$\[ k_{\theta }=\frac{2Eb{t}^{\frac{5}{2}}}{9\pi R^{\frac{1}{2}}} \]$

(3)

2.2.1 노치의 강성 실험

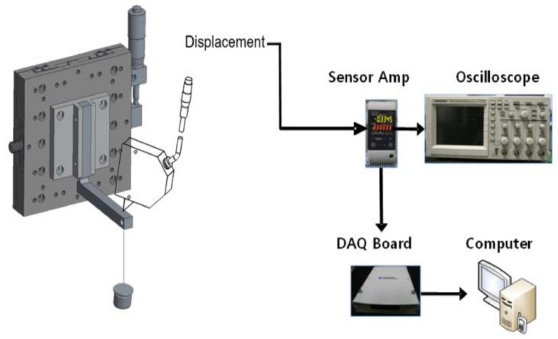
노치의 강성을 측정하기 위해 Fig. 2와 같이 하중점에 추를 매달고 레이저 변위센서(Keyence LK-G3, Table 1)로 하중점의 변위를 측정하였다. 노치변형을 탄성범위 내로 제한하기 위해 각 노치 마다 재료 항복강도(Yield Strength)의 1/1.5배(즉, 안전계수 1.5)에 도달하는 이론적인 최대하중을 구하고, 이것의 20, 40, 60, 80, 100% 값을 하중으로 하여 모든 노치에 대해 하중-변위를 측정하여 Table 2처럼 구하였다.

Fig. 2

Weight-deflection measurement for rotational stiffness of notch

Table 1

Specifications of laser displacement sensor

Table 2

Experimental results of weight-deflection for notches with different thickness/materials

2.2.2 재료와 노치 두께별 강성 측정값 분석

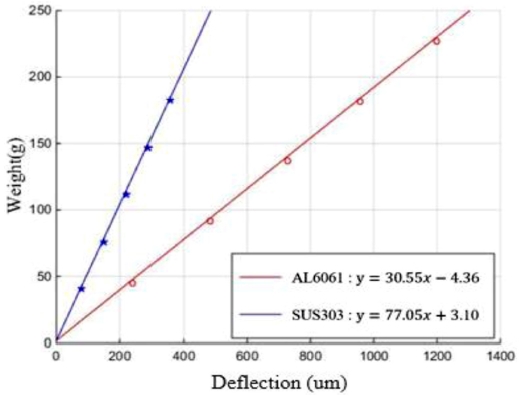
하중(F_in), 하중위치(L), 변위(δ_in), 회전강성(k_θ)의 관계는 식(1) 처럼 표시할 수 있다. 노치 두께 1.2 mm 일 때 두 재료에 대한 하중-변위 측정값을 그림으로 나타내면 Fig. 3과 같이 모두 선형적인 관계가 있음을 알 수 있고, 회귀(Regression) 분석으로 선형계수(k_θ/L²)를 구하면 회전강성을 구할 수 있다. T = 1.2mm일 때 두 재료(AL6061, SUS3043)의 회전강성은 각각 39880 N mm/rad, 122460 N mm/rad이고, 모든 두께에 대해 이런 과정을 거쳐 구하여 정리한 것이 Table 2의 실험값(Experimental) k_θ이다.

Fig. 3

Regression analysis results of weight-deflection for notch of t = 1.2 mm

2.2.3 노치의 두께와 강성의 관련성 분석

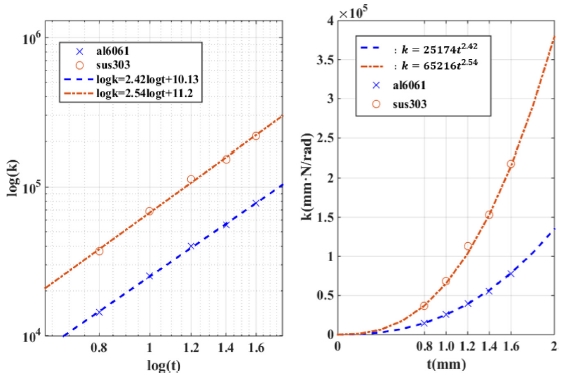
노치 형상에 따라 이론 강성을 나타내는 식(3)에서 b, R을 일정하게 두면 k_θ = Ct^5/2이다. 양쪽에 log 취하면 logk_θ= 2.5logt + logC, 여기서 log 변수를 각각 k'_θ, t', C'로 치환하면 k_θ' = 2.5t' + C'로 된다. Table 2의 강성 측정값을 두께에 따라 원좌표계와 치환 좌표계 그림으로 나타내면 Fig. 4와 같고, 회귀분석으로 구한 두 재료(AL6061, SUS3043)의 강성값은 각각 2.42, 2.54이다. 재료가 다름에도 식(3)의 이론값인 2.5와 ± 2%이내에서 일치한다. 이로써 노치 두께가 힌지의 회전강성에 2.5제곱 만큼 영향을 주는 이론식은 잘 정립되었다고 볼 수 있다. Table 2에 보이는 것처럼 실험값이 이론값보다 약 15% 정도 작은 것은 노치의 가공 변형이나 재료의 불완전과 다른 인자들 때문에 생긴 것으로, 완벽할 때를 전제로 한 이론 강성보다 작아진 것으로 생각된다.

Fig. 4

Regression analysis of relationship between rotational stiffness and notch thickness

3. 다단 유연 힌지의 구조와 증폭비

3.2 2단 유연 힌지의 해석

Fig. 5는 2단 유연힌지 구조와 강체 지렛대의 자유물체도를 나타낸다. 1단의 입력점(L)의 변위가 δ_in 만큼 생기도록 입력점에 변위 δ_in을 입력하면 회전강성 k_θ1인 노치1에서 θ₁ 만큼 회전이 일어나고 강체 지렛대1의 출력점의 변위(δ₁)가 Nδ_in 만큼 발생한다. 이어서 지렛대1의 출력점의 변위(δ₁)와 힘(f₁)이 단 힌지의 작용점(L₂)에 전달되어 회전강성 k_θ2인 노치2에서 회전각도 θ₂ 만큼 회전이 생기고 지렛대2의 출력점 변위(δ_out)가 최종 변위로 발생한다. 이들 변수간의 관계식을 유도하면 다음과 같다.

Fig. 5

2-layer flexure hinge mechanism

$\[ \begin{array}{c}{\theta }_1=\frac{{\delta }_{in}}{L},M_1={k_{\theta 1}·\theta }_1=\frac{{\delta }_{in}·k_{\theta 1}}{L},{\delta }_1=N{\delta }_{in},\\ {\theta }_2=\frac{N{\delta }_{in}}{L},M_2={k_{\theta 2}·\theta }_2=\frac{{N\delta }_{in}·k_{\theta 2}}{L},{\delta }_{out}=N^2{\delta }_{in}\\ F_{in}=\frac{k_{\theta 1}+N^2{k}_{\theta 2}}{L^2}{\delta }_{in},MR=\frac{{\delta }_{out}}{{\delta }_{in}}=N^2\end{array} \]$

(4)

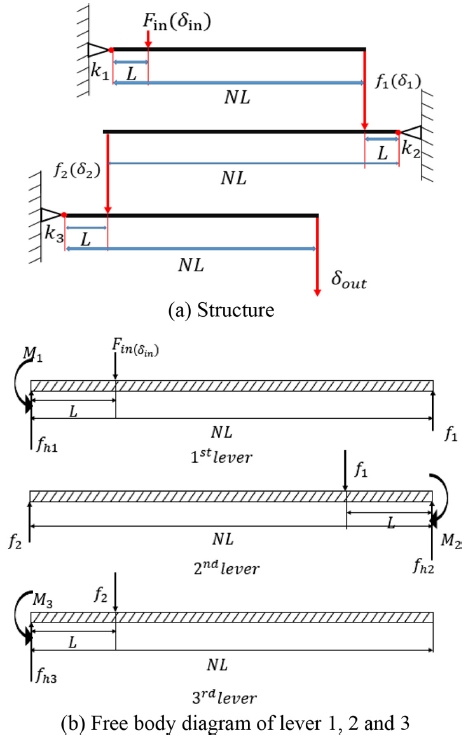
3.3 3단 유연 힌지의 해석

Fig. 6은 3단 유연 힌지구조와 강체 지렛대 1, 2, 3의 자유물체도를 나타낸다. 앞에서 구한 지렛대2의 출력점의 변위(δ₂)는 3단 힌지의 작용점에 전달되어 회전강성 k_θ3인 노치3에서 회전각도 θ₃만큼 회전이 생기고 지렛대3의 출력점 변위(δ_out)가 최종 증폭 변위가 된다. 여기서도 노치 1, 2, 3에 모멘트 M₁, M₂, M₃가 작용하여 각각의 회전각을 유지한다. 이들 변수간의 관계식을 유도하면 다음과 같다.

Fig. 6

3-layer flexure hinge mechanism

$\[ \begin{array}{c}{\theta }_1=\frac{{\delta }_{in}}{L},M_1={k_{\theta 1}·\theta }_1=\frac{{\delta }_{in}·k_{\theta 1}}{L},\mathrm{ }{\delta }_1=N{\delta }_{in},\\ {\theta }_2=\frac{N{\delta }_{in}}{L},M_2={k_{\theta 2}·\theta }_2=\frac{{N\delta }_{in}·k_{\theta 2}}{L},{\delta }_2=N^2{\delta }_{in},\\ {\theta }_3=\frac{{N^2\delta }_{in}}{L},M_3={k_{\theta 3}·\theta }_3=\frac{{N^2\delta }_{in}·k_{\theta 3}}{L},{\delta }_{out}=N^3{\delta }_{in},\\ F_{in}=\frac{k_{\theta 1}+N^2{k}_{\theta 2}+N^4{k}_{\theta 3}}{L^2}{\delta }_{in},MR=\frac{{\delta }_{out}}{{\delta }_{in}}=N^3\end{array} \]$

(5)

3.5 고증폭 다단 힌지의 탄성한계 내 성능 비교

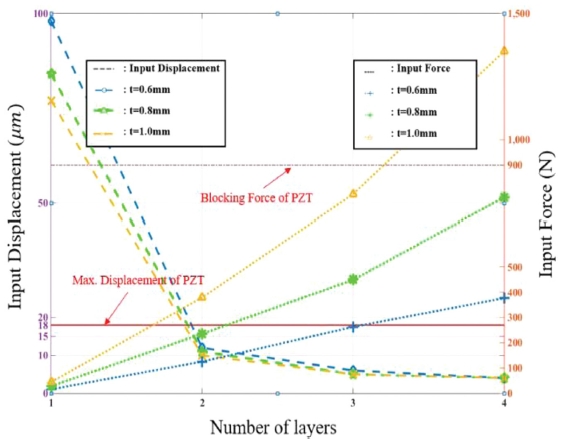
본 연구에서 PZT엑추에이터는 PI사의 P-885.50 (최대변위 18 μm, 최대 지지력(Blocking Force) 900 N, 강성(k_p) 50 N/μm)로 하고, 최종 증폭비(MR)를 64, 입력점 거리(L)를 7 mm로 고정할 때, 힌지의 회전강성 3가지(노치 두께 0.6, 0.8, 1.0 mm)에 대한 다단(1, 2, 3, 4단) 힌지의 특성을 비교하였다.

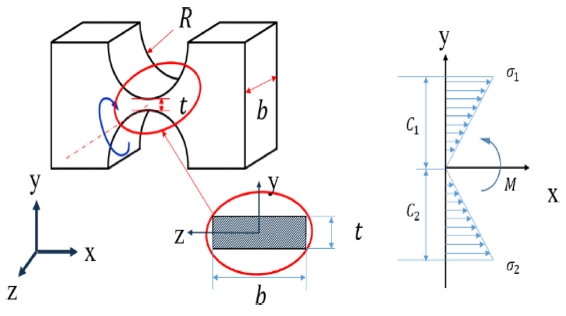
다단 힌지의 경우 회전변위의 증폭이 배가되므로 마지막 단의 노치 회전변위가 탄성한계 내에 있어야 한다. 따라서 Fig. 7에 보이듯이 노치 단면이 y축에 대해 대칭일 때, 굽힘공식에 따르면 탄성범위 내 최대 회전변위는 식(7)에 의해 제한된다.

Fig. 7

Stress distribution in the cross section of a notch

$\[ \begin{array}{c}{C}_1=C_2=\frac{t}{2},S=\frac{\frac{b{t}^3}{12}}{\frac{t}{2}}=\frac{b{t}^2}{6}\\ {\theta }_{\text{max}}=\frac{M_{\text{max}}}{k}=\frac{S·{\sigma }_y}{k}\end{array} \]$

(7)

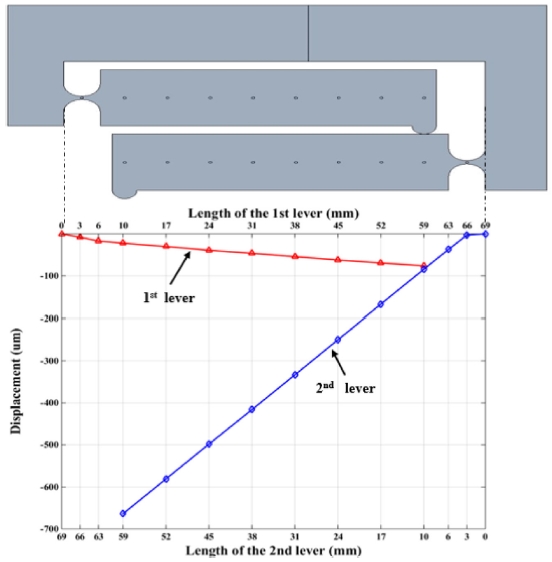
Table 3은 식(7)을 만족하는 각 힌지의 입력변위, 작용력, 손실변위, 출력변위의 최대값을 계산하여 정리한 것이다. 여기서 손실변위는 입력하중(F_in)으로 인한 PZT의 수축량(F_in/k_p)이다. 다단 힌지에서 입력 지렛대에 필요한 입력변위와 하중을 그림으로 표현하면 Fig. 8과 같다. 단이 높아질수록 입력변위가 작아지는 걸 알 수 있다. 1단 힌지에서는 입력 변위가 너무 커서 PZT의 작동 범위를 넘어서지만 2단에서 크게 감소하고 3단 이후는 그 감소폭이 아주 작아진다. 입력하중은 2단 이후 거의 비례적으로 증가하여 4단에서는 PZT의 최대 지지력을 넘어선다. 따라서 2, 3단이 적용가능하고 이중에서 출력변위 측면에서 2단이 훨씬 좋은 걸 알 수 있다. 따라서 2단 유연힌지를 최적으로 선택한다. 3가지 노치 두께를 비교하면 두께가 증가할수록 강성도 증가하는 반면에 최대 회전변위는 작아진다. 따라서 최대 출력변위 측면에서 0.8 mm를 최적으로 선택한다.

Table 3

Comparison of multi-layer flexure hinges in terms of displacements and forces at input/output points. (MR = 64)

Fig. 8

Input displacement/force vs. number of hinge layers for MR = 64

4. 2단 유연 힌지의 구조 해석

앞에서 최적이라고 판단한 2단 유연 힌지의 변형해석을 유한 요소로 실시하여, 노치와 지렛대를 단순화하여 구한 Table 3의 입출력점 변위량이 실제 힌지 변형량과 얼마나 잘 맞는지 확인할 필요가 있다. 노치 반경 3 mm, 노치 폭 10mm, 노치 두께 0.8 mm, 지렛대 입/출력점을 7/56 mm로 고정하고, 지렛대의 두께를 10, 12, 14 mm로 변화시켜 ANSYS Workbench를 사용하여 해석하였다.

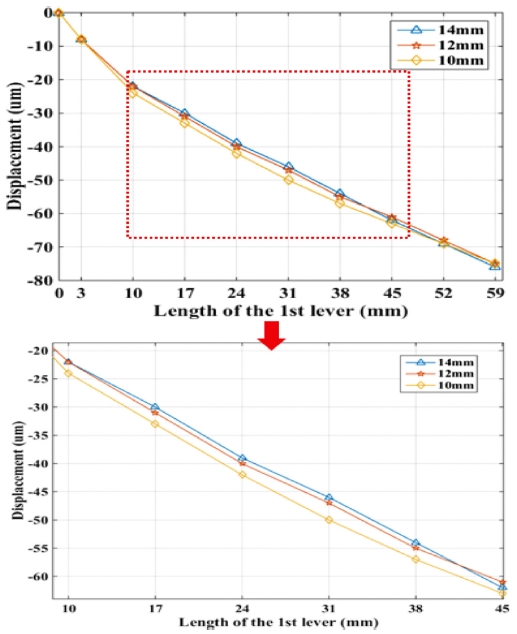
Fig. 9는 지렛대의 두께에 따른 1단 지렛대의 변위를 나타낸다. 두께가 10 mm일 때 굽힘 변형이 나타나므로 강체로 보기 위해 지렛대 두께를 12 mm 이상으로 할 필요가 있다.

Fig. 9

FEM simulated displacement of the 1st levers with 10 mm, 12 mm and 14 mm in thickness

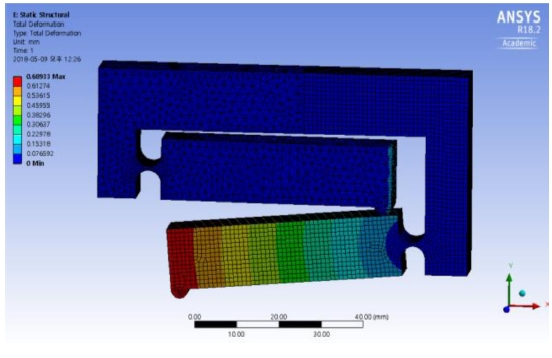
Fig. 10는 두께가 14 mm일 때 힌지 전체의 해석결과를 나타내고, Fig. 11은 노치와 지렛대의 중심선의 변형을 자세히 살피기 위해 1단과 2단 지렛대의 노치 시작점에서 3 mm(노치 중심점), 10 mm(입력점), 59 mm(출력점) 위치의 변위를 표시하였다. 1단과 2단 지렛대의 변위는 거리에 따라 거의 선형적으로 나타나 강체로 작동하고 있음을 알 수 있다. 2단 힌지의 최종 출력 변위가 664 μm로서 Table 3에서 t = 0.8mm일 때 2단 힌지로 64배 증폭할 때 예상 출력 변위 704 μm에 비해 10% 정도 작다. 이것은 설계 때 고려하지 않았던 1단과 2단의 노치 변형(각각 8 μm, 3 μm) 때문으로 생각된다.

Fig.10

FEM structural analysis of 2-layer flexure hinge with lever thickness of 14 mm

Fig.11

FEM simulated displacement of notches and levers of 2-layer flexure hinge

5. 결론

고증폭을 위한 다단 유연 힌지를 설계할 때 주요한 인자가 무엇인지, 단의 수가 커지면서 그들의 특성이 어떠한지를 연구하면서 얻은 결론은 다음과 같다.

(1) 노치의 회전 강성은 두께(t)의 영향을 가장 크게 받으며, 재료에 관계없이 t^5/2에 비례하다는 이론을 실험적으로 확인하였다.

(2) 다단 유연 힌지의 설계에서 최종단의 노치 변형이 탄성 범위를 넘어서지 않는 최대변형에서 1단 지렛대의 입력점에 필요한 변위와 하중이 PZT의 최대 변위와 최대 지지력(Blocking Force) 보다 작아야 하고, 하중에 의한 PZT의 변위 손실을 고려하면 최대 지지력의 50%보다 작아야 한다.

(3) 요구되는 입력 지렛대의 입력 변위는 2단부터 크게 감소하여 3단 이후 그 폭은 아주 작아지고, 하중은 단 증가에 따라 거의 비례적으로 증가하여 변위 손실도 비례하므로 출력 변위 측면에서 2단이 가장 좋다.

(4) FEM에 의한 2단 유연 힌지의 구조해석 결과 지렛대가 변형 없이 강체로서 작동하기 위해 지렛대 두께를 적어도 12 mm로 하여야 하고, 노치(두께 0.8 mm) 변형해석으로 1단과 2단의 노치 중심점의 변위는 각각 8 μm, 3 μm이고, 항복강도에 대한 안전계수가 각각 2.5, 1.6으로 탄성 범위 내 있음을 확인하였다.

(5) FEM 의한2단 유연 힌지(지렛대 두께 14 mm)의 구조해석 결과 최종 출력 변위가 664 μm로서 설계 때 예상했던 704 μm에 비해 10% 정도 작았다.

Acknowledgments

이 성과는 2017년도 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(No. NRF-2017R1A2B1011506).

REFERENCES

• Lee, C. H., “Ultraprecision Positioning Technology,” Journal of the Korean Society for Precision Engineering, Vol. 17, No. 12, pp. 9-15, 2000.
• Gao, P., Swei, S.-M., and Yuan, Z., “A New Piezodriven Precision Micropositioning Stage Utilizing Flexure Hinges,” Nanotechnology, Vol. 10, No. 4, p. 394, 1999. [https://doi.org/10.1088/0957-4484/10/4/306]
• Kim, D., Kang, D., Shim, J., Song, I., and Gweon, D., “Optimal Design of a Flexure Hinge-Based XYZ Atomic Force Microscopy Scanner for Minimizing Abbe Errors,” Review of Scientific Instruments, Vol. 76, No. 7, Paper No. 073706, 2005. [https://doi.org/10.1063/1.1978827]
• Ye, S.-D., Min, B.-H., and Lee, J.-K., “Design of Ultra-Precision Micro Stage Using Response Surface Methodology,” Journal of the Korean Society of Manufacturing Process Engineers, Vol. 5, No. 1, pp. 39-44, 2006.
• Choi, J. S., Cui X., Ahn J. H., “A Study on High Speed Control Mechanism of Micro-Depth Using PZT Actuator,” Journal of the Korean Society for Precision Engineering, Vol. 35. No. 1, pp. 103-109, 2018. [https://doi.org/10.7736/KSPE.2018.35.1.103]
• Paros, J. and Weisbord, L., “How to Design Flexure Hinges,” Machine Design, Vol. 37, No. 27, pp. 151-156, 1965.
• Yong, Y. K., Lu, T.-F., and Handley, D. C., “Review of Circular Flexure Hinge Design Equations and Derivation of Empirical Formulations,” Precision Engineering, Vol. 32, No. 2, pp. 63-70, 2008. [https://doi.org/10.1016/j.precisioneng.2007.05.002]
• Jouaneh, M. and Ping, G., “Modeling and Control of a Micro-Positioning Tower,” Mechatronics, Vol. 7, No. 5, pp. 465-478, 1997. [https://doi.org/10.1016/S0957-4158(97)00016-0]
• Choi, J. Y., Eom, S. I., and Kim, J. H., “Optimal Design for Parallelogram Type Flexure Hinge,” Journal of the Korean Society for Precision Engineering, Vol. 32, No. 1, pp. 107-111, 2015. [https://doi.org/10.7736/KSPE.2015.32.1.107]
• Jouaneh, M. and Yang, R., “Modeling of Flexure-Hinge Type Lever Mechanisms,” Precision Engineering, Vol. 27, No. 4, pp. 407-418, 2003. [https://doi.org/10.1016/S0141-6359(03)00045-X]
• Kim, J. H., “Design of Piezo Driven Motion Stage Using Novel Cross Hinge Structure,” Journal of Korean Society of Mechanical Technology, Vol. 14, No. 1, pp. 7-11, 2012. [https://doi.org/10.17958/ksmt.14.1.201202.7]
• Wu, Y. and Zhou, Z., “Design Calculations for Flexure Hinges,” Review of Scientific Instruments, Vol. 73, No. 8, pp. 3101-3106, 2002. [https://doi.org/10.1063/1.1494855]
• Xu, W. and King, T., “Mechanical Amplifier Design for Piezo-Actuator Applications,” Proc. of Innovative Actuators for Mechatronic Systems conference, pp. 1-5, 1995. [https://doi.org/10.1049/ic:19951045]