장착물 자동고정장치의 작동 원리 분석 및 실험적 검증
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
The Store Automatic Fixing Equipment operates as an external force acting on fixing the Store during the flight and as a device designed to prevent the Store from being shaken when the aircraft is flying with the Store. In this paper, we derived the mathematical modeling of the Store Automatic Fixing Equipment through the analysis of the operating principles of the Equipment. The gap occurred by the external vibration forces was calculated through the mathematical model and structure analysis. And then the shape and stiffness design of the wedge, i.e., the Store Automatic Fixing Equipment was derived by the mathematical modeling and structural analysis. We made the Store Automatic Fixing Equipment and took the vibration testing under the aircraft flight conditions. We used the load cell to measure the reaction forces acting on the gap between the Store Automatic Fixing Equipment and the Store. The results of the reaction force measurements were compared with the analysis results of the design and the suitability of the Store Automatic Fixing Equipment’s design was verified based on the analysis.
Keywords:
Store, Automatic fixing equipment, Analysis of operating mechanism, Experimental verification, Wedge키워드:
외부장착물, 자동고정장치, 작동원리의 분석, 실험적 검증, 쐐기1. 서론
항공기 특히, 군용 항공기의 경우에는 비행 중 다양한 임무를 수행하기 위하여 여러 종류의 외부장착물을 장착 한 상태로 비행 임무를 수행하게 된다. 비행기에 장착된 외부장착물이 고정되지 않으면 비행 중 발생하는 진동이나 비행 기동에 의하여 흔들리게 되며 이러한 외부장착물의 흔들림은 비행 안정성에 악영향을 미치게 된다. 또한, 장착물의 흔들림에 의하여 구조물에 충격을 가하게 되어 항공기 기체 구조에 손상을 입힐 수도 있다. 반면에 너무 강한 힘으로 장착물을 고정하게 되면 장착물을 분리하는데 어려움이 발생하게 된다.
따라서, 항공기에 장착된 외부장착물을 비행 중 적절한 하중으로 고정하는 것은 비행 안정성, 구조 건전성 그리고 운용성을 위한 중요한 요소이다.
외부장착물을 고정하는 방법에는 크게 수동고정 방식과 자동 고정 방식이 있으며, 본 논문에서는 항공기 외부장착물을 설계된 목표 선하중(Pre-Load)으로 자동고정 하기 위한 장착물 자동고정장치에 대한 연구결과를 게재한다.
항공 장착물 자동고정장치를 개발하기 위하여 우선 장착물 자동고정장치의 작동 원리를 분석하고, 장착물 자동고정장치를 수학적으로 정식화 하였다.
수학적 정식화를 바탕으로 비행진동에 의한 구조 틈새를 고려하여 목표 선하중(Pre-Load) 발생을 위한 자동고정 장치의 설계 변수를 설정하였다.
구조 틈새의 산출은 항공기의 불규칙 진동 하중2을 정적 가속도화하여 정하중으로 변환한 다음,1 장착물 자동고정 장치 구조물의 유한요소해석에 변환된 정하중을 적용하여 장착물 자동고정장치와 장착물 사이에 발생되는 공간을 산출하였다. 틈새 공간에 물리는 장착물 자동고정 장치의 설계 형상에 따라서 선하중(Pre-Load)이 제어됨을 입증하기 위하여 다양한 선하중(Pre-Load)을 발생하도록 다양한 형상의 장착물 자동고정장치를 제작하였다.
설계된 목표 선하중(Pre-Load)이 발생되는지 장착물 자동고정장치의 설계 신뢰성을 입증하기 위하여 항공기 비행 진동 조건으로 시험을 수행하였고4 로드셀(Load Cell)을 이용하여 자동고정장치에 의하여 발생하는 선하중(Pre-Load)을 측정하였다.3
설계 분석에 의한 계산결과와 시험결과를 상호 비교하여 장착물 자동고정장치 설계의 신뢰성을 입증하였다.
2. 수학적 정식화
2.1 장착물 자동고정장치 수학적 모델링
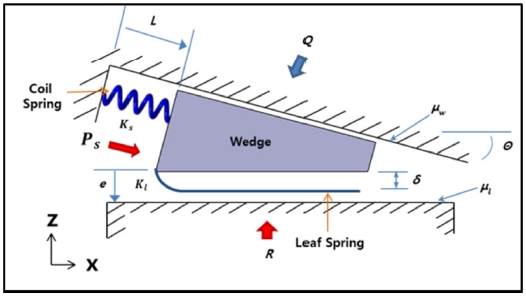
장착물 자동고정장치는 비행 중 장착물에 작용되는 외력에 의하여 Fig. 1과 같이 장착물 자동고정장치의 쐐기와 장착물 사이에 틈새가 발생하게 되면 Coil Spring Force (Ps)에 의하여 쐐기가 틈새에 들어가게 되고 이후 외력이 소멸되면 구조 복원력에 의하여 장착물에 선하중(Pre-Load)이 발생되어 장착물이 흔들리는 것을 방지하게 한다. 여기서 Coil Spring Force에 의하여 쐐기를 밀어주는 힘(Ps)은 식(1)과 같으며, Leaf Spring에 의하여 발생하는 하중(Pl)은 식(2)와 같다.
| (1) |
| (2) |
2.2 쐐기 위치 평형함수
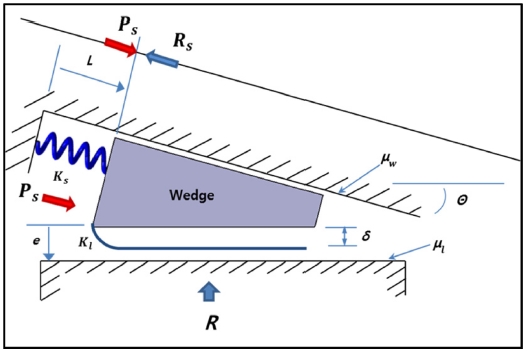
Coil Spring Force (Ps)와 하부면에서 밀어주는 하중(R)에 의하여 쐐기의 위치가 평형을 이루는 함수는 식(3)과 같이 도출되며 다음의 가정으로 식(3)을 단순화할 수 있다.
| (3) |
가정(1) - 쐐기와 쐐기의 상하부의 구조물이 동일한 재질 이라면, 식(4)와 같이 마찰력을 정의할 수 있고, 식(3)은 아래 식(5)와 같이 단순화된다.
| (4) |
| (5) |
가정(2) - 하부면과 쐐기 하부면이 닿는다면, 식(6)과 같이 Leaf Spring 발생 하중과 하부면에서 밀어주는 하중을 정의할 수 있고, 식(5)는 아래 식(7)과와 같이 단순화된다.
| (6) |
| (7) |
따라서, 쐐기가 평형상태인 위치에 의하여 선하중(Pre-Load)이 결정됨으로 아래 식(8)의 평형함수를 도출할 수 있다.
| (8) |
3. 장착물 자동고정장치 설계
3.1 쐐기 각도
비행 중 장착물 자동고정장치에 의하여 장착물에 선하중(Pre-Load)을 발생시키기 위해서는 기본적으로 비행 중 장착물에 작용하는 외력에 의하여 쐐기가 뒤로 밀려나가지 않아야 한다. 외력에 의하여 쐐기가 뒤로 밀려나가지 않기 위해서는 쐐기와 구조물간의 마찰력과 쐐기 각도가 중요한 변수이며 다음과 같이 설계값을 정해야 한다. Fig. 3과 같이 쐐기 아래면에 높은 하중(R)이 작용하였으나 쐐기가 위로 밀려 올라가지 않고 고정이 되기 위해서는 아래 식(9)의 조건을 만족하여야 한다.
| (9) |
여기서 장착물 자동고정장치 구조물의 재질과 도금에 따라서 마찰계수(μ)가 결정되면 상기 식(9) 조건에 맞는 쐐기 각도(θ)를 결정할수 있다.
3.2 Leaf Spring 변형량 결정
3.1절을 통하여 마찰계수(μ)와 쐐기 각도(θ)가 결정되면 쐐기 위치 평형함수 식(8) 은 아래 식(10)과 같이 단순화될 수 있다.
| (10) |
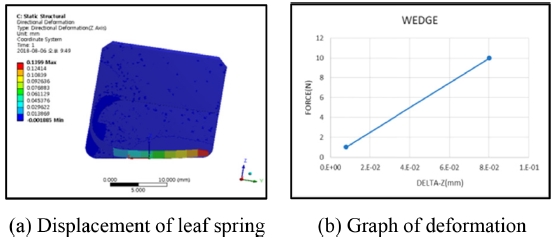
상기 식(10)에서 Ks, Kl Spring 계수는 시행착오법으로 적절한 값을 찾아야 한다. 4.2.2항의 유한요소해석을 통하여 획득한 Kl Spring 계수에 따라 Leaf Spring의 변형량을 확인하여 설계값을 설정한다.
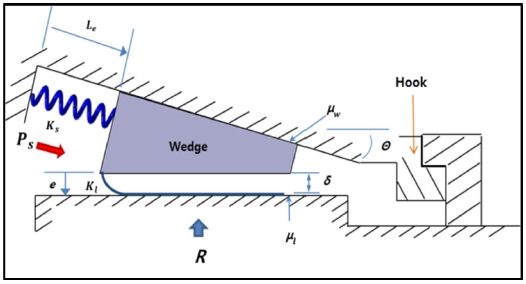
Fig. 3에서의 길이(Le)는 평형상태에서 쐐기의 위치로써 전체 구조물 시스템 설계를 통하여 길이(Le)를 결정할 수 있다. 따라서, 식(10)은 아래 식(11)과 같이 단순화될 수 있다.
| (11) |
α = 0이면 Coil Spring Force (Ps)에 의하여 Leaf Spring이 완전히 눌리는 것을 의미한다.
4장의 장착물에 발생하는 외력에 의한 틈새(변형량)를 고려하여 α 값을 조절하며 최적 δ 설계값을 결정해야 한다.
4. 비행진동에 의한 구조 변형
4.1 장착물에 발생하는 외력 계산
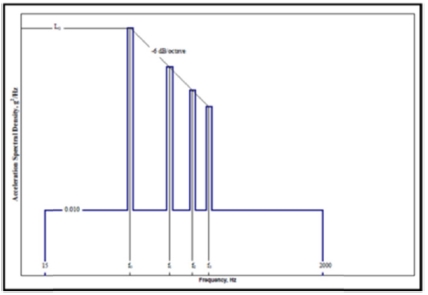
본 시스템은 강체구조물로 재질 및 구조 상 구조물의 고유치가 진동 외란과 반응하지 않는 점을 고려하여 입력 외란에 의한 장착물 자동고정장치는 공진 증폭이 발생하지 않는다고 가정하였다. 비행 진동 Profile에서 입력 진동량 Grms를 계산하였으며, 불규칙 진동의 특성을 고려하여 마이너 지수(Miner’s Index)에 의한 3σ 수준의 진동량 Grms를 장착물 자동고정장치에 입력되는 정적 가속도 하중으로 계산하였다.1
Grms는 Fig. 4의 ASD vs Frequency 진동 프로파일을 바탕으로 ASD 면적의 제곱근으로 계산한다.2
| (12) |
가속도를 계산하기 위하여 입력 불규칙 진동 현상을 분석하여 정적 가속도화 하여 적용한다. 실제 상황에서 자동고정장치는 6 자유도로 운동을 하지만 자동고정장치 동작의 주요 인자는 Z축 진동이며 입증 시험 또한 Z축 1 자유도계 진동시험을 통한 시험 결과값과 비교를 수행하기 때문에 정적 가속도 적용이 가능하다.
또한, 장착물 자동고정장치는 진동에 의하여 지속적으로 쐐기가 틈새로 들어가기 때문에 마이너 지수(Miner’s Index)에 의한 3σ 수준의 진동량에 의한 가속도로 수렴이 될 것으로 판단된다.
따라서, 자동고정장치에 입력되는 하중은 불규칙 진동의 3σ 수준의 가속도 하중을 적용하여 계산한다.
장착물에 발생되는 외력은 비행 진동에 의하여 Z축 방향으로 ±가 발생이 되나 +가 발생될 때는 쐐기가 뒤로 밀려나가지 않고 쐐기의 위치가 유지되고 −가 발생될 때 틈새가 발생이 되어 쐐기가 밀려들어가게 된다.
따라서, 장착물의 중량에 를 곱하여 장착물에 발생되는 외력을 계산하였다.
4.2 유한요소해석 결과
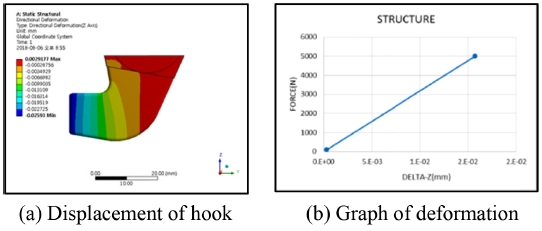
4.1절에서 계산한 비행 진동에 의하여 발생되는 외력으로 유한요소해석을 수행하여 구조물에서 발생되는 변형량을 계산할 수 있다. 메쉬 크기(Mesh Size)는 0.5 mm으로 설정하여 해석을 수행하였고, 960,770개의 절점(Node)와 697,333개의 요소(Element)를 이용하여 해석을 수행하였다. 해석을 위한 경계조건으로, Hook 상부면을 완전고정(Fixed Support) 조건으로 설정하였다.
구조물의 변형에 의하여 발생되는 틈새는 Fig. 3에서 e 값이며 틈새(변형량) 만큼 쐐기가 파고들고 구조물의 복원력에 의하여 선하중(Pre-Load)이 발생하게 된다.
-Z 축 외부하중에 의한 구조물의 변형량을 유한요소 해석을 통하여 측정 하였으며 외부 하중에 의한 변형량은 아래 Fig. 5와 같다.
Fig. 6과 같이 하중에 따른 Leaf Spring의 변형량을 유한요소해석을 통하여 측정한다. 메쉬 크기(Mesh Size)는 0.5 mm으로 설정하여 해석을 수행하였고, 288,907개의 절점(Node)와 200,701개의 요소(Element)를 이용하여 해석을 수행하였다. 해석을 위한 경계조건으로, 구속조건은 쐐기 윗면을 완전고정(Fixed Support) 조건으로 설정하였다. Coil Spring Force (Ps)에 의하여 Leaf Spring이 평형상태에 도달할 때까지 쐐기가 틈새로 이동함으로 Coil Spring Force (Ps)에 의한 Z축 하중을 계산하여 유한요소해석을 통한 Leaf Spring의 변형량을 산출하였다.
5. 진동 시험 결과 및 분석
5.1 진동 시험 결과
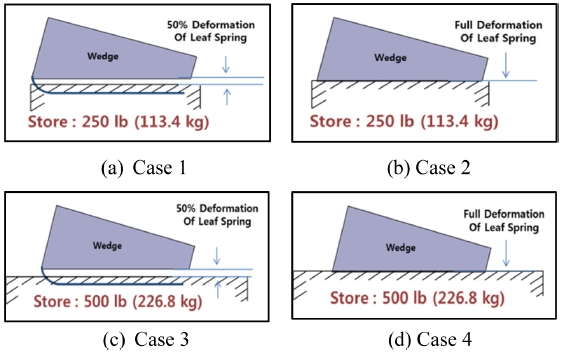
Leaf Spring 변형량에 따른 여러 종류의 장착물 자동고정장치 시제를 제작하였고 외부장착물 중량별로 시험을 수행하였다.
시험 Case별로 시험 초기 조건은 Table 1과 Fig. 7과 같다.
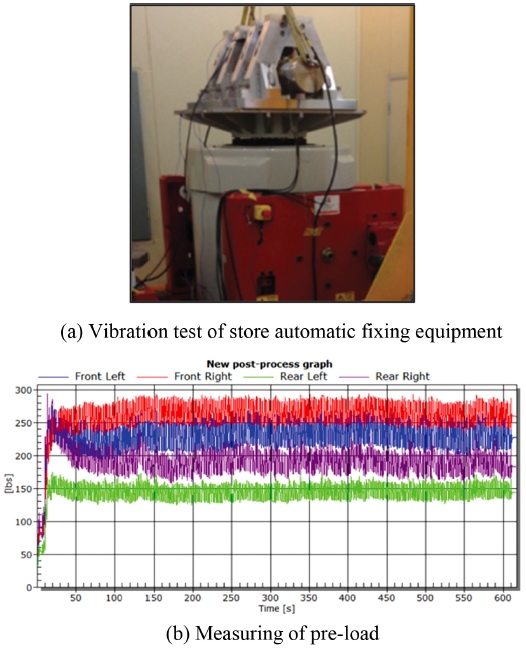
쐐기와 맞닿는 부위의 장착물에 로드셀(Load Cell)을 부착하여 진동에 의하여 발생되는 선하중(Pre-Load)을 Fig. 8(b)와 같이 실시간으로 계측하였다.
Fig. 4의 진동 프로파일을 적용하여 Fig. 8(a)와 같이 Z축으로 진동시험기에서 진동을 가하게 되면 Fig. 8(b)와 같이 선하중(Pre-Load)이 점차 상승하며, 진동을 가하는 시간이 지속되어 최대 가속도가 발생하게 되면 그 이후로는 선하중(Pre-Load)이 상승하지 않고 일정한 값에 수렴하게 된다.3
시험 Case별로 아래 Table 2와 같은 선하중(Pre-Load) 결과를 도출하였다.
5.2 Leaf Spring 변형에 따른 영향성 분석
평형상태에서 Leaf Spring 변형량에 따른 선하중(Pre-Load) 영향을 확인하기 위하여 평형상태에서 Leaf Spring이 절반으로 휘어지는 경우와 완전히 휘어지는 경우의 쐐기를 제작하여 시험을 수행하였다.
Table 2에서 Case 1과 Case 2 그리고 Case 3과 Case 4 결과와 같이 평형상태에서 δ 값의 감소에 따라 쐐기 이동량이 증가함으로 선하중(Pre-Load)이 각각 2.4배, 1.7배로 비례하여 증가하는 결과를 확인하였다.
5.3 장착물 중량에 따른 영향
동일한 진동 조건에서 장착물 중량에 따른 영향을 확인하기 위하여 장착물 중량을 250.0 lb (113.4 kg)와 500.0 lb (226.8 kg) 경우로 두 종류의 장착물을 제작하여 비교 시험을 수행하였다.
Table 2에서 Case 1과 Case 3 그리고 Case 2와 Case 4의 결과와 같이 장착물 중량의 증가에 따라 구조 틈새의 증가에 의한 쐐기 이동량이 증가함으로 선하중(Pre-Load)이 각각 3.0배, 2.0배로 증가하는 결과를 확인하였다.
5.4 시험결과와 계산결과 비교 분석
진동에 의하여 발생되는 선하중(Pre-Load) 의 총하중은 Table 2의 각 Load Cell에서 계측한 하중을 더하여 계산하였다.
그리고 4.1 절을 따라서 최대 선하중(Pre-Load)을 계산하였다. 진동 Profile으로 Grms를 구한 후 불규칙 진동 동적 가속도 값의 3σ 수준을 적용하여 장착물 중량에 따른 최대 하중을 구할 수 있다.1
적용 장착물 중량과 Leaf Spring 변형량에 따른 구조 복원력을 적용하여 하기 Table 3과 같이 최대 선하중(Pre-Load)을 계산하였다.
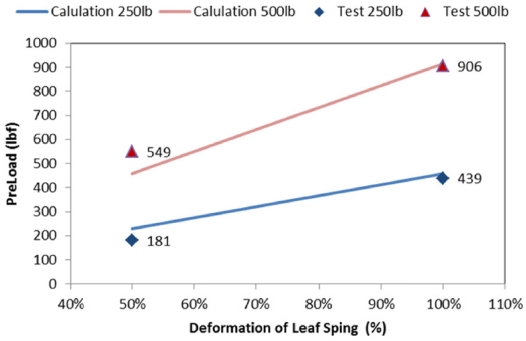
Table 3과 Fig. 9에서 두 결과값을 비교하면 장착물 중량별 그리고 Leaf Spring 변형량별로 선하중(Pre-Load)이 비슷한 경향으로 변하는 것을 확인할 수 있으나 최대 21.0% 정도로 다소 큰 오차가 발생하는 것을 확인할 수 있다.
이러한 오차는 장착물 체결 초기 형상에 따른 영향 그리고 계측 오차 등의 영향으로 인한 것으로 실제 진동 시험 시 이러한 요인들이 계측값에 영향을 주게 된다.
그리고 불규칙 진동의 동적 하중을 정적 하중으로 변환한 것으로, 불규칙 진동 동적 가속도 값의 3σ 수준을 고정장치에 적용되는 정적 가속도로 계산하는 방식이기 때문에 두 데이터 간에 오차가 발생하는 것으로 판단된다.1
6. 결론
본 연구에서는 장착물 자동고정장치의 작동 원리를 분석하여 수학적 모델링을 통하여 평형함수를 도출하였다. 평형함수를 바탕으로 설계 변수를 변화함으로써 선하중(Pre-Load)을 제어할 수 있다는 것을 확인하였고 이를 증명하기 위하여 다양한 선하중(Pre-Load)을 발생하도록 장착물 자동고정장치를 제작한 후 항공기 비행 진동 조건으로 진동시험을 수행하였고 로드셀(Load Cell)을 이용하여 선하중(Pre-Load)을 측정하였다.
불규칙 진동 동적 가속도 통계 분석에 따른 진동에 의한 선하중(Pre-Load) 계산 결과와 진동 시험을 통한 선하중(Pre-Load)이 Fig. 9를 보면 조건에 따라 이론치와 실험치가 아주 일치하며 분석결과와 시험결과의 분석을 바탕으로 설계한 자동고정장치가 신뢰성있다고 판단된다.1
NOMENCLATURE
| Ks : | Coil spring coefficient |
| K1 : | Leaf spring coefficient |
| μ : | Friction coefficient |
| μw : | Friction coefficient of wall |
| μl : | Friction coefficient of leaf spring |
| θ : | Angle of wedge |
| Le : | Distance of wedge at equilibrium condition |
| L : | Distance of wedge |
| e : | Deformation of structure |
| δ : | Height of leaf spring |
| Ps : | Coil spring force |
| Ps0 : | Initial coil spring force |
| Pl : | Leaf spring force |
| R, Q : | Reaction forces |
| ε : | Strain |
| : | Acceleration |
REFERENCES
- Lee, W.-B. and Kim, G.-W., “Random Vibration Analysis for Satellite Design,” Aerospace Engineering and Technology, Vol. 5, No. 2, pp. 102-107, 2006.
- Wang, F. F., “Relating Sinusoid to Random Vibration for Electronic Packaging Testing,” Proc. of Thermal and Thermomechanical Phenomena in Electronic Systems 8th Intersociety Conference, pp. 892-895, 2002.
- Schoppert, T. C., “Dynamic Model of the Interface Reactions in an Aircraft Bomb Rack Due to an External Store,” Department of Mechanical and Aerospace Engineering, pp 20-31, 2002.
- MIL-STD-810G, “Environmental Test Methods and Engineering Guidelines,” United States Department of Defense, 2008.

Research engineer in LIGNex1. His research interest is Dynamics, Structural Analysis and Heat Transfer.
E-mail: jungpil.kim@lignex1.com

Master degree in the Department of Mechanical Engineering, Yonsei University. His research interest is Shock/Vibration and Dynamics.
E-mail: donghun.son@lignex1.com

Research engineer in LIGNex1. His research interest is Composite and Structural Analysis.
E-mail: dhnam1234@lignex1.com

Researcher in Agency for Defense Development(ADD). His research interest is hydraulic system. E-mail: jychoi@add.re.kr

Senior researcher in Agency for Defense Development(ADD). His research interest is structural mechanics.
E-mail: chatory@add.re.kr