포신 수명 증대를 위한 최적 강선 형상 설계


Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
The rifling is applied to most of the conventional gun barrels to stabilize the projectile using the spin. The rifling force (torque) acting on the projectile inside the barrel also wears the rifling itself and shortens the gun lifespan. To reduce the rifling wear, the increasing rifling angle is designed. The starting-part low angle decreases the rifling force while the increased muzzle angle creates the required projectile spin. With the advance of the computer-aided design and manufacturing, a smooth rifling curve is introduced using the Fourier functions. The method shows a high performance in decreasing the maximum rifling forces, but applying the design constraints is limited due to the sinusoidal features of Fourier functions. In this research, a node-point-based rifling-angle design method is introduced. The optimization algorithm and the interpolation method are used to create the smooth profile from the discrete parameters. With the piecewise cubic hermite interpolating polynomial (PCHIP) monotonicity, it is possible to apply various constraints easily while maintaining the design feasibility. To verify the performance, the design results and the comparisons with the previous methods are presented.
Keywords:
Wear, Optimization키워드:
마모, 최적화1. 서론
탄에 회전을 주어 탄도를 안정하게 만들기 위한 강선은 18세기에 개발되어 오늘날까지 대부분의 총포에 적용되어 있다. 초기에 수공업으로 제작되던 강선은 이후 대량생산 체계를 거쳐 오늘날 컴퓨터가 활용된 자동 가공이 가능해졌다. 연소에 의한 가스 압력이 세어나가지 않도록 압착된 상태에서 동시에 탄을 강제로 회전시키기 위해 탄에 가해지는 강선력은 강선 자체도의 수명을 감소시키는데, 수명증대를 위해 탄자가 시작부터 일정한 각도로 휘어진 강선을 통과하는 고정형 강선이 아닌 각도가 서서히 증가하는 증가형 강선이 적용되기 시작했다. 탄체가 강선을 지나가는 것은 직선운동이 회전운동으로 변환되는 비교적 단순한 동작으로 기구학적 모델링이 가능하며, 강선력은 강선의 휜 정도인 강선각, 강선각의 증분과 탄체 운동의 두 요소인 강내압력(후방 추진제연소 가스 압력)과 탄체 속도에 영향을 받는다.1 일반적인 고정형 강선의 경우 탄체가 출발해 강선을 지나 포구로 나가기 전까지 강내압력이 증가함에 따라 강선력이 증가하다가 이후 함께 감소하는 형태로 나타난다. 이에 비해 증가형 강선을 적용하면 강선초기와 중기에 강선의 마모를 줄일 수 있다는 장점이 있는데, 보통 마모가 많이 발생하는 초기와 중기에 강선각을 완화시켜 강선력을 줄이는 방식이다. 이후 강선각을 증가시켜 종말단에서 원하는 회전수로 탄자가 포구를 탈출하게 한다. 증가형 강선의 이런 장점은 이전부터 알려져 있었으며, 1차함수형, 지수함수 증가형 등의 강선들이 적용되어 왔다. 이후 컴퓨터 프로그램 기반의 제작공정이 가능해짐에 따라 기존의 단순한 설계보다 더 강선력을 줄 일 수 있는 복잡한 형태의 증가형 강선설계 방법론이 요구되었다.
Krumman은 1992년에 특허를 통해 최적의 부드러운 곡선 프로파일의 각도 증가형 강선을 설계하는 방법2을 제시한다. 최적곡선을 설계를 위해 고차 푸리에 식의 계수를 최적화 알고리즘을 통해 산출하는 방식을 사용하였다. 이 때 최적화의 목적함수는 강선력의 최댓값이 최소가 되도록 하는 것이며 최대-최소화(Minimax) 문제로 볼 수 있다. 해당 특허에서는 포구 끝단에서 포탄의 안정성이 높아지는 효과를 추가적으로 최적 강선율의 장점으로 제시하였다.
2010년에 차기업 등의 연구3에서는 Krumman의 푸리에 함수 방법론에 낮은 차수의 다항식을 추가하여 함께 최적화하여 강선율을 설계하는 방법을 제안하였다. 이 방법에는 증가형 강선각의 시작부(낮은 각도)에서 종말부(최종 각도)에서 각도의 도함수에 제한조건을 부여할 수 있다는 장점이 있다. 포구 끝에서 탄체가 탈출하기 직전에 지속적으로 증가하고 있는 각도가 이후의 탄도에 악영향을 미칠 것으로 예상될 때에는 해당 연구의 결과가 적용될 수 있다. 한편 위에서 제시한 두 연구는 모두 최대강선력의 최소화를 위해 휴리스틱 최적화 방법을 적용시켜 문제를 해결했다는 공통점이 있다. 이러한 이유는 본 문제에서 목적함수에 포함된 포열의 길이에 대한 탄체의 속도와 강내압력 선도가 비선형성이 강하여 해석적 방식의 적용이 어렵기 때문이다.
비교적 최근에는 2017년에 Sun 등의 연구4에서 가변형 강선의 장점과 실제 적용 결과를 제시하였으나 새로운 방식의 강선설계 방법론은 제시하지 않았다.
본 연구에서는 PCHIP (Piecewise Cubic Hermite Interpolating Polynomial)5를 이용한 노드점 기반의 최적 강선율 설계방법을 제시한다. 본 방법에서는 시작 강선각과 종말 강선각 사이에 특정 수량의 노드를 분포시키고, 단조증가성이 보장되는 보간법을 활용하여 부드러운 곡선을 만들어 내는 방식이다. 기존의 푸리에 계수 설계 방식에 비해 다양한 제한조건을 적용시킬 수 있다는 점이 장점이며, 이에 대해서는 본문에서 설명하였다. 초기에 자유롭게 배치된 노드점들은 최적화 알고리즘을 통해 최대 강선력을 감소시키는 강선율 곡선을 만들어내도록 정렬된다. 강선율 설계에 관해서는 유사한 방식이 적용된 사례가 없으며, 철도 차륜/레일의 형상 설계를 위해 해당 방식이 적용된 연구들이 발표되어 있다.6,7 해당 연구에서는 마모를 저감시키기 위한 최적형상 설계를 수행했으며, 5개의 노드점을 활용하였다.
제시한 방법론에는 노드점의 개수가 설계정밀도의 한계를 고려하여 무수히 많아질 수는 없기 때문에 높은 수준(고차원)의 최적화 알고리즘이 요구되지는 않는다. 다만 노드점들을 크기에 따라 정렬(Sorting)하는 과정이 포함되기 때문에 그라디언트를 이용하는 방식의 최적화는 적용이 불가능하다. 본 연구에서는 최적화 알고리즘으로는 CMA-ES를 사용했다. 이는 무리최적화 PSO (Particle Swarm Optimization)와 비슷한 예측해 분산의 방식으로 10개 이상의 계수의 동시 최적화를 다루는 본 문제에 적합하다고 할 수 있다.
이와 함께 푸리에 함수 기반의 기존에 제시되었던 설계 방식과 비교 결과를 수록하여 본 연구에서 제시하는 설계 방법론의 장점을 보여주고자 한다.
2. 강선 설계
2.1 문제 정의
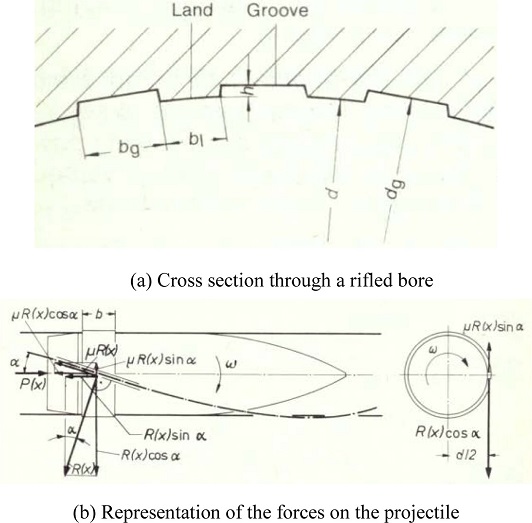
강선력은 탄체가 강선을 따라 회전하며 포강을 진행할 때 강선의 수직방향으로 전단방향으로 작용하는 힘을 의미한다. 이와 같이 작용하는 힘은 지속적으로 강선을 마모시키는 효과를 내게 된다. 강선의 형상과 강선력의 작용구조는 Fig. 1과 같으며, 강선력의 결과식은 식(1)과 같이 표현할 수 있다.1
| (1) |
| (2) |
| (3) |
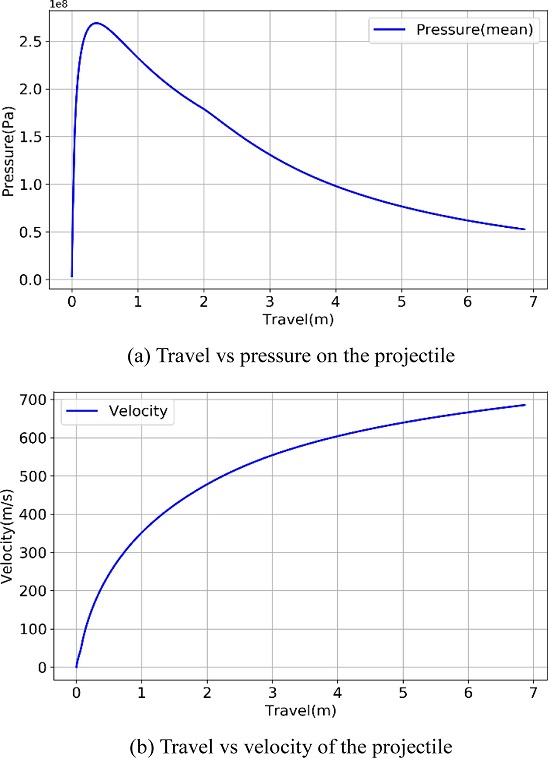
식(1)에서 강선력은 탄체 이동거리에 따른 강선각, 강선각의 도함수, 강내압력, 탄체 속도로 정의되는 것을 확인할 수 있다. 대부분의 화포에서 강내압력 P(x)는 빠르게 최대 압력에 도달한 후 감소하는 추세로, 속도 v(x)의 곡선은 증가율이 낮아지는 증가 형태로 Fig. 2의 예시와 같이 나타난다. 예시는 105 mm 곡사포의 경우이며, 실험을 통해 얻은 결과이다. 이러한 곡선은 이동거리에 대한 간단한 식으로 정의하기 어려우므로, 증가형 강선의 설계문제에서 오일러-라그랑주 방정식을 통한 변분법 역시 적용하기 어렵다.
한편 강선력 프로파일의 설계문제에서 적용될 수 있는 제한조건은 Table 1과 같다. 1번 항목을 제외한 나머지 제한조건은 이전에 수행되었던 푸리에 방식의 증가형 강선설계 방법론에 적용되어있다.2,3
최적 강선율의 설계문제는 이러한 제한조건들을 만족시키며 탄체의 이동 전 구간에 대해 최대로 작용하는 강선력을 감소시키는 문제로 볼 수 있다. 낮은 강선각으로 프로파일을 시작하는 경우 초기의 강선력을 줄일 수 있으나 결과적으로 탈출 강선각까지 큰 기울기를 만들어야 하므로 적절한 시작 강선각을 선정하는 것이 중요한 문제가 된다.
제한조건 1의 단조증가성은 탄체의 회전속도가 감소했다가 다시 증가하는 것이 회전탄대에 악영향을 미치기 때문에 적용되었다. 황동으로 이루어진 회전탄대는 강선으로 인해 소성 변형되어 탈출 이후 강선 형상과 같은 문양이 새겨지게 된다. 강선각이 증가하는 경우, 더 큰 각도로 일정하게 소성변형이 일어나게 되는데, 도중에 각도가 감소하면 이미 소성변형이 일어난 회전탄대에 다시 힘을 가하게 되어 결과적으로 탄대가 소실될 가능성이 있다.
이와 같은 이유로 강선각이 감소하다가 증가하는 설계는 이용되지 않는다. 해당 제한조건은 실제 증가형 강선의 설계와 제작 과정에서 필수적인 조건이지만, 기존의 방법론을 통해서는 적용할 수 없는 문제가 있었다. 이에 대하여 3.2에서 추가적으로 설명하였다.
탈출 강선각을 일정하게 하는 이유는 최종적으로 탄자가 탈출할 때 탄도 안정성을 위해 적절한 값으로 미리 결정된 회전속도를 유지하도록 하기 위함이다. 시작 강선각과 탈출 강선각의 격차를 일정 값 이하로 제한하는 조건은 탄체의 진행과정에서 지나친 강선각의 변화가 회전 탄대를 손상시킬 위험을 방지하기 위함이다. 회전탄대는 황동으로 제작되며 강선모양으로 변형되며 회전을 만들어 내게 된다. 그러나 각도의 변화가 5o 이상으로 클 경우 회전을 만들어 낼 수 있는 살 부위가 남아있지 않아 제 역할을 못하게 되는 현상이 나타난다. 이는 Krumman의 연구에서 제시된 바가 있다.2
제한조건 4번과 5번의 경우, 강선 시작부와 종말부의 강선각도함수가 탄도에 미치는 영향은 밝혀지지 않았으나, 강선 가공 과정에서의 오차에 대한 안전율을 고려하여 기존 연구3에서 적용하였다. 본 연구에서 제시하는 강선설계 방법론을 통해 이러한 제한 조건들 역시 추가적으로 만족시킬 수 있음을 보여주고자 한다.
2.2 설계 방법론
강선율 프로파일의 설계를 위해서 노드점 기반 설계방식을 사용하였다. 강선각 설계문제와 같은 경로 최적화 문제를 경로 사이의 노드를 설정하는 문제로 치환시키면 파라미터 최적화 문제로 치환이 가능하다.
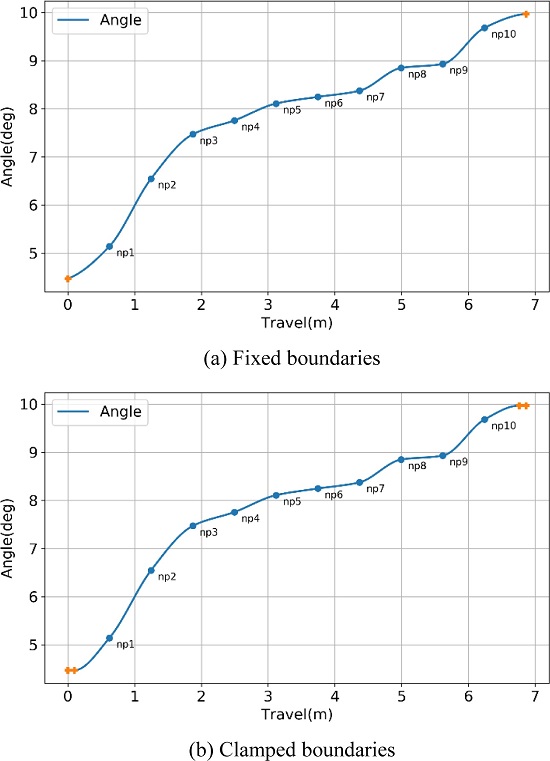
각 노드점들을 부드러운 곡선으로 연결하기 위해서 PCHIP (Piecewise Cubic Hermite Interpolating Polynomial)를 사용하였다. 위의 방식은 1차 미분 가능하도록 하면서 각 점들을 연결하는 방식이며 단조 증가가 보장된다. 시작부와 종말부 사이의 노드들은 최초에 무작위로 배열한 후 크기 순서대로 재정렬 시키는 작업을 수행하게 된다(Fig. 3).
이와 같은 방식의 강선율 프로파일 설계의 또 다른 장점은 노드점 수를 통해 프로파일의 곡률을 변화시키는 효과를 줄 수 있다는 점이다. 실제 포열의 강선 제작에서 공정의 정밀도는 경우데 따라 제한될 수 있다. 본 연구를 통해 제시하는 방법을 통해 공정의 정밀도를 고려하며 프로파일의 곡률을 바꿀 수 있다.
2.1에서 제시된 제한조건은 개별 노드에서 기울기가 연속으로 주어지는 것과 PCHIP의 단조 증가성을 이용하여 시작부와 종말부에 특정 노드점들을 추가하여 정의할 수 있다. Table 2에 해당하는 내용을 나타내었다.
Table 2에서 추가적으로 부여되는 제한조건에 따라 노드점을 추가하여 만족시키는 것을 보여준다. 단조증가함수의 특성상 같은 값의 두 점은 기울기가 0인 직선으로 구성하게 된다. 이것을 이용하여 시작단과 종말단에 기울기에 대한 제한조건을 적용하는 것이 가능하다(Fig. 3).
위에서 정리한 것과 같이 노드점 배치부터 각종 제한조건들을 만족시켰기 때문에 목적함수는 본래 정의된 것에서 수정 없이 사용이 가능하다. 식(4)와 같은 일반적인 최대최소화 문제로 나타낼 수 있다.
| (4) |
2.3 최적화 알고리즘
최적화 알고리즘으로는 CMA-ES (Covariance Matrix Adaptation – Evolutionary Strategy)가 사용되었다. CMA-ES는 분산형 최적화 알고리즘의 일종으로 해 분산의 방식을 진화적으로 변화하는 평균과 공분산으로 정의한 것이다. 대표적으로 PSO (Particle Swarm Optimization)가 해당되는 분산형 최적화 알고리즘에서는 한 차례 또는 수 차례 다수의 초기해(시드)를 뿌리는 과정을 거치게 된다. CMA-ES에서는 이 과정에서 초기해를 평균과 공분산으로 정의되는 다변수 정규분포를 이용하여 분산시키게 된다. 이후 평균과 공분산은 분산된 예상해 집합에서 상위 60%의 해를 활용하여 변화시키게 된다. 이러한 방식은 탐색범위 안에 해가 존재할 경우 해 분포의 공분산을 빠르게 줄여가며 수렴하게 되며, 국소해들이 발생하는 경우 공분산을 유지 또는 증가시키며 지속적으로 해를 탐색하는 과정을 거친다. 고차 최적화 문제에 대해서도 이 알고리즘의 성능은 Hansen에 의해 발표되어 있다.8,9
3. 결과
3.1 강선율 설계안
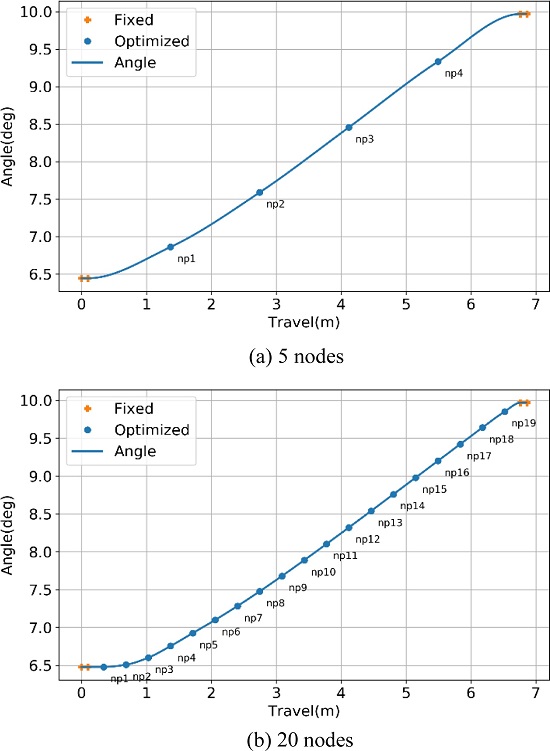
본 연구에서 제시하는 노드점 기반의 최적화 방식은 일반적으로 노드점의 개수가 증가할수록 최대 강선력 감소 성능이 향상되지만, 실제 제작 정밀도를 고려하여 너무 미세한 설계가 되지 않도록 노드점의 개수를 설정해야 한다.
초기에 무작위로 배치된 각 노드점들은 최적화 알고리즘을 통해 배열되고 이후에 부드러운 곡선으로 연결된다. 위의 두 설계안은 고정된 탈출 강선각과 정의되지 않은 시작 강선각이 적용되었으며, 끝 단의 기울기는 0으로 고정되었다. Fig. 5에서 노드점 개수에 따라 다른 두 가지의 설계안을 제시하였으며, 전체적인 형상은 유사하나 노드점이 많아질수록 곡률이 커지는 경향이 있다. 본 연구에서 사용하는 최소 가공 정밀도(5 cm)를 고려하면, 20개의 노드점 설계안에서 노드점 사이를 약 7개의 분할점으로 나누어 제작하게 되며, 따라서 20개의 노드점 설계안도 이론상의 곡선과 유사하도록 제작이 가능하다.
3.2 기존 방법론과의 비교
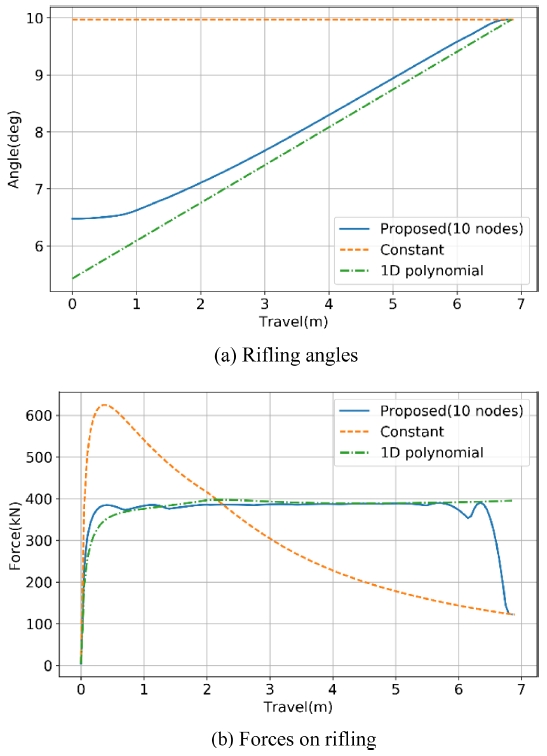
기존 강선율 설계안은 대표적으로 고정형과 1차함수 증가형이 있다. 고정형의 경우 강선의 시작부부터 일정한 강선각이 유지되며, 1차함수 증가형의 경우 같은 비율로 계속해서 증가하는 형상이며, 이 경우에는 종말부에서 강선력의 기울기가 0이 되지 않는다. Fig. 5에서 기존 강선율 설계인 고정형 강선, 1차 함수 증가형 강선과 비교를 수행하였다. 1차 함수 증가형 강선 역시 최대강선력을 가장 최소화하는 설계안이다. 비교를 위한 최적 설계안에는 시작부와 종말부에 강선력의 기울기가 0인 제한조건이 부여되었다.
최대 강선력의 감소를 목적함수로 하는 최적 강선설계안이 적용된 경우에 강선력 프로파일은 Fig. 6(b)와 같이 사다리꼴 형태로 윗쪽 프로파일이 납작한 형상으로 나타나게 된다. Table 3에서 기존의 설계안과 비교한 내용을 나타내었으며, 제한조건을 만족하면서도 더 우수한 강선력 감소 효과를 보여주는 것을 확인할 수 있다.
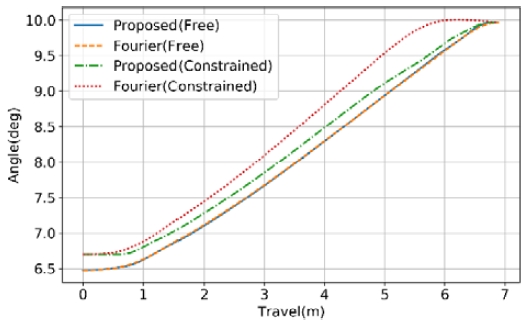
노드점 기반의 설계방식에는 선행연구에서 제시된 푸리에 함수 방식에 비해 각종 제한조건을 적용하기 쉽다는 장점이 있다. 실제로 적용되지는 않았지만, 예를 들어 중간 지점에 특정 각도를 유지하도록 하는 설계안 역시 가능하다. 푸리에 방식의 설계안의 경우 강선 시작부나 단조 증가하도록 하는 제한조건을 적용하기 위해서는 최적화 함수에 페널티를 적용하는 방식을 사용해야 해야 하는데, 이 경우 강선력 최적화 성능에 영향을 미치게 된다. Fig. 7에서 시작 강선각을 제한하는 경우에 푸리에 방식과 노드점 방식을 비교한 결과를 보여준다.
제한조건이 주어지지 않는 경우에는 두 가지 설계 방법론 모두 양호한 결과를 보여주며, 이는 다양한 설계방식을 통해서도 거의 유사한 형태를 보이는 최적 설계이다(Table 4). 그러나 제한 조건이 주어지는 경우에 푸리에 방식의 설계안에서는 종말부 근처에서 강선율이 감소하는 현상이 나타나며, 실제 제작에 적용하기 어렵게 된다. 그러나 본 연구의 설계 방법론을 통해서는 항상 제한조건과 단조증가성을 보장하는 강선율 프로파일의 생성이 가능하다.
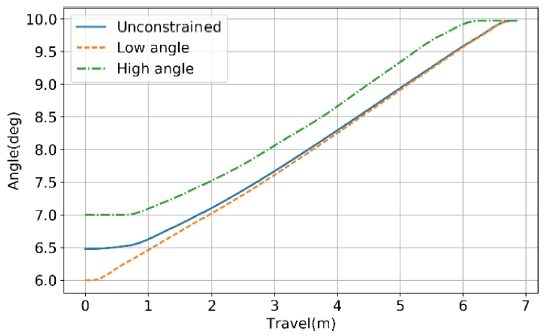
Fig. 8에서는 제시한 방법론을 통해 다양한 시작각에 대해서도 강선력 프로파일을 생성할 수 있음을 보여준다. 실제 설계 과정에서 마모 수명뿐만 아니라 여러 가지 제한 조건을 고려하는 경우에 유용함을 보여준다.
4. 결론
포탄이 포강을 지나갈 때의 높은 열과 압력은 지속적으로 강선을 마모시킨다. 포신의 수명을 늘리기 위해서는 특정 부위에 높은 강선이 작용하지 않도록 하는 증가형 강선 설계가 요구된다. 본 연구에서는 기존의 푸리에 함수를 활용하는 계수최적화 방식에서 벗어나 PCHIP를 활용하여 최적으로 배열된 노드점을 부드러운 곡선으로 연결하는 방식의 설계방법을 제시하였다. 기존 설계방법에 적용되는 제한조건을 모두 만족시키면서 추가적으로 강선율의 단조증가성을 보장할 수 있도록 한 것이 본 설계방법론의 장점이다. 최대 강선력을 감소시키는데 있어서 기존 설계안들과 비교했을 때 동등 이상의 성능을 보였고, 기존의 설계방법으로 적용이 불가능했던 단조증가성을 보장하는 제한조건을 추가시킬 수 있음을 통해 방법론의 유용성을 제시하였다.
NOMENCLATURE
| bg : | Groove width |
| bl : | Land width |
| h : | Groove depth |
| bg : | Diameter above the grooves |
| d : | Caliber and Projectile diameter |
| Jp : | Moment of inertia of projectile about longitudinal axis |
| mp : | Mass of projectile |
| P(x) : | Gas force on the base of projectile at point in the bore |
| p(x) : | Pressure on the bass of projectile at point in the bore |
| R(x) : | Rifling force on the base of projectile at point in the bore |
| v(x) : | Velocity of projectile at point in the bore |
| x : | Longitudinal direction of bore |
| xi : | Starting point in the bore |
| xf : | End point in the bore |
| y : | Unwound peripheral direction |
| α(x) : | Rifling angle at point in the bore |
REFERENCES
- Backstein, G., “Handbook on Weaponry,” Rheinmetall GmbH, D, pp. 576-578, 1982.
- Krumm, H., “Gun Barrel Equipped with Optimized Rifling,” Google Patents, https://patents.google.com/patent/US5077926A/en, (Accessed 12 JUL 2018)
- Cha, K.-U., Cha, Y.-H., Lee, S.-B., and Cho, C.-K., “A Study on the Optimal Design of Rifling Rate,” Journal of the Korea Institute of Military Science and Technology, Vol. 13, No. 6, pp. 998-1005, 2010.
-
Sun, J., Chen, G., Qian, L., and Liu, T., “Analysis of Gun Barrel Rifling Twist,” Proc. of AIP Spring Conference, No. 1, P 020096, 2017.
[https://doi.org/10.1063/1.4982461]

-
Fritsch, F. N. and Carlson, R. E., “Monotone Piecewise Cubic Interpolation,” Society for Indusrtial and Applied Mathematics on Numerical Analysis, Vol. 17, No. 2, pp. 238-246, 1980.
[https://doi.org/10.1137/0717021]

-
Choi, H.-Y., Lee, D.-H., Song, C.-Y., and Lee, J.-S., “Design of Wheel Profile to Reduce Wear of Railway Wheel,” Journal of the Korean Society for Precision Engineering, Vol. 29, No. 6, pp. 607-612, 2012.
[https://doi.org/10.7736/KSPE.2012.29.6.607]

- Choi, H. Y., Seo, J. W., Byon, S. K., Kim, Y., Ma, J. B., et al., “Wheel Profile Design Suitable for Dual Rail Profile,” Proc. of KSPE Autumn Conference, pp. 753-754, 2014.
-
Hansen, N., Müller, S. D., and Koumoutsakos, P., “Reducing the Time Complexity of the Derandomized Evolution Strategy with Covariance Matrix Adaptation (CMA-ES),” Evolutionary Computation, Vol. 11, No. 1, pp. 1-18, 2003.
[https://doi.org/10.1162/106365603321828970]

-
Hansen, N. and Kern, S., “Evaluating the CMA Evolution Strategy on Multimodal Test Functions,” Proc. of Parallel Problem Solving from Nature International Conference, Vol. 8, pp. 282-291, 2004.
[https://doi.org/10.1007/978-3-540-30217-9_29]