블레이드 실험 및 구조해석을 통한 소형풍력발전기 블레이드 구조 안정성 평가와 블레이드 설계 개선
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
This paper examines the stability of the blades that convert the wind kinetic energy into the mechanical energy among the small wind power-generation systems, and proposes the design improvement for blades with a higher rigidity and a lighter weight than the conventional blades. The composite-specimen tensile test and static-load test are conducted to verify the reliability. To design the lightweight blade with the high stiffness, the displacement and the safety factor of the blade composed of the composite material are calculated from the structural-analysis results, and the optimal dimensional and material designs are performed. The optimal design parameters are selected by the shear-web lamination angle and the lamination thickness. The objective function is selected by the safety factor and the weight. For the optimum material design, the GFRP is converted into the CFRP. In this paper, the structural improvement is performed by optimizing the dimensional and material designs, the blade stiffness and weight are redesigned and compared with those of the designed blades, and the structural stability of the redesigned blades is also examined.
Keywords:
Small wind turbine, Composite blade, Tensile test, FEA, Structural design키워드:
소형풍력발전기, 복합재 블레이드, 인장 시험, 유한요소해석, 구조설계1. 서론
국내 소형풍력터빈 시장의 확장으로 소형 풍력터빈 개발의 필요성이 증가하고 있고, 시스템의 안정성 확보 및 기술개발이 필수적인 요소이다. 하지만 국내 소형풍력시장은 상대적으로 규모가 작으며 대형풍력터빈 비해 기술력이 낮은 편이다.
본 연구는 풍력발전 시스템 중 바람의 운동에너지를 기계적 에너지로 변환하는 풍력발전용 블레이드(Wind Turbine Blade)의 구조 안정성 평가 및 설계개선을 목적으로 수행하였다. 이러한 블레이드의 구조재료는 비강도(Specific Strength), 비강성(Specific Stiffness) 및 피로특성 등이 우수한 복합재료가 주로 사용되며, 기본구조는 외부의 표피(Skin), 내부의 시어 웹(Shear Web), 폼(Foam) 등으로 구성된다. 이러한 복합재로 적층 되어 있는 블레이드는 이방성 재질이기 때문에 주로 유한요소법(FEM)을 사용하여 구조해석을 수행한다.1,2 본 논문에서는 구조해석을 검토하기 위해 상용 소프트웨어인 Abaqus3를 이용하여 극한조건에서의 해석을 수행하였다. 그러나 시뮬레이션을 통한 구조 해석은 입력 값에 대한 의존도가 높아서 정확성에 대한 검증이 요구된다. 이에 따라 시편 인장시험 규격인 ISO 5474를 통해 복합재 인장시편시험을 하여 재료의 물성에 대한 검증을 수행하였다. 또한, 설계된 블레이드의 안정성 검증과 시뮬레이션 해석결과 비교를 위해 소형 풍력터빈 관련 국제 규격인 IEC 61400-25에서 규정된 실규모 구조 시험(Full Scale Structural Test)를 수행하였다.
본 연구에서는 기존 블레이드의 굽힘 테스트와 구조해석을 통해 구조 안정성을 평가 하였고, 설계개선을 위해 시어 웹의 두께에 따른 굽힘강도를 분석하여 기존 블레이드보다 경량화된 블레이드를 설계하였다. 풍력터빈용 블레이드의 대한 기존연구는 대부분이 중대형 블레이드의 구조해석과 전체적인 반응을 고려하는 것에만 집중되어 있으며 소형 풍력터빈용 블레이드에 대한 설계 및 해석에 대한 연구는 거의 없다.7 또한 풍력발전기의 특성상 설치 시 장기간 작동되며 유지보수가 어렵기 때문에 연구 단계에서의 높은 신뢰성을 요구된다.8 따라서 구조적으로 강성이 높고 경량화 된 블레이드가 필요하다. 이러한 점을 고려하여 구조해석 결과로부터 복합재료로 구성된 블레이드의 변위량과 강도 비를 계산하고 이를 통해 중량 최적설계와 재료변경을 하여 설계개선을 수행하였다.
본 논문에서 블레이드 중량 최적설계를 위해 사용 소프트웨어인 Isight9를 사용하였다. 소형 풍력터빈용 블레이드의 중량 감소를 위해 블레이드의 구조에서 굽힘에 대한 하중을 지지하고 있는 시어 웹으로 최적설계를 수행하였다. 중량 최적설계 시 설계변수는 시어 웹의 두께로 선정하였고, 목적함수는 안전계수와 중량으로 선정하였다. 시어 웹의 적층 두께에 따른 안전계수와 중량을 분석하여 기존 블레이드보다 최소로 요구되는 안전계수를 만족하고 경량화된 블레이드의 재설계를 수행 하였다. 또한, 재료변경을 위해 기존 블레이드에 적층된 GFRP (Glass Fiber Reinforce Plastics)에서 CFRP (Carbon Fiber Reinforced Plastics)으로 변경하여 강성이 높고 경량화 된 블레이드를 재설계하였다.
2. 기존 블레이드 해석 및 시험
본 연구에서 사용된 풍력발전기의 사양은 정격 풍속 12 m/s, 정격 용량 10 kW, 로터 지름 7.5 m, 제어 방식은 Furling이며 수평축 3 엽 블레이드 소형풍력발전기이다.
2.1 복합재 인장시편 시험
복합재로 구성된 블레이드의 물성에 대한 검증을 수행하기 위해 ISO 547-1, 4, 5의 규정된 절차에 따라 복합재 인장시편 시험을 수행 하였다.
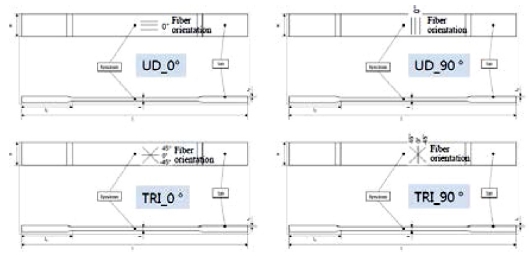
본 연구에 사용된 블레이드는 GFRP (Glass Fiber Reinforced Plastics)로 적층 되어 있다. GFRP는 단축 UD (Unidirectional)과 삼축 TRI (Tri-Directional)로 구성되어 있으며 UD의 경우 0°, 90°로 시편을 제작하였으며 TRI의 경우 0°, 45°, 90°를 0°, 90°로 등가하여 시편을 제작하였다. 시편의 타입은 UD_ 0°, 90°, TRI_0°, 90°로 총 4종류 이며 시편 수는 5개로 시험을 진행하였다. Fig. 2은 GFRP 인장시편에 대한 도면을 나타내고 있으며 Table 1은 시편 타입 별 너비, 전체 길이, 두께를 나타낸 것이다.
인장시편시험 조건과 방법으로 시험장치는 810 MTS (Material Test System, Load Cell 100 kN)과 MM (SYSTEM 7000, Maximum 88 ch)을 사용하였고 Fig. 3은 인장시험 장치를 나타낸 것이다. 시험 속도는 1 mm/min으로 하였고, 데이터 측정 속도는 10 Hz (SYSTEM 7000)이다. 변형률 측정 방법으로는 Strain Gages를 선택하였다. 시험 환경은 대기온도 -25°C, 상대 습도 50% 이하에서 실시하였다. Table 2는 시편인장시험 결과로서 시편 타입별 인장강도, 탄성계수, 포아송 비를 나타내며 5개 시편의 평균값으로 표시하였다.
2.2 정하중 시험
블레이드 구조 안정성 평가를 위해 IEC 61400-2에서 극한 하중 상태인 Case H (Parked Wind Loading)의 조건을 적용하여 규정된 절차에 따라 소형풍력 발전 블레이드 정적 성능 측정 (Measurement of Static Structural Performance for Small Wind Turbine Blade)을 수행하였다.
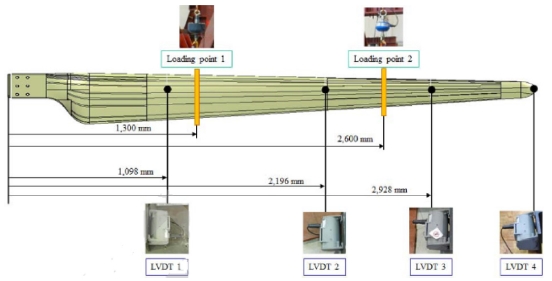
정하중 시험은 Positive Flapwise Test를 실시 하였으며 극한하중 시험과 블레이드가 파손이 발생할 때까지 하중을 부하하는 파괴시험을 수행하였다. 시험 방법으로는 블레이드의 연결 부를 지그에 고정하고 연결 부로부터 1,300 m, 2,600 m 떨어진 위치에 폭 50 mm 의 하중부하장치를 설치하여 하중을 부하하였다. 이때 사용된 계측기는 부하하중 측정용 로드셀(Loadcell)을 사용하였고 변위 측정을 위해 LVDT (Linear Variable Displacement Transducer)를 사용하였다. Fig. 4는 Loading Point 와 LVDT의 설치 위치를 나타낸 것이고 Fig. 5는 Positive Flapwise Test 준비상태를 나타낸 것이다. 총 3번의 시험을 통해 시험하중, 변위, 변형률을 측정하였고 파손이 발생할 때까지 하중을 증가 시켜 파손하중을 얻을 수 있다. 블레이드 파단 시험 결과 블레이드의 표면에서 파손이 발생한 위치를 확인하였다.
2.3 구조해석
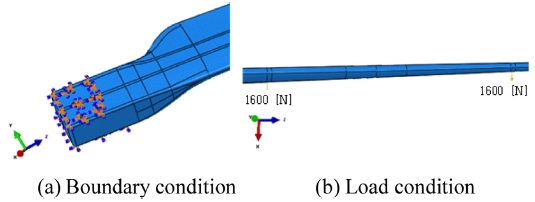
10 kW소형 풍력발전기 복합재 블레이드의 구조해석 신뢰성을 검토하기 위해 상용 소프트웨어인 ABAQUS를 사용하여 정하중 시험과 동일한 극한 하중 조건에서 굽힘 해석(Bending Analysis)을 수행하였다. 블레이드 형상은 두께의 수치가 작기 때문에 쉘 요소(Shell Element)로 모델링 하였고, Elastic의 Type로 Lamina로 설정하여 적층하였다. 또한, 메쉬(Mesh)는 S4R 29110개, S3 331개로 총 29,441개이고, 절점(Node)의 개수는 28,910개이며 Fig. 6에 나타냈다. 그리고 Fig. 7(a)와 같이 경계조건(Boundary Condition)은 블레이드 연결 부에 볼트 체결 면을 X, Y, Z 방향 및 X, Y, Z 회전 방향에 구속조건을 부여 하였고, Fig. 7(b)와 같이 하중조건(Load Condition)은 시험에 사용된 하중부하장치 위치와 하중을 동일하게 하여 해석을 수행하였다.
2.4 시험 및 해석 결과
정하중 시험은 설계하중의 0 - 100%까지 10% 간격으로 하중을 작용한 후 파손이 발생하지 않을 경우 파손이 발생할 때까지 하중을 증가시켰다. 극한 하중 조건에서의 정하중 시험은 총 3번에 걸쳐서 시행 하였으며 블레이드의 연결부로부터 1098 mm, 2196 mm, 2928 mm, 3659 mm에 위치한 변위량을 측정하였고 설계하중의 100%에 대해서 Table 3에 나타내었다. 또한, 파손이 발생할 때까지 하중을 증가시켰을 때 파손 위치는 시어 웹이 끝나는 단에서 발생하였고, 하중부하장치가 설치된 Loading Point 1, 2에 설계하중의 170%에 해당하는 각 2720(N)에서 파손되는 것을 확인할 수 있었다.
2.4.2.1 정하중 해석
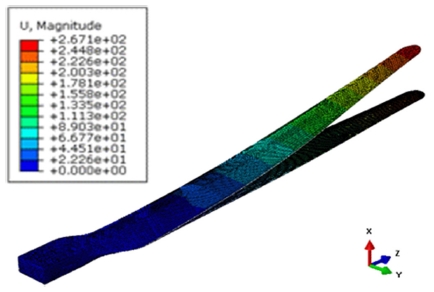
복합재로 구성된 블레이드에 대해서 정적해석(Static Analysis)을 수행하였다. 해석결과 블레이드의 끝단에서 267 mm의 변위가 발생하였고, Fig. 8에 나타내었다. 또한, 블레이드 연결 부에서 최대응력(Maximum Stress)이 분포함을 확인할 수 있다.
복합재료는 등방성 물질이 아니므로 일반적인 등방성 물질에 대한 파손이론 적용이 불가능하다. 따라서 블레이드와 같은 이방성 재질에 대표적으로 사용되는 Tsai-Wu 파손이론을 적용하여 안정성 평가를 수행하였다. Tsai-Wu 파손이론을 정리하면 Tsai와 Wu는 응력장(Stress Space) 내에 파손면(Failure Surface)이며 다음과 같이 식(1)의 형태로 존재한다고 가정한다.6
| (1) |
Fi: Second Rank Strength Tensor
Fij: Fourth Rank Strength Tensor
식(1)의 좌변은 파손지수(Failure Index)라고 불리며, 좌변이 1과 같거나 큰 경우 파손이 발생한다고 판단 한다. 본 연구에 사용된 블레이드의 경우 극한하중조건을 적용한 해석 결과 Fig. 9을 통해 파손지수가 1보다 작은 0.48이며 이로부터 기존에설계된 블레이드는 안전함을 확인할 수 있다.
2.4.2.2 모달 해석
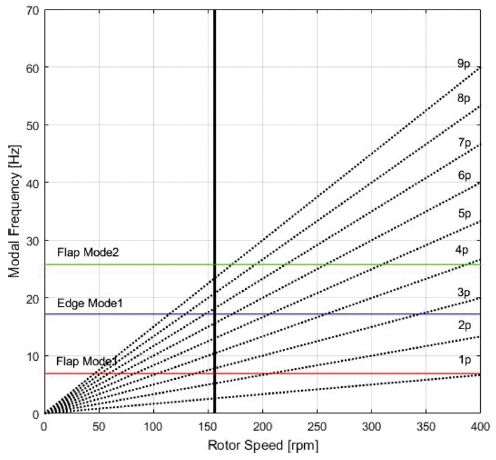
풍력발전기는 회전구조물로 발전기 구동속도 및 풍속의 변화 등에 따라 진동이 발생하게 되므로 공진(Resonance)을 피하도록 설계되어야 한다. 중량과 강성이 있는 구조는 고유 진동수(Natural Frequency)가 존재하며 고유진동수와 외란 진동수(Disturbance Frequency)가 일치 하는 부분에서 공진이 발생하게 된다. 공진 발생 시 응력과 변형이 순간적으로 증가하여 구조적으로 불안정한 상태가 된다. 이러한 공진의 유무를 판단하기 위해 모드해석을 통해 Fig. 10과 같이 블레이드 회전속도에 따른 모드의 고유 진동수와 블레이드 회전속도의 배수와의 관계를 Campbell Diagram으로 나타내었다. 정하중해석과 같은 경계조건 상태이며 그 결과 Flap 1차 모드에서는 6.93 Hz, Edge 1차 모드에서는 17.18 Hz, Flap 2차 모드에서는 25.86 Hz 발생하였다. 본 논문의 대상인 3엽 블레이드의 경우 1배수(1p)의 공진 가능성을 검토하여야 한다. 관심 대상인 Flap 1차 모드 고유 주파수와 1배수 선과 정격 회전속도 156 rpm과 비교한 결과 충분한 차이가 발생하는 것을 그림을 통해 확인할 수 있다. 기계구조물의 공진 여부를 판단할 경우 일반적으로 고유주파수와 외란주파수의 간격이 5% 이상이라는 기준을 만족하는 것을 알 수 있다.2 따라서 본 논문에 사용된 블레이드는 공진이 발생하지 않는 것을 확인할 수 있다.
2.4.2.3 좌굴 해석
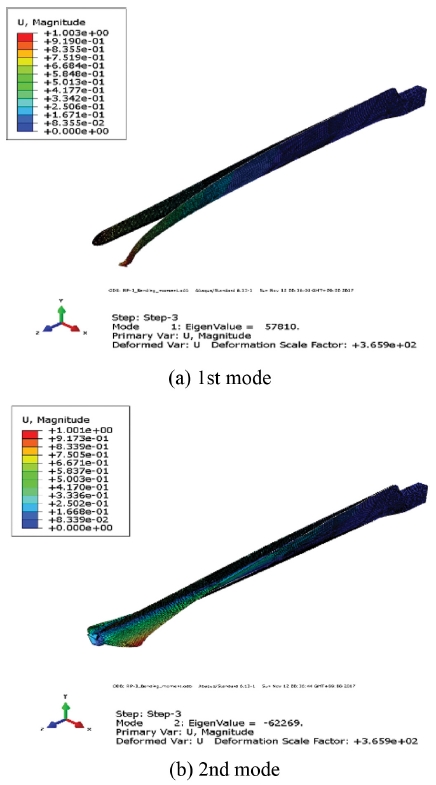
가로에 비해 세로의 길이가 긴 구조물은 축 방향에 작용하는 압축력의 크기가 작은 경우 일반적으로 하중을 받아 수축을 하게 되나, 압축력의 크기가 임계값을 초과하게 되면 가로 방향으로 국부 변형이 발생하여 좌굴(Buckling) 현상이 발생한다. 블레이드의 경우 세장부재(Slender Member)의 형태를 가진 구조물로 대변형 상황에서 심각한 파손 결과를 가져온다. 그러므로 구조 안정성을 평가하기 위해 좌굴해석은 필수요소 중 하나이다. 임계하중의 경우 Fig. 11과 같이 단위하중이 작용한 좌굴해석을 통해 1차 모드 57.8 kN, 2차 모드 -62.3 kN이 발생하는 것을 확인할 수 있고, 압축력의 경우는 블레이드의 끝단에서 1.5 kN의 하중이 발생한다. 계산결과 1차 모드에서의 BLF (Buckling Load Factor)는 38.7, 2차 모드에서의 BLF는 -41.7으로 IEC 61400-2에 규정한 안전계수와 비교하여 안전함을 확인할 수 있다.
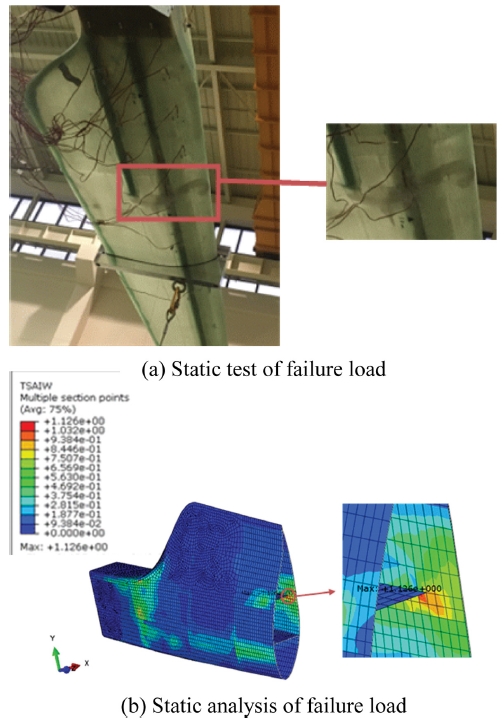
해석 결과의 신뢰성 검증을 위해 동일한 조건에서 결과 비교 및 분석을 하였다. 시험과 해석결과를 비교하기 위해 극한 하중조건에서 블레이드 연결부로부터 일정한 위치의 변위량을 비교하여 오차율을 Table 4에 나타내었다. 시험 값과 해석결과 블레이드 변위량의 오차율이 7%이하로 발생하는 것을 확인 하였고, 이를 통해 해석 결과 대한 신뢰성을 검증하였다. 실제 시험에서 파손이 발생한 지점에 대해서 Fig. 12(a)에 나타내었다. 또한 정하중 시험을 통해 나온 설계하중의 170%에 해당하는 파손하중 각 2721, 2708 N을 구조해석에 적용하여 파손위치와 파손지수가 최대로 발생하는 것을 Fig. 12(b)를 통해 확인하였다. 파손이 발생한 결과와 해석을 통해 파손이 예상되는 영역을 비교한 결과 실제 파손이 일어난 위치와 동일한 위치에서 파손지수가 1을 넘어 파손이 발생함을 확인하였다.
3. 블레이드 설계개선
3.1 중량 최적설계
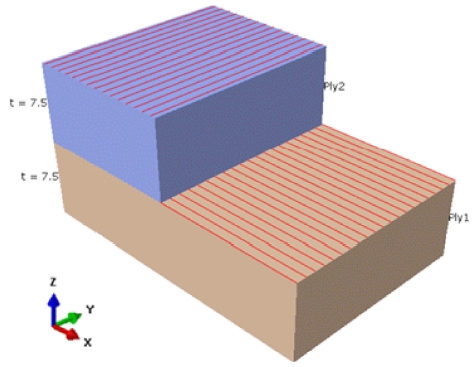
시어 웹의 중량 최적설계를 수행하기 위해 설계변수는 적층 두께로 ply 1, 2를 선정하였고 Fig. 12를 통해 확인 가능하다. 설계 범위는 시어 웹의 ply 1, 2의 두께를 각각 2.5 mm에서 7.5 mm까지 선정하였고, 간격은 1 mm로 설정하였다. 설계 제한조건으로 IEC 61400-2에 7.8.1.1에 해당하는 극한하중에 대한 부분 안전계수 1.35에 정하중 시험과 구조해석의 오차율을 고려해 안정계수 10%를 더한 1.49로 선정하였다. 또한 목적함수는 중량으로 선정하였다. 시어 웹의 적층두께에 의해 계산되는 중량 최적설계 문제를 정식화하여 나타내면 식(3)과 같이 표현된다.
| (2) |
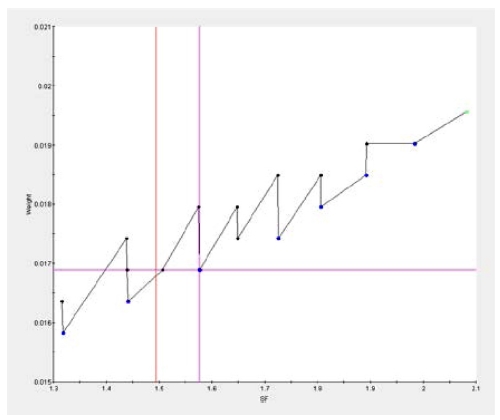
중량 최적설계 총 18회 실시되었고 그 중 제한조건을 만족하는 하여 설계가능 한 값이 13개였다. Fig. 13을 통해 중량과 안전계수와의 관계를 확인할 수 있으며, 빨간색 선은 제한조건을 의미하고 분홍색선은 최적 값을 나타낸다.
중량 최적설계를 통해 시어 웹 적층두께의 경우 ply 1, 2가 각각 3.5 mm, 6.5 mm일 때 중량이 최소가 되는 것을 확인 하였고, 스파 캡의 경우 제작 특성상 기존 블레이드에서 스파 웹의 두께 1 mm보다 얇게 제작하는 것은 불가능하기 때문에 중량 최적화를 적용하지 않았다. 중량 최적설계에 대한 결과는 설계 전 블레이드와 최적설계 후 블레이드의 전체중량과 설계변수를 비교하여 Table 5에 나타내었다. 비교 결과 규격에서 요구하는 안전계수를 만족하는 조건에서 전체 중량은 13.7%, 시어 웹의 중량은 33.6% 경량화 된 모델을 도출하였다.
3.2 재료변경
기존 블레이드에 사용된 GFRP에서 CFRP로 변경한 재료변경결과 CFRP를 적용한 블레이드의 전체 중량은 14.63 kgf으로 GFRP가 적용된 기존 블레이드 전체 무게 19.56 kgf보다 25% 경량화 된 결과를 확인하였다. 또한 기존 블레이드의 안전계수 2.08에 비해 CFRP가 적용된 블레이드의 안전계수는 3.57로 향상된 결과를 얻을 수 있었고, 블레이드의 끝단에서 발생한 변위는 기존 블레이드 267 mm에서 CFRP가 적용된 블레이드 60 mm로 설계 전 블레이드의 변위에 비해 설계 후 블레이드의 변위가 77% 감소된 것을 확인 하였다.
3.3 설계개선
중량 최적설계와 재료변경이 적용된 블레이드의 안정성 검토를 수행하였다. 앞서 수행한 기존 블레이드 안정성 검토와 같은 방법으로 극한하중에서 정적해석, 모드해석, 좌굴해석을 수행하였다. 정적해석 결과는 파손지수가 0.28로 1보다 작아 극한하중에서 파손이 발생하지 않는 것을 확인 하였다. 모드해석 결과는 Flap 1차, Edge 1차, Flap 2차 고유 진동수는 각각 17.17 Hz, 46.01 Hz, 64.43 Hz가 발생하며, 공진에서 안전함을 확인할 수 있다. 좌굴해석 결과는 1차 모드 144 kN, 2차 모드 -156 kN가 발생하였고, BLF는 1차, 2차 모드에서 각각 96, 104로 좌굴에서 안전함을 확인 하였다.
본 논문에서 중량 최적설계와 재료변경이 적용된 블레이드의 설계개선 결과 블레이드의 전체 중량은 12.68 kgf으로 기존 블레이드 전체 무게 19.56 kgf보다 35% 경량화 되었고, 기존 블레이드의 안전계수 2.08에 비해 설계개선 된 블레이드의 안전계수는 3.56으로 향상된 블레이드를 재설계 하였다.
4. 결론
본 논문의 10 kW급 소형풍력발전기 블레이드 구조 안정성 평가 및 설계개선에 대한 결론은 다음과 같다.
(1) 구조해석에 대한 신뢰성을 위해 복합재 인장시편 시험을 통해 물성치를 확보 하였고, 블레이드 정하중 시험을 해석과 비교하여 오차가 거의 발생하지 않는 것을 검증하였다.
(2) 중량 최적설계를 통해 시어 웹 적층두께의 경우 규격에서 요구하는 안전계수를 만족하는 조건에서 ply 1, 2가 각각 3.5 mm, 6.5 mm일 때 중량이 최소가 되는 것을 확인하였다.
(3) 중량 최적설계 후 블레이드와 기존 블레이드 비교 결과 전체 중량은 13.7%, 시어 웹의 중량은 33.6% 경량화 된 모델을 도출하였다.
(4) 재료변경 결과 CFRP를 적용한 블레이드의 전체 중량은 GFRP가 적용된 기존 블레이드 전체 무게보다 25% 경량화 된 결과를 확인 하였다. 또한 기존 블레이드의 안전계수 2.08에 비해 CFRP가 적용된 블레이드의 안전계수는 3.57로 향상된 결과를 얻을 수 있었다.
(5) 치수최적설계와 재료변경이 적용된 블레이드의 설계개선 결과 블레이드의 전체 중량은 12.68 kgf으로 기존 블레이드 전체 무게 19.56 kgf보다 35.2% 경량화 되었고, 기존 블레이드의 안전계수 2.08에 비해 설계개선 된 블레이드의 안전계수는 3.56으로 향상된 블레이드를 재설계 하였다. 또한 치수최적설계와 재료변경이 적용된 블레이드의 안정성 검토를 수행하였다.
(6) 본 연구를 더욱 발전시키기 위해서는 블레이드의 구조안정성을 위한 피로해석, 블레이드의 스킨에 대한 구조 최적화, 공력 특성을 고려한 형상최적화가 동시에 수행되어야 될 것이다. 또한 블레이드 강성향상과 경량화가 전체발전량에 미치는 영향에 대한 연구도 필요할 것으로 예상된다.
NOMENCLATURE
| W[mm] : | Width |
| T[mm] : | Thickness |
| L[mm] : | Length |
| Fm[N] : | Maximum load |
| σm[MPa] : | Tensile strength at Fm |
| E11[GPa] : | Young’s modulus on the fiber direction (the longitudinal modulus) |
| E22[GPa] : | The transverse Young’s modulus |
| υ12, υ21 : | Poisson’s ratios |
Acknowledgments
본 연구는 2015년도 산업통상자원부의 재원으로 한국에너지기술평가원(KETEP)의 지원을 받아 수행한 연구과제입니다(No. 20153010024470).
REFERENCES
- Lee, S.-P., Kang, K.-W., Chang, S.-M., and Lee, J.-H., “Structural Design for 2kW Class Wind Turbine Blade by Using Design of Experiment,” Journal of the Korean Society of Manufacturing Technology Engineers, Vol. 20, No. 1, pp. 28-33, 2011.
-
Kim, H.-K., Lee, J.-H., Jang, S.-M., and Kang, K.-W., “Structural Analysis and Testing of 1.5 kW Class Wind Turbine Blade,” Journal of Korean Fluid Machinery Association, Vol. 13, No. 4, pp. 51-57, 2010.
[https://doi.org/10.5293/KFMA.2010.13.4.051]

- Dassault Systemes, “Abaqus 6.14,” Dassault Systemes Simulia, 2016.
- ISO 547-1, “General Principles,” ISO 547-4, “Test Conditions for Isotropic and Orthotropic Fibre-Reinforced Plastic Composites,” ISO 547-5, “Test Conditions for Unidirectional Fibre-Reinforced Plastic Composites,”.
- IEC 61400-2, “Design Requirements for Small Wind Turbines,” 2006.
- Hahn, H. T. and Tsai, S. W., “Introduction to Composite Materials,” CRC Press, 1980.
-
Choi, C.-W., Jin, J.-W., and Kang, K.-W., “Structural Optimization for Small Scale Vertical-Axis Wind Turbine Blade Using Response Surface Method,” Journal of the Korean Society Fluid Machinery, Vol. 16, No. 4, pp. 22-27, 2013.
[https://doi.org/10.5293/kfma.2013.16.4.022]

-
Lee, S. P., “Reliability-Based Design Optimization for Composite Wind Turbine Blades Considering Material Uncertainty,” New & Renewable Energy, Vol. 13, No. 3, pp. 41-50, 2017.
[https://doi.org/10.7849/ksnre.2017.9.13.3.041]

- Dassault Systemes, “Isight 4.0,” Dassault Systemes simulia, 2016.