이동타겟 추적을 위한 데이터이동법을 이용한 로봇비젼 제어기법 개발

1. 서론

최근 들어 산업용 로봇 활용범위가 지능화와 자동화로 확대되면서 정밀한 측정시스템에 대한 요구가 강조되고 있으며, 휴머노이드 로봇과 의료로봇 분야에서는 머신비젼을 넘어서 로봇 비젼으로 진화하고 있다.

현재 로봇비젼 인식기술은 사람의 얼굴을 인지 하는 수준의 실용화에는 도달했지만, 복잡한 형상의 물체를 구분하기 위해서는 많은 변수들을 사용해서 접근해야 하기 때문에 로봇에게는 매우 복잡하고 어려운 일이 된다.

특히, 최근의 산업현장에 인공지능 로봇이 적용되기 위해서는 로봇 스스로 주변 환경을 인식하고 이동할 수 있어야 할 뿐만 아니라, 불규칙적인 주변환경의 변화를 인식하고 유연하게 대처할 수 있어야 하는데, 이를 위해서는 시각 기능을 담당하는 이미지 처리기술과 시각 이미지의 분석 알고리즘에 대한 연구가 절실히 요구된다.

로봇에 비젼센서를 이용하여 로봇의 자율적인 주행경로 결정 기술, 2차원 시각정보의 3차원 공간재현, 물체 추적기술 등에 대한 많은 연구가 수행되고 있다.^1,2 또한, 많은 양의 데이터처리를 위해 1970년대 후반부터 이루어진 대규모 기억 소자의 꾸준한 개발로 인해 메모리 문제를 해결 하였으며, 이치화 기법이나 큐(Cue)를 사용해 데이터의 양을 최소로 하여 작업의 조건과 특성을 명확히 함으로써 획득되는 데이터의 양을 최소로 줄이는 등의 물리적인 작업환경을 통해 데이터 처리시간을 줄이는 방법들이 연구되었다.^3,4

Kobayashi⁵는 목표물체의 3차원 위치를 스테레오 비전시스템의 삼각측량 기술로 추정하고 카메라 좌표계에서 이동속도를 계산하여 추적지연 없이 움직이는 물체를 시각적으로 추적하는 방법을 제안하였으며, 최근 들어 Asl⁶은 비행 로봇의 동적 설계문제를 해결하여 비행 로봇이 이동 타겟을 추적할 수 있도록 비젼기반의 IBVS 방식을 이용한 제어장치를 제안하였다. 또한, Assa⁷는 단일 카메라에 기초하여 물체의 모습을 추정하는 방법에 다중 카메라 센서 융합기법을 보완하여 비젼을 기반으로 한 단계 높은 정확도와 정밀도를 제공하며 실시간으로 물체의 모습을 추정하는 센서 융합기법을 제안하였다.

위에서 언급된 대부분 연구들은 비젼시스템을 로봇에 적용할 때에 가장 중요한 요소인, 카메라의 위치, 방향 및 초점거리에 대한 보정이 정확하지 않으면 로봇은 정상적인 위치보정을 하지 못하고 오동작할 우려가 있다. 특히, 카메라와 로봇 사이의 상대적인 위치와 카메라 방위 및 초점거리가 변하면 카메라에 대한 보정계수를 다시 계산해야 하는 번거로움이 있다.

이러한 문제점을 해결하기 위해 고정된 타겟의 물체배치 작업에 관한 선행연구^8,9를 통해 증명된 카메라 및 로봇위치 변화에 대해 카메라 매개 변수를 능동적으로 조절할 수 있는 비젼시스템 모델을 공간상 위치값이 알려지지 않은 상태에서 연속적으로 이동하는 이동타겟 추적작업에 적용 하였다. 로봇이 타겟을 향해 이동하는 동안 얻어진 비젼데이터를 처리하는 방법에는 획득된 데이터를 모두 사용하는 일괄처리법(Batch Method)과 일정한 데이터만을 사용하는 데이터 이동법(Data Moving Method)으로 구분할 수 있다.

이리하여 본 연구는 로봇이 이동타겟 추적시 정확도 및 처리속도 향상을 위해 데이터이동법을 이용한 로봇비젼 제어기법을 제안하였다.

제안된 제어기법은 로봇이 타겟을 향해 이동하는 동안 얻어진 비젼데이터 개수를 줄이기 위해 오래된 데이터를 배제하고 최근 타겟 근처에서 획득된 일정한 데이터만을 사용하기 위해, 타겟 근처의 최적의 로봇 이동지점수를 추정하여 한정된 데이터 개수만을 사용하였다.

그리고 제안된 제어기법의 효율성을 보이기 위해 일괄처리법을 사용한 제어기법을 기준으로 설정하여 얇은 막대 이동타겟 추적실험을 통해 정확도 및 처리속도 결과를 비교하여 평가하였다.

2. 시스템 모델

2.1 로봇 기구학 모델

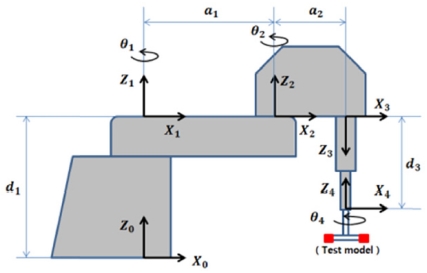
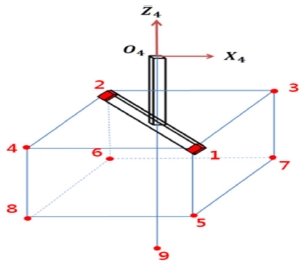
Fig. 1은 본 연구에서 이동타겟 추적실험에 사용 한 삼성 4축 스카라 타입 로봇의 링크 인자와 관절 좌표계의 설정을 보여주며, Table 1은 3개의 회전관절과 1개의 미끄럼 관절을 갖는 로봇의 4개 관절에 대한 Denavit-Hartenberg 규약¹⁰에 따른 링크인자를 보여준다.

Fig. 1

Link parameters and link frame assignments of 4 axis robot

Table 1

Link parameter of 4 axis robot

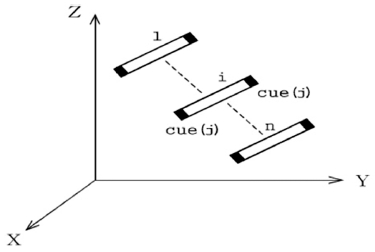
Fig. 2는 로봇이 j개 큐를 갖는 물체를 가지고 설정된 n개 이동 지점을 따라 운동할 때 i번째 이동지점에서 j번째 큐에 대한 운동 상태를 보여 준다. Fig. 2에 근거하여 Table 1의 링크인자를 사용하여 계산된 로봇 기구학 모델의 성분별 위치는 식(1)에서 보여준다.^8,9

Fig. 2

Robot’s movement

$\[ \begin{array}{c}{F}_x^{i,j}=\cos \left({\theta }_1^i+{\theta }_2^i+{\theta }_4^i\right)P_x^j-\sin \left({\theta }_1^i+{\theta }_2^i+{\theta }_4^i\right)P_y^j\\ +250\cos \left({\theta }_1^i+{\theta }_2^i\right)+400\cos {\theta }_1^i\\ F_y^{i,j}=\sin \left({\theta }_1^i+{\theta }_2^i+{\theta }_4^i\right)P_x^j+\cos \left({\theta }_1^i+{\theta }_2^i+{\theta }_4^i\right)P_y^j\\ +250\sin \left({\theta }_1^i+{\theta }_2^i\right)+400\sin {\theta }_1^i\\ F_z^{i,j}=P_z^j-d_3^i+387\end{array} \]$

(1)

여기서, i는 로봇의 운동궤적에서의 이동지점, θ₁ⁱ, θ₂ⁱ, d₃ⁱ, θ₄ⁱ는 i번째 이동지점에서 로봇 관절값, j는 큐(Cue)의 번호를 나타낸다. 또한, $$ P_x^j, P_y^j, P_z^j$$는 마지막 관절 좌표계{4} 원점에 대해 부착된 물체에 있는 j번째 큐의 위치를 나타낸다.

2.2 비젼시스템 모델

본 논문에서 제시한 비젼시스템 모델은 6개의 불확실한 매개변수를 사용하여 3차원 공간상에 움직이는 로봇의 끝점에 부착된 물체의 위치 벡터를 2차원 카메라 좌표계로 변환시키는 모델이다. 비젼시스템 모델은 카메라 모델과 2.1절의 로봇 기구학 모델이 이용된다.

(1) 카메라 모델

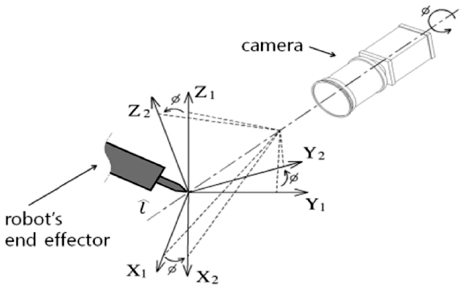
Fig. 3과 같이 임의의 기준계에 대한 카메라의 회전은 오일러 매개변수(Euler Parameter)를 사용하여, 카메라가 원하는 영상을 얻기 위하여 카메라가 회전하는 축 방향으로 단위벡터 $$ \widehat{l}$$(l_x, l_y, l_z)를 설정하고 회전축에 대한 회전각을 Ø라 하면 이때, 오일러 매개변수는 식(2)와 같이 주어진다.¹¹

Fig. 3

Camera rotation and Euler parameters

$\[ c_1=\cos \frac{1}{2}\varnothing ,c_2=l_x\sin \frac{1}{2}\varnothing ,c_3=l_y\sin \frac{1}{2}\varnothing ,c_4=l_z\sin \frac{1}{2}\varnothing \]$

(2)

여기서, $$ c_1^2+c_2^2+c_4^2+c_4^2=1$$인 오일러 매개변수에 대한 제한조건이 주어진다.

식(2)의 제한 조건을 만족하는 카메라 회전모델은 오일러 매개변수들의 항으로 나타내어진 방향 코사인 행렬(Direction Cosine Matrix)을 사용함 으로써 식(3)과 같이 주어진다.¹¹

$\[ \left[\begin{array}{c}{X}_m^{i,j}\\ Y_m^{i,j}\end{array}\right]=\left[\begin{array}{ccc}{K}_{11}\left(C_i\right)& K_{12}\left(C_i\right)& K_{13}\left(C_i\right)\\ K_{21}\left(C_i\right)& K_{22}\left(C_i\right)& K_{23}\left(C_i\right)\end{array}\right]\left[\begin{array}{c}{F}_x^{i,j}\\ F_y^{i,j}\\ F_z^{i,j}\end{array}\right] \]$

(3)

여기서,

$\[ \begin{array}{c}{K}_{11}=C_1^2+C_2^2-C_3^2-C_4^2,K_{12}=2\left(C_2{C}_3+C_1{C}_4\right)\hfill \\ K_{13}=2\left(C_2{C}_4-C_1{C}_3\right),K_{23}=2\left(C_2{C}_3-C_2{C}_4\right)\hfill \\ K_{22}=C_1^2-C_2^2+C_3^2-C_4^2,K_{23}=2\left(C_3{C}_4+C_1{C}_2\right)\hfill \end{array} \]$

(2) 비젼시스템 모델

카메라 평면에 대한 로봇 위치의 불확실성을 보완하기 위해 시각 매개변수 C₅와 C₆을 식(3)의 카메라 회전모델에 첨가하면 아래와 같이 비젼 시스템 모델이 주어진다.^8,9

$\[ \begin{array}{c}{X}_m^{i,j}=\left(C_1^2+C_2^2-C_3^2-C_4^2\right)F_x^{ij}+2\left(C_2{C}_3+C_1{C}_4\right)F_y^{ij}\hfill \\ +2\left(C_2{C}_4-C_1{C}_3\right)F_z^{i,j}+C_5\\ Y_m^{i,j}=2\left(C_2{C}_3+{-C}_1{C}_4\right)F_x^{ij}+\left(C_1^2-C_2^2+C_3^2-C_4^2\right)F_y^{i,j}\hfill \\ +2\left(C_3{C}_4+C_1{C}_2\right)F_z^{i,j}+C_6\end{array} \]$

(4)

여기서, $$ X_m^{i,j}$$과 $$ Y_m^{i,j}$$은 각각 3차 공간상의 i번째 이동지점에서 j번째 큐에 대한 위치 벡터를 2차원 카메라 좌표계로 변환했을 때 x, y성분을 나타 낸다. 6개 시각 매개변수 중 C₁-C₄는 카메라의 방향 및 초점거리의 변화성을 나타내고, C₅, C₆은 카메라에 대한 로봇 위치의 불확실성을 나타낸다.

3. 매개변수 추정을 위한 수학적 모델링

본 연구에서 필요로 하는 수학적 모델링은 카메라 매개변수 추정모델과 로봇 관절값 추정 모델로 구분하여 Newton-Raphson 방법을 사용하여 개발하였다.

4. 이동타겟 추적을 위한 제어기법

Newton-Raphson 방법을 통해 3장에서 보여준 매개변수 수학적 모델링을 이용하여 이동타겟 추적을 위해 일괄처리법과 데이터이동법을 사용한 로봇비젼 제어기법을 제안하였다.

4.1 일괄처리 제어기법

4.1.1 비젼데이터 획득 및 처리

일괄처리법은 임의의 운동궤적을 갖는 로봇 초기화단계를 설정하여 로봇이 이동하는 동안 획득한 모든 비젼데이터를 사용하여 이동타겟 추적을 위한 초기의 카메라 매개변수와 로봇 관절값을 계산한다

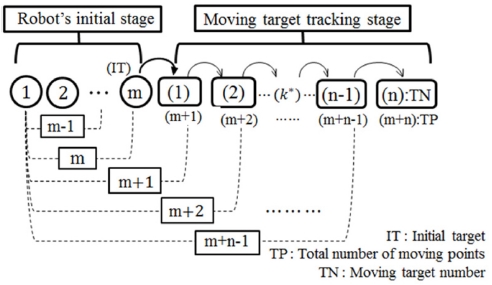
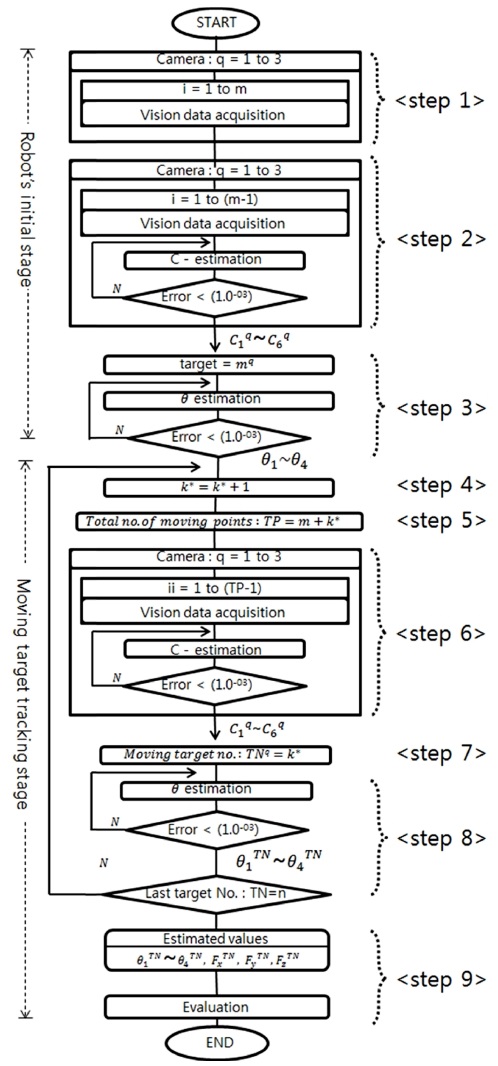
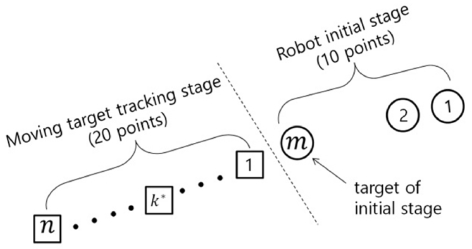
Fig. 4에서 보여준 것 같이 m개 이동지점을 갖는 로봇 초기화 단계에서 m번째 이동지점을 타겟으로 설정하고 (m-1)개 로봇 이동지점의 비젼데이터를 사용하여 이동타겟 추적단계에서 필요한 초기 카메라 매개변수와 로봇 관절값을 추정한다. 이동타겟 추적단계에서 첫 번째 이동타겟을 추정할 때는 로봇 초기화단계에서 타겟으로 사용된 m번째가 추가되어 m개 이동지점의 비젼데이터를 사용하여 카메라 매개변수를 추정한 후, 추정된 카메라 매개변수를 이용하여 타겟에 대한 로봇 관절값을 추정하여 타겟의 위치값을 계산한다. 이와 같이 k*번째 이동타겟 추정시 (k*-1)번째 이동타겟이 추가되어 (m+k*-1)개 이동지점의 비젼데이터를 사용하여 각 카메라 매개변수를 추정하고, 추정된 카메라 매개변수를 이용하여 로봇 관절값을 추정하여 타겟의 위치값을 계산한다.

Fig. 4

Data processing method of the batch scheme

4.1.2 제어기법

Fig. 5는 일괄처리 제어기법에 대한 전체적인 흐름을 보여주며, 각 단계별 설명은 다음과 같다.

Fig. 5

Robot’s vision control scheme of the batch method

(1) Step 1; 로봇 초기화 단계에서 초기 타겟지점(m)으로 이동하는 동안 3 대의 카메라를 사용하여 로봇의 각 이동지점에서 2개의 큐에 대한 비젼 데이터를 획득한다.

(2) Step 2; 각 카메라에서 획득한 2개의 큐에 대한 (m-1)로봇 이동지점까지 비젼데이터를 사용하여 카메라 매개변수 추정방법에 적용하여 각 카메라에 대한 매개변수를 추정한다.

(3) Step 3; <Step 2>에서 추정된 각 카메라 매개변수와 각 카메라에서 획득한 초기 타겟(m)에 대한 비젼데이터를 관절값 추정방법에 적용하여 로봇 관절값을 추정한다. <Step 2>와 <Step 3>에서 추정된 카메라 매개변수와 로봇 관절값은 이동타겟 추정시 초기값으로 사용한다.

(4) Step 4; 이동타겟 추적단계에서 이동타겟의 지점(k*)을 나타내기 위해 정의하였으며, 이동 타겟의 지점을 1부터 n까지 1씩 증가시킨다.

(5) Step 5; k*번째 이동타겟 추정시 사용되는 비젼데이터의 전체 이동지점개수(TP)를 정의 하였으며, 로봇 초기화단계의 m개 이동 지점수와 k*번째까지 이동타겟에 대한 지점을 합한 전체값을 나타낸다.

(6) Step 6; 각 카메라에서 획득한 2개의 큐에 대한 (TP-1)개 지점까지의 비젼데이터를 카메라 매개변수 추정방법에 적용하여 각 카메라에 대한 매개변수를 추정한다.

(7) Step 7; 각 카메라에서 획득한 k*번째 이동타겟 번호(TN)를 나타낸다.

(8) Step 8; <step 6>에서 각 카메라에 대해 추정된 카메라 매개변수와 <Step 7>의 각 카메라에서 정의된 k*번째 이동타겟에 대해 획득된 비젼데이터를 관절값 추정방법에 적용하여 로봇 관절값을 추정한다. 이동타겟 번호(TN)가 마지막 값(n)이 아니면 <Step 4>로 되돌아가서 다음 이동타겟 지점에 대한 계산을 반복한다.

(9) Step 9; 각 이동타겟 지점에서 추정된 관절값을 로봇기구학 식(1)에 대입하여 계산된 2개 큐의 위치값을 실제 위치값과 비교하여 오차값을 계산한다.

4.2 데이터이동 제어기법

4.2.1 비젼데이터 획득 및 처리

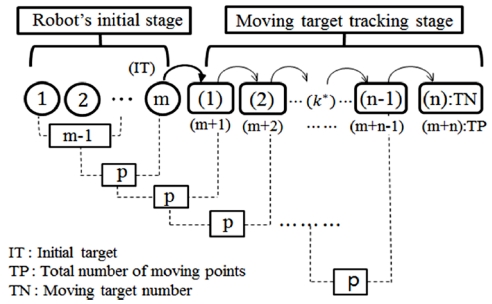
로봇이 이동하는 동안 획득된 비젼데이터를 처리시 데이터 양을 최소화하기 위해 데이터이동 제어기법을 제안하였다. Fig. 6에서 보여준 것 같이 데이터이동법은 m개 이동지점을 갖는 로봇 초기화단계에서 m을 초기 타겟지점으로 설정하고 (m-1)점의 비젼데이터를 사용하여 이동타겟 추적단계에서 이용되는 최적의 로봇 이동지점개수(P)를 계산한 후, 이에 상응하는 초기 카메라 매개변수와 로봇 관절값을 얻는다. 이동타겟 추적단계에서 첫번째 타겟을 추정할 때는 가장 최근 이동지점(m)까지 P개의 이동 지점 비젼데이터만을 사용하여 계산을 수행한다. 이와 같이 k*번째 이동타겟 추정시 이전단계에서 사용된 (k*-1)번째 타겟지점을 포함한 최근 이동지점 개수 P개의 비젼데이터 만을 사용하여 계산한다.

Fig. 6

Data processing method of the data moving scheme

4.2.2 제어기법

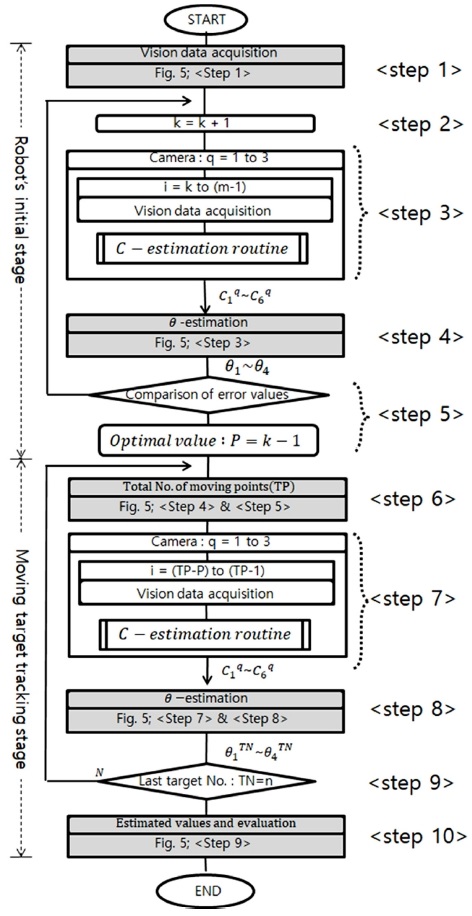
이동타겟 추적을 위해 데이터이동 제어기법은 Fig. 7에서 보여준 것 같이 로봇 초기화단계에서 4.2.1절의 데이터 처리방법을 기초로 최적 데이터 이동지점수(P)를 계산하여, 이동타겟 추적단계에서 타겟 추정시 사용되는 비젼데이터를 최소화 하고자 한다. 이에 대한 각 단계별 내용은 다음과 같다. 특히, Fig. 7에서 음영으로 표시된 부분은 Fig. 5에서 설명된 것과 같은 방법을 사용하고 있다.

Fig. 7

Robot’s vision control scheme of the data moving method

(1) Step 1; 일괄처리 제어기법 Fig. 5의 <Step 1>과 같이 초기화 단계에서 필요한 비젼데이타를 획득한다.

(2) Step 2; 최적의 이동지점수 (P)를 계산하기 위해 로봇 이동지점수를 1씩 변화시키기 위해 정의 하였다.

(3) Step 3; 최초 로봇 이동지점 1부터 (m-1)지점까지 2 큐에 대해 획득한 비젼데이터를 매개변수 추정방법에 적용하여 각 카메라에 대한 매개변수를 계산한다. 이후, 최적의 로봇 이동지점수를 계산하기 위해 로봇 이동지점 수를 1씩 줄이면서 계산한다.

(4) Step 4; Fig. 5의 <Step 3>과 같이 로봇 관절값을 추정한다.

(5) Step 5; 로봇 이동지점수의 변화에 따라 초기타겟에 대해 추정된 위치값과 실제 위치값을 비교한 오차값이 이전에 계산된 오차값 보다 작으면 <Step 2>로 되돌아가고, 크면 이전 단계의 로봇 이동지점수를 최적의 로봇이동 지점수(P)로 다음과 같이 결정한다.

P = (m-1) − (k-1) + 1 = m-k+1

(6) Step 6; Fig. 5의 <Step 4>와 <Step 5>와 같은 방법을 사용하여 k*번째 이동타겟에 대한 총이동지점수(TP)를 계산한다.

(7) Step 7; TP = (m+k*) 이동지점수를 갖는 k*번째 타겟을 추정하기 위해 (TP-P) 부터 (TP-1)까지 P개 이동지점수의 2개 큐에 대한 비젼 데이터를 가지고 카메라 매개변수 추정방법을 사용하여 각 카메라에 대한 매개 변수를 추정 한다.

(8) Step 8; Fig. 5의 <Step 7> 및 <Step 8>과 같은 방법으로 k*번째 이동타겟에 대한 로봇관절값을 추정한다.

(9) Step 9; 이동타겟 k*가 마지막 지점(n)이 아니면 <Step 6>로 되돌아가서 다음 이동 타겟지점에 대한 계산을 반복한다.

(10) Step 10; Fig. 5의 <Step 9>와 같이 추정된 이동타겟값을 이용하여 오차값을 계산하여 효율성을 평가한다.

5. 실험장치 및 실험방법

5.1 실험장치

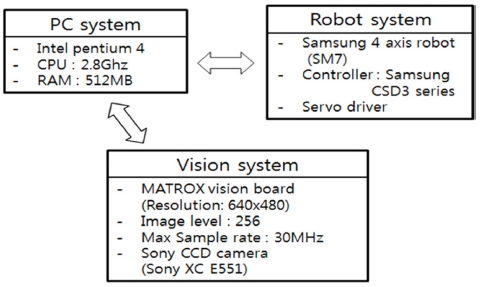
본 연구에 사용된 실험장치의 구성은 Figs. 8과 9와 같이 크게 비젼시스템, 로봇시스템, PC시스템으로 구성되었다.

Fig. 8

Experimental set-up

Fig. 9

Experimental schematic diagram

또한, 비젼데이터의 양을 최소화하여 처리속도를 향상시키고자 물체 형상 전체를 사용하지 않고 여러 개의 큐를 이용하여 다양한 물체를 형상화할 수 있도록 Fig. 10와 같이 시험모형을 제작하였다.

Fig. 10

Test model used for experiment

본 연구에서는 Fig. 10의 1번과 2번 큐를 이용 하여 얇은 막대 형상을 만들어 진행하였으며, 각 큐의 O₄에 대한 위치값은 아래와 같다.

$\[ \begin{array}{c}{P}^1=\left(P_x^1,P_v^1,P_z^1\right)=\left(15 \text{mm}, -18 \text{mm}, -103 \text{mm}\right)\\ P^2=\left(P_x^2,P_v^2,P_z^2\right)=\left(15 \text{mm}, -18 \text{mm}, -103 \text{mm}\right)\end{array} \]$

5.2 실험방법

본 실험에서 삼성 SM7 로봇의 운동궤적은 Fig. 11과 같이 m = 10개의 로봇 초기단계와 n = 20개의 이동타겟 추적단계로 설정하고, 3대의 카메라를 사용하였다. 그리고 4장에서 제안된 로봇비젼 제어기법을 사용하여 이동타겟의 위치값을 추정하였다.

Fig. 11

Robot’s trajectory

6. 실험결과

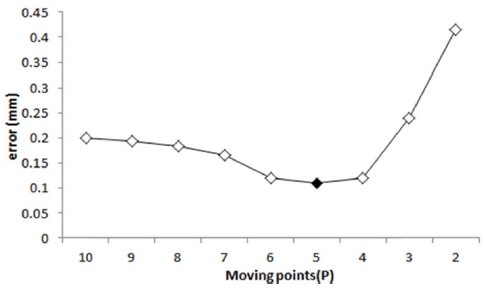
6.1 초기화 단계에서 최적의 로봇 이동 지점수(P) 추정

데이터이동 제어기법을 사용하여 얇은 막대 이동타겟을 추적하기 위해 Fig. 7의 <step1>에서 <step 5>를 이용하여 최적의 로봇 이동지점수(P)를 계산하였다. Fig. 12에서 보여준 것 같이 이동 지점수가 5일 때 0.1099 mm로 가장 적은 오차값이 발생하여 P를 5로 설정하였다.

Fig. 12

Errors according to the variation of robot moving points in the data moving scheme

6.2 비젼시스템 모델의 적합성 결과

Newton-Raphson 방법을 사용한 일괄처리 제어기법과 데이터 이동 제어기법에 대해 비젼시스템 모델의 적합성을 보였다.

일괄처리 제어기법은 Fig. 5 제어기법에 따라 이동타겟 추적단계에서 k* 번째 이동타겟을 추정하기 위해서는 로봇 초기단계 이동지점수(m)와 이동타겟 추적단계의 (k*-1)까지 이동지점을 합한(m+k*-1) 이동지점에 대한 비젼 데이터를 사용하여 매개변수를 추정한다. 이리하여 (k*-1)번째 이동지점에 대해 추정된 매개변수를 사용한 비젼시스템 모델값과 획득된 실제 비젼 데이터값을 비교하여 비젼시스템 모델의 적합성을 보였다.

데이터이동 제어기법은 Fig. 7의 제어기법에 따라 로봇 초기화 단계에서 계산된 최적의 이동 지점수(P)를 이용하여 이동타겟 추적단계에서 k*번째 이동타겟을 추정하기 위해서는 로봇 초기화 단계 이동지점수 (m)개를 포함한 k*번째 이동지점까지 (m+k*) 이동지점수에서 P를 뺀 (m+k*-p)로부터 (m+k*-1) 이동지점까지 비젼데이터를 사용하여 카메라 매개변수를 추정한다. 이리하여, (k*-1)번째 이동지점에 대해 추정된 매개변수를 사용한 비젼시스템 모델값과 실제 비젼데이터값을 비교하여 비젼시스템의 적합성을 보였다.

그러므로 (k*+1)번째 이동타겟을 추정하기 위해 필요한 k*번째 지점에서 각 카메라에 대해 추정된 비젼시스템 모델값과 실제 비젼데이터를 비교한 오차값 $$ e_{r.m.s}^{k\mathrm{*}}$$을¹² 식(11)과 같이 정의하였다. 특히, 첫번째 타겟을 추정하기 위해서, 로봇 초기화 단계의 m번째까지의 비젼데이터를 사용하였다.

$\[ e_{r.m.s}^{k\mathrm{*}}=\sqrt{\frac{{\sum }_{j=1}^{j\mathrm{*}}\left\{{\left(e_x^{k\mathrm{*},j}\right)}^2+{\left(e_y^{k\mathrm{*},j}\right)}^2\right\}}{2\times j^{\mathrm{*}}}} \]$

(11)

여기서 j*는 큐의 개수(j*=2), $$ e_x^{k\mathrm{*},j}$$와 $$ e_y^{k\mathrm{*},j}$$는 k*번째 이동지점의 j번째 큐에 대한 실제 비젼데이터와 비젼시스템 모델 추정값 사이의 x축과 y축의 오차값이다. 또한 이동타겟 추적 단계에서 평균오차값 e_avg는 식(12)와 같이 정의하였다.

$\[ e_{avg}=\frac{{\sum }_{k\mathrm{*}}^n{e}_{r.m.s}^{k\mathrm{*}}}{n} \]$

(12)

여기서, n은 타겟 추적단계에서 필요한 이동 지점수(n = 20)을 나타낸다.

6.2.1 일괄처리 제어기법 결과

로봇이 타겟을 향해 이동하는 동안 각 이동 지점에서 3대 카메라에 대해 추정된 매개 변수를 식(4)에 적용하여 계산된 비젼시스템 모델값과 획득된 실제 비젼데이터를 비교하여 1번 카메라 의 결과만을 Fig. 13에서 보여 주었으나, 2번과 3번 카메라에서도 비슷한 결과를 얻었다. Table 2는 각 이동 지점에서 식(11)을 통해 계산된 3대 카메라의 실제 비젼데이터와 비젼시스템 모델값 사이의 r.m.s. 오차와 식(12)를 사용한 평균오차를 보여준다. 평균오차는 1번 카메라에서 0.7053 Pixel, 2번 카메라에서 0.4814 Pixel, 3번 카메라에서 0.8472 Pixel로 모든 카메라에서 비젼시스템 모델이 적합함을 보여준다.

Fig. 13

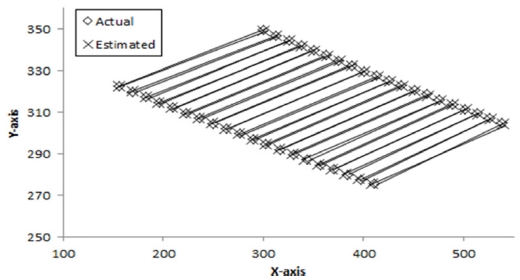
For camera 1, comparison of the actual and estimated values of vision system model in the moving target tracking stage based on the batch scheme (unit: pixel)

Table 2

The r.m.s errors of vision system model based on the batch scheme (unit: pixel)

Tables 2와 3에서 m은 초기화 단계의 타겟값으로서 첫번째 이동타겟을 추정하기 위해 사용 되어지는 각 카메라에서 비젼시스템 모델값의 r.m.s 오차값을 보여준다.

Table 3

The r.m.s errors of vision system model based on the data moving scheme (unit: pixel)

본 연구는 m = 10을 사용하였으며, 실험을 통해 임의로 선택된 m의 크기는 2개 제어기법에서 이동타겟 추정값에 큰 영향을 미치지 않으나, m의 크기가 클수록 처리시간이 늦어짐을 알 수 있었다.

6.2.2 데이터이동 제어기법 결과

6.1절에서 계산된 최적 이동지점수 (P = 5)를 사용하여 얇은 막대 이동타겟 위치추정에 적용하였다. 로봇이 타겟을 향해 이동하는 동안 각 지점에서 3대 카메라에 대해 추정된 매개변수를 식(4)에 적용하여 계산된 비젼시스템 모델값과 획득된 실제 비젼데이터를 비교한 결과 중 1번 카메라에 대한 결과만을 Fig. 14에서 보여주고 있으나 2번과 3번 카메라에서도 비슷한 결과를 얻었다. Table 3은 식(11)을 통해 계산된 3대 카메라에 대한 실제 비젼데이터와 비젼시스템 모델값 사이의 r.m.s. 오차값과 식(12)를 사용한 평균오차를 보여준다. 평균오차가 1번 카메라에서 0.1922 Pixel, 2번 카메라에서 0.1324 Pixel, 3번 카메라에서 0.1378 Pixel로 모든 카메라에서 일괄처리기법을 사용한 경우보다 더 높은 정확도를 보여 주었다.

Fig. 14

For camera 1, comparison of the actual and estimated values of vision system model in the moving target tracking stage based on the data moving scheme (unit: pixel)

6.3 이동타겟 추적 결과

이동타겟 추적단계에서 로봇이 이동하는 동안 공간상 위치가 알려지지 않은 각 타겟지점에서 획득된 실제 비젼데이터만을 사용하여 일괄처리 제어기법과 데이터이동 제어기법을 적용하여 각 이동 타겟지점에 대해 로봇 관절값을 추정하였다. 추정된 관절값을 식(1)의 로봇기구학 모델에 적용하여 타겟에 대해 위치값을 계산하였다.

k*번째 타겟에 대해 추정된 위치값과 실제 타겟지점 위치값 사이의 오차값 ($$ e_{r.m.s}^{k\mathrm{*}}$$)¹²은 식(13)과 같이 정의하였다.

$\[ e_{r.m.s}^{k\mathrm{*}}=\sqrt{\frac{{\sum }_{j=1}^{j\mathrm{*}}\left\{{\left(e_x^{k\mathrm{*},j}\right)}^2+{\left(e_y^{k\mathrm{*},j}\right)}^2+{\left(e_z^{k\mathrm{*},j}\right)}^2\right\}}{3\times j\mathrm{*}}} \]$

(13)

여기서, j*는 큐의 개수(j*=2), $$ e_x^{k\mathrm{*},j},e_y^{k\mathrm{*},j},e_z^{k\mathrm{*},j}$$는 k*번째 타겟지점의 j번 큐에 대한 x성분, y성분, z성분 오차를 나타낸다.

또한 추정된 이동타겟들에 대한 평균오차 e_avg는 식(14)에 정의하였다.

$\[ e_{avg}=\frac{{\sum }_{k\mathrm{*}=1}^n{e}_{r.m.s}^{k\mathrm{*}}}{n} \]$

(14)

여기서, n은 이동타겟 추적단계에서 이동타겟 지점수 (n = 20)를 나타낸다.

6.3.1 일괄처리 제어기법 결과

(1) 관절값 추정

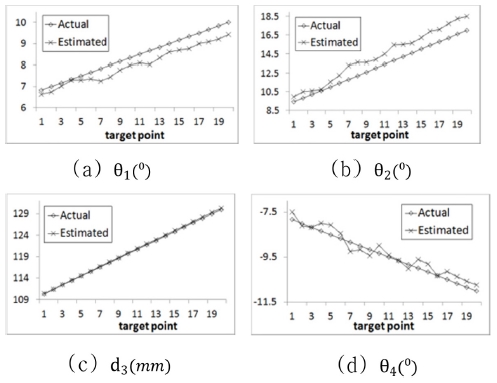
Fig. 15는 각 타겟지점에서 로봇관절값 추정 방법 에 의해서 계산된 관절값과 실제 관절값을 비교한 결과를 보여주고 있으며, 오차값 범위는 θ₁= 0.043 − 0.632 degree, θ₂= -1.651 − -0.137 degree, d₃ = -0.332 − -0.04 mm, θ₄ = -0.419 − 0.4227 degree로, 각 관절값은 아주 적은 오차범위 내에 존재한다.

Fig. 15

Comparison of the actual and estimated values of robot joint values using the batch scheme

(2) 타겟 위치 추정

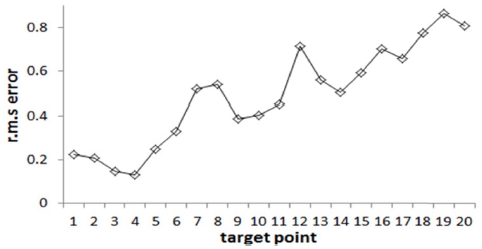
각 이동타겟에서 추정된 관절값을 식(1)에 대입하여 계산된 타겟의 위치값을 식(13)을 사용하여 계산된 r.m.s 오차값(e_r.m.s)을 Fig. 16과 Table 4에서 여준다. 오차값은 타겟이 이동함에 따라 처리하는 데이터의 양이 증가하기 때문에 증가하는 양상을 나타낸다. 식(14)를 이용한 이동타겟 20개에 대한 평균오차값(e_avg)은 0.488 mm의 정확도를 가지며, 본 연구에서 개발한 프로그램 처리시간은 344 ms가 소요되었다.

Fig. 16

The r.m.s errors for 20 moving targets using the batch scheme (unit: mm)

Table 4

The r.m.s errors for 20 moving targets using the batch scheme (unit: mm)

6.3.2 데이터이동 제어기법 결과

(1) 관절값 추정

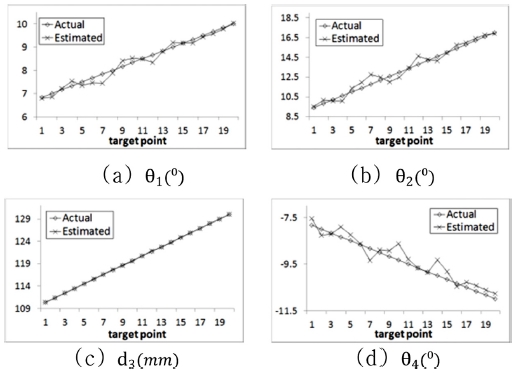
데이터이동 제어기법의 (P = 5)를 사용한 로봇 관절값 추정방법에 의해서 계산된 관절값과 실제 관절값을 비교한 결과를 Fig. 17에서 보여주고 있으며, 오차값 범위는 θ₁ = -0.247 − 0.395 degree, θ₂= -0.978− 0.61 degree, d₃= -0.091− 0.073mm, θ₄= -0.699 − 0.518 degree로서, 각 관절값은 아주 적은 오차범위 내에 존재한다.

Fig. 17

Comparison of the actual and estimated values of robot joint values using the data moving scheme

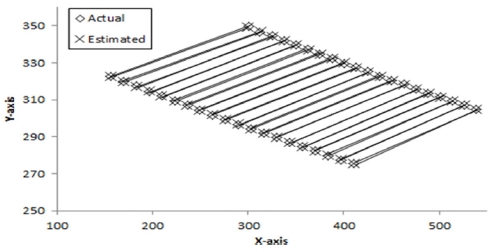
(2) 타겟 위치 추정

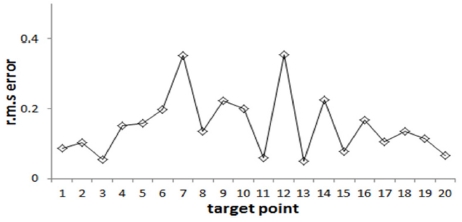
Fig. 18과 Table 5는 각 타겟지점에서 추정된 로봇 관절값을 식(1)에 대입하여 계산된 20개 이동타겟에 대한 위치값을 식(13)에 적용하여 계산된 r.m.s 오차값 ($$ e_{r.m.s}^{k\mathrm{*}}$$)을 보여준다. 타겟이 이동하여도 일정한 이동 지점수 만을 이용하여 데이터를 처리하기 때문에 일정한 범위 내에서 변화한다. 또한, 식(14)를 사용한 이동타겟 20개의 평균 오차값 (e_avg)은 0.152 mm, 프로그램 처리시간은 281 ms가 소요되었다.

Fig. 18

The r.m.s. errors for 20 moving targets using the data moving scheme (unit: mm)

Table 5

The r.m.s errors for 20 moving targets using the data moving scheme (unit: mm)

결과적으로, 연속적으로 이동하는 타겟을 어떤 지점에서 위치값을 추정하기 위해서 일괄처리기법은 로봇이 이동하는 동안 획득된 모든 비젼데이터를 사용하여 추정한 반면, 데이터이동기법은 획득된 오래된 비젼데이터를 배제하고 타겟근처에서 최근 얻어진 일정한 비젼데이터만을 사용하기 때문에 정확도 및 처리시간에서 일괄처리기법과 비교하여 더 좋은 결과를 얻었다.

7. 결론

본 논문은 일괄처리 제어기법을 기준으로 설정하고 데이터이동법을 이용한 로봇비젼 제어기법을 제안하였으며, 얇은 막대 이동타겟 추적을 통해 얻은 결과는 다음과 같다.

(1) 로봇이 이동하는 동안 획득한 방대한 비젼데이터를 처리하는데 있어서 양을 최소화하기 위해 제안된 데이터이동 제어기법에서 최적의 로봇 이동지점수(P)를 결정하는 방법을 제시하여(P = 5)를 추정하였다.

(2) 비젼시스템 모델 적합성에서 타겟 근처의 최근 로봇 이동지점수(P = 5)를 사용한 데이터이동 제어기법은 일괄처리 제어기법과 비교하면 3개 카메라 모두에서 적은 오차값은 보여준다.

(3) 데이터이동 제어기법은 획득된 데이터 중 오래된 데이터를 삭제하고 타겟 근처의 일정한 최근 데이터를 사용하기 때문에 획득한 모든 비젼데이터를 사용하는 일괄처리 제어기법에 비해 약 3배 정도 정확도가 향상됨을 보여 주었다.

(4) 모든 데이터를 사용하는 일괄처리 제어기법에 비해 한정된 일정한 개수의 데이터를 사용하는 데이터이동 제어기법의 데이터 처리시간이 더 빠름을 알 수 있었다.

이리하여 본 논문에서 제안된 데이터이동 제어기법은 일괄처리 제어기법보다 정확도 향상 및 처리속도를 빠르게 할 수 있다는 장점을 가지고 있어 그 효율성을 입증할 수 있었다. 향후, 이 결과를 토대로 작업환경이 급변하는 산업 현장에서 사용자가 상황에 맞는 제어기법을 선택할 수 있도록 제시하였다.

Acknowledgments

이 논문은 2017 학년도 조선대학교 학술연구비 지원을 받아 연구되었음.

REFERENCES

• Kelly, R., Carelli, R., Nasisi, O., Kuchen, B., and Reyes, F., “Stable Visual Servoing of Camera-in-Hand Robotic Systems,” IEEE/ASME Transactions on Mechatronics, Vol. 5, No. 1, pp. 39-48, 2000. [https://doi.org/10.1109/3516.828588]
• Yoshihiro, T., Yasuo, K., and Hiroyuki, I., “Positioning-Control of Robot Manipulator Using Visual Sensor,” Proc. of International Conference on Control, Automation, Robotics and Vision, pp. 894-898, 1996.
• Horn, B. K. H., “Robot Vision,” Cambridge, Massachusetts, MIT Press, pp. 46-48, 1986.
• Sandon, P. A., “Control of Eye and Arm Movements Using Active, Attentional Vision,” International Journal of Pattern Recognition and Artificial Intelligence, Vol. 8, No. 6, pp. 1471-1491, 1994. [https://doi.org/10.1142/S0218001494000711]
• Kobayashi, N. and Shibata, M., “Visual Tracking of a Moving Object Using a Stereo Vision Robot,” Electronics and Communications in Japan, Vol. 91, No. 11, pp. 19-27, 2008. [https://doi.org/10.1002/ecj.10184]
• Asl, H. J. and Bolandi, H., “Robust Vision-Based Control of an Underactuated Flying Robot Tracking a Moving Target,” Transactions of the Institute of Measurement and Control, Vol. 36, No. 3, pp. 411-424, 2014. [https://doi.org/10.1177/0142331213502747]
• Assa, A. and Janabi-Sharifi, F., “A Robust Vision-Based Sensor Fusion Approach for Real-Time Pose Estimation,” IEEE Transactions on Cybernetics, Vol. 44, No. 2, pp. 217-227, 2014. [https://doi.org/10.1109/TCYB.2013.2252339]
• Jang, M. W., “A Study on the Devaluation of the Development Robot Vision Control Schemes in Real Time for the Estimation of the Fixed Target,” M.Sc. Thesis, Chosun University, 2017.
• Jang, M. W., Kim, J. M., and Jang, W. S., “Real-Time Robotic Vision Control Scheme Using Optimal Weighting Matrix for Slender Bar Placement Task,” Journal of the Korean Society of Manufacturing Technology Engineers, Vol. 26, No. 1, pp. 50-58, 2017. [https://doi.org/10.7735/ksmte.2017.26.1.50]
• Craig, J. J., “Introduction to Robotics: Mechanics and Control,” Addison Wesley Publishing Company, pp. 62-76, 1989.
• Morton, H. S., Junkins, J. L., and Blanton, J. N., “Analytical Solutions for Euler Parameters,” Celestial Mechanics, Vol. 10, No. 3, pp. 287-301, 1974. [https://doi.org/10.1007/BF01586859]
• Freedman, D., Pisani, R., and Purves, R., “Statistic Fourth Edition,” W. W. Norton & Company, pp. 66-67, 2007.