런플랫 타이어의 내구 예측을 위한 사이드월 온도 해석 방법

1. 서론

차량의 고속화, 고성능화에 따라 타이어에 대한 요구사항도 다양해지고 있다. 최근 안전에 대한 관심이 증대되고, 주행 중 갑작스러운 타이어 펑크로 인한 위급 상황에서도 차량의 안정이 보장된다는 인식으로 런플랫 타이어의 소비자 관심이 커지고 있는 추세다. 런플랫 타이어는 1세대의 기본적인 런플랫 기능을 제공하는 수준에서 현재는 연비, 승차감 등 일반 타이어 수준의 성능을 원하는 소비자의 요구로 계속해서 진화하고 있다.

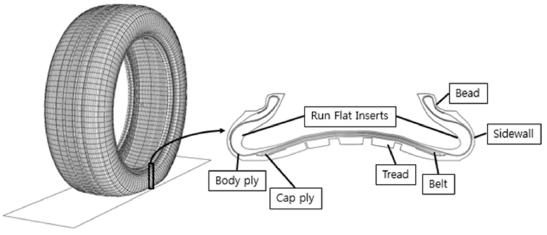
런플랫 타이어는 공기입 타이어의 펑크에 대비해서 여러 가지 방안들로 고안되었으며, 현재는 타이어 내부의 사이드월(Sidewall)에 보강고무(Run Flat Inserts, RFI)를 삽입한 방식의 런플랫 타이어가 주로 사용되고 있다. 런플랫 타이어는 내부 공기압이 없더라도 시속 80 km/h로 일정거리를 주행할 수 있어야 할 뿐만 아니라, 일반 주행 시 승차감, 핸들링, 연비 등 적절한 성능도 발휘되어야 한다. 따라서, 런플랫 타이어는 기본적인 런플랫 내구성을 만족함과 동시에 다양한 요구 성능을 고려한 RFI의 설계가 요구된다. 특히, 사이드월의 반복적인 굴신 운동으로 인한 열발생은 런플랫 타이어의 내구성에 영향을 미치므로, 최근 열발생량 및 온도 감소를 위한 다양한 방법의 설계가 고안되고 있다.

일반적으로 회전하는 타이어에서 발생되는 열원(Heat Source)은 타이어의 대부분을 구성하는 고무의 점탄성적 특성과 접촉, 마찰 등의 결과에 기인한 매우 복잡한 메커니즘을 가진다. 이러한 복잡한 메커니즘과 동적 해석을 필요로 하는 회전하는 타이어의 온도 분포예측은 이미 여러 사람들에 의해 순차적 접근 방식(Sequential Approach)으로 적용되고 있다. Park,¹ Kwon,² Futamura 등³은 순차적 접근 방식을 적용하여 회전 상태의 래디얼 타이어에 대한 열발생량 산출 및 열전달 해석을 수행하였다. 하지만 상기 연구는 일반 래디얼 타이어에 대한 연구이며 런플랫 타이어에 대한 내부온도 예측과 검증에 대한 연구는 전무한 실정이다.

본 연구에서는 래디얼 타이어가 아닌 런플랫 타이어를 대상으로 주행중 사이드월 부의 온도 분포를 예측하고자 한다. 내구성능의 경우 래디얼 타이어는 공기와 하중 조건 하에서 내구성 검토가 필요하다면, 런플랫 타이어는 그 목적에 맞게 Zero 공기압 조건에서의 내구성능이 주목적이라 할 수 있다. 따라서, Zero 공기압 조건에서 사이드월부는 가장 큰 변형을 받을 뿐만 아니라 차체 하중을 지지해야 하는 중요한 역할을 수행할 수 있어야 한다. 그러므로 이러한 가혹한 조건에서 런플랫 성능을 달성하기 위해서는 설계단계에서부터 사이드월 부의 내구성을 예측할 필요가 있다.

일반적으로 가황 고무가 상온에서 가지고 있는 특성(강성, 점탄성적 특성 등)들은 온도에 따라 변화된다. 하지만 그 한계를 벗어난 가혹한 온도 변화는 타이어 강성을 위한 고무의 요구 특성을 상실시켜 더 이상 타이어 역할을 수행할 수 없는 상태로 만들어 버린다. 그러므로 가혹 조건에서 운용되는 런플랫 타이어의 경우 사이드월의 반복 변형으로 발생된 고온의 열에 의한 내구성 감소를 고려해야 한다.

따라서, 본 연구에서는 런플랫 타이어의 내구성을 예측하기 위해, 주행상태의 런플랫 타이어의 사이드월 온도 분포를 예측하고자 한다. 실제로 일반 래디얼 타이어와 런플랫 타이어의 실내 내구 주행 평가 방법이나 조건은 동일하기 때문에 일반 래디얼 타이어의 해석 방법과 동일한 조건을 적용하였으며, 이를 위해 순차적 접근 방식을 이용하였다. 순차적 접근 방식은 변형 해석(Structural Analysis) 단계, 에너지 손실 계산 단계(Calculation of Energy Loss), 열전달 해석 단계(Heat Transfer Analysis)로 구성된다. 타이어 변형 해석을 통해 하중 상태에서의 변형률을 산출하고, 다음 단계에서 고무의 점성적 성질에 기인하는 에너지 손실을 산출하여 최종적으로 열전달 해석을 통해 타이어 온도 분포를 예측할 수 있다. 회전하는 타이어의 온도 분포 예측은 몇 가지 가정들이 존재한다. 즉, 에너지 손실(Energy Loss)만이 내부의 열원으로 전환되고, 원주방향의 온도 구배는 존재하지 않으며, 지면과의 마찰로 인한 온도 증가는 무시한다.⁴

본 연구는 런플랫 타이어 내구 시험을 열화상 장비를 통해 온도 분포를 측정하였고, 고안된 예측 기법 결과와 비교함으로써 예측 기법의 효용성을 검증해 보았다.

2. 에너지 손실 (Energy Loss)

2.1 고무의 동적 거동⁵

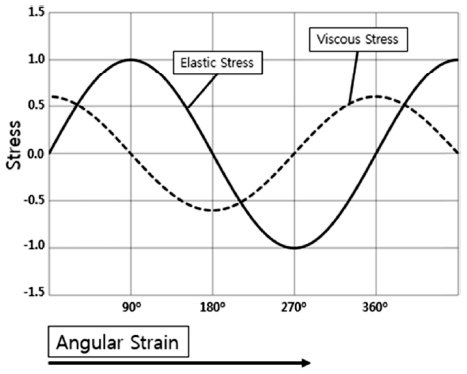
점성 응력(Viscous Stress) 곡선은 Fig. 1과 같이 최고 신장 값(90^o변형)에서 점성 응력이 Zero가 된다. 이러한 현상을 뉴턴(Isaac Newton)이 발견하였고, 이를 뉴턴의 점성 법칙으로 표현하다. 즉, 점성 응력은 변형 속도에 비례하며, 다르게 표현하면 응력/변형 속도의 값은 상수이며, 이 상수가 바로 물질의 점성이 된다. 그러므로 고무는 액체의 성질도 가지고 있기 때문에 완전히 신장했다가 되돌아오려고 하는 지점(90^o 또는 270^o)에서 그 ‘속도’ 또는 ‘변형 속도’는 제로이며, 점성 응력 또한 Zero가 된다.

Fig. 1

The curve of elastic stress and viscous stress

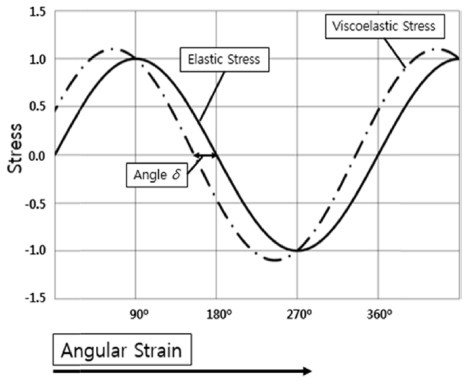
따라서, 점탄성 성질을 가진 고무에 정현파의 주기적인 변형이 주어 질 때 고무의 점성에 의해 Fig. 2와 같이 탄성 응력(Elastic Stress)과 점탄성 응력(Viscoelastic Stress)은 δ만큼 위상차가 나타나게 된다.

Fig. 2

Phase difference of viscoelastic stress and elastic stress

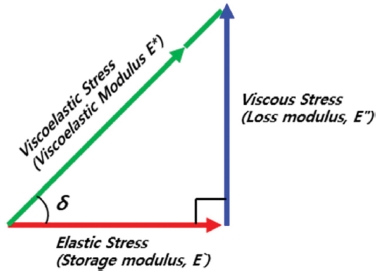
각 δ와 Modulus 사이엔 간단한 수학적 관계가 있는데, Fig. 3과 같이 삼각법을 이용하여 벡터로 나타낼 수 있다.

Fig. 3

The complex of viscoelastic stress and elastic stress

Fig. 3의 관계로부터 탄성 성분과 90°위상 차이의 점성 성분으로 Viscoelastic Modulus를 분해하면 식(1)과 식(2)로 나타낼 수 있다.

$\[ E*=E^{\text{'}}+iE\text{'}\text{'} \]$

(1)

$\[ E^{\text{'}}=E*\cos \text{δ},E^{\text{'}\text{'}}=E*\sin \text{δ} \]$

(2)

여기서, E*는 Viscoelastic Modulus, E'은 Storage Modulus, E''은 Loss Modulus를 의미한다.

2.2 런플랫 타이어 사이드월의 거동

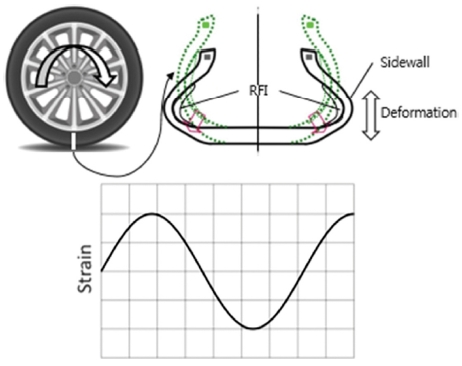
주행중 타이어는 여러 가지 복잡한 변형을 받는다. 특히, 타이어 사이드월 부의 고무는 주행중 주기적인 굴신 운동을 하게 되는데, 공학적 접근을 위해 단순화 시켜보면 Fig. 4처럼 정현파 형태인 주기적인 반복 변형으로 생각해 볼 수 있다.

Fig. 4

The sinusoidal cyclic deformation of sidewall on rolling

정현파의 주기적인 변형 하에서 점탄성 물질의 에너지 손실 Q는 식(3)과 같이 나타낼 수 있다.

$\[ {\sigma }_0=E*{\epsilon }_0,\sin \delta =E^{\text{'}\text{'}}/E* \]$

(3)

여기서, σ₀는 응력(Stress Amplitude), ε₀는 변형률(Strain Amplitude), T는 1회전 동안의 시간 그리고 δ은 응력과 변형률과의 위상차를 의미한다.

이때 σ₀와 sinδ는 식(4)와 같은 관계를 가지며, 에너지 손실은 식(5)와 같이 나타낼 수 있다.

$\[ Q={\int }_0^T\sigma \dot{\epsilon }dt=\pi {\sigma }_0{\epsilon }_0\sin \text{δ} \]$

(4)

$\[ Q=\pi {\sigma }_0{\epsilon }_0\sin \text{δ}=\pi {\epsilon }_0^{2}E\text{'}\text{'} \]$

(5)

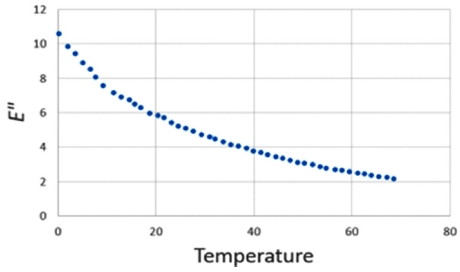
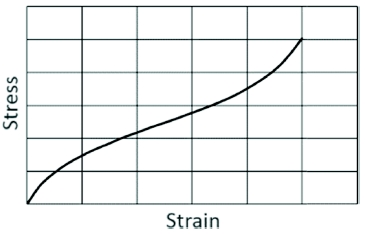
즉, 에너지 손실은 변형률과 Loss Modulus로 나타낼 수 있다. Loss Modulus는 온도에 의존적이므로 해석 적용 시 온도 의존성을 고려해야 한다. Loss Modulus와 온도와의 관계는 Fig. 5와 같이 반비례관계이다.

Fig. 5

Relation between loss modulus and temperature

3. Heat Build-Up 해석 프로세스

Zero 공기압에서 주행중인 런플랫 타이어의 사이드월 부의 열발생은 사이드월과 RFI 고무의 주기적인 반복 거동에 기인한다고 볼 수 있다. 주기적인 변형으로 에너지 손실이 발생되며 이는 열로써 나타난다. 열발생량은 Loss Modulus와 관련이 있으며 이는 재료의 고유 특성으로써 온도에 의존하다. 따라서, 재료의 온도 의존성을 해석에 반영하기 위해서는 Heat Build-Up 해석 프로세스를 통해 반복적으로 온도 의존성을 고려한 Loss Modulus 및 에너지 손실을 산출해야 한다.

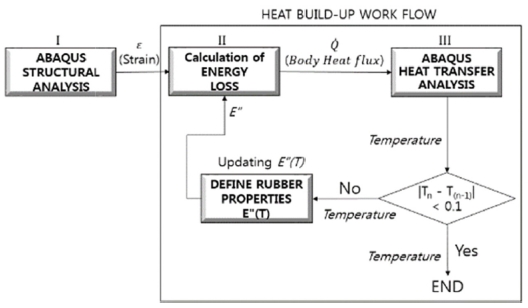
Heat Build-Up 해석 프로세스는 Fig. 6과 같이 나타낼 수 있다. Heat Build-Up 해석 프로세스는 3단계로 구성되어 있으며, 변형 해석(Structural Analysis)을 통해 계산된 변형률을 바탕으로 재료의 Loss Modulus와 식(5)를 이용하여 에너지 손실을 산출하고, 속도 효과를 반영하여 열전달 해석(Heat Transfer Analysis)을 수행하는 단계로 구성된다. 이때, 주행 속도에 따른 효과는 식(6)을 통해 에너지 손실에 속도 효과(Frequency)를 부여함으로써 해석적으로 속도 증가에 따른 온도 상승을 구현할 수 있다.

Fig. 6

Heat build-up work flow

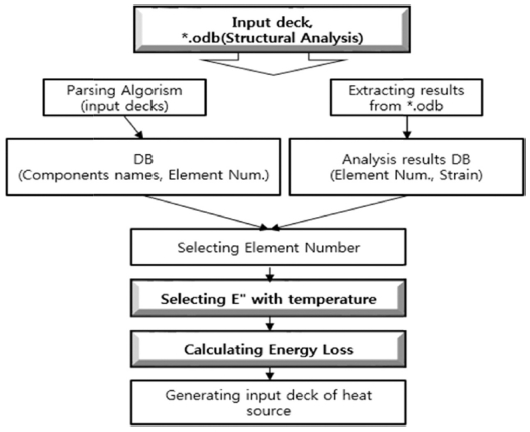
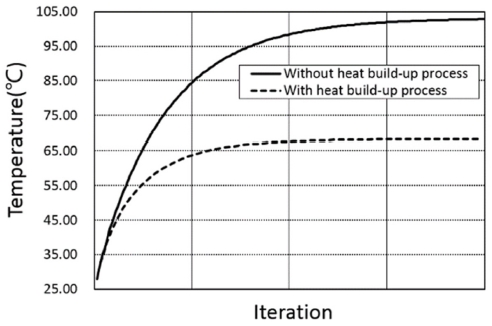
Heat Build-Up 해석 프로세스의 자동 반복 해석을 위해 Fig. 7과 같은 In-House Code를 개발하였다. ABAQUS Input 파일(*.inp)과 구조 해석의 결과 파일(*.odb)에 접근해서 반제품 별로 나누어진 요소정보와 변형률 결과를 Data Base 화해서 각 요소의 손실계수를 자동으로 산출한 후, 열전달 해석을 위한 Input (Body Heat Flux)파일을 최종적으로 생성함으로써 Heat Build-Up 자동 반복 해석을 수행할 수 있다. Heat Build-Up을 적용한 열전달 해석은 Fig. 6에서, 이전의 열전달 해석으로부터 계산된 온도 분포를 다음 열전달 해석의 초기 온도로 적용되고, 이때 새롭게 계산된 Body Heat Flux를 적용하여 열전달 해석을 수행하게 된다. 따라서, 온도 의존성이 해석에 반영되므로 Fig. 8과 같이 Heat Build-Up의 적용 유무에 따라 확연히 다른 온도 증가 양상을 볼 수 있다. 즉, 반복 열전달 해석의 Input 조건인 Body Heat Flux는 고무의 Loss Modulus의 온도 의존성에 따라 낮아지고, 이전 온도 결과가 다음 해석의 초기 온도로 Update 됨으로써 Heat Build-Up을 적용하지 않은 경우보다 온도가 낮아지게 된다.

Fig. 7

Generating heat source work flow for heat transfer analysis

Fig. 8

The results of temperature using the heat build-up analysis

4. 유한요소해석⁶

4.1 구조 해석

런플랫 타이어의 Zero 공기압에서의 주행중 온도 분포 예측을 위해 구조 해석을 수행해야 한다. 구조 해석은 Zero 공기압 상태에서 하중이 부가 되었을 때, 각 요소들의 변형률을 계산하기 위해 실시된다.

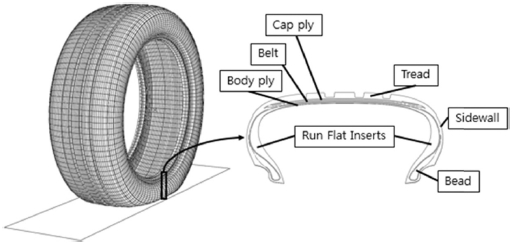
런플랫 타이어의 유한요소 모델은 Fig. 9와 같이 트레드(Tread), 사이드월(Sidewall), 보강고무(Run Flat Inserts) 등으로 구성되어 있다. 3D 모델은 2D 단면 모델을 3차원 모델로 확장 시키는 방법으로 생성된다.

Fig. 9

The finite element model of run flat tire

바디 플라이(Body Ply), 벨트(Belt) 등 복합재는 상용유한요소 소프트웨어 ABAQUS에서 지원하는 REBAR LAYER 요소로 구성되어 있다. 트레드, 사이드월, 보강고무 등은 Hyperelastic으로 가정하고, 해석에 사용되는 고무의 물성은 Fig. 10 단축 인장 시험 Data를 적용하였으며, 그 외 Cord류의 물성은 시험을 통한 탄성계수가 적용된다.

Fig. 10

The stress-strain data of rubber

해석 대상 규격은 225/50RF17로써, 공기압은 Zero, 하중은 규정 하중을 받는 타이어의 구조 해석을 수행하였다. 타이어의 구조는 Table 1과 같이 BP Trun-Up 높이에 따라 사이드월 강성이 서로 상이하며, 본 해석에서는 사이드월 부가 주 관심 대상이며 트레드 영향이 적기 때문에 트레드 패턴은 고려하지 않았다. 해석시간은 ABAQUS를 사용하여 CPU 16 Core로 Ver.당 약 1시간이 소요되었다.

Table 1

Construction of the tire for verification

4.2 열전달 해석

열전달 해석에 적용될 열원은 구조해석을 통해 계산된 변형률의 최대 진폭(Max. Strain Amplitude)으로 Heat Build-Up 프로세스를 통해 산출된다. 이때, 주행 속도는 80 km/h로 속도 효과가 반영되었다.

유한요소 모델은 Fig. 11과 같이 3D모델로 구성되며, 각 부위에 적용되는 열전도, 비열, 밀도는 런플랫 타이어 사이드월에 발생하는 변형율 내에서 유사하기 때문에 Table 2와 같이 적용하였다. 단, 대류 열전달 계수는 정확한 측정이 어렵기 때문에 문헌을 참조하였다.^1,2 그리고 각 요소에 적용된 Body Heat Flux는 원주방향으로 동일한 값을 가진다.¹

Fig. 11

The finite element model for heat transfer analysis

Table 2

The properties of materials

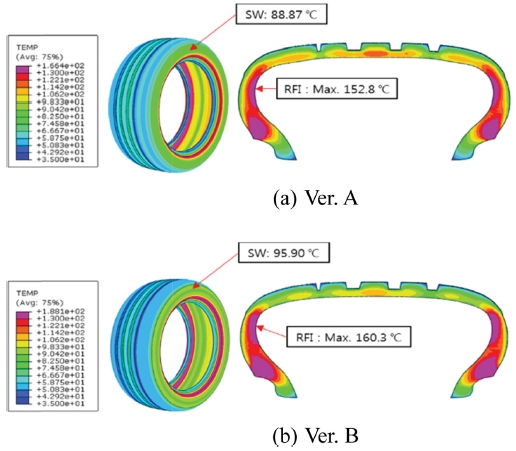
해석이 완료된 온도 분포는 Fig. 12와 같다. 사이드월부의 최대 온도는 보강 고무에서 나타나며, 이때 사이드월 부의 표면 온도는 Ver. A, Ver. B 각각, 88.87^oC, 95.90^oC로써, 사이드월의 변형률이 낮을 수록 온도가 낮다. 즉 사이드월 강성이 높은 Ver. A가 내구성에 유리할 것으로 판단된다.

Fig. 12

The results of heat transfer analysis

5. 실험 결과 및 고찰

5.1 런플랫 타이어 내구성 시험

런플랫 타이어의 내구성 시험은 공기가 없는 상태에서 주행성을 평가하는 것으로 규정 속도에서 일정 시간 이상 주행 가능한지를 평가한다.

본 연구에서는 ASM (Akron Special Machinery) 고속 주행 시험기와 열화상 측정 장비를 사용하여 런플랫 타이어 내구 시험을 실시하였다. 열화상 촬영 시간은 타이어 파손으로 주행 불가 시점까지 진행하였다.

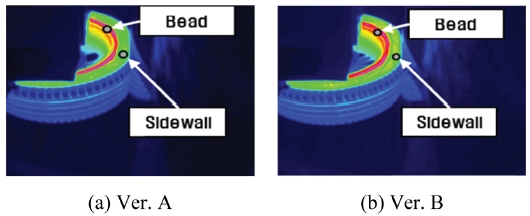
열화상 측정 결과는 Fig. 13과 같으며, 열화상 측정 결과에서 타이어 파손 시 사이드월 부의 최대 온도와 이때 주행 시간을 Table 3에 나타내었다.

Fig. 13

The thermal test results using thermo-graphic camera

Table 3

Results of run flat test

런플랫 시험 모드에서 파손 위치는 Fig. 14처럼 사이드월이며, Fig. 13에서 비드부를 제외하고 가장 높은 온도가 측정되는 위치 또한 사이드월이다. 열화상 측정에 있어, 타이어 외부만 촬영이 가능하다는 한계가 있지만 Fig. 15처럼 타이어 내부의 보강고무가 위치한 부분이 열화로 파손된 점을 고려해 볼 때, 보강고무에서 많은 열이 발생되었음을 추정해 볼 수 있다. 이를 해석 측면에서 살펴보면, Fig. 12에서 사이드월보다 RFI의 온도가 높은 것을 재차 확인할 수 있다. 따라서, 런플랫 타이어의 사이드월 파손은 RFI의 열화에 의한 것으로 유추할 수 있다.

Fig. 14

The thermal test results using thermo-graphic camera

Fig. 15

The thermal test results using thermo-graphic camera

5.2 시험 및 해석 결과 비교

런플랫 타이어의 내구성을 온도 측면에서 시험과 해석을 진행하였으며, 그 결과를 Table 4에 나타내었다.

Table 4

Results of run flat test and analysis

Table 4의 시험 결과에서 Ver. A가 내구성(Running Time)이 우세하게 나타났고, 온도는 낮게 측정되었다. 해석에서도 시험과 동일한 경향이 보여진다. 단, 절대값에서는 차이가 발생하는데, 유추되는 원인으로는 실 타이어의 측정 포인트에 대한 오차, 대류 열전달 계수 및 트레드부의 접촉에 따른 마찰열, Zero 공기압의 가혹 조건에 따른 비선형성 등 전산 모사의 한계와 여러 가지 가정으로 인해 발생된 오차라 생각된다.

하지만 실제 런플랫 타이어 개발 시, 사전 성능이 예측 가능하여 버전별 우선 순위를 가늠할 수 있는 수준이므로 개발 기간 단축이나 제작 샘플 수 선정 등에 충분한 가치가 있는 것으로 판단된다.

결과적으로, 내구성과 온도와의 상관관계는 반비례 관계로써 사이드월의 변형에 의해 발생된 열은 사이드월의 강성이 상대적으로 컸던 Ver. A가 Ver. B보다 열 발생량이 적었기 때문에, Ver. A가 내구성에서 우세한 결과가 나타난 것으로 파악된다.

6. 결론

본 연구에서는 런플랫 타이어의 내구성 향상을 위해 온도 측면에서 살펴보았다. Heat Build-Up 해석 프로세스를 적용하여 재료의 온도 의존성을 고려한 열전달 해석을 수행하였고, 런플랫 타이어의 주행중 온도 분포 예측 및 시험과의 비교를 통해 예측 기법의 효용성을 검증하였다. 런플랫 타이어 개발 시, 이 기법을 활용하여 Zero 공기압에서의 내구 성능을 사전에 예측함으로써 샘플 타이어 제작에 수반되는 시간적, 비용적 손실을 최소화하는데 큰 가치가 있다. 본 연구에서는 런플랫 타이어의 내구성 향상을 위해 온도 측면에서 살펴보았다. Heat Build-Up 해석 프로세스를 적용하여 재료의 온도 의존성을 고려한 열전달 해석을 수행하였고, 런플랫 타이어의 주행중 온도 분포 예측 및 시험과의 비교를 통해 예측 기법의 효용성을 검증하였다. 런플랫 타이어 개발 시, 이 기법을 활용하여 Zero 공기압에서의 내구 성능을 사전에 예측함으로써 샘플 타이어 제작에 수반되는 시간적, 비용적 손실을 최소화하는데 큰 가치가 있다.

또한 본 연구를 통해, 런플랫 타이어의 내구성에 영향을 미치는 주인자는 보강고무(RFI)이며, 보강고무의 설계는 열발생량을 줄이는 방향으로 설계가 이루어져야 된다고 판단된다.

REFERENCES

• Park, H.-C., Youn, S.-K., Song, T.-S., and Kim, N.-J., “Analysis of Temperature Distribution in a Rolling Tire due to Strain Energy Dissipation,” Tire Science and Technology, Vol. 25, No. 3, pp. 214-228, 1997. [https://doi.org/10.2346/1.2137541]
• Sarkar, K., Kwon, Y., and Prevorsek, D., “A New Approach for the Thermomechanical Analysis of Tires by the Finite Element Method,” Tire Science and Technology, Vol. 15, No. 4, pp. 261-275, 1987. [https://doi.org/10.2346/1.2148793]
• Futamura, S. and Goldstein, A., “A Simple Method of Handling Thermomechanical Coupling for Temperature Computation in a Rolling Tire,” Tire Science and Technology, Vol. 32, No. 2, pp. 56-68, 2004. [https://doi.org/10.2346/1.2186774]
• Yavari, B., Tworzydlo, W., and Bass, J., “A Thermomechanical Model to Predict the Temperature Distribution of Steady State Rolling Tires,” Tire Science and Technology, Vol. 21, No. 3, pp. 163-178, 1993. [https://doi.org/10.2346/1.2139527]
• Ciesielski, A., “Introduction to Rubber Technology,” RAPRA Technology Ltd., pp. 139-141, 1999.
• Systèmes, D., “Abaqus Analysis User’s Guide,” Solid (Continuum) Elements, Vol. 6, 2014.