초정밀 대형 머시닝센터의 바닥 지반 설계에 관한 연구
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
With the advent of high-tech products, the need for ultra-precision machining has become increasingly necessary, along with the need for a jig center machining center capable of precision machining. A jig center maintains the accuracy of a jig borer, and also has an automatic tool changer like that of a machining center. It performs various machining functions in addition to hole machining and is the most precise and rigid machine tool. Various control methods and analytical techniques to improve machining accuracy are currently being developed in the field of ultra-precise large-scale machine tools. One relevant finding is that the degree of deformation varies depending on the weight of the machine tool as well as the ground conditions. It is therefore necessary to optimize ground conditions before installing the machine tools so as to improve the machining accuracy. The depth of concrete as well as the depth and diameter of grout were selected as variables. We developed the simulation case through structural analysis to consider the position of columns and tables. As a result of optimizing the foundation condition, it was found that the relative displacement error was reduced by up to 98% compared to the rigid foundation condition.
Keywords:
Highly precision, Machining center, Optimal foundation, Processing precision키워드:
고정밀, 머시닝센터, 지반 최적화, 가공정밀도1. 서론
첨단기술이 발달하여 다양한 분야에서 정밀가공제품의 수요가 급증함에 따라 높은 수율로 정밀 가공이 가능한 머시닝 센터 도입이 필수적이다. 또한 가공대상의 모양, 크기, 재질에 국한되지 않고 전반적인 가공물에 대해 가공 정밀도의 중요성이 높아지고 있기 때문에 고정밀 고강성 장비의 수요가 확대되고 있다.
머시닝 센터의 가공 정밀도를 향상시키기 위해 다양한 제어방법과 분석기술 개발 등이 이루어 지고 있으며,1-8 그 중에서도 초정밀 대형 머시닝센터 같은 경우는 자중에 의한 변형량 차이가 크기 때문에 머시닝 센터의 가공정밀도를 향상시킬 수 있도록 바닥 지반 최적화가 필요하다.
본 연구에서는 초정밀 대형 머시닝센터의 가공정밀도를 향상시키기 위해 최적화 된 바닥 지반 형상을 제시한다. 바닥 지반 형상을 최적화 하기 위해 가공장비 구조물과 바닥 지반의 일체형 모델을 설계하고9-13 바닥 지반의 기초 조사를 통해 재료를 선정하여 최적화의 변수로 선정하였다. 또한 구조해석을 통해 이송 유닛인 컬럼과 테이블의 위치변화를 고려한 시뮬레이션 케이스를 결정하였고 목적함수를 두어 가공장비 구조물의 최적 지반 조건을 도출하였다.
2. 바닥 지반 형상 최적화
2.1 시뮬레이션 모델 선정
공작기계의 주요 연구 내용인 구조의 정적 변형, 고유진동수, 모드형상 등의 시뮬레이션을 통하여 바닥 지반을 최적화 하기 위해 공작기계 구조물과 바닥 지반을 일체화하여 모델을 구성하였다.14 가공장비 구조물과 바닥 지반의 일체형 모델 사용시 실시간으로 변화하는 운동 유니트를 고려하기 어렵기 때문에 가공 위치에 따른 가공장비 구조물의 케이스를 분류하였다.
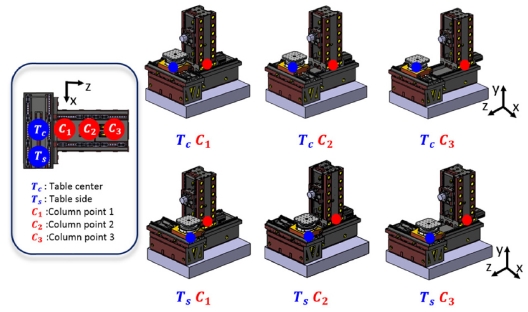
Fig. 1은 이송 유니트 위치에 따른 구조물 케이스에 대한 그림으로 가공 장비 구조물 케이스는 X축으로 2지점 Z축 3지점을 선정하여 총 6개의 케이스로 구분하였다. 시뮬레이션 케이스를 선정하기 위해 가공 장비의 스핀들 중앙(Tool Center Point)과 워크피스 중앙(Workpiece Center Point)의 초기 변위와 바닥기초 조건에 따른 변위를 이용하여 6개 케이스에 따른 상대변위 오차를 구하였다. 상대변위 오차가 가장 큰 케이스를 시뮬레이션 케이스로 선정하여 최적화된 바닥 지반 조건이 다른 케이스에도 적용될 수 있도록 시뮬레이션 케이스를 선정하였다.
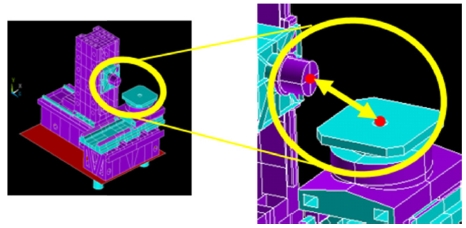
Fig. 2는 상대 변위 오차의 측정 위치를 나타내며 상대 변위 오차는 가공 장비의 스핀들 중앙(Tool Center Point)과 워크피스 중앙(Workpiece Center Point)의 거리와 각 지점의 변형량을 이용하여 설정하였으며, 상대 변위 오차는 식(1)과 같이 나타낼 수 있다.
| (1) |
최대 상대 변위 오차가 발생하는 케이스를 얻기 위하여 대형 가공장비의 3점 지지점을 고정하여 가공장비의 하중으로 인한 구조해석을 실행하였다. 모든 케이스의 T.C.P (Table Center Point), W.C.P (Workpiece Center Point)간의 상대 변위 오차를 구하여 Table 1에 나타내었다.
케이스 TcC2에서 최대 상대 변위 오차가 발생하는 것을 확인할 수 있으며 TcC2를 시뮬레이션 모델로 선정하여 가공 장비 구조물과 바닥 지반이 일체화 된 시뮬레이션 모델을 설계하였다.
2.2 통합구조 모델 설계 및 구속 조건
가공 구조물과 바닥 지반의 통합구조 모델을 설계하기 위해 바닥 지반 기초를 설계하였다. 바닥 지반 기초 구조는 총 3개의 물성으로 가정하였으며 소일, 콘크리트, 그라우트 층으로 구성된다.
소일층은 실제로 다양한 물성과 형태를 지니고 있으나 일반적으로 사용하는 소일의 물성치를 이용하여 시뮬레이션을 진행하였다. 시뮬레이션에 사용된 소재의 물성치는 Table 2에 나타냈다.
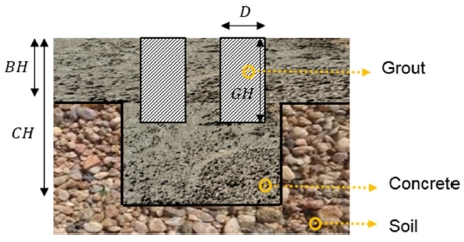
바닥 지반 기초 구조의 단면은 Fig. 3과 같으며 BH는 공장 지반 콘크리트의 기본 깊이를 나타내고, 200 mm로 설정하였다. CH는 장비를 지지하는 전체적인 콘크리트 깊이를 나타내며, GH는 가공장비 구조물의 3점 지지점 지반의 그라우트의 깊이를 나타내며 D는 그라우트의 직경을 나타낸다.
시뮬레이션 모델은 가공장비와 바닥 지반이 일체화된 통합구조를 사용하여 전체적인 지반 최적화 시뮬레이션을 진행한다.
컬럼과 테이블의 위치변화에 따라 최대 상대 변위 오차를 가지는 TcC2 모델을 이용하여 가공 장비 구조물과 바닥 지반 통합구조 모델을 구성하였다. 소일층은 콘크리트의 깊이, 그라우트의 깊이와 직경조건이 변하더라도 전체 소일층의 크기는 동일하도록 모델링하였다.
전체 지반 구조의 4개 라인의 자유도를 구속하고 중력조건을 부여하였고 가공에 있어서 운동 유니트에 대한 이송체가 움직일 때 발생하는 마찰과 진동에 의한 바닥 지반 형상을 최적화 하는 것이 중요하기 때문에 스핀들에 가진력을 부여하여 변형량을 도출하였다.
또한 기존 장비 구조물은 3점 지지이기 때문에 가공 구조물과 바닥 지반의 연결 부는 3점으로 모델링하여 가공 구조물과 바닥 지반을 연결하였다.
3. 최적화 결과 및 검토
3.1 설계 변수
실제 공작기계가 설치 되기 전 바닥기초 공사를 진행할 때 사용하는 2가지 재료의 형상에 따라 설계변수를 선정하였다. Table 3은 설계변수와 설계변수의 범위를 나타낸다. 콘크리트 깊이, 그라우트 깊이와 직경으로 3개의 설계변수를 선정하였다. 재료의 형상을 설계변수로 선정한 이유는 부피에 따라 바닥 기초 공사의 초기 비용이 결정되기 때문이다. 설계변수의 범위는 현장에서 경험적으로 사용되는 데이터를 기준으로 선정하였다.
최적화에 앞서 설계변수가 상대 변위 오차에 미치는 경향을 알아보기 위하여 Fig. 4를 통하여 설계변수가 상대 변위 오차에 미치는 영향을 파악했다.
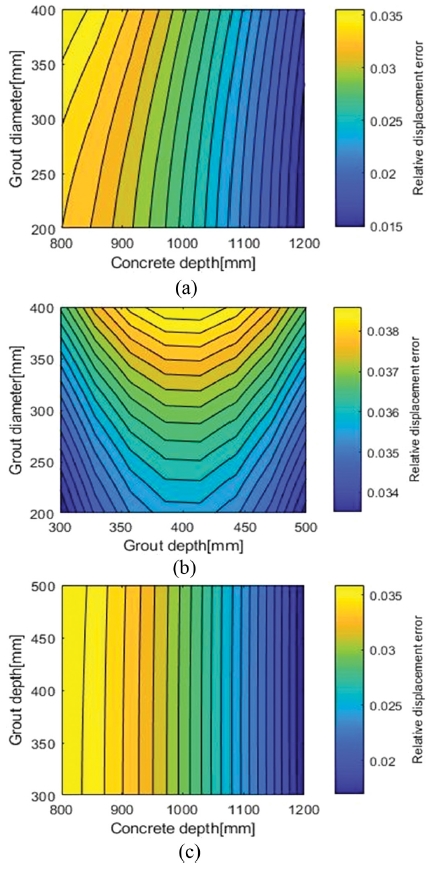
(a) Contour plot of relative displacement error vs grout diameter, concrete depth (b) Contour plot of relative displacement error vs grout diameter, grout depth (c) Contour plot of relative displacement error vs concrete depth, grout depth
콘크리트 깊이가 깊어질수록 상대 변위 오차는 줄어들고, 그라우트는 깊이보다 넓이가 넓어질수록 상대 변위 오차가 줄어드는 것을 볼 수 있다.
전체적으로 다른 변수에 비해 콘크리트 깊이가 상대 변위 오차에 민감하게 반응하는 것을 볼 수 있으며, 다음으로 그라우트 직경, 그라우트 깊이 순서로 상대 변위 오차에 더 민감하게 반응하는 것으로 분석할 수 있다.
3.2 최적화 목적 함수
가공장비의 바닥 지반 형상 최적화의 목적 함수는 무게와 상대변위 오차의 최소화로 설정하였다. 각각의 목적 함수에 가중치를 부여하였고 두 개의 목적함수를 동시에 고려하기 위해 최종적인 목적 함수를 설정하여 최적화하였다.
| (2) |
식(2)는 최적화 목적함수를 나타내는 식이다.
3.3 지반 형상 최적화 결과
가공장비 구조물과 바닥 지반이 일체화된 통합 FEM 모델의 구조해석 결과로 T.C.P와 W.C.P의 상대 변위 오차와 무게를 얻은 후 그 결과를 목적함수에 맞추어 최적화 결과값을 얻었다.
3.4 최적 지반 형상 도출
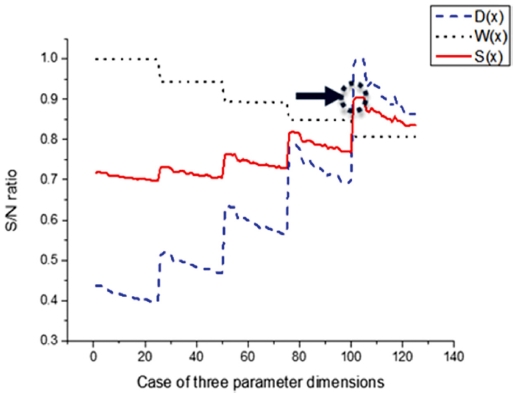
Fig. 5는 바닥 지반 형상의 최적화 결과값을 S/N비로 나타낸 것이다. 가로축은 시뮬레이션의 계산 횟수이고, 세로축은 S/N비를 나타낸 것이다. S/N비는 높을수록 좋은 값이며, 무게와 상대변위의 목적함수와, 최종 목적함수를 그래프로 나타내었다.
무게와 상대변위 오차의 가중치를 α : β = 1 : 1로 두어 최적화한 결과 Table 4에 나타난 것과 같이 무게와 상대 변위 오차의 S/N비 합을 통해 최적의 바닥 지반 형상을 도출하였다.
3.5 케이스 별 상대 변위 오차 비교
Table 5는 지반 조건에 따른 상대 변위 오차 값의 비교를 나타낸다. 강체 지반 조건에서는 TcC2 케이스에서 최대 상대 변위 오차인 29.49 μm의 상대 변위 오차가 발생하며, 최적화 된 지반조건을 사용할 경우 TsC1 케이스에서 최소 상대 변위 오차인 0.19 μm가 발생하는 것을 볼 수 있다. 강체 지반 조건에 비해 최적화 된 지반의 상대 변위 오차는 전체적으로 감소한 것을 확인하였다.
컬럼이 C3에 위치한 경우에는 실제 가공이 일어나는 위치가 아닌 공구를 교환하는 위치이기 때문에 가공정밀도에 영향을 미치지 않으므로 해당 위치의 상대 변위 오차는 고려하지 않았다.
지반 조건에 따른 변형량과 경향은 Fig. 6에서 볼 수 있다. Fig. 6(a)는 강체 지반 조건에서의 변형량을 나타내고 Fig. 6(b)에서는 최적화 된 지반에서의 변형량을 나타낸다. 최적 지반 조건일 때 가공 장비 구조물의 최대 처짐 변형량은 강체 지반 조건에 비해 증가하지만, 상대 변위 오차는 줄어드는 것을 볼 수 있다. 이는 상대 변위 오차의 기준이 되는 T.C.P, W.C.P가 함께 변형되기 때문에 지반의 형태에 따라 강체 지반 조건에 비해 상대 변위 오차가 줄어들기 때문이다.
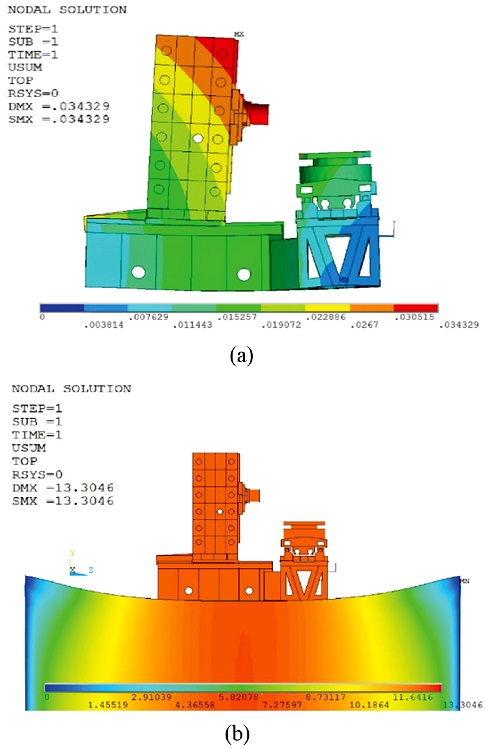
(a) Contour plot of deformation of machining center in rigid foundation (b) Contour plot of Deformation of machining center in optimal foundation
TsC1에서 상대 변위 오차가 최대 98% 줄었으며 무게는 최대 무게 대비 0.1% 감소하였다.
4. 결론
본 연구는 대형 가공 장비의 가공정밀도를 향상시키기 위해 컬럼과 테이블의 위치 변화에 따른 지반 조건을 최적화하여 최적 지반 조건을 도출하였다.
(1) 가공장비의 정밀도를 향상시키기 위하여 T.C.P.와 W.C.P의 상대 변위 오차를 최소화하고 지반의 무게를 최소화 하기 위한 목적함수를 구성하였다.
(2) 콘크리트 깊이가 깊어질수록 상대 변위 오차는 크게 줄어들며, 콘크리트 깊이가 다른 변수에 비해 상대 변위 오차에 대한 영향도가 큰 것을 볼 수 있다.
(3) 최적화된 지반이 강체 조건의 지반에 비해 상대 변위 오차값이 작은 이유는 강체 지반 조건일 경우 하중으로 인한 기계적 변형을 기계 구조물 내에서 나타나게 되고 최적화된 지반은 지반의 변형으로 인해 기계 구조물 내에서의 변형을 줄이기 때문에 상대 변위 오차도 함께 줄어들기 때문이다.
(4) 본 연구 결과를 통해 바닥 지반 조건을 최적화하여 대형 가공 기계뿐만 아니라 대형 기계, 장비 등 다양한 분야의 가공정밀도를 향상시킬 수 있을 것이다.
NOMENCLATURE
| De(i, j, k) : | Relative displacement error by variable |
| W(i, j, k) : | Weight of foundation by variable |
| S(i, j, k) : | Multipurpose function for optimal foundation |
| xw : | Workpiece center point(W.C.P) x-aixs coordinate |
| : | Workpiece center point(W.C.P) x-aixs variation |
| xT : | Tool center point(T.C.P) x-aixs coordinate |
| : | Tool center point(T.C.P) x-aixs variation |
| yw : | Workpiece center point(W.C.P) y-aixs coordinate |
| : | Workpiece center point(W.C.P) y-aixs variation |
| yT : | Tool center point(T.C.P) y-aixs coordinate |
| : | Tool center point(T.C.P) y-aixs variation |
| zw : | Workpiece center point(W.C.P) z-aixs coordinate |
| : | Workpiece center point(W.C.P) z-aixs variation |
| zT : | Tool center point(T.C.P) z-aixs coordinate |
| : | Tool center point(T.C.P) z-aixs variation |
| : | Minimum relative displacement error |
| W* : | Minimum weight of foundation |
| α : | Weighting factor on relative displacement error |
| β : | Weighting factor on weight of foundation |
Acknowledgments
본 연구는 2018년도 산업통상자원부(10052978)의 연구비 지원으로 수행된 연구 결과임.
REFERENCES
-
Park, B. H. and Lee, C. W., “A Development on the Fault Prognosis of Bearing with Empirical Mode Decomposition and Artificial Neural Network,” Journal of the Korean Society for Precision Engineering, Vol. 33, No. 12, pp. 985-992, 2016.
[https://doi.org/10.7736/KSPE.2016.33.12.985]

-
Yun, S. H., Park, B. H., and Lee, C. W., “A Study on Fault Diagnosis Algorithm for Rotary Machine Using Data Mining Method and Empirical Mode Decomposition,” Journal of the Korean Society of Manufacturing Process Engineers, Vol. 15, No. 4, pp. 23-29, 2016.
[https://doi.org/10.14775/ksmpe.2016.15.4.023]

-
Kim, D. H., Lee, C. M., and Choi, H. J., “Static and Dynamic Analysis and Optimization Design of 40,000-rpm High-Speed Spindle for Machine Tools,” Transactions of the Korean Society of Mechanical Engineers A, Vol. 37, No. 1, pp. 105-111, 2013.
[https://doi.org/10.3795/KSME-A.2013.37.1.105]

-
Jang, S. H., Choi, Y. H., Kim, S. T., An, H. S., Choi, H. B., et al., “Development of Core Technologies of Multi-tasking Machine Tools for Machining Highly Precision Large Parts,” Journal of the Korean Society for Precision Engineering, Vol. 29, No. 2, pp. 129-138, 2012.
[https://doi.org/10.7736/KSPE.2012.29.2.129]

-
Choi, Y. H., Ha, G. B., and An, H. S., “Stiffness Evaluation of a Heavy-Duty Multi-Tasking Lathe for Large Size Crankshaft Using Random Excitation Test,” Journal of the Korean Society for Precision Engineering, Vol. 31, No. 7, pp. 627-634, 2014.
[https://doi.org/10.7736/KSPE.2014.31.7.627]

-
Kim, B.-S., “Integrated Dynamic Simulation of a Magnetic Bearing Stage and Control Design,” Journal of The Korean Society of Manufacturing Technology Engineers, Vol. 22, No. 4, pp. 730-734, 2013.
[https://doi.org/10.7735/ksmte.2013.22.4.730]

- Lee, C.-M., Gwon, B.-D., Go, T.-J., Jeong, J.-Y., and Jeong, W.-J., “A Study on the Improvement of Machining Accuracy in High Speed Machining using Design of Experiments,” Journal of the Korean Society for Precision Engineering, Vol. 19, No. 7, pp. 88-96, 2002.
-
Oh, N.-S., Kim, D.-H., and Lee, C.-M., “A Study on the Analysis of 20,000 rpm Heavy-Cutting Spindle for Precision Machining,” Journal of the Korean Society for Precision Engineering, Vol. 32, No. 1, pp. 57-61, 2015.
[https://doi.org/10.7736/KSPE.2015.32.1.57]

-
Dutta, S. C. and Roy, R., “A Critical Review on Idealization and Modeling for Interaction Among Soil–Foundation–Structure System,” Computers & Structures, Vol. 80, Nos. 20-21, pp. 1579-1594, 2002.
[https://doi.org/10.1016/S0045-7949(02)00115-3]

-
Kocak, S. and Mengi, Y., “A Simple Soil–Structure Interaction Model,” Applied Mathematical Modelling, Vol. 24, Nos. 8-9, pp. 607-635, 2000.
[https://doi.org/10.1016/S0307-904X(00)00006-8]

-
Padron, L., Aznárez, J., and Maeso, O., “Dynamic Structure–Soil–Structure Interaction between nearby Piled Buildings under Seismic Excitation by BEM–FEM Model,” Soil Dynamics and Earthquake Engineering, Vol. 29, No. 6, pp. 1084-1096, 2009.
[https://doi.org/10.1016/j.soildyn.2009.01.001]

-
Wang, S. and Schmid, G., “Dynamic Structure-Soil-Structure Interaction by FEM and BEM,” Computational Mechanics, Vol. 9, No. 5, pp. 347-357, 1992.
[https://doi.org/10.1007/BF00370014]

-
Wolf, J. P. and Song, C., “Some Cornerstones of Dynamic Soil–Structure Interaction,” Engineering Structures, Vol. 24, No. 1, pp. 13-28, 2002.
[https://doi.org/10.1016/S0141-0296(01)00082-7]

- Park, C.-H., Hwang, J.-H., Lee, C.-H., and Song, C.-G., “Development of an Accuracy Simulation Technology for Mechanical Machines,” Journal of the Korean Society for Precision Engineering, Vol. 28, No. 3, pp. 259-264, 2011.