육각 격자구조를 갖는 원통형 복합재 격자 구조물의 유한요소 모델링 기법 연구
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
In this paper, finite element modeling methods for cylindrical composite lattice structures were verified through natural frequency test. Finite element models for cylindrical composite lattice structure were developed using beam, shell and solid elements. Natural frequency test was measured using impact test method under free-boundary condition. The analysis result of the beam element model showed up to 23% errors because the beam element could not consider the degradation of mechanical properties of non-intersection parts of the composite lattice structures. On the other hand, the natural frequencies of finite element analysis for shell and solid element models showed good results with natural frequencies test. From the analysis of the experiment, finite element model for composite lattice structures should use shell or solid element which takes into consideration the intersection and non-intersection parts.
Keywords:
Cylindrical composite lattice structure, Finite element modeling method, Natural frequency test키워드:
원통형 복합재 격자 구조물, 유한요소 모델링 기법, 고유진동수 시험1. 서론
복합재 격자 구조물은 최적의 형상 설계와 경량 재료인 복합재를 적용하여 경량화를 극대화한 구조물이다. 구조하중을 지지하기 위한 최소의 두께를 가진 단위 격자 형상이 반복되는 구조를 가지고 있다. 복합재 격자 구조물은 주로 원통형 및 콘(Cone)형으로 제작되어 경량화가 구조물의 성능 향상에 매우 큰 영향을 미치는 고성능 유도무기, 위성 발사체의 페어링 등에 적용되고 있다. 러시아, 미국 등에서는 우주항공과 군수 분야에서 항공기 동체, 미사일 그리고 우주 발사체 등에 적용하여 사용되고 있다. 복합재 격자 구조물에 대한 기술은 유도 무기, 위성 발사체 등의 성능에 직접적으로 영향을 미치기 때문에 선진국에서는 기술 보호를 통해 유출을 방지하고 있어 자체적인 연구가 필수적이다.
복합재 격자 구조물이 적용된 대표적인 사례로는 러시아에서 필라멘트 와인딩 공법을 이용하여 제작된 복합재 격자구조체를 항공기 동체와 Proton-M 로켓의 단 연결부에 적용한 사례가 있다.1-3 그 외에 Belardo 등4은 탄소 섬유 복합재 격자 구조물을 적용한 재진입 운반체의 설계를 수행하였고, Krishna 등5은 우주발사체 내부 탱크에 적용하기 위한 복합재 격자 구조물을 설계하였으며 Querin 등6은 항공기 동체에 적용하기 위한 복합재 격자 구조물의 최적 설계 연구를 수행하였다. Kanou 등7은 수치해석적 방법을 통한 원통형 복합재 격자 구조물의 구조성능 평가에 대한 연구를 수행하였다.
국내에서는 도영대 등8,9이 필라멘트 와인딩 공법을 이용한 복합재 격자 구조물의 설계, 제작 그리고 시험에 대한 연구를 수행한 사례가 있으나 이는 매우 기초 단계로 기술 보유국과 격차가 매우 큰 실정이다.
또한 Vasiliev가 정립한 복합재 격자 구조물의 설계 이 론은 보이론을 기반으로 설계를 수행하는 이론이며10 식(1)을 통해 질량을 최소화 하는 것을 목적으로 하고 있다.
| (1) |
필라멘트 와인딩 공법을 통해 제작되는 복합재 격자 구조물은 공정의 특성상 섬유 교차부가 발생되는데 이는 비교차부와 섬유 체적률이 다르기 때문에 밀도, 기계적 물성 등의 차이가 발생된다. 그러나 보 이론을 적용할 경우, 섬유 교차부를 고려할 수 없기 때문에 복합재 격자 구조물의 정확한 구조 안전성 평가를 수행할 수 없다.
이에, 본 논문에서는 원통형 복합재 격자 구조물의 수치 해석적 구조 안전성 평가를 위한 유한요소 모델링 기법에 대해 연구를 수행하였다. 필라멘트 와인딩 공법을 이용해 제작된 복합재 격자 구조물을 사용하여 연구를 수행하였으며 고유진동수 시험 및 해석 결과를 비교하여 유한요소 모델링 기법을 검증하였다.
2. 복합재 격자 구조물의 고유진동수 해석
2.1 원통형 격자 구조물의 형상
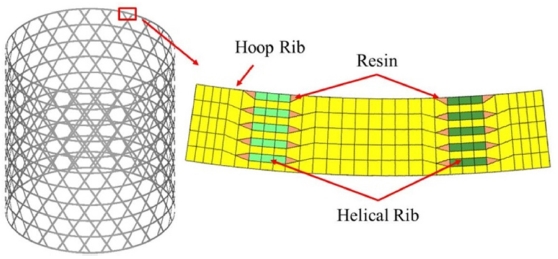
필라멘트 와인딩 공법을 통해 제작되는 원통형 복합재 격자 구조물은 Fig. 1과 같이 격자 형상을 갖는 실리콘 금형 위에 수지가 함침된 섬유를 와인딩하여 제작하게 된다.
복합재 격자 구조물은 공정 특성상 섬유 교차부가 발생된다. 섬유 교차부는 비교차부와 비교하여 두 배수의 섬유가 와인딩되는 부분으로 구조물의 두께 불균형에 원인이 된다. 복합재 격자 구조물의 두께 불균형을 극복하기 위해 Fig. 2와 같이 섬유 교차부의 압착 공정을 수행한다. 압착 공정을 통해 섬유 교차부의 두께가 감소하며 이탈되는 잉여 수지가 비교차부로 이동해 구조물의 두께가 균일하게 제작된다.
그러나 섬유 교차부 경계에는 와인딩된 섬유 수의 차이로 인해 Fig. 3과 같이 수지 응집부가 존재하며 이를 고려할 수 있는 유한요소 모델링 기법을 도출할 필요가 있다.
본 연구에서는 선행 연구를 통해 설계된 직경 600 mm, 높이 617.87 mm를 갖는 원통형 복합재 격자 구조물을 적용하였다.11 복합재 격자 구조물은 필라멘트 와인딩 공법을 통해 제작되었으며 Fig. 4와 같은 형상을 갖는다. Table 1은 복합재 격자 구조물의 설계 치수를 보여준다.
이때 섬유는 25층으로 와인딩 되었으며 섬유 교차부의 경우는 두 배수인 50층이 와인딩 되어 제작 되었다.
2.2 원통형 격자 구조물의 유한요소 모델
원통형 복합재 격자 구조물의 유한요소 모델은 상용 유한요소해석 프로그램인 ABAQUS v.6.13을 사용하여 각각 빔(Beam), 쉘(Shell) 그리고 솔리드(Solid) 요소를 사용 하여 생성하였다.
빔 모델은 B31 요소를 적용하여 53,376개의 절점과 54,096개의 요소, 쉘 모델은 S4R 요소를 적용하여 134,928개의 절점과 114,624개의 요소, 솔리드 모델은 C3D8R 요소를 적용하여 809,568개의 절점과 573,568개의 요소로 유한요소모델을 생성하였다. 빔 모델은 요소의 특성상 섬유 교차부가 고려되지 않았으며, 쉘과 솔리드 모델은 섬유 교차부를 고려하여 모델링을 수행하였다. 솔리드 모델의 경우, 섬유의 연속성을 모사할 수 있도록 Fig. 5와 같이 섬유 교차부를 모델링하였다.
원통형 복합재 격자 구조물은 Toray사의 T700 탄소 섬유와 에폭시 타입의 수지를 사용하여 제작되었으며 Table 2의 소재 물성이 고유진동수 해석에 적용되었다. 이때 섬유 교차부와 비교차부의 섬유 체적률을 측정하여 각각 0.7과 0.3을 확인하였으며 식(2)와 식(3)의 혼합물 법칙(Rule of Mixture)을 통해 비교차부의 물성과 밀도를 도출하여 적용하였다.
| (2) |
| (3) |
빔 모델은 섬유 비교차부의 기계적 물성 저하를 고려할 수 없기 때문에 섬유 교차부의 물성을 적용하였으며 밀도는 원통형 복합재 격자 구조물의 무게를 부피로 나눈 1,512 kg/m3을 적용하였다.
2.3 원통형 격자 구조물의 고유진동수 해석
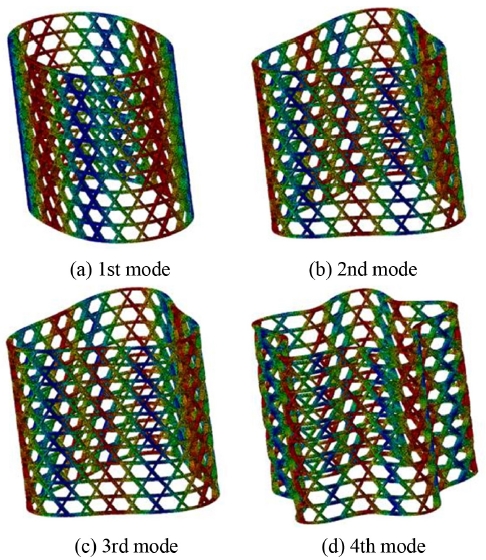
원통형 복합재 격자 구조물의 고유진동수 해석은 ABAQUS v.6.13을 사용하였으며 구조물을 구속하지 않는 자유 경계조건 하에서 Lanczos 알고리즘을 사용하여 고유진동수 해석을 수행하였다. 고유진동수 해석 결과는 Table 3과 같이 도출되었으며 빔 모델의 결과가 쉘과 솔 리드 모델의 결과와 큰 차이가 발생하는 것을 확인하였다. 섬유 비교차부의 기계적 물성 저하를 고려하지 못하는 빔 요소와 이를 고려하는 쉘과 솔리드 요소의 차이 때문으로 판단된다. Fig. 6은 솔리드 모델의 모드 형상을 보여준다. 원통형 복합재 격자 구조물의 모드 형상은 일반적인 원통의 모드 형상과 유사하게 발생하였다.
3. 복합재 격자 구조물의 고유진동수 시험
원통형 복합재 격자 구조물의 고유진동수 시험은 고유진동수해석과 동일한 조건으로 수행하였다. 지름 1.168 mm의 금속 와이어를 격자 사이로 관통시켜 Fig. 7과 같이 공중에 매달아 자유경계조건을 모사하였다.
원통형 복합재 격자 구조물의 상단에 왁스를 이용해 3축 가속도 센서를 부착하고 임팩트 해머와 오실로스코프를 이용해 충격 시험법으로 고유진동수를 측정하였다. 이때 고유진동수는 10회 측정하여 평균값을 고속 푸리에 변환을 통해 도출하였다. Fig. 8(a)는 3축 가속도 센서의 부착 모습을 보여주고 Fig. 8(b)는 시험에 사용된 오실로스코프를 보여준다.
시험을 통해 도출된 고유진동수는 4차 모드까지 측정하여 해석 결과와 비교하였다. Table 4와 같이 빔 모델의 경우, 시험 결과와 비교하여 4차 모드에서 최대 22.93%의 오차가 발생하였으며 전체적으로 큰 오차가 발생하는 것을 확인하였다. 쉘과 솔리드 모델의 경우, 최대 오차는 각각 4차 모드와 2차 모드에서 14.60%와 14.50%로 발생하 였으나 그 외의 모드에서는 10% 이하의 오차가 발생하였다.
쉘과 솔리드 모델의 고유진동수 해석 결과는 시험 결과와 유사하게 도출되었으나 섬유의 연속성 및 수지 응집부를 고려해 모델링을 수행한 솔리드 모델의 결과가 상대적으로 시험 결과와 잘 일치하는 것을 확인하였다. 따라서 원통형 복합재 격자 구조물의 유한요소 모델은 섬유 교차부와 비교차부를 고려할 수 있는 쉘 또는 솔리드 요소를 적용해 생성해야 할 것으로 판단된다.
발생된 오차는 원통형 복합재 격자 구조물의 부분별 섬유 체적률을 측정하여 정확한 밀도와 기계적 물성을 적용하면 감소할 수 있을 것으로 판단된다.
4. 결론
본 논문에서는 필라멘트 와인딩 공법을 통해 제작된 원통형 복합재 격자 구조물의 구조 안전성 평가를 위한 유한요소 모델링 기법에 대해 연구를 수행하였으며 다음과 같은 결론을 얻었다.
(1) 필라멘트 와인딩 공법으로 제작되는 복합재 격자 구조물의 섬유 교차부 및 수지 응집부를 고려할 수 있는 유한요소 모델링 기법을 도출하였다.
(2) 빔, 쉘 그리고 솔리드 요소를 사용하여 생성한 유한요소 모델의 고유진동수 해석 및 시험을 비교한 결과, 쉘과 솔리드 모델의 해석 결과가 시험 결과와 유사한 결과가 도출되었으나 섬유 연속성 및 수지 응집부를 고려한 솔리드 모델의 해석 결과가 상대적으로 잘 일치하는 것을 확인하였다.
(3) 빔 모델의 해석 결과는 시험과 비교하여 큰 오차가 발생하였으며 이는 섬유 비교차부의 기계적 물성 저하를 고려할 수 없는 빔 요소의 한계 때문으로 판단되어 원통형 복합재 격자 구조물의 유한요소 모델은 섬유 교차부와 비교차부를 모사할 수 있는 쉘 또는 솔리드 요소를 적용해야 할 것으로 판단된다.
(4) 원통형 복합재 격자 구조물의 각 부분별 섬유 체적률 측정을 통해 정확한 밀도와 기계적 물성을 적용하면 더욱 정확도가 향상될 것으로 판단된다.
(5) 연구를 통해 도출된 원통형 복합재 격자 구조물의 유한요소 모델링 기법은 향후 연구될 콘형 복합재 격자 구조물의 유한요소 모델링에 활용할 수 있을 것으로 사료된다.
NOMENCLATURE
| ac : | Distance of hoop rib |
| ah : | Distance of helical rib |
| δc : | Width of hoop rib |
| δh : | Width of helical rib |
| ρc : | Density of hoop rib |
| ρh : | Density of helical rib |
| H : | Thickness of rib |
| L : | Length of lattice structure |
| R : | Radius of cylindrical lattice structure |
| Ef : | Elastic modulus of fiber |
| EL : | Longitudinal modulus of composite |
| EM : | Elastic modulus of matrix |
| ET : | Transverse modulus of composite |
| Vf : | Fiber volume fraction |
| Vm : | Matric volume fraction |
Acknowledgments
This paper was presented at KSPE Spring Conference 2017
본 연구는 민군협력진흥원(ICMTC)의 재원으로 복합재 Lattice 격자구조체 기술개발(15-CM-MA-12)의 지원을 받아 수행한 연구과제입니다.
REFERENCES
-
Vasiliev, V., Barynin, V., and Rasin, A., “Anisogrid Lattice Structures-Survey of Development and Application,” Composite Structures, Vol. 54, Nos. 2-3, pp. 361-370, 2001.
[https://doi.org/10.1016/S0263-8223(01)00111-8]

-
Vasiliev, V. and Razin, A., “Anisogrid Composite Lattice Structures for Spacecraft and Aircraft Applications,” Composite Structures, Vol. 76, Nos. 1-2, pp. 182-189, 2006.
[https://doi.org/10.1016/j.compstruct.2006.06.025]

-
Vasiliev, V. V., Barynin, V. A., and Razin, A. F., “Anisogrid Composite Lattice Structures-Development and Aerospace Applications,” Composite Structures, Vol. 94, No. 3, pp. 1117-1127, 2012.
[https://doi.org/10.1016/j.compstruct.2011.10.023]

-
Belardo, M., Paletta, N., and Mercurio, U., “Conceptual Design of the Composite Sandwich Fuselage of a Re-Entry Vehicle,” Materialwissenschaft und Werkstofftechnik, Vol. 46, Nos. 4-5, pp. 420-433, 2015.
[https://doi.org/10.1002/mawe.201500417]

- Krishna Prasanth, K. and Muruganantham, P., “Design and Analysis of a Typical Inter-Tank Structure of a Launch Vehicle Using Integrally Stiffened Construction,” International Journal of Research in Engineering & Technology Vol. 1, No. 1, pp. 21-34, 2013.
- Querin, O. M., Toporov, V., Liu, D., Busch, L., and Hühne, C., et al., “Topology and Parametric Optimization of a Lattice Composite Fuselage Structure,” https://altairuniversity.com/wp-content/uploads/2014/04/Topology_and_Parametric_Optimization-of-a-Latice_Composite_Fuselage_Structure_as_published.pdf, (Accessed 2 MAY 2018)
-
Kanou, H., Nabavi, S., and Jam, J., “Numerical Modeling of Stresses and Buckling Loads of Isogrid Lattice Composite Structure Cylinders,” International Journal of Engineering, Science and Technology, Vol. 5, No. 1, pp. 42-54, 2013.
[https://doi.org/10.4314/ijest.v5i1.4]

- Doh, Y.-D., Chung, S.-K., Lee, S.-W., and Son, J.-H., “Design and Fabrication of Filament Wound Composite Lattice Structures,” Proc. of the Korean Society of Propulsion Engineers Conference, pp. 421-427, 2010.
- Doh, Y.-D., Chung, S.-K., Lee, S.-W., and Chang, H.-B., “Design and Fabrication of Cone Type Composite Lattice Structures,” Proc. of the Korean Society of Propulsion Engineers Conference, pp. 307-311, 2011.
- Barynin, V. A., Bunakov, V. A., Rasin, A. F., and Vasiliev, V. V., “Aerospace Composite Lattice Structures,” Proc. of ICCM, 1999.
- Im, J. M, Shin, K. B., and Lee, S. W., “A Study on Finite Element Modeling for Composite Lattice Structure with Hexagonal Cell,” Proc. of KSPE Autumn Conference, p. 295, 2016.