공작기계의 체적 오차 향상을 위한 주기적 검사 및 기하학적 오차 보정
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
In the manufacture of mechanical components, volumetric errors of a machine tool should be checked and reduced to meet the required tolerance levels. In this paper, we propose a quick and simple method of measurement for checking and compensating geometric errors which include scaling and squareness errors. During the measurement, which usually takes approximately 5 minutes to complete, the machine tool is first commanded into four vertices sequentially on a virtual regular tetrahedron. Subsequently, the six lengths between four vertices are measured using a double ball-bar and geometric errors are calculated from the measured lengths. In order to verify the measurement result, the measured geometric errors are compensated using NC-code and the six lengths are re-measured to confirm the error correction. In conclusion, a double ball-bar circular test on XY-, YZ-, ZX-plane is done, first without compensation and then with the compensation of the measured geometric errors to check the effect of compensation practically.
Keywords:
Interim check, Geometric errors, Virtual regular tetrahedron, Volumetric error, Machine tools키워드:
주기적 검사, 기하학적 오차, 가상 정사면체, 체적 오차, 공작기계1. 서론
공작기계에서 기하학적 오차(Geometric Errors)는 공구와 공작물 사이의 체적 오차(Volumetric Error)를 야기하고 가공품의 형상정확도를 저하시키는 주요 요인이다.1 기하학적 오차는 이송축자체의 오차인 위치종속오차(Position Dependent Geometric Errors, PDGEs)와 이송축 사이의 오차인 위치독립오차(Position Independent Geometric Errors; PIGEs)로 구분한다. 3축 공작기계의 체적 오차는 18개의 PDGEs(한 축당 6개)와 3개의 PIGEs를 사용하여 나타낸다.2 PDGEs는 이송축을 구성하는 정밀 부품인 위치 센서의 정확도와 안내면의 형상정확도에 많은 영향을 받으며, 이에 따라 ISO에서는 ‘Component Errors’라고 명기한다.3 또한 3축 공작기계에서 PIGEs는 직각도 오차이며 작업자의 조립 숙련도에 많은 영향을 받는다. PIGEs는 ISO에서 ‘Location and Orientation Errors’라고 명기한다. 21개의 기하학적 오차에서 상대적으로 큰 값의 주요 기하학적 오차는 선형위치오차와 작업자의 숙련도에 의한 직각도 오차이다.4 공작기계의 체적 오차는 준정적(Quasi-Static) 특징의 주요 기하학적 오차를 주기적으로 측정하고 보정하여 향상시킨다.
기하학적 오차는 레이저 간섭계, 스트레이트 에지와 정전용량센서, 전자레벨, 레이저 트레이서 등의 장비를 사용하여 측정하며,5,6 체적 오차는 측정한 기하학적 오차를 NC 보정하여 향상한다.7
공작기계의 성능은 (a) 볼바(Ball-Bar)를 사용한 대각측정,8 (b) 더블 볼바(Double Ball-Bar, DBB)를 사용한 원호측정9 및 (c) 정밀 정사면체 치구의 3차원 측정10을 통해 주기적으로 검사(Interim Check)하고, 측정값이 기준을 벗어나는 경우에는 기하학적 오차를 측정하고 보정하여 일정 수준으로 유지한다. 하지만 앞서 언급한 측정방법은 고가의 측정기 셋업이 다소 복잡하고 긴 측정시간이 필요하여 다수의 공작기계에 주기적으로 적용하는 것은 장비 활용성과 제품 생산성을 고려하는 경우 비효율적이다. 이러한 단점은 DBB를 사용한 원호시험방법에서 일부 개선되지만,11,12 2축 동시구동의 원호시험은 태생적으로 이송축의 동적 특성이 측정결과에 나타나기 때문에 정적 특성의 기하학적 오차를 측정하는 경우에는 상당한 주의를 요구한다.
본 연구는 공작기계의 체적 오차를 주기적 검사하고 주요 기하학적 오차(직선축의 스케일링 오차 및 직선축 사이의 직각도 오차)를 측정하는 방법을 현장 적용한다.13 또한 측정한 기하학적 오차의 타당성은 오차 보정 전/후의 정적 원호시험에서 반경 방향 오차의 개선여부를 통해 검증한다. 여기서, 직선축의 스케일링 오차는 선형위치오차에서 일반적으로 큰 값을 가지는 선형(Linear) 성분이다. 측정방법은 공작기계를 순차적으로 가상 정사면체(Virtual Regular Tetrahedron)의 꼭지점에 위치시킨 후 DBB를 사용하여 꼭지점 사이의 길이를 순차적으로 측정하고, 꼭지점 좌표와 기하학적 오차의 관계 정의 및 최소자승법을 통한 주요 기하학적 오차 계산으로 구성한다.
2. 체적 오차의 주기적 검사 및 주요 기하학적 오차 측정방법
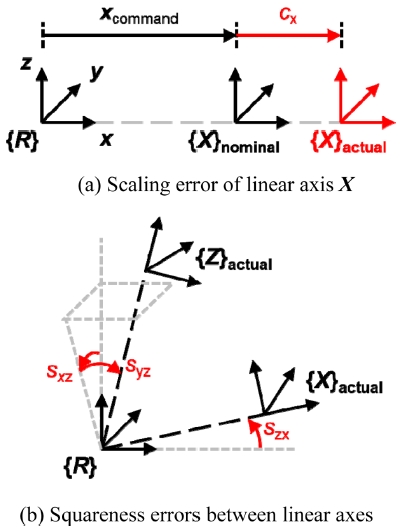
직선축의 스케일링 오차와 직선축 사이의 직각도 오차는 Fig. 1과 같으며, 본 연구는 3축 공작기계의 스케일링 오차 ci (i = x, y, z)와 직각도 오차 szx, sxz, syz를 측정 및 보정한다.
공작기계의 주기적 검사 및 주요 기하학적 오차 측정은 (1) 공작기계를 사용한 가상 정사면체 형성, (2) DBB를 사용하여 정사면체 꼭지점 사이의 길이 측정, (3) 꼭지점의 좌표 계산 및 기하학적 오차 측정으로 구성한다. 주기적 검사는 정사면체 꼭지점 사이의 길이가 기준 범위를 벗어나는지 여부를 통해 용이하게 진행하며, 기하학적 오차는 꼭지점의 좌표를 분석하여 계산한다.
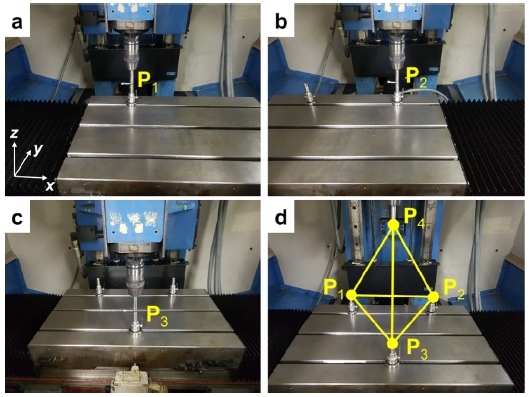
가상 정사면체는 Fig. 2와 같이 공작기계의 공구 끝단을 순차적으로 꼭지점에 이송 후 DBB 치구를 사용하여 공구 끝단의 위치를 유지함으로써 형성한다. 여기서 꼭지점 Pi,m (i = 1,…,4) 사이의 길이 Lij는 DBB를 사용하여 측정한다. 측정 길이 Lij와 꼭지점 좌표는 다음과 같다.
| (1) |
여기서,
를 나타낸다.
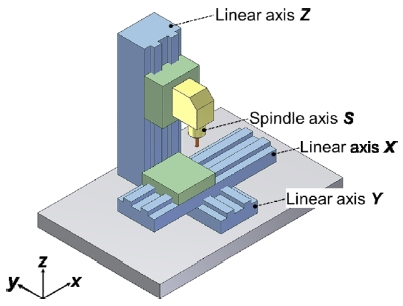
체적 오차는 주요 기하학적 오차를 사용하여 나타내며, 체적 오차와 기하학적 오차의 관계는 공작기계의 기구학적 구조에 의해 결정한다.14 본 연구는 Fig. 3에 나타낸 구조의 수직형 공작기계를 모델링 및 실험한다. 직선 이송축 X, Y, Z와 공구 및 공작물의 위치 및 방향은 식(2)와 같이 모델링하며, 체적 오차 V는 식(3)과 같이 주어진다.
| (2) |
| (3) |
여기서,
ci: i축의 스케일링 오차(i = x, y, z), ppm
sij: j축의 i에 대한 직각도 오차(i, j = x, y, z), μrad
(xi, yi, zi): 가상 정사면체 꼭지점의 공칭 좌표(i = 1,…,4), mm(xi,m, yi,m, zi,m): 가상 정사면체 꼭지점의 측정 좌표(i=1,…,4), mm
: 4×4 균일변환행렬이며 좌표계 {j}에서 좌표계 {i}로 변환을 나타낸다.
가상 정사면체의 꼭지점 좌표와 기하학적 오차의 관계는 식(4)와 같이 주어지며, 기하학적 오차는 최소자승법을 사용하여 계산한다.
| (4) |
3. 기하학적 오차 측정, 보정 및 검증
3.1 기하학적 오차 측정, 보정
측정에 사용한 공작기계는 Komatec 社의 SPT-T30이며, DBB는 Renishaw 社의 QC20-W이다.
가상 정사면체 변의 공칭길이 L는 QC20-W가 제공하는 최대값 300 mm이다. 가상 정사면체 변의 길이 Lij는 Fig. 4와 같이 DBB를 사용하여 측정한다. 측정 시간은 약 5분이며, 기하학적 오차는 3회 측정한 길이의 평균값을 사용하여 계산한다.
측정한 길이는 최대 16.1 μm의 편차를 나타내며, 측정한 공작기계는 기하학적 오차를 보정하여 성능을 개선해야 하는 것을 나타낸다. 기하학적 오차는 식(4)를 사용하여 계산하고 Table 1에 나타내었으며, 측정 결과의 타당성은 보정 NC-code를 통해 생성한 가상 정사면체를 재 측정하여 검증한다. 최근 개발된 NC는 기하학적 오차를 NC 변수를 설정하여 보정하지만, 실험에 사용한 공작기계 NC는 초기 모델로써 주요 기하학적 오차의 NC 보정 기능이 없으며 이에 보정 NC-code를 사용하였다. 기하학적 오차의 보정 후 측정한 변의 길이는 최대 2.9 μm의 편차를 가지며, 이는 측정한 기하학적 오차 및 보정이 유효한 것을 나타낸다.
3.2 정적 원호시험의 검증
가상 정사면체를 사용한 방법의 타당성은 반지름 100 mm의 DBB 원호시험을 정적으로 진행하고, Table 1의 기하학적 오차 보정에 따른 DBB의 반경오차(Radial Deviation)을 비교하여 검증한다. 원호시험은 상용 DBB에서 제공되는 최대각도(XY 평면: [0°, 360°], YZ평면: [-20°, 200°], ZX 평면: [-110°, 110°])에서 진행하며, 각 평면에서 DBB의 원호경로와 측정점은 Fig. 5와 같다.
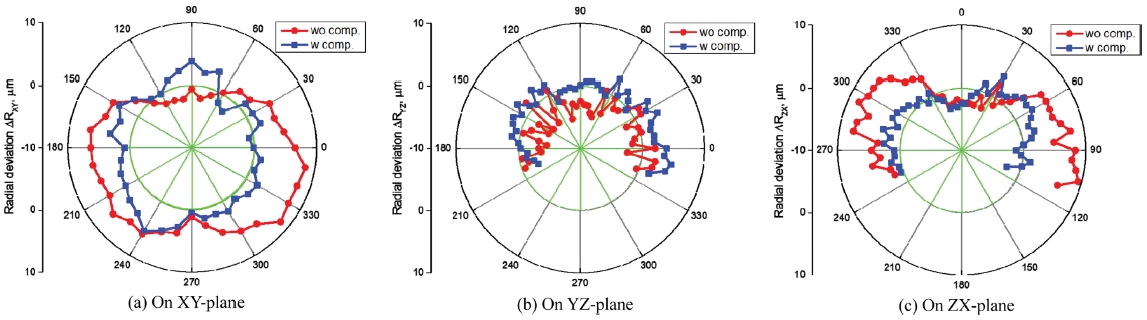
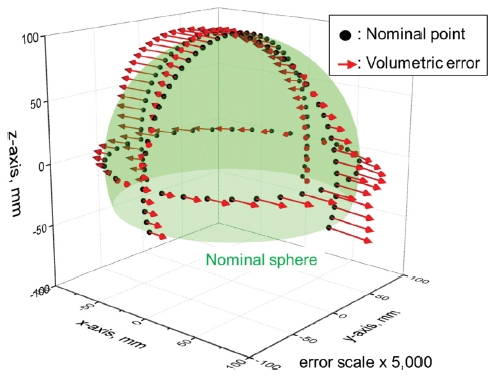
측정한 반경오차는 Fig. 6과 같으며, 상대적으로 큰 cx의 값에 의해 XY, ZX 평면에서 x 방향의 오차가 큰 것을 나타낸다. 체적 오차 V는 Table 1의 기하학적 오차를 사용하여 Fig. 7과 같이 계산한다. 체적 오차 V의 보정은 DBB 정적 원호시험을 위한 보정 NC-code를 생성하여 진행한다. 보정 후 반경오차는 일부 영역에서는 공작기계의 반복정밀도 수준에서 다소 증가한 값을 보이지만, 보정 전/후에서 반경오차의 RMSE (Root Mean Square Error)는 XY, YZ, ZX 평면에서 각각 54%, 23%, 64%의 향상을 나타낸다.
4. 결론
본 연구는 공작기계의 주기적 검사 및 기하학적 오차 측정/보정 방법을 소개하고 현장 적용하여 타당성을 검증하였으며, 결론은 다음과 같다.
(1) 가상 정사면체에서 꼭지점 사이 길이의 측정을 통한 공작기계의 체적 오차 진단
(2) 꼭지점 좌표와 공작기계의 기구학적 구조 분석을 통한 스케일링 오차와 직각도 오차 측정
(3) 측정한 기하학적 오차의 보정을 통한 공작기계의 체적 오차 향상
Acknowledgments
이 논문은 한국연구재단의 대학중점연구소지원사업, 이공학개인기초연구지원사업으로 수행된 연구임(2010-0020089, 2017R1D1A1B03028396).
REFERENCES
-
Ramesh, R., Mannan, M., and Poo, A., “Error Compensation in Machine Tools—A Review: Part I: Geometric, Cutting-Force Induced and Fixture-Dependent Errors,” International Journal of Machine Tools and Manufacture, Vol. 40, No. 9, pp. 1235-1256, 2000.
[https://doi.org/10.1016/S0890-6955(00)00009-2]

-
Lee, J. H., Liu, Y., and Yang, S. H., “Accuracy Improvement of Miniaturized Machine Tool: Geometric Error Modeling and Compensation,” International Journal of Machine Tools and Manufacture, Vol. 46, Nos. 12-13, pp. 1508-1516, 2006.
[https://doi.org/10.1016/j.ijmachtools.2005.09.004]

- ISO 230-1, “Test Code for Machine Tools – Part 1: Geometric Accuracy of Machines Operating under No-load or Quasi-Static Conditions,” 2012.
-
Pahk, H. J., Kim, Y. S., and Moon, J. H., “A New Technique for Volumetric Error Assessment of CNC Machine Tools Incorporating Ball Bar Measurement and 3D Volumetric Error Model,” International Journal of Machine Tools and Manufacture, Vol. 37, No. 11, pp. 1583-1596, 1997.
[https://doi.org/10.1016/S0890-6955(97)00029-1]

-
Schwenke, H., Knapp, W., Haitjema, H., Weckenmann, A., and Schmitt, R., “Geometric Error Measurement and Compensation of Machines—an Update,” CIRP Annals, Vol. 57, No. 2, pp. 660-675, 2008.
[https://doi.org/10.1016/j.cirp.2008.09.008]

-
Ibaraki, S. and Knapp, W., “Indirect Measurement of Volumetric Accuracy for Three-Axis and Five-Axis Machine Tools,” International Journal of Automation Technology, Vol. 6, No. 2, pp. 110-124, 2012.
[https://doi.org/10.20965/ijat.2012.p0110]

-
Schwenke, H., Schmitt, R., Jatzkowski, P., and Warmann, C., “On-the-Fly Calibration of Linear and Rotary Axes of Machine Tools and Cmms Using a Tracking Interferometer,” CIRP Annals, Vol. 58, No. 1, pp. 477-480, 2009.
[https://doi.org/10.1016/j.cirp.2009.03.007]

-
Kruth, J. P., Zhou, L., Van Den Bergh, C., and Vanherck, P., “A Method for Squareness Error Verification on a Coordinate Measuring Machine,” The International Journal of Advanced Manufacturing Technology, Vol. 21, Nos. 10-11, pp. 874-878, 2003.
[https://doi.org/10.1007/s00170-002-1408-x]

-
Curran, E. and Phelan, P., “Quick Check Error Verification of Coordinate Measuring Machines,” Journal of Materials Processing Technology, Vols. 155-156, pp. 1207-1213, 2004.
[https://doi.org/10.1016/j.jmatprotec.2004.04.337]

-
Asano, Y., Furutani, R., and Ozaki, M., “Verification of Interim Check Method of CMM,” International Journal of Automation Technology, Vol. 5, No. 2, pp. 115-119, 2011.
[https://doi.org/10.20965/ijat.2011.p0115]

-
Bryan, J., “A Simple Method for Testing Measuring Machines and Machine Tools Part 1: Principles and Applications,” Precision Engineering, Vol. 4, No. 2, pp. 61-69, 1982.
[https://doi.org/10.1016/0141-6359(82)90018-6]

- ISO 230-4, “Test Code for Machine Tools – Part 4: Circular Tests for Numerically Controlled Machine Tools,” 2005.
-
Lee, K. I., Lee, H. H., and Yang, S. H., “Interim Check and Practical Accuracy Improvement for Machine Tools with Sequential Measurements Using a Double Ball-Bar on a Virtual Regular Tetrahedron,” International Journal of Advanced Manufacturing Technology, Vol. 93, Nos. 5-8, pp. 1527-1536, 2017.
[https://doi.org/10.1007/s00170-017-0582-9]

-
Lee, D. M. and Yang, S. H., “Mathematical Approach and General Formulation for Error Synthesis Modeling of Multi-Axis System,” International Journal of Modern Physics B, Vol. 24, Nos. 15-16, pp. 2737-2742, 2010.
[https://doi.org/10.1142/S0217979210065556]