다축응력 성분간의 위상차를 고려한 등가본미세스응력을 이용한 피로수명예측

1. 서론

실제 환경에서 기계부품 및 기계시스템은 정하중(Static Load)과 더불어 동하중(Dynamic Load)에 의해 가진되어 진다. 이러한 하중은 기계적 파손을 야기하는 항복강도 이상으로 부품을 응력을 발생시키지 않더라도, 충분한 하중 횟수를 작용한다면 피로파괴를 발생시킬 수 있다.

대부분의 피로해석은 시간영역에서 수행되어 왔는데, 모든 입력하중 및 출력응력은 시간 영역에서 측정되거나 해석을 통해 구해졌다.¹ 시간 영역 피로해석은 불규칙 응력진폭이력의 반복수를 산정하고 구조물의 재료에 상응하는 S-N선도와 Miner²의 선형누적법칙을 이용하여 피로수명을 예측하는 방법이다. 이 방법은 통계적인 불확실성을 줄이고 안정된 피로수명을 예측하기 위하여 충분히 긴 시간 동안의 국부지점의 응답이력이 필요하다. 따라서 구조물이 복잡할 경우 많은 시간과 비용이 필요하게 된다.^3-5 응력이력을 유한요소모델(Finite Element Model)로부터 구할 경우, 모든 순간에서의 복잡한 모델의 해는 매우 길어지게 된다. 따라서 시간영역에서의 일반적인 접근방법은 구조물이 동하중 하에 있지 않다고 가정하여 정적해석을 수행하고 정적해석의 결과에 충격인자(Impact Factor)를 곱하여 동적 응력이력을 구하는 보정방법을 이용하였다.⁶ 특히 랜덤(Random) 진동가진 구조물에 서는 동하중의 가진주파수가 구조물의 고유진동수와 일치하는 공진문제가 발생할 수 있고, 이 경우에 시간영역기법은 구조물의 동적 정보의 부족으로 정확한 피로수명의 예측이 어렵게 된다.⁷

주파수영역기법의 경우 대상 구조물이 선형적이라고 가정하고 랜덤진동이론에 근거하여 스펙트럴해석(Spectral Analysis)을 통해 구한 전달함수와 입력하중에 이용하여 출력응력의 파워스펙트럼밀도함수(Power Spectral Density, PSD)을 예측하게 된다. Bendat와⁸ Dirlik에⁹ 의해 제안된 주파수영역 피로해석은 응력진폭 이력을 FFT (Fast Fourier Transform)를 이용하여 PSD를 구하고, 응력범위 스펙트럼의 모멘트를 이용하여 응력진폭범위 분포에 대한 확률밀도함수(Probability Density Function, PDF)를 구하고, 이를 S-N선도와 선형누적법칙에 적용하여 피로수명을 예측하게 된다.

실제 기계구조물의 응력은 단축(Uniaxial)보다는 평면응력(Biaxial) 또는 실제 대부분의 경우에서 다축(Multi-Axial)응력에 해당한다.¹⁰ 지금까지 대부분 다축응력 피로해석은 시간영역에서 제안되어 왔는데, 대부분 임계 평면법(Critical Plane Approach)^11,12와 등가 응력방법(Equivalent Method)에^13,14 근거를 두고 있다. 등가응력방법은 다축응력으로부터 계산된 등가응력에 단축피로 수명기법을 적용하여 피로수명을 예측하는 방법으로, 본미세스응력(Von Mises Stress), 최대주응력(Maximum Principle Stress), 최대전단응력(Maximum Shear Stress)이 등가응력으로 많이 이용된다. 다축응력 피로해석은 대부분 시간영역에서 수행되어 계산된 등가응력에 대한 응력-수명 방법에 의해 피로수명이 예측된다. 그러나 기계구조물에서 랜덤진동가진에 의해 다축응력이 발생할 경우 위에서 제시된 문제점으로 인해 다축응력 PSD들에 근거하여 주파수영역에서 피로해석을 수행하여야 한다. Premont는 주파수영역에서 PSD들을 이용하여 등가응력을 계산하는 방법을 제안하였는데, 등가본미세스응력 PSD를 계산하는 과정에서 다축응력성분간의 위상차(Phase Difference)를 고려하지 않았다.¹⁵

본 연구에서는 랜덤진동 가진된 실제구조물에서 나타날 수 있는 위상차를 고려하여 다축응력 PSD로부터 등가응력을 계산할 수 있는 주파수영역 피로해석기법을 제안하고자 하였다. 또한 이러한 방법의 검증을 위하여 간단한 시뮬레이션 모델에서 제안된 주파수영역기법과 기존의 시간영역기법인 다축레인플로우 방법(Multi-Axial Rainflow Method)과의 비교분석을 수행하였다. 그리고 다축응력성분간의 위상차의 고려여부에 따른 다축응력 PSD를 구하여 특정 주파수 영역에서 차이점을 분석하였다.

2. 다축응력에 대한 진동피로해석

2.1 평면응력의 등가본미세스응력¹⁴

일반 구조물에서 동적피로는 평면응력 상태인 표면에서 발생하는데, 평면응력 상태에서의 등가본미세스응력 σ_VM(t)은 수직응력과 전단응력의 이차식 형태로 표현될 수 있다.

$\[ \begin{array}{c}{\sigma }_{VM}^2\left(t\right)={\sigma }_{xx}^2\left(t\right)+{\sigma }_{yy}^2\left(t\right)-{\sigma }_{xx}\left(t\right){\sigma }_{yy}\left(t\right)+{\tau }_{xy}^2\left(t\right)\\ =\text{Re}{\left(\sigma \right)}^{T}Q\text{Re}\left(\sigma \right)\end{array} \]$

(1)

이 때, 상수행렬 Q와 응력벡터 σ다음과 같다.

$\[ Q=\left\{\begin{array}{ccc}1& -0.5& 0\\ -0.5& 1& 0\\ 0& 0& 3\end{array}\right\} \]$

$\[ \sigma ={\left\{{\sigma }_{xx},{\sigma }_{yy},{\tau }_{xy}\right\}}^T \]$

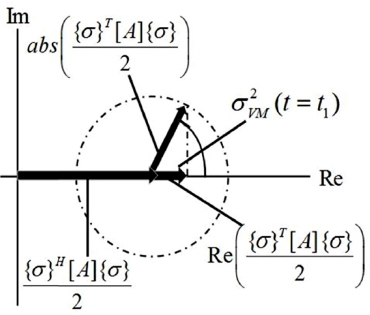
식(1)의 등가본미세스응력은 식(2)과 같이 표현할 수 있는데, Fig. 1과 같이 Re(σ^TQσ) 부분은 각각의 위상에 따라 달라질 수 있게 되어 등가본미세스응력에 영향을 주게 된다.

Fig. 1

von-Mises stress for in-phase

$\[ {\sigma }_{VM}\left(t\right)=Re{\left(\sigma \right)}^{T}Qre\left(\sigma \right)=\frac{{\sigma }^{H}Q\sigma }{2}+\frac{\text{Re}\left({\sigma }^{T}Q\sigma \right)}{2} \]$

(2)

여기서, σ^T, σ^H는 각각 전치(Transpose) 행렬과 허미션(Hermitian) 행렬을 의미한다. 식(1)의 양변에 기대치 E[·]를 수행하여 다음과 같이 주파수영역에서 등가본미세스응력 PSD를 구하였다.

$\[ {\Phi }_{{\sigma }_{VM}}\left(f\right)=Trace\left[Q{\Phi }_{\sigma \sigma }\left(f\right)\right] \]$

(3)

여기서, Φ_σσ(f)는 각각의 다축응력성분의 PSD행렬을 의미하고, Φ_σVM(f)는 등가본미세스응력 PSD를 의미한다.

3. 피로해석 시뮬레이션

3.1 해석모델 및 기본특성

다축진동 가진 조건에서의 피로수명 예측기법을 적용하기 위해서 상용 유한요소해석 기법으로 널리 쓰이는 ABAQUS를 이용하여 랜덤 진동가진을 이용한 강제진동해석 시뮬레이션을 시행하였다.

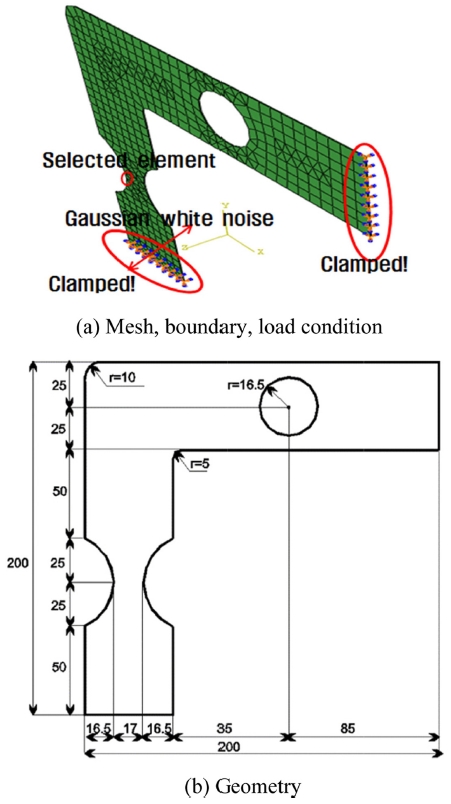
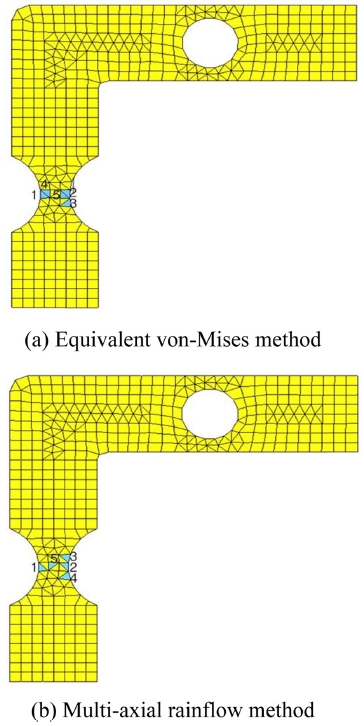
Fig. 2는 시뮬레이션에 이용된 L자형 철(Steel) 구조물로 평면구조이며 좌측 하단 부분에 원형으로 파인 부분과 위쪽 큰 구멍에 응력이 집중되도록 설계되었는데, 예상되는 응력집중 부위에 매쉬를 더 세밀하게 해주었다. Fig. 2(a)와 같이 평면 구조물 전체를 400 Hz이하의 저역통과(Low-Pass)된 가우시안(Gaussian) 랜덤가진을 적용하였고, 구조물의 양쪽 끝은 고정경계(Clamp) 조건으로 이렇게 고정된 부분을 제외하고는 전체가 동일한 가진력이 작용하도록 하였다.

Fig. 2

L-Shaft steel plate

구조물의 재료 물성치를 Table 1에 나타내었는데 이를 이용하여 구조물 고유치해석(Eigenvalue Analysis)를 수행하였다. 구조물 고유진동수(Natural Frequency)는 1차 고유진동수는 27 Hz, 2차 고유진동수는 107 Hz, 3차 고유진동수는 127 Hz, 4차 고유진동수는 288 Hz, 5차 고유진동수는 291 Hz로 나타났는데 주목하는 주파수 범위 이내에 5개 이상의 고유진동수가 분포함을 알 수 있다.

Table 1

Material properties of L-shaft steel plate

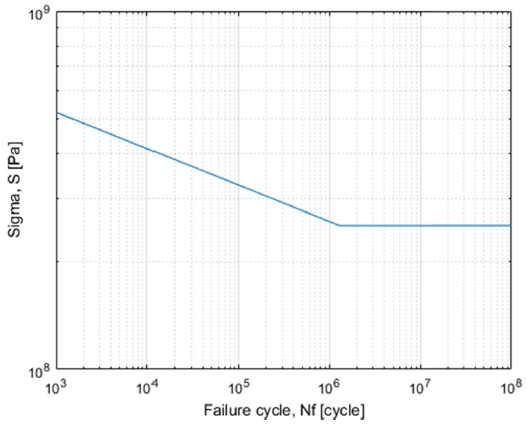
Table 2의 파라미터를 이용하여 NS^m = K의 S-N선도를 Fig. 3과 같이 구할 수 있었는데, 내구한도(Endurance Limit) S_e은 252 × 10⁶ Pa이고, 해당 사이클 N은 1.28 × 10⁶번에 해당한다.

Table 2

Material parameters of fatigue model

Fig. 3

S-N curve of fatigue model

3.2 등가본미세스응력 PSD를 이용한 수명 예측

평면응력 조건에서 먼저 주파수영역의 피로수명 예측방법인 식(3)의 등가본미세스응력 PSD를 이용하는 방법과 시간영역에서의 방법인 식(8)의 다축레인플로우기법을 비교하기 위하여 각각의 기법을 이용하여 구한 등가피로하중(EFL)을 계산하여 서로 비교하였다.

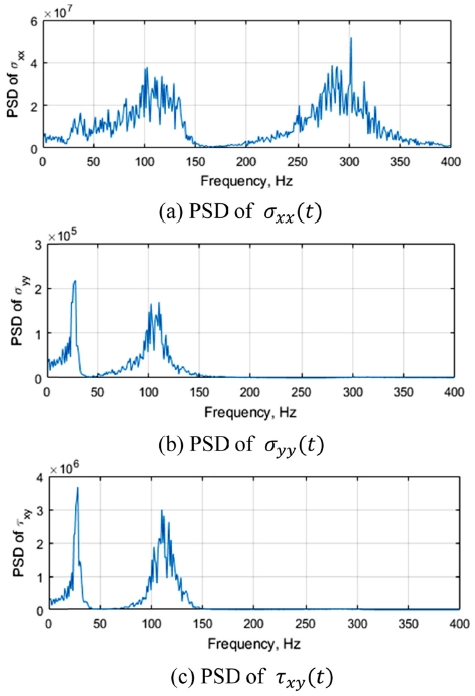
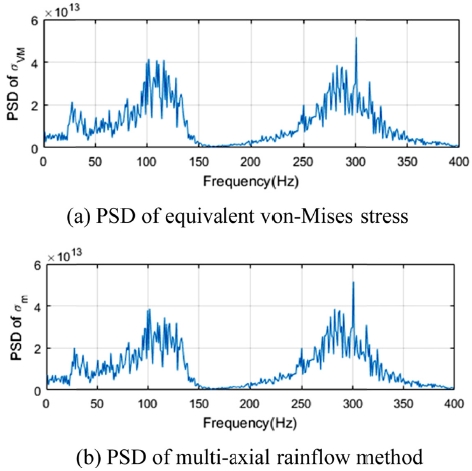
Fig. 2(a)의 구조물에서 응력집중 부분의 임의의 한 요소를 택하였고, 그 요소에서의 다축응력의 PSD 응답을 Fig. 4와 같이 구하였고, 제안된 두 방법을 이용하여 구한 등가응력 PSD를 Fig. 5에 나타내었다. Fig. 5(a)의 등가본미세스응력 PSD 방법보다 Fig. 5(b)의 다축레인플로우기법이 해석시간 측면에서 10배 이상의 시간을 소요되었다. 두 방법을 이용하여 구한 등가응력 PSD는 전반적인 주파수 특성에서 매우 유사함을 알 수 있지만, 해석시간의 차이로 인한 비용 측면에서 등가본미세스응력 PSD 기법이 우수함을 알 수 있었다.

Fig. 4

PSD of multi-axial stress in target element

Fig. 5

Comparison of equivalent stress PSD

구조물의 모든 요소에서의 등가피로하중을 계산하였으며 Table 3에 상위 5개 요소에서의 등가피로하중 결과를 나타내었다. 상위 5개 요소의 위치는 Fig. 6의 손상맵(Damage Map)에 표시하였으며 두 방법 모두 상위 5개의 손상 위치가 예상되는 응력 집중부위에 밀집되어 있었으며 두 방법을 이용하여 구한 등가피로하중의 크기가 비슷하였다.

Table 3

EFL of five critical areas

Fig. 6

Damage map of critical areas

3.3 위상차를 고려한 등가 본미세스응력 PSD를 이용한 수명예측

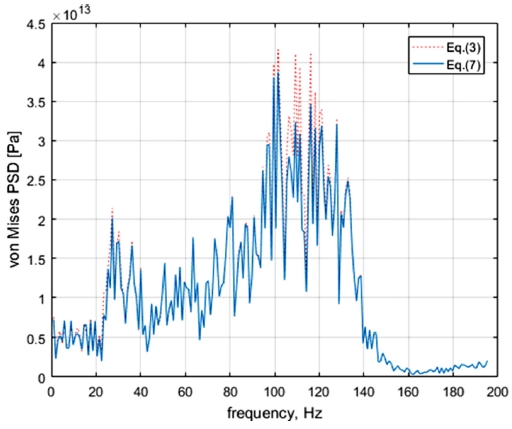
먼저 가진입력 지점과 응력집중이 예상되는 지점에서의 다축응력 사이의 각 주파수별 전달함수를 구하고, 400 Hz이하의 저역 통과된 랜덤가진을 곱하여 다축응력의 스펙트럼과 구하였다. 이를 이용하여 구한 각 주파수별 진폭과 위상을 이용하여 본 연구에서 제안한 식(7)에 적용하여 등가본미세스응력 PSD를 구하였다. 그리고 기존의 식(3)을 이용하여 구한 등가본미세스응력 PSD와의 비교 결과를 Fig. 7에 나타내었는데, 두 수식에 소용되는 해석시간은 거의 동일하게 나타났다.

Fig. 7

Equivalent von-Mises PSDs with two methods

기존의 다축응력 사이의 위상을 고려하지 않고 구한 등가본미세스응력 방법의 PSD 값은 특정 주파수 범위(100-125 Hz)에서 본 연구에서 제시된 위상을 고려한 등가본미세스응력 방법의 PSD 값보다 더 크게 나타났다. 이것은 특정주파수 영역에서 다축응력사이의 위상을 고려하지 않고 주파수영역에서 등가본미세스응력 PSD를 이용한 피로수명의 경우 실제와 많이 오차가 발생할 수 있음을 알 수 있다.

4. 결론

본 연구에서는 각각 시간영역과 주파수영역에서 평면응력 상태의 구조물에서 피로수명예측에 관한 연구를 수행하였다.

첫째로 주파수영역에서 등가본미세스응력 PSD를 이용하는 방법과 시간영역에서 다축레인플로우방법을 각각 이용하여 대상되는 구조물에서 구한 등가피로하중을 계산한 결과에서 상위 5개 지점의 위치가 동일하였으며, 등가피로하중이 8% 이내의 오차율을 보였다. 따라서 제안된 등가본미세스응력 PSD를 이용하여 피로수명을 예측하는 방법의 절차 및 성능을 검증할 수 있었다.

둘째로 다축응력 사이의 위상차의 고려 유무에 따른 등가본미세스응력 PSD를 예측한 결과의 차이를 보여주었는데, 기존의 방법이 제안된 위상차를 고려한 경우보다 일부 주파수영역에서 큰 PSD를 가지는 것을 알 수 있었다. 따라서 다축응력 사이의 위상차를 고려하여 등가본미세스응력 PSD를 구하는 제안된 방법의 타당성을 검증하였다. 향후 본 연구에서 제안된 시험편 모델에 대한 다축가진시험을 수행할 수 있는 시뮬레이터를 구성 중에 있으며, 시뮬레이션 결과에 대한 검증을 계속적으로 수행하고자 합니다.

Acknowledgments

이 논문은 2016년 미래창조과학부의 재원으로 한국연구재단의 지원을 받아 수행된 지역신산업선도인력양성사업의 성과임(No. 201 6H1D5A1910490).

REFERENCES

• Choi, S.-W., Kang, D.-H., Lee, J.-K., and Kim, T.-W., “Fatigue Crack Propagation and Fatigue Life Evaluation of High-Performance Steel Using Modified Forman Model,” Transactions of the Korean Society of Mechanical Engineers A, Vol. 35, No. 11, pp. 1361-1368, 2011. [https://doi.org/10.3795/KSME-A.2011.35.11.1361]
• Miner, M. A., “Cumulative Damage in Fatigue,” Journal of Applied Mechanics, Vol. 67, pp. 159-164, 1945.
• Rice, R. C., Leis, B. N., and Nelson, D., “Fatigue Design Handbook,” Society of Automotive Engineers, 1988.
• Bannantine, J., “Fundamentals of Metal Fatigue Analysis,” Prentice Hall, 1990.
• Ragan, P. and Manuel, L., “Comparing Estimates of Wind Turbine Fatigue Loads Using Time-Domain and Spectral Methods,” Wind Engineering, Vol. 31, No. 2, pp. 83-99, 2007. [https://doi.org/10.1260/030952407781494494]
• JIS B 8821, “Calculation Standards for Steel Structures of Cranes,” Japanese Standards Association, pp. 2-14, 2004.
• Sutherland, H. J., “On the Fatigue Analysis of Wind Turbines,” Sandia National Labs., No. D00-0089, 1999. [https://doi.org/10.2172/9460]
• Bendat, J. S. and Piersol, A. G., “Random Data: Analysis and Measurement Procedures,” John Wiley & Sons, 2011. [https://doi.org/10.1002/9781118032428]
• Dirlik, T., “Application of Computers in Fatigue Analysis,” Ph.D. Thesis, University of Warwick, 1985.
• Aykan, M. and Celik, M., “Vibration Fatigue Analysis and Multi-Axial Effect in Testing of Aerospace Structures,” Mechanical Systems and Signal Processing, Vol. 23, No. 3, pp. 897-907, 2009. [https://doi.org/10.1016/j.ymssp.2008.08.006]
• Beste, A., Dresler, K., Kötzle, H., and Krüger, W., “A Consequent Continuation of Professor Tatsuo Endo's Work,” The Rainflow Method in Fatigue, 2013.
• Dressler, K., Kottgen, V., and Kotzle, H., “Tools for Fatigue Evaluation of Non-Proportional Loading,” Fatigue Design, Vol. 1, pp. 261-277, 1995.
• Pitoiset, X., Rychlik, I., and Preumont, A., “Spectral Methods to Estimate Local Multiaxial Fatigue Failure for Structures Undergoing Random Vibrations,” Fatigue & Fracture of Engineering Materials & Structures, Vol. 24, No. 11, pp. 715-727, 2001. [https://doi.org/10.1046/j.1460-2695.2001.00394.x]
• Pitoiset, X. and Preumont, A., “Spectral Methods for Multiaxial Random Fatigue Analysis of Metallic Structures,” International Journal of Fatigue, Vol. 22, No. 7, pp. 541-550, 2000. [https://doi.org/10.1016/S0142-1123(00)00038-4]
• Bonte, M., de Boer, A., and Liebregts, R., “Determining the von Mises Stress Power Spectral Density for Frequency Domain Fatigue Analysis Including Out-of-Phase Stress Components,” Journal of Sound and Vibration, Vol. 302, Nos. 1-2, pp. 379-386, 2007. [https://doi.org/10.1016/j.jsv.2006.11.025]
• Daniel, J. I., “Engineering Vibration,” Prentice Hall New Jersey, 2001.
• Dowling, N. E., “Fatigue Failure Prediction for Complicated Stress Strain Histories,” Journal of Materials, pp. 71-87, 1972. [https://doi.org/10.21236/AD0736583]