상수 기본전하 e를 이용한 암페어 재정의 및 실현
1한국표준과학연구원 전자기표준센터2부산대학교 물리학과
 ; Myung-Ho Bae1 ; Ye-Hwan Ahn1 ; Wan-Seop Kim1 ; Dong-Hun Chae1 ; Changki Hong2 ; Yunchul Chung2
; Myung-Ho Bae1 ; Ye-Hwan Ahn1 ; Wan-Seop Kim1 ; Dong-Hun Chae1 ; Changki Hong2 ; Yunchul Chung2
2Department of Physics, Pusan National University
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
It is often overlooked that so far, there has been inconsistency between the definition of the ampere in SI units and its realization. For instance, the ampere is defined based on the classical Ampere’s law, while its representation has been made through the Ohm’s law, that is, the ratio of the Josephson voltage to the quantum Hall resistance that do not belong to the SI units. However, in the revised SI units that are slated to take effect in 2019 on World Metrology Day, 20 th of May, it is significant to note that the ampere will be defined as a flow of electrons with the numerical value of the elementary charge fixed. In this instance, all three of the electrical units, such as the current, voltage and resistance will become defined on the basis of quantum physics. As a candidate for the quantum current standard, the various types of single electron pump devices are reviewed in relation to the redefinition of the ampere.
Keywords:
ampere, Current standard, Elementary charge, Quantum metrology triangle, Single electron pump, SI redefinition키워드:
암페어, 전류표준, 기본전하, 양자 측정 삼각체계, 단전자 펌프, 단위 재정의1. 서론
전류의 단위인 암페어는 1948년도 제 9회 국제도량형 총회(CGPM)에서 다음과 같이 정의되었다. ‘1 암페어는 무한히 길고 무시할 수 있을 만큼 작은 원형 단면적을 가진 두 개의 평행한 직선 도체가 진공 중에서 1 미터 간격으로 유지될 때 두 도체 사이에 매 미터 당 2 × 10-7 뉴톤의 힘을 생성하는 일정한 전류의 크기이다.1 이 정의는 ‘무한히 긴’, ‘직경을 무시할 수 있는’과 같은 현실적으로 실현 불가능한 가정을 전제하고 있기 때문에, 실험실에서는 다른 방식으로 암페어를 구현하고 있다. 각국의 표준기관(NMI)에서는 저항표준기와 전압표준기 상호간에 유지되는 옴의 법칙을 이용하여 암페어를 구현하고 있는데, 불확도는 10-7 수준이다. 현재의 양자 전기표준기인 양자홀 저항표준기와 조셉슨 전압표준기의 10-9 수준의 불확도에 비하면 전류표준기의 불확도 개선이 요구된다. 이처럼 현재의 암페어 단위는 정의와 구현 사이의 괴리가 있고, 또한, 국제단위계(SI)의 기본 단위임에도 이를 실현하기 위해서는 세 개의 다른 기본단위인 ‘초’, ‘킬로그램’ 및 ‘미터’ 표준기에 의존하게 정의되어 있어서 실현 자체가 매우 복잡하며 결과적으로 불확도가 상대적으로 매우 높은 상황이다.
이러한 암페어에 대한 SI 정의와 현실적인 구현 사이의 불일치 문제를 해소하기 위해서, 이미2005년 CIPM에서 기본전하 e에 기초해서 암페어 재정의를 준비하기 시작하였고, 향후2019년도에 재정의가 선포될 예정이다. 재정의될 암페어는 전자의 전하 즉 기본전하를 물리 상수로 고정하고(e = 1.602 176 634 × 10-19 C), A = e/(1.602 176 634 × 10-19 s)로 정의하게 된다.2,3 즉 1 암페어는 1 초당 6.241 509 07 × 1018 [1/(1.602 176 634 × 10-19)]개의 기본 전하의 흐름에 해당하는 전류이다. 새로운 암페어의 정의는 기본 전하 물리상수에 근거하기 때문에 정의 자체의 모호성이 사라졌고, 시간 단위 초(s)에만 의존하여 정의 되었으므로 논리적인 측면에서 매우 단순해졌다. 그러나 현재까지 새로운 암페어 단위를 실현할 수 있는 양자 전류표준기는 확립되지 않은 상태다.
새로운 암페어 정의를 실현하는 방법으로 각국의 표준기관에서는 소위 ‘단전자 펌프 소자’를 유력한 후보로 보고 있다. 단전자 펌프 소자는 단일 전자를 현재 가장 정확한 물리단위인 시간 단위 초에 소급되는 rf 주파수에 동기화함으로써 I = ef 크기의 전류를 발생시키는 소자이다(f는 rf의 주파수). 단전자 펌프 소자는 ‘단전자 투과 현상’(부록 참고)을 이용하여 전자를 한 개씩 제어하여, 단일 전자를 소스 전극에서 드레인 전극으로, 양 전극 사이에 전위차가 존재하더라도, 이를 극복하여 한 개씩 전송하는 소자를 일컫는다.4 단전자 펌프 소자를 이용하여 발생시킬 수 있는 최대 출력은 인가하는 rf 주파수에 의존하는데, 현재까지 개발된 소자의 출력은 1 nA 이하이다.4 향후로도 단전자 펌핑 방식으로 1 A를 직접 실현하는 것은 불가능하다고 예견되지만, 단전자 펌프 소자를 이용한 양자 전류표준기 개발이 갖는 의미는 다음과 같다. 첫째로 비록 출력은 1 nA 이하로 작지만 10-8 수준의 불확도가 달성되면 극소 전류 영역에서 재정의에 입각한 양자 전류표준이 실현되었다고 판단할 수 있다. 또한 양자 전류표준기와 조셉슨 전압표준기, 양자홀 저항표준기 등 세 개의 서로 다른 양자 표준기 상호간의 일치성을 검증할 수 있는 기회를 제공하게 된다. 이와 같은 일치성 검증 실험은 Quantum Metrology Triangle (QMT) 검증실험이라고 불리는데, QMT 일치성이 확인되어야, 조셉슨 전압표준기, 양자홀 저항표준기 상호간의 옴의 법칙을 이용한 전류표준기의 정당성이 확보되는 것이다. 또한, 과학적인 관점에서는 양자홀 효과, 조셉슨 효과 및 단전자 투과 효과 등 각기 다른 세 개의 물리 이론이 QMT 측정 불확도 이내에서 정확하다는 검증도 가능하게 된다.
다음 절부터는 현재까지, 한국표준과학연구원(KRISS)을 포함하여, 범 세계적으로 연구되고 있는 양자 전류원의 개발현황, 정밀측정 방법 및 원리에 대하여 개략적으로 소개하겠다. 본 논문에서, 소자 특성평가 및 정밀측정 방법에 대한 자세한 기술은 KRISS의 연구 결과를 기초로 하였다.
2. 양자전류원 개발 동향
2.1 반도체 양자점 단전자 펌프
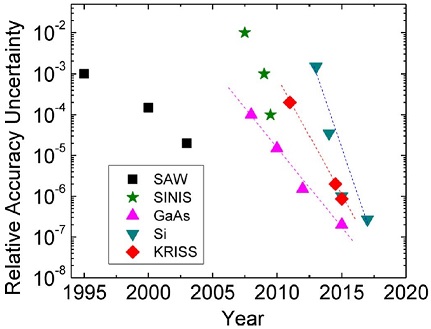
반도체 양자점 기반 단전자 펌프는 유럽의 표준기관을 중심으로 활발히 연구되는 분야이다. 과거 20년 동안 연구가 진행되었는데, 현재까지 개발된 최고의 양자 전류원 출력과 불확도 수준은 다음과 같다 출력 ~100 pA, 불확도 ~2 × 10-7. Fig. 1은 각 기관별 개발 중인 양자점 기반 단전자 펌프 소자의 사진이고 Table 1에는 각 소자별 출력과 불확도가 명시되어있다. 이와 같은 불확도 측정결과를 근거로 단전자 펌프 소자의 보편성이 확인되었다고 판단할 수 있다. 왜냐하면, 각 기관의 펌프 소자의 구조와 재질은 모두 다르고 제작 방법도 상이하지만 동일한 물리 이론으로 펌핑 현상이 설명되고 불확도도 비슷한 수준에서 측정되고 있기 때문이다. 다음 절에서 설명되겠지만, 소자의 작동 안정성도 검증되었기 때문에 양자 전류표준기로서 개발되는데 있어서 한 단계 진보가 있었다고 볼 수 있다. 또한 Fig. 2를 살펴보면 단전자 펌프 소자의 상대 불확도가 해마다 빠르게 개선되고 있음을 알 수 있다. 따라서 단전자 펌프 소자가 표준기로 공인될 수 있는 필요조건인 상대불확도 10-8 수준에 점차 다가가고 있다고 판단된다.
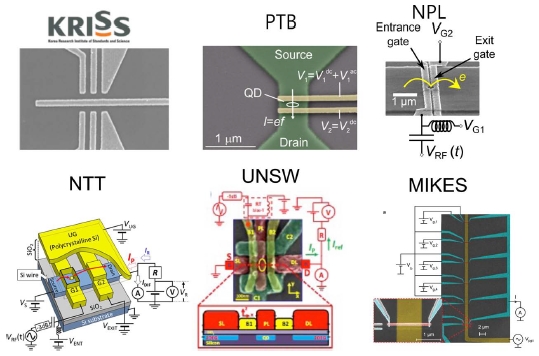
Various types of single electron pumps; GaAs/AlGaAs-based QD pumps by KRISS, PTB and NPL. Si-based QD pumps by NTT and UNSW. SINIS pump by MIKES5-15
각 기관별 소자의 구조 및 물성은 각각 다르지만, 작동 원리는 다음과 같이 동일하다. Fig. 3에 양자화된 전자의 펌핑 순서가 도식적으로 표현되어 있다 전자의 적재(Loading), 포획(Capturing) 그리고 방출(Unloading)의 단계를 순차적으로 묘사하고 있다. 양자점(Quantum Dot, QD)의 출구 포텐셜을 고정한 상태에서 입구 포텐셜을 제어하는 입구 전압(Vent)을 주기적(T = 1/f)으로 변조하면 전자가 한개씩 순차적으로 변조 신호에 동기화되어서, 소스 전극에서 드레인 전극으로 양자화된 전자가 이송된다. 이 때 중요한 점은, 전자의 적재 및 방출 과정에서는 전자가 전극과 에너지적으로 평형 상태가 유지되어야 하고, 포획단계에서는 비평형상태(Non-Adiabatic)가 유지되어야 양자화된 전자가 펌핑될 수 있다. 이와 같은 조건이 만족되려면, 적재 및 방출 단계에서는 hf≪ΓL, hf≪ ΓR 조건을 각각 만족해야 하고, 포획 단계에서는 hf≫ΓL 조건이 만족되어야 한다. 여기서 ΓL, ΓL은 각각 전자의 소스 및 드레인 전극으로의 투과율을 나타낸다. Fig. 3은 logΓ(t) 곡선에서 이와 같은 조건을 만족시킬 때 적재, 포획 및 방출되는 순간을 묘사하고 있다.
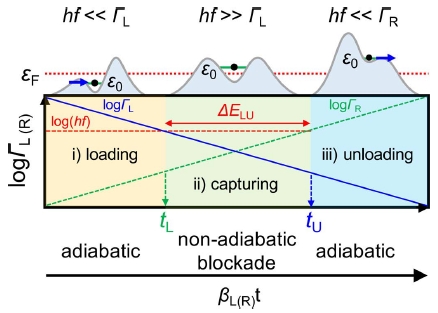
Sequence of quantized electron pumping. Schematic diagram showing the loading or capturing timing as the entrance potential barrier modulates as a function of time. ΓL(R) ∝ exp(±βL(R)) where βL(R) is a barrier-shape dependent parameter16
Fig. 4는 단전자 펌핑 현상을 설명하는 붕괴하강 모델(Decay Cascade Model)의17 핵심 개념인 후방 투과율(Back-Tunneling Rate)을 묘사하고 있다. 이 이론 모델에 의하면, 단전자 펌핑에 의한 출력 전류는 출구 포텐셜 전압 Vexit의 함수로 다음과 같이 표현된다.5,18
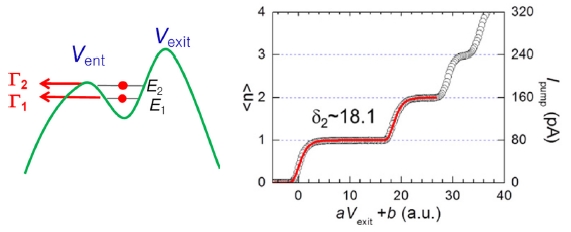
Left; back-tunneling process during the capturing stage. Right. an example of fitting the decay-cascade model (red solid line) to the experiment data. <n> = Ipump/ef 18
| 〈n〉=Ipump/ef=exp[-exp(-aVexit-b)]+exp[-exp(-aVexit-b+δ2)] | (1) |
여기서 a, b는 게이트 전압의 전환변수 및 오프셋 값이고 δ2는 피팅 파라미터이다. δ2 = log(Γ2/Γ1)으로 표시되는데, 물리적으로 Γ2가 Γ1에 비해서 클수록 δ2 값이 커지는데, δ2 크기는 첫 번째 평평 구간의 길이와 비례한 다. 따라서 이 수치는 평평도와 비례하므로 단전자 펌프 전류의 품질을 나타내는 지표 즉 성능지수(Figure of Merit)로 받아 들여진다.
Fig. 4에서 제시된 일반측정 결과를 모델 식(1)에 피팅해서 얻어진 δ2 값은 극저온 정밀측정의 불확도 값과 일정한 연관성을 갖는다. 즉 δ2 값이 크면 불확도가 작다는 경향성이 실험적으로 확인되었다. 예컨데 20 이상이면 정밀측정 상대 불확도는 10-7 수준이었다. 따라서 이 모델을 이용하면 정밀측정(Precision Measurement) 전에 간단한 일반측정(Normal Measurement)을 통해서 상대 불확도 값을 예측할 수 있다.
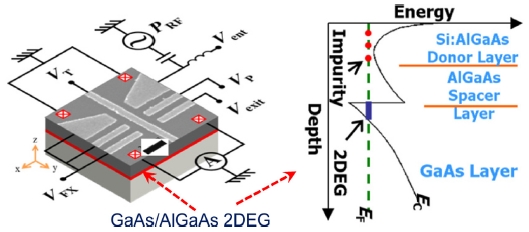
Fig. 5는 KRISS 단전자 펌프 소자의 예시이다. GaAs/AlGaAs 이차원 전자계 기반의 양자점 펌프를 구현하기 위하여 금속 양자점접촉(Quantum Point Contact, QPC) 게이트를 이용하였다. 세 조의 QPC 게이트로 구성되어 있어서, 두 조의 QPC는 양자점을 형성하고 가운데 위치한 QPC가 형성된 양자점의 에너지 레벨을 조절하는 막대 게이트(Plunger Gate) 역할을 하도록 설계되었다. 3 쌍의 QPC 게이트를 관통하는 1차원 금속 게이트[이하 ‘트렌치 게이트(Trench Gate)’]를 추가하였는데, 트렌치 게이트에 양의 전압(VT)을 인가하면 양자점의 포텐샬 우물을 더 깊게 만들어 양자점 에너지 준위의 간격을 증가시킬 수 있다. 성능지수 δ2는 양자점 에너지 준위간격에 비례하는 특성이 있다.18 트렌치 게이트를 이용하여 1차원 채널 및 양자점 에너지 준위 간격을 증가시킬 수 있음은 이미 실험적으로 검증되었다.18,19 펌프 측정 실험은 트렌치 게이트 전압을 +0.3 V 이상으로 인가한 상태에서 수행되게 된다. 각 게이트 전극의 선폭은 75 nm, 각 게이트 사이의 간격 또한 75 nm로 설계되었다.
단전자 펌프 소자의 측정불확도 측정 방법 및 측정 결과를 기술하기에 앞서서 먼저 일반측정 방법을 설명하겠다. 측정 실험에선, 일반측정 결과가 먼저 도출되고 그 결과에 기초해서 정밀측정이 진행된다.
단전자 펌프 소자의 특성 평가를 위한 일반측정은 액체헬륨 온도 4.2 K에서 수행된다. 모든 게이트에 음의 전압을 인가하여 전자 채널이 완전히 닫히는 영역에서 각 게이트의 인가 전압을 적절히 조절하여 전자의 펌핑 조건을 탐색한다. 이때, 입구 게이트(Entrance Gate)에 인가되어 있는 직류 전압에 rf 신호가 더해지면 입구 포텐셜 장벽이 순차적으로 그리고 주기적으로 증감을 반복하게 되고, 포획된 전자는 인가된 rf의 주기 f로 전자 펌핑이 진행되어서 유도되는 전류의 크기는 I = nef를 만족시킨다. Fig. 6는 소위 ‘펌핑지도’(Pumping Map)이라 불리는 측정 데이터이다. 입구 및 출구 게이트 전압을 변수로 펌핑된 전류의 크기를 2차원 그림으로 표현한 데이터인데, 빨간색 테두리로 둘러싸인 영역이 전류 고원(Current Plateau)이고 전류 고원 영역에 표시되어 있는 숫자는 펌핑된 전자의 개수를 나타낸다. Fig. 6의 오른쪽 그림은 ‘펌핑지도’에 점선으로 표시된 단면 프로파일에 해당되는 펌핑 전류 곡선이다. 전류 고원 3개가 선명하게 보인다. 이 때 사용된 rf 신호의 주파수 대역은 ~100 MHz이었고, rf의 파워(Prf)는 −3 dBm~+1 dBm이었다.
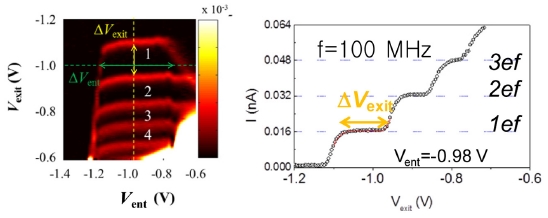
Left; pumping map, dIp/dVexit density plot as a function of Vexit and Vent. Right; an example of pumped current at a fixed entrance voltage corresponding to the vertical dotted yellow line in the left panel
KRISS와 NPL 공동으로 수행한 단전자 펌프의 전류 크기 정밀 측정 방법은 다음과 같다. 양자홀 저항표준기와 조셉슨 전압표준기에 소급해서 교정된 표준저항(Rs~1 GΩ)과 전압측정기를 이용해서 기준 전류 IR을 생성한다. 단전자 펌프 전류 Ip와 기준 전류 IR의 차이를 영점검출기(Null Signal Detector)로 측정 비교함으로써 단전자 펌프에서 발생된 전류의 크기를 결정한다.
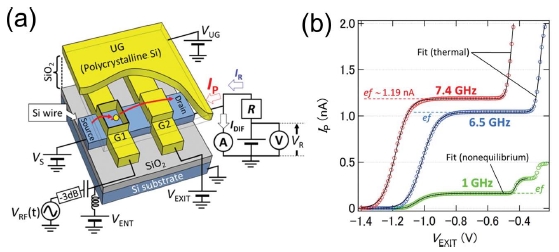
여기서, 시스템 불확도(uB)는 표준저항(Rs), 전압측정기(V) 및 영점검출기의 교정 단계에서 발생되는 불확도의 제곱의 합의 근으로 결정된다. 1 GΩ 표준저항의 불확도가 약 0.98 × 10-6, 전압측정기(V)는 약 0.66 × 10-6로 평가되었다. 따라서 전체 정밀측정 시스템의 총 불확도는 uB= 1.2 × 10-6이었다.5 KRISS 단전자 펌프 소자는 온도 300 mK, 자기장 14 T 냉동기에 설치되고 표준전압기와 표준저항, 영점검출기등은 상온에 설치된다. 펌프 전류의 불확도 평가 과정은 다음과 같은 교정 과정을 포함한다. 표준저항(Rs) 교정, 그리고 전압측정기(V) 교정, 그리고 영점검출기 교정이다. 각 표준기의 교정이 완료된 후에 단전자 펌프 전류 크기에 대한 정밀측정이 진행된다. 방법은 표준기의 교정 방법과 유사한 방법에 따라 수행된다. 단지 차이점은, 펌프 소자에 인가되는 rf 신호의 On/Off를 기준전류 IR와 기준전압의 On/Off와 동기화 시켰다는 점이다. Fig. 7에 묘사되어 있듯이 IR와 Ip를 동기화된 상태에서 On/Off 했을 때 영점검출기에 읽히는 전류값의 변화폭이 ΔI이면 실제 펌프 전류 값은 IR + ΔI × FI이 된다. 여기서 FI는 영점검출기의 교정 인자이다. 이때 평균은, 영점검출기 교정 때와 동일하게, On/Off 20번씩 시행하여 평균하게 된다. 이때 소요되는 시간은 16초이고, 이렇게 200번을 반복해서 평균값 Ipm과, 표준 분산값 σ, 표준 불확도 σ/√N 등의 통계 값을 얻게 된다. 여기서 N = 200. 이렇게 해서 측정 불확도 uA=(σ/√N/Ipm)가 구해진다.
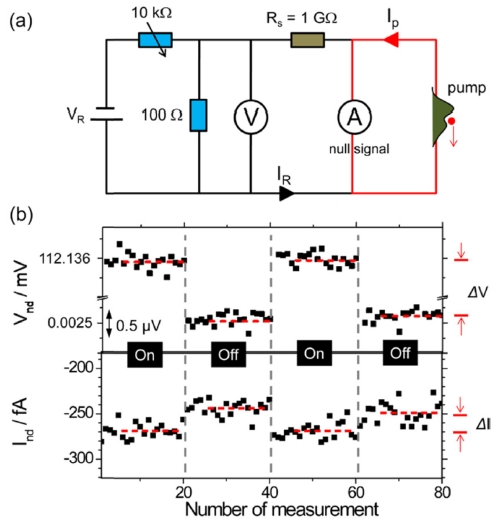
(a) NPL precision measurement configuration to evaluate the accuracy of the electron pump device. A combination of a voltage source VR and a 1 GΩ standard resistor Rs generates a reference current IR. A current amplifier, a null detector, reads the difference between IR and pump current IP. (b) Null detection technique process for pump operation with f = 0.7 GHz, where ΔV and ΔI are voltage and current differences, respectively, between ‘On’ and ‘Off’ states of both the voltage and rf sources6 (doi:10.1088/0026-1394/52/2/195)
Fig. 8은 KRISS 단전자 펌프의 정밀측정 결과를 보여준다. 결론적으로 단전자 펌프의 상대 불확도 δI/ef는 <IP - ef>/ef ± uT = (-0.92 ± 1.37) × 10-6이다. 여기서 주파수 f = 0.95 GHz, 자기장 B = 11 T, 온도 T = 0.3 K, uT=√(u2A+u2B) ~ 1.37 × 10-6. 시스템 불확도가 uB= 1.2 × 10-6이므로, 시스템 불확도 아래로 펌프 소자의 정확한 불확도 평가는 불가능하였지만, 최소한 시스템 불확도 보다 작다는 것은 확인되었다. 그리고, 모델 이론에 근거한 예상치 보다 측정 결과의 불확도 크기가 더 작게 관찰되었다. 이런 경향성은 종종 발견되는데, 정확한 이유는 심도있는 연구가 필요하겠지만, 이것이 의미하는 바는 모델이 예상한 불확도보다 실제로 단전자 펌프 소자의 불확도는 더 낮을 수 있다는 것을 의미한다.
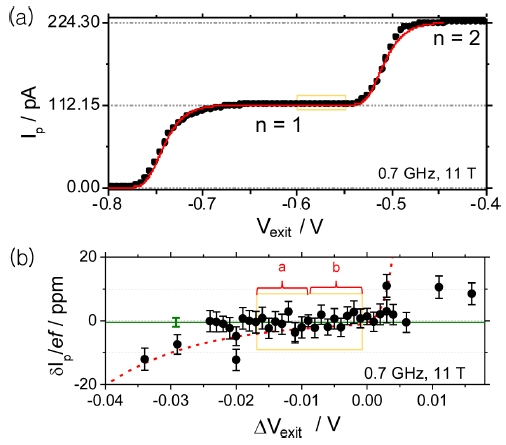
Pump current Ip as a function of exit gate voltage Vexit [scattered points: experimental result, solid curve: a fitted line with Eq. (1)] at f = 0.7 GHz under B = 11 T. (b) Relative deviation from ef, δIp/ef in ppm (parts per million) as a function of an offset gate voltage scale, ΔVexit [scattered points: results of the precision measurement with 200 on–off cycles, dashed red curve: theoretical data predicted by Eq. (1)]. The horizontal green line shows the average value of the sixteen points in the blue box region with an error bar indicating the total uncertainty uT=uA2+uB26 (doi:10.1088/0026-1394/52/2/195)
향후 단전자 펌프가 양자 전류표준기로 공인받기 위해서는 소자 작동의 안정성 및 보편성 또한 담보되어야 한다. 안정성 관련해서는, 단전자 펌프의 작동 조건이 실험 환경 변수에 얼마나 의존하는 가에 대한 정량적인 분석 결과가 필요하다. 예컨대, 게이트 전압, 자기장, 온도 및 주파수 의존도 등에 대한 양자 전류원의 성능 변화에 대한 측정 평가가 필요하다. 즉, 단전자 펌프가 양자전류 표준기로 채택되기 위해서는 전류 고원의 평평도가 외부 변수 영향으로부터 자유로워야 한다. 따라서 최적의 펌핑 조건에서 전류 고원의 외부 영향 평가를 수행하였다.
정밀측정한 실험 조건은 다음과 같다; T = 0.3K, f = 0.5 GHz, Prf= 3 dBm, B = −14 T. Fig. 9(a)는 일반측정 방법으로 측정된 펌핑지도이고, 이론에 근거해서 추산된 상대 불확도 등고선을 첫 번째 전류 고원 영역에 그려 넣었다. 정밀측정 결과 양자점의 입출구 게이트 전압 Vent와 Vexit의 변화폭이 각각 100 mV와 50 mV정도에서는 불확도 2 × 10-6이 유지됨을 검증하였다.21 Fig. 9(b)는 자기장의 변화에 대한 불확도 변화를 보여주고 있는데, 자기장 1 T 정도의 변화폭에 대한 전류 고원의 안정도를 확인할 수 있었다. 마지막 그림은 온도를 1.3 K까지 상승해서 전류 고원의 상대불확도를 정밀측정한 결과다. 여기서 붉은 선은 이론 추산 값을 그린 곡선이다. 이론에서 얻어진 붉은색 선이 정밀측정한 초록색 선과 잘 일치함을 알 수 있고, 상대적으로 높은 온도인 1.3 K에서도 0.3 K 결과와 일치하는 0.87 × 10-6정도의 불확도 평가를 확인하였다.21 앞절에서의 불확도 수치보다 감소한 이유는 이 실험을 수행할 때는 전보다 시스템 불확도가 개선되었기 때문이다.
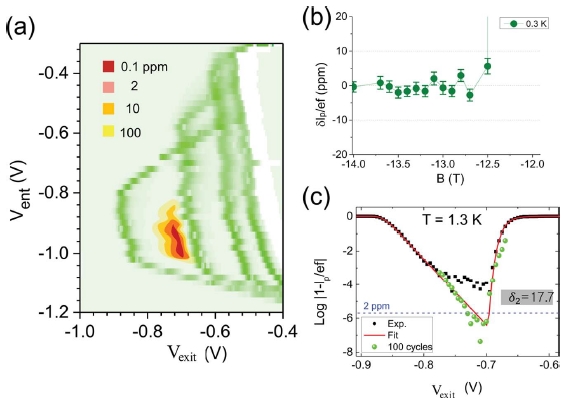
Robustness characterization. (a) Pumping map with colored contour representing expected uncertainty in ppm unit, (b) Precision measurement results with error bars of uT, (c) Precision (green solid circle) and normal (black solid circle) measurement data with a theoretical curve (red line)20
결론적으로, KRISS 단전자 펌프 소자는 최적의 작동 조건에서 0.87 × 10-6 불확도가 유의미한 외부환경(전압, 자기장, 온도)의 변화에도 유지되었다. 이와 같은 소자의 안정성은 향후 양자 전류표준기로 채택되기 위해서 매우 중요한 특성이다.
위와 같은 정밀측정 결과는 단전자 펌프 소자가 소자의 구조 및 기판의 종류에 관계없이 보편적인 결과라는 것을 보여준다고 말할 수 있다. 왜냐하면, NPL 정밀측정 시스템에서 KRISS 소자와 NPL 소자가 거의 유사한 정밀측정 결과를 보여줬기 때문이다.5,6 앞에서 언급되었지만, NPL 소자의 구조(Fig. 1)는 KRISS 소자와 다르고, 제작 방식도 다르다. 보편성 검증을 보다 확대 심화하기 위해서 국제 표준기관 상호간에 단전자 펌프 소자를 상호 교환하여 교차적으로 상대불확도 측정이 필요하고 이를 계획하고 있다.
단전자 펌프 소자가 양자홀 저항표준기와 조셉슨 전압표준기와 비견할 수 있는 양자 전류표준기로 공인되어 양자 전기표준체계가 완성되기 위해서는 단전자 펌프의 불확도도 10-8 수준이 유지될 수 있음이 검증되어야 한다. 현재의 정밀측정 기술로는 출력이 ~100 pA인 단전자 펌프 소자의 경우, 출력이 너무 낮아서10-8 불확도 검증이 불가능하다. 현재의 단전자 펌프 소자의 출력이 최소한 10 배 이상 증가되어야 가능하다. 단전자 펌프 소자의 출력을 높이는 방법으로는 소자의 작동 주파수를 상승시키거나 소자의 병렬화 등 두 가지 방법이 있다.
그러나 GaAs/AlGaAs 이종접합 반도체 기반의 단전자 펌프 소자가 작동할 수 있는 최대 주파수(fm) 가 존재한다는 것은 경험적으로 알려져 있다. 그런데, 우리는 KRISS 펌프 소자를 이용하여 양자점 포텐셜 모양을 제어함으로써 최대주파수 fm를 상승시킬 수 있음을 밝혔다(Fig. 10).16 그러나 fm은 증가하지만 반대로 펌프 소자 성능지수 δ2 즉 첫 번째 전류고원의 불확도가 악화된다는 사실도 확인하였다.16 KRISS 단전자 펌프 소자의 경우 fm은 최대 0.6 nA에 해당하는 4 GHz를 넘지 못하였다. 따라서 nA 수준 이상을 달성하기 위해서는 소자의 병렬화가 요구된다.
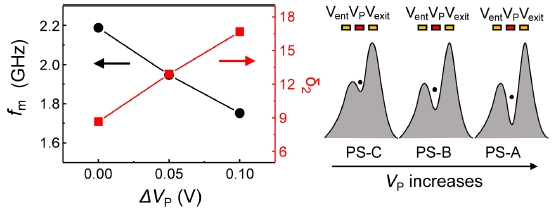
Left; Measured maximum operation frequency fm and d2 vs offset plunger gate voltage. Right; a schematic illustrating how plunger voltage VP deepens the QD potential well16 (https://doi.org/10.1063/1.5000319)
펌프 소자 병렬화 관련해서는, GaAs/AlGaAs 이종접합 반도체 기반의 단전자 펌프의 경우, 2개까지 병렬화를 성공한 사례가 보고되었다.22,23 그 이상의 소자 개 수에서 성공한 사례는 아직 없다. KRISS에서도 두개의 펌프 소자를 병렬로 연결하여 출력을 두배로 상승시킬 수 있음을 확인하였다.24 각각의 펌프 소자를 튜닝함으로써 두 개의 펌핑 맵이 서로 겹쳐지게 제어가 가능했다. 따라서 한 쌍의 펌프 소자가 마치 한 개의 소자처럼 전류의 출력 제어가 가능하므로, 펌핑 모델식 (1)을 데이터에 피팅하여 성능지수 δ2 값을 얻을 수 있었다. 이때 얻어진 δ2 수치는 각각의 펌핑지도에서 얻어진 값과 대동소이하였다. 즉, 병렬화로 기인한 추가 불확도 증가는 관찰되지 않았다.
2.2 기타 단전자 펌프
90년대 초에 금속기반의 단전자 소자를 이용한 단전자 펌프 소자가 세계 최초로 시연되었고,25,26 그 후에NIST에서 보고한 단전자 펌프가 현재까지 가장 정확한 단전자 펌프 소자(불확도 1.5 × 10-8)로 기록되었다.10,11 그러나 금속기반 단전자 펌프 소자는 터널 접합의 저항(R)과 정전용량(C)의 존재때문에 최대 동작 속도가 1/RC 변수에 의해서 제한을 받기때문에 100MHz를 넘기 힘들었다.
금속 기반 단전자 펌프 소자 중에서 가장 간단한 예가 Fig. 11에 사진과 개략도로 묘사되어 있다.27 3개의 터널 접합으로 연결된 두개의 금속 아일랜드(Island)와 두개의 게이트 전극으로 구성된 펌프 소자이다. 이 펌프 소자의 전기 에너지 U(n, m Vg1, Vg2)는 게이트 전압 Vg1, Vg2에 의해서 조절되고 각각의 금속 아일랜드에 존재하는 전자의 개수(n, m)는 전기 에너지 U(n, m Vg1, Vg2)의 최저값 조건에서 결정된다. 전기 에너지 계산에 의하면, 전자의 상태도는 Fig. 11(b)에 그려진 것과 같은 안정화 다이아그램으로 설명된다. 전자의 개수(n, m)가 안정적인 상태는 Vg1, Vg2로 이루어진 2차원 공간에서 육각형 벌집 모양을 이루고 있다. 육각형의 각 꼭지점은 에너지적으로 삼중축퇴점(Triple Degenerate Point)을 형성한다. 삼중축퇴점에서는 3가지 다른 전자배치(n, m)에 대해서 같은 에너지를 가지므로, 삼중축퇴점에서 펌프 소자는 최고의 전도도를 보여준다. 반면에 육각형 내부는 쿨롱봉쇄(Coulomb Blockade)된 상태로 펌프 소자는 절연상태에 있게 되어 전자의 개수(n, m)는 고정된다(부록 참조).
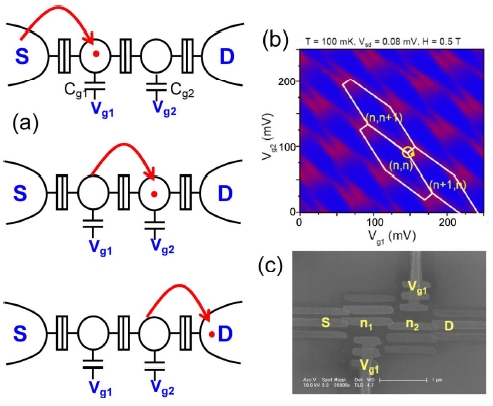
(a) Schematic diagram illustrating the sequence of pumping an electron from source to drain when gate voltages are driven along the circle path around a triple degenerate point in (b). (b) Conductance density plot as a function of Vg1 and Vg2. The red color represents high conductance while blue one low conductance. The honeycomb structure represents the energy stability diagram for double QD device. (n, m) represents the number of excess electrons existing on each QD. (c) SEM photo of a metallic pump device made by KRISS27
Fig. 11(b)에서, 삼중축퇴점 중심으로 노랑색 원으로 표시된 길을 따라서 게이트 전압을 조절하면, 한개의 전자가 첫 번째 금속 아일랜드에서 두 번째 금속 아일랜드로 순차적으로 전송되는 단전자 펌핑 현상이 발생한다[Fig. 11(a) 참조]. 단전자 펌핑에 의해서 소스와 드레인 사이에 발생하는 전류 크기는 인가하는 게이트 전압의 주파수 f에 비례한다. 이 펌프 동작에서 오류를 주는 주요인은 코터널링(Co-Tunneling)에 의한 누설 전류이다. 코터널링 현상은 수 개의 접합에 걸쳐서 전자 투과가 동시에 일어나는 현상을 말한다. 이론적으로, 접합의 개수 N이 증가하면 코터널링 확률이 각 접합의 터널링 확률의 N곱으로 줄어듦이 알려져있다.28 90년대에 미국 NIST에서 N = 7인 7-접합 펌프 소자를 이용하여 작동 주파수 10 MHz에서 ~1.5 × 10-8의 불확도를 확인하였다.10,11 이 결과는 지금까지 세계에서 가장 높은 정확도의 결과이지만 전류 크기가 너무 작아서 전류 표준기로 사용되지 않았고 정전용량 표준기 개발에 이용되고 있다.11 PTB에서는 터널접합의 개수 증가 없이 코터널링 확률을 줄이는 방법을 개발하여 접합 개수 3개의 펌프 소자에서 불확도 3.9 × 10-6을 달성하였다.29,30
초전도 하이브리드소자(SINIS 소자); MIKES(핀란드 NMI) 및 Aalto 대학(핀란드) 공동으로 단전자 펌프 소자를 초전도-금속-초전도 하이브리드 터널 접합(SINIS)으로 개발하였다. 이 소자를 SINIS 턴스타일(Turnstile)이라고 부른다(Fig. 12). SINIS 턴스타일의 구동 방법은 게이트에 DC 전압과 rf 신호를 인가하여 전자를 한 번에 하나씩 금속 양자점을 통해 운반하는 것이다(Fig. 12(b)). Fig. 12(c)는 rf 신호 진폭과 게이트 DC 전압 변화에 의존하는 I = nef 전류 고원을 3차원 플롯으로 보여주고 있다. SINIS 단전자 펌프 소자의 장점은 터널 접합이 2개임에도 코터널링 현상이 초전도 갭에 의해서 억제되어서, 예상 불확도 10-7수준을 기대할 수 있고, 또한 병렬화가 가능하다는 장점이 있다. 현재 10개의 SINIS 병렬화 펌프 소자가 개발되어 있다.15 그러나 소자의 최대 작동 주파수는 RC 파라미터에 제한을 받아서 100 MHz를 넘지 못하고 있다. 그리고, 가장 큰 불확도 요인으로는 준입자의 열적 요동으로 알려져있다. 단일 SINIS 단전자 펌프 소자의 출력은 약 10 pA, 불확도는 10-7이 예상되고 있다.
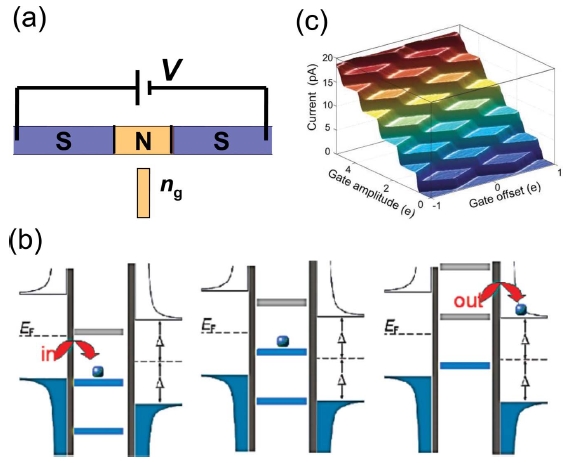
(a) Schematic diagram of SINIS device, (b) Sequence of a single electron pumping in accordance with the modulation of the energy levels on the QD, (c) Current plateaus as a function of gate voltage and rf amplitude31 arXiv:0708.1995v2
SAW 단전자 펌프 소자, Fig. 13에서 보는 바와 같이 파장이 λ인 표면음파(Surface Acoustic Wave, SAW)를 QPC에 의해서 형성된 1차원 양자선에 주입하면, 표면음파에 의해서 형성된 전기적 포텐샬 우물이 1차원 양자선을 통과하면서 포획된 전자와 함께 QPC 포텐셜 장벽을 넘어설 수 있다.32-34 포획된 전자는 음속으로 이동하는 표면음파와 함께 양자선을 따라서 전송된다. 여기서 전자의 수송은 열손실이 전혀 없는 서행(Adiabatic) 과정이다. 그런데, SAW에 의해서 유도되어서 음속으로 진행되는 전기적 포텐샬의 우물 크기가 충분히 작아서 양자점으로 간주될 수 있으므로 쿨롱봉쇄 현상에 의해서 포획되는 전자의 갯수는 양자화 되어서 유도된 전류의 크기는 I = nef 식을 만족한다. 여기서 n은 포획된 전자의 개수이다. Fig. 13에서 보듯이 소자의 구성은 QPC와 SAW 발생장치인 IDT (Inter Digital Transducer)로 이루어져 있고, GaAs/AlGaAs 이차원 전자계를 이용해서 소자가 제작된다. 펌프의 작동 주파수는 IDT의 공진주파수에 의해서 결정된다. 대체로 2~3 GHz에 해당되고, 영국 그룹에서 발표한 소자의 경우 예상 불확도는 10-5였다.32 불확도의 가장 큰 요인은 다음의 두 가지로 믿어지고 있다. SAW에 의해서 전기적인 포텐셜 우물을 형성시키기 위해서는 상대적으로 높은 rf 출력이 필요한데(~10 dBm) 이때문에 발생되는 열화 현상이 불확도의 가장 큰 요인일 수 있다. 또 다른 하나는 rf 신호와 QPC 금속게이트의 상호작용이다. 이 때문에 전자의 서행이 깨질 수 있다.
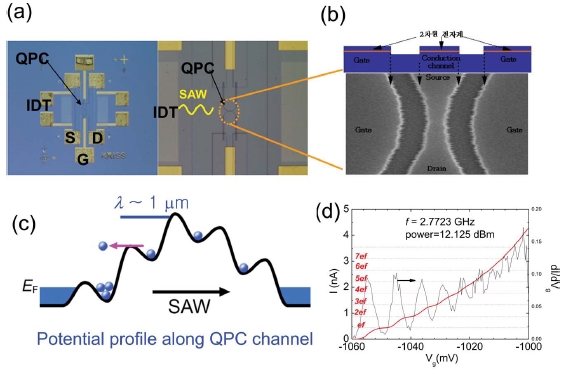
(a) SEM photo of a SAW pump device, (b) Photo of QPC. (c) Illustration for the SAW-driven quantized charge pumping across the QPC potential barrier, (d) An example of the observed quantized current as a function of QPC-gate voltage32-34
Si 양자점 단전자 펌프, 반도체 기반 단일변수 단전자 펌프로는 세계 최초로 개발된 소자가 Si 반도체 기반의 NTT 소자였다(Fig. 1참조).35 작동주파수가 상대적으로 높다(~7 GHz)는 사실(Fig. 14)과8 병렬화가 가능하다는 가능성때문에 최근에 NTT7, UNSW9, MIKES9 등에서 연구가 활발히 진행중이다.
3. 양자 전류원 정밀측정 방법
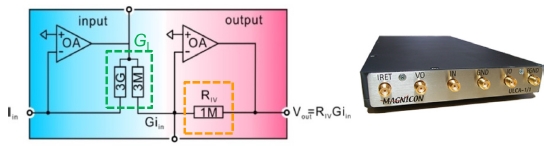
현재까지 개발된 양자점 단전자 펌프의 출력은 최대 출력 1 nA 이하이다. 따라서 10-8 불확도를 검증하기 위해서는 최소한 10-18A의 해상도를 갖는 전류 검출기가 필요하지만, 현재는 그보다 약 10 배 나쁜 10-17 A 해상도가 세계 최고 수준이다. 현재까지 개발된 극소전류 측정 방식은 크게 3가지 방식이다. 첫째는 앞 절에서 소개된 NPL 방식이다. 표준저항과 표준전압기를 이용하여 발생시킨 표준전류와 단전자 펌프 전류의 차이를 영점검출기를 이용하여 비교하는 방식이다. 현재 100 pA 크기의 전류에 대해서 불확도 ~2 × 10-7 검증이 가능한 수준이다.9 두번째 방식은 PTB에서 개발된 방식인데, ULCA (Ultrastable Low-Noise Current Amplifier)로36,37 명명된 전류 증폭기를 이용하여 극소 전류를 측정하는 방식이다. 이 방법으로 100 pA 수준에서 2 × 10-7불확도 측정이 가능하다고 보고되었다. ULCA는, Fig. 15에 개략도가 묘사되어 있듯이, 입력단과 출력단으로 구성되어 있다. 입력단은 입력된 극소 전류를 증폭율 GI (~1000) 배로 증폭하여 출력단으로 보내게 되고, 출력단에서는 트랜스 저항 RIV를 이용하여 전류를 전압으로 변환하여 출력하게 된다. 그래서 ULCA의 GI (= 3 GΩ/3 MΩ)와 RIV의 교정이 필요한데, CCC (Cryogenic Current Comparator)라는 저온 전류 비교기와(부록참조)38 양자홀 저항표준기를 이용하여 입력단 저항비와 출력단의 저항을 교정함으로써 가능하다. GI와 RIV가 10-8 수준으로 불확도 교정이 가능하다고 보고되었다. 최종적으로 ULCA의 총 불확도는 100 pA 전류 측정시에 2 × 10-7 불확도 수준이다.36,37
세번째 방식은 프랑스 표준기관인 LNE에서 시도되는 방식으로, 단전자 펌프의 전류를 CCC를 이용하여 약 2만배 증폭하여 양자홀 저항표준기에 입력하면, 이 때 저항표준기 양단에 유도되는 전압을 조셉슨 전압표준기와 직접적으로 비교하는 방식으로 100 pA 크기의 극소 전류에 대해서 ~3 × 10-7 수준의 불확도를 검증할 수 있을 것으로 예상된다.13
4. 양자 전류원 활용분야
4.1 QMT
새로운 전류 표준(양자 전류표준)이 기존의 양자 전기표준체계(조셉슨 전압 및 양자홀 저항표준)와 일치함을 증명하기 위하여 QMT에 대한 연구가 필수적이다. Fig. 16은 이와 같은 양자 전기 표준의 일치성을 삼각형 도형으로 도식화해서 표현하고 있다. 양자 전기표준 확립을 위해서는 적어도 10-8 불확도 수준에서 일치성 검증이 요구된다. 일치성 검증이 필요한 이유는 다음의 두 가지로 요약될 수 있다. 첫째, 현재의 전류표준 정의(고전 전자기 역학에 기초한 정의)와 전류표준 구현(조셉슨 전압과 양자홀 저항의 옴의 법칙에 의존) 사이의 괴리를 해결할 미래의 새로운 전류 표준(‘양자 전류표준’)은 기존의 양자 전기표준체계(조셉슨 전압 표준과 양자홀 저항표준)와 일치함을 증명해야 한다. 두 번째 이유는, 물리학적인 이유로서, 양자 전기표준의 근간이 되는 물리학 이론의 정확성에 대한 확인이다. 즉, 물리학에서 제공하는 이론에 기반을 둔 공식들의 유효성 한계를 가늠할 수 있는 중요한 수단이 될 수 있다. 이 밖에 QMT 검증의 또 다른 의의는 물리상수 측정이라는 측면에서 다음과같은 의미가 있다. 조셉슨 상수 KJ= 2e/h와 폰 클리칭 상수 RK = h/e2 그리고 기본 전하 상수 QS = e에 대한 CODATA(2010)40 불확도 불일치 이슈를13,40,41 해소하는데 기여한다. 양자홀 효과, 조셉슨 효과 및 단전자 효과를 표현하는 상수의 관계식이 εK, εJ, εs 만큼 부정확하다고 가정하면, KJRKQS-2의 불확도가 ~5 × 10-7 수준으로 산출될 수 있다는 문제 제기가 있었다.41 이와 같은 불일치 이슈에 대한 원인이 무엇인지 밝혀져야 한다.
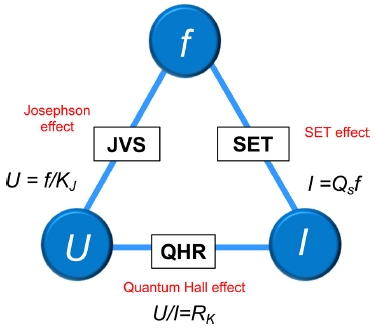
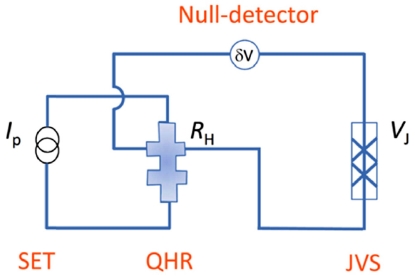
Quantum metrology triangle links the Josephson effect (JVS), the quantum Hall effect (QHR) and the singleelectron tunneling effect (SET) by using Ohm’s law. Josephson voltage U = f/KJ = hf/2e, quantum hall resistance RK = h/e2, and single electron current I = ef39
Fig. 17은 QMT 실현을 위한 측정의 기본 구성도를 보여준다. QMT의 일치성은 영점검출기를 통하여 검증된다. 영점검출기는 단전자 펌프의 전류 Ip = QSfS에 의해서 양자홀 저항 RH = RK에 유도되는 홀 전압 VH = IpRH과 조셉슨 전압 VJ = fJ/KJ과의 차이를 측정한다. 여기서, QS, RK, KJ는 각각, 전자의 전하상수, 폰 클리칭 상수, 그리고 조셉슨 상수를 나타낸다. Fig. 17에서처럼 δV가 측정되면 다음의 관계식이 성립된다.
| δV=IpRH-Vj | (2) |
이 식을 물리상수를 이용하여 전개하면 다음과 같이 된다.
| KJRKQs-2=δ | (3) |
여기서, δ ≡ δV × KJ/fS로 재정의 하였다. 즉 영점검출기 신호 δV가 제로로 측정되면 위 식(3)도 제로가 되어서 QMT 일치성이 검증되었다고 판단할 수 있다. 그러나 δ만큼 불일치가 존재한다고 가정하면, 다음과 같이 물리 상수에 ε만큼 오차가 있다고 판단할 수 있다. 즉, QS = e(1 + εs), RK = h/e2(1 + εK), KJ= 2e/h(1 + εJ). 여기서 εs, εK, εJ는 불일치 파라미터이다. 이 관계식들을 식(3)에 대입하여, ε 파라미터에 대해서 1차 항만 유지하면, 다음 식(4)가 유도된다.
| εs+εK+εJ=δ | (4) |
그러면 이식의 실험 측정 결과는 다음 식(5)와 같이 표현될 수 있다.
| εs+εK+εJ=δexp±uexp | (5) |
여기서 δexp는 영점검출기에서 측정되는 불일치 측정값이고 uexp는 측정 불확도가 된다. 따라서, δexp 값이 uexp 보다 작다면QMT는 측정 불확도 uexp 내에서 일치한다고 결론 내릴 수 있다. 반대의 경우는 불일치 결론이 나오게 되는데, 이 때는 불일치 원인에 대한 새로운 추가 연구가 필요하다.
현재까지 QMT 검증 실험이 성공하지 못하였는데, 가장 큰 이유는 양자 전류원의 출력이 현재의 측정기술과 비교해서 10-100 배 정도 적기 때문이었다.11,13,14 현재까지 시도되었던 QMT 실험은 모두 간접적인 방법이었다고 할 수 있는데 사례를 간단히 살펴보면 다음과 같다. LNE 그룹은 CCC 회로를 이용하여 금속 단전자 펌프의 출력을 증폭하여 표준저항에 인가함으로써, 표준저항 양단에 유도된 전압을 조셉슨 전압표준기와 비교하여 측정 불확도를 평가하였다. 불확도는 1.5 × 10-5 수준이었다.13 NIST그룹은 금속 단전자 펌프 소자를 이용하여 개수가 제어된 전자를 표준 커패시퍼에 주입하고, 이 때 커패시터에 유도된 전압을 조셉슨 전압표준기와 비교함으로써 간접적으로 QMT 일치성 검증 실험을 수행하였는데, 불확도는 9 × 10-7이었다.11
4.2 저전류 교정 분야
앞에서 100 pA 수준의 단전자 펌프의 불확도 측정을 10-7 수준 이하로 낮추려면 극소전류 측정 능력을 현재보다 10배이상 향상시켜야 한다고 언급하였다. 즉 aA (10-18 A) 수준까지 분해능이 향상되어야 한다. 그런데, 극소전류 측정 능력 개선은 단전자 펌프의 측정 불확도 개선뿐만 아니라, 저전류 교정이 필요한 계측 분야에서도 필수적이다. 상용 전류계는 고이득 증폭기를 사용하는데, 고이득 증폭기가 불안정해서 상용 전류계에서는 fA (10-15A) 이하의 전류를 측정하기가 어렵다. 극소 전류 측정 교정이 불량하면, 극소량의 물질을 검출하는 물질량 검출기의 정밀도가 저하되는 문제가 있다. 예를 들어, 파라데이컵(Faraday-Cup) 측정 방식을 이용하는 에어로졸 입자 계수기의 분해능은 입방 센티미터 당 약 1000 개 이상의 입자수를 필요로 한다. 왜냐하면, 입자 계수 측정 단계에서 발생되는 전류 크기가 fA 크기의 극소 전류이기 때문이다.42 언급한 저전류의 정밀측정 능력은 요즘 문제가 대두되고 있는 미세먼지 측정 능력의 향상을 가져올 수 있을 것으로 기대한다. 또한, 방사능 치료에서 이용되는 기기의 방사성 핵종의 수명과 방사선량의 측정에도 동일한 논리가 적용되는데, pA (10-12 A) 이하의 전류를 분석 할 수 있다면 더 나은 정확도로 핵종 수명과 방사선 량의 측정이 가능해진다.43 이는 양전자 방출 단층 촬영에 사용되는 15O, 13N 및 11C와 같은 극도로 수명이 짧은 방사성 핵종 측정에 특히 중요하다. 또한 향상된 극소전류 검출기 기능은 또 다른 중요한 장점을 가지게 되는데 다음과 같다. 독성 가스 또는 방사능 물질량을 검출하기 위해서 현재 일정 용적을 맞추는 희석식 방법이 채용되고 있는데, 이런 방식은 측정의 불확도를 높일뿐만 아니라 고비용을 유발하고 실험자의 건강을 위협하기 때문에 직접적으로 극소전류를 검출하는 검출기가 개발되면 이러한 현재 상황을 극복할 수 있다.
4. 결론
전류단위 암페어의 재정의에 대해서 그 의의 및 실현 방법에 대해서 고찰하였다. 또한 재정의될 암페어의 실현 방안으로 유력한 단전자 펌프의 원리, 개발 현황 및 문제점 등을 KRISS 연구결과 및 타 연구기관의 결과를 기초로 하여 기술하였다. 현재 소자 제작 기술과 정밀 측정 기술이 진보하고 있고, 또한 세계 NMI 기관들이 협력 연구를 강화하고 있기 때문에 재정의를 실현할 수 있는 저출력의 양자 전류원은 개발이 될 것이라고 낙관적으로 전망한다.
NOMENCLATURE
| CCC : | Cryogenic current comparator |
| CODATA : | Committee on data for science and technology |
| CGPM : | General conference on weights and measures |
| CIPM : | International committee for weights and measures |
| IDT : | Inter digital transducer |
| JVS : | Josephson voltage standard |
| KRISS : | Korea research institute of standards and science |
| LNE : | Laboratoire national de métrologie et d'essais (French metrology laboratory) |
| MIKES : | Centre for metrology and accreditation, Finland |
| NIST : | National institute of standards and technology, USA |
| NMI : | National measurement institute |
| NPL : | National physical laboratory, UK |
| PTB : | Physikalisch-technische bundesanstalt (the national standards laboratory of Germany) |
| QD : | Quantum dot |
| QHR : | Quantum Hall resistance |
| QMT : | Quantum metrology triangle |
| QPC : | Quantum point contact |
| SAW : | Surface acoustic wave |
| SEM : | Scanning electron microscope |
| SET : | Single electron tunneling |
| SI : | International system of units |
| SINIS : | Superconductor/insulator/normal-metal/insulator/superconductor junction |
| ULCA : | Ultrastable low-noise current amplifier |
| UNSW : | University of new south wales, Sydney, Australia |
| A : | ampere, unit of current |
| Ip, Ipump : | Pump current |
| Prf : | Power of rf in unit of dBm |
| aA : | Atto ampere (10-18 A) |
| e : | Elementary charge |
| fA : | Femto ampere (10-15 A) |
| fm : | Maxiumu operation frequency |
| h : | Plank constant |
| m : | Meter, unit of length |
| nm : | Nano meter |
| pA : | Pico ampere (10-12 A) |
| ppm : | Parts per million |
| rf : | Radio frequency |
| s : | Second, unit of time |
| uA : | Measurement uncertainty (random) |
| uB : | System uncertainty (systematic) |
| uT : | Total uncertainty |
| δ2 : | Figure of merits for single electron pump |
| Γ : | Electron tunneling rate |
Acknowledgments
이 연구는 2018년도 한국표준과학연구원의 양자 측정 삼각체계 실현 사업 재원으로 지원을 받아 수행된 연구임(한국표준과학연구원-GP2018-003). 저자 중 한 명(김남)은 EMPIR 15SIB08 e-SI-Amp 과제를 통해서 국제협력을 할 수 있었고, 한국연구재단(NRF-2016K1A3A7A03951913)의 일부 지원을 받았다.
REFERENCES
- BIPM, “SI Brochure: The International System of Units (SI),” https://www.bipm.org/en/publications/si-brochure/ampere.html, (Accessed 23 MAR 2018)
-
Newell, D. B., Cabiati, F., Fischer, J., Fujii, K., Karshenboim, S. G., et al., “The Codata 2017 Values of h, e, k, and Na for the Revision of the SI,” Metrologia, Vol. 55, No. 1, pp. L13-L16, 2017.
[https://doi.org/10.1088/1681-7575/aa950a]

- BIPM, “Concise Summary of the SI,” https://www.bipm.org/utils/en/pdf/si-revised-brochure/Draft-Concise-summary-2018.pdf, (Accessed 23 MAR 2018)
-
Pekola, J. P., Saira, O.-P., Maisi, V. F., Kemppinen, A., Mottonen, M., et al., “Single-Electron Current Sources: Toward a Refined Definition of the Ampere,” Reviews of Modern Physics, Vol. 85, No. 4, Article No. 1421, 2013.
[https://doi.org/10.1103/RevModPhys.85.1421]

-
Giblin, S., Kataoka, M., Fletcher, J., See, P., Janssen, T., et al., “Towards a Quantum Representation of the Ampere Using Single Electron Pumps,” Nature Communications, Vol. 3, Article No. 930, 2012.
[https://doi.org/10.1038/ncomms1935]

-
Bae, M.-H., Ahn, Y.-H., Seo, M., Chung, Y., Fletcher, J., et al., “Precision Measurement of a Potential-Profile Tunable Single-Electron PUMP,” Metrologia, Vol. 52, No. 2, pp. 195-200, 2015.
[https://doi.org/10.1088/0026-1394/52/2/195]

-
Stein, F., Scherer, H., Gerster, T., Behr, R., Gtz, M., et al., “Robustness of Single-Electron Pumps at Sub-PPM Current Accuracy Level,” Metrologia, Vol. 54, No. 1, pp. S1-S8, 2017.
[https://doi.org/10.1088/1681-7575/54/1/S1]

-
Yamahata, G., Giblin, S. P., Kataoka, M., Karasawa, T., and Fujiwara, A., “High-Accuracy Current Generation in the Nanoampere Regime from a Silicon Single-Trap Electron Pump,” Scientific Reports, Vol. 7, Paper No. 45137, 2017.
[https://doi.org/10.1038/srep45137]

-
Zhao, R., Rossi, A., Giblin, S., Fletcher, J., Hudson, F., et al., “Thermal-Error Regime in High-Accuracy Gigahertz Single-Electron PUMPING,” Physical Review Applied, Vol. 8, No. 4, Paper No. 044021, 2017.
[https://doi.org/10.1103/PhysRevApplied.8.044021]

-
Keller, M. W., Martinis, J. M., Zimmerman, N. M., and Steinbach, A. H., “Accuracy of Electron Counting Using a 7-Junction Electron Pump,” Applied Physics Letters, Vol. 69, No. 12, pp. 1804-1806, 1996.
[https://doi.org/10.1063/1.117492]

-
Keller, M. W., Zimmerman, N. M., and Eichenberger, A. L., “Uncertainty Budget for the NIST Electron Counting Capacitance Standard, ECCS-1,” Metrologia, Vol. 44, No. 6, p. 505, 2007.
[https://doi.org/10.1088/0026-1394/44/6/010]

-
Steck, B., Gonzalez-Cano, A., Feltin, N., Devoille, L., Piquemal, F., et al., “Characterization and Metrological Investigation of an R-PUMP with Driving Frequencies Up to 100 Mhz,” Metrologia, Vol. 45, No. 4, p. 482, 2008.
[https://doi.org/10.1088/0026-1394/45/4/015]

-
Devoille, L., Feltin, N., Steck, B., Chenaud, B., Sassine, S., et al., “Quantum Metrological Triangle Experiment at LE: Measurements on a Three-Junction R-PUMP Using a 20 000: 1 Winding Ratio Cryogenic Current Comparator,” Measurement Science and Technology, Vol. 23, No. 12, Paper No. 124011, 2012.
[https://doi.org/10.1088/0957-0233/23/12/124011]

-
Scherer, H., Schurr, J., and Ahlers, F., “Electron Counting Capacitance Standard and Quantum Metrology Triangle Experiments at PB,” Metrologia, Vol. 54, No. 3, p. 322, 2017.
[https://doi.org/10.1088/1681-7575/aa65f9]

-
Maisi, V. F., Pashkin, Y. A., Kafanov, S., Tsai, J.-S., and Pekola, J. P., “Parallel Pumping of Electrons,” New Journal of Physics, Vol. 11, No. 11, Paper No. 113057, 2009.
[https://doi.org/10.1088/1367-2630/11/11/113057]

-
Ahn, Y.-H., Hong, C., Ghee, Y.-S., Chung, Y., Hong, Y.-P., et al., “Upper Frequency Limit Depending on Potential Shape in a QD-based Single Electron Pump,” Journal of Applied Physics, Vol. 122, No. 19, Paper No. 194502, 2017.
[https://doi.org/10.1063/1.5000319]

-
Kashcheyevs, V. and Kaestner, B., “Universal Decay Cascade Model for Dynamic Quantum Dot Initialization,” Physical Review Letters, Vol. 104, No. 18, Paper No. 186805, 2010.
[https://doi.org/10.1103/PhysRevLett.104.186805]

-
Seo, M., Ahn, Y.-H., Oh, Y., Chung, Y., Ryu, S., et al., “Improvement of Electron PUMP Accuracy by a Potential-Shape-Tunable Quantum Dot PUMP,” Physical Review B, Vol. 90, No. 8, Paper No. 085307, 2014.
[https://doi.org/10.1103/PhysRevB.90.085307]

-
Um, Y., Oh, Y., Seo, M., Lee, S., Chung, Y., et al., “Quantum Point Contact with Large Subband Energy Spacings,” Applied Physics Letters, Vol. 100, No. 18, Paper No. 183502, 2012.
[https://doi.org/10.1063/1.4710522]

-
Ahn, Y.-H., Seo, M., Giblin, S., Kataoka, M., Chung, Y., et al., “Robustness of Potential-Profile-Tunable Electron PUMP,” Proc. of the Conference on Precision Electromagnetic Measurements, pp. 1-2, 2016.
[https://doi.org/10.1109/CPEM.2016.7540623]

-
Giblin, S., Bae, M., Kim, N., Ahn, Y.-H., and Kataoka, M., “Robust Operation of a GaAs Tunble Barrier Electron PUMP,” Metrologia, Vol. 54, No. 3, pp. 299-306, 2017.
[https://doi.org/10.1088/1681-7575/aa634c]

-
Wright, S., Blumenthal, M., Pepper, M., Anderson, D., Jones, G., et al., “Parallel Quantized Charge Pumping,” Physical Review B, Vol. 80, No. 11, Paper No. 113303, 2009.
[https://doi.org/10.1103/PhysRevB.80.113303]

-
Mirovsky, P., Kaestner, B., Leicht, C., Welker, A., Weimann, T., et al., “Synchronized Single Electron Emission from Dynamical Quantum Dots,” Applied Physics Letters, Vol. 97, No. 25, Paper No. 252104, 2010.
[https://doi.org/10.1063/1.3527940]

- Ahn, Y.-H., Ghee, Y.-S., Hong, C., Chung, Y., Kim, B.-K., et al., “Parallelized Single Electron PUMP Based on Gate Tunable Quantum Dots,” Preparation.
-
Pothier, H., Lafarge, P., Orfila, P., Urbina, C., Esteve, D., et al., “Single Electron PUMP Fabricated with Ultrasmall Normal Tunnel Junctions,” Physica B: Condensed Matter, Vol. 169, Nos. 1-4, pp. 573-574, 1991.
[https://doi.org/10.1016/0921-4526(91)90332-9]

-
Geerligs, L., Anderegg, V., Holweg, P., Mooij, J., Pothier, H., et al., Frequency-Locked Turnstile Device for Single Electrons,” Physical Review Letters, Vol. 64, No. 22, Article No. 2691, 1990.
[https://doi.org/10.1103/PhysRevLett.64.2691]

- KRISS Research Report, KRISS/IR-2005.
-
Jensen, H. D. and Martinis, J. M., “Accuracy of the Electron PUMP,” Physical Review B, Vol. 46, No. 20, Paper No. 13407, 1992.
[https://doi.org/10.1103/PhysRevB.46.13407]

-
Zorin, A., Lotkhov, S., Zangerle, H., and Niemeyer, J., “Coulomb Blockade and Cotunneling in Single Electron Circuits with On-chip Resistors: Towards the Implementation of the R PUMP,” Journal of Applied Physics, Vol. 88, No. 5, pp. 2665-2670, 2000.
[https://doi.org/10.1063/1.1286328]

-
Lotkhov, S., Bogoslovsky, S., Zorin, A., and Niemeyer, J., “Operation of a Three-Junction Single-Electron PUMP with On-Chip Resistors,” Applied Physics Letters, Vol. 78, No. 7, pp. 946-948, 2001.
[https://doi.org/10.1063/1.1347017]

-
Pekola, J. P., Vartiainen, J. J., M ̈otto ̈nen, M., Saira, O.-P., Meschke, M., et al., “Hybrid Single-Electron Transistor as a Source of Quantized Electric Current,” Nature Physics, Vol. 4, No. 2, pp. 120-124, 2008.
[https://doi.org/10.1038/nphys808]

-
Cunningham, J., Talyanskii, V., Shilton, J., Pepper, M., Simmons, M., et al., “Single-Electron Acoustic Charge Transport by Two Counter-Propagating Surface Acoustic Wave Beams,” Physical Review B, Vol. 60, No. 7, Article No. 4850, 1999.
[https://doi.org/10.1103/PhysRevB.60.4850]

- Kim, N., Woo, B., Kim, J., Seo, M., and Chung, Y., “Quantization of the Current Induced by a Surface Acoustic Wave through a Quantum Point Contact,” Journal of the Korean Physical Society, Vol. 50, No. 5, pp. 1290-1293, 2007.
-
Seo, M., Kim, H., Chung, Y., Kim, N., Woo, B.-C., et al., “The Frequency Dependence of Quantized Current Plateaus Induced by Surface Acoustic Waves through a Quantum Point Contact,” Journal of the Korean Physical Society, Vol. 55, No. 6, pp. 2482-2485, 2009.
[https://doi.org/10.3938/jkps.55.2482]

-
Fujiwara, A., Zimmerman, N. M., Ono, Y., and Takahashi, Y., “Current Quantization due to Single-Electron Transfer in Si-Wire Charge-Coupled Devices,” Applied Physics Letters, Vol. 84, No. 8, pp. 1323-1325, 2004.
[https://doi.org/10.1063/1.1650036]

-
Drung, D., Krause, C., Becker, U., Scherer, H., and Ahlers, F., “Ultrastable Low-Noise Current Amplifier: A novel Device for Measuring Small Electric Currents with High Accuracy,” Review of Scientific Instruments, Vol. 86, No. 2, Paper No. 024703, 2015.
[https://doi.org/10.1063/1.4907358]

-
Drung, D. and Krause, C., “Ultrastable Low-Noise Current Amplifiers with Extended Range and Improved Accuracy,” IEEE Transactions on Instru- Mentation and Measurement, Vol. 66, No. 6, pp. 1425-1432, 2017.
[https://doi.org/10.1109/TIM.2016.2611298]

-
Kim, W.-S., Yu, K. M., Kim, M.-S., Park, P. G., and Kim, K.-T., “Precise Measurement of Quantized Hall Resistance on the Basis of a Cryogenic Current Comparator,” Journal of the Korean Physical Society, Vol. 58, No. 1, pp. 1339-1342, 2011.
[https://doi.org/10.3938/jkps.58.1339]

-
Likharev, K. and Zorin, A., “Theory of the Bloch-Wave Oscillations in Small Josephson Junctions,” Journal of Low Temperature Physics, Vol. 59, Nos. 3-4, pp. 347-382, 1985.
[https://doi.org/10.1007/BF00683782]

- Mohr, P. J., Taylor, B. N., and Newell, D. B., “CODATA Recommended Values of the Fundamental Physical Constants: 2010,” Journal of Physical and Chemical Reference Data, Vol. 84, No. 4, Aritcle No. 1527, 2012.
-
Scherer, H. and Camarota, B., “Quantum Metrology Triangle Experiments: A Status Review,” Measurement Science and Technology, Vol. 23, No. 12, Paper No. 124010, 2012.
[https://doi.org/10.1088/0957-0233/23/12/124010]

-
Flagan, R. C., “History of Electrical Aerosol Measurements,” Aerosol Science and Technology, Vol. 28, No. 4, pp. 301-380, 1998.
[https://doi.org/10.1080/02786829808965530]

-
Giblin, S., Bakshandier, E., Fletcher, N., Lines, K., and Sephton, J., “An Si Traceable Electrometer System for Radionuclide Metrology,” Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, Vol. 606, No. 3, pp. 824-828, 2009.
[https://doi.org/10.1016/j.nima.2009.04.023]

- Kim, B. K., “Quantum Dots and Kondo-Correlated Andreev Bound States in Single-wall Carbon Nanotubes,” Ph.D. Thesis, Chonbuk National University, 2014.
-
Kaneko, N.-H., Nakamura, S., and Okazaki, Y., “A Review of the Quantum Current Standard,” Measurement Science and Technology, Vol. 27, No. 3, Paper No. 032001, 2016.
[https://doi.org/10.1088/0957-0233/27/3/032001]

-
Drung, D., Goetz, M., Pesel, E., and Scheter, H., “Improveing the Traceable Measurement and Generation of Small Direct Currents,” IEEE Transactions on Instru-Mentation and Measurement, Vol. 64, No. 11, pp. 3021-3030, 2015.
[https://doi.org/10.1109/TIM.2015.2440564]

Appendix
APPENDIX
A1. 단전자 투과 현상
Fig. A1은 ‘단전자 효과’를 보여주는 ‘단전자 소자’의 구조를 보여주고 있다. 서브마이크로 크기의 작은 도체(도체점 또는 양자점)가 전극과는 얇은 두께의 절연체(터널링 장벽)를 사이에 두고 연결되어 있어서 전자의 양자 투과가 가능하다. 그리고, 게이트 전압에 의해서 양자점의 전자 에너지준위가 제어될 수 있다. 도체점이 서브마이크로 크기로 작아지면, 도체점의 쿨롱에너지 Ec = e2/2C가 무시할 수 없을 정도로 커지게 되어서, 전극에서 도체점으로 전자가 한개 투과하려면 Ec 크기의 에너지가 추가로 필요하다. 따라서 전극의 페르미에너지 준위의 전자는 도체점으로의 투과가 봉쇄되는 현상이 발생하는데 [Fig. A1(b)] 이런 현상을 쿨롱 봉쇄 현상 또는 쿨롱봉쇄 효과라고 한다. 전극의 에너지를 Ec 보다 높여서 전자를 도체점으로 투과하게 할 수도 있지만, 게이트 전압에 의해서 도체점의 에너지준위를 제어하여 Fig. A1(c)에서 처럼 전자의 투과를 가능하게 할 수도 있다. 따라서 그림에서 묘사되어 있듯이 게이트 전압을 변화시키면 도체점이 도체 상태와 절연체 상태를 반복하게 되는데 [Fig. A1(d)] 이런 현상을 쿨롱진동이라고 한다. 쿨롱봉쇄 효과에 의해서 도체점에 존재하는 전자의 개수는 양자화되고 전자 투과 시에도 단일전자 형태로 투과된다. 따라서 게이트 전압을 적절히 제어하여 도체점의 전자 개수를 임의로 제어하는 것이 가능하다. 그런데, 이러한 단전자 투과 효과가 실제로 발생하기 위해서는 Ec가 열적에너지보다 커야하고(Ec >> kBT) 또한 도체점의 에너지 준위가 잘 정의될 정도로 투과 장벽의 저항이 커야한다는 조건(R >> h/e2)이 만족되어야 한다. 그러면, 게이트 전압에 의해서 전자를 한 개씩 제어하는 것이 가능해진다.
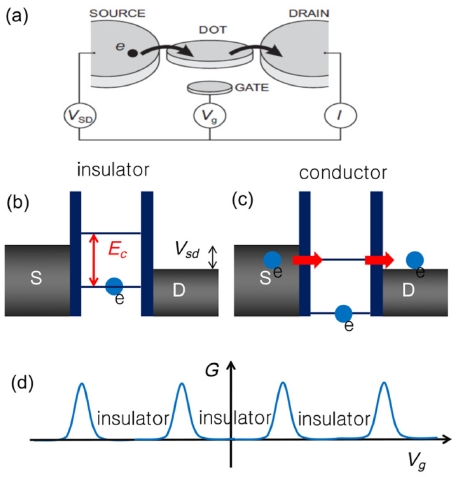
(a) Schematic diagram showing a single electron tunneling (SET) device. (b) Electron tunneling is blockaded due to the charging gap energy Ec. (c) Electrons can tunnel through the QD when energy levels are aligned. (d) SET can be switched between insulator and conductor states44
A2. 저온 전류 비교기; CCC
저온 전류 비교기(CCC, cryogenic current comparator)는 한 쌍의 코일(권선수 > 10 회)에 흐르는 1차와 2 차 직류 전류 크기의 비율을 10-10 이하로 정확하게 측정할 수있는 장치이다(Fig. A2).45 CCC는 이를 달성하기 위해 초전도 센서인 초전도 양자 간섭 장치(supeconducting quantum interference device, SQUID)를 이용하므로 낮은 온도, 일반적으로 액체 헬륨 온도(4.2 K)에서 작동한다. 동작 원리는 초전도체의 자속 차폐 원리(Meissener Effect, 마이스너 효과)를 이용한다. Fig. A2(a)처럼, 두 개의 도선에 각각 직류 I1, I2가 초전도 튜브 안쪽으로 관통해서 흐를 때 암페어법칙에 의해서 자기장이 유도되는데, 마이스너 효과때문에 자기장은 초전도체 튜브의 벽을 통과할 수 없으므로, 즉 초전도 튜브의 벽 내부에서 자속 밀도가 0이 되도록, 스크린 전류 I가 그림처럼 튜브 초전도체 표면으로 유도된다. 유도된 전류 I는 I1 + I2에 비례하는데, I 전류를 SQUID 센서로 측정한다. SQUID에 연결된 검출 코일을 사용하여 튜브의 표면 전류를 측정할 수 있다.
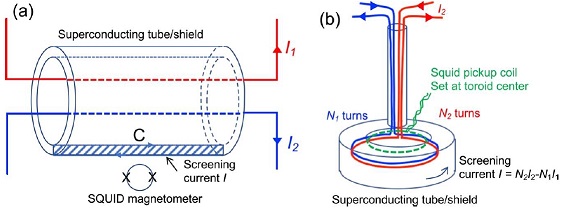
(a) Cryogenic current comparator (CCC) operation principle. Any magnitude in the currents carried by the two conductors I1 + I2 causes an equal and opposite screening current I along the surface of the superconducting tube cancelling the net magnetic flux inside the tube material (the Meissner effect). In reality, this screening current is distributed around the tube and the diagram only shows a representative path. (b) Practical structure of CCC and superconducting quantum interference device (SQUID) readout system45
오른쪽 Fig. A2(b)은 도넛 모양을 갖는 전형적인 CCC의 구조를 보여주고 있다. N1, N2의 서로 다른 권선수를 갖는 한 쌍의 코일에 전류 I1, I2 가 공급되면, 초전도 표면으로 자속 차폐 전류 I = N1I1 − N2I2가 유도되고, 유도된 전류의 크기는 SQUID 센서로 측정하게 된다. 따라서 I = 0가 되도록 전류의 크기 I1, I2을 제어하면, 코일에 흐르는 전류의 I2/I1 비율을 매우 정확하게 다음과 같이 측정할 수 있다.
| I2/I1=N1/N2 | (A1) |
그러므로 CCC 장치를 이용하면, 코일에 공급되는 전류의 비율을 매우 정밀하게 SQUID 센서를 이용하여 측정할 수 있을 뿐만 아니라, 권선수 비율만큼 이차 코일에 유도되는 전류를 증폭할 수도 있다. 참고로, 14 bit CCC의 경우, 극소 전류 해상도를 나타내는 전류 노이즈 수치는 100 pA에서 약 65 aA/√Hz이다.46