켈빈의 재정의

1. 서론

열역학이나 통계역학에 등장하는 열역학적 방정식에는 온도 T가 항상 볼츠만 상수 k와 곱해져 kT로 등장한다. 혹은 기체상수와 곱해져 RT로 등장할 수 있으나 기체 상수와 볼츠만 상수는 아보가드로수로 엮어져 있어서(k = R/N_A) 언제나 kT로 치환된다. 그리고 아보가드로수의 상대불확도가 기체상수나 볼츠만 상수의 상대 불확도에 비해서 무시할 수 있을 정도로 작으므로 실질적으로 볼츠만 상수 측정 불확도는 기체 상수 측정 불확도와 동일하다.¹

즉, 열역학적 방정식에 등장하는 다른 물리량을 측정하면 그 상황에서 kT를 얻어낼 수 있으며, 이것을 일차온도계(Primary Thermometer)라고 부른다. 일차온도계를 이용하여 kT를 측정하는 실험에서 온도 T를 알고 있다면 k를 산출할 수 있고, k를 알고 있다면 이 실험의 T를 산출할 수 있다. 2019년 5월 20일을 기점으로 일어날 켈빈 단위의 재정의는 정확히 위의 과정으로 이루어진다. 즉, 현재 정의에 의해 알고 있는 T에서 열역학 방정식을 적용하여 k를 정확하게 산출한 후에, 재정의 후에는 이렇게 산출한 k를 이용하여 T를 정의한다.

현재의 열역학적 온도단위인 켈빈(Kelvin)의 정의는 다음과 같다.²

열역학적 온도의 단위인 켈빈은 물의 삼중점의 열역학적 온도의 1/273.16이다.

즉, 물의 삼중점 상태를 만들면 이것과 열적 평형을 이루는 열역학적 상태의 온도를 273.16 K로 정하는 것이 현재 온도의 정의이다. 이 정의를 적용하여 과학계는 볼츠만 상수를 가능한 정밀하게 측정하려는 노력을 해 왔다. 2017년 7월 1일까지 결과를 마감한 후 합의하여 조정한 볼츠만 상수의 값은 k = 1.380 649 03 × 10^-23 J K^–1이며, 그 상대 불확도는 3.7 × 10^-7이다.¹ 이 조정값을 바탕으로 2019년 5월 이후 열역학적 온도의 단위인 켈빈(Kelvin)의 정의는 다음과 같이 바뀔 예정이다.³

켈빈(기호: K)은 열역학적 온도의 SI 단위이다. 그 크기는 볼츠만 상수의 값을 단위 J K^-1 = kg m² s^-2 K^-1으로 표현할 때 정확히 1.380 649 × 10^-23으로 고정시킴으로써 정해진다.

이것은 물질의 고유한 성질인 물의 삼중점을 이용한 기존의 정의를 물리학의 기본 상수인 볼츠만 상수를 이용하여 재정의하는 것이다. 전체적인 국제단위계의 관점에서 보면 켈빈을 포함하여 킬로그램, 암페어, 몰의 네 가지 SI 기본단위의 정의가 같은 시점을 기준으로 모두 기본 상수를 이용한 정의로 바뀌는 SI 단위 재정의 중 일부이다. Fig. 1은 SI 재정의를 홍보하기 위하여 국제도량형국(Bureau International des Poids et Mesures, BIPM)에서 준비한 그래픽 로고 중 열역학적 온도의 단위인 켈빈과 켈빈 정의에 사용하게 될 볼츠만 상수를 강조한 그림을 보여주고 있다.⁴

Fig. 1

SI illustration prepared by the BIPM for the redefinition of the kelvin and the Boltzmann constant

물의 삼중점은 킬로그램의 원기와는 달리 인공 구조물이 아니다. 따라서 파손, 분실, 마모의 위험이 없이 누구나 물의 삼중점을 제작할 수 있는 충분한 기술만 있다면 현재의 정의로부터 켈빈을 실현시킬 수 있다. 그럼에도 불구하고 기본 물리 상수를 이용한 정의를 선택한 것은 다른 기본 단위의 재정의와 조화를 이루고 과학적인 완결함을 이루려는 목적이 더 크다.

이 리뷰 논문에서는 볼츠만 상수의 결정에 이용되었던 일차온도계 실험을 리뷰한 후 켈빈의 재정의가 미치는 과학적 효과와 향후 온도 눈금 체계의 변화를 논의해 본다. 앞서 설명한 바와 같이 지금의 정의에 의해서 볼츠만 상수를 측정하는 동일한 실험이 재정의 후에는 정해진 볼츠만 상수값을 이용하여 열역학적 온도를 측정하는 실험이 되기 때문에 켈빈의 재정의 이후에도 이런 일차온도계 실험은 여전히 중요성을 갖는다.

2. 볼츠만 상수 결정에 이용된 실험

이 장에서는 과학기술 데이터 위원회(Committee on Data for Science and Technology, CODATA)에서 볼츠만 상수를 최종적으로 결정하는데 인용된 세 가지 종류의 일차온도계 실험의 물리적 원리와 해당 방법을 이용하여 기여한 연구 결과를 소개한다.

Fig. 2은 2017년 CODATA의 마지막 볼츠만 상수 조정에 기여한 실험값을 나타낸 것이다.¹ 그림에서 표시한 것과 같이 총 11개의 결정값이 최종적으로 사용되었는데 그 중 9개의 결정값이 음향기체온도계(Acoustic Gas Thermometer, AGT)를 이용한 것이다. 나머지 둘은 각각 유전상수기체온도계(Dielectric Constant gas Thermometry, DCGT)와 잡음온도계(Noise Thermometry) 방법을 이용하였다.⁵ 이 결과를 바탕으로 2017년 CODATA는 볼츠만 상수의 최종 조정값으로 k = 1.390 649 03(51) × 10^-23 J K^–1을 결정하였다. 이 값이 그림에서 실선으로 표시된 값이며 그 주변에 음영으로 처리된 것이 최종 조정값의 불확도이다. 최종 조정값의 상대 불확도는 u_r= 3.7 × 10^-7이다.

Fig. 2

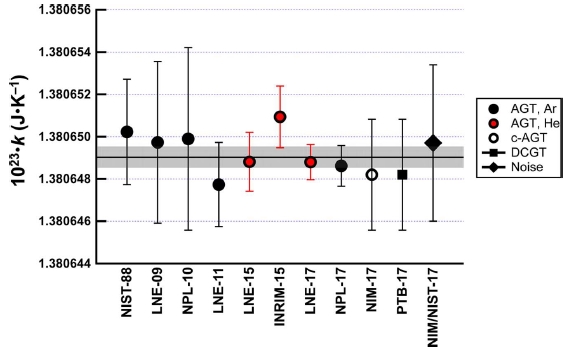
The Boltzmann constant determinations used for the final CODATA least square adjustment in 2017. The horizontal solid line represents the adjusted Boltzmann constant with standard uncertainty shown as a shaded band. The error bar for each determination represents standard uncertainty of the determination. (AGT: acoustic gas thermometry, c-AGT: cylindrical AGT, DCGT: dielectric constant gas thermometry)

2.1 음향기체온도계

음향기체온도계는 Fig. 2에서 보는 바와 같이 볼츠만 상수 측정을 위해서 가장 많이 이용된 값이고 가장 불확도가 낮은 측정이 이루어졌다. 음향기체온도계의 물리적 원리는 다음과 같다.

열역학적 온도가 T인 단원자 이상기체 내에서 소리의 속도, 즉 음속을 u₀라고 할 때 기체의 압력이 0에 접근하는 극한에서 다음의 관계가 성립한다.

$\[ k=\frac{u_0^{2}M}{\gamma N_{A}T} \]$

(1)

여기서, γ는 정압 몰비열과 정적 몰비열의 비로서 이상기체에서는 5/3이며, 이상기체와 가까운 실제 기체에서는 이론적인 계산으로 구할 수 있다.⁶ 그리고 M은 기체의 몰질량이며 N_A는 아보가드로 상수로서 볼츠만 상수보다 훨씬 낮은 상대불확도로 알려져 있기 때문에 볼츠만 상수 측정에 실질적으로 영향을 미치지 않는다.¹ 따라서 음향기체온도계를 이용한 볼츠만 상수 측정을 위해서는 u₀, M, T를 실험적으로 결정해야 한다.

음속 u₀는 공진구 내의 음파의 공진 주파수와 공진구의 크기를 측정함으로써 결정한다. 또 공진구의 크기는 공진구 내에 설치된 마이크로파 안테나를 이용하여 마이크로파 공진 주파수를 측정함으로써 결정한다. 따라서 음속 측정을 위해서는 음향 공진과 마이크로파 공진이 결합된 공진기가 사용된다.

음향기체온도계 실험을 위해서 초기에는 구형 공진기가 사용되었다.⁷ 그러나 구형 공진기는 마이크로파 공진에서 3개의 Degenerate된 공진 신호가 겹쳐져 나오면서 가공 오차에 의해서 넓게 벌어져서 공진구의 내경을 정확하게 측정하는데 한계가 있다. 이러한 한계를 극복하기 위해 3축 타원체 공진구가 개발되어 세 축 방향으로 미세하게 크기가 다른 타원체로 3개의 공진 Peak를 분리하는 방법이 사용되어 왔다.⁸ Fig. 3은 이와 같은 음향 기체 온도계에 사용되는 공진기의 사진을 보여주고 있다.

Fig. 3

Quasi-spherical resonator for acoustic gas thermometry.

Fig. 4는 Quasi-Spherical Resonator의 마이크로파 공진 중 가장 간단한 Mode인 TM11 Mode가 관찰된 것을 보여주고 있다. 이 공진구의 내경은 대략 50 mm이다. 그림에서 보여주는 데이터는 공진구 내부에 설치한 두 마이크로파 안테나를 통한 전달산란 계수 S₂₁를 측정한 것이다. 세개의 미세하게 분리된 공진 Peak는 미세하게 크기가 다른 세 개의 기본축의 내경에 해당한다. 공진주파수를 중심으로 일정한 범위내의 주파수에서 S₂₁을 측정한 후, 측정값을 수학적 모델에 따라서 Fitting하면 세개의 분리된 공진주파수를 상대 불확도 10^-7보다 훨씬 정밀하게 측정하는 것이 가능하다.

Fig. 4

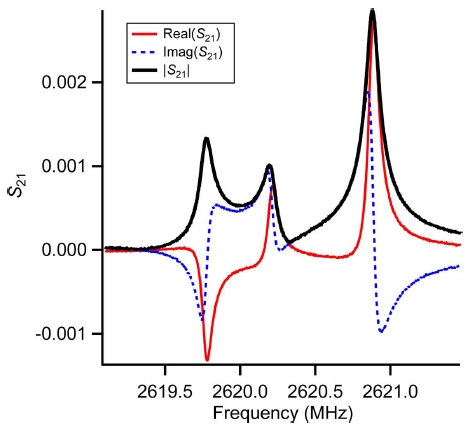
Electromagnetic resonance of TM11 mode for quasi-spherical resonator used for acoustic gas thermometry

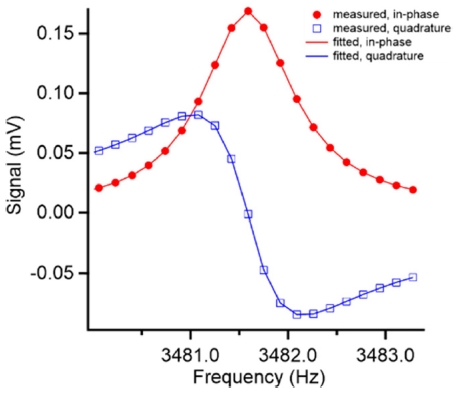
마이크로파 공진을 통해서 직경을 충분한 정밀도로 잘 알고 있는 공진기의 음향 공진 주파수를 측정하면 공진기 내부 기체에서의 음속을 정확하게 계산할 수 있다. Fig. 5는 Quasi-Spherical Resonator에서 측정할 수 있는 공진 중 가장 간단한 공진인 (0, 2) Mode의 음향 공진을 보여주고 있다. 그림과 같은 공진 신호를 바탕으로 Fitting을 통하여 측정된 공진 주파수를 구한 후 기체와 공진구의 물리적 특성을 고려한 보정을 하고, 마이크로파 공진으로 측정한 공진구의 Dimension을 고려하면 열역학적 이론으로 예측한 음속을 산출할 수 있다.⁶

Fig. 5

Acoustic resonance of (0, 2) mode for quasi-spherical resonator used for acoustic gas thermometry

볼츠만 상수 측정을 위해서는 음속을 측정하는 기체의 평균 분자량 M을 정밀하게 측정해야 한다. 음향기체온도계에는 지금까지 아르곤 혹은 헬륨 기체가 사용되었다.⁶ 아르곤 기체는 음향 공진 신호의 감도가 크지만 연구용 고순도 시료들끼리 평균 분자량의 차이가 큰 것이 문제가 될 수 있다. 연구용 시료 내에 함유된 동위원소 ³⁶Ar의 함유량 차이에 의하여 분자량이 상대적으로 10^-6 까지 차이가 날 수 있음이 밝혀졌다.⁹ 따라서 볼츠만 상수 측정과 같은 정밀한 측정에서는 사용하는 아르곤 기체 시료의 평균 분자량, 즉 동위원소 함유량을 정밀하게 측정해야 한다.

헬륨 기체는 음향 공진 신호의 감도가 낮지만, 제일 원리를 이용한 기체의 물리적 성질이 낮은 불확도로 알려져 있고 거의 하나의 동위원소로 이루어져 있다는 장점이 있다. 공기 중에 있는 헬륨 내의 함유된 ³He는 전체 헬륨에 대해 1.38 μmol mol^-1 정도의 몰비율로 함유되어 있는 것으로 알려져 있다. 그러나 연구용 고압 실린더는 대부분 천연 가스 추출물에서 만들어지며, ³He 함유량은 그 보다 더 낮은 0.6 μmol mol^-1혹은 그 이하의 몰비율인 것으로 알려져 있다. 이 함유량 전체를 불확도로 잡더라도 평균 분자량에 미치는 상대 불확도는 0.15 × 10^-6정도로써 그 영향이 작다는 이점이 있다.

볼츠만 상수 측정에서 온도 T는 공진구 내에 있는 기체의 온도인데, 실험은 언제나 물의 삼중점에서 수행하므로 T는 273.16 K이거나 그와 매우 가까운 온도이다. 이것은 볼츠만 상수의 측정이 지금 현재의 켈빈 정의 아래에서 이루어져야 하기 때문이다. 볼츠만 상수 측정이 물의 삼중점 이외의 온도에서 이루어진다면 그 온도를 정확하게 측정하기 위하여 어떤 열역학적 방정식을 이용한 추가의 측정이 이루어져야 하고, 그로 인해 불확도가 추가되므로 물의 삼중점에서 측정한 볼츠만 상수의 불확도에 비해서 원리적으로 그 불확도가 커질 수 밖에 없다. 따라서 모든 볼츠만 상수 측정은 정확하게 물의 삼중점에서 이루어졌다.⁵ 볼츠만 상수의 최종적인 결정을 위해서 사용된 실험 중 가장 불확도가 낮은 실험은 프랑스의 표준기관인 LNE에서 Pitre 등이 수행한 실험으로서 그 상대불확도는 0.6 × 10^-6이다.¹⁰ 헬륨 기체를 이용한 Quasi-Spherical Resonator에서 실험하였으며, 볼츠만 상수를 최종적으로 결정하는데 가장 큰 역할을 했다.

3. 켈빈 재정의와 열역학적 온도, 온도 눈금

물의 삼중점의 열역학적 온도는 재정의 이전에 불확도 없이 정의에 의해 정확하게 273.16 K이다. 재정의 이후에는 그 최상의 추정값은 여전히 273.16 K임에도 불구하고 상대불확도 3.7 × 10^-7를 갖게 되며, 이를 온도로 환산하면 0.1 mK에 해당한다. 이것은 재정의 직전의 볼츠만 상수의 상대 불확도가 재정의 직후에 물의 삼중점의 열역학적 온도의 상대 불확도로 그대로 옮겨온 것이다.

Fig. 6는 열에너지와 열역학적 온도 사이의 관계를 나타낸 것이다. 열역학적 온도는 열역학적 방정식에 의해서 평균 열에너지와 비례하는 양으로 정의되기 때문에 두 물리량 사에에는 열역학적 온도의 정의에 의해 비례식이 성립한다. 비례관계를 유일하게 정의하기 위하여 재정의 이전에 사용하던 방법은 상태가 잘 알려지고 매우 안정한 물의 삼중점에 273.16 K이라는 숫자를 지정한 것이다. 이렇게 되면 원점을 지나는 선이 유일하게 정해지기 때문에 열역학적 온도가 열에너지를 이용하여 정의된다. 그러나 현실적인 실현에서는 물의 삼중점에 포함된 동위원소 함량의 차이 때문에 제작에 사용되는 물의 근원, 지역과 계절에 따라서 삼중점의 온도 차이가 측정 가능한 정도로 크게 날 수도 있다. 이를 반영하여 최근에는 켈빈의 정의에 사용되는 물에 포함된 H와 O원자의 기준 동위원소 함량을 지정해주는 수정을하였다.² 이러한 수정에 의해서 켈빈의 정의가 갖고 있는 모호함은 해소되었지만, 그 정의가 원래 의도한 것에 비해 복잡해졌다는 단점이 있었다.

Fig. 6

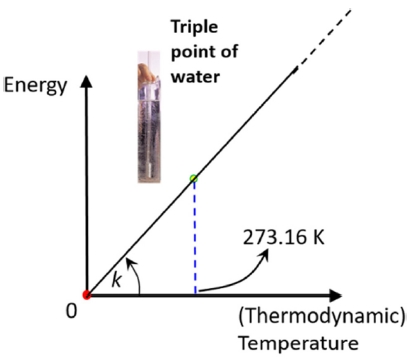
Relationship between thermal energy and thermodynamic temperature. The current definition of the thermodynamic temperature assigns a number to a specific state (triple point of water), whilst the revised definition specifies the conversion factor between the thermal energy and thermodynamic temperature (Boltzmann constant)

반면 재정의 이후의 방법은 두 물리량 사이를 관계 짓는 비례 상수인 볼츠만 상수에 정해진 값(1.380 649 × 10^-23 J K^-1)을 지정하여 1 K의 크기를 지정하는 것이다. 이렇게 했을 때 가장 큰 이점은 어떤 온도에서도 물의 삼중점과 연관지을 필요없이 해당 온도에서 잘 정의된 열역학적 방정식만 실험적으로 실현할 수 있으면 열역학적 온도를 측정할 수 있는 것이다. 즉, 20 K 이하의 저온이나 1000 K 이상의 고온에서 열역학적 온도의 실현과 측정의 불확도가 줄어드는 효과가 있을 것으로 보인다. 특정한 물질, 특히 그 물질의 지구 상에 존재하는 정도의 동위원소 비율로 정의를 한정하지 않는다는 것도 과학적으로 좀 더 바람직한 방향의 정의이다.

단위의 정의의 관점에서 물의 삼중점은 그 전에 갖던 유일한 지위를 잃게 되었다. 물의 삼중점의 열역학적 온도는 다른 물질의 상변화 온도와 마찬가지로 불확도를 갖는 측정량이 되었다. 볼츠만 상수의 불확도에서 물의 삼중점의 열역학적 온도로 전파된 불확도 0.1 mK은 물의 삼중점의 국제적 재현성인 약 0.02 mK보다 다섯배나 큰 값이다. 따라서 물의 삼중점 혹은 그와 매우 가까운 온도에서는 재정의 이전에 비해 불확도에서 손실을 보게 된다. 그러나 이 손실은 물의 삼중점과 아주 가까운 점으로 한정된 것이고, 다섯배가 늘어난다고 하더라도 불확도가 0.1 mK 수준으로서 실용적인 측면에서는 큰 차이가 없다. 아주 낮은 온도와 아주 높은 온도에서 얻을 수 있는 불확도의 개선 효과가 큰 장점이 될 수 있기 때문에 실용적인 측면에서도 전체적으로 바람직하게 재정의 되었다고 볼 수 있다.

그러나 여전히 국제온도눈금-1990 체계 아래에서는 가장 중요한 고정점으로서의 위치가 유지된다.¹⁴ 즉, 열역학적 온도를 근사하는 온도눈금인 국제온도눈금 내에서는 물의 삼중점의 온도가 T₉₀(TPW) = 273.16 K으로 불확도 없는 정확한 값이다. 이런 이중적인 물의 삼중점의 지위 때문에 개정된 단위의 정의과 기존의 국제온도눈금이 모순을 일으키므로 국제온도눈금이 조속히 개정되어야 한다는 주장도 있다. 그러나 물의 삼중점의 열역학적 온도에 대한 최상의 추정값이 273.16 K인 한, 이런 모순은 잠정적인 것일 뿐 실질적인 문제를 일으키지 않는다. 여전히 물의 삼중점의 열역학적 온도를 273.16으로 나눈 온도가 새 정의에 의한 1 K과 일치하기 때문이다.

물의 삼중점의 열역학적 온도의 추정값이 업데이트되기 위해서는 단위 개정 이전에 볼츠만 상수를 측정에 사용한 실험과 동일한 실험이 이루어져야 한다. 그러나, CODATA의 볼츠만 상수 마지막 조정값의 상대불확도는 3.7 × 10^-7이고, 이 조정값이 나오기까지의 여러가지 결정값 중에 가장 상대 불확도가 낮은 것이 6.0 × 10^-7 임을 감안하면, 당분간 그러한 실험을 하는 것은 현실적으로 어려울 것으로 예상된다. 즉, 볼츠만 상수의 최종 결정 직전까지 수행되던 볼츠만 상수 측정 실험의 최종 불확도를 절반으로 낮추는 실험을 해야만이 재정의 이후에 물의 삼중점의 열역학적 온도 측정에 대한 유의미한 실험이 되는 것이다. 따라서 당분간은 재정의된 켈빈과 국제온도눈금-1990이 모순을 일으키지 않고 공존할 것으로 예상된다.

4. 결론

2019년 5월에 발효되는 켈빈의 새정의는 켈빈을 다른 역학적 단위(킬로그램, 미터, 초)와 연결시켰다. 즉, 열역학적 온도가 특정한 물질의 열역학적 상태를 이용하여 정의되는 것이 아니라, 에너지의 크기를 이용하여 정의됨으로서 켈빈이 다른 물리량과 더 밀접하게 연결되는 결과를 가져온다.

이런 과학적인 진보에도 불구하고 일반 사용자에게 켈빈의 재정의가 미치는 영향은 미미하다. 켈빈의 정의 변화가 단위의 사용자 일반에 미치는 영향을 정확하게 알리기 위하여 BIPM에서 준비한 정보에 대한 번역을 제시하는 것으로 본 리뷰 논문을 마친다.¹⁵

켈빈(K)의 재정의는 일반적인 온도 측정이나 측정 소급성에 곧바로 영향을 미치지 않으며, 대부분의 사용자들이 재정의로 인한 차이를 인지하지 못할 것이다. 그러나 재정의는 향후 발전의 기초가 된다. 물질에 의존적이거나 기술적인 제한을 받지 않는 새로운 켈빈의 정의는 특히 극한의 온도에서 SI 단위를 소급할 수 있는 새롭고 정확한 기술 개발을 가능하게 한다. 재정의 이후 켈빈의 실현에 대한 지침은 정의된 눈금인 ITS-90 및 PLTS-2000과 함께 열역학적 온도 측정을 위한 일차적 방법을 설명함으로써 켈빈의 전 세계적인 보급을 지원할 것이다.

REFERENCES

• Newell, D., Cabiati, F., Fischer, J., Fujii, K., Karshenboim, S., et al., “The CODATA 2017 Values of h, e, k, N_A for the Revision of the SI,” Metrologia, Vol. 55, No. 1, 2018. [https://doi.org/10.1088/1681-7575/aa950a]
• BIPM, “SI Brochure: The International System of Units (SI),” https://www.bipm.org/en/publications/si-brochure/, (Accessed 23 MAR 2018)
• BIPM, “On the Future Revision of the SI,” https://www.bipm.org/en/measurement-units/rev-si/#communication, (Accessed 23 MAR 2018)
• BIPM, “Revised SI: Download Ares,” https://www.bipm.org/en/si-download-area/, (Accessed 23 MAR 2018)
• Fischer, J., “Low Uncertainty Boltzmann Constant Determinations and the Kelvin Redefinition,” Philosophical Transactions of the Royal Society A, Vol. 374, No. 2064, 2016. [https://doi.org/10.1098/rsta.2015.0038]
• Moldover, M. R., Gavioso, R. M., Mehl, J. B., Pitre, L., de Podesta, M., et al., “Acoustic Gas Thermometry,” Metrologia, Vol. 51, No. 1, pp. R1-R19, 2014. [https://doi.org/10.1088/0026-1394/51/1/R1]
• Moldover, M. R., Trusler, J. P. M., Edwards, T. J., Mehl, J. B., Davis, R. S., “Measurement of the Universal Gas Constant R Using a Spherical Acoustic Resonator,” Physical Review Letters, Vol. 60, No. 4, Article No. 249, 1988. [https://doi.org/10.1103/PhysRevLett.60.249]
• Mehl, J. B., Moldover, M. R., Pitre, L., “Designing Quasi-Spherical Resonators for Acoustic Thermometry,” Metrologia, Vol. 41, No. 4, pp. 295-304, 2004. [https://doi.org/10.1088/0026-1394/41/4/011]
• Yang, I., Pitre, L., Moldover, M. R., Zhang, J., Feng, X., et al., “Improving Acoustic Determinations of the Boltzmann Constant with Mass Spectrometer Measurements of the Molar Mass of Argon,” Metrologia, Vol. 52, No. 5, pp. S309-S409, 2017. [https://doi.org/10.1088/0026-1394/52/5/S394]
• Pitre, L., Sparasci, F., Risegari, L., Guianvarc’h, C., Martin, C., et al., “New Measurement of the Boltzmann Constant k by Acoustic Thermometry of Helium-4 Gas,” Metrologia, Vol. 54, No. 6, pp. 856-873, 2017. [https://doi.org/10.1088/1681-7575/aa7bf5]
• Gaiser, C., Fellmuth, B., Haft, N., Kuhn, A., Thiele-Krivoi, B., et al., “Final Determination of the Boltzmann Constant by Dielectric-Constant Gas Thermometry,” Metrologia, Vol. 54, No. 3, pp. 280-289, 2017. [https://doi.org/10.1088/1681-7575/aa62e3]
• Łach, G., Jeziorski, B., and Szalewicz, K., “Radiative Corrections to the Polarizability of Helium,” Physics Review Letters, Vol. 92, No. 23, Paper No. 233001, 2004. [https://doi.org/10.1103/PhysRevLett.92.233001]
• Qu, J., Benz, S. P., Coakley, K., Rogalla, H., Tew, W. L., et al., “An Improved Electronic Determination of the Boltzmann Constant by Johnson Noise Thermometry,” Metrologia, Vol. 54, No. 4, pp. 549-558, 2017. [https://doi.org/10.1088/1681-7575/aa781e]
• Preston-Thomas, H., “The International Temperature Scale of 1990 (ITS-90),” Metrologia, Vol. 27, No. 1, pp. 3-10, 1990. [https://doi.org/10.1088/0026-1394/27/1/002]
• BIPM, “Information for Users on the Proposed Redefinition of the SI,” https://www.bipm.org/cc/CCTF/Allowed/Revised_SI/CommonStatement_FinalVersion_June2017.pdf, (Accessed 23 MAR 2018)