물질의 양에 대한 SI 기본단위 몰과 아보가드로 상수를 이용한 재정의


Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
The mole, symbol mol, is the International System of Units (SI) unit of the amount of substance which is the quantity referring to a measure of the number of specified elementary entities, such as chemical elements or compounds in a sample. In the current SI, the mole is defined by specifying the mass of carbon-12. But this base unit is not an invariant of nature because the mass is defined by the material artefact. According to efforts to define the base units in SI using true invariants of nature, the mole will be redefined by fixing the numerical value of a fundamental constant, the Avogadro constant. In the new SI, the definition of the mole can be realized through the experiments that lead to the determination of the Avogadro constant. The best experimental value of the Avogadro constant has been obtained by the X-ray crystal density experiment using silicon-28 highly enriched silicon sphere in the frame work of the International Avogadro Coordination. In this paper, the current definition of the mole and practical aspects of this unit are introduced, then the principle and technical challenges in X-ray crystal density experiment for redefinition of the mole are discussed.
Keywords:
Mole, Amount of substance, Avogadro constant, XRCD, SI redefinition키워드:
몰, 물질의 양, 아보가드로 상수, x선 결정 밀도, 국제단위계 재정의1. 서론
국제단위계(SI)는 과학적 측정에 기반한 국제적으로 일관되고 합의된 측정단위의 체계이다. 어떤 양(Quantity)은 측정(Measurement)을 통해서 정확한 크기와 불확실한 정도를 갖게 되고, 비로소 의미 있게 사용될 수 있다. 즉, 측정의 결과는 양의 값(Value of a Quantity)과 측정불확도(Measurement Uncertainty), 측정 단위(Measurement Unit)의 세 가지가 모두 갖추어져야 완전한 의미를 나타내게 된다. 여기서 단위는 결국 어떤 측정표준(Measurement Standard)과 비교하였는지를 의미한다. 예를 들어 주어진 막대의 길이를 측정하였을 때 측정결과는(5.32 ± 0.05) m라고 표시할 수 있다. 여기서 단위 “m”는 국제단위계(SI)의 길이에 대한 측정단위인 미터(Meter)의 정의로부터 구현된 측정표준과의 비교를 통해 얻었다는 것을 알려준다. 과학적인 측정량(Measurand)은 최종적으로 국제단위계의 7개의 기본단위, 미터(meter, 기호: m), 킬로그램(kilogram, 기호: kg), 초(second, 기호: s), 암페어(ampere, 기호: A), 켈빈(kelvin, 기호: K), 몰(mole, 기호: mol), 칸델라(candela, 기호: cd)로 표현될 수 있다.1
몰(mole)은 7개의 기본단위 중에서 물질의 양(amount of substance)에 대한 단위이다. 화학에서는 원자, 분자와 같은 물질을 구성하는 특정 입자들의 개수에 의해 특성이 결정되는 과학법칙들이 많이 발견되어 왔다. 그런데, 거시적인 현상에서 거기에 관련된 구성 입자들의 수는 매우 많을 뿐 아니라 그 수를 미시적으로 직접 측정하는 것은 매우 어렵다. 그래서, 일정한 수를 묶어서 그 입자들로 이루어진 물질의 양을 나타내는데 사용하게 되었다. 이렇게 구성 입자들의 일정한 수와 그에 해당하는 질량과의 관계에서 물질의 양에 대한 단위인 몰이 만들어지게 되었고, 결국 그 중요성을 인정받아 국제단위계(SI)의 기본단위로까지 도입되게 되었다.
본 논문에서는 몰에 대한 설명과 함께 2019년부터 시행될 새로운 국제단위계에서 몰의 재정의를 위한 방법에 대해 기술한다. 2장에서는 몰에 익숙하지 않은 독자들을 위해 물질의 양에 대한 단위 몰에 대해 소개하고, 3장에서는 몰의 재정의의 필요성과 그 내용을 간략히 기술한다. 그리고, 4장에서는 몰의 재정의를 위한 기본상수인 아보가드로 상수를 결정하는 방법인 XRCD 실험에 대해서 소개한다. 키블저울에 대한 내용은 질량의 재정의에 대한 다른 논문에서 자세히 기술하고 있으므로 본 논문에서는 XRCD 실험에 대해서만 기술한다. 5장은 결론으로써 몰의 재정의에 따른 영향을 간략하게 논의하는 것으로 본 논문을 끝맺는다.
2. 물질의 양을 나타내는 단위 몰
몰은 물질의 양에 대한 국제단위계의 기본단위이다. 본 논문에서는 의미전달의 명확성을 높이고, 대한화학회에서 편찬한 화학술어집에 따라 “물질량”보다는 “물질의 양”으로 표기하였고, 이를 권고하고자 한다.2
물질의 양이라는 개념은 이름 그대로 거시적인 자연현상에서 관여하는 물질들의 양에서 출발한다. 다만, 질량과 구별되는 부분은 물질의 구성과 그 구성 단위의 수(Number of Entity)에 대한 정보를 함께 담고 있다는 점이다. 예로써 이상기체상태 방정식 같은 기초적인 열역학적 관계식에서 물질의 양으로써 질량을 사용할 경우에는 기체의 화학적 구성에 따라 달라지는 보정상수를 사용해야 한다. 이 보정상수는 추후 설명할 몰질량(Molar Mass)이 된다.
| (1) |
식(1)에서 PX, VX, TX는 각각 어떤 n(X) 몰의 이상기체 X의 압력, 부피, 온도이고, mX는 질량, M(X)는 몰질량, R은 기체 상수(Gas Constant)이다.
물질의 양으로써 질량을 사용하지 않을 경우에는 기체상수가 가진 기체입자의 수와 볼츠만 상수(Boltzmann Constant)의 관계를 사용하여 아래와 같이 구성 입자의 수를 바탕으로 이상기체상태 방정식을 사용할 수 있다. 하지만, 앞서 기술한 바와 같이 거시적인 반응계의 입자의 수를 측정해서 사용하는 것은 매우 어렵고 불편함을 감수해야 한다.
| (2) |
식(2)에서 N(X)는 이상기체 입자의 수, kB는 볼츠만 상수이다.
자연현상들에서는 이렇게 물질을 구성하는 특정한 입자들의 수에 의해 결정되는 과학법칙들이 있으며 몰을 사용함으로써 구성입자들의 수를 고려한 거시적인 양을 나타낼 수 있게 된다. 몰의 현재 정의는 1971년 채택되었고 다음과 같다.1
(1) 몰은 탄소-12의 0.012 킬로그램에 있는 원자의 개수와 같은 수의 구성요소를 포함한 어떤 계의 물질의 양이다. 그 기호는 “mol”이다.
(2) 몰을 사용할 때에는 구성요소를 반드시 명시해야 하며 이 구성요소는 원자, 분자, 이온, 전자, 기타 입자 또는 이 입자들의 특정한 집합체가 될 수 있다.
그리고, 1980년에 몰의 정의에 대해서 아래의 내용이 추가되었다.
이 정의에서 탄소-12는 정지상태에 있고, 바닥상태에 있으며, 속박되어 있지 않은 원자를 말한다.
몰의 정의로부터 탄소-12의 몰질량 M(12C)의 값은 정확하게 0.012 kg/mol이 된다. 그리고, 1 몰의 물질의 양에는 항상 일정한 구성요소의 개수가 들어있게 되므로 보편상수가 되고, 이 상수를 아보가드로 상수라고 하는데 NA로 표시하며 단위는 몰의 역수가 된다. 현재의 정의에서는 측정을 통해 아보가드로 상수의 값과 측정불확도를 구하게 된다. 실제 몰을 활용할 때는 아래 식(3)과 같이 아보가드로 상수로부터 몰을 구하거나 물질을 구성하는 원자나 분자의 몰질량을 식(4)와 같이 탄소-12의 몰질량에 대한 상대적인 비율로부터 구한 다음 이것을 사용하여 식(5)와 같이 몰을 구하는 경우가 많다.
| (3) |
| (4) |
| (5) |
식(4)에서 Ar(X)는 X의 상대질량으로 M(12C)에 대한 비율을 나타내는 상수이고 단위가 없다. Mu는 몰질량 상수로써 M(12C)/12와 같은 0.001 kg/mol이 된다.
3. 몰의 재정의 필요성과 내용
현재 몰의 정의는 탄소-12의 질량을 바탕으로 정의되어 있기 때문에 질량의 정의와 직접 연결되어 있다. 하지만, 현재 질량 단위는 약속으로 정한 인공물인 “국제 킬로그램 원기(IPK)”를 사용하여 정의되어 있기 때문에 변동 가능성을 포함한 여러 가지 문제점을 안고 있으며 몰 역시 이런 문제점들의 영향을 받을 수 있다. 또한, 몰은 물질의 양으로써 구성요소의 수에 대한 개념을 포함하고 있기 때문에 주로 사용되는 분야인 화학과 생물학에서는 몰이 아보가드로 상수와 밀접하게 관련되어 인식되고 있다. 하지만, 몰의 정의에서는 이에 대한 명시적인 기술이 없이 탄소-12의 질량만으로 정의가 이루어져 있음으로 인해 혼란을 줄 수 있었다. 따라서, 국제도량형위원회(CIPM), 국제도량형국(BIPM) 등의 국제기구 및 각 나라의 국가측정표준기관(NMI) 등에서 측정학(Metrology)을 연구하는 과학자들은 이런 문제점을 해결하고 앞으로도 변하지 않는 단위의 정의를 확립하기 위해서 국제단위계의 재정의를 진행하였으며 몰도 새롭게 재정의를 하게 되었다.
새로운 국제단위계에서는 변하지 않는 기본상수를 사용하여 단위의 정의를 하게 되며 몰의 경우에는 아보가드로 상수를 고정하여 이를 바탕으로 재정의를 한다. 아보가드로 상수는 정해진 물질의 양에 대해서 물질을 구성하는 특정 입자들의 수를 연결해주는 기본상수가 된다. 몰의 재정의를 위해 검토되고 있는 2018년 2월 5일 잠정안(Draft)은 다음과 같으며 추가로 보완되고 검토된 후 2018년 11월 국제도량형총회(CGPM)에서 최종본이 채택될 예정이다. 한글로 된 몰의 재정의 역시 최종본의 채택 후 한국표준과학연구원에서 공식 발간될 예정으로 여기서는 한글 잠정안을 싣는다.
몰(기호: mol)은 물질의 양(물질량)을 나타내는 SI 단위이다. 1몰은 정확하게 6.022 140 76 × 1023 개의 구성요소를 포함한다. 이 숫자는 아보가드로 상수 NA를 mol-1 단위로 나타낼 때 정해진 수치로 아보가드로 수라고 부른다.
어떤 계의 물질의 양(기호: n)은 명시된 특정 구성요소들의 수를 나타내는 척도이다. 특정 구성요소들이란 원자, 분자, 이온, 전자, 그 외의 입자 또는 그런 입자들의 특정한 집합체가 될 수 있다.
몰의 재정의를 위해서는 아보가드로 상수를 고정해야 할 뿐 아니라 재정의가 되더라도 이전과 연속성을 가져야 한다. 따라서, 현재의 정의 하에서 측정을 통하여 가능한 가장 정확하게 아보가드로 상수를 결정한 다음 그 값을 고정하여 새로운 정의에 활용하게 된다. 아보가드로 상수를 결정하기 위해서는 현재로써는 두 가지 방법이 가장 정확한 값을 얻을 수 있는 것으로 알려져 있다. 두 가지 방법 모두 질량의 재정의를 위한 방법과 동일하게 XRCD (X-Ray Crystal Density) 실험에 의한 방법과 키블저울(Kibble Balance)을 사용한 방법이다. 이는 몰이 물질의 양에 관한 단위이고, 몰의 현재 정의가 질량과 직접적으로 연결되어 있기 때문이다. XRCD 실험은 순수한 물질에 들어있는 입자의 수와 물질의 질량을 정확하게 측정하여 아보가드로 상수를 결정하는 방법이다. 키블저울을 사용한 방법은 플랑크 상수를 먼저 정확하게 결정한 다음 리드버그 상수의 관계식을 통해 아보가드로 상수를 결정하는 방법이다. XRCD 실험은 아보가드로 상수를 직접 결정할 수 있는 방법으로 몰의 재정의에 가장 적합하지만, 농축동위원소를 사용한 순수한 실리콘 구를 제조해서 여러 가지 측정량을 매우 정확하게 측정해야 하기 때문에 물리, 화학, 재료공학, 기계공학 등 다양한 분야의 전문가들의 협력이 필요하다. 이를 위해서 국제도량형국(BIPM)과 유럽의 JRC-IRMM, 독일의 PTB, 이탈리아의 INRIM, 미국의 NIST, 호주의 NMIA, 일본의 NMIJ, 영국의NPL 등 여러 나라의 국가측정표준기관(National Metrology Institute)들의 주도로 “아보가드로 프로젝트(Avogadro Project)”라고도 불리는 “International Avogadro Coordination (IAC)”라는 국제적인 협력 프로젝트가 2004년 시작되었고, 각 국가측정표준기관들간에 서로 가능한 영역을 분담하여 XRCD 실험이 수행되었다.3
4. XRCD 실험에 의한 아보가드로 상수의 결정 방법
4.1 XRCD 실험의 원리
XRCD (X-Ray Crystal Density) 실험은 실리콘 단결정(Single Crystal)의 밀도를 측정하고, x선 결정법에 의해 측정한 격자 상수(Lattice Constant)를 사용하여 실리콘 결정에 있는 실리콘 원자의 개수로부터 아보가드로 상수를 구하고자 하는 방법이다. 실리콘 단결정으로 Fig. 1(a)와 같이 구(Sphere)를 만들었을 때 실리콘 결정의 단위 격자(Unit Cell)는 Fig. 1(b)와 같이 8개의 실리콘 원자로 구성되어 있고, 격자 상수를 정확히 측정하면 단위 격자의 부피를 구할 수 있다.
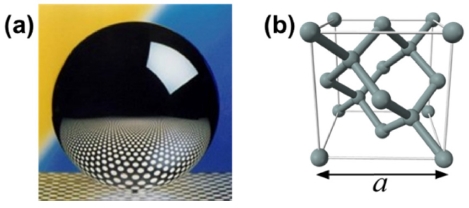
(a) Photo of a highly pure silicon sphere, (b) The crystalline structure of single-crystal silicon unit cell with lattice constant, a4
그럼, 실리콘 구에 있는 실리콘 원자의 개수는 아래 식(6)과 같게 된다.
| (6) |
식(6)에서 N은 실리콘 원자 개수, V는 실리콘 구의 부피, Vuc는 실리콘 단위 격자의 부피, a는 실리콘 격자 상수이다.
실리콘의 물질의 양(Amount of Substance), 몰은 정의에 따라 실리콘 원자의 개수를 아보가드로 상수로 나누어준 값이 되고, 실리콘 구에 대해서는 실리콘 구의 질량과 실리콘의 몰질량(Molar Mass)으로부터 아래와 같이 구할 수 있다.
| (7) |
식(7)에서 n(Si)은 실리콘의 몰, msphere은 실리콘 구의 질량, M(Si)는 실리콘의 몰질량이다.
식(6)과 식(7)을 아보가드로 상수에 대해 정리하면 아래와 같은 관계식(8)을 얻을 수 있다.
| (8) |
식(8)에서 ρ는 실리콘 구, 곧 실리콘 결정의 밀도이다.
결국, 아보가드로 상수는 실리콘 결정의 몰질량, 밀도, 격자 상수를 정확하게 측정함으로써 구할 수 있다. 20세기 초기 실험에서는 격자 상수의 경우에는 X-선 광학계를 사용하여 측정하였고, 밀도의 경우에는 물을 사용한 Hydrostatic Weighing을 통해 측정하여 아보가드로 상수의 측정을 시도하였기 때문에 X-Ray Crystal Density 실험이라는 이름이 붙게 되었다.5,6 하지만, 밀도 측정의 측정불확도 개선이 한계에 부딪침에 따라 최근에는 구의 질량과 부피를 직접 측정하고 있다.7,8 실리콘의 몰질량은 실리콘의 세가지 안정동위원소 실리콘-28, 실리콘-29, 실리콘-30의 동위원소 조성을 측정하여 구할 수 있다. 이와 같이 XRCD 실험에 의한 아보가드로 상수의 결정 원리는 매우 단순하고 명확하다. 하지만, 불순물 없이 순수하고, 결함이 없는 완벽한 결정(Perfect Crystal)의 실리콘으로 이상적인 구를 만드는 것은 불가능에 가깝기 때문에 XRCD 실험을 통한 아보가드로 상수의 결정은 현실적으로는 매우 복잡하고 어려운 과정이다. 다행히도 실리콘의 경우에는 현대 반도체 산업의 발달로 인해 다른 원소들에 비해 고순도 물질의 정제 기술, 단결정 성장 기술, 가공 기술이 매우 높은 수준에 올라있다. 여기에 아보가드로 상수를 결정하기 위한 각각의 측정량에 대해서 가장 첨단의 다양한 측정방법들을 활용함으로써 재정의 조건을 만족시킬 수 있을 정도의 정확한 측정이 가능하게 되었다. 다음 절에서는 실리콘 구의 제조과정과 각 측정량에 대한 측정법들을 간략히 설명한다.
4.2 실리콘-28 농축 실리콘 단결정 구의 제조
아보가드로 상수 결정에 필요한 실리콘 구의 제조를 위해서는 불순물이 거의 없는 매우 고순도의 실리콘 단결정이 필요하다. 그리고, 실리콘 몰질량 측정의 측정불확도를 줄이기 위해서는 거의 한가지 동위원소로만 이루어진 실리콘 구를 만드는 것이 유리하다. 이를 위해서 자연적인 동위원소조성을 가진 실리콘으로부터 테트라플루오로실레인(Tetrafluorosilane, SiF4)을 만들고, 원심분리를 통해 실리콘-28테트라플루오로실레인(28SiF4)을 분리해서 농축한다. 이것을 실리콘-28실레인(28SiH4)으로 변환해서 Flat-Zone(FZ) 방법에 의해 실리콘 결정을 성장시킨다(Fig. 2). 이렇게 얻은 실리콘 단결정을 가공하여 1 kg의 실리콘 구를 제조할 수 있다(Fig. 3).9,10 IAC에서는 XRCD 실험을 위해 2007년 실리콘-28 농축 실리콘 단결정으로 첫 실리콘 구를 제조하였는데 “AVO28”로 명명하였고, 실리콘-28의 농축도(Enrichment)는 99.9956%이었다. 그리고, PTB에서는 2012년 시작한 “Kilogram-2 Project”를 통해 실리콘-28의 농축도가 “Avo28”보다 높은 두 개의 실리콘 단결정을 추가로 생산할 계획을 세워 추진 중인데 2015년 “Si-28-23Pr11”로 명명된 실리콘 단결정을 만들었고, 농축도는 99.9985%였으며 이로부터 두 개의 실리콘 구를 제조하였다.10

The float-zone single crystals of highly 28Si enriched silicon. These photographs are courtesy of the Leibniz institute for crystal growth (IKZ)9
4.3 실리콘 구의 불순물 및 결정 결함 측정
제조한 실리콘 구가 XRCD 실험의 가장 기본적인 요구조건인 완벽한 실리콘 결정에 얼마나 가깝게 만들어졌는지를 확인하기 위해 불순물과 이로 인한 결정 결함 측정이 이루어졌다. 시료의 채취가 필요한 경우에는 실리콘 구의 손상이나 변형을 피하기 위해서 실리콘 구를 제작한 실리콘 결정에서 실리콘 구에 최대한 가까운 여러 부분을 선택적으로 채취하여 측정결과가 실리콘 구에 대해 대표성과 균질성을 가질 수 있도록 하였다. 실리콘 결정에서 주요 불순물은 탄소(C), 산소(O), 질소(N)로 알려져 있으며 이들의 농도(Number Density)는 적외선 분광법(Infrared Absorption Spectroscopy)를 적용하여 측정한다. 적외선 분광법의 측정한계는 탄소의 경우 5 × 1014 cm-3 정도이고, 산소와 질소는 5 × 1013 cm-3 정도로써 상대적으로 좋지 못한 편이다. 하지만, 측정을 통해 계산된 실리콘 구의 이들 불순물 질량은 약 4 μg으로써 실리콘 구의 질량 1 kg에 비해서는 매우 작다. 붕소(B), 인(P), 갈륨(Ga), 비소(As), 안티모니(Sb)에 대한 적외선 분광법의 측정한계는 약 1011cm-3 수준으로 좋은 편이며 붕소를 제외하면 거의 측정한계 이하로 검출되었다.11 수소(H)에 대해서는 DLTS (Deep Level Transient Spectroscopy)를 적용하였는데 측정한계는 약 2 × 1013 cm-3이고, 이 방법을 통해 측정한 수소에 의한 결함은 측정한계 이하였다.12 다른 원소들에 대해서는 기기 중성자 방사화 분석법(Instrumental Neutron Activation Analysis, INAA)를 적용하여 13개 원소에 대해서 정량분석이 이루어졌고, 53개 원소에 대해서는 측정한계 이하로 측정되었는데 이들 원소들이 실리콘 구에서 차지하는 영향은 약 1 μg 정도로써 매우 작음을 확인할 수 있었다.13 실리콘의 구조적 결정 결함인 공공(Vacancy)이나 자기침입(Self-Interstitial) 결함의 정량적인 측정은 매우 어렵기 때문에 결정 성장 조건을 바탕으로 계산을 병행하여 구할 수 있다. 공공 결함의 경우 Annihilation Experiment를 통해 양전자(Positron)의 Lifetime으로부터 측정할 수 있고, 자기침입 결함은 실리콘 결정의 성장 조건에서 공공 결함보다 작은 것으로 계산되었다. 그 외에도 Self-Referenced Lattice Comparator 등을 활용하여 결정 결함에 대한 연구가 진행되었다.14
4.4 실리콘 몰질량 측정
실리콘은 서로 다른 질량을 갖고 있는 세가지 실리콘 동위원소원자들로 구성되어 있기 때문에 실리콘의 몰질량을 알아야만 실리콘 구의 질량과의 관계에서 몰을 구할 수 있다. 실리콘의 몰질량은 각 실리콘 동위원소 원자들의 몰질량과 몰분율로부터 구할 수 있다.
| (9) |
식(9)에서 M(iSi)는 실리콘 동위원소 iSi (i ∈{28, 29, 30})의 몰질량이고, x(iSi)는 몰분율(Amount of Substance Fraction)로써 아래와 같이 동위원소비로부터 구할 수 있다.
| (10) |
식(10)에서 Ri,j는 iSi의 개수(또는 몰)를 다른 동위원소 jSi의 개수(또는 몰)로 나누어 준 실리콘의 동위원소비이다. 실리콘의 동위원소비는 다중검출기 유도결합플라즈마 질량분석법(Multicollector Inductively Coupled Plasma Mass Spectrometry, MC-ICP-MS)을 사용한다(Fig. 4). MC-ICP-MS는 7000 K이상의 고온의 유도결합플라즈마를 생성하고, 여기에 액체 상태의 시료를 분무하여 만든 수 μm 이하의 입자나 기체를 주입해서 원자화와 이온화가 일어난다. 이렇게 만들어진 실리콘 동위원소 이온들을 고분해능 질량분석기로 질량 대 전하량비(Mass to Charge Ratio, m/z)에 따라 분리해서 여러 개의 검출기로 동시에 검출하면 실리콘의 동위원소비를 측정할 수 있다.
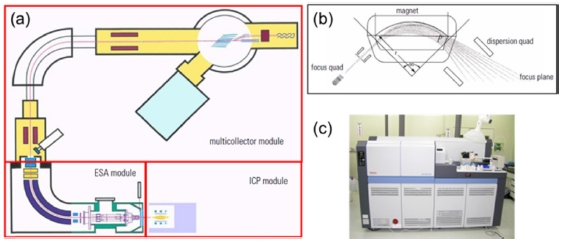
(a) Schematic diagram of MC-ICP-MS (Neptune, Thermo Scientific Inc. Bremen, Germany), (b) schematic diagram describing separation of ion beams of isotopes with different m/z in magnetic field of MC-ICP-MS, and (c) photo of MC-ICP-MS installed in KRISS
재정의를 위해서는 상대 측정불확도 2 × 10-8 이하로 아보가드로 상수를 결정해야 하는데 측정불확도에 가장 큰 영향을 미치는 측정량은 실리콘의 몰질량이었다. 실리콘-28 농축 실리콘을 사용하고, MC-ICP-MS을 실리콘 동위원소비 측정에 적용하면서 측정불확도의 개선이 이루어졌지만, 실리콘-28에 대한 실리콘-29와 실리콘-30의 동위원소비는 너무 작은 비율이기 때문에 그 정밀한 측정이 매우 어려워서 측정불확도의 개선은 더딘 상태였다.
이의 해결을 위해서 독일의 국가측정표준기관(National Measurement Institute)인 PTB가 주도하는 연구팀에서는 가상원소 동위원소희석 질량분석법(Virtual Element Isotope Dilution Mass Spectrometry, VE-IDMS)을 개발하였다.15-17 이 방법을 Fig. 5에 간략하게 나타내었는데 이름 그대로 실리콘-29와 실리콘-30에 대해서 두 가지 안정동위원소를 갖고 있는 어떤 가상의 원소(Virtual Element)를 가정한다. 그럼, 실리콘-28로 농축된 실리콘은 실리콘-28로만 이루어진 고순도 물질에 가상원소가 극미량 불순물로 존재하는 것으로 생각할 수 있다. 매질 시료에 극미량으로 들어있는 어떤 원소의 양은 동위원소희석 질량분석법(Isotope Dilution Mass Spectrometry, IDMS)이라는 방법으로 매우 정확하게 측정할 수 있다. 그리고, 실리콘-28에 대한 동위원소비는 10-5수준으로 매우 작은 값을 측정해야 하는 반면에 실리콘-29에 대한 실리콘-30의 동위원소비는 0.1부터 100사이의 상대적으로 큰 값을 측정하게 되기 때문에 좀더 정밀한 측정이 가능해진다. 정리하면 실리콘 전체에서 불순물인 가상원소의 양을 빼면 실리콘-28의 양을 얻을 수 있고, 가상원소의 두 동위원소인 실리콘-29와 실리콘-30의 동위원소비와 가상원소의 양으로부터 실리콘-29와 실리콘-30의 양을 계산할 수 있다. 즉, 실리콘의 각 동위원소들의 몰분율을 구할 수 있게 되어 실리콘의 몰질량을 결정할 수 있다.
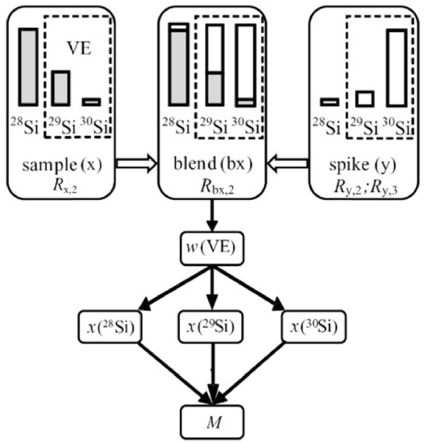
Schematic diagram of VE-IDMS: 29Si and 30Si isotopes in 28Si enriched silicon smaple (x) can be considered as a VE. The isotope ratios R = x(29Si)/x(30Si) are measured in the sample, isotope dilution blend (bx), and spike (y)9
여기에 새롭게 개발된 K-factor질량편향 보정방법(Mass Bias Correction Method)를 함께 적용하면 실리콘의 몰질량은 상대 측정불확도 5 × 10-9이하의 정밀도로 결정할 수 있다. IAC에서 “AVO28”에 대해 보고한 실리콘 몰질량은 M(Si) = (27.976 970 09 ± 0.000 000 15) g/mol이고, PTB의 “Si28-23Pr11”의 실리콘 구 하나에 대해서는 M(Si) = (27.976 942 674 ± 0.000 000 041) g/mol이었다.18
4.5 격자 상수 측정
실리콘 단결정의 격자 상수는 Fig. 6과 같이 X-선 간섭계(X-Ray Interferometer)와 광학 간섭계(Optical Interferometry)를 함께 이용하여 측정한다. X-선 간섭계는 실리콘 {2 2 0}면에 대해서 수직인 세 개의 실리콘 단결정 블레이드(Blade)로 구성되어 있고, 17 keV의 Mo Ka선을 사용한다. 고정된 두 개의 블레이드는 각각 Splitter와 Mirror 역할을 해서 X-선의 회절이 일어나서 Analyzer역할을 하는 세 번째 블레이드에 간섭을 일으킨다. 세 번째 블레이드는 {2 2 0}면에 대해 수직으로 이동이 가능하고, 이동에 따라 주기적인 X-선의 강도(Intensity)의 변화에 의해 생성된 프린지 패턴을 관측할 수 있다. X-선 간섭계에서 Analyzer블레이드의 이동 거리는 광학 간섭계를 이용하여 측정하게 되면 광학 프린지 패턴을 얻을 수 있고, X-선 프린지 패턴을 비교하여 실리콘 단결정 {2 2 0}면의 간격(Spacing)을 구할 수 있다.
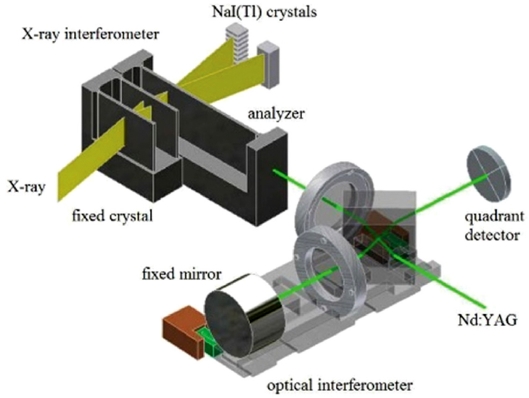
Schematic diagram of a combined x-ray and optical interferometer for the measurement of lattice constant of silicon crystal9
| (11) |
식(11)에서 d220은 실리콘 {2 2 0} 격자면의 간격, m은 광학 프린지의 수, λ/2는 광학프린지의 주기, n은 X-선 프린지의 수이다.
실제 측정에서는 Analyzer 블레이드를 이동이 가능한 영역에서 반복적으로 움직이면서 양쪽 끝에서 X-선 프린지를 관측하여 Least-Square 방법을 적용하여 d220을 측정한다. 측정불확도를 줄이기 위해서는 가급적 Analyzer 블레이드의 이동 폭을 증가시킬 필요가 있으며 간섭계의 구조와 움직임에 있어서의 정확도와 정밀도의 개선도 필수적이다. 이를 위해 이탈리아의 INRIM에서는 간섭계의 실리콘 결정들의 위치와 움직임을 원자 수준의 정확도로 조절 가능하면서 50 mm에 이르는 이동 폭을 줄 수 있는 간섭계를 개발하여 측정불확도의 획기적인 개선을 이루어내었다. 그외의 여러 가지 노력을 더해서 “AVO28” 실리콘 단결정에 대해서 보고된 20.000oC, 0 Pa에서의 격자면 간격은 d220 = (192.014 712 65 ± 0.000 00033) pm이다.18-21
4.6 질량 측정
실리콘 구의 질량은 질량비교기(Mass Comparator)를 사용하여 현재 질량의 정의인 국제킬로그램 원기로부터 연속적인 비교를 통해 질량측정의 측정소급성(Measurement Traceability)를 가지고 수 μg 이하의 측정불확도로 측정한다. 부력이나 물체의 표면흡착 등의 영향을 함께 고려하여 공기 중에서와 진공 중에서 실리콘 구의 질량을 측정한다. 하지만, 실리콘은 공기 중에서 표면에 산화물 층을 형성하기 때문에 XRCD 실험에서 실리콘 구의 질량을 정확하게 측정하기 위해서는 실리콘 구의 표면특성에 대한 연구가 필수적이다. 이를 바탕으로 실리콘 구의 정확한 질량은 실리콘 구의 질량에서 표면층의 질량과 실리콘 구 내부의 불순물과 결함으로 인한 질량 차이를 보정해주어야 한다.
| (12) |
식(12)에서 mSL은 실리콘 구 표면층의 질량, mdeficit는 불순물과 결정 결함으로 인한 질량차이, mcore는 표면층과 불순물, 결정 결함 등을 제외한 실리콘 중심부의 질량이다.
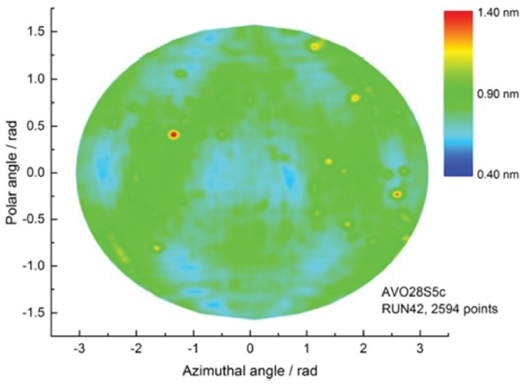
실리콘 구의 표면층은 주로 흡착에 의한 물 층과 탄소화합물 계열의 오염, 실리콘 산화물 층으로 나눌 수 있다. 산화물 층의 두께는 타원계측법(Ellipsometry)과 XRR (X-Ray Reflectometry)을 사용하여 측정한다. 그리고, 표면층의 화학적 조성은 엑스-선 형광분석법(X-Ray Fluorescence, XRF), NEXAFS (Near Edge X-Ray Absorption Fine Structure), 엑스-선 광전자 분광법(X-Ray Photoelectron Spectroscopy, XPS)를 사용하여 측정할 수 있다. 실리콘 구 “AVO28-S5c”에 대해 산화물 층의 두께를 측정한 topography의 예를 Fig. 7에 나타내었고, 측정결과 진공 중 표면층의 질량은 77.7 μg으로 보고되었다.12
4.7 부피 측정
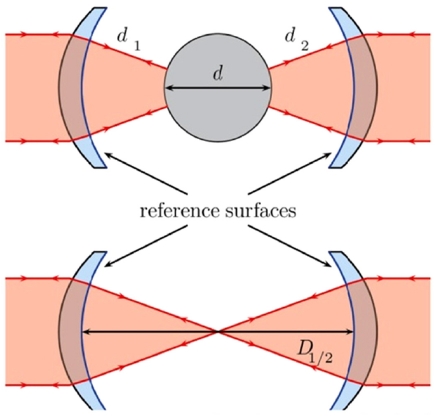
실리콘 구의 부피는 Fig. 8과 같이 광학 간섭계(Optical Interferometry)를 사용하여 구의 여러 지점에서 지름을 측정하여 얻은 평균지름으로부터 구한다. 실리콘 구의 제조 및 가공을 통해서 완벽한 구에서 벗어난 정도는 100 nm이내 수준으로 측정되고 있으며 구의 부피 측정의 상대 측정불확도는 약 2 × 10-8수준이다. 실제 측정에서는 표면층에 의해 간섭계에 Phase Retardation의 영향이 발생하므로 질량과 마찬가지로 표면층의 영향을 고려하여 중심부의 부피를 구한다. 또한, 공기굴절률을 보정하기 위해 진공 중에서 측정하며, 실리콘 구의 열 팽창의 효과를 보정하기 위해 정확한 온도 측정도 병행되어야 한다.9
5. 결론
2019년이면 물질의 양에 대한 단위 몰은 아보가드로 상수에 기반하여 새롭게 정의된다. 아보가드로 상수는 1 몰의 물질의 양에서 구성요소들의 수를 나타내는 기본상수로써 측정불확도가 없는 정확하게 고정된 값을 가지게 된다. 새롭게 정의가 된다고 해서 몰의 사용에 있어서 큰 변화가 있거나 그 동안 측정한 몰 단위의 측정량의 값에 큰 차이가 발생하는 것은 아니다. 새로운 정의에서 아보가드로 상수 자체가 현재의 정의를 바탕으로 측정을 통해 결정된 것을 고정한 값이기 때문에 이미 사용되고 있는 몰과 연속성을 가지고 있기 때문이다. 따라서, 몰 단위를 사용한 기존의 측정결과들은 기존의 아보가드로 상수의 값과 새로운 정의에서의 아보가드로 상수의 값의 차이 정도의 매우 작은 차이가 발생할 뿐이며 측정불확도 역시 1 × 10-9이하의 상대 측정불확도가 주는 매우 작은 영향을 받게 될 것이다.
하지만, 새롭게 정의되는 몰은 질량과의 직접적인 관계를 끊어내고 물질의 양에 대한 측정단위로써 구별되는 역할이 가능하게 되었다. 그리고, 물질을 구성하는 입자들의 개수가 물질의 양이라는 개념을 좀더 명확하게 해줌으로써 몰 단위의 사용자들에게 정확한 의미 전달을 통해 혼란을 줄여줄 수 있다. 또한, 구성요소들의 수에 대한 단위라는 점이 강조됨으로써 몰을 사용하여 무차원의 양(Dimensionless Quantity)이었던 입자의 수가 비로소 물리학적 차원(Physical Dimension)을 가질 수 있게 해주는 측면이 좀더 부각될 수 있게 되었다.
NOMENCLATURE
| SI : | International system of units |
| NA : | Avogadro constant, unit: mol-1 |
| n(X) : | The amount of substance of a specific entity X, unit: mol |
| M(X) : | Molar mass of X, unit: kg/mol |
| IPK : | International prototype of the kilogram |
| CIPM : | International committee for weights and measures |
| BIPM : | International bureau of weights and measures |
| NMI : | National metrology institute |
| CGPM : | General conference on weights and measures |
| IAC : | International avogadro coordination |
| XRCD : | X-Ray crystal density |
| JRC-IRMM : | Joint research center - institute for reference materials and measurement |
| PTB : | Physikalisch-Technische bundesanstalt (Germany) |
| INRIM : | Istituto nazionale di ricerca metrologica (Italy) |
| NIST : | National institute of standards and technology (USA) |
| NMIA : | National measurement institute australian government (Australia) |
| NMIJ/ : | National metrology institute of japan (Japan) |
| NPL : | National physical laboratory (UK) |
Acknowledgments
한국표준과학연구원에서 몰질량 측정에 도움을 준 연구자들에게 감사를 드립니다. 황의진은 한국표준과학연구원에 화학측정에서 측정소급성을 확보하기 위해 다중검출기 유도결합플라즈마 질량분석기가 필요함을 설득 및 기획하였고, 임용현은 실질적인 도입과 지속적인 연구가 가능하도록 지원해 주었습니다. 그리고, 황의진, 이종화, 최종오, 이경범은 몰의 재정의를 한글로 나타낼 때 엄밀한 의미전달이 될 수 있도록 좋은 의견을 제시해 주었습니다.
REFERENCES
- BIPM, “SI Brochure: The International System of Units (SI),” https://www.bipm.org/en/publications/si-brochure/download.html, (Accessed 23 MAR 2018)
- Korean Chemical Society, “Terminology of Chemistry in Korean,” http://kcsnet.or.kr/cheminfo, (Accessed 23 MAR 2018)
-
Becker, P., Bettin, H., Danzebrink, H-U., Gläser, M., Kuetgens, U., et al., “Determination of the Avogadro Constant via the Silicon Route,” Metrologia, Vol. 40, No. 5, pp. 271-287, 2003.
[https://doi.org/10.1088/0026-1394/40/5/010]

- BIPM, “International Avogadro Project,” https://www.bipm.org/en/bipm/mass/avogadro/, (Accessed 23 MAR 2018)
-
Henins, I. and Bearden, J. A., “Silicon-Crystal Determination of the Absolute Scale of X-ray Wavelengths,” Physical Review, Vol. 135, No. 4A, pp. A890-A898, 1964.
[https://doi.org/10.1103/PhysRev.135.A890]

-
Deslattes, R. D., Henins, A., Bowman, H. A., Schoonover, R. M., Carroll, C. L., et al., “Determination of the Avogadro Constant,” Physical Review Letter, Vol. 33, No. 8, pp. 463-466, 1974.
[https://doi.org/10.1103/PhysRevLett.33.463]

-
Fujii, K., Tanaka, M., Nezu, Y., Nakayama, K., Fujimoto, H., et al., “Determination of the Avogadro Constant by Accurate Measurement of the Molar Volume of a Silicon Crystal,” Metrologia, Vol. 36, No. 5, pp. 455-464, 1999.
[https://doi.org/10.1088/0026-1394/36/5/7]

-
Becker, P., “History and Progress in the Accurate Determination of the Avogadro Constant,” Reports on Progress in Physics, Vol. 64, No. 12, pp. 1945-2008, 2001.
[https://doi.org/10.1088/0034-4885/64/12/206]

-
Fujii, K., Bettin, H., Becker, P., Massa, E., Rienitz, O., et al., “Realization of the Kilogram by the XRCD Method,” Metrologia, Vol. 53, No. 5, pp. A19-A45, 2016.
[https://doi.org/10.1088/0026-1394/53/5/A19]

-
Abrosimov, N. V., Aref’ev, D. G., Becker, P., Bettin, H., Bulanov, A. D., et al., “A New Generation of 99.999% Enriched 28Si Single Crystals for the Determination of Avogadro’s Constant,” Metrologia, Vol. 54, No. 4, pp. 599-609, 2017.
[https://doi.org/10.1088/1681-7575/aa7a62]

-
Zakel, S., Wundrack, S., Niemann, H., Rienitz, O., and Schiel, D., “Infrared Spectrometric Measurements of Impurities in Highly Enriched ‘Si28,” Metrologia, Vol. 48, No. 2, pp. S14-S19, 2011.
[https://doi.org/10.1088/0026-1394/48/2/S02]

-
Azuma, Y., Barat, P., Bartl, G., Bettin, H., Borys, M., et al., “Improved Measurement Results for the Avogadro Constant Using a 28Si-Enriched Crystal,” Metrologia, Vol. 52, pp. 360-75, 2015.
[https://doi.org/10.1088/0026-1394/52/2/360]

-
D’Agostino, G., Luzio, M., D., Mana, G., Oddone, M., Bennett, J., W., et al., “Purity of 28Si-Enriched Silicon Material Used for the Determination of the Avogadro Constant,” Analytical Chemistry, Vol. 88, No. 13, pp. 6881-6888, 2016.
[https://doi.org/10.1021/acs.analchem.6b01537]

-
Fujimoto, H., Waseda, A., and Zhang, X., W., “Homogeneity Characterization of Lattice Spacing of Silicon Single Crystals by Self-Referenced Lattice Comparator,” Metrologia, Vol. 48, No. 2, pp. S55-S61, 2011.
[https://doi.org/10.1088/0026-1394/48/2/S09]

-
Rienitz, O., Pramann, A., and Schiel, D., “Novel Concept for the Mass Spectrometric Determination of Absolute Isotopic Abundances with Improved Measurement Uncertainty: Part 1 - Theoretical Derivation and Feasibility Study,” International Journal of Mass Spectrometry, Vol. 289, No. 1, pp. 47-53, 2010.
[https://doi.org/10.1016/j.ijms.2009.09.010]

-
Rienitz, O., Pramann, A., Schiel, D., and Güttler, B., “Novel Concept for the Mass Spectrometric Determination of Absolute Isotopic Abundances with Improved Measurement Uncertainty: Part 2 - Development of an Experimental Procedure for the Determination of the Molar mass of Silicon Using MC-ICP-MS,” International Journal of Mass Spectrometry, Vol. 299, Nos. 2-3, pp. 78-86, 2011.
[https://doi.org/10.1016/j.ijms.2010.09.023]

-
Mana, G., Rienitz, O., and Pramann, A., “Measurement Equations for the Determination of the Si Molar Mass by Isotope Dilution Mass Spectrometry,” Metrologia, Vol. 47, No. 4, pp. 460-463, 2010.
[https://doi.org/10.1088/0026-1394/47/4/012]

-
Bartl, G., Becker, P., Beckhoff, B., Bettin, H., Beyer, E., et al., “A New 28Si Single Crystal: Counting the Atoms for the New Kilogram Definition,” Metrologia, Vol. 54, No. 5, pp. 693-715, 2017.
[https://doi.org/10.1088/1681-7575/aa7820]

-
Ferroglio, L., Mana, G., and Massa, E., “Si Lattice Parameter Measurement by Centimeter X-Ray Interferometer,” Optics Express, Vol. 16, No. 21, pp. 16877-16888, 2008.
[https://doi.org/10.1364/OE.16.016877]

-
Massa, E., Sasso, C. P., Mana, G., and Palmisano, C., “A More Accurate Measurement of the 28Si Lattice Parameter,” Journal of Physical and Chemical Reference Data, Vol. 44, No. 3, Paper No. 031208, 2015.
[https://doi.org/10.1063/1.4917488]

-
Mana, G., Massa, E., Sasso, C., Stock, M., Fujii, K., et al., “The Correlation of the NA Measurements by Counting 28Si Atoms,” Journal of Physical and Chemical Reference Data, Vol. 44, No. 3, Paper No. 031209, 2015.
[https://doi.org/10.1063/1.4921240]