모델 불확실성과 외란을 고려한 로봇 매니퓰레이터의 채터링이 없는 2차 슬라이딩 모드 기반 유한-시간 제어
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
This paper presents a finite-time tracking control for a robot manipulator in the presence of a modeling uncertainty and an external disturbance. To solve the large chattering phenomenon that is caused by the high switching gain of the sliding-mode control, a novel second-order sliding-mode controller that generates a continuous control input is designed with a robust differentiator. The finite-time stability of the closed-loop system is ensured using a constructive Lyapunov-stability analysis. Finally, a numerical simulation of the 2-Axis Pan-Tilt system is performed to verify the effectiveness of the proposed controller.
Keywords:
Second order sliding mode control, Robust differentiator, Finite-time stability, Lyapunov stability analysis, Robot manipulator키워드:
2차 슬라이딩 모드 제어, 강건 미분기, 유한-시간 안정성, 리아푸노프 안정성 해석, 로봇 매니퓰레이터1. 서론
로봇 매니퓰레이터의 동역학 방정식은 상태변수에 대하여 비선형 방정식으로 구성되며, 정밀제어를 위해서는 비선형 제어기법이 적용되어야 한다. 또한 로봇 매니퓰레이터 제어 시 모델의 불확실성과 외란은 시스템의 제어성능을 악화시킬 뿐 아니라 시스템의 불안정성을 야기할 수 있기 때문에 제어기 설계 시 반드시 고려되어야 한다.
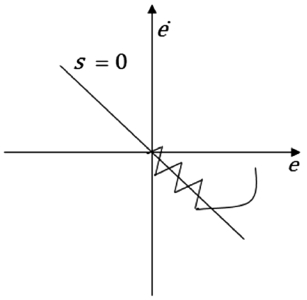
슬라이딩 모드 제어는 모델 불확실성과 외란에 강인한 제어기로 알려져 있으며, 비교적 간단하고 사용하기 쉬운 제어 법칙 덕분에 로봇 매니퓰레이터 제어에도 많이 사용되어 왔다.1 하지만 CSMC (Conventional Sliding Mode Control)는 제어 입력에 시스템의 불확실성과 외란에 대한 영향을 억제하기 위한 비연속 함수를 포함하기 때문에 고주파의 떨림 현상(Chattering Phenomenon)이 나타나게 된다. 이는 구동기에 악영향을 끼칠 뿐만 아니라 로봇 매니퓰레이터에 물리적 진동현상을 야기한다. 이러한 문제점을 해결하기 위해 적응슬라이딩모드,4 외란관측기 기반의 슬라이딩모드,3 경계층기반의 슬라이딩모드11들과 같은 다양한 방법들이 제안 되어왔다. 하지만 위에서 언급한 방법들은 떨림 현상은 감소시켰지만 모두 슬라이딩평면을 상태변수에 대하여 선형으로 정의하였기 때문에 점근안정성(Asymptotic Stability)밖에 보장하지 못한다는 한계점을 가지고 있다.
한편, 점근안정성에 비해 수렴시간이 짧고 강건성이 향상된다는 장점덕분에 유한-시간 안정성(Finite-Time Stability)기반의 제어 연구가 활발히 이루어져 왔다. 특히 슬라이딩 모드 제어에서는 유한-시간 안정성을 얻기 위해 상태변수에 대하여 비선형으로 슬라이딩평면을 정의하는 방법인 TSMC (Terminal Sliding Mode Control)가8 제안 되었고, TSMC에서 발생하는 특이점 문제(Singularity Problem)를 해결한 NTSMC (Nonsingular Terminal Sliding Mode Control)기법이7 로봇 매니퓰레이터에 적용되었다. 하지만 NTSMC도 외란에 대한 강인성을 보장하는 제어 입력으로 인해 떨림 현상이 불가피하게 존재한다. 이를 위하여 유한-시간 비선형 외란관측기가 결합 된 방법,5 퍼지와 신경망 이론이 결합된 연구,6 적응형 슬라이딩 모드가2 연구되었다. 하지만 이 연구들은 추가적인 해석이론이 필요하여 해석과 구현이 어려워진다는 단점이 있다.
본 연구에서는 로봇 매니퓰레이터를 제어 하기 위해 강건미분기(Robust Differentiator)를 이용한 새로운 형식의 SOSMC (Second Order Sliding Mode Control)기법을 제안한다. 이 제어기법은 강건 미분기를 활용하여 비선형 슬라이딩 평면을 정의하고, 슬라이딩 변수뿐만 아니라 상태변수를 유한 시간 내에 평형점에 도달시키는 제어 입력을 산출 시킨다. 결과적으로 본 연구에서 제안 된 제어 기법은 구현이 간단한 제어입력을 통해 유한-시간 안정성을 보장할 뿐만 아니라, 외란에 대한 강건성을 유지하면서도 떨림 현상이 존재하지 않는 연속적인 제어 입력을 산출한다.
본 논문의 남은 구성은 다음과 같다. 2장에서는 로봇 매니퓰레이터의 수학적 표현과 함께 기존 슬라이딩 모드가 포함하고 있는 떨림 현상문제를 수학적으로 도출된다. 3장에서는 본 연구에서 핵심적으로 제안하는 슬라이딩 평면 정의, 강건 미분기 도입, 제어법칙설계와 시스템의 안정성해석이 이어지며, 4장에서는 제안된 제어기를 2축 팬-틸트(2-Axis Pan-Tilt)에 적용한 모의실험을 통한 제어기법의 성능을 검증한다. 마지막으로 5장은 본 제어 기법에 대한 결론과 향후 연구가 이어진다.
마지막으로 본문에 들어가기에 앞서 본 논문에 쓰인 수학적 표현을 다음과 같이 정의하였다.
2. 문제정의(Problem Statement)
2.1 모델의 불확실성과 외란이 포함된 로봇 매니퓰레이터의 수학적 표현
우리는 로봇 매니퓰레이터의 동역학 방정식을 구성하는 관성 모멘트, 질량 그리고 길이와 같은 값을 대략적으로 측정 및 추정된 값으로 이용 할 수 밖에 없다. 이런 모델의 불확실성과 함께 현실적으로 동역학 방정식으로 표현 할 수 없는 마찰력이나 외부에서 오는 외란을 아래와 같이 통합 외란이 포함된 비선형 방정식으로 표현한다.
| (1) |
여기서, 통합 외란 D의 미분 값은 조건 을 만족한다.
위에서 표현된 것과 같이 통합 외란이 존재 할 경우 시스템의 제어성능이 악화 되고, 심할 경우 안정성을 잃기도 한다. 따라서 로봇 매니퓰레이터 정밀제어를 위해 합리적인 제어 기법이 반드시 적용되어야 하며, 이를 위해 본 연구에서는 강건성이 보장되는 새로운 형식의 슬라이딩 모드 제어 기법을 제안한다.
2.2 슬라이딩 모드에서 떨림 현상
이번 절에서는 기존 슬라이딩 모드 제어의 문제점을 언급하기 위해 CSMC를 설명한다. CSMC 소개를 통해 슬라이딩 모드 제어에서 떨림 현상이 수학적으로 어떻게 야기 되는지를 서술한다.
우선 슬라이딩 변수를 식(2)와 같이 정의한다.
| (2) |
여기서, 에러 벡터를 식(3)과 같이 정의 하였다.
| (3) |
안정성판별을 위해 리아푸노프 함수를 정의 하고 시간에 대해서 미분을 하면 식(5)와 같이 전개 된다.
| (4) |
| (5) |
위 식(5)를 토대로 제어입력을 식(6)과 같이 설계하면 리아푸노프 안정성을 만족하게 된다.
| (6) |
여기서, 제어 입력을 살펴보면 알 수 없는 값 D에 대한 영향을 억제 하기 위해 입력에 Ksign(s)를 도입하고 있다. 이를 도입함에 따라 외란에 대한 영향을 억제 하지만 Signum Function에 의해 슬라이딩 평면 근처에서 떨림 현상이 발생한다.
본 연구에서는 이 한계를 극복하기 위해 외란에 대해서 강건성을 유지하면서 떨림 현상이 존재 하지 않는 슬라이딩 모드 제어기법을 제안한다.
3. 2차 슬라이딩 모드 제어
3.1 슬라이딩 평면 정의
슬라이딩 평면의 정의는 슬라이딩 변수가 0으로 수렴한 후 시스템 상태 변수의 수렴 특성을 결정하는 매우 중요한 역할을 한다. 본 연구에서는 시스템의 유한-시간 안정성을 보장하기 위해 슬라이딩 평면을 다음과 같이 상태변수에 대한 비선형방정식으로 정의한다.
| (7) |
여기서 χ은 0 < χ < 1을 만족 한다.
식(7)의 슬라이딩 변수가 0으로 수렴 후 미분 방정식의 형태는 다음을 만족한다.
| (8) |
위의 식을 만족하는 비선형 미분방정식은 유한 시간 안정성이 보장이 되며,10 이를 만족하기 위하여 본 연구에서는 슬라이딩 모드와 결합하여 슬라이딩 변수를 0으로 구속시키도록 한다.
3.2 강건미분기
앞선 3.1절에서 정의한 슬라이딩 평면은 e의 2차 미분 항이 포함되어 있기 때문에 로봇 매니퓰레이터의 각가속도() 값을 요구한다. 따라서 본 연구에서는 강건미분기를 사용하여 각가속도 값을 얻는다.
가정 1: 미분기의 입력 값인 로봇 매니퓰레이터의 각속도() 값은 이용가능 하다.
실제로 최근에는 센서를 통해 각속도 값이 출력되는 로봇 매니퓰레이터 시스템이 존재하고, 비선형상태관측기를 통해 각속도를 추정하는 연구결과도 많이 발표되었다.12 가정 1을 바탕으로 본 연구에서는 다음 식(9)의 강건 미분기를9 활용한다.
| (9) |
여기서, 입력은 u는 입력 신호이고 출력 미분 값은 z1이다.
4. 시뮬레이션
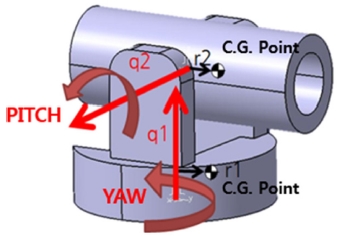
본 연구에서 제안 된 제어 기법의 효과를 확인하기 위해 다음과 같은 2축 팬-틸트(2Axis Pan-Tilt) 시스템에 제어기법을 적용하였다.
먼저 모델의 불확실성을 부여하기 위해 시스템의 동역학 방정식과 제어를 위한 동역학 방정식이 다르다고 가정하였다. 이는 제작 시 발생하는 질량중심, 링크의 길이, 관성모멘트 오차에 의한 것 이라고 할 수 있다. 또한 2축은 1축에 비해 비교적 가볍고 지면(Ground)과 떨어져 있는 것을 고려해 외부에서 오는 외란에 의한 영향까지 가해주었다(자세한 동역학 방정식의 구성은 APPENDIX에 첨부하였다).
시뮬레이션은 MATLAB/SIMULINK로 수행하였으며, 제안된 SOSMC와 TSMC의13 비교를 통해 제어 기법의 효과를 검증하였다. 제어기 성능 비교를 위해 외란이나 모델 불확실성에 의해 시스템이 발산하지 않으면서도 수렴시간이 비슷한 수준을 유지하도록 각 제어기의 설계변수를 Table 1과 같이 설정하였다.
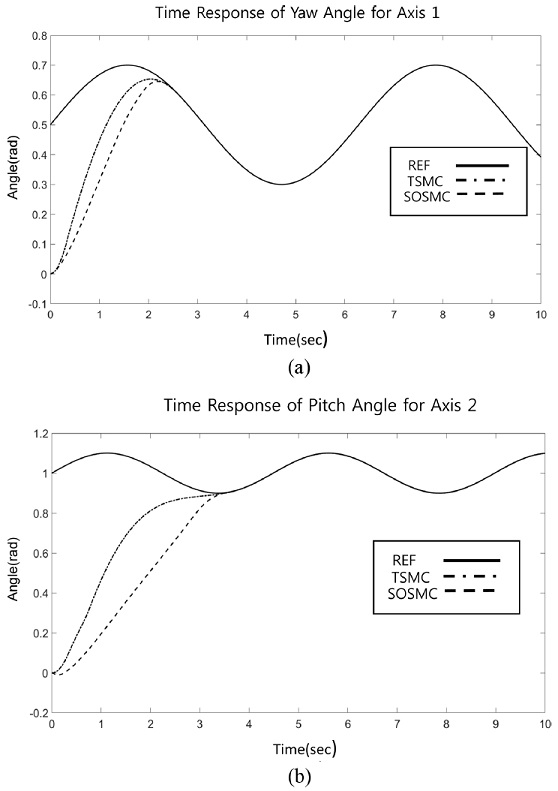
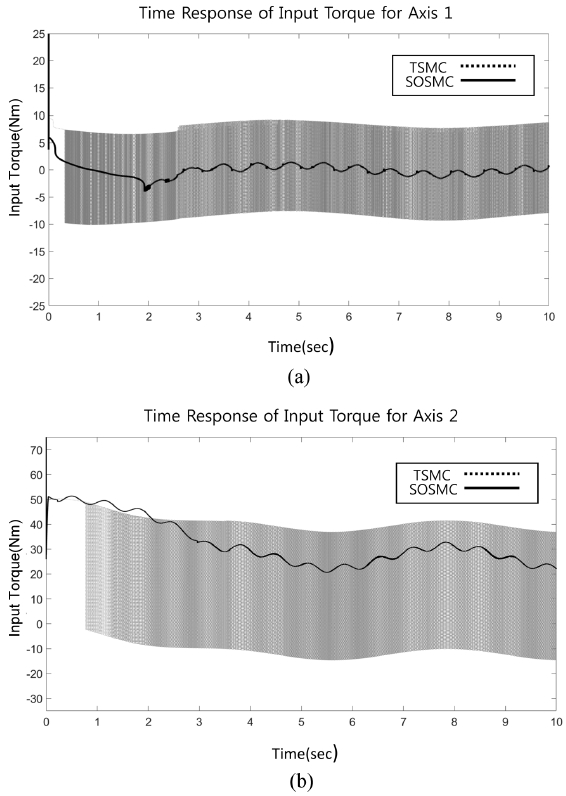
Figs. 3(a)와 3(b)는 1축과 2축에 대한 각도의 추종성능을 보여주고 있으며, Figs. 4(a)와 4(b)는 추종제어를 위한 각 축의 입력토크를 보여주고 있다. 각도의 추종성능을 보면 과도응답(Transient Response) 구간에서는 TSMC가 조금 빠르지만 최종적인 레퍼런스에 대한 정착시간(Settling Time)은 1축은 3초 2축은 2.5초로 비슷한 성능 수준을 보이고 있다.
하지만 그림 4를 보면 각도에 대한 정착 시간은 비슷한 성능을 보이고 있다 하더라도 제어 입력의 양상은 상당한 차이를 보이고 있다. TSMC의 경우 모델의 불확실성과 외란을 극복하기 위해 비연속적인 제어 신호를 산출하고 있으며, 본 연구에서 제안된 제어기의 경우 연속적인 제어 입력을 산출해내고 있다. 특히 2축의 경우 중력, 모델의 불확실성, 외란을 모두 보상 해야 하기 때문에 TSMC의 비연속신호의 게인 값이 커져서 제어 입력의 비연속적인 특성이 심하게 나타나고 있다. 이로 인해 TSMC의 경우 시스템을 구동하는 액추에이터에 악영향을 주게 되고 실제로 액추에이터가 고주파의 스위칭 입력을 구현하는 것도 불가능하다. 반면, 본 연구에서 제안한 제어기의 경우 비연속적인 항이 미분 항에 들어가 있기 때문에 연속적인 제어 입력을 산출하면서도 모델의 불확실성이나 외란에 영향을 받지 않고 있는 추종 성능을 보여준다. 이는 기존의 슬라이딩 모드 제어의 장점을 모두 유지하면서도 떨림 현상 단점을 극복 하는 것을 보이고 있는 것이다.
5. 결론
본 연구에서는 기존 슬라이딩 모드 제어의 단점들을 해결하기 위한 2차 슬라이딩 모드 제어 기법을 제안하였고 그 결론을 다음과 같이 요약하였다.
(1) 본 논문에서는 새로운 형식의 2차 슬라이딩 모드 제어기법을 위한 강건 미분기 기반의 비선형 슬라이딩 평면을 제안 하였다.
(2) CSMC의 한계점인 점근안정성을 개선하여 유한시간 안정성을 보장하는 제어 입력을 설계 하였고, 이를 리아푸노프 안정성 판별을 통해 증명하였다.
(3) 슬라이딩 모드 제어 기법의 특징인 강건성을 유지하면서도 떨림 현상이 없는 연속적인 제어 입력을 산출하는 제어입력을 설계 하였다.
본 연구의 제어 효과를 MATLAB/SIMULINK 기반으로 시뮬레이션을 통해 검증하였지만, 더욱 신뢰성 있는 연구 결과를 위해 실제 실험 기반의 결과 도출이 추후 진행되어야 한다.
NOMENCLATURE
| n : | The number of robot manipulator’s links |
| M : | Inertia matrix ∈ Rn×n |
| C : | Coriolis vector ∈ Rn×1 |
| G : | Gravitational force vector ∈ Rn×1 |
| D : | Lumped disturbance vector ∈ Rn×1 |
| τ : | Control input vector ∈ Rn×1 |
| K1, K2 : | Design parameter matrix ∈ Rn×n |
| α, χ : | Design Parameter vector ∈ Rn×1 |
Acknowledgments
이 논문은 국방과학연구소 생존성 기술 특화연구센터의 사업으로 지원받아 연구되었다(계약번호 UD1500131D).
REFERENCES
- Lee, M. C., Jin, S. Y., and Lee, M. H., “A Study on the Trajectory Control of a SCARA Robot Using Sliding Mode,” Transactions of the Korean Society of Mechanical Engineer, Vol. 19, No.1, pp. 99-110, 1995.
-
Mondal, S. and Mahanta, C., “Adaptive Second Order Terminal Sliding Mode Controller for Robotic Manipulators,” Journal of the Franklin Institute, Vol. 351, No. 4, pp. 2356-2377, 2014.
[https://doi.org/10.1016/j.jfranklin.2013.08.027]

-
Kawamura, A., Itoh, H., and Sakamoto, K., “Chattering Reduction of Disturbance Observer Based Sliding Mode Control,” IEEE Transactions on Industry Applications, Vol. 30, No. 2, pp. 456-461, 1994.
[https://doi.org/10.1109/28.287509]

- Piltan, F., Sulaiman, N., Allahdadi, S., Dialame, M., and Zare, A., “Position Control of Robot Manipulator: Design a Novel SISO Adaptive Sliding Mode Fuzzy PD Fuzzy Sliding Mode Control,” International Journal of Artificial Intelligence and Expert System, Vol. 2, No. 5, pp. 208-228, 2011.
-
Yu, S., Yu, X., Shirinzadeh, B., and Man, Z., “Continuous Finite-Time Control for Robotic Manipulators with Terminal Sliding Mode,” Automatica, Vol. 41, No. 11, pp. 1957-1964, 2005.
[https://doi.org/10.1016/j.automatica.2005.07.001]

-
Wang, L., Chai, T., and Zhai, L., “Neural-Network-Based Terminal Sliding-Mode Control of Robotic Manipulators Including Actuator Dynamics,” IEEE Transactions on Industrial Electronics, Vol. 56, No. 9, pp. 3296-3304, 2009.
[https://doi.org/10.1109/TIE.2008.2011350]

-
Feng, Y., Yu, X., and Man, Z., “Non-Singular Terminal Sliding Mode Control of Rigid Manipulators,” Automatica, Vol. 38, No. 12, pp. 2159-2167, 2002.
[https://doi.org/10.1016/S0005-1098(02)00147-4]

-
Jin, M., Lee, J., Chang, P. H., and Choi, C., “Practical Nonsingular Terminal Sliding-Mode Control of Robot Manipulators for High-Accuracy Tracking Control,” IEEE Transactions on Industrial Electronics, Vol. 56, No. 9, pp. 3593-3601, 2009.
[https://doi.org/10.1109/TIE.2009.2024097]

-
Cruz-Zavala, E., Moreno, J. A., and Fridman, L. M., “Uniform Robust Exact Differentiator,” IEEE Transactions on Automatic Control, Vol. 56, No. 11, pp. 2727-2733, 2011.
[https://doi.org/10.1109/TAC.2011.2160030]

-
Bhat, S. P. and Bernstein, D. S., “Continuous Finite-Time Stabilization of the Translational and Rotational Double Integrators,” IEEE Transactions on Automatic Control, Vol. 43, No. 5, pp. 678-682, 1998.
[https://doi.org/10.1109/9.668834]

-
Chen, M.-S., Hwang, Y.-R., and Tomizuka, M., “A State-Dependent Boundary Layer Design for Sliding Mode Control,” IEEE Transactions on Automatic Control, Vol. 47, No. 10, pp. 1677-1681, 2002.
[https://doi.org/10.1109/TAC.2002.803534]

-
Du, H., Qian, C., Yang, S., and Li, S., “Recursive Design of Finite-Time Convergent Observers for a Class of Time-Varying Nonlinear Systems,” Automatica, Vol. 49, No. 2, pp. 601-609, 2013.
[https://doi.org/10.1016/j.automatica.2012.11.036]

-
Zhao, D., Li, S., and Gao, F., “A New Terminal Sliding Mode Control for Robotic Manipulators,” International Journal of Control, Vol. 82, No. 10, pp. 1804-1813, 2009.
[https://doi.org/10.1080/00207170902769928]

-
Moulay, E. and Perruquetti, W., “Finite Time Stability and Stabilization of a Class of Continuous Systems,” Journal of Mathematical Analysis and Applications, Vol. 323, No. 2, pp. 1430-1443, 2006.
[https://doi.org/10.1016/j.jmaa.2005.11.046]

Appendix
APPENDIX
A1. 시뮬레이션을 위한 동역학 방정식
동역학 방정식은 위와 같이 M, C, G 항으로 구성이 된다.시뮬레이션 상에서 실제 시스템이라고 정의한 동역학 방정식의 요소들을 다음과 같이 정의하였다.
제어기 구성을 위해 우리가 사전에 알고 있는, 일반적으로 공칭모델이라고 표현하는 요소들을 다음과 같이 정의하였다.