크레인 붐의 형상 최적화

1. 서론

2012년 기준 전국에는 총 1,578 개소의 터널이 시공되어 있고, 이는 약 1,148 Km에 달한다.¹ 산간지역이 많은 국내의 특성상 터널을 많이 시공하고 있고, 터널이 증가함에 따라 유지관리를 위한 청소 업무가 증가하고 있으며, 이를 위해 더 많은 예산과 장비가 요구되고 있다. 유지관리 업무를 수행하는데 있어서 안정성, 유지보수 비용, 작업 환경 등을 만족시키기 위해 터널 청소 방식의 기계화를 통해 효율을 제고하려는 노력을 하고 있다.²

Lee 등²은 터널 청소 분야에서 빈번하게 발생하는 안전사고문제 및 터널 유지 보수를 위한 비용 상승 등의 문제 등을 해결하기 위해 터널 청소장비의 고찰 및 개선된 모델에 관한 연구를 통해 기존의 방식을 개선할 수 있는 방안을 제안 하였다. Hong³은 고소작업차의 붐대 및 프레임을 위상 최적설계, 형상 최적 설계, 두께 최적설계 기법을 적용 하여 경량 설계를 수행하였다. Lee⁴는 너클 크레인의 비선형 동적 상태를 고려 할 수 있는 등가정하중법을 이용하여 최적 설계를 수행하였다. Yoo 등⁵은 이동식 크레인 붐의 경량화를 위하여 최대 응력이 걸리는 하중상태에 대해 육각형 붐의 단면을 트러스 구조로 변환한 최적설계를 수행하여, 최대응력의 감소 및 경량화 효과를 얻었다. Hong 등⁶은 천장크레인의 경량화를 위해 직교배열의 S/N 비를 이용하여 구조 최적화하였다. Lim⁷은 Solid Edge를 이용하여 너클크레인을 모델링 한 후 Optistruct을 이용하여 유한요소 해석을 진행하고, 초기설계의 구조 강도에 대한 적정성을 검사하였으며, 크레인의 경량화를 위한 구조 최적화를 정식화 하였다. Park⁸은 직진식 크레인의 경량화를 위한 최적설계를 위하여 Pro-e를 이용해 삼차원 모델링 한 후 Ansys Workbench를 이용하여 안전성을 검토하고, 최적화된 설계 값을 제시하였다. Kim⁹은 이동식 크레인의 종류 및 사고 사례와 유형 분석을 통해 이동식 크레인의 선정 및 안전성 검토를 위한 방법을 제안하여 이동식 크레인의 선정 및 안전성을 객관적으로 검토할 수 있는 가이드를 제시하였다. Shim¹⁰은 이동식 크레인 구조물의 안전성능을 평가하기 위하여 근사계산식과 유한요소해석을 동시에 진행하여 비교 분석하였다. Savkovic 등¹¹은 텔레스코픽 유압 크레인의 붐간 접촉부위에서 발생하는 응력을 유한요소법으로 해석하고 최적화하는 방안을 제시하였다. Rauch¹² 등은 이동식 크레인의 전도안전성을 연구하였다.

본 논문은 이러한 노력의 일환으로 터널 청소용 굴절식 유압크레인의 안전성 확보를 위하여 유압 크레인 붐의 형상최적설계를 진행하였다. 이를 통해 추후 설계되는 이동식 크레인의 형상최적화 과정에 도움이 될 것이라 판단된다.

2. 유한요소해석

2.1 크레인 모델

터널 청소용 크레인의 실제 사진은 Fig. 1(a)와 같으며 살수 노즐을 통해 넓은 각도의 청소업무를 수행한다. Fig. 1(b)와 같이 가이드(Guide), 브라켓(Bracket) 베이스(Base), 칼럼(Column), 이너 붐(Inner Boom), 아우터 붐(Outer Boom), 엔드 붐(End Boom)으로 구성 되어 있으며, 브라켓은 특장차량의 프레임에 고정된다. 각각의 붐은 유압실린더로 작동된다. 유한요소해석을 위해 SolidWokrs로 3D 모델링 하였고, Ansys Workbench를 사용하여 해석을 진행하였다.

Fig. 1

Crane structure

2.2 요소분할 및 경계조건

한국산업표준 ‘크레인-하중 및 복합하중에 관한 설계원리’(KS B ISO 8686-2)에서는 간헐적인 하중요소인 바람에 의한 풍 하중, 눈 및 얼음에 의한 하중 등 기후효과에 따른 간헐적인 하중 및 접지된 하중에 의한 인양 시험하중, 긴급차단 등의 예외적 하중에 의한 효과를 고려하지 않고 크레인의 질량, 정격하중의 질량에 의한 중력 가속 및 충격에 일상적인 하중만 고려할 경우 안전율 1.48을 적용하여 설계하도록 제시하고 있다. 따라서 본 연구에서는 안전율을 고려하여 정격하중의 무게인 브러시 질량 및 크레인의 질량만 고려하여 해석을 진행하였다.¹³

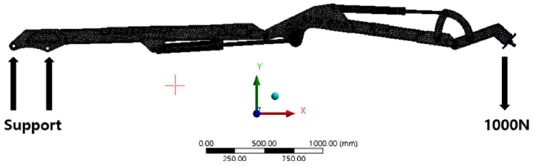
구조해석을 진행하기 위한 경계조건은 Fig. 2와 같다. 크레인에 하중을 가했을 때 크레인 붐의 안전성을 평가하기 위해 붐만 따로 해석을 진행 하였으며 칼럼과 실린더에 조립되는 이너 붐 끝 단의 핀 홀에 원통형 지지조건(Cylindrical Support)을 주었으며 반경(Radial) 방향은 구속하지 않았다. 엔드 붐 끝 단에 하중을 부가하였으며, 하중의 크기는 터널청소용 브러시의 질량인 약 100 kg을 고려하여 1000 N을 적용하였다.

Fig. 2

Boundary conditions

사용된 요소(Element)는 Tetra Mesh이며, 자동요소 생성기능을 이용하여 생성하였다. 전체 Mesh 크기는 10 mm로 적용하였으며, 핀으로 조립되는 힌지(Hinge) 부분의 요소크기는 2 mm로 조밀하게 나누었다. 유한요소모델의 요소 수는 203,871개, 절점 수는 361,251개이다. 핀의 재질은 S45C, 붐의 재질은 ATOS60이다.

2.3 해석 결과

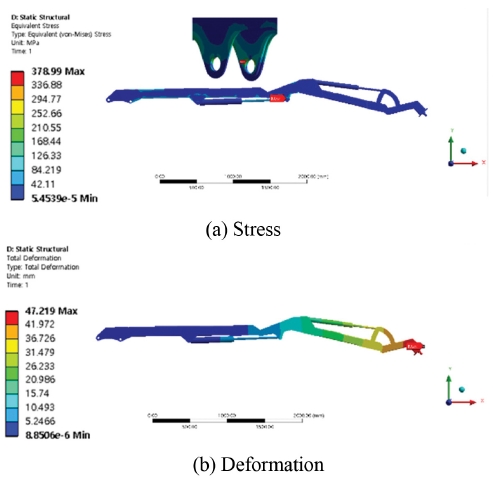
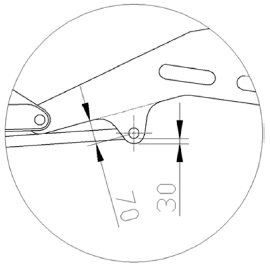
응력해석 결과 최대등가응력(Maximum Von Misses Stress)은 Fig. 3(a)와 같이 아우터 붐과 유압실린더가 핀으로 조립되는 부분에서 발생하였고, 그 값은 378.99 MPa이다. 크레인의 질량 및 정격하중의 질량 등 일상적 하중의 범주만을 고려한 복합하중의 경우 한국산업표준(KS B ISO 8686-2)에서는 안전율 1.48을 적용할 것을 제시하고 있다. 이를 고려하였을 때의 ATOS60의 항복강도 440 MPa을 초과하여 파손의 위험성이 있다. 하중이 가해지는 크레인의 엔드 붐 끝 단에서 최대 처짐이 발생하였으며 그 값은 47.219 mm이다. 따라서 최대응력발생 부위의 응력개선을 위하여 Fig. 4와 같이 핀 홀로부터 힌지 구조의 오프셋거리를 15 mm에서 30 mm로, 두께를 4.5 mm에서 6 mm로 보강하고, 핀 홀의 중심점의 거리를 65 mm에서 70 mm로 변경하여 다시 해석을 진행하였다.

Fig. 3

Stress and deformation results (initial)

Fig. 4

Modified design

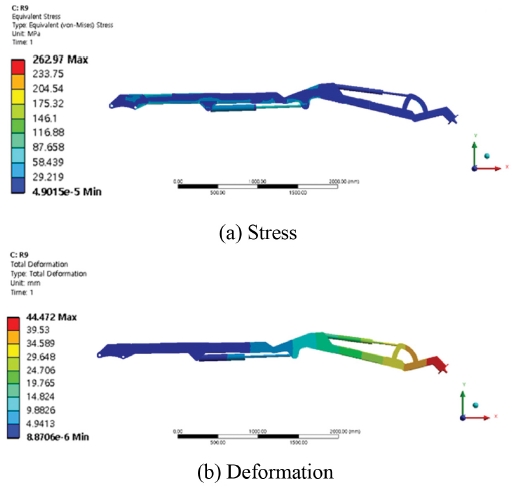
개선 된 모델을 재해석한 결과, 초기모델과 같은 부분에서 최대응력과 최대 처짐이 발생하였으며 응력 값은 262.97 MPa로 약 30.6%의 응력감소 효과를 얻었다. 최대 처짐은 약 44.47 mm의 값을 나타내었다.

Fig. 5

Stress and deformation results (improved)

3. 실험계획법

개선 후 최대응력은 262.97MPa로 안전율 1.48을 고려하였을 때, ATOS60의 항복강도 440 MPa을 초과하지 않아 파손의 위험은 없을 것으로 판단하였으며, Fig. 4의 개선형상의 최적 형상을 찾기 위해 수치해석 통계프로그램인 MINITAB을 사용하여 실험계획법을 진행하였다.

3.1 실험 인자와 수준 선정

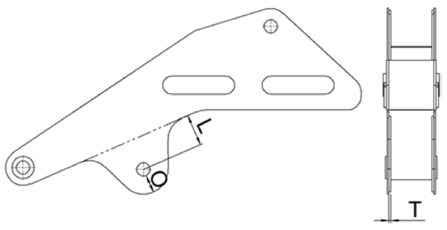
실험인자는 Fig. 6과 같이 길이 L과 오프셋 거리 O, 그리고 Reinforced Plate의 두께 T로 선정하였다. 그 이유는 이 인자들이 최대응력이 발생한 힌지의 Hole 주변을 구성하는 설계요소들이기 때문이다. L은 크레인 조립 시 실린더의 간섭을 고려하여 인자 수준을 최소 60 mm에서 최대 80 mm까지 정하였다. O는 최소 20 mm에서 최대 40 mm로 정하였다. T는 사용화된 Plate의 규격에서 위아래로 두 단계를 수준으로 설정하여 최소 3 mm에서 최대 9 mm로 설정하였다.

Fig. 6

Factors for design of experiment

3.2 완전 요인 배치법(3인자 2수준)

최대등가응력 Y (MPa)가 요인의 수준에 따라 어떻게 반응하는지 알아보기 위해 3인자 2수준의 완전요인 배치를 통해 실험을 계획하였으며 그 결과 Table 1과 같이 최대등가응력 반응 값 Y를 유한요소해석을 통해 얻었다.

Table 1

Full factorial design of 2-level 3-factor

Table 1에 대한 수치 통계 분석결과는 Table 2와 같다. 여기서 P-Value의 값이 유의수준인 0.05를 넘게 되면, 각 인자별 수준간 차이가 없고 그 인자가 결과에 영향을 미치지 못한다고 판단한다. T-Value의 절대값이 크면 회귀방정식(Regression Equation)에서 계수(Coefficient)에 대한 유의성이 크다는 것을 나타낸다.¹⁴ P-Value를 분석해보면 L, O, T는 각각 0.007, 0.011, 0.045로, 각각의 인자들의 교호작용인 L*O, L*T, O*T의 P-Value값은 0.064, 0.899, 0.031로 나타났다.

Table 2

Results of DOE of 2-level 3-factor

P-Value가 가장 크게 나온 L*T항은 유의하지 않은 것으로 판단했고, 따라서 L*T항을 오차항에 포함시킨 후 타 인자들을 정밀검정하는 풀링(Pooling) 결과는 Table 3과 같다. 그 결과, L*T를 제외한 모든 인자가 유의한 것으로 해석되었다.

Table 3

Pooling results of DOE for 2-level 3-factor

수치해석 통계프로그램인 MINITAB을 사용하여 구한반응 값 Y에 대한 회귀방정식은 식(1)과 같이 표현할 수 있다.

$\[ \begin{array}{c}Y=655.0400-3.9565L-5.5610O-8.1620T\\ +0.0324L*O+0.2205O*T\end{array} \]$

(1)

식(1)의 신뢰도는 99.99%로 나타나 데이터를 적합하게 표현한다고 판단하였다.

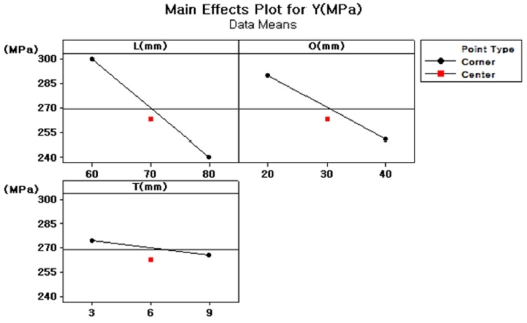
각각의 인자가 반응 값 Y에 미치는 영향을 보기 위해 Fig. 7와 같이 요인이 결과에 영향을 미치는 정도를 나타내는 주효과도(Main Effect)로 표현하였다. 주효과도에서 X축은 각 인자의 수준을 나타내며 Y축은 각 수준에 대한 반응 값, 즉 등가응력을 나타낸다. 각각의 인자가 반응 값 Y에 미치는 영향이 클수록 주효과도의 기울기가 크다. 2 수준의 완전요인배치를 통한 실험계획법에서는 낮은 수준과 높은 수준의 관계를 직선적으로 보여주어 각각의 인자와 수준의 관계가 선형인지 비선형인지 판단할 수 없다. 따라서 중간점(Center Point)에서의 실험을 추가하여 곡률효과(Curvature Effect)의 유무를 판단할 필요가 있다.

Fig. 7

Main effect plot

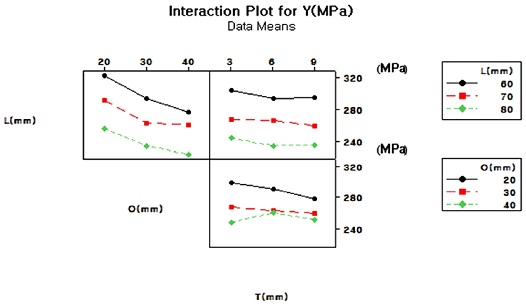
Fig. 7의 주효과도를 통해 반응 값 Y에 대해 L의 효과가 가장 큰 것을 그래프의 기울기를 통해 알 수 있고, 상대적으로 T의 효과가 작은 것을 확인 할 수 있다. 또한 각 인자 수준의 중간 값에서의 반응 값이 비선형이므로 곡률효과를 예측할 수 있다. 주효과도의 분석 결과뿐만 아니라 통계 분산분석 결과도 곡률효과의 P-Value가 0.010으로 나타나 유의수준인 0.05보다 작으므로 비선형성을 가지고 있음을 예상할 수 있다. 따라서 3 수준 이상의 반응표면분석법을 이용한 추가적인 실험이 필요하다.

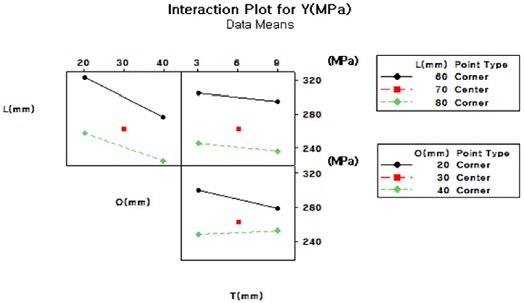
인자간 상호작용을 나타내는 교호작용도를 Fig. 8과 같이 나타내었으며, X축은 각 인자의 수준을 나타내고 Y축은 각 수준에 대한 반응 값을 나타내어 교호작용이 반응 값 Y에 미치는 영향을 파악할 수 있다. O와 T의 기울기의 부호는 반대이므로 O*T의 교호작용이 크게 작용함을 확인하였다.

Fig. 8

Interaction plot

3.3 반응표면분석법

반응표면분석법에 대한 실험 계획은 Table 4와 같다. 요인의 수준을 초과하지 않는 범위 내에서 실험을 계획하기 위해 중심합성 내접설계를 통해 실험을 계획했으며 반응 값 Y는 유한요소해석을 통해 구한 결과이다.

Table 4

Central composite design

반응표면분석법의 수행 결과는 Table 5와 같으며 L*L, T*T, L*T는 P-Value가 각각 0.211, 0.146, 0.897로 유의 수준인 0.05보다 크게 나와 유의하지 않은 것으로 판단했다. 이를 바탕으로 풀링을 한 결과는 Table 6과 같다.

Table 5

Results of central composite design

Table 6

Pooling results

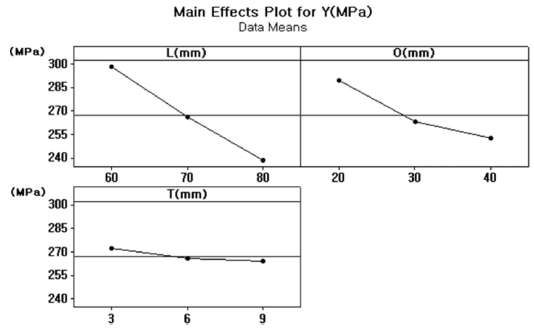
반응표면분석법을 통해 각각의 요인들이 반응 값 Y에 어떻게 작용하는지를 Figs. 9와 10과 같이 주효 과도와 교호작용도를 통해 나타내었다. L, O, T 세 개의 인자 모두 수준이 커질수록 반응값 Y가 작아지는 효과를 보였고, 2수준 3요인의 완전요인배치법에서 확인한 것과 같이 곡률 효과가 있는 것으로 확인되었다. 교호작용도에서는 O*T의 기울기가 반대로 나타나 교호 효과가 크게 나타나는 것을 확인하였다.

Fig. 9

Main effect plot

Fig. 10

Interaction effect plot

Fig. 11

Optimization plot from MINITAB

통계검증을 통해 확인한 결과, 유의한 인자는 L, O, T, O*O, L*O, O*T이고 이를 회귀방정식(2)와 같이 표현할 수 있다.

$\[ \begin{array}{c}Y=719.6000-4.0810L-10.2100O-7.6300T\\ +0.0764O^2+0.0360L*O+0.2064O*T\end{array} \]$

(2)

식(2)의 신뢰도는 99.22%로 나타나 데이터를 적합하게 표현한다고 판단하였다

3.4 반응최적화

위 식(2)의 수학적 모형을 통해 최저의 응력 값을 구하면 반응값 Y = 223.9415 MPa이고 이때의 각각의 인자의 수치는 Table 7과 같다.

Table 7

Results of the optimization

반응최적화를 통해 얻은 각 인자의 수준 값으로 유한요소해석을 통해 재해석한 결과는 222.55 MPa이다. 반응최적화 결과와 약 99.38%일치하였다.

4. 결론

본 논문에서는 터널 청소용 이동식 크레인에 대해 유한요소 해석결과와 재질의 항복강도를 비교 분석하였으며, 안전율을 고려하여 파손을 예측하였다. 최대등가응력이 발생한 부분을 개선 및 최적화 하기 위해 실험계획법을 통하여 최적화를 진행하였고, 그 결과는 아래와 같다.

(1) 크레인 붐에서 발생하는 최대등가응력은 378.99 MPa로 안전율 1.48을 고려하였을 때, 재질의 항복강도 440 MPa를 초과하여 파손이 예측된다. 최대응력이 발생하는 부분은 크레인 붐과 유압실린더가 핀으로 조립되는 힌지 부분이다. 때문에 힌지 형상을 구성하는 설계인자 L, O, T를 각각 70 mm, 30 mm, 6 mm로 변경하여 재해석한 결과, 최대등가응력이 262.97 MPa로 약 30.6%의 개선효과를 얻었다.

(2) 개선형상에 대한 최적화를 위해 3인자 2수준의 완전요인배치 실험을 수행한 결과, 각각의 인자 수준이 커질수록 반응치가 낮아지는 경향을 나타내었으나 인자간의 교호작용에 의해 곡률효과가 있을 것으로 예상하였다.

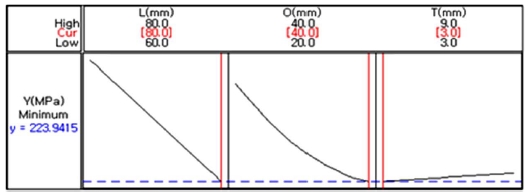
(3) 반응표면분석법을 통해 3인자 3수준의 실험을 다시 계획하였고, 그 결과 L = 80 mm, O = 40 mm, T = 3mm일 때 223.94 MPa로 최적인자를 도출하였다. 최적의 인자를 바탕으로 유한요소해석을 진행한 결과 222.55 MPa로서 99.38%의 정확도를 보였다. 이를 통해 초기 모델에 비해 약 41.28%의 응력감소 효과를 얻었다.

Acknowledgments

본 연구는 케이에이치특장㈜의 지원으로 수행 되었음.

REFERENCES

• Statics Korea, “Road Bridge and Tunnel Status,” http://www.index.go.kr/potal/main/EachDtlPageDetail.do?idx_cd=1213#link, (Accessed 16 MAR 2018)
• Lee, T. S., Kim, Y. H., Jang, K. S., and Koo, J. S., “A Study on Introducing Advanced Tunnel Cleaning Automation Equipment,” Proc. of the Korean Society Civil Engineers Conference, pp. 3705-3708, 2006.
• Hong, S. K., “Structural Optimum Design for the Lightweight of an Aerial Work Platform Truck’s Telescopic Boom and Frame System,” M.Sc. Thesis, Sejong University, 2012.
• Lee, D. K., “Structural Optimization of the Knuckle Crane Using Equivalent Static Loads Method,” M.Sc. Thesis, Hanyang University, 2013.
• Yoo, K. S., Park, J. W., Sinichi, H., and Han, S. Y., “Optimum Design of Movable Hydraulic Crane Booms,” Journal of the Korean Society of Machine Tool Engineers, Vol. 19, No. 6, pp. 776-781, 2010.
• Hong, D. K., Choi, S. C., and Ahn, C. W., “Optimal Design for Weight Reduction of Magnet Over Head Crane by using Taguchi method,” Journal of the Korean Society for Precision Engineering, Vol. 20, No. 3, pp. 50-57, 2003.
• Lim, H. B., Shin, M. K., and Yang, H. I., “Structural Optimization of the Knuckle Crane Installed in Truck,” Journal of the Korean Society of Manufacturing Technology Engineers, Vol. 21, No. 2, pp. 344-348, 2012. [https://doi.org/10.7735/ksmte.2012.21.2.344]
• Park, J. Y., “Design Optimization for Weight Reduction of the Boom Crane on Vehicle by Finite Element Method,” M.Sc. Thesis, Chungbuk National University, 2012.
• Kim, A. K., “A Study on Mobile Crane Interactive Selection and Stability Evaluation,” M.Sc. Thesis, Kyunghee University, 2008.
• Shim, S. Y., “Evaluation on the Performance Criteria of the Movable Hydraulic Crane's Structural Safety,” M.Sc. Thesis, Hanyang University, 2014.
• Savković, M., Gašić a, M., Pavlović, G., Bulatović, R., and Zdravković, N., “Stress Analysis in Contact Zone between the Segments of Telescopic Booms of Hydraulic Truck Cranes,” Thin-Walled Structures, Vol. 85, pp. 332-340, 2014. [https://doi.org/10.1016/j.tws.2014.09.009]
• Rauch, A., Singhose, W., Fujioka, D., and Jones, T., “Tip-Over Stability Analysis of Mobile Boom Cranes With Swinging Payloads,” Journal of Dynamic Systems, Measurement, and Control, Vol. 135, No. 3, Paper No. 031008, pp. 1-6, 2013. [https://doi.org/10.1115/1.4023276]
• ISO 8686-2:2006 “Cranes – Design principles for Loads and Load Combinations - Part 2: Mobile Cranes,” 2006.
• Lee, S. B., “MINITAB Example with Design of Experiment,” ERETEC, 4th Ed., 2014.