망각인자를 이용한 순환최소자승 기반 DC모터의 적응형 모델 독립 속도 제어 알고리즘

1. 서론

직류(Direct Current) 전동기는 직류 전력을 기계적인 회전 동력으로 변환하는 장치이며 일반적으로 계자코일, 전기자, 정류자편, 그리고 브러시로 구성되어 있다. 또한 계자권선과 전기자권선의 접속방식에 따라 타여자전동기, 자여자전동기, 직권전동기, 분권전동기, 복권전동기, 가동복권전동기, 그리고 차동복권전동기로 다양한 종류로 구분될 수 있다. 이러한 직류전동기는 다양한 분야에서 활용되고 있으며 Kirchhoff's Voltage Law와 Newton’s Second Law를 기반으로 수학적으로 표현될 수 있고, 이를 기반으로 최적 속도제어가 가능하다. 하지만 두 지배법칙은 상태에 따라 서로 다른 영향을 주고, 도출된 수학적 모델의 불확실성으로 인해 최적제어 입력을 도출하는 것은 현실적으로 어려우며 이러한 문제점을 해결하기 위해 직류전동기의 최적 속도제어를 위한 다양한 분야에서의 연구가 수행되고 있다.

E. Dursun¹은 Sliding Mode Control을 이용하여 다양한 산업현장과 로봇에 많이 사용되는 직류전동기의 속도제어 방법을 제시하고 부하변화에 따른 성능평가를 수행하였다. M. Ahmed²는 Brushless 직류전동기의 속도제어를 위한 PI와 Fuzzy PI 기반 속도제어 알고리즘을 개발하고 평가하였다. N. Kiran³은 P-I, I-P, Fuzzy Logic 등 다양한 제어기를 이용한 직류전동기의 속도제어에 관한 비교연구를 수행함으로써 장단점을 비교/분석하였다. A. Ali⁴는 직류전동기의 변수 변화에 강건한 성능과 최적 효율을 확보할 수 있도록 Model Reference PID Controller를 제안하였다. M. Saealal⁵는 Multiple Motor의 정착시간을 줄이기 위해 Linear Quadratic Regulator Controller를 제안하였으며 기존의 PID Controller와 비교검증 하였다. K. Premkumar⁶는 Adaptive Neuro-Fuzzy Inference System (ANFIS) 기반 Brushless 직류 전동기를 위한 속도제어 알고리즘을 제안하고 MATLAB 기반 시뮬레이션 결과를 보여주었다.

본 연구에서는 직류전동기의 수학적 모델 없이 입력(전압)과 출력(속도)만을 이용한 적응형 속도제어 기법을 제안하였다. 제어기 설계를 위해 망각인자 기반 순환최소자승 기법과 외란추정기가 사용되었다. 직류전동기의 입력과 출력과의 관계는 구간 별 1계 시스템으로 근사화할 수 있다는 개념을 이용하여 Lyapunov Direct Method 기반 최적제어 입력(전압)을 도출하였다. 적용된 망각인자는 구간별 최적 근사화를 위해 출력(속도)의 변화율에 따른 갱신규칙을 정의하였으며 실제 시스템과 근사화된 1계 시스템의 불확실성은 외란 추정기를 이용하여 추정하여 최적제어 입력을 도출하였다. 성능평가는 MATLAB/Simulink 환경에서 구성된 직류전동기를 이용하여 다양한 요구 입력과 변수 변화 시나리오에 대해 수행되었으며 성능평가 결과 제안된 적응형 제어 알고리즘은 직류전동기의 수학적 모델 없이 입력과 출력만을 이용하여 다양한 입력과 부하 변화에 대해 좋은 속도 제어성능을 보여 주었다. 본 논문은 다음과 같이 구성되었다.

2장에서는 개발된 제어기의 개념을 기술하고, 3장에서는 적응형 모델 독립 제어기의 설계에 대해 기술한다. 그리고 4장에서는 제어기의 성능평가 결과를 보여주고 마지막 5장에서는 향후 계획과 함께 본 논문의 결론에 대해 기술한다.

2. 적응형 모델 독립 제어기의 개념

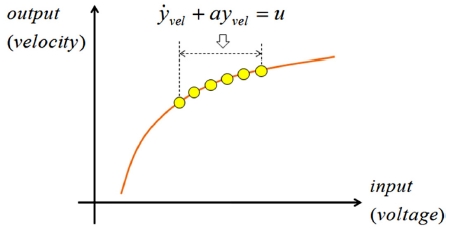
본 연구에서 제안한 적응형 모델 독립 속도제어기는 직류전동기의 입력(전압)과 출력(속도)의 관계는 특정 구간별 서로 다른 1계 미분방정식으로 근사화할 수 있다는 개념을 기반으로 설계되었다. Fig. 1은 직류전동기의 입력과 출력 관계에 따른 1계 시스템으로의 근사화를 보여준다.

Fig. 1

Input and output relation approximated as 1st order system

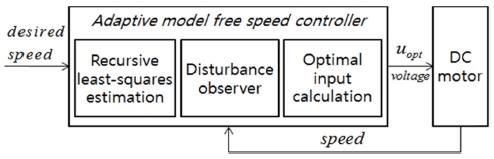
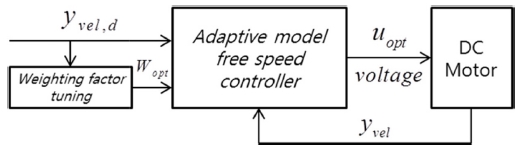
근사화된 1계 시스템과 실제 직류전동기 시스템의 오차는 항상 존재할 수 밖에 없기 때문에 외란 추정기를 기반으로 오차를 추정하여 최적제어입력 도출에 사용하였다. 입력과 출력만을 이용한 적응형 속도제어 알고리즘의 모델 개략도는 다음의 Fig. 2에 나타나 있다.

Fig. 2

Model schematics of an adaptive model free control algorithm

Recursive Least-Squares Estimation 블록에서는 직류 전동기에 인가된 입력과 회전속도인 출력을 이용하여 근사화된 1계 시스템의 계수 a를 추정한다. 근사화된 1계 시스템과 실제 시스템의 오차는 Disturbance Observer 블록에서 추정되며 추정된 계수와 오차는 Optimal Input Calculation 블록에서 최적제어 입력(u_opt: Voltage)을 계산하기 위해 사용된다. Fig. 2에서 볼 수 있듯이 제안된 적응형 모델 독립 알고리즘은 직류전동기의 속도제어를 위해 입력과 출력만을 이용하며 다음 장에서는 각 블록에 대해 세부적으로 기술한다.

3. 적응형 모델 독립 제어기 설계

3.4 가중치 망각인자 결정 규칙

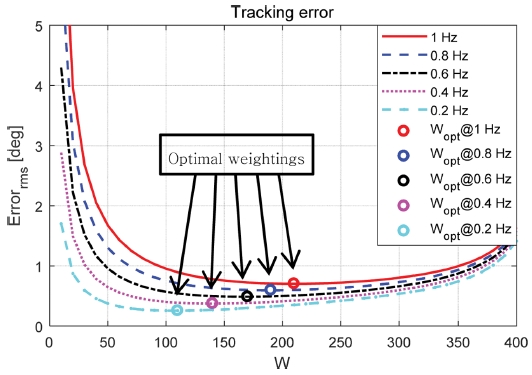
제안된 속도제어 알고리즘은 망각인자와 외란의 독립적인 추정성능을 가지고 있기 때문에 제어성능 확보를 위해 전동기의 요구속도의 변화율 $$ {\dot{y}}_{vel,d}$$에 따른 합리적인 가중치(W) 필요로 한다. 그러므로 본 연구에서는 요구속도 변화율 $$ {\dot{y}}_{vel,d}$$에 따른 최적 가중치(W_opt)를 시뮬레이션을 기반으로 도출하였다. 최적가중치 도출을 위해 구성된 제어알고리즘을 이용하여 Sinusoidal 입력 기반 추종 오차의 실효값(Root Mean Square, RMS)을 분석하였다. Fig. 3은 Sinusoidal 입력(1 Hz, 0.8 Hz, 0.6 Hz, 0.4 Hz, 0.2 Hz)을 인가하였을 때 W 값에 따른 추종오차(RMS) 결과와 주파수 별 오차를 최소화하는 최적가중치(W_opt)를 보여준다.

Fig. 3

Tracking error (RMS) with respect to W

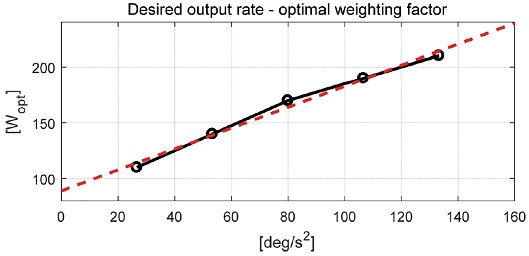
정의된 요구속도 변화율 $$ {\dot{y}}_{vel,d}$$에 대한 최적 가중치 규칙을 정의하기 위해 인가된 Sinusoidal 입력 변화율의 실효값을 도출하였으며 Fig. 3의 최적가중치와 연결하여 선형화된 규칙을 도출하였다. Fig. 4는 최적가중치와 Sinusoidal 입력 변화율의 실효값 그리고 선형화된 규칙을 나타낸다.

Fig. 4

Optimal W and linearized rule (dashed red line)

Fig. 4의 선형화된 규칙을 1차 함수로 나타내면 아래와 같이 요구속도 변화율에 대해 1차 근사화된 함수로 표현될 수 있다.

$\[ W_{opt}=0.94{\dot{y}}_{vel,d}+89 \]$

(12)

도출된 최적 가중치 결정 규칙을 이용하여 성능평가를 수행하였으며 다음 절에서는 개발된 모델 독립 제어기의 성능평가 결과에 대해 기술한다.

4. 제어기 성능평가

4.1 성능평가를 위한 직류전동기 모델링

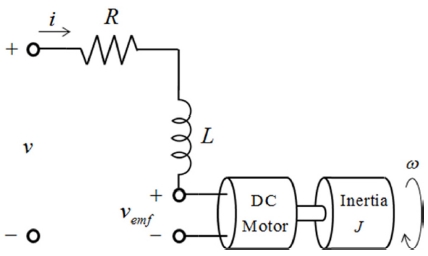
제안된 모델 독립 제어 알고리즘의 합리적인 성능평가를 위해 본 논문에서는 아래 Fig. 5와 같은 직류전동기 모델을 MATLAB/Simulink 환경에서 모델링 하여 사용하였다.

Fig. 5

Circuit for DC motor

R과 L은 각각 저항과 인덕턴스이고, v과 v_emf 그리고 i는 인가전압, 역기전력, 그리고 전류를 의미한다. 직류전동기에 직접적으로 연결되어 있는 부하의 등가관성은 J, 등가 댐핑계수는 b로 정의하고, 키르히호프 법칙과 오일러 법칙을 이용하여 직류전동기의 수학적 모델을 아래와 같이 정리할 수 있다.

$\[ \frac{di}{dt}=\frac{v}{L}-\frac{R}{L}i-\frac{K_{\mathrm{\Phi }}}{L}\omega \]$

(13)

$\[ \frac{d\omega }{dt}=\frac{K_{\mathrm{\Phi }}}{J}i-\frac{b}{J}\omega \]$

(14)

K_Φ는 EMF Constant를 의미하며 사용된 직류전동기의 계수들은 아래 Table 1과 같다.

Table 1

Used parameters of DC motor

개발된 적응형 모델 독립 제어알고리즘의 성능평가를 위해 직류전동기에 직접적으로 연결된 부하의 시간에 따른 변화를 적용하였다. 이를 위해 연결된 부하모델의 관성이 시간에 따라 변화되도록 성능평가 시나리오를 구성하였다. 평가를 위해 인가된 요구 직류전동기의 속도는 계단입력과 사인파입력을 인가하였으며 모든 경우에 대해 합리적인 제어성능을 확보하는 것을 확인할 수 있었다. 다음 절에서는 구성된 직류전동기 모델과 제어기를 이용한 성능평가 결과를 보여준다.

4.2 시뮬레이션 기반 성능평가 결과

Fig. 6는 성능평가를 위해 구성된 직류전동기와 적응형 모델 독립 제어기를 포함하는 시뮬레이션 모델을 보여준다.

Fig. 6

Integrated simulation model for performance evaluation

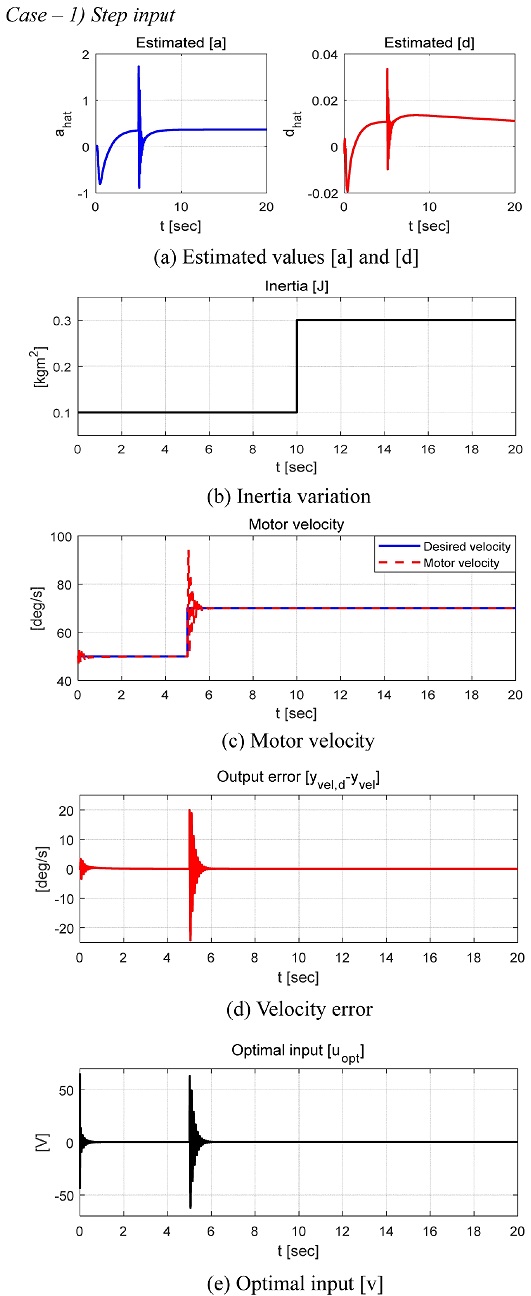
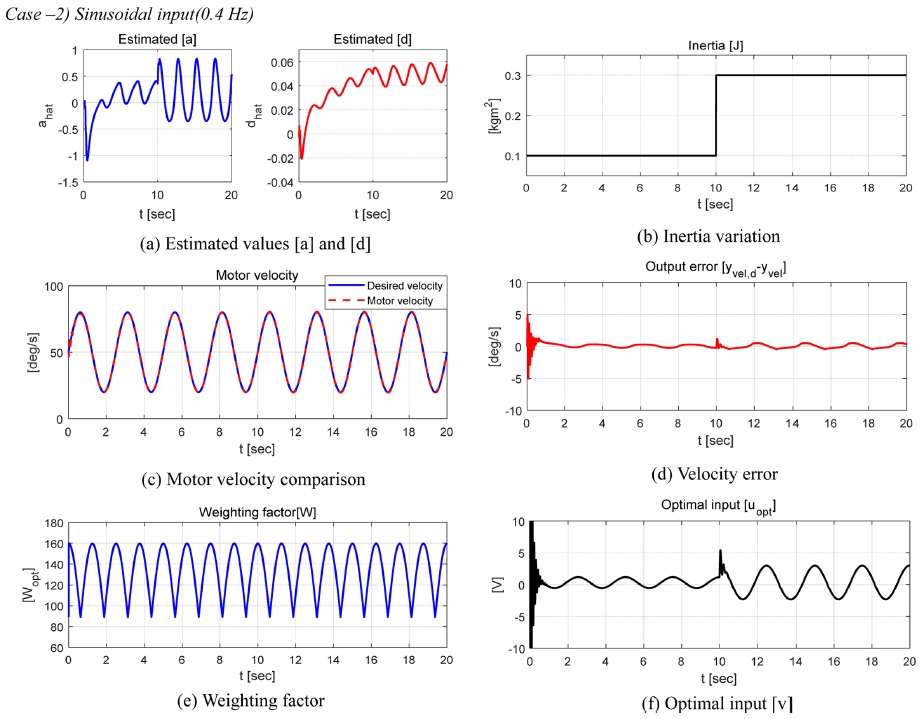
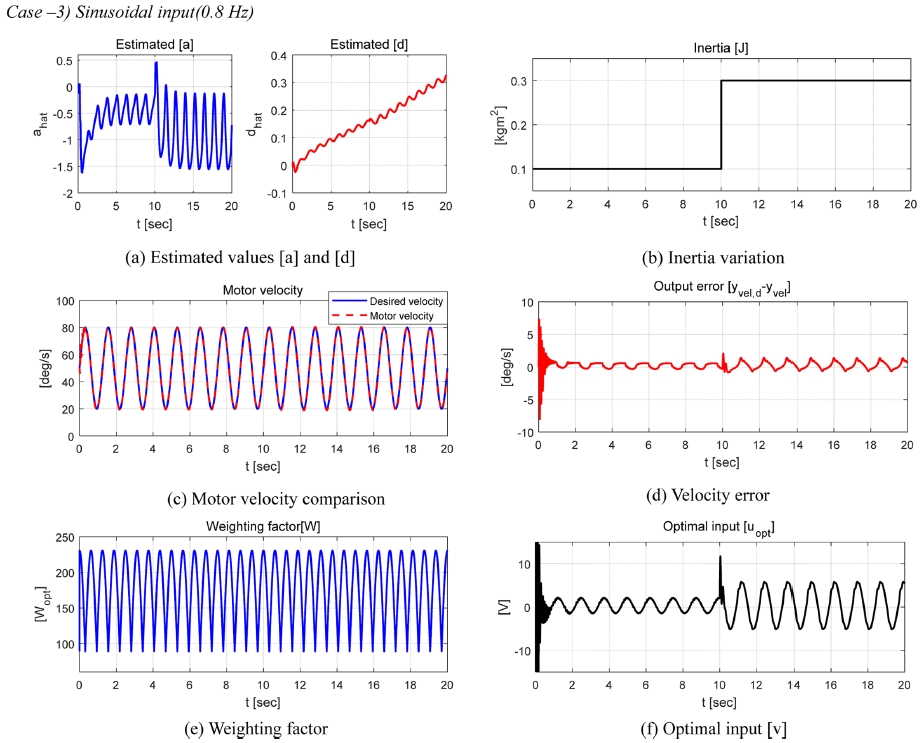
성능평가를 위해 적용된 y_vel,d는 스텝입력과 사인파가 적용되었으며 최적제어 입력 도출을 위해 필요한 $$ {\dot{y}}_{vel,d}$$는 선형 칼만필터를 이용하여 추정되었다. 성능평가를 위해 정의된 변수는 아래 Table 2와 같으며 Figs. 7-9는 평가 결과를 보여준다.

Table 2

Used parameters for controller

Fig. 7

Performance evaluation results (step input)

Fig. 8

Performance evaluation results (sinusoidal input, 0.4 Hz)

Fig. 9

Performance evaluation results (sinusoidal input, 0.8 Hz)

4.3 실험 기반 성능평가 결과

제시된 제어 알고리즘의 현실적 성능평가를 위해 실제 직류전동기를 이용한 실험환경을 구축하였다. 구축된 실험환경은 직류전동기, 회전각도 계측을 위한 엔코더, 데이터 수집장치, 전압공급장치, 그리고 컴퓨터로 구성되었으며 다음 Fig. 10에서 구성요소들을 보여준다.

Fig. 10

Elements for experiment setup

구성된 실험장치의 제어기를 설계하고 적용하기 위해 MATLAB/Simulink를 이용하여 제어기를 구성하고, 직렬통신 기법을 이용하여 데이터 수집 및 명령입력을 수행하였다. 하지만 실험에 적용된 제어 알고리즘은 실험장치의 성능(엔코더의 각도 계측성능)을 고려하여 직류전동기의 속도제어가 아닌 회전각 제어 알고리즘을 적용하였다. 그러므로 동일 알고리즘 내 시스템 출력이 직류전동기의 각도로 정의되었다. 제안된 알고리즘의 성능은 시스템 출력의 변화율에 민감하기 때문에 향후 회전 각가속도 정보를 추정할 수 있는 고성능 계측센서를 이용하여 속도제어 실험환경을 구축할 계획이다. 실험은 회전관성의 변화에 대한 두 가지 입력조건(계단입력, 정현파 입력)이 적용되었으며 Fig. 11에서 보여준다.

Fig. 11

Experimental conditions: rotational inertia change

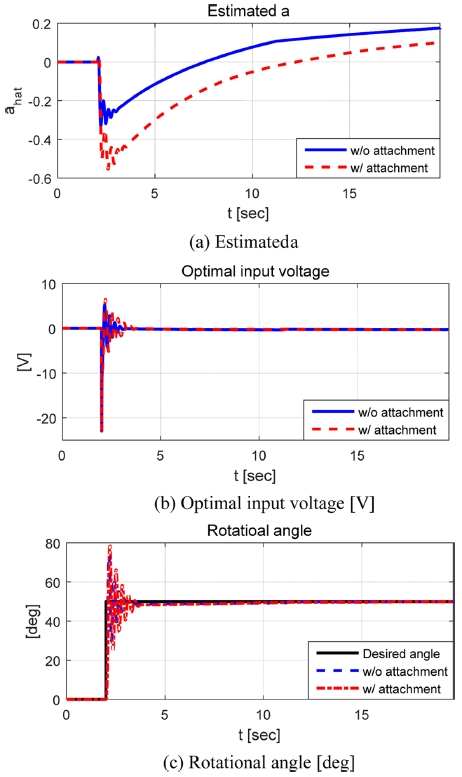
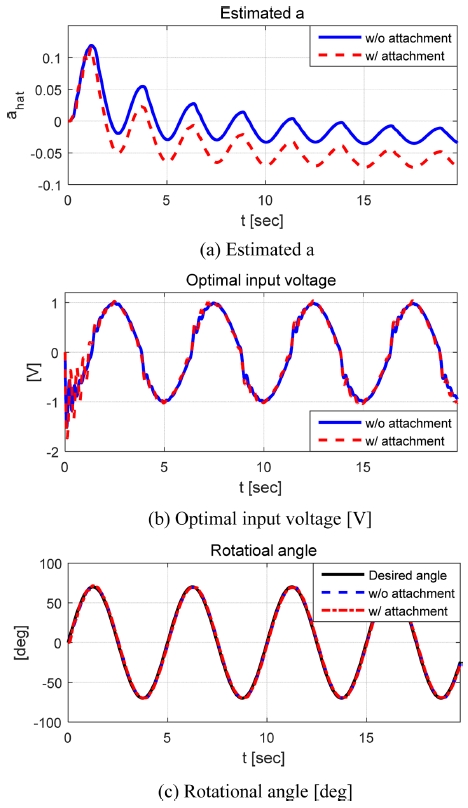
Fig. 11의 왼쪽 사진은 부착물이 없는 상태의 직류전동기를 보여주고, 오른쪽 사진은 부착물이 연결된 직류전동기를 보여준다. Figs. 12와 13, Table 4는 회전관성의 변화에 대한 계단 및 정현파 각도입력이 인가되었을 때 직류전동기의 회전각도 제어 결과를 보여준다.

Fig. 12

Experimental results: step input

Fig. 13

Experimental results: sine wave input

Table 3

Tracking error comparison (RMS value)

Table 4

Experimental tracking error comparison (RMS value)

Figs. 7-9에서 볼 수 있듯이 제안된 적응형 모델 독립 속도제어 알고리즘은 회전관성의 변화와 요구 속도의 다양한 주파수에 대해 강건한 제어성능을 보여주었다. 스텝입력이 인가된 Case-1의 경우 요구속도에 대한 제어결과 급격한 요구속도의 변화시점(5초)에서 약 0.5초 내 수렴하는 성능을 보였다. 요구속도의 변화율이 0이기 때문에 칼만필터의 추정오차 또한 0에 가까우며, 이는 합리적인 근사화 및 최적제어 입력 도출을 가능하게 하기 때문에 회전관성이 급변하는 10초 구간에서 근사화 및 제어오차가 발생하지 않는 것을 확인할 수 있다. 요구속도의 변화율이 시변하는 Case-2와 Case-3의 경우 스텝입력일 때와는 다르게 근사화 및 추정에 따른 제어성능이 상대적으로 낮아지는 것을 확인할 수 있었지만 합리적으로 1계 시스템의 계수와 오차를 추정하면서 평균적인 오차의 크기가 1 deg/s 미만을 유지하는 것을 확인할 수 있었다. 또한 10초 때 직류전동기에 적용된 등가 회전관성이 3배 증가하더라도 약 0.5초 내 수렴하는 제어성능을 확인할 수 있었다. 그리고 실험환경 구축에 따른 제어 알고리즘의 성능평가 결과 회전관성의 변화 조건에서 시스템의 출력이 요구되는 계단입력과 정현파 입력을 합리적으로 추정하는 것을 확인할 수 있었으며, 회전관성의 변화에 따른 추정오차는 계단입력의 경우 약 1.1 deg의 차이를 보였으나 정현파 입력의 경우 약 0.1 deg의 차이를 보였다. 본 연구에서 제안한 제어 알고리즘은 시뮬레이션 및 실험적으로 합리적인 성능을 보였지만 사용된 고정된 망각인자 값은 Steady State Error를 0으로 수렴시킬 수 있는 최적제어를 위한 값이 아니며 계측된 직류전동기의 속도는 잡음이 없는 값으로 가정하여 수행된 평가결과이다. 그러므로 향후 제어성능 향상을 위해 전동기의 속도 변화율에 따른 망각인자의 적응형 변경규칙 적용 및 잡음에 대한 강건한 성능을 확보하고, 고성능 계측센서의 사용을 통한 직류 전동기 속도제어 알고리즘의 실험적 검증을 추가적으로 계획하고 있다. 다음 장에서는 본 논문의 결론을 기술한다.

5. 결론

본 논문에서는 입력(전압)과 출력(속도)만을 이용하는 직류전동기의 모델 독립 속도제어 알고리즘을 제안하였다. 이를 위해 망각인자 기반 최소순환자승 기법과 외란추정기를 이용하였다. 제안된 모델 독립 제어 알고리즘은 대상 전동기의 입력(전압)과 출력(속도)만을 이용하여 수학적 모델 없이 입출력 관계를 1계 시스템으로 근사화 하고 근사화된 1계 시스템과 실제 시스템의 오차를 외란추정기를 이용하여 추정하도록 설계되었다. 근사화된 1계 시스템과 추정된 외란을 이용하여 Lyapunov Direct Method 기반 최적제어 입력(전압)을 도출하였으며, 제어성능 향상을 위해 최적 가중치 규칙을 시뮬레이션을 기반으로 도출하여 적용하였다. 합리적 성능평가를 위해 직류전동기의 수학적 모델을 구성하고, 합리적인 파라미터를 적용하여 성능평가를 수행하였다. 성능평가 조건은 스텝과 사인파 형태(다양한 주파수)의 요구 회전속도가 인가되는 가운데 평가의 중간에서 부하의 관성이 약 3배 변하는 조건이 적용되었다. 시뮬레이션 기반의 평가결과 모든 조건에서 제안된 속도제어 알고리즘은 합리적인 제어성능을 확보할 수 있었으며, 실험환경 구성을 구성함으로써 제안된 알고리즘 기반 직류 전동기의 회전각도 제어성능을 평가하였다. 실험환경에서의 제어성능 평가결과 다양한 평가조건에 대해 합리적 결과를 보여주었다. 하지만 알고리즘에 적용된 망각인자는 최적화된 적응규칙이 아닌 고정된 값이고 계측된 직류전동기의 회전속도는 잡음이 없다고 가정하였기 때문에 향후 외란 관측기의 수렴성능을 고려한 망각인자의 적응규칙 최적화 및 잡음에 대해 강건한 성능확보를 위해 알고리즘을 고도화할 계획이다. 그리고 1계 시스템으로의 근사화 과정을 주기적으로 갱신함으로써 구간별 수학적 수렴성능 및 안정성을 확보하는 것을 계획하고 있다. 또한 이를 기반으로 실제 직류전동기 시스템에 적용하여 성능평가를 수행하고 다양한 시스템으로의 확장 가능성 분석을 수행할 것이다. 본 연구에서 제안한 적응형 모델 독립 제어 알고리즘은 향후 다양한 시스템에 적용된 직류전동기의 실용적인 각도 및 속도제어를 위해 사용될 수 있을 것이라 기대한다.

REFERENCES

• Dursun, E. H. and Durdu, A., “Speed Control of a DC Motor with Variable Load Using Sliding Mode Control,” International Journal of Computer and Electrical Engineering, Vol. 8, No. 3, pp. 219-226, 2016. [https://doi.org/10.17706/IJCEE.2016.8.3.219-226]
• Ahmed, A. M., Ali-Eldin, A., Elksasy, M. S., and Areed, F. F., “Brushless DC Motor Speed Control Using Both PI Controller and Fuzzy PI Controller,” International Journal of Computer Applications, Vol. 109, No. 10, pp. 29-35, 2015. [https://doi.org/10.5120/19227-0933]
• Kiran, N., Raju, N., and Kumar, A., “Performance Comparison of Speed Control of Chopper Fed DC Motor for Various Controllers,” International Journal of Innovation and Scientific Research, Vol. 11, No. 2, pp. 273-282, 2014.
• Ali, A. T. and Tayeb, E. B. M., “Adaptive PID Controller for DC Motor Speed Control,” International Journal of Engineering Inventions, Vol. 1, No. 5, pp. 26-30, 2012.
• Saealal, M., Ramachandran, A., Abas, M., and Saad, N. M., “Synchronize Speed Control for Multiple DC Motors Using Linear Quadratic Regulator,” Proc. of the International Conference on Computing in Mathematics and Statistics, pp. 85-92, 2017. [https://doi.org/10.1007/978-981-10-2772-7_9]
• Premkumar, K. and Manikandan, B., “Adaptive Neuro-Fuzzy Inference System Based Speed Controller for Brushless DC Motor,” Neurocomputing, Vol. 138, pp. 260-270, 2014. [https://doi.org/10.1016/j.neucom.2014.01.038]
• Vahidi, A., Stefanopoulou, A., and Peng, H., “Recursive Least Squares with Forgetting for Online Estimation of Vehicle Mass and Road Grade: Theory and Experiments,” Vehicle System Dynamics, Vol. 43, No. 1, pp. 31-55, 2005. [https://doi.org/10.1080/00423110412331290446]
• Liu, C.-S. and Peng, H., “Disturbance Observer Based Tracking Control,” Journal of Dynamic Systems, Measurement, and Control, Vol. 122, No. 2, pp. 332-335, 2000. [https://doi.org/10.1115/1.482459]