Polymer Microlens 제작을 위한 Thermal Reflow 공정 해석
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Polymer microlens manufacturing using thermal reflow was simulated and optimized by a numerical approach. Microlenses are used in various industrial fields, such as optical, semiconductor, and observation experiment equipment. Therefore, polymer microlens fabrication using an economical thermal reflow process is important for mass production and cost reduction. The feasibility of a thermal reflow process for microlens fabrication was analyzed in this paper by numerical methods. First, we refer to the previous studies and papers for the theoretical shape of the microlens. Second, for numerical simulation of the process above Tg (Glass Transition Temperature), we studied the multiphase flow simulation using a VOF method and adopted a Cross-WLF model to consider the rheological characteristics of PMMA. Finally, several parametric studies were carried out to compare the simulation profile and the theoretical lens shape in order to optimize the thermal reflow process. The numerical approach presented in this paper would enable a more efficient analysis and provide better understanding of reflow behavior to obtain the optimal process.
Keywords:
Microlens, Thermal reflow, Mutiphase, Numerical analysis키워드:
마이크로렌즈, 열 재유동, 다상유동, 수치 해석1. 서론
마이크로렌즈(Microlens)란 통상적으로 수 μm를 기준으로 수 mm, 수 nm까지의 지름을 갖는 구형 형상으로, 구형의 곡면(Curvature)으로 광원이 통과하여 광원의 조절과 분기, 분파와 같은 기능을 하는 크기가 작은 렌즈를 말한다. 이러한 마이크로렌즈는 광원의 퍼짐을 막거나 광원을 한 곳으로 집적시켜 광감지 센서의 센싱 효율을 증대시키는 등의 기능을 통해 디스플레이, 광통신, 광학기기와 같은 다양한 산업 및 연구 분야에서 응용 되고 있는 광학 시스템과 관련된 분야에서 필수적인 부품이다.1
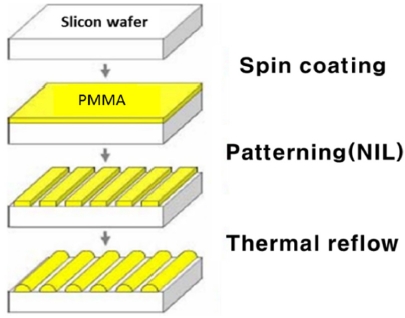
이러한 기능의 마이크로렌즈는 응용 기술의 발전에 따라 수요가 급증하고 있으며, 렌즈의 크기를 세밀한 공정을 통해 더욱 작게 성형하는 동시에 낮은 비용으로 높은 수율을 얻는 공정에 대한 연구 또한 활발히 이루어지고 있다. 이러한 저비용 고정밀 렌즈 성형 방법으로 활용되는 다양한 공정 방법 중 대표적인 방법이 Thermal Reflow 공정을 이용한 방법이다. 일반적으로 기존 마이크로렌즈를 제작하는 방법은 몰딩(Molding) 또는 엠보싱(Embossing) 공정을 주로 사용하는데, 이러한 공정에서 필수적인 마스터(Master) 몰드의 경우, 마이크로렌즈의 곡면(Curvature) 형상으로 기계적 가공하는 것이 상대적으로 어렵고 고비용이며 연속적인 곡률을 담보할 수 없다는 점에서 공정상 어려움이 있다. 따라서, 대안으로 렌즈 형상을 1차 성형한 후에 이어지는 후속공정을 통해 렌즈 형상을 제작하는 방법이 각광되고 있다. 1차 성형의 경우, 반도체 공정에서 쓰이는 레이저 펄스를 이용한 건식 에칭(DRIE)이나 마이크로 밀링(Milling), E-Beam 가공법을 통한 직접적인 가공을 사용하거나, Photoresist를 활용한 광학적인 리소그래피와 잉크젯 프린팅 기술 등의 간접적인 방법을 사용할 수 있다.2 그리고, 마스터 몰드를 이용한 저비용 공정 방법도 넓게 사용되고 있으며 대표적으로는 핫엠보싱(Hot Embossing) 및 나노임프린트 리소그래피(Nano Imprint Lithography, NIL) 공정을 예로 들 수 있다. 이들 공정의 경우, 다양한 고분자 재료의 성형이 가능하고 특히 열가소성(Thermo-Plastic) 수지의 성형을 통해 후속 공정으로 Thermal Reflow 공정을 적용하기 위한 연계성에서 유리하다. 3
이러한 이유로 본 연구에서는, 저비용 고정밀 고분자 마이크로렌즈의 제작을 위해 리소그래피 기술 중 하나인 핫엠보싱 또는 나노임프린트 공정과 연계가 가능한 Thermal Reflow 공정의 마이크로렌즈 성형 가능성을 확인하고 최적화를 위한 해석모듈 확보와 변수최적화에 대한 연구를 진행하였다. 즉, 나노임프린트 기술을 활용해 가공이 용이한 직각 마스터 몰드를 통해 Line&Space 패턴을 1차 성형하고, 고분자의 유리전이온도(Glass Transition Temperature, Tg) 이상의 온도 공정조건에 따라 용융되는 고분자 수지 계면의 표면장력으로 렌즈 곡면을 성형하는 후속 Thermal Reflow 공정에4-6 대한 해석적 연구를 진행하였다. 연구를 통해 렌즈 제작과 관련된 종횡비에 따른 초점거리와 같은 이론적 형상(Theoretical Geometry)을 구현할 수 있는 조건을 제시하고 공정 최적화에 따른 곡률형상의 구현 가능성에 대해 살펴보았다.7
2. 마이크로렌즈 형상 이론 설계
마이크로렌즈의 광학 성능은 렌즈의 곡률 반경에 따라 달라지는 초점거리(Focal Length)에 연관이 있다. 따라서 이론적으로 제시되는 곡률(Curvature Radius)을 구현할 수 있는 성형공정을 확보하는 것이 중요하다. 이론적 측면에서 마이크로렌즈를 위한 Reflow 전후의 패턴 형상은 부피는 같고, 모양은 시간에 따라 변화하므로, 이러한 구속조건에 따라 원하는 곡률반경과 너비 그리고 높이를 갖는 이론적인 마이크로렌즈 형상을 계산할 수 있다. 이러한 이론적 렌즈설계를 위한 계산과 유도과정에 대한 수식은 아래와 같다.8
먼저 본 연구에서 설계 목표로 설정한 실린더 형태의 마이크로렌즈의 부피를 Vcyl이라고 두고, 처음 Reflow되기 전 Line 형태의 초기 부피를 VO라고 뒀을 때 두 형태의 부피 관계는 다음과 같다.
| (1) |
식(1)에서 초기 Line 형태의 부피와 Reflow 후 Lens 형태의 부피가 부피 감소율(Volume Reduction) E를 대입함으로써 같다. 부피 감소율은 일반적으로 큰 차이가 없으므로 100% 설정하였다. Reflow 전과 후의 부피에 대해 표시하면,
| (2) |
| (3) |
로 나타낼 수 있다.
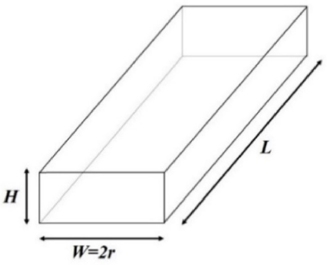
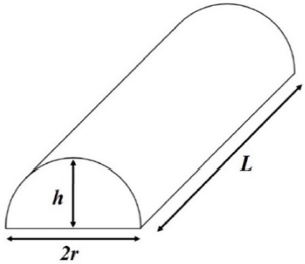
Figs. 2와 3에서 L은 렌즈의 길이(Length), W는 렌즈의 너비(Width)이며 Reflow 후 렌즈의 지름은 2r과 같다고 가정한다. H는 Reflow 전의 높이(Height), h는 Reflow 후의 높이일 때, h는
| (4) |
로 계산된다. 식(4)에서 R은 Constant Radius of Curvature로 렌즈의 초점거리를 정하는 주요 파라미터이다. 즉, 초점거리는 곡률반경 R과의 관계를 통해 나타나며, 그 관계식은
| (5) |
이다. 여기서 n은 물질 고유의 굴절률(Refractive Index)로써 연구에서 고려된 고분자는 PMMA (PolyMethyl-Methacrylate)이므로 n = 1.49의 값으로 설정하였다.
θ는 곡률반경이 이루는 호의 각도로, 이 변수를 통해 렌즈의 단면적 A를 구할 수 있다. 또한 θ는 다음과 식으로 나타날 수 있는데
| (6) |
이러한 관계식 들을 통해 렌즈의 Reflow 전과 후의 부피가 식(1)과 같이 같다라고 할 때, 결과적으로 Reflow 전의 높이(Height) H를 구할 수 있다.
| (7) |
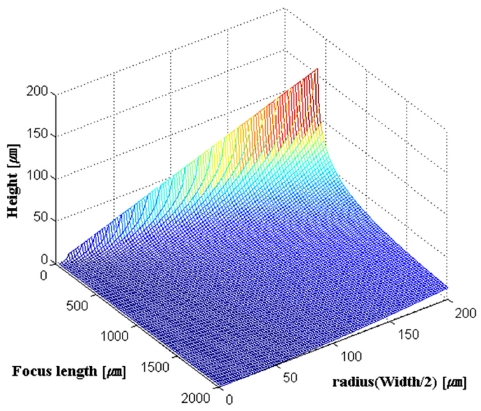
이처럼 너비, 높이, 초점거리와 같은 구조파라미터를 통해 렌즈의 형상적인 설계를 진행하였다. 각각의 파라미터는 서로에게 종속되어 변화하므로 위 식들로부터 렌즈의 형상을 결정 짓는 맵핑(Mapping) 그래프를 Fig. 4와 같이 나타낼 수 있다.
위와 같이 마이크로렌즈의 이론적 설계를 바탕으로 구조 파라미터에 따른 실제 성형가능성을 예측하기 위하여 6가지 Case(Table 1)에 대한 Reflow 공정 후 프로파일을 해석을 통해 예측하였다.
3. 공정 설계를 위한 해석 조건
3.1 마이크로렌즈 재질의 유변학적 특성
일반적으로 렌즈의 재질은 굴절률의 중요성으로 인해 투과성이 높은 유리로 많이 생산되어 왔다. 그러나 렌즈 스케일의 미소화로 인해 유리와 같이 미세가공이 어려운 재질보다, 성능은 유지하면서 가공 및 성형 또한 용이한 다른 재질의 선정이 필요한 상황이다. 본 연구에서는 대체 가능 재질로 성형성 및 비용차원에서 유리하고 Thermal Reflow 공정에 적합한 용융성과 굴절률(Refractive Index)을 가지고 있어 마이크로/나노 스케일의 부품에 적용이 용이한 PMMA (Polymethyl-Methacrylate) 고분자 재료를 선정하여 해석을 진행하였다.
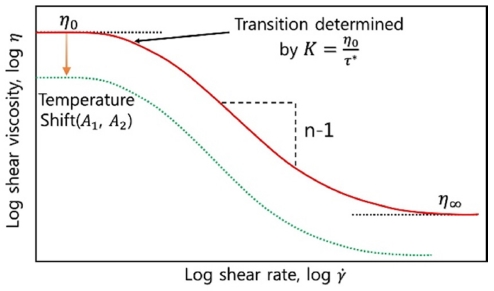
Fig. 5와 같이 고분자의 경우는 열을 이용한 성형 시 용융점 아래의 유리전이온도(Glass Transition Temperature)를 기준으로 유동성을 보이며 유변학적(Rheological) 특성을 나타낸다. 일반적으로 고분자의 점도는 온도와 전단변형률(Shear Rate)에 따른 비뉴턴(Non-Newtonian) 유체 특성을 가지고 있다. 이러한 고분자의 유변학적 특성을 구현하기 위하여 다양한 점도모델(Viscosity Model)들이 있으나, 본 연구에서는 다양한 수지 종류에 대해서 데이터가 충분히 알려져 있는 Cross-WLF 모델을 사용하여 PMMA(Polymethyl-Methacrylate)의 고분자 특성을 모델링하였다.9
Cross-WLF Model 관계식은 Fig. 5와 같은 형태의거동을 보이며 다음과 같은 식으로 나타낼 수 있다.
| (8) |
여기서 는 전단변형률(Shear Rate), η0는 Zero Shear Viscosity, τ*은 Shear Tinning 구간으로 변화하는 시점의 critical stress를 의미하며 n은 Power Law Index이다. 식(8)에서 Zero-Shear Viscosity 는 다음 식(9)로 표현된다.
| (9) |
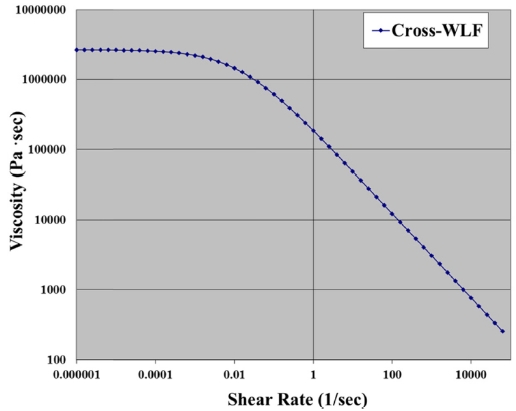
위의 관계식과 PMMA에 해당하는 아래의 상수값(Table 2)을 통해 연구에서 적용한 Cross-WLF Model의 전단변형률과 점도에 따른 그래프를 Fig. 6과 같이 표현하였다.
3.2 지배방정식
연구에서는 고분자의 유변학적 특성과 동시에 표면장력으로 인한 유체 거동을 모사하기 위하여 질량 보존 및 운동량 보존의 2차원 비압축성 유체 지배방정식을 고려하여 해석을 진행하였다. 렌즈의 크기가 마이크로 스케일로 매우 작으므로 열전도에 따른 위치별 온도 차이는 무시할 정도로 작으므로 에너지 보존식은 해석에서 제외하였다. 따라서, 해석에서 고려한 지배방정식(Governing Equations)은 아래와 같이 연속 방정식(Continuity Equations)과 나비에-스톡스(Navier-Stokes) 방정식으로 나타낼 수 있다.
| (10) |
| (11) |
여기서 ui, ρ, P, T는 속도 벡터, 밀도, 압력, 온도이며, fi는 체적력(Body Force)이고 τij는 점성응력텐서(Viscous Stress Tensor)로 나타내었다. 식(11)은 비압축성 유체의 운동량방정식을 표현하며, 구성방정식은 아래와 같다.
| (12) |
| (13) |
여기서 Dij는 strain rate tensor이고 σij는 total stress tensor, δij, η는 각각 kronecker delta tensor와 viscosity를 나타낸다.10
3.3 자유표면 및 표면장력 모델링
공정 해석을 위한 수치해석 프로그램은 상용 CFD S/W인 Ansys-Fluent 16.0를 사용하였으며, 액체-기체-고체가 존재하는 다상(Multi-Phase) 유동이므로 VOF(Volume of Fluid) 방법을 적용하여 해석을 진행하였다. VOF 방법은 고정격자계에서 자유표면 경계 유동을 추적하기 위한 대표적인 자유표면 해석 방법으로, 해석 모델의 전체 도메인에서 유체로 채워진 영역과 미충전 상태의 비유체영역을 나누어 수치로 표시한다. 즉, 완전하게 유체로 채워진 부분을 1로, 비어있는 부분을 0으로 부피분율(Fractional Volume)을 설정하고 경계면을 추적(Tracking)하는 방법이다. VOF의 지배방정식은 이송방정식(Advection Equation)의 형태를 가지며 수식은 아래와 같다.
| (14) |
여기서 C는 부피분율의 값을 나타내는 Color Function이다.
또한 고정된 격자시스템에서 표면장력의 영향을 고려하기 위하여, Brackbill’s CSF Model 식을 차용하였다. CSF Model은 표면장력을 체적력으로 변환 시키는데 자세한 수식은 아래와 같다.11
| (15) |
여기서, γ는 표면장력계수이며 κ는 곡률, 그리고 n은 경계면의 단위 수직 벡터이고 |C|는 각 경계면을 교차하는 인자이다.
해석 조건은 실린더 타입의 렌즈 패턴들 중 하나를 도메인으로 구성하여 진행하였고, 구조적으로 단면 모양을 반으로 나누어 대칭이므로 수치적으로도 대칭 모델로 구성하였다. 또한, 시간에 따른 변화를 보기 위해 Unsteady (Transient) 다상 유동 해석을 진행하였다. 패턴이 마이크로스케일이므로 미세 유체 특성으로 인해 중력의 영향이 작고, 관성력(Inertial Force)보다는 점성력(Viscous Force)에 의한 거동을 하므로 층류유동(Laminar Flow)으로 가정하였다. 앞서 제시한대로 마이크로렌즈 제작에 사용되는 재료는 성형 및 광학특성에 유리한 PMMA를 사용하였고, Cross-WLF Model을 적용하여 유변학적 거동을 구현하였다. PMMA의 표면장력계수로는 Reflow 전 상온의 경우 41.1 mN/m를 적용하였고, 온도증가에 대한 표면 장력의 변화는 0.076 mN/m·K 로 감소하는 것으로 설정하였다.
4. 해석결과 분석
Fig. 7은 180oC의 온도에서 일정 시간에 따라 Reflow된 마이크로렌즈의 프로파일을 나타낸 해석 결과이다. 시간에 따른 Reflow 유동 경계면은 높은점도의 영향으로 수 분에서 수십 분의 공정 제어 가능한 시간대에서 변형이 일어나며, 표면장력의 영향으로 초기 표면 형태와 아랫면의 접촉각에 따라 천천히 렌즈 형상으로 변화한다.
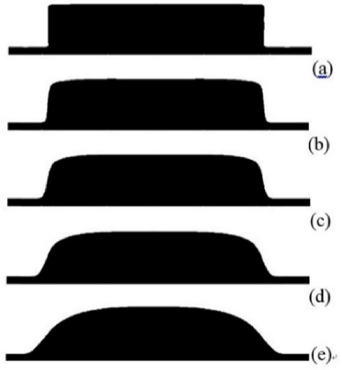
Curvature profile after thermal reflow at 180oC with time: (a) before Reflowing, (b) 60 sec, (c) 600 sec, (d) 1800 sec, (e) 2400 sec
앞선 이론설계를 통해 제시한 렌즈의 기준 형상과 일정 공정시간(30 min)이 지났을 때의 곡률반경, 그리고 이론적 형상과 가장 일치하는 것으로 파악되는 시간에 대한 렌즈 형상 프로파일을 Figs. 8부터 11까지 각각 그래프로 나타내었다.
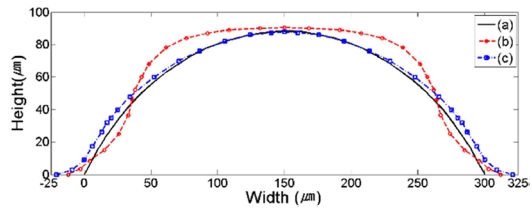
Width: 300 μm, height: 60 μm, focal length: 350 μm: (a) Theoretical profile, (b) Thermal Reflow profile at 180oC for 30 min, (c) 55 min. reflowed profile
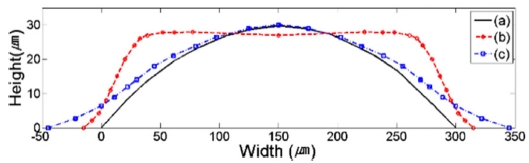
Width: 300 μm, height: 20 μm, focal length: 800 μm: (a) Theoretical profile, (b) Thermal reflow profile at 180oC for 30 min, (c) 45 min. reflowed profile
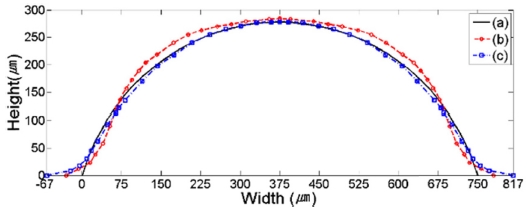
Width: 750 μm, height: 200 μm, focal length: 800 μm: (a) Theoretical profile, (b) Thermal reflow profile at 180oC for 30 min, (c) 1hr 15min. reflowed profile
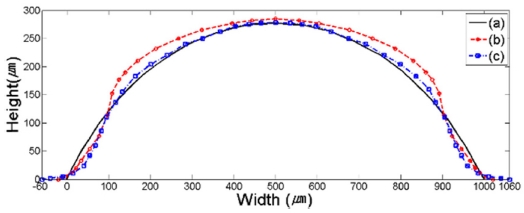
Width: 1000 μm, height: 200 μm, focal length: 1200 μm: (a) Theoretical profile, (b) Thermal reflow profile at 180oC for 30 min, (c) 1 hr 30 min. reflowed profile.
해석 결과인 프로파일 형상을 정성적으로 관찰해보면 종횡비가 작을수록(Figs. 8-10) 이론적인 렌즈 형상에 근접하는 것을 확인할 수 있었다. 즉, 종횡비가 가장 작은 Fig. 9의 경우보다 종횡비가 큰 Fig. 10의 경우 렌즈의 이론적 형상에 근접함을 관찰할 수 있었으며 그 중간 정도의 종횡비에 해당하는 Fig. 8의 경우는 형상 또한 중간 정도의 일치성을 보였다. 또한, 동일 종횡비인 Figs. 8과 11의 경우를 보면 패턴의 스케일이 클수록 Reflow되는 공정 시간은 비례하여 증가하는 것을 관찰할 수 있었다. 즉, 이론적 곡률과 가장 근접하게 Reflow 됐을 시간의 프로파일 형상은 각 패턴의 종류에 따라 다양하게 나타나지만, 일반적으로 스케일이 클수록 공정 시간은 자연스럽게 길어지는 것을 확인할 수 있었다.
정성적인 분석과 더불어 정량적인 비교를 위해 곡률반경의 이론적 형상과 해석을 통한 예측 결과를 수치적으로 서로 비교하였다. 이를 위해, 아래와 같이 형상 일치성을 Consistency Rate이라는 변수로 정의하였다.
| (16) |
위 수식이 의미하는 바는 렌즈의 너비를 n개의 Point로 나누었을 때 각 너비의 Point에서 이론적인 높이 hth,i와 수치적인 해석으로 예측된 높이 hi의 차이 평균을 패턴의 높이 h로 나눈 값으로, 이를 통해 기하학적 일치성을 수학적으로 표현하였다.
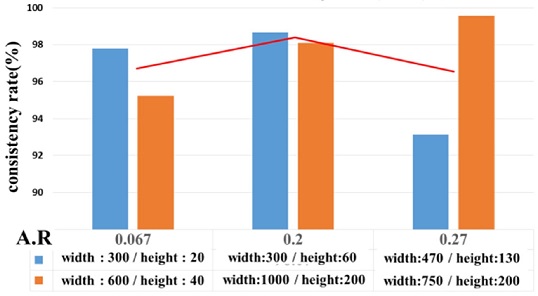
앞서 비교한 Figs. 8-11의 4가지 Case의 결과와 더불어, 동일 종횡비의 다른 스케일의 패턴영향을 추가로 관찰하기 위해 Table 1의 5, 6번 Case를 추가로 고려하여 일치성을 확인하였다. 이론적인 렌즈 형상에 가장 근접할 때의 형상 프로파일을 기준으로 전체적인 렌즈 형상에 대한 일치성, 그리고 광학성능에 주된 영향을 미치는 렌즈 중앙부분(너비 기준 25%)의 곡률 일치성을 각각 비교한 결과를 Table 3과 Fig. 12에 도시하였다.
Fig. 12에서 볼 수 있듯이, 렌즈의 이론적 형상과 Reflow 공정 후의 형상 프로파일 오차를 일치성이라는 지표로 표현할 때, 같은 종횡비라 하더라도 패턴 스케일에 따라 차이가 있음을 알 수 있다. 즉, 마이크로 렌즈의 형상에 따라 패턴의 종횡비와 스케일을 함께 고려하여야 이론적인 형상에 근접할 수 있음을 알 수 있는데, 이러한 점을 통해 Reflow 공정의 최적화를 위해서는 주어진 렌즈 형상에 따라 종횡비와 스케일을 적절히 설계하는 것이 필요함을 알 수 있다. 본 해석 케이스를 기준으로 볼 때, 가장 높은 일치성을 위해서는 가능한한 높은 종횡비의 패턴을 설계한 후 스케일을 조정하면서 최적화하는 렌즈 형상 케이스가 이론적인 렌즈 형상으로 구현하기에 적절한 것으로 판단된다.
또한, 두 가지 주요한 구조변수인 종횡비와 스케일 외에도 렌즈의 재질 또한 주요한 변수로 파악된다. 앞서 패턴의 종횡비와 스케일, 두 가지 함수가 Reflow 공정 최적화에 관련이 되어 있는 이유는 Reflow 공정의 유동특성과 관련이 있다. 따라서 고분자의 유변학적 특성에 영향을 미치는 렌즈의 재질까지 변수로 고려한다면 총 세 가지의 변수가 혼재되어 있음을 알 수 있다. 고분자 마이크로 렌즈의 형상은 광학 성능에 따라 다양한 구조로 디자인되며, 재질 또한 선택 가능한 변수이므로 Reflow 형상의 최적 형상 프로파일을 확보하기 위해서는, 세가지 변수를 고려하여 Reflow 온도에 따른 수치적인 해석을 진행하여 공정을 예측하고 공정을 설계, 적용하는 것이 필요할 것으로 판단된다.
5. 결론
본 연구에서는 고분자 마이크로렌즈의 Thermal Reflow 공정에 대한 해석적인 접근을 통해 주요 공정 변수에 대해 도출하는 연구를 진행하였다. 렌즈를 성형하기 위한 1차 성형 패턴의 스케일 및 종횡비에 따른 유변학적 고분자 유동특성을 해석에 적용하여 공정시간에 따른 곡률반경 일치성에 대해 수치적으로 살펴보았다. 이론적인 렌즈 형상과 일치하는 정도를 수치적으로 정량 분석하기 위해 일치성이라는 변수를 정의하여 패턴의 종횡비와 스케일, 그리고 고분자 재질이 Reflow 공정의 주요 변수임을 확인하였다. 다양하게 사용되는 고분자 마이크로 렌즈를 Thermal Reflow 공정을 통해 구현하기 위해서는 구조변수와 유변학적 거동을 고려하여야 하며, 최적화된 공정설계를 적용할 때 너비 기준 25%내 중앙부의 95% 이상의 일치도를 보이는 이론적 렌즈 형상을 제작할 수 있음을 확인하였다. 렌즈의 기본적인 형상이 표면장력으로 인한 반구(Hemisphere)로의 형상 변화와 유사함을 고려할 때, 보다 복잡한 렌즈의 형상에 대해서도 Thermal Reflow 공정을 예측하는 해석 모듈을 이용해 최적화 설계 및 구현이 가능함을 확인하였다.
Acknowledgments
본 연구는 한국연구재단 기본연구지원사업의 지원(NRF-2017R1D1A1B03035636)과 2018년도 한국기술교육대학교 교수 교육연구진흥과제 지원으로 수행된 연구결과입니다.
REFERENCES
-
Tuantranont, A., Bright, V., Zhang, J., Zhang, W., Neff, J., et al., “Optical Beam Steering Using Mems-Controllable Microlens Array,” Sensors and Actuators A: Physical, Vol. 91, No. 3, pp. 363-372, 2001.
[https://doi.org/10.1016/S0924-4247(01)00609-4]

- Ryoo, K., Kim, Y., and Jeon K., “Polymer Microlens Fabrication,” Clean Technology, Vol. 11, No. 4, pp. 205-211, 2005.
-
Tsai, J. C. and Hsu, Y. S., “Profile of Microlens Fabricated by the Thermal Reflow Process,” IEEE Transactions on Magnetics, Vol. 47, No. 3, pp. 598-601, 2011.
[https://doi.org/10.1109/TMAG.2010.2102010]

-
Yoo, J. H. and Jung, H. S., “Characteristics of Plastic Lens Dimensional Deviation according to Injection Mold Clamping Force,” J. Korean Soc. Precis. Eng., Vol. 32, No. 12, pp. 1081-1086, 2015.
[https://doi.org/10.7736/kspe.2017.34.10.739]

- Lee, E. S., Lee, M. K., Park, J. B., and Kim, K. H., “Development of an automatic Measuring System for Aspheric Lenses,” Proc. of the Korean Society of Manufacturing Technology Engineers Spring Conference, p. 77, 2012.
-
Yang, S. W., Kim, S. H., Kim, B. H., and Cho, Y. H., “Fabrication and Characterization of Polymer Microlens using Solvent-vapor-assisted Reflow,” J. Korean Soc. Precis. Eng., Vol. 32, No. 3, pp. 299-305, 2015.
[https://doi.org/10.7736/KSPE.2015.32.3.299]

-
Kim, S. H., Song, J. Y., Lee, P. A., Kim, B. H., Oh, Y. T., et al., “Surface Polishing of Polymer Microlens with Solvent Vapor,” J. Korean Soc. Precis. Eng., Vol. 30, No. 6, pp. 644-649, 2013.
[https://doi.org/10.7736/KSPE.2013.30.6.644]

-
O'Neill, F. T. and Sheridan, J. T., “Photoresist Reflow Method of Microlens Production Part I: Background and Experiments,” Optik, Vol. 113, No. 9 pp. 391-404. 2002.
[https://doi.org/10.1078/0030-4026-00186]

- Rudolph, N. and Osswald, T. A., “Polymer Rheology: Fundamentals and Applications,” HANSER, pp. 70-71, 2014.
-
Kim, S., Kang, J., and Lee, W., “Analysis of Polymer Flow in Embossing Stage During Thermal Nanoimprint Lithography,” Polymer Engineering & Science, Vol. 51, No. 2, pp. 209-217, 2011.
[https://doi.org/10.1002/pen.21772]

-
Brackbill, J., Kothe, D. B., and Zemach, C., “A Continuum Method for Modeling Surface Tension,” Journal of Computational Physics, Vol. 100, No. 2, pp. 335-354, 1992.
[https://doi.org/10.1016/0021-9991(92)90240-Y]