5축 CNC 가공을 위한 실시간 NURBS 곡선 보간기
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
In CAD/CAM, NURBS (Non-Uniform Rational B-Spline) is used to represent a wide variety of free-form curves. NURBS interpolation is advantageous in the processing of smooth curves and is capable of high-speed and high-precision CNC machining. In this paper, a real-time 5-axis NURBS curve interpolator is proposed. The proposed interpolator is based on tool center point control and can produce smooth tool orientations as well as accurate tool paths, thereby realizing high precision and efficient 5-axis machining. Using newly defined G codes, tool orientations are described by vectors and the proposed interpolator can be applied to any 5-axis machines regardless of their rotary axis configurations. In addition, the proposed interpolator calculates both tool positions and orientations simultaneously using a shared interpolation routine and we can reduce the computation load. The proposed NURBS interpolator is implemented on a PC-based 5-axis CNC testbed. The performance of the proposed interpolator is compared with the conventional linear interpolator in terms of smoothness of feedrate, contour errors, and tool orientation errors.
Keywords:
CNC, 5-axis machining, NURBS curve interpolator, Tool center point control, Tool orientation vectors키워드:
컴퓨터 수치제어, 5축 가공, NURBS 곡선 보간기, 공구선단점 제어, 공구방향벡터1. 서론
기존의 동시 5축 가공 방식에서는 CAD/CAM 프로그램을 이용하여 3차원 형상을 정의하고 공구경로를 생성한 뒤, 후처리기(Post Processor)를 통해 CNC 운동축의 모션을 기계좌표계의 이송량과 회전각으로 표현하는 것이 일반적이었다. 근래에는 공작물좌표계에서 공구선단점의 직선 이송과 공구의 자세각으로 NC 데이터를 입력하는 TCP (Tool Center Point) 제어 방식을 주로 사용한다. 이 방법의 NC 데이터는 기계 구조(Configuration)에 무관하게 사용될 수 있다는 장점을 갖는다. NC 데이터는 기본적으로 3차원 형상을 좀 더 유사하게 근사하기 위하여 이론적으로는 NC 블록의 분할 수를 최대화하는 것이 바람직하다. 그러나 실제적으로 근사에 따른 기하학적 형상오차와 공구축 방향오차가 수반되는 등의 문제가 발생할 수 있다.
이러한 문제점을 해결하기 위하여 기존의 연구에서 정밀한 CL 데이터 생성과 포스트 프로세싱,1,2 이송속도 조정,3,4 NC 데이터 수정을 통한 가공 최적화5,6 등의 알고리즘이 제시되었다. 5축 NURBS (Non-Uniform Rational B-Spline) 곡선 보간기도 상기의 문제점을 해결할 수 있는 방법인데, 두 개의 NURBS 곡선을 이용하여 곡선의 위치를 공구위치점(CL Position)과 공구축 자세로 표현하는 방식이 제시된 바 있다.7-9 이 방식은 공구축 자세 벡터를 두 개의 NURBS 곡선으로 처리하기 때문에 자유도가 높아 보이지만 또 다른 NURBS 곡선 정보를 부가적으로 요구하며, 대부분 회전축 각도를 입력하는 방식을 사용한다. CAM에는 CAD 데이터를 기반으로 추출되는 CL 데이터가 기본적으로 벡터 형태이기 때문에 부가적인 파싱(Parsing) 과정과 명령어 처리 프로세스가 요구된다. 이 외에도 이 방식을 이용하여 CAM의 CL 데이터를 Fanuc의 5축 NURBS 곡선 보간 G 코드로 변환시키는 연구가 수행되었다.10 5축 머시닝센터는 3축의 직선 이송축과 더불어 2개의 회전 운동축을 갖추고 있기 때문에 3축 장비에 비하여 공구의 효율적인 움직임이 가능하기에 앞으로 이에 관련된 연구개발이 활발할 것으로 예상된다.
5축 NURBS 보간기를 포함하여 이와 유사한 5축 전용 곡선 보간 기능을 갖춘 CNC는 Fanuc과 Siemens, Heidenhain의 제품을 꼽을 수 있다. Fanuc은 NURBS의 조정점과 함께 두 개의 회전각을 입력하여 처리하는 방법을 사용하고 있다.11 Siemens는 두 개의 스플라인 곡선을 이용하여 하나의 스플라인은 공구의 하단점을, 나머지 스플라인은 공구의 상단점을 가리키도록 입력하여 공구위치점과 공구축 벡터를 설정하는 방식을 사용하고 있다.12 Heidenhain은 공구위치와 회전축 경로를 수식으로 직접 입력하는 방식을 사용하고 있다.13 그 외 다른 대부분의 업체들은 현재까지 3축 곡선 보간만을 지원하고 있다.
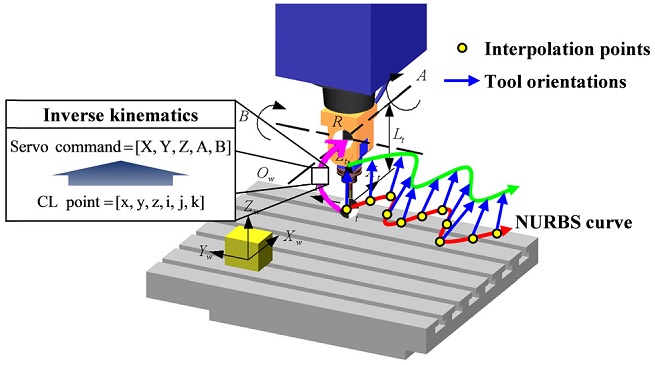
본 논문에서는 새로운 방식의 동시 5축 실시간 NURBS 곡선 보간기를 제시하며, 그 개략도를 Fig. 1에 도시하였다. 제시된 보간기는 CAD/CAM에서 설계한 곡선과 곡면들을 직선 분할화(Discretization)하는 과정을 거치지 않고 직접 해석하여 보간하는 것이 가능하기 때문에 가공에 필요한 대용량의 NC 데이터를 획기적으로 줄일 수 있고, 곡선과 곡면의 분할 근사 과정에서 발생되는 기하학적 형상오차를 최소화하여 가공정밀도를 높일 수 있으며, 보간기 수준에서 균일하고 연속적인 이송속도 출력을 얻을 수 있으므로 기존의 보간 방식보다 고품위 가공이 가능하다. 본 논문에서 제시된 보간기를 PC기반 개방형 5축 CNC 시스템에 구현하여 그 성능을 기존 보간 방식과 비교 평가하였다.
2. 제시된 5축 NURBS 곡선 보간기
2.1 3차원 NURBS 곡선의 계산
NURBS 곡선은 매개변수 형식을 사용하여 표현되며, NURBS의 기본이 되는 B-스플라인(B-Spline)은 단순한 스플라인과는 달리 해당 곡선 상에 놓일 필요가 없는 조정점들에 의해 정의된다. B-스플라인은 아래 식(1)과 같이 블렌딩(Blending) 함수 Ni,k(u)에 의해 표현된다.14
| (1) |
여기서 Pi는 조정점, n은 (조정점의 개수 - 1), Ni,k는 해당 블렌딩 함수, k는 블렌딩 함수의 차수(Degree)를 나타낸다. 그리고 i번째 블렌딩 함수 Ni,k(u)는 다음과 같이 재귀적으로 계산된다.
| (2) |
| (3) |
여기서 ui는 블렌딩 함수의 구성에 필요한 매듭(Knot)을 의미한다. B-스플라인 곡선은 볼록포 특성(Convex-Hull Property)과 정규화 특성(Normalizing Property)을 가진다. B-스플라인을 정규화시키면 그 블렌딩 함수는 아래의 식을 만족하게 된다.
| (4) |
그리고 매듭 U = [u0,...,um]는 다음과 같은 조건식을 만족해야 한다.
| (5) |
| (6) |
B-스플라인 곡선은 생성되는 매듭의 개수와 매듭들의 구성 방식이 균일한지 그리고 주기적인지의 여부에 따라 몇 가지 형식으로 분류된다. NURBS는 B-스플라인을 구성하는 매듭들의 간격이 균일하지 않다는 의미를 갖는다. 곡선의 모양을 제어하기 위해서 불규칙 매듭 벡터를 사용하는 경우는 실제적으로 드물지만, 불규칙 매듭 벡터는 주로 두 가지 목적으로 사용된다. 즉, 곡선의 형상을 형성할 때 주어진 시점과 종점을 지날 필요가 있을 경우와 B-스플라인 곡선이 갖는 부드러움을 포기하고 조정점들 사이의 뾰족한 부분이나 각진 모서리를 표현하는 경우에 사용된다.
곡선의 부드러움을 나타내는 수학적 연속성(Continuity)은 두 개의 구간 곡선(Curve Segment)끼리 만나는 연결부에서의 연결 상태에 의해 구분된다. B-스플라인의 연결부는 매듭의 구성에 따라 쉽게 구분할 수 있으며, 오더(Order) k인 곡선은 연결부에서 C(k-2)의 연속성을 갖는다. 이 때 매듭 값이 한 번 중복될 때마다 연속성이 1차씩 감소한다. 따라서 곡선의 중간을 모나게 혹은 뾰족하게 만들려면 그 부분의 매듭 값을 원하는 만큼 중복시키면 된다. 아래 식(7)은 가중치 Wi가 반영된 유리(Rational) B-스플라인 곡선식을 나타내며, 항상 Wi ≥ 0의 조건을 갖는다.
| (7) |
조정점을 동차 좌표계(Homogeneous Coordinate)로 표현할 경우(xi·W, yi·W, zi·W, W)의 형태로 표시할 수 있고 곡선의 설계에 있어서 가중치를 부여한 개념으로서 형상의 자유도를 한 단계 높일 수 있다.
2.2 공구자세의 계산
본 논문에서는 하나의 NURBS 곡선을 기반으로 공구위치 좌표와 축방향 벡터를 직접 입력하여 쉽게 공구축을 운용할 수 있는 방법을 제시한다. 기본적으로, 제시하는 5축 NURBS 곡선 보간 방법은 기본 3축 보간 알고리즘에 자유롭게 공구축을 기울일 수 있도록 하여 보간기에 더 많은 자유도를 부여하는 방식이다.
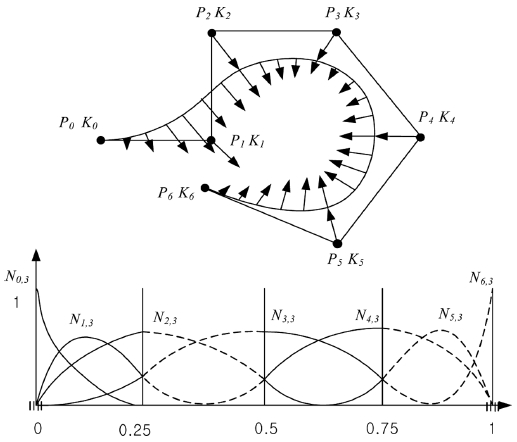
NURBS는 사용자가 입력한 조정점 사이를 지나는 부드러운 자유곡선을 생성해낸다. 곡선의 매개변수 u가 변화되며 곡선을 따라 공구가 이동될 때, 보간점이 각 조정점에 근접하는 만큼 해당 조정점이 곡선에 미치는 영향력이 커지게 된다. 따라서 사용자는 보통 조정점의 위치를 개별적으로 조정하여 NURBS가 생성하는 자유곡선의 형상을 조절한다. 마찬가지로, 본 논문에서는 공구자세의 조정 방법으로, 공구경로의 각 조정점과 함께 짝을 이룰 NURBS 곡선의 공구축 중간 자세벡터를 지정함으로써 공구경로 진행 방향의 매개변수 u에 따라 공구자세를 변화시키는 방법을 제시한다. 이것의 개념도는 Fig. 2와 같다.
즉, 제시된 방법에서는 NURBS 곡선의 각 조정점에서 B-스플라인의 조정점의 좌표와 함께 취하고 싶은 공구축 중간 자세벡터 Ki를 입력할 수 있으며, 식(8)을 이용하여 입력된 각 공구축 벡터 Ki 사이의 자세 벡터를 계산하도록 하였다. 이 때 반드시 |Ki| ≥ 0이어야 공구축 자세 벡터를 결정할 수 있다.
| (8) |
식(7)와 식(8)로 표현되는 NURBS 곡선식과 Fig. 2의 NURBS 블렌딩 함수를 고려하면, 실시간으로 변화될 매개변수 u가 NURBS의 각 블렌딩 함수의 특성에 기인하여 공구 좌표와 공구축 벡터에 미치는 영향을 예측할 수 있다. 즉, 각 구간 블렌딩 함수의 영향력이 최대가 되는 곳에서 지정된 조정점과 중간 자세벡터의 국지적 영향력이 최대가 된다. 공구축 중간 자세벡터는 조정점과 달리 공구가 취할 자세만이 중요하므로 입력된 공구축 벡터는 처리 과정에서 정규화(Normalization)하여 사용한다.
식(8)을 사용하면 NURBS 곡선 보간기의 실시간 보간점 연산 시에 공구자세가 함께 계산된다. 따라서, 공구경로를 따라 공구축 자세가 부드럽게 변화되는 결과를 예상할 수 있다. 식(8)의 계산에는 조정점의 개수 와 같은 수의 공구축 자세를 자유롭게 설정할 수 있다.
2.3 공구위치 및 공구자세 NURBS 보간 알고리즘의 통합
전술한 바와 같이 본 연구에서는 공구축 자세 계산을 식(8)로 정의하였으며, 제시된 공구자세 보간을 위한 알고리즘은 식(7)로 표현되는 NURBS 곡선식과 식(8)를 통합하여 식(2)와 식(3)의 블렌딩 함수 Ni,k의 배열값을 재사용할 수 있도록 하였다. 즉, 해당 프로그램은 식(7)로 표현된 곡선의 좌표 계산과 식(8)로 표현되는 공구자세 보간 계산부를 통합하여 불필요한 중복 계산을 줄일 수 있도록 고려되었다.
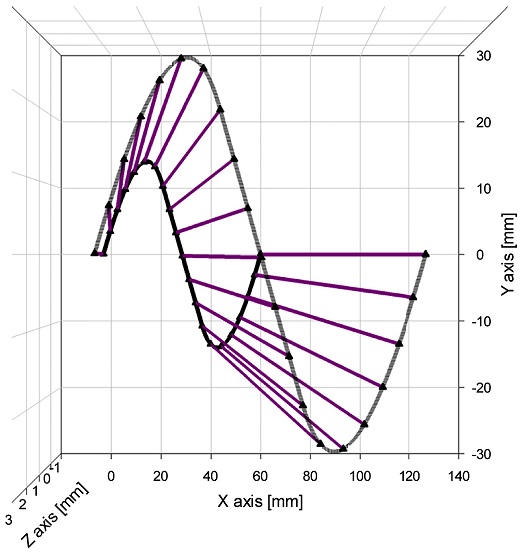
Fig. 3은 통합된 계산 모듈이 실시간 실행되어 보간된 공구위치와 공구축 자세 벡터가 함께 계산된 결과를 보여준다. Fig. 3의 보간에는 5개의 조정점과 5개의 기준 공구축 방향이 입력된 3차(Third-Order) NURBS 곡선이 사용되었다. 그림에 3축 공구위치 보간 결과와 계산된 공구자세를 확인할 수 있도록 보간점과 공구자세 방향 벡터를 1 mm 크기의 벡터 놈(Norm)으로 함께 표시하였다.
보간된 공구위치 좌표와 공구방향 벡터는 CNC 내부에서 실행되는 역기구학 변환을 거쳐 기계좌표계의 이송과 회전량으로 전환되어 해당 서보 드라이브에 지령값으로 전송된다. Table 1은 제시된 5축 NURBS 보간을 위해 본 논문에서 새로이 정의된 G코드 형식을 나타낸다.
3. PC기반 개방형 5축 CNC 시스템에서의 구현 결과
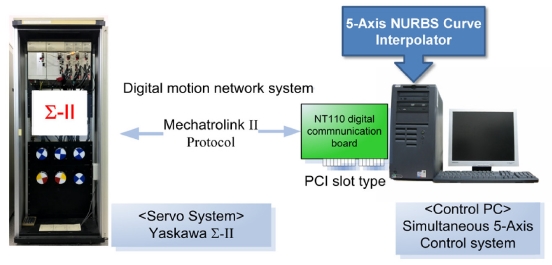
제시된 5축 NURBS 곡선 보간기의 실효성을 평가하기 위하여 Fig. 4와 같은 구조의 PC기반 개방형 5축 제어시스템에 제시된 알고리즘을 구현하였다. 이 시스템은 디지털 서보제어 시스템을 사용하는 Yaskawa사의 MechatroLink-II 모션 네트워크를 채용하고 있다. 제어시스템의 샘플주기는 1 ms이며 시스템의 BLU (Basic Length Unit)는 0.1 μm이고, PCI 인터페이스 방식의 NT-110 통신제어 카드를 통하여 5개의 서보 모터를 동시에 제어할 수 있다. 이 제어시스템을 이용하여 실제 동시 5축 보간 및 제어 실험을 수행하였으며, 제시된 NURBS 보간기의 성능을 TCP 제어 방식의 기존 직선 보간기와 비교, 분석하였다.
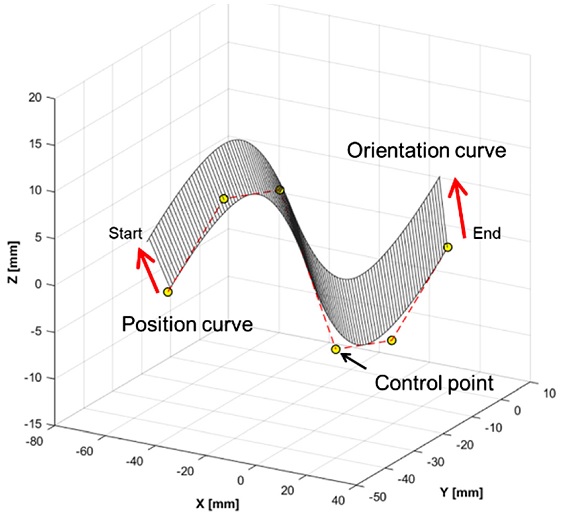
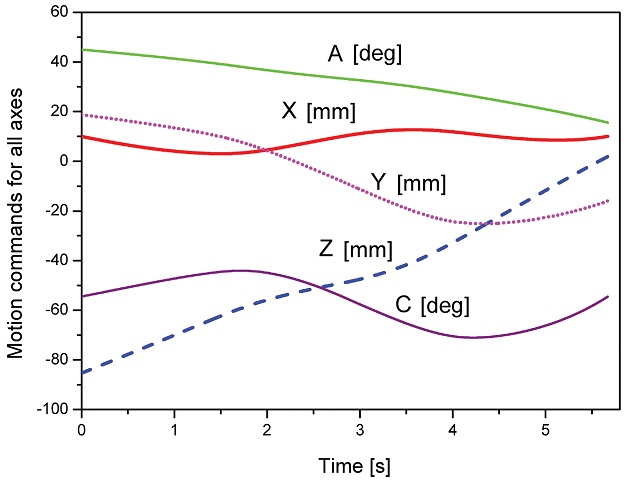
실험에는 Fig. 5와 같이 굴곡이 있는 NURBS 기준 곡선을 사용하였다. 기계가공 영역 내의 공작물 좌표계 즉, 프로그래밍 좌표계에서 정의한 사인 파형(Sine Wave)의 공구경로를 따라 공구위치와 공구자세가 보간되도록 하였으며, 기본적으로 곡선의 시작점에서 공구축 벡터가 약 40° 정도 기울어진 상태에서 시작하여 종점에 이를 때까지 공구를 80° 가까이 세우는 움직임을 주었다. Fig. 5의 두 개 곡선 중 위쪽 곡선은 공구의 축방향 벡터가 움직이는 공구방향 곡선(Orientation Curve)이고 아래쪽 곡선은 공구 접촉점에서의 공구위치 곡선(Position Curve)을 나타낸다. 실험 대상 장비는 A축의 틸팅 축과 C축의 로터리 축(Table-Tilting/Rotating)을 갖는 형태의 수직형 5축 머시닝센터를 가정하였으며, 회전축의 마스터 축과 슬레이브 축 사이의 피봇 길이는 40 mm, 피봇점에서 공작물의 게이지 길이는 50 mm로 설정하였다. Fig. 6에는 역기구학 변환을 통해 계산된 각 축의 운동지령을 나타냈으며, 이는 기계좌표계에서의 기계 움직임에 해당한다.
주어진 공구경로에 대해 TCP 제어를 기반으로 제시된 NURBS 보간 방식과 직선 보간 방식의 이송속도, 윤곽오차, 공구방향오차를 비교하였다. NURBS 보간의 경우 Table 2와 같이 NC 데이터를 정의하여 사용했으며, 직선 보간 NC 데이터는 곡선을 직선으로 분할할 때 곡선 중심점과의 코드 오차(Chordal Deviation) 구속을 1 μm로 설정한 뒤 후처리하여 167개의 블록을 생성하였다.
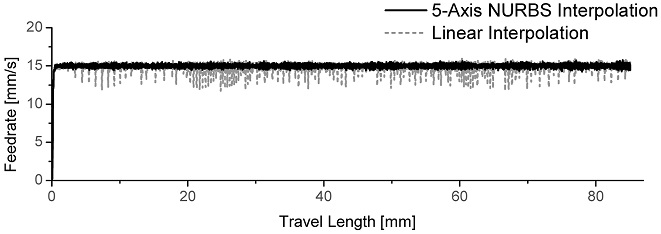
아래 Fig. 7은 이송속도 0.9 m/min인 Fig. 6의 운동지령에 대하여 서보 드라이브로부터 얻어진 엔코더 출력을 기반으로, 정기구학 변환을 통해 공작물 좌표계에서 공구선단점의 이송속도 출력을 계산하여 나타낸 것이다. 직선 보간 방식은 NURBS 보간과 비교하여 이송속도 프로파일이 진동하는 양상을 확인할 수 있다. 이것은 각 직선 구간의 종단점에서 가감속에 의한 영향에 기인한다. Fig. 7의 결과에서 직선 보간 방식의 경우 최대 20% 이상의 이송속도 오차가 발생하였다.
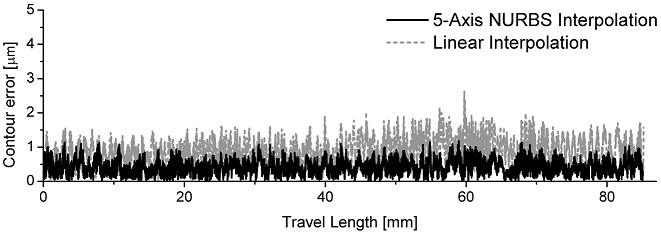
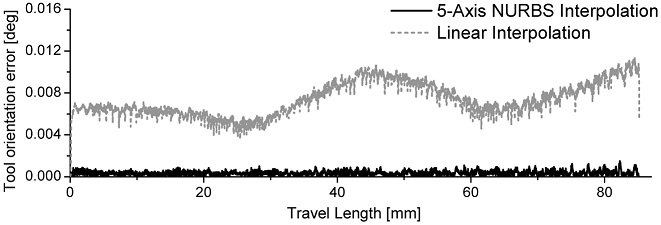
Fig. 8에 상기 두 보간 방식에 대한 윤곽오차를 비교하였는데, 기준 공구경로로부터 벗어난 거리를 계산하여 나타내었다. 이때 0.2 μm의 간격으로 세밀하게 보간된 기준 공구경로 상의 보간점들과 서보 드라이브로부터 출력된 실제 위치를 비교하여, 실제 위치점에서 가장 가까운 거리의 두 보간점을 지나는 직선과 실제 위치점 사이의 거리를 계산하여 윤곽오차를 구하였다. 이 결과에서 직선 보간 방식에 비해 NURBS 보간 방식의 제어시스템 출력이 50% 이상 저감된 윤곽오차의 평균값를 갖는 것을 확인할 수 있다. 또한 Fig. 9의 공구방향오차 비교 결과로부터 NURBS 보간 방식의 경우 공구방향오차가 윤곽오차 결과와 비슷한 양상과 보였으나, 직선 보간 방식의 경우에는 기본적으로 공구방향오차가 크게 발생함을 알 수 있다. 직선 보간 방식은 근사화 과정으로 인한 윤곽오차와 공구방향오차를 수반하며, 직선 분할된 각 구간 내에서 보간점과 공구방향 벡터가 선형적으로만 계산되는 문제점이 존재한다. 반면에 NURBS 보간 방식에서는 보간점과 공구방향 벡터가 항상 기준 곡선상에 위치하며, 공구방향 벡터가 비선형적으로 보간되어질 수 있으므로 직선 보간과 큰 차이를 보이며 공구자세의 정확도를 개선할 수 있다.
4. 결론
본 논문에서는 동시 5축 CNC 가공에서 사용할 수 있는 5축 실시간 NURBS 곡선 보간기를 제시하였다. 제시된 보간 알고리즘을 PC기반 5축 제어 시뮬레이터에 구현하여 5축 NURBS 곡선 보간기에 의한 제어시스템 구동 시 획득한 서보 드라이브의 엔코더 출력을 바탕으로 이송속도, 윤곽추적 및 공구자세의 정확도를 계산하여 제시된 5축 NURBS 곡선 보간기의 성능을 기존 직선 보간 방식과 비교 평가하였다. 실험 결과로부터 기존 직선 보간 방식 대비 제시된 NURBS 보간기의 우수성을 확인할 수 있었다. 제시된 5축 NURBS 곡선 보간을 통해 매끄러운 공구경로 보간과 동시에 공구자세의 자유로운 운용이 가능함으로써 상용 CNC에 적용하여 동시 5축 고속/고정밀 가공을 위한 필수 기능을 확보할 수 있을 것으로 기대된다.
Acknowledgments
본 연구는 산업통상자원부의 “중소형 공작기계용 2계통 제어 CNC와 서보, 스핀들 구동 유닛 국산화 개발” 과제의 지원에 의해 수행되었음.
REFERENCES
- Jun, C. S., Park, S. H., and Jun, Y. T., “Development of CAM System for 5-Axis NC Machining of Sculptured Surfaces,” J. Korean Soc. Precis. Eng., Vol. 10, No. 1, pp. 52-61, 1993.
- Cho, H. D., “A Study on the 5-Axis Precision Machining for Sculptured Surfaces,” Korea Advanced Institute of Science and Technology, 1993.
- Lee, C. S. and Lee, J. P., “Calculating the Feedrate of 5-Axis NC Machining Data for the Constant Cutting Speed at a CL-Point,” Korean Journal of Computational Design and Engineering, Vol. 6, No. 2, pp. 69-77, 2001.
- Oh, J. Y., Hwang, J. D., and Jung, Y. G., “Development of Post-Processor for Constant Feedrate Controlled 5-Axis Machining,” Proc. of KSPE 2008 Spring Conference, pp. 385-386, 2008.
- So, B. S. and Jung, Y. H., “Machining Speed Enhancement for 5-Axis Milling by Step Length Optimization,” Korean Journal of Computational Design and Engineering, Vol. 11, No. 6, pp. 422-428, 2006.
-
Ho, M.-C. and Hwang, Y.-R., “Machine Codes Modification Algorithm for Five-Axis Machining,” Journal of Materials Processing Technology, Vol. 142, No. 2, pp. 452-460, 2003.
[https://doi.org/10.1016/S0924-0136(03)00625-3]

-
Li, Y., Wang, Y., Feng, J., and Yang, J., “The Research of Dual NURBS Curves Interpolation Algorithm for High-Speed Five-Axis Machining,” Proc. of the International Conference on Intelligent Robotics and Applications, pp. 983-992, 2008.
[https://doi.org/10.1007/978-3-540-88518-4_105]

-
Chen, L., “Method of 5-Axis Spline Interpolation and Realization in CNC System,” Proc. of the International Asia Conference on Informatics in Control, Automation and Robotics, pp. 398-401, 2009.
[https://doi.org/10.1109/CAR.2009.8]

-
Wang, Y., Liu, Y., Han, Z., and Shao, Z., “Integration of a 5-Axis Spline Interpolation Controller in an Open CNC System,” Chinese Journal of Aeronautics, Vol. 22, No. 2, pp. 218-224, 2009.
[https://doi.org/10.1016/S1000-9361(08)60090-4]

-
Li, W., Liu, Y., Yamazaki, K., Fujisima, M., and Mori, M., “The Design of a NURBS Pre-Interpolator for Five-Axis Machining,” International Journal of Advanced Manufacturing Technology, Vol. 36, Nos. 9-10, pp. 927-935, 2008.
[https://doi.org/10.1007/s00170-006-0905-8]

- Fanuc Co., “FANUC Series 30i/31i/32i-MODEL A User’s Manual (B-63944EN/03),” 2007.
- Siemens Co., “SINUMERIK 840D/840Di/810D Advanced Programming Guide,” 2002.
- Heidenhain Co., “User's Manual HEIDENHAIN Conversational Format iTNC 530,” 2007.
-
Piegl, L. and Tiller, W., “The NURBS Book,” Springer, 2nd Ed., pp. 47-50, 1995.
[https://doi.org/10.1007/978-3-642-97385-7_2]