[ REGULAR ]

Journal of the Korean Society for Precision Engineering - Vol. 35, No. 2, pp.169-177

ISSN: 1225-9071 (Print) 2287-8769 (Online)

Print publication date 01 Feb 2018

Received 28 Apr 2017 Revised 06 Sep 2017 Accepted 27 Sep 2017

DOI: https://doi.org/10.7736/KSPE.2018.35.2.169

솔라 패널 청소 로봇을 위한 새로운 진공 캐터필러 구조의 구동 시스템 해석

성벽경¹ ; 옥서원¹ ; 김동환²^{, #}

1서울과학기술대학교 대학원 기계설계로봇공학과
2서울과학기술대학교 기계시스템디자인공학과

Analysis of New Vacuum Caterpillar Structure Drive System for Solar Panel Cleaning Robot

Byuck Kyung Seong¹ ; Seo Won Ok¹ ; Dong Hwan Kim²^{, #}

1Department of Mechanical Design and Robot Engineering, Graduate School, Seoul National University of Science and Technology
2Department of Mechanical System Design Engineering, Seoul National University of Science and Technology

Correspondence to: ^#E-mail: dhkim@seoultech.ac.kr, TEL: +82-2-970-6362

Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract

In this paper, we studied a new vacuum caterpillar drive system that can be used for solar panel cleaning robots. The conventional vacuum caterpillar structure has an issue, in that the vacuum hose becomes twisted. As a result, we designed a new vacuum caterpillar structure with no vacuum hose kinks. Also, we verified that no issues concerning flow analysis exist with this new system. We found that this system with the proposed vacuum caterpillar structure has an appropriate performance as a solar panel cleaning robot for practical use.

Keywords:

Vacuum, Caterpillar system, Solar panel, Flow analysis

키워드:

진공, 캐터필러 시스템, 솔라 패널, 유동해석

1. 서론

솔라 패널은 태양광발전의 효율을 높이기 위하여 약 40도의 경사로 설치된다. 따라서 이 솔라 패널을 청소하기 위해서는 로봇이 40도의 경사면에서도 미끄러지지 않아야 한다. 이를 만족시키기 위하여 솔라 패널 청소 로봇은 Wall-Climbing 로봇의 구조를 참고, 활용하게 된다.^1-4

벽에서 미끄러지지 않기 위하여 많이 선택하는 방식은 진공을 통한 방식이며,^5-8 구동 방식은 바퀴 구동, 링크 구동 등 여러 방식이 있다. 본 논문에서는 여러 방식들 중 진공 캐터필러 구동 시스템을 주목하였다.⁹ 기존의 Wall-Climbing 로봇은 크기가 크고 무거우며 속도가 느리다는 문제점을 가지고 있었으나, 진공 캐터필러 구동시스템은 캐터필러 구조 속에 흡착시스템과 이동시스템을 모두 갖추어 이러한 문제점을 개선하였다.⁹

그러나 이 진공 캐터필러 구동 시스템 또한 문제점들을 가지고 있다. 본 논문에서는 그러한 문제점들 중, 캐터필러의 회전에 따라 진공 패드와 진공 펌프를 연결하여주는 진공 호스 또한 회전함으로 인하여 생기는 문제점에 대하여 주목하였다. 로터리 조인트를 사용하여도, 캐터필러의 타원형 구조 상 진공 호스는 일정한 길이를 유지하는 것이 아닌, 늘었다 줄었다를 반복하게 되고, 이 과정에서 호스의 꼬임, 접힘 등으로 인하여 진공 손실이 일어나는 문제이다.

이러한 문제점을 해결하기 위하여 캐터필러 및 진공 패드는 회전하지만, 진공 호스는 회전하지 않는 새로운 진공 캐터필러 구동시스템을 제시할 것이다. 또한 전체 구동 시스템 중 진공 손실이 유발 될 수 있는 경우에 대해 유동 해석을 진행하여, 구동시스템에 대한 검증을 진행할 것이다.

2. 새로운 진공 캐터필러 구조의 개념

2.1 솔라 패널 청소 로봇을 위한 새로운 진공 캐터필러 구조

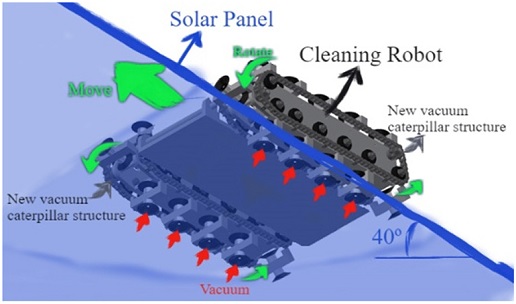
새로운 진공 캐터필러 구조는 약 40도의 경사를 가진 솔라 패널을 청소하는 로봇을 위한 구조이다. Fig. 1에서 보다시피 청소 로봇은 양쪽에 하나씩 총 두 개의 진공 캐터필러를 가지며, 캐터필러는 진공을 이용하여 솔라 패널에서 미끄러지지 않고 이동할 수 있도록 해준다. 로봇의 길이와 폭은 60 cm, 무게는 20 kg, 속도는 13 cm/s이며, 이를 기준으로 패드 및 진공 라인 길이 등을 정할 것이다.

Fig. 1

A cleaning robot for a solar panel with a new vacuum caterpillar structure

2.2 기존 진공 캐터필러 구조와의 차이점

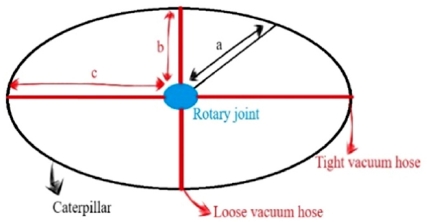
기존의 진공 캐터필러는 진공 패드와 진공 펌프를 진공 호스로 연결하고, 로터리 조인트를 이용하여 진공 호스를 회전시킨다.⁹ 그러나 Fig. 2에서 보다시피 로터리 조인트를 사용하더라도 진공 호스들은 매우 엉키게 되는데, 그 이유는 캐터필러의 타원형 모양 때문이다.

Fig. 2

Tangled vacuum hoses of conventional vacuum caterpillar9

Fig. 3에서 로터리 조인트로부터 캐터필러까지의 간격을 a라고 했을 때, a의 값은 시간 t에 따라 간격의 최소값인 b와 최대값인 c 사이에서 변화하는 값을 가진다.

Fig. 3

Variation of vacuum hose length due to elliptical shape of caterpillar

b ≤ a t ≤ c

(1)

그러나 실제로 로터리 조인트로부터 캐터필러까지 연결시켜주는 진공 호스의 길이를 d라고 하면, d값은 최대 간격인 c값을 고정 값으로 가진다.

이렇게 되면, 진공 호스가 회전함에 따라 간격 a(t)와 진공 호스 길이 d사이의 차이 값, 값은 계속 변화하는 값을 가지게 된다. 즉,

b - d ≤ a t - d ≤ c - d

(2)

이고, 진공 호스의 길이 d값은 c를 고정 값으로 갖기 때문에, 식 (2)의 d에 c를 대입하여 식을 정리해보면,

0 ≤ c - a t ≤ c - b

(3)

가 된다.

따라서 로터리 조인트로부터 캐터필러까지의 간격과 진공 호스 길이 사이의 차는 0에서부터 c-b 값까지 변화하는 값을 가지게 되며, 이에 따라 진공 호스는 접혔다 펴졌다를 반복하고, 이 과정에서 진공 호스가 꼬이고 엉키게 된다.

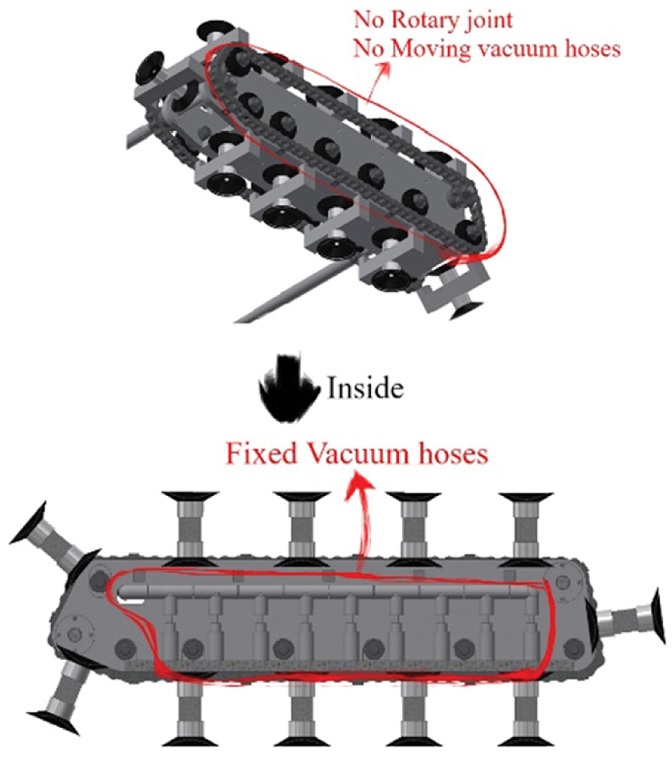
이러한 문제를 해결하기 위하여 새로운 진공 캐터필러는 진공 호스를 고정시켜 사용한다. Fig. 4의 윗부분을 보면, Fig. 2와는 다르게 캐터필러의 옆 부분에 로터리 조인트 및 진공 호스가 전혀 없고, 내부에 진공호스들이 고정되어 있다.

Fig. 4

Fixed vacuum hoses of new vacuum caterpillar structure

그렇기 때문에 새로운 진공 캐터필러는 진공 호스가 타원형의 캐터필러를 따라 회전해서 생기는 진공 호스의 접힘, 꼬임, 엉킴 등으로 인한 진공 손실이 전혀 없다.

3. 새로운 진공 캐터필러 구조의 구동 시스템

3.1 흡착 시스템

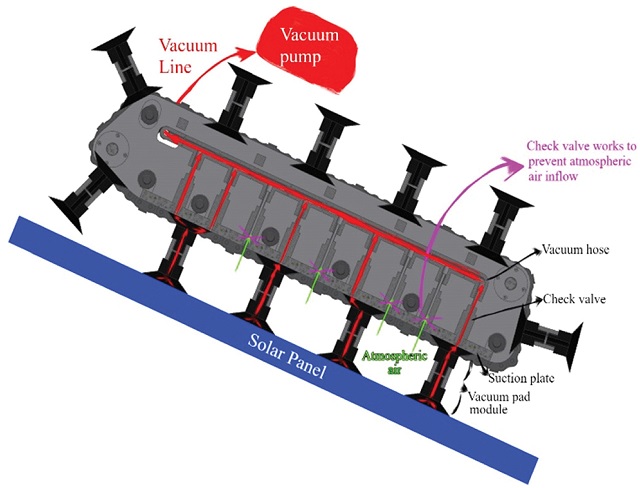
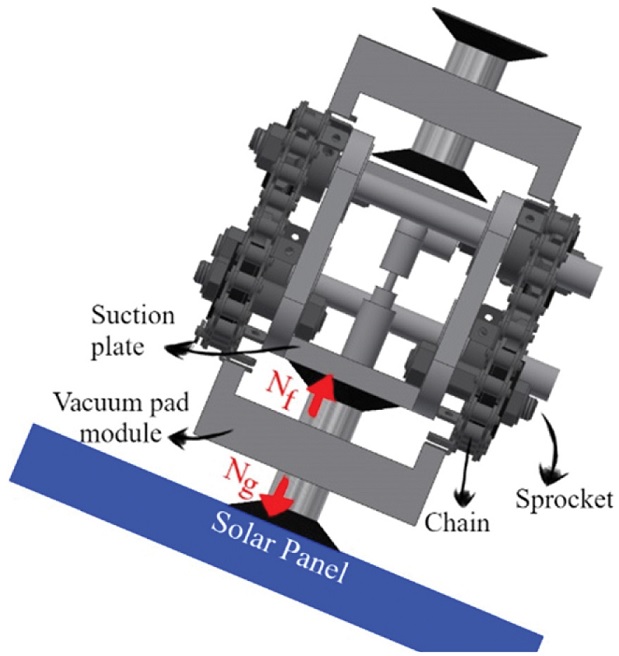
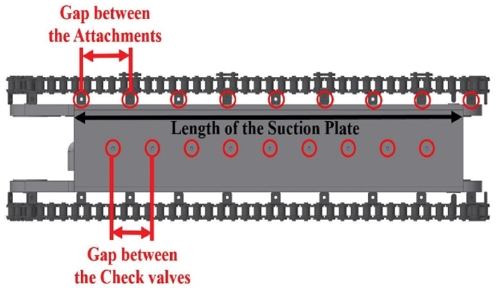
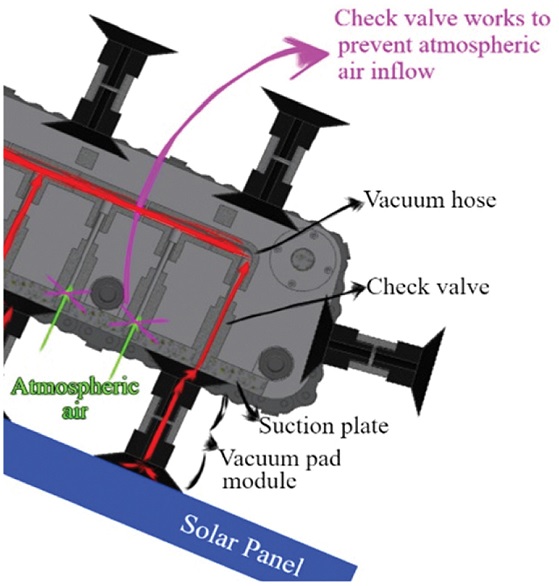
새로운 진공 캐터필러 구조의 흡착시스템은 Fig. 5와 같이 구성되어 있다. 진공 패드 모듈, 흡착 판 및 체크 밸브, 진공 펌프와 진공 호스로 구성되어 있으며, 공기는 솔라 패널과 붙어있는 진공 패드 모듈 안에서 시작하여 흡착 판 및 체크밸브를 지나 진공 호스를 통해 진공 펌프로 이동한다.

Fig. 5

Caterpillar with fixed vacuum line system

먼저 진공 패드 모듈은 유일하게 움직이는 파트이며, 2개의 진공 패드를 사용한다. 각각의 진공 패드는 솔라 패널과 진공 패드 모듈 사이, 진공 패드 모듈과 흡착 판 사이를 연결해주어 진공 손실 없이 공기가 진공 펌프로 이동할 수 있도록 해준다

흡착 판은 진공 패드 모듈에서 들어오는 공기를 안전하게 진공 호스까지 전달해주는 역할을 하는데, 여기에 더해 체크 밸브는 흡착 판의 구멍 중 진공 패드 모듈과 연결되어있지 않아 대기 중에 노출되어 있는 구멍을 막아주는 역할을 한다. 일정 압력 차 이상이 되면 체크밸브가 작동하여 공기를 차단하는데, 진공 호스와 같은 압력을 가지는 진공 패드 모듈과 연결 되어있을 때는 작동하지 않는다.

3.2 이동 시스템

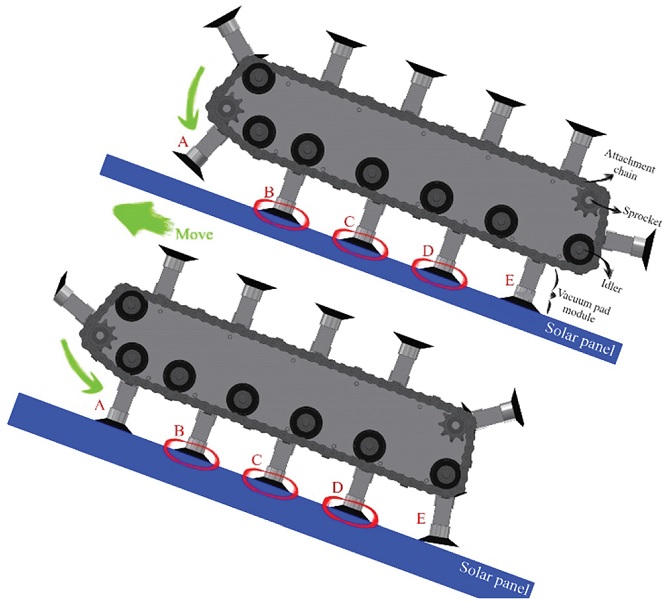
이동시스템은 체인-스프라켓 구동 방식이며, 체인의 텐션 및 지지를 위하여 아이들러를 사용하였다. 진공 패드 모듈은 체인의 어태치먼트와 체결 되어있어 체인이 회전하면 같이 회전한다.

Fig. 6의 그림에서 진공 패드 모듈 B, C, D는 솔라 패널에 흡착되어 고정된 상태인데, 체인-스프라켓을 회전시키게 되면 진공 패드 모듈 B, C, D는 솔라 패널 기준으로 위치 변화가 없지만, 캐터필러를 기준으로 했을 때는 뒤로 물러나게 되므로, 물러난 양만큼 캐터필러는 솔라 패널을 기준으로 앞으로 나아가게 된다.

Fig. 6

Chain-Sprocket moving system

이를 위해서는 솔라 패널과 진공 패드 모듈 사이에서는 미끄러짐이 일어나지 않고, 진공 패드 모듈과 흡착 판 사이에서는 미끄러짐이 일어나야 한다. 이는 마찰력 차이를 통하여 해결할 수 있는데, Fig. 7을 보면 솔라 패널과 진공 패드 모듈 사이에는 힘을 분산시켜줄 수 있는 기구가 없기에 진공 패드에 로봇의 무게가 그대로 실려 수직 항력 값이 매우 높은 반면, 진공 패드 모듈과 흡착 판 사이에는 체인-스프라켓이 힘을 분산시켜 주기 때문에 값은 값에 비해 낮다. 즉,

Fig. 7

Difference in frictional force between two pads due to difference in vertical drag

N f < N g

(4)

이고, 마찰력 공식에 따라

f f = μ N f

(5)

f g = μ N g

(6)

로 나타낼 수 있으며, 수직항력간의 차이가 커 마찰계수 는 큰 차이를 주지 못하기 때문에,

f f < f g

(7)

라고 할 수 있다.

따라서 진공 패드 모듈과 흡착 판 사이에서는 상대적으로 마찰력이 낮아 미끄러짐이 일어나고, 솔라 패널과 진공 패드 모듈 사이에서는 마찰력이 높아 미끄러짐이 일어나지 않을 것이다.

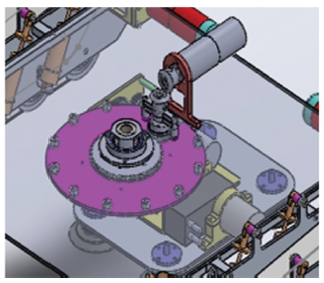
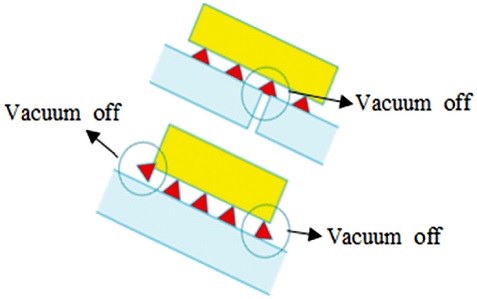
또한, 일반적인 캐터필러의 회전은 두 캐터필러의 속도 차이를 이용하여 회전하나, 진공 패드를 이용한 캐터필러에서는 두 캐터필러의 속도 차이를 이용한 회전 방법을 사용하게 되면, Fig. 8에서 볼 수 있듯이 진공 패드가 솔라 패널 위에서 미끄러져야 회전이 가능해지는 모순된 상황이 생기기 때문에, 캐터필러의 속도 차이를 이용한 회전 방법은 사용할 수 없다. 따라서 본 논문에서 제안하는 진공 캐터필러 구조만으로는 로봇이 회전할 수 없으며, 로봇이 회전하기 위해서는 진공 캐터필러 구조 외에 별도로 Fig. 9와 같은 회전 장치를 로봇 본체의 중앙에 설치하여, 로봇이 이 회전 장치 만으로 회전할 수 있도록 하여야 한다.

Fig. 8

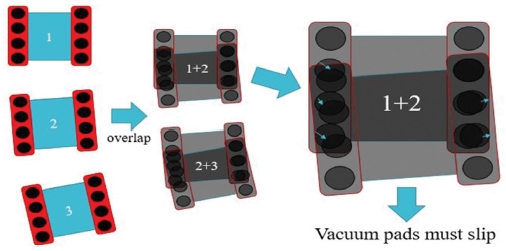
The rotation method using the difference in speed of the caterpillar cannot be used with the vacuum pad caterpillar because the vacuum pad must slide on the solar panel

Fig. 9

Another rotating device added to the robot body part

4. 새로운 진공 캐터필러 구조의 설계

4.1 진공 패드의 선정

진공 패드는 VF30, VF40, VF50, VF75의 네 가지 모델 중에서 필요한 힘 및 길이 조건을 고려하여 모델 및 개수를 선정할 것이다. 각각 모델의 지름 및 수평방향으로 버틸 수 있는 힘은 Table 1과 같다.

Table 1

Vacuum pad model

4.1.1 솔라 패널 조건 및 힘 계산

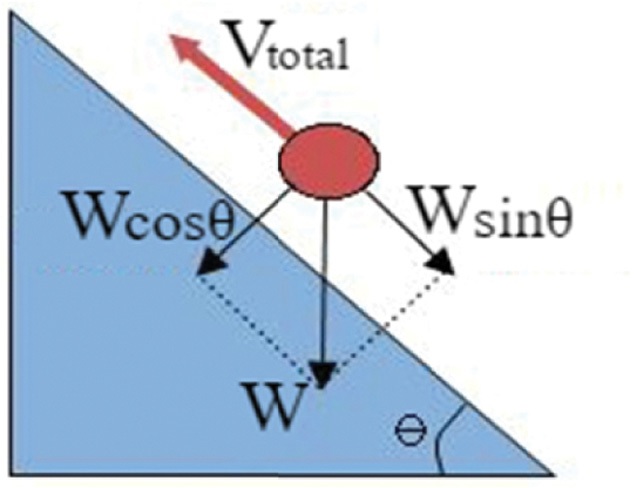
Fig. 10에서, 솔라 패널의 각도는 40이며, 로봇의 질량은 20 kg이다. V_total은 로봇이 미끄러지지 않기 위해 진공 패드에 필요한 총 수평방향 힘으로, V₁을 진공 패드 하나의 수평방향 힘이라 가정하였을 경우

Fig. 10

Force calculation according to solar panel condition

V t o t a l = 2 N p a d V 1

(8)

로 나타낼 수 있다. N_pad는 한쪽 캐터필러에서 솔라 패널에 흡착하는 패드의 개수이며, 캐터필러를 양쪽에 사용하므로, 2를 곱하였다.

이를 토대로 V_total을 구해보면,

W = m g = 20 × 9.81 = 196.2 N

(9)

V t o t a l = W s i n θ = 196.2 s i n 40 ° = 126.1 N

(10)

이고, kgf 단위로 바꾸면, 12.85 kgf가 된다.

이 힘을 토대로 선정 가능한 진공패드별로 각각 몇 개의 패드가 솔라 패널에 붙어야 하는지 계산한 것을 표로 나타내면, Table 2와 같다.

Table 2

Number of vacuum pads to attach to the solar panel according to force calculation

4.1.2 흡착 판 및 기타 길이 조건

본 논문에서 사용하는 흡착 판의 길이는 407 mm이고, 진공 패드 모듈은 어태치먼트 붙이 체인에 연결되는데, 어태치먼트 붙이 체인은 총 88 링크를 사용하며, 어태치먼트 사이의 간격은 1 링크별 어태치먼트 사용 시 12.7 mm에서 2 링크별 사용 시 25.4 mm, 4 링크별 사용 시 50.8 mm로까지 확대하여 사용할 수 있다.

어태치먼트 붙이의 조건에 더해 양쪽에 캐터필러를 사용하기 때문에 바닥에 붙는 진공 패드의 개수는 짝수가 되어야한다는 점과, Fig. 12처럼 틈새를 지나거나 주행 중 진공 패드가 떨어지는 경우를 고려하여 한쪽 캐터필러에서 솔라 패널에 붙는 진공 패드의 개수가 최소 3개 이상은 되어야 안전한 시스템인 것까지 모두 고려하여 힘 조건에 더해 길이조건까지 고려하였을 때 솔라 패널에 붙어야 하는 진공 패드의 개수는 Table 3과 같다.

Fig. 11

Length conditions to consider when placing a vacuum pad

Fig. 12

Vacuum pad loses power during operation

Table 3

Number of vacuum pads to be attached to solar panel considering length condition

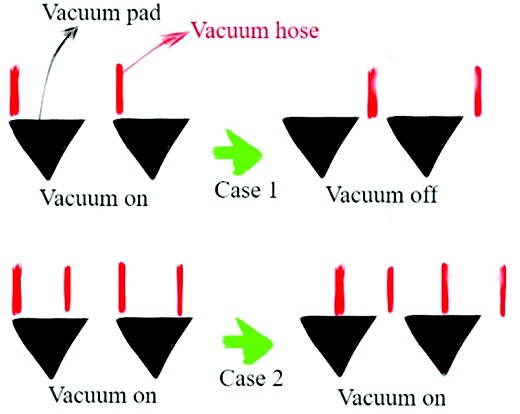
또한, Fig. 11에서 볼 수 있듯이 흡착 판에는 체크 밸브와 연결되는 구멍이 있는데, 구멍 크기는 진공 패드의 구멍 크기와 동일한 지름 3 mm이며, 구멍의 간격은 진공 패드와 진공 호스를 계속 연결시켜줄 수 있는 간격으로 선정하는 것이 중요한데, Fig. 13을 보면 Case 1은 진공 호스의 간격이 진공 패드의 지름보다 큰 경우이며, Case 2는 진공 호스의 간격이 진공 패드의 지름보다 작은 경우이다. Case 1의 경우에는 진공 패드가 이동할 때 진공 호스와 연결이 끊기는 부분이 생기게 되지만, Case 2의 경우에는 연결이 끊이지 않는 것을 볼 수 있다. 따라서 진공 호스 간격은 진공 패드 지름보다 같거나 작아야 하며, 진공 패드의 지름에서 외곽 실링 부분을 양쪽에서 각각 1 mm, 흡착 판 구멍의 크기 3 mm 및 여유분을 뺀 값을 사용한다. 각 진공 패드 모델의 지름에 따라 계산되는 모델 별 흡착 판 구멍 사이의 간격 및 흡착판 길이와 흡착 판 구멍 사이의 간격을 고려하여 한쪽 캐터필러의 흡착 판에 사용되는 체크 밸브의 개수를 표로 나타내면, 다음과 같다.

Fig. 13

Difference when the vacuum hose spacing is larger than the vacuum pad diameter or smaller

Table 4

The number and interval of the check valves used for the suction plate of the one side caterpillar by the vacuum pad model

4.1.3 진공 패드 모델 별 비교에 따른 진공 패드의 선정

힘 계산 및 길이 조건에 따른 계산에 따라 진공 패드 각 모델별로 구한 계산 값들을 비교하여 가장 최적의 진공 패드 및 개수를 결정할 것이다. 비교 값은 진공 패드의 크기 및 개수에 따른 진공 패드의 총 부피 값, 체크 밸브의 개수에 따른 체크 밸브의 총 무게 값을 비교 값으로 선정하였으며, 표로 정리한 것은 다음과 같다.

첫 번째 비교 값인 진공 패드의 총 부피 값은 같은 로봇의 무게를 버티면서도 적은 용량의 진공 펌프를 사용할 수 있기 때문에 그 값이 적을수록 좋은 값이며, 두 번째 비교 값인 체크 밸브의 총 무게 값 또한 로봇의 무게를 절감시켜 주기 때문에 그 값이 적을수록 좋은 값이다.

따라서 이 값들을 활용하여 어느 진공 패드가 가장 적합한 지선정 할 수 있으나, Table 5의 값 자체로는 각 비교 항목 속에서 어느 진공 패드가 가장 적합한 것인지는 알 수 있어도, 두 비교 항목을 종합하였을 때 어느 진공 패드가 가장 적합한 것인지는 알 수 없다. 따라서 Table 5의 두 비교 항목 모두 그 값이 적을수록 좋은 값이라는 것을 활용하여 각 비교 항목의 수치 값들을 각 비교 항목의 최소 수치 값, 즉 부피를 활용한 비교 항목에서는 64 cm³으로, 무게를 활용한 비교 항목에서는 120 g으로 수치 값들을 나누어 적합성 점수로 표현하여, 두 비교 항목을 종합하였을 때 어느 진공 패드가 가장 적합한 것인지를 선정할 수 있도록 하였다.

Table 5

Comparison by vacuum pad model

Table 6

Fitness score of comparison by vacuum pad model

Table 5의 각 비교 항목의 수치 값들을 최소 수치 값들로 나누어 적합성 점수로 표현하였기에, 각 비교 항목 안에서의 진공 패드의 비교뿐만 아니라, 두 비교 항목을 종합하였을 때에도 진공 패드를 비교할 수 있게 되었으며, 앞서 설명하였듯이 두 비교 항목 모두 그 값이 적을수록 좋은 값이기 때문에, 따라서 각 비교 항목의 적합성 점수, 그리고 두 비교 항목의 적합성 점수를 합한 총 적합성 점수 또한 그 값이 적을수록 좋은 값이다. 따라서 진공 패드들 중, VF50이 총 적합성 점수 4점으로 가장 적기 때문에, VF50이 가장 적합하다고 결론지을 수 있다.

그러므로 진공 패드 모델은 지름 53 mm의 VF50 모델을 사용하며, 한쪽 캐터필러에서 솔라 패널에 붙는 진공 패드의 개수는 4개를 사용한다.

4.2 진공 패드가 솔라 패널에 흡착할 때 패드의 휘어짐을 방지하기 위한 흡착 각도 선정

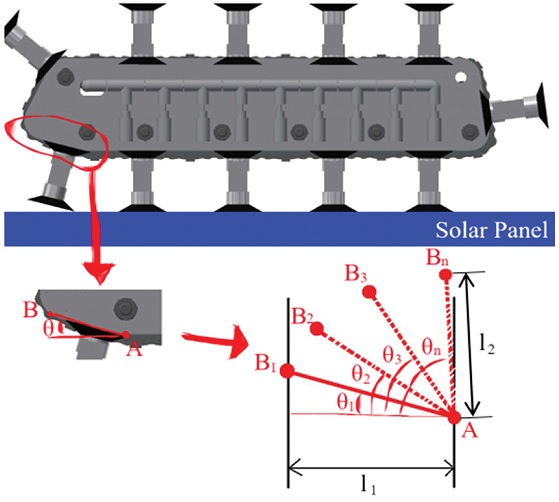
Fig. 14에서 보듯이 진공 패드가 트랙을 따라 회전하면서 솔라 패널에 최초로 닿기 시작할 때 진공 패드의 휘어짐의 문제없이 솔라 패널에 안전하게 흡착하기위해서, 캐터필러 가이드 인입 각도 θ의 결정은 매우 중요하다.

Fig. 14

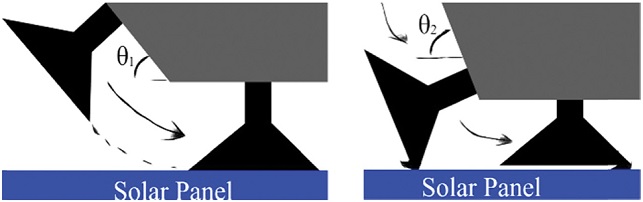
The θ may cause the vacuum pads to come into contact with the smoother on the solar panel or cause no smooth contact

이 θ값은

0 < θ ≤ 90

(11)

의 사이의 값을 가지는 데, θ가 0에 가까우면 가까울수록 안전한 접촉이 가능하나, 경로의 폭 및 길이가 길어지는 문제점이 있다.

따라서 θ 값은 정해진 경로의 폭과 경로의 길이 값의 한계 로부터 정할 수 있는 값 중 0에 가장 가까운 값을 경로의 θ 값으로 결정한다. 즉, Fig. 15에서 정해진 경로의 폭 l₁과 정해진 경로의 길이 l₂를 토대로, θ 값을 θ₁에서 θ_n까지 다양하게 하여 경로를 설정할 수 있으나, 솔라 패널에 안전하게 흡착하기 위해서는 경로의 폭 l₁ 값을 한계 값까지 모두 사용하여 θ 값을 0에 가장 가깝게 해야 한다. 따라서 가장 0에 가까운 값으로 θ 값을 결정하면 θ₁으로 값을 결정할 수 있으며, 이 θ₁ 값은 Fig. 15에서 볼 수 있듯이 l₁과 l₂로 그 값을 구할 수 있는데,

Fig. 15

Design of pass angle to allow pads to come into safe contact

c o s θ 1 = l 1 l 2

(12)

의 수식을 통하여 그 값을 구할 수 있으며, l₁을 46 mm, l₂를 약 47.8 mm로 정하였기 때문에 식(12)를 통하여 구한 결과에 따라 경로의 각도를 약 16도로 결정하였다.

4.3 체크 밸브 선정

체크 밸브는 진공 패드 구멍의 크기인 3 mm와 같은 구멍 크기를 가지는 체크밸브를 선정하였으며, 체크밸브가 작동하여 공기를 차단하는 압력 차는 2.85 kPa이다.

앞서 기술한 방법을 토대로 최종적으로 진공 패드 기반의 캐터필러 구조에 대한 설계 수치들을 Table 7에 정리하였다.

Fig. 16

Check valve connection

Table 7

Design results

5. 진공 캐터필러 구조에 대한 수치적 검증

5.1 검증 방법

진공 캐터필러 구조는 구동 과정 중에 진공 손실이 일어나지 않아야 한다. 따라서 이에 대한 검증이 필요하나, 전체 시스템 모두를 해석하여 검증하는 것은 비효율적이기 때문에 전체 시스템 중 진공 손실이 일어날 가능성이 있는 부분에 대해서 검증을 진행하여 새로운 시스템 및 설계에 대한 검증을 마칠 것이다.

5.2 진공 패드 외곽 실링 두께와 흡착 판 구멍 크기에 다른 진공 손실 검증

5.2.1 해석 개요

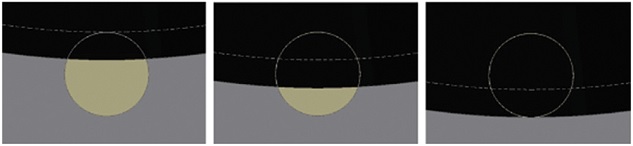
진공 패드의 외곽 실링 부분의 두께는 1 mm인 반면, 흡착 판에 있는 구멍의 지름은 3 mm이다. 따라서 진공 패드가 이동하는 과정에서 이 차이로 인한 진공 손실이 일어날 수 있다. Fig. 17을 보면, 1 mm 실링 부분이 3 mm 지름의 구멍과 만난 후 구멍을 완전히 덮기까지 이동하는 과정에서 3 mm 지름 구멍의 중앙에 1 mm 실링 부분이 위치하게 되어 대기 중의 공기와 진공 패드 내부의 공기가 연결되는 현상이 생기게 된다. 이는 모듈 내의 진공도를 손실 시킬 가능성이 있으며, 유입되는 공기로 인하여 진공 패드 내부의 압력이 진공 호스 내부의 압력 보다 2.85 kPa 이상 커지게 되면, 체크밸브가 작동하게 되어 진공펌프와의 연결이 끊길 수도 있다. 이 경우 흡착이 불가능하여 로봇이 미끄러지는 상황이 발생한다. 따라서 이에 대해 유동 해석을 진행하여 정확한 흡착이 유지되는지를 확인하고자 한다.

Fig. 17

Overview of flow analysis

5.2.2 해석 모델

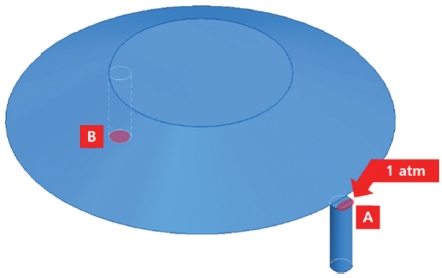
3 mm 지름 구멍의 정 중앙에 1 mm 실링 부분이 위치할 경우에 대해 해석 모델을 세웠으며, 진공 패드와 흡착 판의 구멍 안에 있는 공기를 모델링 하였다. 모델링 된 기체는 25도의 공기이며, 압력은 81.325 kPa이다. Fig. 18에서 A와 B를 제외한 모든 면의 경계 조건은 기체의 출입이 없는 Wall 경계이다. A면은 구멍의 지름과 실링 두께의 차이로 인하여 대기압의 공기가 들어오는 면으로, 기체의 출입이 자유로운 Open 경계로 설정하였으며, 대기압 1 atm의 압력을 받도록 설정하였다. B면은 진공 패드 내부에 있으면서 진공 펌프와 진공 패드를 연결시켜주는 진공 호스 및 체크 밸브와 연결된 면으로, 기체의 출입이 자유로운 Open 경계로 설정하되, 진공 패드 내부 압력인 81.325 kPa과 같은 압력 수준을 갖도록 하였다. 해석 시간은 캐터필러의 규정 속도 13 cm/s에 따라 2 mm를 이동하는데 걸리는 시간인 0.015초로 하였으며, ANSYS Flow Analysis 프로그램을 사용하였다.

Fig. 18

Analysis model of flow analysis

5.2.3 해석 결과

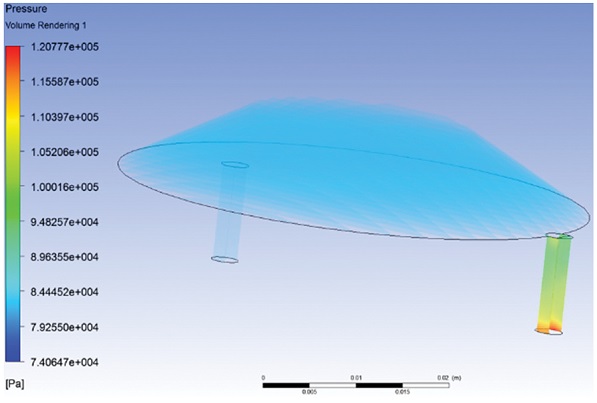
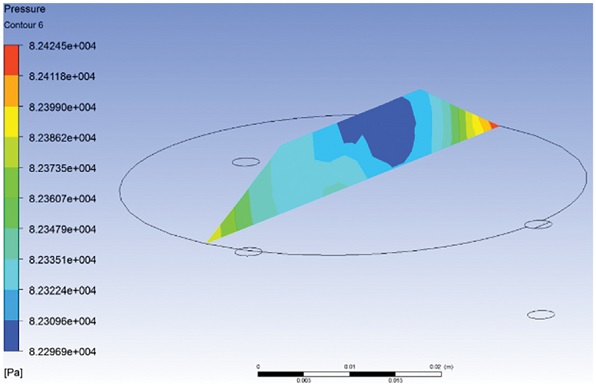
Fig. 19에서 볼 수 있듯이 실링 두께와 구멍 지름의 차이로 인한 대기 중의 공기 유입은, 외부에 노출된 구멍 속 기체에 일부 영향을 줄 수는 있지만, 진공 패드 내부까지는 영향을 주지 않았다.

Fig. 19

Result of flow analysis 1

보다 구체적인 압력 값을 보기 위하여 진공 패드 내부 기체의 단면 압력 값을 본 Fig. 20을 보더라도, 진공 패드 내부의 압력 값은 약 82.3 kPa으로 81.325 kPa에서 0.975 kPa 상승하는데 그쳤다. 따라서 체크 밸브는 작동하지 않으며, 흡착이 유지되어 시스템의 구동에 전혀 영향을 끼치지 않는다는 것을 확인할 수 있었다.

Fig. 20

Cross section result of flow analysis

5.2.4 이동 시간에 대한 Case Study

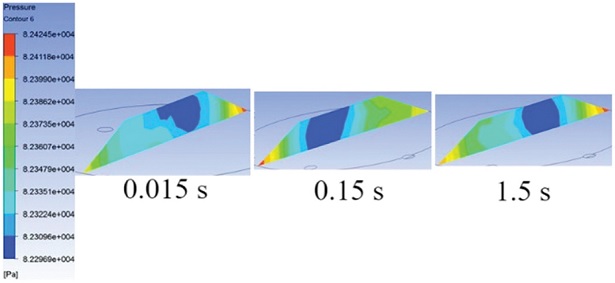
정확한 분석을 위하여 Case Study를 진행하였다. 1 mm의 실링 부분이 구멍을 완전히 덮기까지 캐터필러가 이동하는데 걸리는 시간이 늘어나, 구멍이 노출되는 시간이 길어지는 것이 결과에 영향을 끼치는지 해석 시간을 0.015초, 0.15초, 1.5초로 다르게 두어 결과를 확인하였다.

그 결과 Fig. 21에서 볼 수 있듯이 진공 패드 내부 기체의 단면 압력 분포는 같지 않지만, 그 평균값은 Table 8에서 볼 수 있듯이 차이가 없다. 따라서 구멍이 노출되는 시간이 압력 값에 주는 영향은 없음을 알 수 있었다.

Fig. 21

Cross section result of case study of travelling time

Fig. 22

Result of case study of suction plate hole diameter variations on A and B

Table 8

Case study of travelling time

Table 9

Case study of suction plate hole diameter A

5.2.5 흡착 판의 구멍 지름에 대한 Case Study

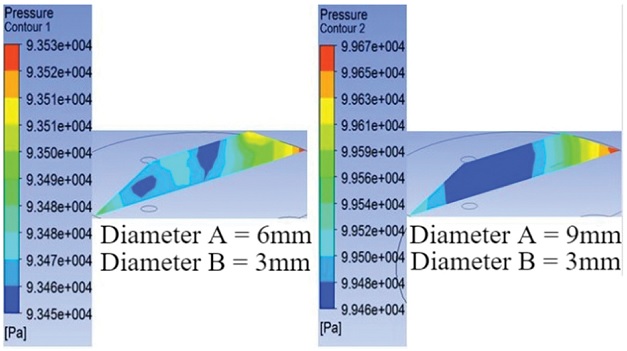
흡착 판의 구멍, 즉 Fig. 18에서 A면 및 B면의 구멍 지름을 조절하여 해석한 후 압력 값에 변화가 있는지 확인하였다. 먼저 B면의 구멍 지름은 고정시킨 채, A면의 구멍 지름만 6 mm, 9 mm로 늘려 해석하였으며, 두 번째로 A면과 B면 구멍 모두 지름을 6 mm, 9 mm로 늘려 해석하였다. 첫 번째 경우는 대기 중의 공기가 들어오는 양만 늘린 형태이며, 두 번째 경우는 들어오는 양과 진공 펌프와 연결되어 나가는 양 두 가지 모두를 늘린 경우이다.

그 결과, 대기 중의 공기가 들어오는 양만 늘린 경우에는 구멍의 지름이 늘어남에 따라 압력 값 또한 증가함을 볼 수 있었다. 지름을 6 mm로만 늘려도 체크밸브가 닫히는 수준을 뛰어 넘었으며, 9 mm의 경우에는 대기압과 비슷한 수준을 보였다.

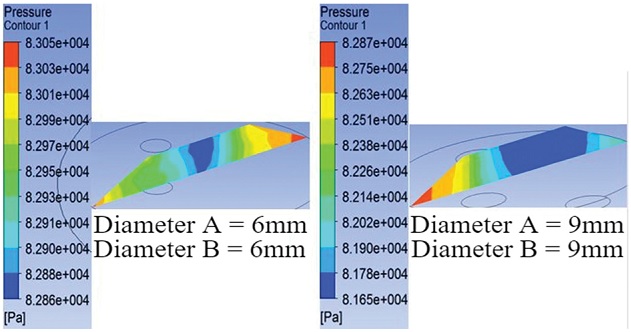
반면, 들어오는 양과 나가는 양 모두 늘린 경우에는 Fig. 23 및 Table 10에서 볼 수 있듯이 압력 차가 비교적 일정하게 유지됨을 볼 수 있었다.

Fig. 23

Result of case study of increased suction plate hole diameter B

Table 10

Case study of suction plate hole diameter A with B

즉, 5.2 해석에서 중요한 부분은 공기가 들어오는 양과 나가는 양의 비율이며, 비율만 잘 조절한다면 구멍의 지름을 크게 늘려도 상관이 없다는 것을 확인할 수 있었다.

5.3 해석 결과에 따른 설계 결과에 대한 검증

진공 캐터필러 구동 시스템 중에서 진공 손실이 일어날 가능성이 있는 부분에 대해 해석 및 두 가지 Case Study를 한 결과, 진공 손실은 없는 것으로 검증되었다. 즉 본 논문에서 제시한 새로운 진공 캐터필러 시스템은 문제가 없으며, 또한 4장에서 선정한 설계 값들도 문제가 없다고 결론지을 수 있다.

6. 결론

본 연구에서는 기존의 진공 캐터필러 구조에서 발생하는 캐터필러의 회전에 따른 진공 호스의 꼬임 또는 접힘 문제를 해결하기 위하여 새로운 유형의 메커니즘을 제안하였다. 이러한 문제점을 해결하기 위하여 별도의 진공라인을 구성하는 매니폴더 구조를 제안하여 캐터필러 및 진공 패드가 회전하더라도 진공 호스는 고정되어 있을 수 있는 구조가 가능함을 확인하였으며, 진공 패드, 경로, 흡착 판 등에 대하여 수치적 설계 또한 행하였다. 그리고 이 구조 및 설계 수치들에 대한 검증을 위하여 진공 캐터필러 내부적으로 진공 손실이 생길 수 있는 부분에 대하여 유동 해석을 진행하였으며, 그에 따른 결과 및 Case Study를 통한 결과에 대한 분석을 통하여 이 진공 캐터필러 구조에는 진공 손실 등 심각한 내부적인 문제가 없다는 것을 알 수 있었다.

따라서 본 논문에서 제시한 새로운 진공 캐터필러 구동시스템을 통하여 기존의 진공 캐터필러 구조가 가지고 있던 문제점을 해결하였다. 따라서 기존의 진공 캐터필러 구조를 사용하는 솔라 패널 청소로봇, Wall-Climbing 로봇 등에 이 새로운 진공 캐터필러 구조를 활용한다면, 기존 진공 캐터필러 구조의 장점은 유지하면서도 보다 유연한 운동이 가능함으로 진공방식의 로봇 메커니즘의 확장성을 기대할 수 있다.

NOMENCLATURE


t :	Time
f :	Frictional force
μ :	Friction factor
N :	Normal force
W :	Weight
m :	Mass
g :	Acceleration of gravity

Acknowledgments

본 연구는 중소기업청 “민관공동투자기술개발사업(S2248211)”으로 수행된 연구결과이고 또한 산업통상자원부·한국산업기술진흥원의 “산업융합·연계형 로봇창의인재양성사업(N0001126)”으로 수행된 연구결과임.

REFERENCES

Nishi, A., “Development of Wall-Climbing Robots,” Computers & Electrical Engineering, Vol. 22, No. 2, pp. 123-149, 1996. [https://doi.org/10.1016/0045-7906(95)00034-8]
De Fazio, T. L., “Wall-Climbing Robot,” US Patent, 6793026 B1, 2004.
Kang, B. G., “Wall Climbing Robot,” Universityof Southern Queensland Faculty of Engineering and Surveying, pp. 1-111, 2007.
Kim, H., Seo, K.-C., Kim, J.-W., and Kim, H.-S., “Design of Tracked Wheel Mechanism for Wall Climbing Robot,” Proc. of KSPE Autumn Conference, pp. 215-216, 2010.
Mahajan, R. G. and Patil, S. M., “Development of Wall Climbing Robot for Cleaning Application,” International Journal of Emerging Technology and Advanced Engineering, pp. 658-662, 2013.
Yano, T., Suwa, T., Murakami, M., and Yamamoto, T., “Development of a Semi Self-Contained Wall Climbing Robot with Scanning Type Suction Cups,” Proc. of the International Conference on Intelligent Robots and Systems, pp. 900-905, 1997.
Bahr, B., Li, Y., and Najafi, M., “Design and Suction Cup Analysis of a Wall Climbing Robot,” Computers & Electrical Engineering, Vol. 22, No. 3, pp. 193-209, 1996. [https://doi.org/10.1016/0045-7906(95)00039-9]
Yoshida, Y. and Ma, S., “Design of a Wall-Climbing Robot with Passive Suction Cups,” Proc. of the International Conference on Robotics and Biomimetics, pp. 1513-1518, 2010. [https://doi.org/10.1109/ROBIO.2010.5723554]
Kim, H., Kim, D., Yang, H., Lee, K., Seo, K., et al., “A Wall Climbing Robot with Vacuum Caterpillar Wheel System Operated by Mechanical Valve,” Proc. of the 9th International Conference on Climbing and Walking Robots, pp. 28-33, 2006.

Model	Diameter (mm)	Lifting force (kg) -Parallel (-20 kPa)
VF30	32	1.12
VF40	42	1.53
VF50	53	2.44
VF75	77	6.12

Model	Total vacuum pad volume used in the robot (cm²)	Total check valve weight used in robot (g)
VF30	64	400
VF40	153.6	260
VF50	160	180
VF75	240	120

Model	Fitness score of total vacuum pad volume used in the robot	Fitness score of total check valve weight used in robot	Total fitness score
VF30	1	3.333	4.333
VF40	2.4	2.166	4.566
VF50	2.5	1.5	4
VF75	3.75	1	4.75

Number of vacuum pads adsorbed to solar panel	4
Diameter of vacuum pad	53 mm (VF50)
Absorption angle of vacuum pad	16^o
Diameter of suction plate holes	3 mm
The interval between the suction plate holes	41 mm
Number of check valves used in one caterpillar	9

Diameters of A (mm)	3	6	9
Diameters of B (mm)	3	3	3
Pressure (kPa)	82.3	93.5	99.6