Investigation of Penetration Depth and Efficiency of Applied Heat Flux in a Directed Energy Deposition Process with Feeding of Ti-6Al-4V Wires
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Wire feeding type directed energy deposition (DED) process is able to produce metal parts with high density at high deposition rate. However, the parts are subjected to high residual stresses and distortion due to its large heat input. In order to simulate the thermal stress, a proper heat input parameter is required. The goal of this paper is to investigate the efficiency and penetration depth of the applied heat flux in the DED process. The estimation method for the penetration depth and efficiency of applied heat flux is proposed using the thermal finite element analyses (FEAs). A finite element model is developed according to the cross sectional profile of the actual deposited beads. A top-hat volumetric heat flux is adopted to simulate the transient thermal phenomenon of the laser based wire feeding type DED process. The estimated heat affected zone (HAZ) from the FEAs is compared with the experimental results in order to estimate the proper efficiency and penetration depth of the laser beam for each condition of DED process.
Keywords:
Penetration depth, Efficiency, Ti-6Al-4V wire feeding, Applied heat flux키워드:
침투 깊이, 효율, Ti-6Al-4V 와이어 공급, 적용 열원1. Introduction
Additive manufacturing using directed energy deposition (DED) through the joining methodology of cladding or welding can be used to produce fully dense part.1 The DED process can be performed by either powder or wire feeding. In the wire feeding DED process, the feed wire is melted by laser and deposited onto the substrate under an inert gas shielding environment. Compared with powder feeding, wire feeding type DED process is an environmental friendly and cost effective process that involves high deposition rate and low material wastage.2,3 Besides, wire is preferred for aerospace components because it has a higher purity and is less susceptible to contamination during handling.4
The major challenge in the wire feeding type DED is that it produces parts that have low dimensional accuracy, poor surface finish, high residual stresses and relatively large distortions due to the excessive heat input and deposition rate.5 The weld bead geometry such as width of welded zone heat affected zone (HAZ) are related to the laser power, welding speed and focused position.6 The correct representation of the keyhole of the heat input is one of the important aspects of the simulation.7 In order to investigate the thermal stress using simulation, proper heat input parameters such as beam profile, efficiency and penetration depth are required.
The modelling of heat flux is critical for the estimation of weld pool and HAZ dimensions.8 Past researches have adopted Gaussian heat flux model to represent the heat flux of laser in selective laser melting and laser cladding.7,9,10 Due to energy loss, Tsirkas et al. considered that the absorbed energy as 70% of the laser power and utilized a Gaussian distribution of heat flux with a conical keyhole.7 Instead of using efficiency, Li et al. and Robert et al. applied the laser energy absorptivity of the powder, A, to the Gaussian heat flux.9,10 They applied absorptivity of laser irradiation with a wavelength 1.06 m for pure titanium powder as 0.77.10 Frenk et al. experimentally investigated the powder feed rate on global absorptivity for the laser cladding process for Stellite 6 powder on mild steel using a specially designed cladding calorimeter.11 At the same powder feed rate, the process with slower laser scanning rate has a higher global absorptivity.11
Some researchers have applied a mixed mode of Gaussian and doughnut distribution to represent their top-hat heat intensity profile of laser based on their experimental measurement.12,13 The top-hat power density distribution is preferred for wire feeding type cladding process.2 Li et al. showed that the volumetric heat flux model predicted better surface heat flux in their modelling of laser melting of ceramic materials.12 They applied absorption length of 345 m based on the Beer-Lambert’s law as the penetration depth of laser energy in their volumetric heat flux model.12 These heat flux models are not considering the efficiency of energy conversion from the laser to heat. Therefore, the influence of process parameters such as travel speed and wire feed rate on the applied heat flux is not considered and may result to inaccurate estimation of weld pool and HAZ.
In this study, the efficiency and penetration depth of the laser beam in the DED process is estimated using thermal finite element analyses (FEAs). The methodology for the estimation is proposed. Experiments are carried out using different laser power and travel speed. The measured cross-section of heat affected zone is used to evaluate the proper penetration depth and efficiency of the heat flux model. From the result of FEAs, the influence of the efficiency and penetration depth of the laser beam is discussed.
2. Prediction Method of Penetration Depth and Efficiency of Heat Flux
Fig. 1 illustrates the prediction method of penetration depth and efficiency according to the process parameters. Using the actual profile of the deposited bead, proper finite element models according to the process parameters are created. Thermal finite element analyses using different penetration depth and efficiency of applied heat flux are performed in order to estimate the width and depth of HAZ.
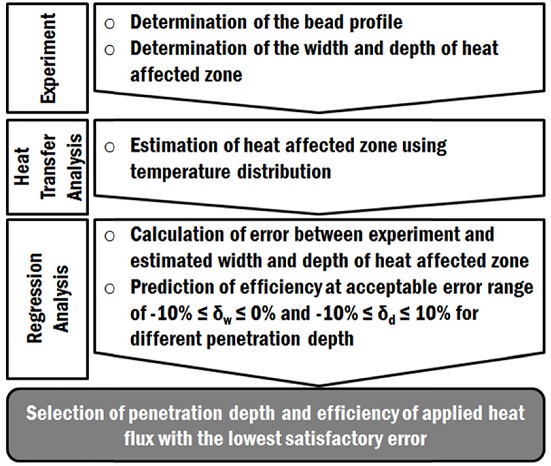
Prediction method of penetration depth and efficiency of applied heat flux according to process parameters
By comparing the estimated and measured HAZ, errors for the width (δw) and depth (δd) are calculated by Eqs. (1) and (2), respectively. In this study, acceptable ranges of errors for the width and depth are set to be -10−0% and -10−10%, respectively. Subsequently, the efficiencies are predicted at error δw = -10%, δw = 0%, δd = -10% and δd = 10% for different penetration depth via linear regression analysis. A common penetration depth that has satisfactory low errors for all process parameters is selected.
Using the selected penetration depth, the efficiency of each process parameter is properly chosen.
| (1) |
| (2) |
3. Experiments and Finite Element Analyses
3.1 Experiments
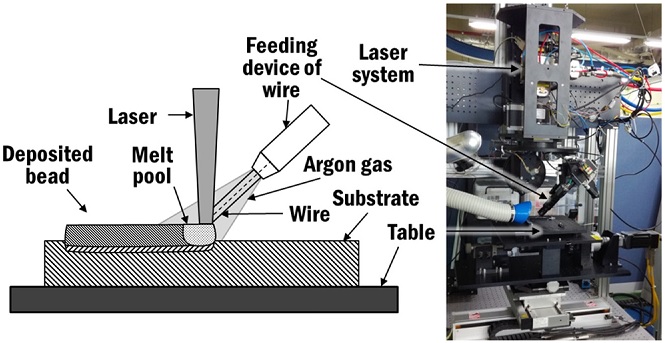
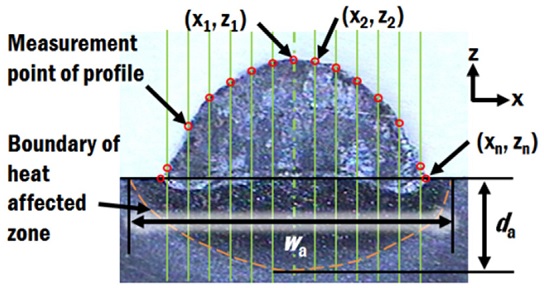
Several straight beads were deposited on a Ti-6Al-4V substrate by front feeding of Ti-6Al-4V wire using a laser DED process, as shown in Fig. 2. In order to obtain the shape of deposited bead, the depositions were made according to different power of laser and travel speed, as tabulated in Table 1. The substrate was clamped to a numerically controlled table at four corners. Cross sectional cuts of the deposited bead were made in order to obtain the bead profile and heat affected zone. The cross sectional views were captured by a video microscope system (ICS, Sometech Inc.). The coordinates of the profile of bead were extracted by measuring the height at fixed interval across the deposited beads, as shown in Fig. 3. The width and depth of heat affected zone were also obtained through measurement from the cross sectional views of the deposited bead.
3.2 Finite Element Analysis
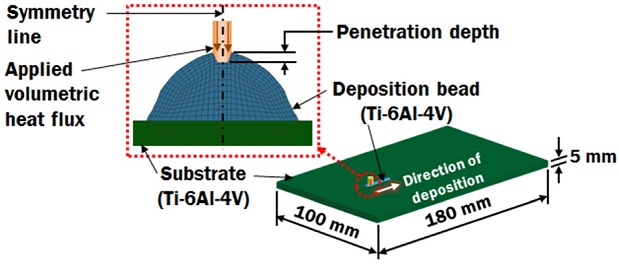
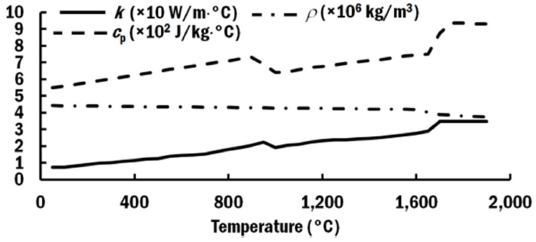
A three-dimensional finite element model containing a 25 mm straight bead on a 180 mm × 100 mm × 5 mm substrate was proposed. The model was created as a symmetry model as shown in Fig. 4. The profile of bead was modeled based on the actual profile of the deposited bead. A three-dimensional non-linear thermal FEA was carried out using Sysweld 12.0. The models were meshed with 8-node solid elements. Fig. 5 shows the temperature dependent material properties of Ti-6Al-4V that had being assigned for the deposited bead and substrate. A volumetric moving heat flux with top hat distribution was applied at the top of the bead. The volumetric heat flux model is given in Eq. (3) which is depending on the effective radius of laser beam as given in Eq. (4). Four corners of the substrate were constrained for translation and rotation in all directions. Convection from the surface of the deposited bead and substrate was considered in the FEA. For this study, different penetration depth and efficiency of laser were applied into the heat flux model as shown in Table 2.
| (3) |
| (4) |
4. Results and Discussions
4.1 Penetration Depth of Applied Heat Flux
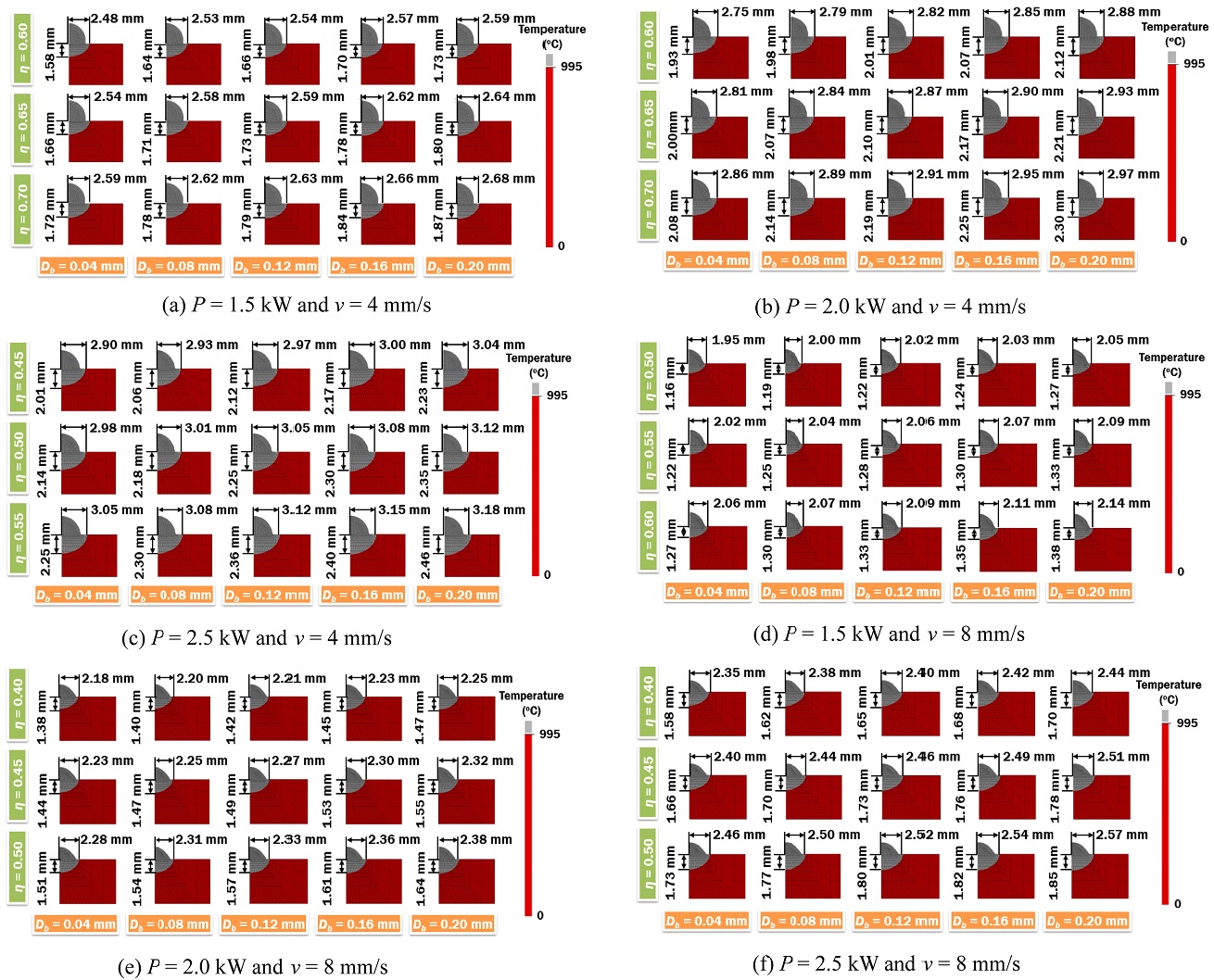
DED experiments at different process conditions were conducted. The deposited beads were sectioned to obtain the width and depth of HAZ as shown in Fig. 6. The microstructure change in heat affected zone (HAZ) is correlated with the peak temperature.16 For this study, the HAZ is estimated by the zone that are heated above the beta transus temperature (Tβ) of 995oC for Ti-6Al-4V.16,17 Fig. 7 shows the estimated width and depth of heat affected zone from the thermal analysis using different penetration depth and efficiency of applied heat flux. At the same process condition, the width and depth of HAZ is increasing with the increasing penetration depth. This is due the fact that the applied heat input is greater with higher penetration depth. The higher heat flux results to the increase in size of HAZ. Therefore, the proper selection of penetration depth for the applied heat flux is important for the proper estimation HAZ using FEAs.
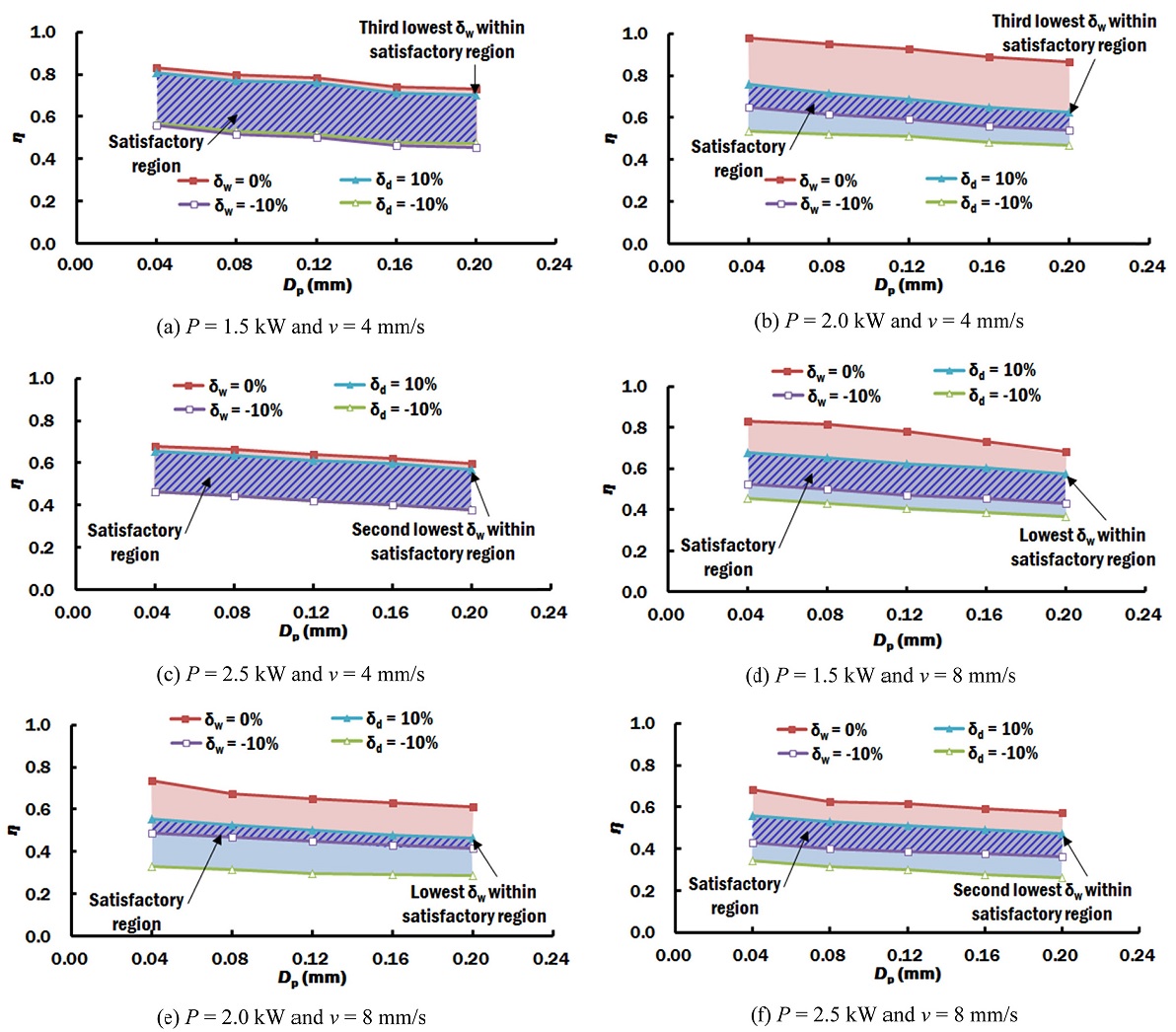
Using the proposed method in Chapter 2, the error between the estimated and measured HAZ has been calculated. The efficiency at error of -10%, 0% and 10% for different penetration depth are predicted via regression analysis, as shown in Fig. 8. The satisfactory region that meets both conditions of acceptable range of -10% ≤ δw ≤ 0% and -10% ≤ δd ≤ 10% is identified. The width of HAZ is more important in this study. Therefore, lowest error in width of HAZ is desired. The error in width of HAZ (δw) is lowest within the satisfactory region when the δd = 10% is located closest to the δw = 0%, as shown in the Fig. 8.
Due to the fact that a laser beam acting on the same material should have the same penetration depth, only one penetration depth should be selected for all the process conditions. In this study, the penetration depth of 0.2 mm gives the best minimal error in width of HAZ within the satisfactory region in most of the test conditions. Thus, the penetration depth of 0.2 mm is selected.
4.2 Efficiencies of Applied Heat Flux
The proper selection of efficiency of applied heat input according to travel speed and laser power is important to ensure that the estimated width of HAZ is accurate. The efficiency of applied heat flux is depending to the process conditions because the heat loss is varying according to the travel speed and temperature gradient between the deposited bead and surrounding.
Using the selected penetration depth of 0.2 mm, the efficiency that is within the satisfactory region for each process condition is selected. For the proper estimation of error, only efficiencies that are used in the FEA are selected. Using the same selection strategy, the efficiency that provides the lowest error in width of HAZ is selected, as listed in Table 3. This is due to the fact that proper estimation of width of HAZ is more appropriate for the DED process using cold wire. A DED process using cold wire produces a shallow peripheral penetration type of fusion zone, as shown in Fig. 6. Therefore, the depth of HAZ is harder to predict properly as compare to the width of HAZ.
From the selected efficiencies in Table 3, it is observed that the efficiency is changing according to the travel speed and power of laser. This dependency of efficiency on the travel speed and power of laser is proper because the width of HAZ is mainly depending on the travel speed and power of laser.6 Thus, the appropriate selection of efficiency for each process condition is related to the accurate estimation of width of HAZ.
4.3 Influence of Power and Travel Speed of the Laser on the Efficiency
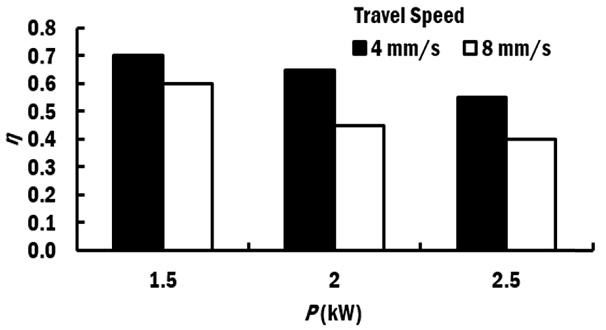
Fig. 9 shows the selected efficiency for different power of laser. It is observed that the higher power of laser has lower efficiency for the same travel speed. The higher power of laser results to higher peak temperature on the bead. The deposited bead becomes wider. Therefore, larger amount of heat loss occurs due to the large temperature gradient between the bead and its surrounding. Subsequently, the efficiency is reduced when the higher power of laser is applied.
Besides, it is observed that the higher travel speed has lower efficiency for the same power of laser. The laser-metal wire interaction time is lower at high travel speed. Therefore, most of the energy is used to rapidly heat the wire before melting of wire can occur. At the same time, the heat is dissipated rapidly at the Ti-6Al-4V substrate via conduction. The input energy is not fully utilized for the melting and deposition of the wire. As a result, a shallower deposition bead is produced at high travel speed. Hence, the deposition efficiency is lower when the travel speed increases for the same input power.
5. Conclusions
In this paper, a novel method has been proposed to estimate the penetration depth and efficiency of applied heat flux in a wire feeding type DED process using FEAs. A three dimensional finite element model with actual profile of the deposited bead has been adopted for the FEAs. The estimation method of the penetration depth and efficiency of applied heat flux has been discussed.
The influence of the penetration depth and efficiency of applied heat flux on the width and depth of HAZ has been examined. It has been revealed that the increase in penetration depth and efficiency produce larger width and depth of HAZ for the same process condition. The error between the estimated and measured HAZ have been investigated. Using linear regression analysis, the satisfactory region has been estimated for each process condition. From these results, a penetration depth of 0.2 mm has been selected within the satisfactory region for this wire feeding type DED process.
The efficiency that has the lowest error in width of HAZ for each process condition has been selected from the FEAs with the selected penetration depth of 0.2 mm. From the results of the selection, it has been shown that the efficiency is depending on the power and travel speed. The efficiency increases when the power of laser and travel speed decrease. The influence of the power and travel speed on the efficiency has been discussed.
In the future, the efficiency should be predicted for different process conditions using regression analysis from these results. In addition, correlation between the deposition bead profile and process condition are required for the creation of proper FEA model without the need to obtain the bead profile from the experiments. In order to verify the validity of the proposed method, additional FEAs should be performed at the predicted efficiency and compared with experimental results.
NOMENCLATURE
| A : | Laser energy absorptivity of the material |
| Dp : | Penetration depth of heat flux |
| E : | Young’s modulus |
| Q : | Heat flux |
| P : | Power of heat flux |
| η : | Efficiency of heat flux |
| wa : | Actual width of heat affected zone |
| we : | Estimated width of heat affected zone |
| da : | Actual depth of heat affected zone |
| de : | Estimated depth of heat affected zone |
| z : | Z-Coordinate of the model |
| ze : | Z-Coordinate at surface of bead |
| zi : | Z-Coordinate at penetration depth |
| r : | Effective radius of laser beam on surface z |
| re : | Effective radius of laser beam on surface z = ze |
| ri : | Effective radius of laser beam on surface z = zi |
| k : | Thermal conductivity |
| v : | Travel speed of table |
| Cp : | Specific heat |
| Tβ : | Beta transus temperature |
| ρ : | Density |
| δd : | Error in depth of heat affected zone |
| δw : | Error in width of heat affected zone |
Acknowledgments
This work was supported by the National Research Council of Science & Technology (NST) grant by the Korea government (MSIT) (No. CRC-15-03-KIMM).
REFERENCES
-
Ahn, D.-G., “Direct Metal Additive Manufacturing Processes and Their Sustainable Applications for Green Technology: A Review,” Int. J. Precis. Eng. Manuf.-Green Tech., Vol. 3, No. 4, pp. 381-395, 2016.
[https://doi.org/10.1007/s40684-016-0048-9]

-
Mok, S. H., Bi, G., Folkes, J., and Pashby I., “Deposition of Ti-6Al-4V Using a High Power Diode Laser and Wire, Part I: Investigation on the Process Characteristics,” Surface and Coatings Technology, Vol. 202, No. 16, pp. 3933-3939, 2008.
[https://doi.org/10.1016/j.surfcoat.2008.02.008]

-
Kim, J.-D. and Peng, Y., “Plunging Method for Nd:YAG Laser Cladding with Wire Feeding,” Optics and Lasers in Engineering, Vol. 33, No. 4, pp. 299-309, 2000.
[https://doi.org/10.1016/S0143-8166(00)00046-4]

-
Brandl, E., Palm, F., Michailov, V., Viehweger, B., and Leyens C., “Mechanical Properties of Additive Manufactured Titanium (Ti-6Al-4V) Blocks Deposited by a Solid-State Laser and Wire,” Materials & Design, Vol. 32, No. 10, pp. 4665-4675, 2011.
[https://doi.org/10.1016/j.matdes.2011.06.062]

-
Ding, D., Pan, Z., Cuiuri, D., and Li, H., “Wire-Feed Additive Manufacturing of Metal Components: Technologies, Developments and Future Interests,” International Journal of Advanced Manufacturing Technology, Vol. 81, Nos. 1-4, pp. 465-481, 2015.
[https://doi.org/10.1007/s00170-015-7077-3]

-
Benyounis, K. Y., Olabi, A. G., and Hashmi, M. S. J., “Effect of Laser Welding Parameters on the Heat Input and Weld-Bead Profile,” Journal of Materials Processing Technology, Vol. 164, pp. 978-985, 2005.
[https://doi.org/10.1016/j.jmatprotec.2005.02.060]

-
Tsirkas, S. A., Papanikos, P., and Kermanidis, T., “Numerical Simulation of the Laser Welding Process in Butt-Joint Specimens,” Journal of Materials Processing Technology, Vol. 134, No. 1, pp. 59-69, 2003.
[https://doi.org/10.1016/S0924-0136(02)00921-4]

-
Mughal, M. P., Fawad, H., and Mufti, R., “Finite Element Prediction of Thermal Stresses and Deformations in Layered Manufacturing of Metallic Parts,” Acta Mechanica, Vol. 183, Nos. 1-2, pp. 61-79, 2006.
[https://doi.org/10.1007/s00707-006-0329-4]

-
Roberts, I. A., Wang, C. J., Esterlein, R., Stanford, M., and Mynors, D. J., “A Three-Dimensional Finite Element Analysis of the Temperature Field During Laser Melting of Metal Powders in Additive Layer Manufacturing,” International Journal of Machine Tools and Manufacture,” Vol. 49, No. 12, pp. 916-923, 2009.
[https://doi.org/10.1016/j.ijmachtools.2009.07.004]

-
Li, Y. and Gu, D., “Thermal Behavior During Selective Laser Melting of Commercially Pure Titanium Powder: Numerical Simulation and Experimental Study,” Additive Manufacturing, Vol. 1, pp. 99-109, 2014.
[https://doi.org/10.1016/j.addma.2014.09.001]

-
Frenk, A., Vandyoussefi, M., Wagniere, J.-D., Kurz, W., and Zryd, A., “Analysis of the Laser-Cladding Process for Stellite on Steel,” Metallurgical and Materials Transactions B, Vol. 28, No. 3, pp. 501-508, 1997.
[https://doi.org/10.1007/s11663-997-0117-0]

-
Li, J. F., Li., L., and Stott, F. H., “Comparison of Volumetric and Surface Heating Sources in the Modeling of Laser Melting of Ceramic Materials,” International Journal of Heat and Mass Transfer, Vol. 47, No. 6, pp. 1159-1174, 2004.
[https://doi.org/10.1016/j.ijheatmasstransfer.2003.10.002]

-
Pinkerton, A. J. and Li, L., “Modelling the Geometry of a Moving Laser Melt Pool and Deposition Track via Energy and Mass Balances,” Journal of Physics D: Applied Physics, Vol. 37, No. 14, pp. 1885-1895, 2004.
[https://doi.org/10.1088/0022-3727/37/14/003]

-
Romano, J., Ladani, L., and Sadowski, M., “Thermal Modeling of Laser Based Additive Manufacturing Processes within Common Materials,” Procedia Manufacturing, Vol. 1, pp. 238-250, 2015.
[https://doi.org/10.1016/j.promfg.2015.09.012]

- ESI Group, “SYSWELD Visual-Weld 12.0,” 2016.
-
Brandl, E., Michailov, V., Viehweger, B., and Leyens, C., “Deposition of Ti-6Al-4V Using Laser and Wire, Part I: Microstructural Properties of Single Beads,” Surface and Coatings Technology, Vol. 206, No. 6, pp. 1120-1129, 2011.
[https://doi.org/10.1016/j.surfcoat.2011.07.095]

- Donachie, M. J., “Titanium: A Technical Guide,” ASM International, 2nd Ed., p. 67, 2000.