방위각 추정용 3축 마그네토미터를 위한 타원체 피팅 방식 보정 기법 비교
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Three-axis magnetometers are widely used in various fields requiring azimuth information. However, accuracy of azimuth estimation based on magnetometer signals may be degraded because of errors such as offset, scale factor, non-orthogonality, hard-iron distortion, and soft-iron distortion. Recently, several ellipsoid-fitting calibration techniques have been proposed and have received much attention. However, comparative analysis of calibration accuracies between these techniques has not been conducted. This study compared and analyzed performance of four ellipsoid-fitting magnetometer calibration techniques such as the linear least square method, the two-step algorithm, and two different nonlinear least square methods. Our analysis and experimental results reveal superiority of the linear least square method compared to other methods in terms of calibration accuracy as well as ease of use in practice.
Keywords:
Magnetometer calibration, Ellipsoid-fitting, Azimuth, Hard-iron distortion, Soft-iron distortion키워드:
마그네토미터 보정, 타원체 피팅, 방위각, 강성 왜곡, 약성 왜곡1. 서론
최근 MEMS (Micro Electro Mechanical System) 기술이 발전함에 따라 크기가 작고 저가의 IMMU (Inertial and Magnetic Measurement Unit)가 차량, 무인 잠수정, 수중 로봇, 스마트폰 등 3차원 자세 정보를 필요로 하는 다양한 분야에서 사용되고 있다.1-5 여기서, IMMU는 3축 가속도계(Accelerometer), 3축 자이로 센서(Gyroscope)와 3축 마그네토미터(Magnetometer)로 구성된 센서모듈로서, 물체의 3차원 자세추정 정확성을 높이기 위해서는 센서 사용 전에 보정(Calibration) 과정이 필요하다. 그 중에서도 방위각(Azimuth) 정보를 제공하는 마그네토미터는 다른 두 센서에 비해 주변환경의 영향을 크게 받기 때문에 반드시 보정 과정을 거쳐야 한다.6-8
3축 마그네토미터는 지구자기장의 크기와 방향을 측정하여 방위각 정보를 얻기 위해 사용된다. 하지만 센서 제조 과정에서 생기는 오차와 주변환경에 의해 발생하는 오차로 인하여 신호 왜곡이 발생할 수 있다. 여기서, 센서 자체가 가지는 오차는 민감도(Scale Factor), 비직교성(Non-Orthogonality)과 오프셋(Offset)이 있고, 주변환경에 의해 발생하는 오차는 강성 왜곡(Hard-Iron Distortion)과 약성 왜곡(Soft-Iron Distortion)이 있다. 이러한 오차들로 인해 보정되지 않은 마그네토미터를 이용하여 방위각 추정시 정확성이 크게 저하될 수 있다.9
마그네토미터를 통한 방위각 추정 정확성을 높이기 위하여 다양한 보정 기법들이 연구되었다. 가장 기본적인 보정 기법으로는 스윙 방식(Swing Method)이 있다. 스윙 방식은 센서의 각 축을 중심으로 회전시켜 얻은 데이터를 통해 오프셋과 강성 왜곡에 해당하는 오차를 보정하는 기법으로 민감도, 비직교성과 약성 왜곡으로 인한 오차는 보정할 수 없다. 또한, 센서를 회전시키는 과정에서 회전축과 센서축을 완벽하게 일치시켜야 한다는 단점이 있다.10
스윙 방식과 달리 (1) 오프셋과 강성 왜곡 외에도 다양한 오차 보정이 가능하며, (2) 일정회전축에 의한 데이터가 아닌 임의 회전에 의한 데이터가 사용가능한 타원체 피팅(Ellipsoid-Fitting) 방식이 연구되어 왔다.11-17 타원체 피팅 방식의 기본 원리는 다음과 같다. 이론적으로 3축 마그네토미터를 임의로 회전시키며 일정한 지구자기장을 측정하여 공간상에 출력하면 구 형태를 형성해야 한다. 하지만 마그네토미터 오차 요인들로 인하여 편향된 타원체 형태를 형성한다. 이에 따라 측정 데이터를 타원체 방정식으로 표현할 수 있으며, 이때 타원체 방정식의 계수는 마그네토미터 오차 파라미터(Parameter)들로 이루어진 함수이다. 즉, 3차원상에서 회전하여 계측된 3축 마그네토미터 측정값을 이용하여 타원체 방정식 계수 및 오차 파라미터를 결정할 수 있다.
최근 들어 다음과 같은 타원체 피팅 방식에 기반한 다양한 방법들이 발표되었다: 타원체 방정식의 대각화 분해(Eigen-Decomposition)를 통한 선형 최소자승법(Least Square)을 사용하는 방법(이하 Method A),11 비선형(Nonlinear) 최소자승법을 적용한 방법(이하 Method B),12 타원체 방정식의 계수를 구하는 단계와 계수로부터 파라미터를 구하는 단계를 명시적으로 구분하여 적용한 2단계 알고리즘(이하 Method C),13 그리고 Method B와 보정 모델과 방정식구성에 차이를 보이는 또다른 비선형 최소자승법 적용방법 (이하 Method D).14 이외에도 최대가능도법(Maximum Likelihood Estimation),15 격차 진화 알고리즘(Differential Evolution Algorithm)16 그리고 확장 칼만 필터(Extended Kalman Filter)17 등을 사용한 기법들이 연구되었다.
위에 기술한 바와 같이 다양한 타원체 피팅 방식 보정기법이 발표되었으나, 현재까지 이들 기법에 대한 성능비교와 장단점 분석은 이루어 지지 않았다. 본 논문에서는 타원체 피팅을 기반으로 하는 보정 기법 Method A-D의 방위각 추정성능을 비교하고자 한다. 이때, Method A와 B에서는 마그네토미터 오차들이 모두 고려된 반면, Method C와 D에서는 약성 왜곡이 고려되지 않았다. 따라서 Method C와 D에서 약성 왜곡 미고려에 따른 영향을 제거하기 위하여 Method C와 D에 Method B의 오차모델을 적용한 Method C′과 D′을 추가로 비교한다. 본 논문은 이러한 비교를 통해 각 방법의 장단점과 특징을 분석하고, 보정성능의 우열을 가늠해 보고자 한다.
2. 마그네토미터 보정 기법
Table 1은 각 마그네토미터 보정 기법의 특성을 나타낸 표이다. Method C와 D에서는 약성 왜곡뿐 아니라 강성 왜곡도 고려되지 않았다. 하지만, 강성 왜곡은 오프셋과 동일한 형태의 오차로 센서 각 축의 출력값을 증감시키므로, Method C와 D에서도 강성 왜곡이 보정된다고 할 수 있겠다.
2.1 선형 최소자승법(Method A)
3축 마그네토미터를 회전시키며 데이터를 수집하게 되면 식(1)과 같이 모델링 할 수 있다.
| (1) |
여기서, Bx, By, Bz는 3축 마그네토미터 측정값이다. 최소자승법을 이용하여 식(1)의 파라미터를 구할 경우 모든 파라미터가 0이 나오는 경우가 발생할 수 있다. 이를 피하기 위해 식(1)을 표준화하는 과정이 필요하여 Rosin이 제안한 j = 1이라는 조건을 적용한 후 다음과 같이 파라미터를 구한다.18
| (2) |
| (3) |
| (4) |
| (5) |
타원체 방정식은 아래와 같이 행렬식으로 나타낼 수 있다.
| (6) |
| (7) |
대칭행렬 A를 대각화하는 행렬을 P(행렬 A의 고유벡터들을 열벡터로 하는 행렬)라 하고 대각화 분해를 통해 B = PB' 을 만족하도록 식(6)을 변환하면 식(8)과 같다.
| (8) |
여기서, λ1, λ2, λ3는 행렬 A의 고유값이고 행렬 D = P-1AP이며, sP = [g′ h′ k′] 이다. 식(8)을 이용하여 오프셋과 민감도 오차에 해당하는 파라미터를 구할 수 있으며, 다음과 같다.
| (9) |
| (10) |
| (11) |
| (12) |
여기서 Braw, Bcal는 각각 3축 마그네토미터의 보정 전후의 데이터이다. Method A의 자세한 내용은 참고문헌11에서 확인할 수 있다.
2.2 비선형 최소자승법 I (Method B)
3축 마그네토미터의 오차 모델링은 다음과 같이 나타낼 수 있다.
| (13) |
여기서, B는 센서 측정값, H는 지구자기장, CSf, CNo, CSi는 각각 민감도, 비직교성, 약성 왜곡의 모델링이다. b는 오프셋과 강성 왜곡으로 인한 오차 성분이다. 식(13)을 전개하면 다음과 같이 나타낼 수 있다.
| (14) |
식(14)를 제곱하여 정리하면 다음과 같다.
| (15) |
d11, d12, d13, d21, d22, d23, d31, d32, d33, bx, by, bz를 구하기 위해서는 12개 이상의 데이터가 필요하며, 비선형 방정식을 풀기 위해서는 Matlab®의 fsolve 기능을 사용하였다.
2.3 2단계 알고리즘(Method C)
3축 마그네토미터의 오차 모델링은 다음과 같이 나타낼 수 있다.
| (16) |
| (17) |
여기서, B는 센서 측정값, H는 지구자기장, Q는 민감도와 비직교성 해당되는 모델링이다. b는 오프셋과 강성 왜곡으로 인한 오차 성분이다. 지구자기장의 크기를 계산하기 위해 식(16)을 제곱하면 다음과 같이 나타낼 수 있다.
| (18) |
식(18)을 정리하면 다음과 같이 나타낼 수 있다.
| (19) |
1단계는 식(19)를 통해 중간 파라미터 M1-M10을 추정한다. 여기서, M1-M10은 식(20)과 같이 Q와 b로 이루어진 함수이다.
| (20) |
2단계는 식(20)을 통해 Q와 b를 추정한다. Method C의 자세한 내용은 참고문헌13에서 확인할 수 있다.
2.4 비선형 최소자승법 II (Method D)
3축 마그네토미터의 오차 모델링은 다음과 같이 나타낼 수 있다.
| (21) |
| (22) |
여기서, B는 센서 측정값, H는 지구자기장, K는 민감도와 비직교성 해당되는 모델링이다. b는 오프셋과 강성 왜곡으로 인한 오차 성분이다. 지구자기장의 크기를 계산하기 위해 식(21)을 제곱하면 다음과 같이 나타낼 수 있다.
| (23) |
| (24) |
참고문헌14에서는 으로 설정하였는데 이럴 경우 비선형 방정식을 푸는데 있어 센서 측정값과 관계없이 파라미터가 0일 경우 항상 만족하기 때문에 식(24)와 같이 변경하였다. 이에 따라 보정 데이터에 따른 오차의 합은 다음과 같다.
| (25) |
비선형 최소자승법을 사용하여 E의 값이 최소가 될 때 K와 b에 해당하는 파라미터를 추정할 수 있다. Method D의 자세한 내용은 참고문헌14에서 확인할 수 있다.
3. 실험
검증 실험에는 GY-87 센서모듈과 광학식 모션 캡쳐 시스템(Optitrack Flex 13)을 사용하였다. 여기서 GY-87 센서모듈은 6축 관성센서(MPU6050)와 3축 마그네토미터(HMC5883L)로 구성된 센서모듈이며, Arduino Uno R3에 연결하여 센서 측정값을 PC로 전송하였다. 광학식 모션 캡쳐 시스템은 방위각 추정 성능을 비교하기 위한 참조값(Reference)을 얻기 위해 사용되었다. 센서 측정값과 참조값을 동일 좌표계에서 얻기 위해 육면체 플라스틱 상자에 GY-87 센서모듈, Arduino Uno R3와 마커를 부착하여 실험하였다 (Fig. 1 참조). 또한, 광학식 모션 캡쳐 시스템과 GY-87 센서모듈의 계측 주기는 100 Hz로 동일하게 설정하였다.
보정 성능 비교를 위해 무작위로 회전시켜 얻은 보정 데이터와 2가지 자세 실험을 실행하였다. 여기서 보정 데이터는 파라미터를 구하기 위해 사용되며, 2300개의 데이터를 사용하였다. 자세 실험은 구한 파라미터를 사용하여 방위각 추정 성능을 비교하기 위한 실험이다. 또한, 다양한 주변환경에 따른 성능 비교를 위해 보정 및 실험 데이터에 추가적으로 임의의 신호 왜곡을 가하였다.
방위각 추정 성능 비교를 위한 자세 실험은 다음과 같다.
(1) Test 1: 1분동안 센서의 Z축을 중심으로 약 45o씩 회전시킨 후 5초간 정적 상태를 유지하였다.
(2) Test 2: 1분동안 센서를 무작위로 자세를 변경시킨 후 5초간 정적 상태를 유지하는 것을 반복하였다.
추가적인 신호 왜곡을 가하기 위하여 다음과 같이 마그네토미터 오차 파라미터를 임의로 설정하였다.
| (26) |
여기서, C는 민감도, 비직교성과 약성 왜곡에 의한 오차에 해당하는 행렬이며, b는 오프셋과 강성 왜곡에 의한 오차로 단위는 [mGauss]이다. 오프셋과 강성 왜곡만이 존재할 경우와 모든 오차 성분이 존재할 경우의 보정 기법 성능 비교를 위해 보정을 위한 데이터와 자세 실험 데이터에 다음과 같이 추가적인 왜곡을 가하였다.
| (27) |
| (28) |
여기서, Borig는 추가적인 왜곡을 가하기 전의 원래(Original) 보정 및 실험 데이터이다. Bdist.1과 Bdist.2는 보정 및 실험 데이터에 임의의 왜곡을 가한 후(Distorted)로 각각 (1) 오프셋과 강성 왜곡만 왜곡을 가한 경우와 (2) 모든 오차 성분에 왜곡을 가한 경우의 데이터이다. 이에 맞추어, 자세실험 데이터 역시, Bdist.1를 적용한 (즉, b만 가한) Test 1-1과 Test 2-1과 Bdist.2를 적용한 (즉, b와 C를 가한) Test 1-2와 Test 2-2로 구분된다. 보정 기법간 방위각 추정 성능 비교를 위해 평균 제곱근 오차(Root Mean Square Error, RMSE)를 사용하였다.
4. 결과 및 고찰
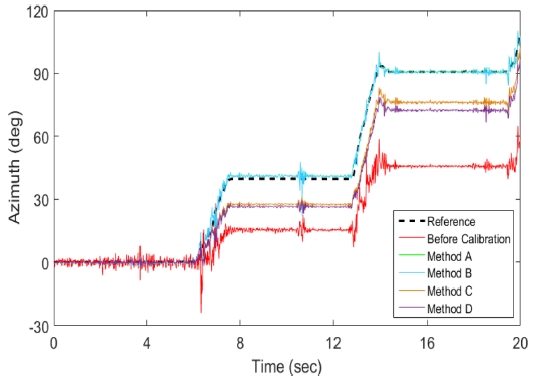
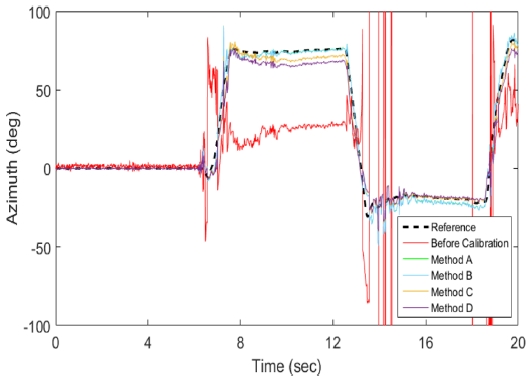
Table 2는 각 실험에 따른 방위각 추정 RMSE 결과이다. 여기서, Method C′과 Method D′은 Method B에서 사용된 오차 모델링을 적용한 후의 결과이다. 또한, Figs. 2와 3은 Method A-D를 사용하였을 때 Test 1-2와 Test 2-2에서의 방위각 추정 결과 중 일부 데이터를 발췌하여 나타낸 그래프이다.
오프셋과 강성 왜곡만이 존재하는 Test 1-1과 Test 2-1에서 결과를 확인해보면, 보정 이전의 데이터를 사용하여 방위각을 추정한 경우 RMSE는 각각 88.61°, 104.09°로 정확성이 매우 저하되었다. Test 1-1에서 Method A를 사용한 경우 방위각 추정 RMSE가 1.11o로 다른 보정 기법들에 비해 성능이 우수하였다. 반면, Method D에서 RMSE가 1.77°로 가장 큰 오차를 보였다. Test 2-1에서는 Method A-D′ 모두 방위각 추정 RMSE가 0.88o 또는 0.89o로 성능 차이를 보이지 않았다.
모든 오차가 존재하는 Test 1-2와 Test 2-2에서도 보정 이전의 데이터를 사용하여 방위각을 추정한 경우 RMSE가 96.34o 이상으로 방위각 추정 성능이 매우 저하되었다. 모든 마그네토미터 오차를 고려한 Method A와 B는 Test 1-2에서는 1.97o, Test 2-2에서는 1.53o 이하의 오차를 보였다. 이에 비해 Method C는 방위각 추정 RMSE가 Test 1-2에서는 7.64o, Test 2-2에서는 4.32o로 이전과 비교하여 오차가 크게 증가하였다. Method C의 경우 오차 모델링 변경 이후에 Test 1-2와 Test 2-2에서 RMSE가 각각 3.62o, 2.27o로 이전과 비교하여 방위각 추정 성능이 향상되었다. 하지만 Method A와 B보다는 여전히 큰 오차를 보였다. Method D는 가장 큰 오차를 보였으며, 오차 모델링 변경 후에도 방위각 추정 성능이 향상되지 않았다. 이는 Method D에서 파라미터를 구하는데 있어 식(25)를 사용하여 발생하는 문제로 판단된다. 식(25)는 데이터마다 생기는 오차의 합으로 이루어져 있어, 이를 통해 파라미터를 구하게 될 경우 각 데이터의 오차는 최소화되지 않을 수 있다. 즉, 각 데이터의 오차는 남아있지만 오차를 더해주는 과정에서 상쇄되어 오차의 합이 최소가 되는 파라미터가 구해질 수 있다.
오프셋과 강성 왜곡만이 존재하는 경우에는 Method A-D′ 모두 방위각 추정 RMSE가 1o 내외로 우수한 성능을 보이면서 방법 간 성능차이는 크지 않았다. 하지만, 모든 오차가 존재하는 경우 Method A와 B가 다른 방법들에 비해 우수한 추정 성능을 보였다. 특히, 전체적으로 Method A가 비교된 6가지 방법 중에서 가장 우수한 성능을 보였다. 또한, 식(26)의 추가적인 왜곡 성분을 약하게 설정하였을 경우에는 전체적으로 방위각 추정 오차가 감소하였다. 그러나 여전히 Method A와 B가 다른 방법들에 비해 우수한 성능을 보였다.
Method A는 Method B-D′와 달리 평면 또는 평면에 가까운 데이터를 사용하여 마그네토미터 오차 파라미터를 추정하는 경우 추정 정확성이 크게 저하된다. 예를 들어, 한 평면내의 측정값들로 제한된 데이터를 사용하여 파라미터를 추정한 경우, Method B는 Test 1-1에서 3.99o, Test 2-1에서 4.74o인 반면, Method A는 Test 1-1에서 12.79o, Test 2-1에서 13.82o의 RMSE를 보였다 –본 실험은 데이터에 따른 추정성능 민감도 확인을 위해 별도로 진행됨. 하지만, 마그네토미터를 3차원 공간상에서 적절히 회전시켜 주면서 계측을 하기만 하면 해결되는 문제이므로, 실제적인 운용에 있어 문제는 없다고 하겠다.
Method A는 우수한 추정성능에 더하여 선형해석과 파라미터수에서 다음과 같은 장점이 있다 (Table 1 참조). Method A를 제외한 나머지는 비선형 방정식을 풀어내야 하므로, Newton법 등과 같이 사용자가 지정하는 초기값에서 반복수정을 거치면 해를 구한다(Iterative Approach). 따라서, 지정된 초기값에 따라 수렴속도와 해에 많은 차이가 발생할 소지가 있다. 반면, Method A는 초기값 지정이 필요없는 선형해석과정을 통해 해가 도출되므로 해석속도는 물론이고, 해의 일관성과 정확성에서 보다 우수하다고 할 수 있다. 또한 보정 파라미터의 개수를 보면 Method B는 12개이고 나머지 방법들은 9개로 동일하지만, 고려되는 오차의 종류를 감안하면 Method A만 모든 오차를 고려하면서도 파라미터 개수가 9개인 것을 확인할 수 있다.
5. 결론
본 논문에서는 타원체 피팅 방식을 기반으로 하는 네 가지 마그네토미터 보정 기법 성능을 비교 분석하였다. 보정 성능 비교를 위해 두 가지 자세 실험에 따른 방위각 추정 성능을 비교하였으며, 다음과 같은 결론을 얻었다.
(1) 마그네토미터를 통해 방위각 추정을 함에 있어, 마그네토미터 자체가 가지는 오차뿐만 아니라 강성 왜곡과 약성 왜곡같이 주변환경에 의해 발생하는 오차도 고려해야 한다.
(2) 모든 실험에서 Method A가 가장 우수한 방위각 추정 성능을 보였다.
(3) 추정성능에 더하여 Method A는 파라미터의 개수가 상대적으로 적으며, 선형적인 특성을 지니기 때문에 다른 보정 기법과는 달리 초기값 설정이 필요하지 않다는 장점을 가지고 있다. 특히, 초기값이 불필요하다는 장점은 마그네토미터를 사용하며 수시로 보정이 필요한 경우, 실제 운용의 편의성 측면에서 매우 중요하다고 판단된다.
Acknowledgments
이 논문은 미래창조과학부 재원으로 한국연구재단 기초연구사업(NRF-2015R1C1A1A02036373)의 지원을 받아 연구되었음.
REFERENCES
-
Kim, Y. and Kim, D. H., “Implementation of a Smartphone Interface for a Personal Mobility System Using a Magnetic Compass Sensor and Wireless Communication,” Journal of Korean Institute of Intelligent Systems, Vol. 25, No. 1, pp. 48-56, 2015.
[https://doi.org/10.5391/JKIIS.2015.25.1.048]

-
Park, Y. S., Choi, W. S., Han, S. I., and Lee. J. M., “Navigation System of UUV Using Multi-Sensor Fusion-Based EKF,” Journal of Institute of Control, Robotics and Systems, Vol. 22, No. 7, pp. 562-569, 2016.
[https://doi.org/10.5302/J.ICROS.2016.15.0213]

-
Hwang, Y. and Choi, S., “Vehicle Orientation Estimation by Using Magnetometer and Inertial Sensors,” Transactions of the Korean Society of Automotive Engineers, Vol. 24, No. 4, pp. 408-415, 2016.
[https://doi.org/10.7467/KSAE.2016.24.4.408]

-
Lee, D. H., Kim, H. W., and Lee, J. M., “Obstacle Recognition and Avoidance of the Bio-Mimetic Underwater Robot Using IR and Compass Sensors,” Journal of Institute of Control, Robotics and Systems, Vol. 18, No. 10, pp. 928-933, 2012.
[https://doi.org/10.5302/J.ICROS.2012.18.10.928]

-
Mangia, A. L., Cortesi, M., Fantozzi, S., Giovanardi, A., Borra, D., et al., “The Use of Immus in a Water Environment: Instrument Validation and Application of 3D Multi-Body Kinematic Analysis in Medicine and Sport,” Sensors, Vol. 17, No. 4, p. 927, 2017.
[https://doi.org/10.3390/s17040927]

-
Guerrero-Castellanos, J. F., Madrigal-Sastre, H., Durand, S., Torres, L., and Munoz-Hernández, G. A., “A Robust Nonlinear Observer for Real-Time Attitude Estimation Using Low-Cost Mems Inertial Sensors,” Sensors, Vol. 13, No. 11, pp. 15138-15158, 2013.
[https://doi.org/10.3390/s131115138]

-
Lee, J. K., “A Parallel Kalman Filter for Estimation of Magnetic Disturbance and Orientation,” Transactions of Korean Society of Mechanical Engineers A, Vol. 40, No. 7, pp. 659-666, 2016.
[https://doi.org/10.3795/KSME-A.2016.40.7.659]

-
Kim, J. T., Kim, M. S., and Hong, J. S., “A Study on the Method for Improving the Localization Accuracy Using the Magnetic Sensors,” J. Korean Soc. Precis. Eng., Vol. 31, No. 2, pp. 133-139, 2014.
[https://doi.org/10.7736/KSPE.2014.31.2.133]

-
Gebre-Egziabher, D., Elkaim, G. H., David Powell, J., and Parkinson, B. W., “Calibration of Strapdown Magnetometers in Magnetic Field Domain,” Journal of Aerospace Engineering, Vol. 19, No. 2, pp. 87-102, 2006.
[https://doi.org/10.1061/(ASCE)0893-1321(2006)19:2(87)]

-
Ghanbarpour Asl, H., Pourtakdoust, S., and Samani, M., “A New Non-Linear Algorithm for Complete Pre-Flight Calibration of Magnetometers in the Geomagnetic Field Domain,” Proc. of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, Vol. 223, No. 6, pp. 729-739, 2009.
[https://doi.org/10.1243/09544100JAERO485]

-
Hwang, J. M. and Kim, J. H., “Development of the Calibration Algorithm of 3 Axis Vector Sensor Using Ellipsoid,” J. Korean Soc. Precis. Eng., Vol. 32, No. 7, pp. 643-651, 2015.
[https://doi.org/10.7736/KSPE.2015.32.7.643]

-
Pang, H., Pan, M., Chen, J., Li, J., Zhang, Q., et al., “Integrated Calibration and Magnetic Disturbance Compensation of Three-Axis Magnetometers,” Measurement, Vol. 93, No. 1, pp. 409-413, 2016.
[https://doi.org/10.1016/j.measurement.2016.06.056]

-
Foster, C. C. and Elkaim, G. H., “Extension of a Two-Step Calibration Methodology to Include Nonorthogonal Sensor Axes,” IEEE Transactions on Aerospace and Electronic Systems, Vol. 44, No. 3, pp. 1070-1078, 2008.
[https://doi.org/10.1109/TAES.2008.4655364]

-
Pang, H., Li, J., Chen, D., Pan, M., Luo, S., et al., “Calibration of Three-Axis Fluxgate Magnetometers with Nonlinear Least Square Method,” Measurement, Vol. 46, No. 4, pp. 1600-1606, 2013.
[https://doi.org/10.1016/j.measurement.2012.11.001]

-
Vasconcelos, J. F., Elkaim, G., Silvestre, C., Oliveira, P., and Cardeira, B., “Geometric Approach to Strapdown Magnetometer Calibration in Sensor Frame,” IEEE Transactions on Aerospace and Electronic Systems, Vol. 47, No. 2, pp. 1293-1306, 2011.
[https://doi.org/10.1109/TAES.2011.5751259]

-
Pang, H., Zhang, Q., Wang, W., Wang, J., Li, J., et al., “Calibration of Three-Axis Magnetometers with Differential Evolution Algorithm,” Journal of Magnetism and Magnetic Materials, Vol. 346, pp. 5-10, 2013.
[https://doi.org/10.1016/j.jmmm.2013.06.051]

-
Kok, M. and Schön, T. B., “Magnetometer Calibration Using Inertial Sensors,” IEEE Sensors Journal, Vol. 16, No. 14, pp. 5679-5689, 2016.
[https://doi.org/10.1109/JSEN.2016.2569160]

-
Rosin, P. L., “A Note on the Least Squares Fitting of Ellipses,” Pattern Recognition Letters, Vol. 14, No. 10, pp. 799-808, 1993.
[https://doi.org/10.1016/0167-8655(93)90062-I]