PZT 구동기를 이용한 미세깊이 고속제어 기구 연구

1. 서론

생산 장비에서 공구와 작업물의 간격을 일정하게 유지해야 할 경우가 많다. 예를 들어 에어컨이나 냉장고 같은 가전제품의 미관을 결정짓는 철판 표면에 흠집이 생기지 않도록 비닐 박막을 철판 표면에 부착하는 경우가 증가하면서,¹ 펀칭 등의 후가공을 위해 펀칭 전에 적절한 형상에 따라 박막을 미리 정밀하게 절단해야 하는데 이때 절단 공구와 철판의 간격을 일정하게 유지해야 한다. 그 외 제품의 표면에 따라 일정한 깊이의 얕은 가공을 해야 할 경우도 표면과 공구 간격을 일정하게 유지해야 한다.

이런 경우 생산성을 높이기 위해 공작물이나 공구를 빠르게 이송하면서 수십 μm 이하의 간격을 유지하려면 제품의 표면 높이 변화를 빨리 검출해서 고속으로 공구 위치를 움직일 수 있는 구동기가 필요하다. 일반적으로 모터를 이용한 구동계는 연결되어 있는 동력전달 부품들의 관성 때문에 아주 빠른 응답을 기대할 수 없다. 이러한 미세 변위를 고속으로 제어하기 위해 압전(PZT) 구동기 혹은 VCM (Voice Coil Motor)이 유력한 후보로 거론된다. VCM의 경우 이송 거리가 압전구동기에 비하여 길지만 주파수 성능이 떨어진다는 단점을 가지고 있고, 반면에 압전구동기는 다른 구동기에 비해 응답속도가 매우 빠르며 정확도가 아주 높지만 변위량이 적어서 변위를 증폭하는 유연힌지와 함께 사용하는 경우가 많다. 유연힌지(Flexure Hinge)는 일체형 구조로 결합오차와 백래쉬가 없고, 탄성 변위를 이용하여 부드럽고 운동을 증폭하는 특징을 가지고 있다.^2-4

선행 연구에서 빠른 응답속도와 높은 분해능을 가진 압전구동기와 변위량을 확대시키는 유연힌지를 조합하여 개회로(Open Loop)에서 미세 깊이를 제어하였지만 피드백(Feedback) 제어하지는 못하였다.⁵ 본 논문에서는 압전구동기와 유연힌지 각각의 정/동특성 및 오차해석 등을 통하여 응답성과 정밀도를 분석하고, 최종 변위의 피드백 제어계를 추가하여 PID 제어기를 LabVIEW에서 실현하였다. 최적의 게인을 구하고, 힌지 출력단에 절삭력 부하가 걸릴 때를 가정하여 제어특성을 조사하였다.

2. 지렛대 유연힌지(Lever Type Flexure Hinge) 설계 및 제작

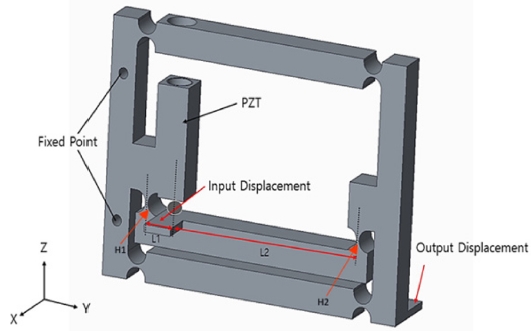
압전구동기의 변위를 증폭하기 위해서 사용되는 유연힌지의 메커니즘으로는 지렛대 메커니즘, 브릿지 메커니즘, 무니 메커니즘 등이 있다. 본 연구에서는 증폭비가 크고, 인가된 힘과 평행한 방향으로 안정된 변위를 일으키는 지렛대 메커니즘(Fig. 1)을 사용하였다.^6,7 지렛대 유연힌지는 PZT 구동기에서 입력 변위를 주면 H1을 지지점으로 해서 H2에서 변위가 증폭되는 구조이다. 정적/동적 특성에 영향을 주는 주요변수는 폭(b), 노치 반경(R), 노치두께(t), 힌지길이(L1, L2)로서,^8-11 필요한 증폭비와 동특성에 맞추어 이들을 설계해야 한다.

Fig. 1

Lever type flexure hinge

2.1 노치두께의 영향

본 연구에서는 선행연구에 따라 유연힌지의 형상을 Fig. 1처럼하고 변위증폭비를 10배로 설정하여 힌지를 설계하였다. 유연힌지를 강체 지렛대로 가정하면 지렛대의 원리에 따라 L1과 L2의 비율은 1 : 9이다. 그러나 유연힌지를 알루미늄으로 만든다면 강체가 아니므로 증폭비가 설계값보다 줄어들 것으로 예측된다.

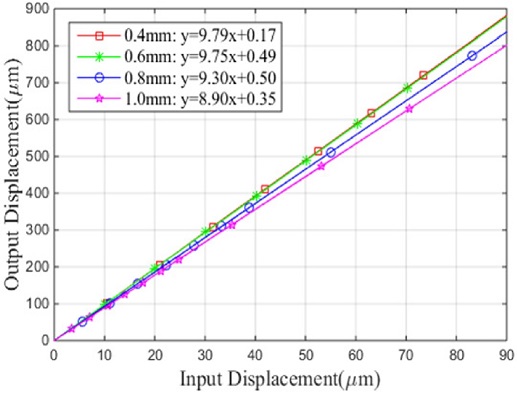
노치의 반경 3 mm으로 고정한 상태에서 노치두께가 변위증폭에 얼마나 영향을 미치는지 조사하였다. 노치두께를 0.4, 0.6, 0.8, 1.0 mm로 설정하고, 출력단에 외력이 없는 경우 입력점에 힘을 20 N에서 최대 160 N까지 20 N씩 증가시키면서 가할 때 입력점 변위(Z_i)와 출력점 변위(Z_o, Y_o)를 ANSYS WORKBENCH를 이용해서 해석한 결과 입/출력점 변위 관계식은 Fig. 2와 같다. 증폭비는 설계값 10보다 작게 나타났고, 두께가 얇을수록 힌지의 강성이 작아져 변위증폭비가 커지는 것을 알 수 있지만 0.6 mm 이하에서는 증폭비가 비슷하고 오히려 힌지의 강도만 떨어지므로 너무 얇은 것은 바람직하지 않다. 따라서 본 연구에서는 노치두께를 0.8 mm 로 선정하였다.

Fig. 2

Effect of notch thickness on displacement magnification ratio

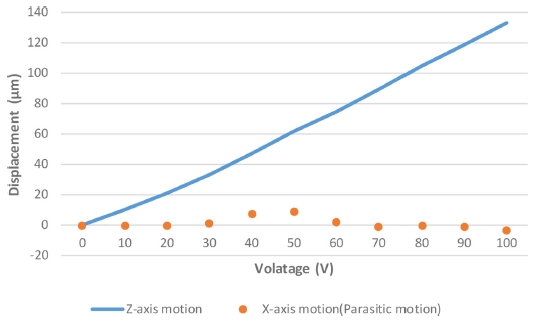
2.2 기생운동(Parasitic Motion) 확인

힌지형상을 완전하다고 가정하면 X축 방향 변위는 없으므로 Y축 변위를 확인하면 기생운동 여부를 확인할 수 있다. 노치두께 0.8 mm 일 때 위의 해석결과를 정리하면 Table 1과 같다. Y축 출력변위(Y_o)는 2 μm 이하로 거의 무시할 수 있어 Z축 한 방향으로 정밀하게 운동하고 있음을 알 수 있다.

Table 1

FEM displacement results of Al flexure hinge with notch thickness of 0.8 mm along with applied input forces (Zo = 9.30 * Zi + 0.50)

2.3 유연힌지의 강성

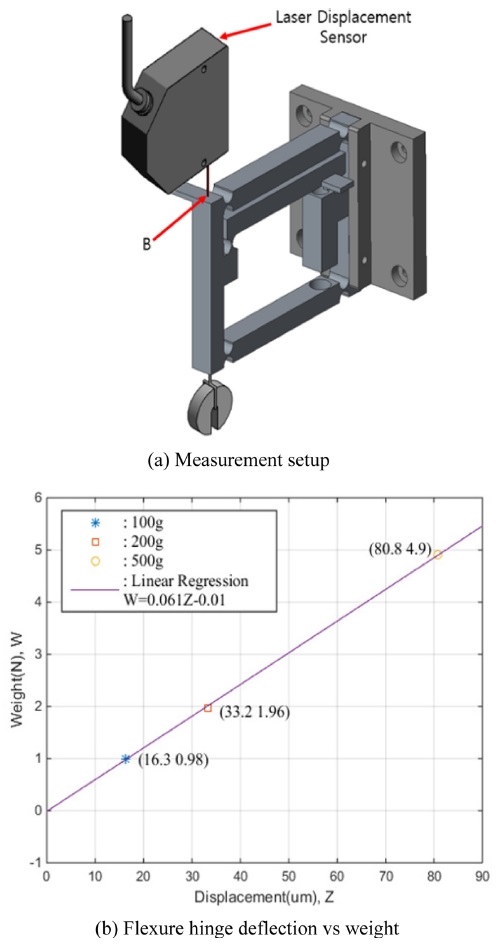
유연힌지의 출력단에 수직 반력이 작용할 때 변위손실을 예측하기 위해 압전구동기를 조립한 상태에서 강성을 측정하였다. Fig. 3(a)와 같이 출력단에 추(100 g, 200 g, 500 g)를 메달고 레이저 변위센서로 B부분 변위를 측정하였고, 회귀분석을 통해 Fig. 3(b)처럼 선형적인 관계식을 구하였다. 강성은 0.06 N/μm로 선행연구에서 필름절단에 필요한 힘이 100 N 정도이었으므로 절단작업 때 힌지 출력단이 약 17 μm 정도의 변위손실이 생길 것으로 생각된다.

Fig. 3

Measurement of flexure hinge stiffness

3. PZT 구동 미세변위 기구의 특성 실험

3.1 실험 장치 구성

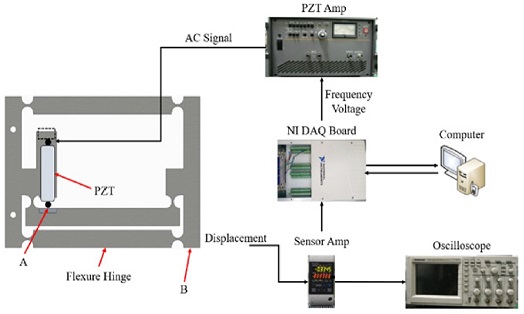
압전구동 유연힌지 기구의 특성을 알아보기 위한 실험장치 구성은 Fig. 4와 같다. DAQ 보드와 압전앰프를 통하여 특정 전압을 인가하면 압전구동기가 특정량만큼 늘어나고 유연힌지를 거쳐 변위가 증폭된다. 변위는 레이저 변위측정기로 측정되고 DAQ를 통해 측정된다.

Fig. 4

Experimental set-up for testing a PZT-hinge mechanism

증폭비 10배, 출력단의 최대 변위 150 μm를 목표로 설정하였기 때문에 최대 이동량이 18 μm인 압전구동기 P-844.40를, 압전앰프는 E-501(PI社)을 사용하였다. Tables 2부터 4는 압전구동기, 압전앰프, 레이저 변위 측정기의 제원을 각각 나타낸다.

Table 2

Specification of PZT actuator

Table 3

Specification of PZT amplifier

Table 4

Specification of laser sensor

3.2 정특성

3.2.1 유연힌지의 변위 증폭비

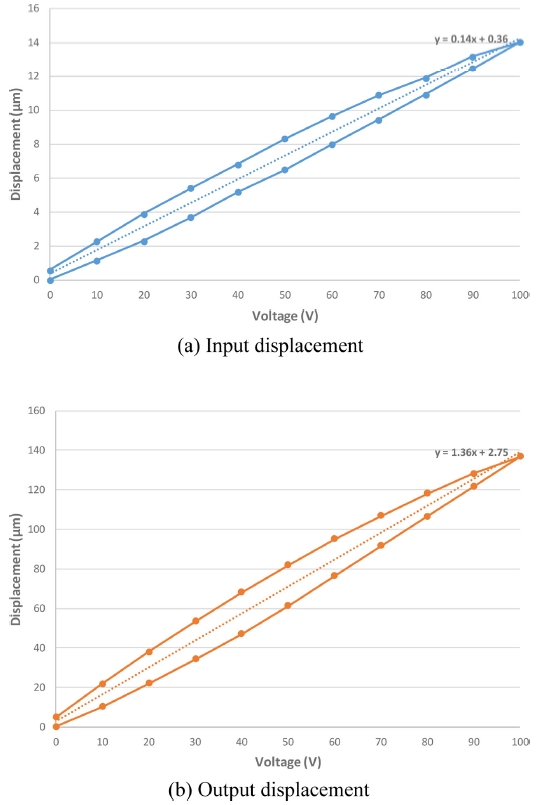
압전구동기와 유연힌지를 결합한 미세변위기구의 실제 변위증폭비를 파악하기 위한 실험을 하였다. 압전구동기에 전압을 0 V에서 100 V까지 증가시키고 감소시켰을 때, A에서 힌지 입력 변위와 B에서 힌지 출력변위를 레이저센서로 각각 측정하였다. Fig. 5는 그 결과를 나타내는 데 각각의 평균변위의 직선기울기는 회귀분석을 통해 0.14, 1.36이므로 평균적인 증폭비는 약 9.8배로 해석 값보다 좀 크다.

Fig. 5

Displacement behavior at input/output point of flexure hinge with applied voltages

3.2.2 히스테리시스 오차

Fig. 5 및 Table 5에서 보듯이 PZT 구동기의 상승과 하강구간에서 힌지 출력변위의 차이 즉 히스테리시스 최대오차가 21 μm 이어서 개회로에서 깊이를 제어할 때 제어위치에 따라 히스테리시스 오차보정이 필요하다.

Table 5

Hysteresis error of hinge input and output displacement

3.2.3 기생운동 오차

앞의 실험처럼 압전구동기의 전압을 10 V 간격으로 증가시키면서 X축 방향의 기생운동 오차를 측정한 결과 Fig. 6에 보이는 것처럼 최소 -2.83 μm에서 최대 8.95 μm까지 발생하였다. 이론 해석값보다 크게 나온 것은 힌지의 가공 및 조립 오차가 누적되었기 때문으로 생각된다. 그렇더라도 여전히 전행정136 μm에 비해 훨씬 작아 무시할 수 있을 정도이다.

Fig. 6

Measurement of parasitic motion of flexure hinge

3.3 동특성

3.3.1 유연힌지의 고유진동수

유연힌지의 고유진동수를 구하기 위해 힌지 출력부를 당겼다 놓을 때 B에서 측정한 변위는 Fig. 7(a)와 같다. 이를 FFT 분석하면 Fig. 7(b)처럼 약 208 Hz에 피크점이 나타나는데 이것은 유연힌지의 고유진동수에 해당한다.

Fig. 7

Measurement of natural frequency of the flexure hinge

3.3.2 주파수 응답 특성

설계한 압전구동 변위기구가 얼마나 빠른 변화를 따라가는지 알아보기 위해 주파수 응답을 조사하였다. 입력신호의 전압을 30, 60 V로 하고 주파수를 1, 10, 20, 40 Hz로 변화시키면서 힌지 출력변위를 측정한 결과는 Table 6과 같으며, 차단(Cut-Off) 주파수는 20 Hz정도라고 추정된다. 이것은 압전구동기의 충방전특성에 의한 것으로 유연힌지의 응답성이 훨씬 빠른 걸 알 수 있다.

Table 6

Response amplitudes with input frequency varied

4. 미세변위 기구의 제어성능 평가

4.1 실험 장치 구성

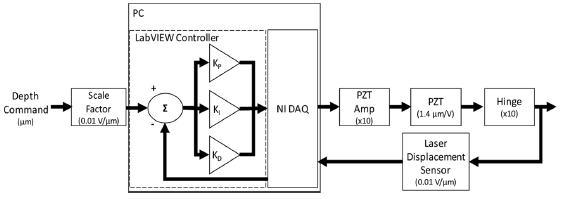
미세변위 기구의 제어성능을 평가하기 위한 실험 장치는 Fig. 8과 같이 크게 LabVIEW 보드, 압전구동기, 압전증폭기, 미세변위 기구(압전구동기 + 힌지), 레이저 변위 측정기 4가지로 구성된다. 깊이 지령에 따라 압전구동기를 구동하고 힌지 출력단의 변위를 레이저 측정기로 측정해서 피드백을 하는 구조이다. 제어 알고리즘은 일반적인 PID 제어로 구성되고 LabVIEW 보드에서 실현된다. 지령과 레이저 출력 값을 일치시키기 위해 단위인자(Scale Factor)(0.01)를 두었고, 지령과 실제 깊이의 오차가 0.1 μm 이내이면 제어를 완료하였다.

Fig. 8

Construction of a PZT driven micro-depth control system

4.2 게인 조정

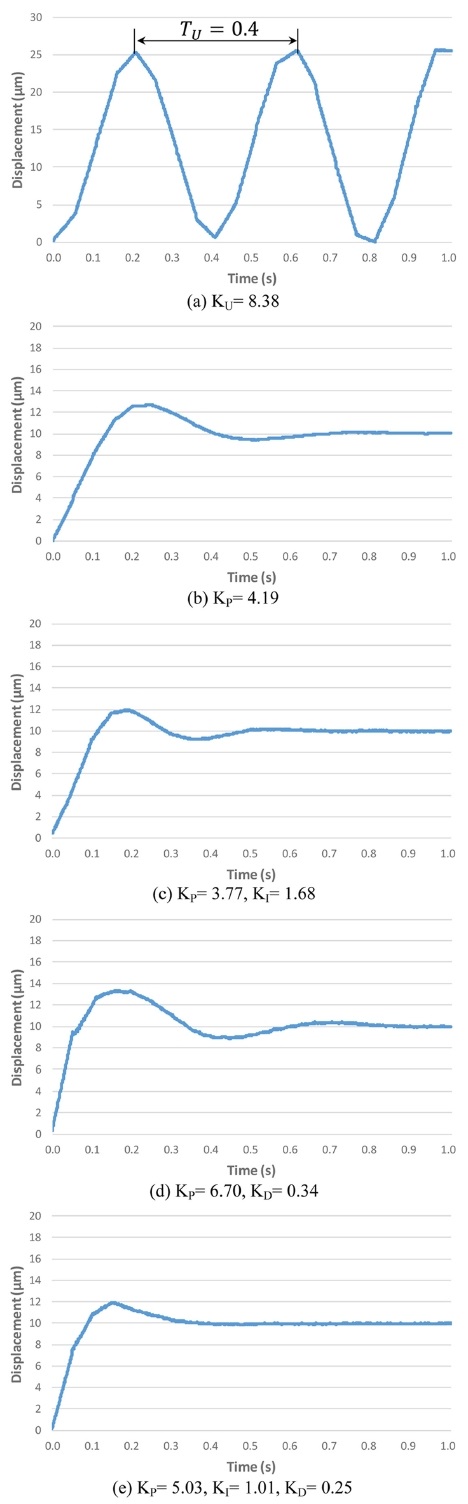
제어 알고리즘에서 최적의 PID 게인을 구하기 위해 경험적(Heuristic) 방법인 Ziegler–Nichols 법^12,13을 적용하였다. Table 7은 이 방법에 의한 P, I, D 제어의 최적게인을 수식화한 것이다. Fig. 9는 게인 조정한 결과를 나타낸다. 깊이지령에 대해 비례게인 K_p를 증가시켜 Fig. 9(a)처럼 안정적으로 진동하는 반응이 나오는 한계 게인 K_u= 8.38, 주기 T_u= 0.4를 얻었고, 이로부터 Table 7에 주어진 네 개 제어기의 게인을 구해서 실험한 결과 Figs. 9(b)-9(e)를 비교하면 오버슈트(Overshoot)와 위치제어 시간 측면에서 PID 제어기가 가장 우수한 것을 알 수 있다. 최적 게인은 K_p= 5.03, K_i= 1.01, K_d= 0.25 이다. (* K_u, T_u: 출력이 안정적이면서 일정한 진동 반응이 나오는 한계 게인과 주기)

Table 7

Ziegler-Nichols chart for tuning a PID controller

Fig. 9

Ziegler-Nichols tuning results for each controller (P, PI, PD, PID) with Ku= 8.38 and Tu= 0.4

$\[ u\left(t\right)=K_p\left(e\left(t\right)+\frac{1}{T_i}{\int }_0^{t}e\left(\tau \right)d\left(\tau \right)+T_d\frac{de\left(t\right)}{dt}\right) \]$

(1)

4.3 미세깊이 추종제어 실험

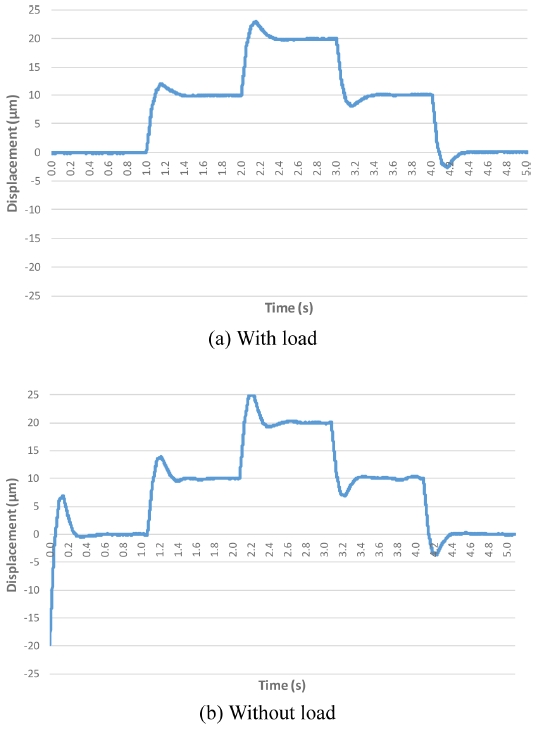
힌지 출력단에 하중이 없을 때와 하중이 걸리는 환경을 가정하여 미세깊이 추종제어 실험을 하였다. 하중은 실제 필름절단에 필요한 약 1 N의 하중을 가정하여 힌지 출력단 B에 100 g 추를 달았다. Figs. 10(a)와 10(b)는 하중이 없을 때와 있을 때 10 μm씩 증가하고, 감소할 때 차례대로 깊이변화를 추종해 가는 것을 나타낸다. Fig. 10(b)에서 시작 위치는 하중에 의해 생긴 변위 20 μm (2.3에서 예상한 17 μm 보다 약간 큼)를 0의 위치로 복원시킨 뒤에 10 μm씩 증가하고, 감소하는 결과를 나타낸다. 0.1 μm의 오차에 도달하는 시간은 무부하 때 0.33 s이고, 부하 때 변위 20 μm 복원에는 0.51 s, 그 이후에는 0.48 s이다. 부하가 걸리면 제어시간이 더 걸림을 알 수 있다.

Fig. 10

Step response of hinge output with/without a load of 1N

5. 결론

본 논문에서 빠른 응답속도와 높은 분해능을 가진 압전구동기와 유연힌지를 이용하여 미세깊이 제어기구를 설계하고, 정·동특성을 분석한 뒤 피드백 제어 알고리즘을 적용하여 이 기구의 미세깊이 제어 특성을 실험하였다. 연구를 통해서 확인한 사실은 아래와 같다.

• (1) 지렛대 유연힌지 기구의 기생운동(Parasitic Motion)은 거의 발생하지 않았고, 힌지의 노치 두께는 변위증폭비 측면에서 0.6 mm 이상이 바람직하다.
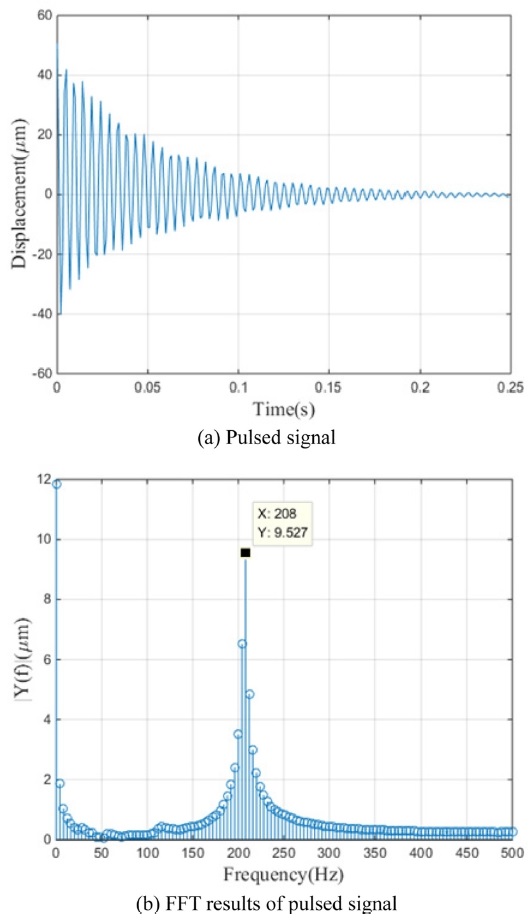
• (2) 개발한 압전구동기 -유연힌지 미세변위 장치의 차단 주파수는 20 Hz 정도이다.
• (3) Ziegler–Nichols 조정법에 의해 최적의 PID 게인은 K_P = 5.03, K_I = 1.01, K_D = 0.25 이다.
• (4) 힌지 출력단에 1N의 부하가 걸렸을 때 0.1 μm 위치정밀도 도달시간은 0.5 s이다.

Acknowledgments

이 과제는 2014년도 부산대학교 교수 국외장기파견지원비에 의하여 연구되었음.

REFERENCES

• Jeong, J.-I. and Yang, J.-H., “Trend and Prospect of Thin Film Processing Technology,” Journal of the Korean Magnetics Society, Vol. 21, No. 5, pp. 185-192, 2011. [https://doi.org/10.4283/JKMS.2011.21.5.185]
• Kim, Y.-S., Kim, J.-I., and Kim, I.-S., “Modeling and Motion Control of the Precision Positioning Stage with Flexible Hinge Mechanism,” Journal of the Korean Society of Manufacturing Process Engineers, Vol. 9, No. 6, pp. 51-58, 2010.
• Choi, H., Lee, J., Jung, M., Yun, D., Han, C., et al., “Review of a High Precision Actuator Mechanism Using PZT,” Proc. of the Korean Society of Machine Tool Engineers Spring Conference, pp. 524-529, 2004.
• Choi, J. P., Lee, K. H., Lee, H. J., Lee, N. G., and Kim, B. H., “Development of Micro Punching System Using PZT Actuator and Displacement Amplification Device,” Proc. of the Korean Society of Machine Tool Engineers Spring Conference, pp. 268-272, 2007.
• Ryu, S.-O., Kim, H.-Y., and Ahn, J.-H., “Characteristics of a PZT-Driven Micro Depth Adjustment Device for Cutting Coated Film,” Journal of the Korean Society of Manufacturing Technology Engineers, Vol. 23, No. 6, pp. 630-635, 2014. [https://doi.org/10.7735/ksmte.2014.23.6.630]
• Kim, J., Kim, S., and Kwak, Y., “Optimization of a Piezoelectric Actuator Using Bridge-Type Hinge Mechanism,” J. Korean Soc. Precis. Eng., Vol. 20, No. 2, pp. 168-175, 2003.
• Chae, K.-W., Bae, J.-H., and Jeong, Y.-H., “Modularized Flexure-Hinge Nanopositioner Based on Four-Bar-Link-Mechanism,” J. Korean Soc. Precis. Eng., Vol. 28, No. 7, pp. 851-858, 2011.
• Ye, S. D. and Min, B. H., “Effects of Flexure Hinge Thickness and Vertical Arm Length on the Design of Ultra-Precision Stage,” Proc. of the Korean Society of Manufacturing Process Engineers Conference, pp. 297-302, 2008.
• Jea, W.-S., Ye, S.-D., and Min, B.-H., “A Study on the Displacement Magnification Mechanism of Two-Lever System Using Flexure Hinge,” Journal of the Korean Society of Manufacturing Process Engineers, Vol. 7, No. 2, pp. 60-65, 2008.
• Choi, S.-C., Kim, Y.-W., Kim, J.-G., Park, J.-W., and Lee, D.-W., “Development of High Precision Nano-Stage Using Mafnified Mechanism,” Proc. of the Korean Society of Machine Tool Engineers Autumn Conference, pp. 61-65, 2008.
• Choi, J. Y., Eom, S. I., and Kim, J. H., “Optimal Design for Parallelogram Type Flexure Hinge,” J. Korean Soc. Precis. Eng., Vol. 32, No. 1, pp. 107-111, 2015. [https://doi.org/10.7736/KSPE.2015.32.1.107]
• Åström, K. J. and Hägglund, T., “Advanced PID Control,” The Instrumentation, Systems and Automation Society, 2006.
• O'Dwyer, A., “Handbook of PI and PID Controller Tuning Rules,” World Scientific, 2009. [https://doi.org/10.1142/p575]