3차 B-스플라인 곡선 기반의 5축 공구 경로 스무딩

1. 서론

동시 5축 공작기계는 가공 방향에 제약이 있는 3축 공작기계와 달리 3개의 직선 이송축(Linear Axes)과 2개의 회전 구동축(Rotary Axes)이 동시에 움직이며 여러 방향에서 가공이 가능하여 3축 공작기계로는 가공이 어려운 복잡한 형상을 갖는 자유 곡면의 공작물 가공에 필수적이다. CAM 소프트웨어를 이용하면 5축 공구 경로는 TCP (Tool Center Point) 제어가 가능한 형식으로 공구 위치(Tool Tip Position)와 공구자세벡터(Tool Orientation Vector)로 이루어진 NC 데이터로 생성되거나, 후처리기(Post Processer)를 통해 공구 위치와 회전 구동축에 대한 좌표 형식의 NC 데이터로 변환될 수 있다.

대부분의 경우 직선 보간의 NC 데이터를 이용하여 공작물을 가공하게 되는데, NC 데이터 생성 조건에 따라 CAD 형상을 근사한 연속적인 미소 직선의 형태로 가공이 되고 설정된 허용 오차 내외로 기하학적 오차가 수반되는 등의 문제가 있다. 또한 미소 직선 간 연결부에서는 공구 방향의 변화로 인해 공구의 가속도, 저크(Jerk)가 발생하고 이로 인해 진동이 유발되어 가공면의 품위를 악화시킬 수 있다. 이러한 문제점을 해결하기 위하여, 공구 경로 수정을 통해 구동계의 운동 성능을 향상시키거나^1-3 기존의 직선 공구 경로의 연결부를 부드러운 곡선으로 대체하는 스무딩(Smoothing) 방법^4-10 등이 제시되었으며, 후자의 경우 3축 공구 경로에 대한 스무딩에 공구 자세 스무딩 방법이 추가되어 5축 공구 경로 스무딩으로 확장하는 연구가 진행되었다.

3축 공구 경로에 대해서는 직선 이송축의 최대 속도, 가속도, 저크 등 구동계에 대한 운동 지령의 한계를 설정하는 방법^1,2과 NURBS (Non-Uniform Rational B-Spline) 등의 매개식을 사용하여 부드러운 곡선으로 미소 직선의 연결부인 코너를 대체하는 스무딩 방법^4-6이 제시되었다. 두 방법 모두 이송축의 가감속을 줄여주어 진동을 억제하므로, 가공 시간의 단축과 가공면 품위의 향상을 가능하게 한다. 또한 미소 직선의 연결부를 지나도록 곡선을 생성하는 방법⁷이 제시된 바 있으며, 반복 알고리즘을 통하여 CAD 형상과의 오차를 줄여주었다.

5축의 공작기계는 공구 위치와 더불어 공구의 자세도 제어를 해야 하며, 공구 자세의 운동이 기계 좌표계(Machine Coordinate System)에서 각 구동축의 운동에 큰 영향을 줄 수 있다. 즉, 공구 자세의 급격한 변화가 있을 때, 구동축에 가속도 및 저크가 발생하게 되어 가공면의 품질에 악영향을 주게 된다. 이를 해결하기 위한 방안으로 공구 자세의 변화가 큰 지점을 선택하고, 그 지점의 공구 자세를 Quaternion 보간하여 공구 경로를 생성하는 연구³가 수행되었다. 이 방법은 공구 접촉점(Cutter Contact Point)과 그 점에서 공구의 자세만을 고려한 기존 방법에 비해 공구 자세의 변동폭을 줄여주는 장점이 있으나 공구 위치 변화를 고려하지 않는 방식이기 때문에 형상 오차가 증가할 수 있다.

또 다른 한편으로, 공구 경로에 의한 형상 오차를 일정 수준 유지시켜 주기 위해, 공작물 좌표계(Workpiece Coordinate System)에서 공구 경로의 코너를 곡선으로 대체하는 방식이 연구된 바 있다.^8-10 공구 자세에 대해서는 기계 좌표계로 변환하여 회전 구동축의 움직임에 대한 스무딩 곡선을 생성하는 방식⁸이 제안되었다. 이 방식은 기계의 구조(Configuration)가 다를 경우, 동일한 NC 데이터에 대해서도 상이한 회전 구동축 운동을 갖게 될 뿐만 아니라,¹¹ 측면 가공 시 가우징(Gouging)이 발생하여 고르지 못한 가공면 형상을 얻을 수 있다.¹² 공구자세벡터로 정규화된 B-스플라인 곡선을 생성하는 방식^9,10도 스무딩 곡선을 생성하는 방식 중 하나인데, 공구 자세를 보간하는 기준이 명확하지 않기 때문에 공구 자세가 불규칙하게 보간될 소지가 있다. 또한 코너를 곡선으로 대체하는 상기의 방식들은 직선과 곡선을 번갈아 보간하는 형태로, 본래 CAD 형상과는 다른 형태의 가공 결과를 가져온다.

본 논문에서는 3차 B-스플라인을 이용한 5축 공구 경로 스무딩 방법을 제시한다. 제시된 방법은 공구자세벡터 간 각도의 불규칙한 편차를 줄여주는 과정을 거치므로 가감속을 줄일 수 있다. 또한 공구의 상단점과 하단점에 대한 경로를 두 개의 곡선으로 생성, 보간하고 공구 위치와 공구 자세를 계산하므로, 기계의 구조에 관계없이 공구의 동일한 움직임을 생성할 수 있다. 스무딩에 이용되는 B-스플라인 곡선은 구간별 다항식(Piecewise Polynomial)으로 이루어져 있으며 연결부가 부드럽게 연결되므로, 미소 직선의 연결부에서 발생할 수 있는 가속도와 저크를 감소시켜 진동의 발생을 억제할 수 있다. 그리고 공구 위치와 공구 자세의 조절을 위해 만들어지는 하단 곡선과 상단 곡선은 공구 접촉점이 CAD의 형상을 추종하도록 생성되므로, NC 데이터 생성 시 발생하는 기하학적 형상 오차를 줄일 수 있다. 본 논문에서 제시된 스무딩 방법을 PC 기반 개방형 5축 제어시스템에 구현하고, 기존 직선 보간 방식과 비교, 평가하였다.

2. 제시된 5축 공구 경로 스무딩 방법

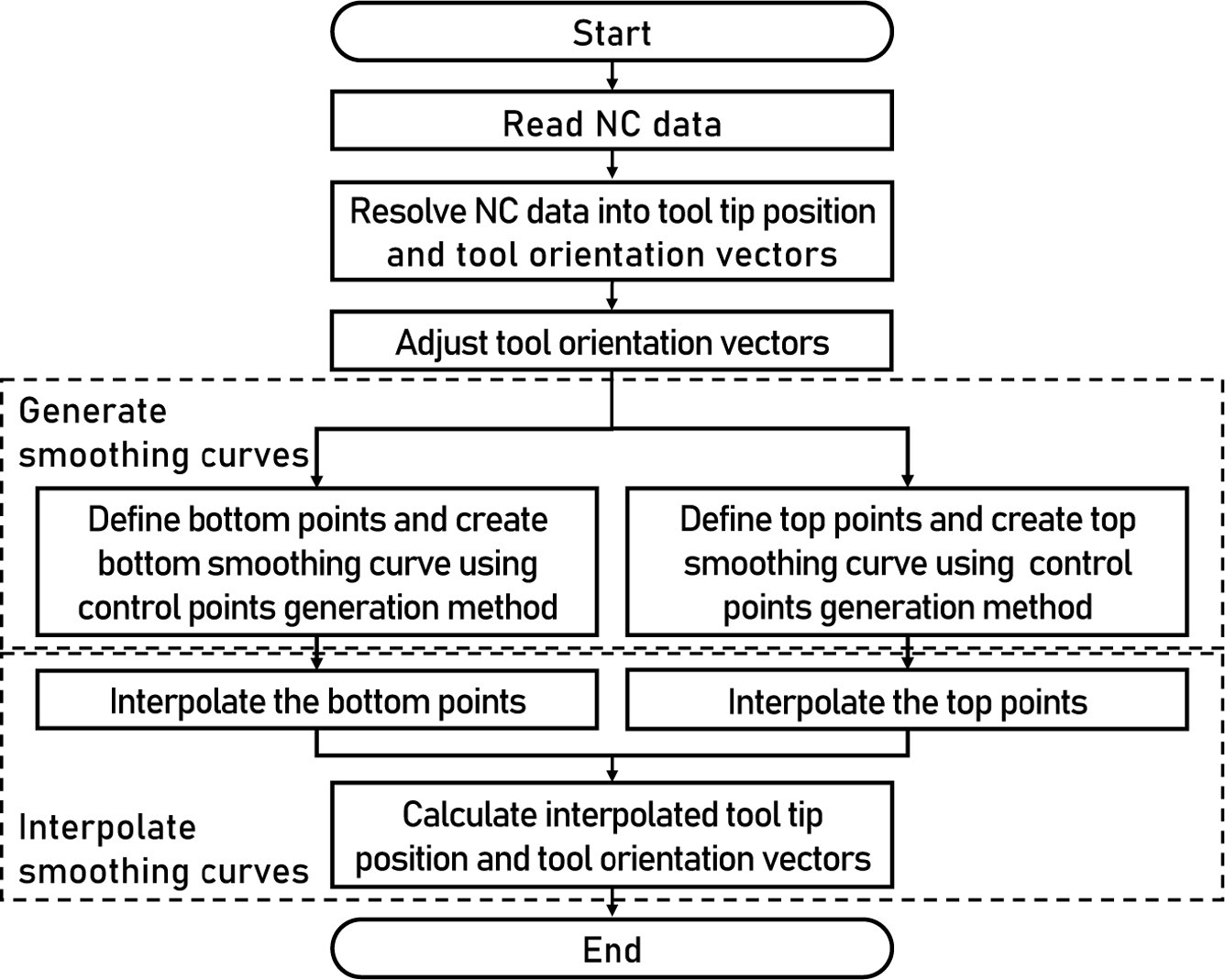
본 논문에서 제시된 5축 공구 경로 스무딩은 NC 데이터를 공구위치벡터와 공구자세벡터로 분리하고, 공구자세벡터를 공구 위치의 간격에 따라 조정하는 과정을 거친다. 그 후, 공구의 상단점과 하단점을 정의하고, 상단점과 하단점을 근사하는 상단 곡선과 하단 곡선을 각각 생성하고 보간하여 공구위치벡터와 공구자세벡터를 계산한다. 일련의 과정에 대한 순서도를 Fig. 1에 나타내었다.

Fig. 1

Flow chart of the proposed smoothing method

2.1 공구 자세의 조정

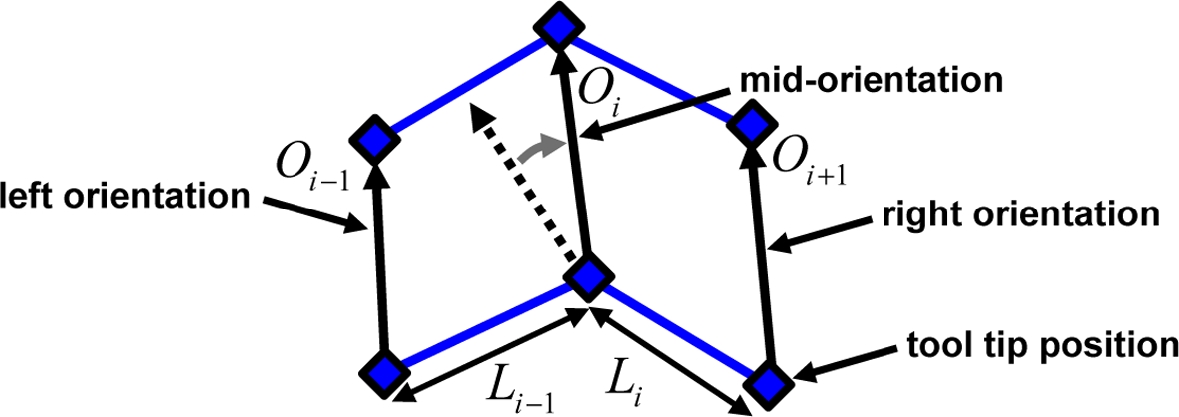
CAM 소프트웨어에서 생성된 NC 데이터의 공구 자세 간 간격을 공구 위치의 간격 비율에 맞춰 조정함으로써, 공구 자세의 급격한 변화나 불규칙한 변동을 줄여줄 수 있다. Fig. 2는 공구 자세 조정 방법의 개념도이다. 주어진 NC 데이터로부터 연속적으로 세 개의 공구 자세를 취한 후, 중간의 공구자세벡터를 조정하여 평활화한다. 조정된 공구자세벡터는 공구 위치 간 거리의 비로 이웃한 두 공구자세벡터를 구면선형보간(Spherical Linear Interpolation)하여 구할 수 있다. 구면선형보간은 아래의 식(1)과 같이 정의된다.

$\[ \mathrm{S}\mathrm{l}\mathrm{e}\mathrm{r}\mathrm{p}\left({\mathbf{V}}_1,{\mathbf{V}}_2,t\right)=\left({\mathbf{V}}_1\sin \left(\left(1-t\right)\theta \right)+{\mathbf{V}}_2\sin \left(t\theta \right)\right)/\mathrm{s}\mathrm{i}\mathrm{n}\theta \]$

(1)

Fig. 2

Adjustment of tool orientation

여기서, V₁과 V₂는 구면 선형보간의 대상이 되는 단위 벡터이고, θ는 두 벡터 간 각도, t는 0과 1 사이의 값을 갖는 보간 비율에 해당한다. 아래 식(2)를 통해 조정된 공구자세벡터를 구할 수 있다.

$\[ {\mathbf{O}}_i=\mathrm{s}\mathrm{l}\mathrm{e}\mathrm{r}\mathrm{p}\left({\mathbf{O}}_{i-1},{\mathbf{O}}_{i+1},L_i/\left(L_{i-1}+L_i\right)\right) \]$

(2)

위 식에서, O_i는 조정 후의 공구자세벡터, O_i-1과 O_i+1은 O_i와 이웃한 공구자세벡터이고, L_i-1과 L_i는 각각 (i-1)번째와 i번째 공구 위치 간 거리이다.

2.2 5축 공구 경로의 스무딩 곡선

스무딩 곡선은 복수 개의 상단점과 하단점을 근사하는 방식으로 생성된다. 이때의 상단점은 공구위치벡터에 공구자세벡터를 더한 좌표로 정의되며, 하단점은 공구위치벡터로 정의된다. 즉, 상단점과 하단점에 대하여 아래 식(3)과 식(4)의 관계가 성립한다.

$\[ {\mathbf{U}}_i={\mathbf{P}}_i+{\mathbf{A}}_i \]$

(3)

$\[ {\mathbf{D}}_i={\mathbf{P}}_i \]$

(4)

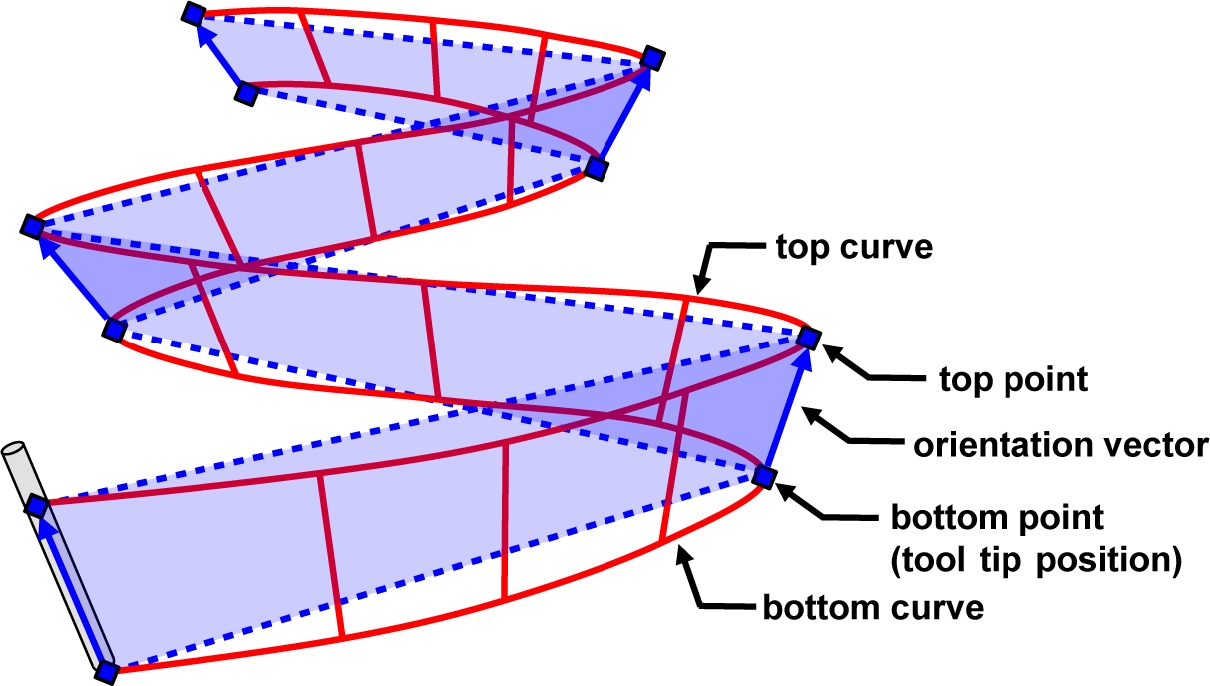
여기서, U_i와 D_i는 상단점과 하단점의 위치벡터이고, P_i는 공구 위치벡터, A_i는 공구자세벡터를 나타낸다. 스무딩을 위한 상단 곡선과 하단 곡선은 상단점과 하단점을 기반으로 생성되기 때문에, 공구 자세를 공작물 좌표계에서 제어하는 것이 가능하다. 이 곡선들은 매듭벡터(Knot Vector)를 공유하며, 각각에 대한 조정점(Control Points)은 동일한 알고리즘으로 생성된다. Fig. 3에 스무딩 곡선의 개념도를 도시하였다.

Fig. 3

Schematic of the proposed smoothing curves

2.2.1 B-스플라인 곡선의 특성

B-스플라인 곡선은 주로 자유 곡선과 같이 매끄러운 곡선을 표현할 때 사용되며, 주어진 여러 개의 조정점을 이용하여 정의되는 매개변수 곡선이다. 곡선 상의 점은 차수(Degree), 조정점, 기저함수(Basis Functions)로 계산되고 구간별 다항식으로 구성되며 아래의 식(5)와 같이 표현된다.¹³

$\[ \mathbf{C}\left(u\right)={\sum }_{i=0}^n{N}_{i,p}\left(u\right){\mathbf{P}}_i \]$

(5)

여기서, P_i는 조정점을 나타내고, N_i,p는 i번째 p차 B-스플라인의 기저함수로서 Cox-De Boor 점화식에 의해 다음 식(6)과 식(7)과 같이 재귀적으로 정의된다.

(6)

$\[ N_{i,p}\left(u\right)=\frac{u-u_i}{u_{i+p}-u_i}{N}_{i,p-1}\left(u\right)+\frac{u_{i+p+1}-u}{u_{i+p+1}-u_{i+1}}{N}_{i+1,p-1}\left(u\right) \]$

(7)

위 식의 u_i는 매듭(Knot)으로, 각 구간별로 정의되는 다항식 곡선의 연결부에서의 매개변수 값이다. 매듭의 집합인 매듭벡터를 U = {u₀, u₁,..., u_m}라 하면 다음의 두 조건식(8)과 식(9)를 만족한다.

$\[ m=n+p+1 \]$

(8)

$\[ u_i\le u_{i+1} \left(i=\mathrm{0,1},\dots ,m-1\right) \]$

(9)

p차 B-스플라인 곡선은 p차 다항식이 매듭에서 연결되는 형태로 만들어진다. 특정 매듭의 다중도(Multiplicity)가 k(k < p)인 경우, 매듭에서의 곡선 간 연속성(Continuity)은 C^(p-k)를 만족한다.

2.2.2 B-스플라인 곡선의 생성

스무딩 곡선은 공구의 상단점과 하단점을 근사하도록 만들어지며, 스무딩 곡선의 조정점은 상단점과 하단점 각각에 대하여 일정한 비율의 내분점을 생성하고, 내분점을 인접한 세 하단점에 의해 정의되는 보정 방향으로 특정 값만큼 보정하여 생성한다.

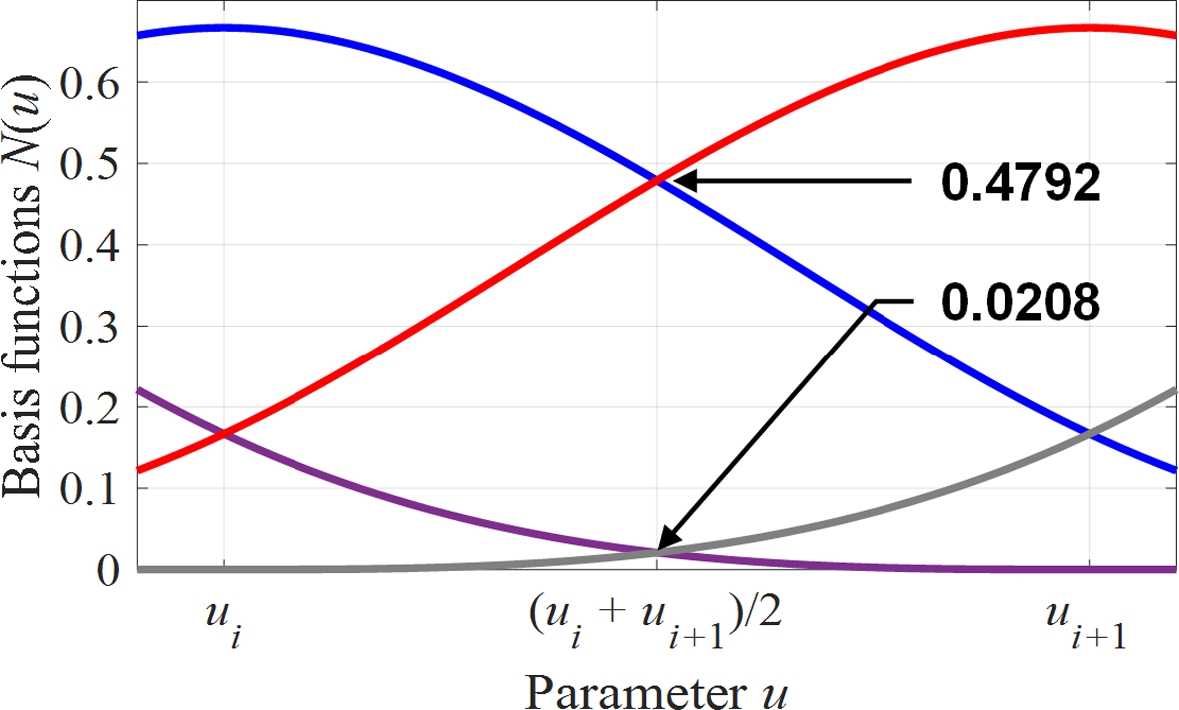
먼저, 두 스무딩 곡선에 대한 매듭벡터로서 식(10)과 같이 매듭 간 간격이 일정한 3차 비균일 B-스플라인의 매듭벡터를 고려한다. 이 경우, B-스플라인은 Fig. 4와 같은 기저함수를 갖는다.

$\[ U=\left\{u_0,u_0,u_0,u_0,u_1,u_2,\dots ,u_{n-3},u_{n-3},u_{n-3},u_{n-3}\right\} \]$

(10)

$\[ u_k-u_{k-1}=u_{k+1}-u_k \left(k=1,\dots ,n-4\right) \]$

(11)

Fig. 4

Basis functions of a non-uniform B-spline

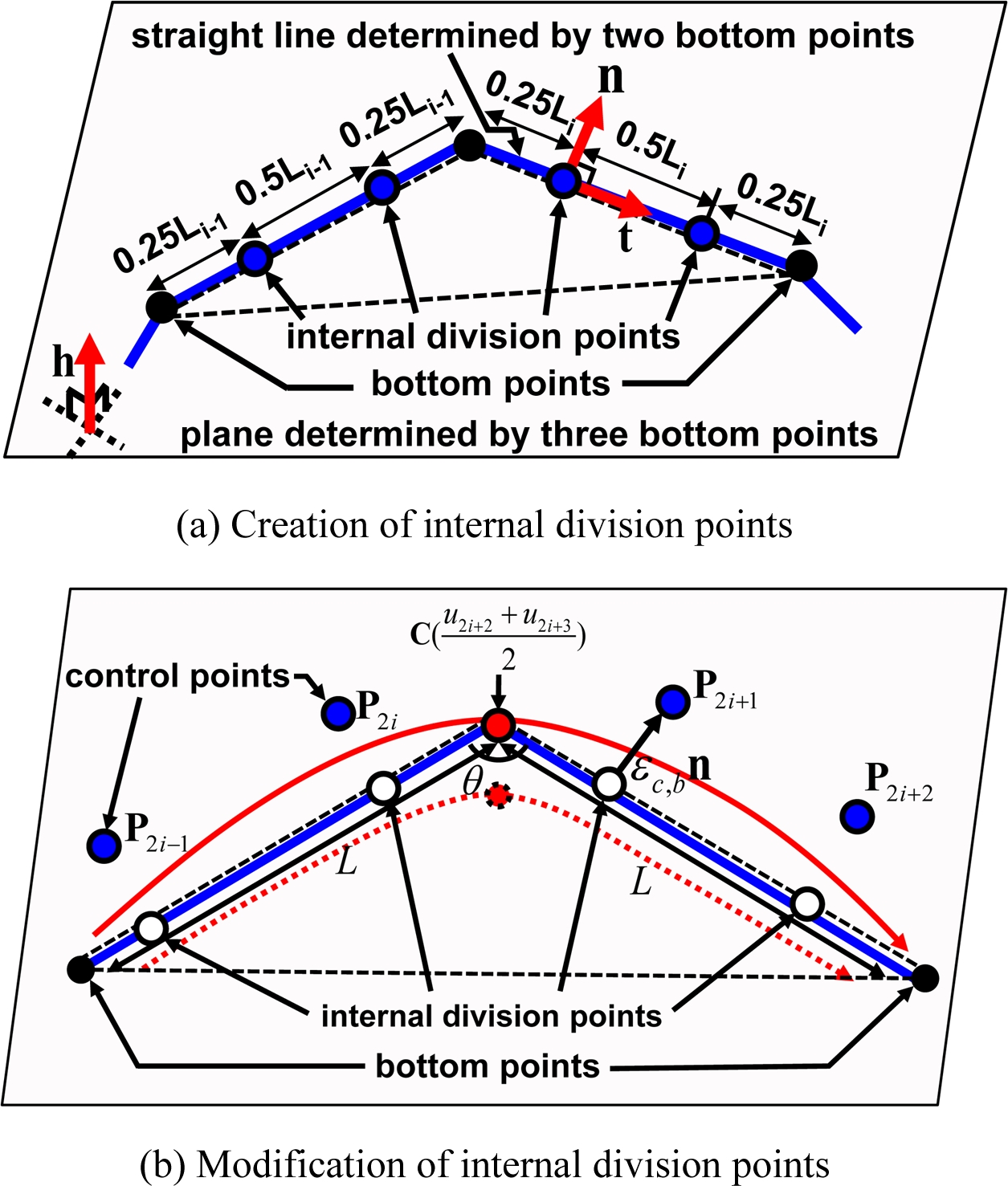
식(10)과 식(11)에서 n은 조정점의 개수이다. 이때, 하단점의 스무딩 곡선에 대한 조정점 생성 방법을 Fig. 5에 나타내었다. Fig. 5(a)에 제시된 바와 같이 생성할 스무딩 곡선의 하단점에 대하여 0.25 : 0.5 : 0.25의 비율로 내분점을 두 개씩 생성할 수 있다. 이 내분점들을, 내분점 생성에 이용한 두 하단점을 잇는 직선 방향 단위 벡터 t와, 내분점에 가장 근접한 세 하단점으로 정의되는 평면의 단위법선벡터 h에 동시에 수직인 벡터 n의 방향으로 보정한다. 보정 방향 n은 식(12)와 같이 두 벡터 t와 h를 외적하여 계산할 수 있다.

$\[ \mathbf{n}=\mathbf{h}\times \mathbf{t} \]$

(12)

Fig. 5

Control points generation

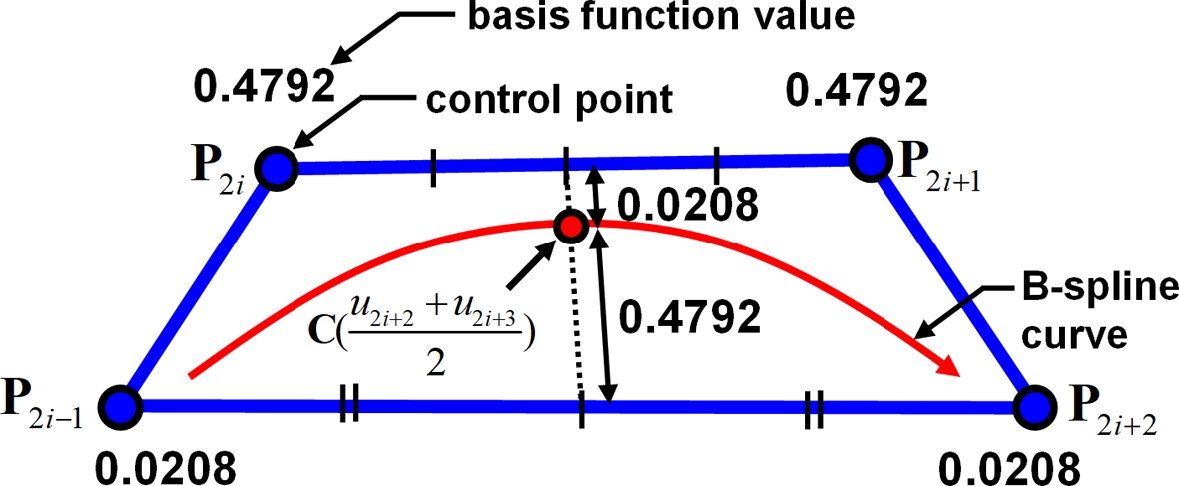
하단점의 내분점에 대한 보정량 ε_c,b에 대한 수식 유도의 편의상 하단점 간 거리가 일정한 경우를 가정하면, Fig. 4의 기저함수 값에 의해 Fig. 6의 곡선과 조정점의 기하적 관계가 정해진다. Fig. 5(b)와 같이 인접한 하단점 간 거리가 같다면, 내분점을 식(13)에서 제시된 값만큼 보정한 후, 보정된 내분점을 B-스플라인 곡선의 조정점으로 하여 하단점의 위치와 곡선상의 한 점 C((u_2i+2+u_2i+3)/2)의 위치를 일치시킬 수 있다.

$\[ {\epsilon }_{c,b}\left(L,\theta \right)=2\left[0.0208L+0.25L\left(0.4792-0.0208\right)\right]/\mathrm{t}\mathrm{a}\mathrm{n}\frac{\theta }{2} \]$

(13)

Fig. 6

Geometric relation between control points and a B-spline curve

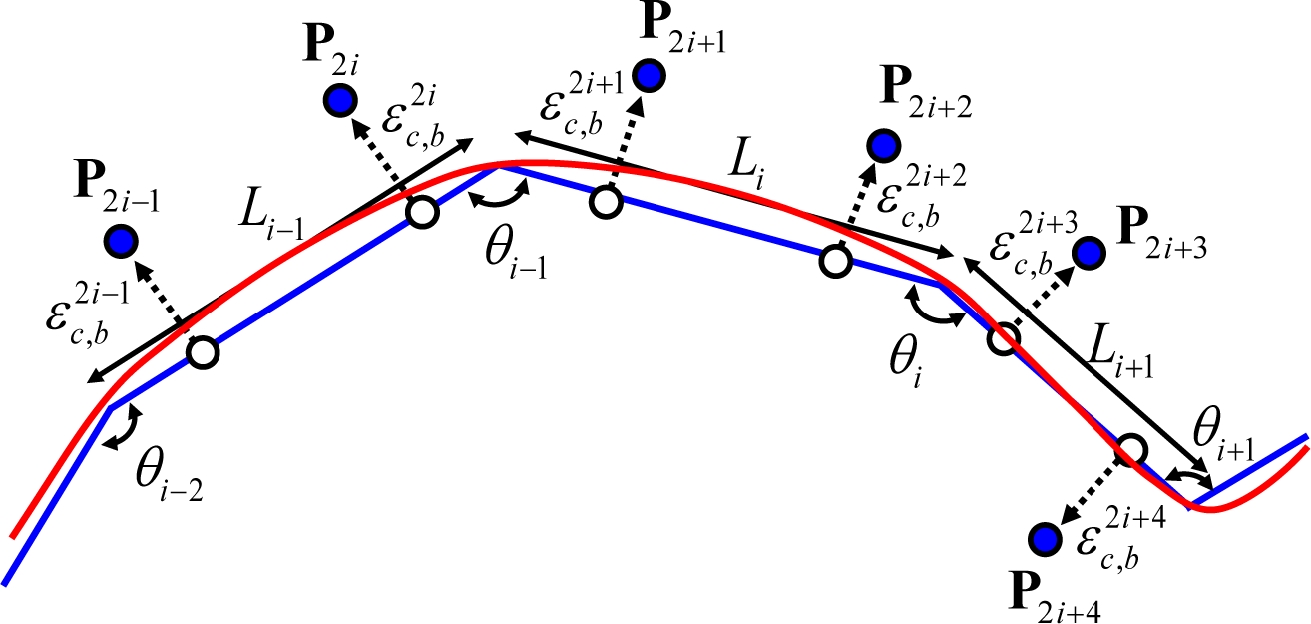
여기서, L은 내분점이 속하는 하단점 사이의 거리, θ는 하단점을 잇는 직선 간 각도이다. 일반적인 경우, 인접한 하단점 간 거리가 같지 않으므로 Fig. 7과 같이 i번째 NC 블록의 두 내분점에 대해 아래 식(14)와 식(15)를 적용하여 보정하면, 하단점을 근사하는 곡선을 생성할 수 있다.

$\[ {\epsilon }_{c,b}^{2i+1}=2\left[0.0208L_i+0.25L_i\left(0.4792-0.0208\right)\right]/\mathrm{t}\mathrm{a}\mathrm{n}\frac{{\theta }_{i-1}}{2} \]$

(14)

$\[ {\epsilon }_{c,b}^{2i+2}=2\left[0.0208L_i+0.25L_i\left(0.4792-0.0208\right)\right]/\mathrm{t}\mathrm{a}\mathrm{n}\frac{{\theta }_i}{2} \]$

(15)

Fig. 7

Modification of internal division points for NC blocks

단, $$ {\epsilon }_{c,b}^1 \mathrm{과} {\epsilon }_{c,b}^{2n} $$의 경우, 첫 하단점을 포함하여 정의되는 첫번째 내분점과 마지막 하단점을 포함하여 정의되는 마지막 내분점에 대한 보정량이므로 하단점을 잇는 직선 사이의 각도θ가 존재하지 않는다. 따라서, 가장 가까운 각도 차를 이용한 아래의 식(16)과 식(17)로 대체한다.

$\[ {\epsilon }_{c,b}^1=2\left[0.0208L_0+0.25L_0\left(0.4792-0.0208\right)\right]/\mathrm{t}\mathrm{a}\mathrm{n}\frac{{\theta }_0}{2} \]$

(16)

$\[ {\epsilon }_{c,b}^{2n}=2\left[0.0208L_{n-1}+0.25L_{n-1}\left(0.4792-0.0208\right)\right]/\mathrm{t}\mathrm{a}\mathrm{n}\frac{{\theta }_{n-2}}{2} \]$

(17)

내분점에 대한 보정 완료 후, 처음과 마지막 하단점과 보정된 내분점들을 조정점으로 갖는 3차 B-스플라인 곡선을 생성할 수 있다. 이러한 방식으로 생성된 B-스플라인 곡선은 공구위치벡터의 보간을 위한 스무딩 곡선이며, 3축 공구 경로에 대한 스무딩에 사용될 수 있다. 5축 공구 경로의 스무딩을 위해서 공구의 상단점에 대한 스무딩 곡선이 추가적으로 요구된다. 이 상단 곡선은 식(3)에서 정의된 상단점에 대해 하단점의 조정점 생성 방법을 동일하게 적용하여 생성하며, 이때 상단점의 내분점에 대한 보정량을 ε_c,t로 정의한다.

2.2.3 스무딩 오차

스무딩 오차(Smoothing Error Tolerance)는 기존의 직선 공구 경로와 스무딩 곡선 사이 거리의 상한 또는 각도 차의 상한으로 정의하며, B-스플라인의 내분점에 대한 보정량을 특정 값으로 제한함으로써 제어된다. 공구 위치와 공구 자세에 대한 스무딩 오차를 각각 e_p와 e_o로 정의하면, 하단점을 잇는 직선과 하단 곡선 사이의 거리 e_b의 상한치 e_b,max, 상단점을 잇는 직선과 상단 곡선 사이 거리 e_t의 상한치 e_t,max는 각각 공구 위치와 공구 자세의 스무딩 오차에 의해 아래의 식(18) 및 식(19)와 같이 계산된다.

$\[ e_{b,\mathrm{m}\mathrm{a}\mathrm{x}}=e_p \]$

(18)

$\[ e_{t,max}={he}_o \]$

(19)

식(19)에서 e_o는 라디안 단위의 각도이며, 상단점과 하단점 사이의 거리 h는 NC 데이터의 위치 지령 단위이므로 e_t,max는 원호의 길이로 근사하여 계산될 수 있다.

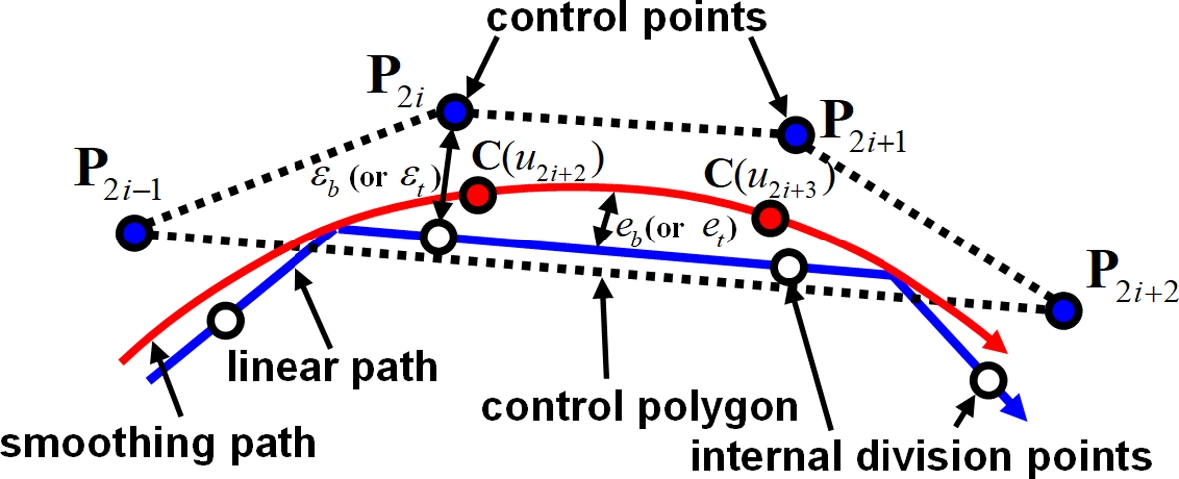
Fig. 8과 같이, 스무딩 곡선의 구간별 다항식은 4개의 조정점을 꼭지점으로 하는 조정 다각형(Control Polygon) 내부에 위치하기 때문에 e_b와 e_t는 각 내분점의 보정량 ε_c,b와 ε_c,t보다 항상 작은 값을 갖게 된다. e_b,max와 e_t,max를 고려한 내분점의 보정량 ε_b와 ε_t는 각각 식(20)과 식(21)에 의해 계산될 수 있다.

$\[ {\epsilon }_b=\min \left(e_{b,\mathrm{m}\mathrm{a}\mathrm{x}},{\epsilon }_{c,b}\right) \]$

(20)

$\[ {\epsilon }_t=\min \left(e_{t,\mathrm{m}\mathrm{a}\mathrm{x}},{\epsilon }_{c,t}\right) \]$

(21)

Fig. 8

Schematic of the smoothing error tolerance

3. PC 기반 5축 제어시스템에서의 실험 결과

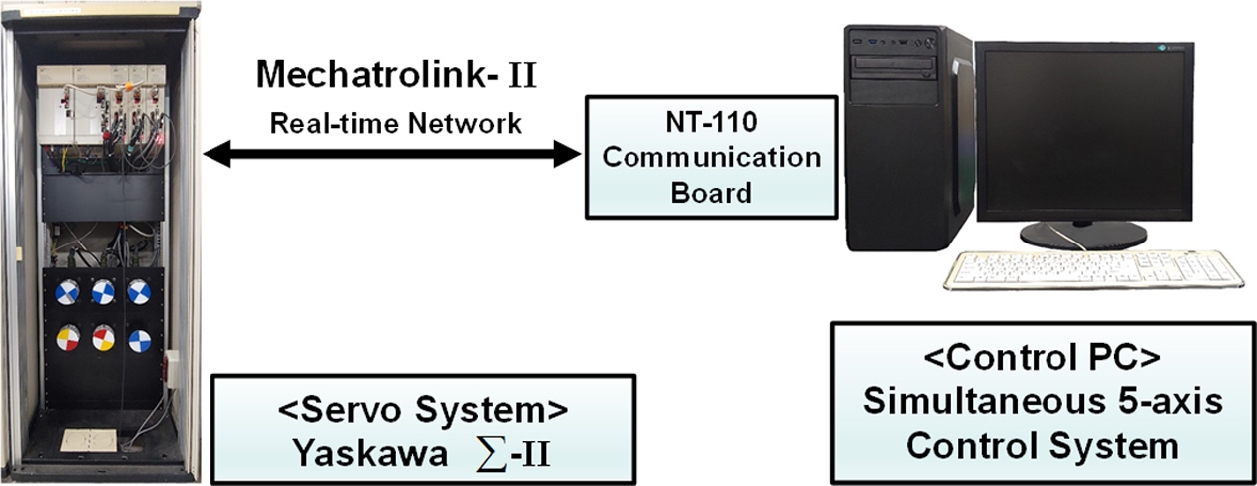
제시된 스무딩 방법을 Fig. 9와 같은 구조의 PC 기반 개방형 동시 5축 제어시스템에 구현하여 기존의 5축 TCP 제어 방식의 직선 보간기와 비교, 분석하였다. 이 시스템은 Mechatrolink-II 통신으로 Yaskawa사의 ∑-II 서보 드라이브를 통해 5개의 서보 모터를 동시 제어하며, 시스템의 제어 주기는 1 ms, BLU (Basic Length Unit)는 0.1 μm로 설정하였다. 테이블에 틸팅축(A)과 로터리(C) 축을 갖는 TRT (Table-Rotary-Tilting) 타입의 수직형 5축 머시닝 센터를 가정하여 역기구학 변환을 통해 각 축의 운동 지령을 계산하고, 무부하 상태로 기계 모션을 제어하였다.

Fig. 9

Simultaneous 5-axis control system

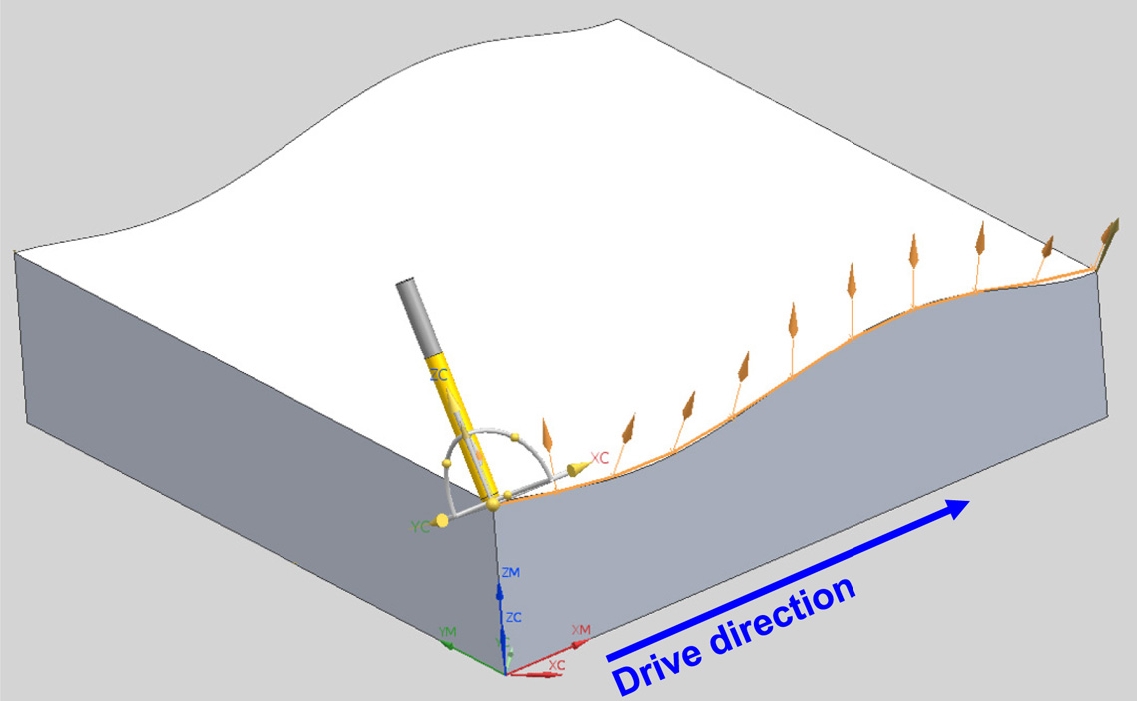
실험 시의 기준 CAD 형상은 Fig. 10의 곡면이고, 상용 CAM 소프트웨어를 이용하여 공구 위치는 공구의 진행 방향으로 이동하면서, 공구 자세가 양옆으로 변하도록 하였으며, 코드 오차(Chordal Deviation) 구속 조건을 5 μm로 설정, 총 134개의 NC 블록을 생성하였다. 스무딩 알고리즘의 공구 위치와 공구 자세의 스무딩 오차는 각각 5 μm와 0.5°로 설정하였다.

Fig. 10

Generation of tool path used in experiment

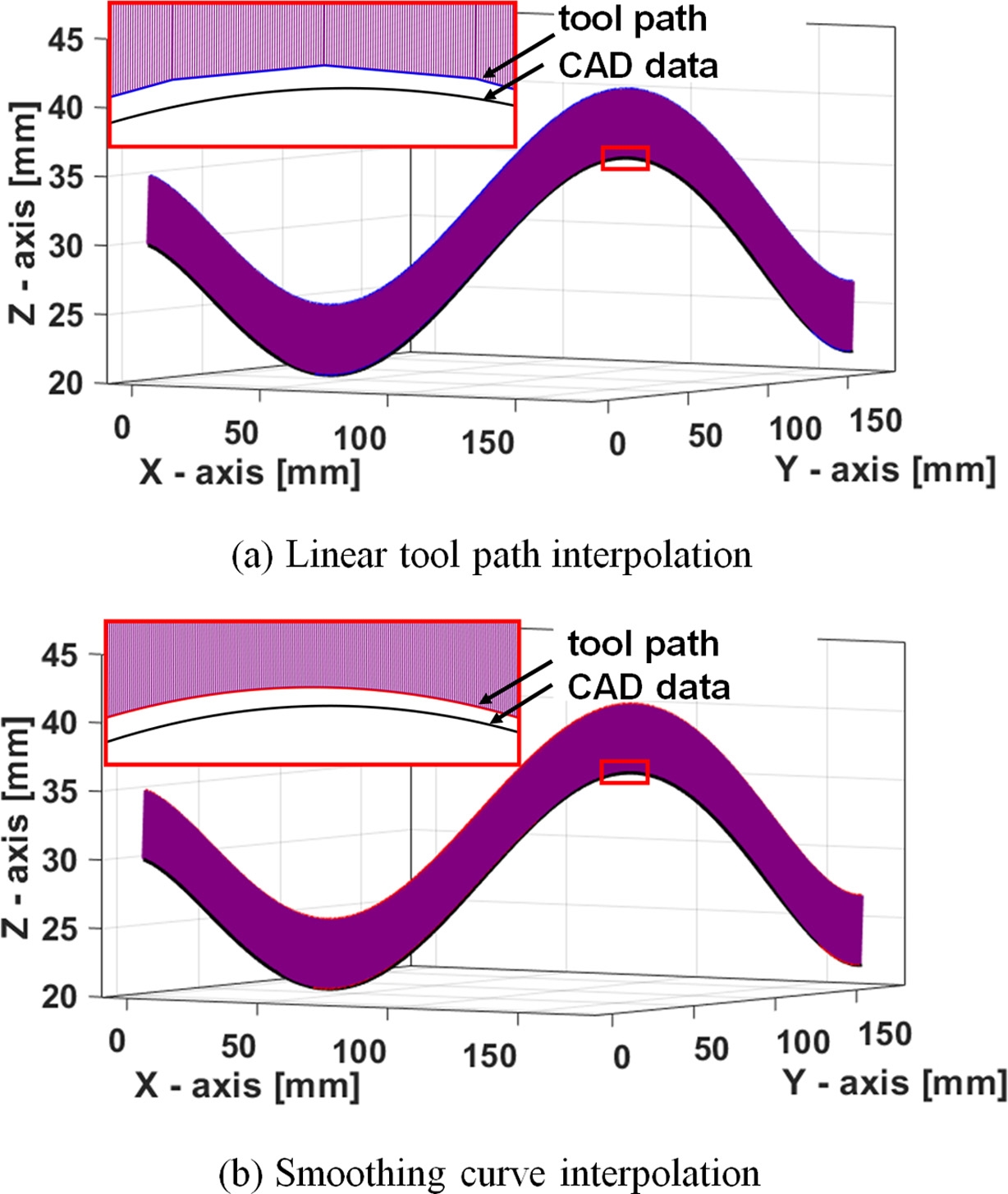
Fig. 11에 기존 직선 보간과 제시된 스무딩 방법을 적용한 보간 결과를 기준 CAD 형상과 비교하여 나타내었다. 공구 위치와 CAD 데이터 간에는 오프셋이 존재한다. Fig. 11(a)와 같이 직선 보간에서는 공구가 연결된 여러 개의 짧은 직선 선분을 따라 이동하므로 공구 접촉점도 이와 같은 직선 형상을 추종하게 되는 반면에, Fig. 11(b)의 결과에서 볼 수 있듯이 제시된 스무딩 방법에서는 보간된 공구 위치의 자취에 따라 공구 접촉점도 매끄러운 곡선 형상을 추종하게 된다.

Fig. 11

Comparison of tool path interpolations

실험에서는 시스템 특성에 의한 응답의 지연이 존재하고 구동계의 운동 성능에 따라 진동이 유발되기도 하여 보간된 형상 대비 실제 윤곽 정확도 등에 차이가 발생할 수 있다. 제시된 방법의 실효성을 검증하기 위하여 직선 보간과 제시된 스무딩 방법에 의한 윤곽 오차와 공구의 이송 속도, 가속도, 저크의 실험 결과를 비교해보았다.

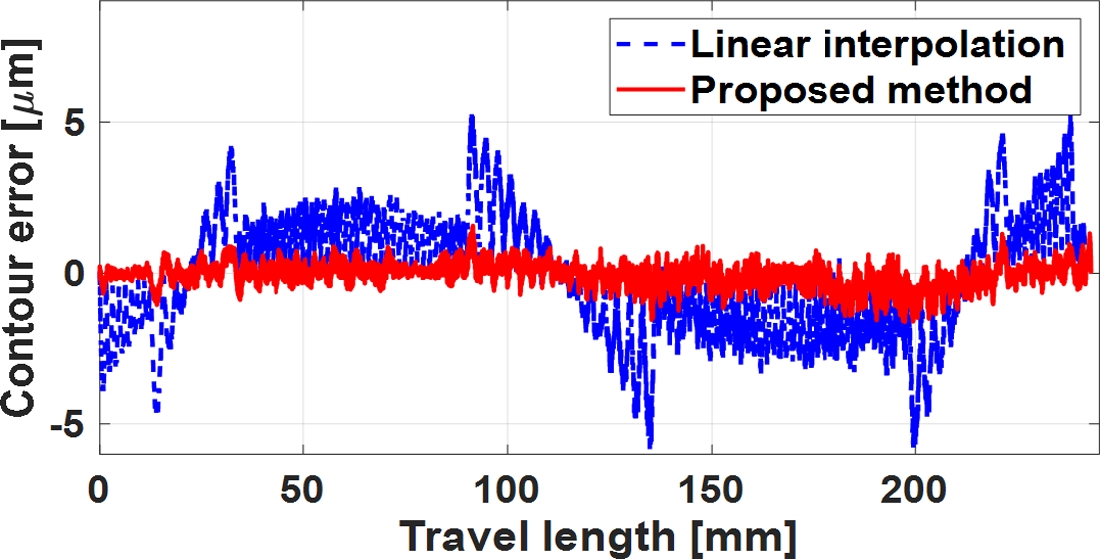
Fig. 12에 직선 보간 방식과 제시된 스무딩 방식에 대한 윤곽 오차를 비교하였는데, 기준 CAD 데이터와 공구 접촉점 사이의 거리를 계산하여 나타내었다. 제시된 스무딩 방법은 직선 보간 방식에 비해 공구 경로 전체에 걸쳐 윤곽 오차의 절대치와 변동 폭이 크게 감소되었음을 볼 수 있다. 직선 보간 방식은 기준 CAD 형상을 연속된 점으로 근사화하고 이 점들을 직선으로 연결한 형태로 보간하기 때문에, 각 직선 구간 내에서 보간점이 선형적으로만 계산되어 윤곽 오차가 설정된 코드 오차 구속 조건 값 내외에서 형성될 수밖에 없다. 반면에 제시된 스무딩 방법은 공구 접촉점이 기준 CAD 형상을 추종하도록 스무딩 곡선을 생성하여 보간하므로 윤곽 정확도를 개선할 수 있다.

Fig. 12

Comparison of contour errors in experiment

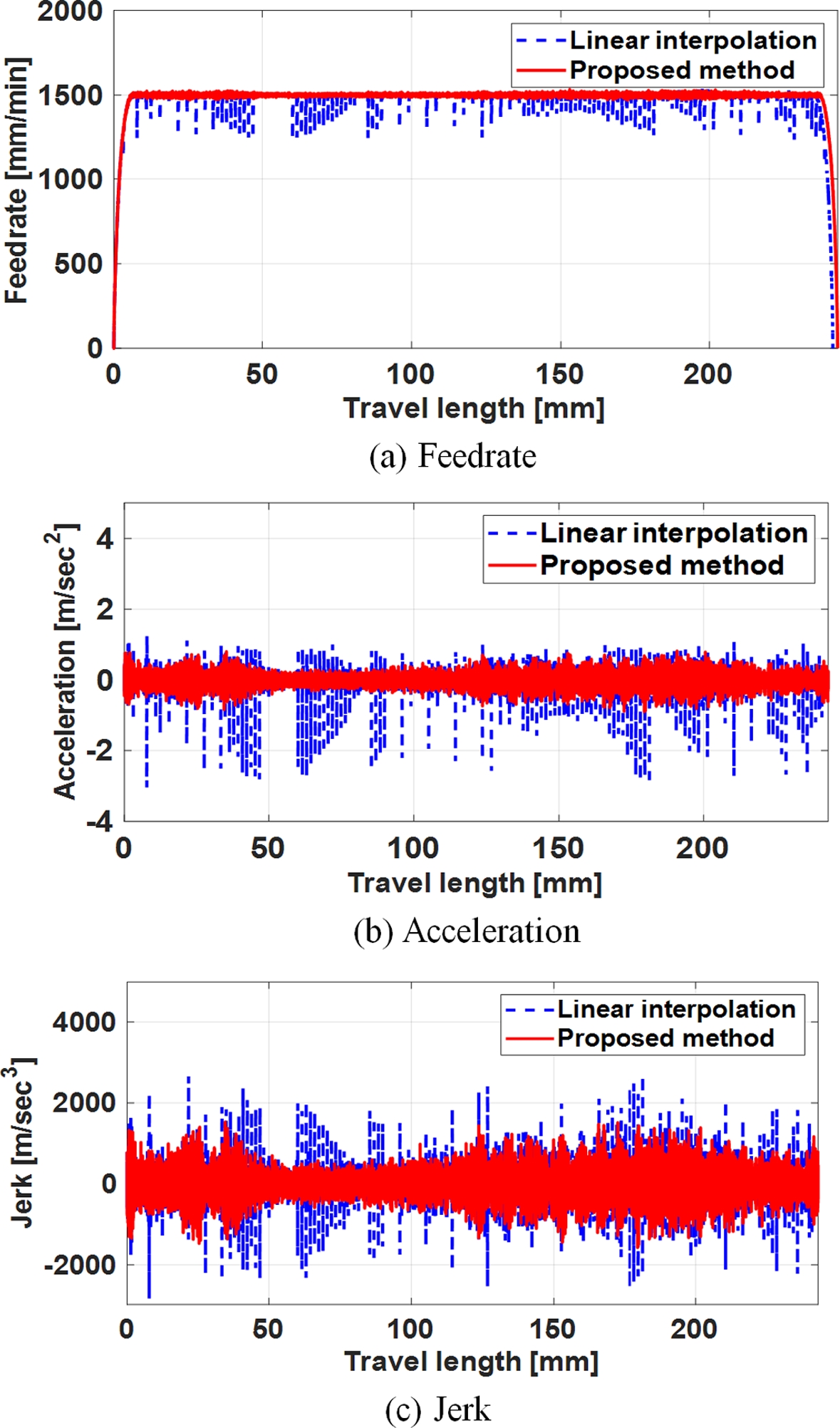
Fig. 13은 구동계의 엔코더 출력에 대해 정기구학 변환식을 적용하여 공작물 좌표계에서 공구의 이송 속도, 가속도와 저크를 나타낸 것이다. Fig. 13(a)의 결과와 같이 직선 보간 방식에서 나타나는 NC 블록 연결부에서의 이송 속도 변동이 제시된 방법에서는 거의 발생하지 않음을 확인할 수 있다. 또한 Figs. 13(b)와 13(c)를 통해 직선 보간 대비 제시된 방법의 가속도와 저크의 전반적인 크기가 감소되었음을 알 수 있다. 이는 직선 공구 경로를 보간할 경우 발생하는 각 연결부에서의 급격한 방향 변화가 제시된 스무딩 방법의 적용으로 완만하게 변환되었음을 알 수 있다. 다시 말해 이 결과는, 직선 보간 방식의 C⁰ 연속성이 스무딩에 의해 C² 연속성으로 바뀌게 되고 방향 변화가 매 보간마다 점진적으로 일어남으로 인해, 부드러운 가공면을 생성할 수 있음을 의미한다.

Fig. 13

Comparison of dynamic motion performance

Table 1에 본 실험을 통해 얻은 직선 보간 방식과 스무딩 방식의 윤곽 오차와 가속도, 저크를 정량적으로 비교 정리하였다.

Table 1

Comparison of experimental results

4. 결론

본 논문에서는 5축 공구 경로에 대한 스무딩 방법을 제시하였다. CAM 소프트웨어로 생성한 NC 데이터로부터 스무딩 곡선을 생성하기 위한 전처리 작업으로, 공구 위치의 간격에 맞춰 공구자세벡터를 조정하여 공구자세벡터 간 불규칙한 변동을 줄여주었다. 또한 공구의 상단점과 하단점을 정의하고, 상단점과 하단점의 경로에 대한 두 개의 B-스플라인 곡선을 생성한 후 동시 보간하여 공구 위치와 공구 자세를 계산하였다.

제시된 스무딩 방법을 PC 기반 5축 제어시스템에 구현하였으며, 보간된 공구 접촉점이 기준 CAD의 형상을 추종함으로써 직선 보간 방식과 비교하여 윤곽 정확도가 향상되고 직선의 연결부에서 발생하는 가속도와 저크가 감소됨을 확인하였다. 제시된 방법을 통해 복잡한 형상을 갖는 자유 곡면의 5축 가공에 대하여 가공물의 치수 정확도 개선과 가공면의 품위 향상이 가능할 것으로 기대된다.

Acknowledgments

본 연구는 산업통상자원부 지원의 “중소형 공작기계용 2계통제어 CNC와 서보, 스핀들 구동 유닛 국산화 개발” 과제에 의하여 수행되었음.

References

• Tajima, S. and Sencer, B., “Kinematic Corner Smoothing for High Speed Machine Tools,” International Journal of Machine Tools & Manufacture, Vol. 108, pp. 27-43, 2016. [https://doi.org/10.1016/j.ijmachtools.2016.05.009]
• Tajima, S. and Sencer, B., “Global Tool-Path Smoothing for CNC Machine Tools with Uninterrupted Acceleration,” International Journal of Machine Tools & Manufacture, Vol. 121, pp. 81-95, 2017. [https://doi.org/10.1016/j.ijmachtools.2017.03.002]
• Ho, M. C ., H wang, Y. R., and Hu, C. H ., “ Five-Axis T ool Orientation Smoothing Using Quaternion Interpolation Algorithm,” International Journal of Machine Tools & Manufacture, Vol. 43, No. 12, pp. 1259-1267, 2003. [https://doi.org/10.1016/S0890-6955(03)00107-X]
• Pateloup, V., Duc, E., and Ray, P., “Bspline Approximation of Circle Arc and Straight Line for Pocket Machining,” Computer-Aided Design, Vol. 42, No. 9, pp. 817-827, 2010. [https://doi.org/10.1016/j.cad.2010.05.003]
• Zhao, H., Zhu, L., and Ding, H., “A Real-Time Look-Ahead Interpolation Methodology with Curvature-Continuous B-Spline Transition Scheme for CNC Machining of Short Line Segments,” International Journal of Machine Tools & Manufacture, Vol. 65, pp. 88-98, 2013. [https://doi.org/10.1016/j.ijmachtools.2012.10.005]
• Yang, J., Hu, Q., and Ding, H., “A Two-Stage CNC Interpolation Algorithm for Corner Smoothing Trajectories with Geometric Error and Dynamics Constraints,” Proc. of the 9th International Conference on Digital Enterprise Technology-Intelligent Manufacturing in the Knowledge Economy Era, Vol. 56, pp. 306-310, 2016. [https://doi.org/10.1016/j.procir.2016.10.022]
• Fan, W., Lee, C. H., and Chen, J. H., “A Realtime Curvature-Smooth Interpolation Scheme and Motion Planning for CNC Machining of Short Line Segments,” International Journal of Machine Tools & Manufacture, Vol. 96, pp. 27-46, 2015. [https://doi.org/10.1016/j.ijmachtools.2015.04.009]
• Yang, J. and Yuen, A., “An Analytical Local Corner Smoothing Algorithm for Five-Axis CNC Machining,” International Journal of Machine Tools & Manufacture, Vol. 123, pp. 22-35, 2017. [https://doi.org/10.1016/j.ijmachtools.2017.07.007]
• Tulsyan, S. and Altintas, Y., “Local Toolpath Smoothing for Five-Axis Machine Tools,” International Journal of Machine Tools & Manufacture, Vol. 96, pp. 15-26, 2015. [https://doi.org/10.1016/j.ijmachtools.2015.04.014]
• Huang, J., Du, X., and Zhu, L. M., “Real-Time Local Smoothing for Five-Axis Linear Toolpath Considering Smoothing Error Constraints,” International Journal of Machine Tools & Manufacture, Vol. 124, pp. 67-79, 2018. [https://doi.org/10.1016/j.ijmachtools.2017.10.001]
• Cho, H. D., Jun, Y. T., and Yang, M. Y., “Five-Axis CNC Milling for Effective Machining of Sculptured Surfaces,” International Journal of Production Research, Vol. 31, No. 11, pp. 2559-2573, 1993. [https://doi.org/10.1080/00207549308956883]
• Langeron, J. M., Duc, E., Lartigue, C., and Bourdet, P., “A New Format for 5-Axis Tool Path Computation, Using Bspline Curves,” Computer-Aided Design, Vol. 36, No. 12, pp. 1219-1229, 2004. [https://doi.org/10.1016/j.cad.2003.12.002]
• Piegl, L. and Tiller, W., “The NURBS Book,” Springer, 2nd Ed., pp. 47-50, 1995. [https://doi.org/10.1007/978-3-642-97385-7_2]