Modeling and Validation of 3DOF Dynamics of Maglev Vehicle Considering Guideway

1. Introduction

Maglev (Magnetic-Levitation) trains and vehicles propel forward without mechanical contacts through the use of magnetic forces.¹ They are a viable transportation means with commercial operations in China and Japan as well as in Korea. The electromagnetic maglev uses attractive magnetic forces to lift up the vehicle and to maintain the levitation.

Since electromagnetic suspension is open-loop unstable, feedback control is necessary. Position sensors are typically used to measure the gap between the electromagnet (or vehicle body) and the guideway for feedback signal which is used by a controller for modulating magnetic forces.^1,2 If the guideways contain irregularities such as jumps, therefore, they would directly affect the performance as well as the stability of suspension. In addition, the safety would be seriously compromised if the vehicle encounters guideway jumps while moving at high speeds.

Fig. 1 shows actual pictures of maglev guideway joints. Some of them are joined across a fairly small gap, while others have somewhat large gaps over complicated depth profile of an intervening plate as shown in the right side of Fig. 1. If the joints contain jumps which are the vertical discrepancy across joints, they not only affect the suspension stability but also create vibrations that degrade the ride quality. Therefore, the regular inspections of guideway anomalies must be done in order to ensure safe and reliable operations. To meet these needs, several authors have proposed guideway monitoring systems (GMS), equipped with various sensors and monitor the irregularities of the guideway.^3-5 These systems collect coil currents, gap signals, and/or accelerations of the vehicle for processing. A method commonly employed is to measure the accelerations of GSM and obtain the guideway profile through double integration of accelerations.⁵ However, double integration amplifies even minute offset,⁶ corrupting the validity of results.

Fig. 1

Pictures of guideway joints. Some of them are joined by intervening plate as shown in the right picture

In order to develop a signal processing algorithm that extracts guideway jumps from sensor data, it is necessary to have well-defined jumps and various signals resulting from the jumps. This can be done either experimentally or by simulations. Experimental data would be a primary and ultimate choice. However, it is very difficult to set up a test rig that controls all parameters except guideway jumps. For example, vertical motions of vehicle due to guideway jumps inevitably induce lateral vibrations which would alter the dynamics. Virtual testing using a simulation model makes it possible to see the exact effects of any input as long as the model describes the actual system accurately. Furthermore, model-based methods⁷ can be used to estimate the guideway jumps if a system model is available.

A literature survey shows several research efforts that present mathematical dynamic models of a maglev vehicle with guideway irregularities. For example, Sinha describes a single DOF model that has the guideway jumps as the input.² Guideway irregularities have also been considered using power spectral density (PSD).⁸ However, little research have been done to specifically deal with guideway jumps and the dynamics due to jumps. In this paper, we present a dynamic model of a maglev vehicle considering guideway jumps and experimental validation of the model.

2. Dynamic Model of Maglev Vehicle System

2.1 Linearized Magnetic Force Model

Although the linearized force model in a maglev vehicle is well known,² the basic principles and the involving variables are essential in the presentation hereafter. Thus, the magnetic force model is described briefly here. Fig. 2 shows the front and side views of a magnetic actuator in a maglev vehicle. The displacement of the actuator assembly holding a gap sensor and an electromagnet is denoted by z, and defined to be upward positive. The actuator assembly is attached to the vehicle body. The magnet clearance, c, is defined as the air gap between the electromagnet and the guideway. The sensor signal, s, is a measure of distance between the sensor head and the guideway. The magnetic force is quadratic with respect to the clearance and the coil current, but it can be linearized if the variations of parameters from their nominal values are small as follows.

$\[ f=K_{z}c+K_{i}i \]$

(1)

Fig. 2

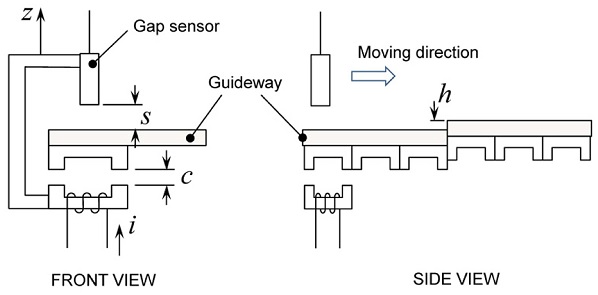
Schematic diagram of an electromagnetic actuator in a maglev vehicle. A guideway jump is denoted as h

Here, K_i is the actuator constant and K_z is the open-loop stiffness with a negative value. If the guideway has irregularities such as jumps, they in effect change the magnet clearance. Therefore, Eq. (1) can be modified as

$\[ f=K_z\left(c+h\right)+K_{i}i \]$

(2)

Since the electromagnet is attached to the vehicle body, the displacement of the body is related to the magnet clearance as

$\[ z=c_0-c \]$

(3)

where c₀ is the nominal clearance.

2.2 Dynamics of Vehicle Body

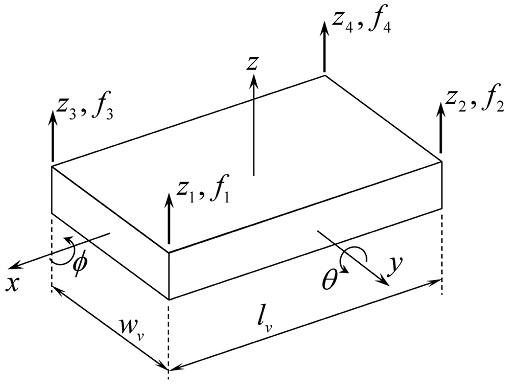
As far as the suspension of the vehicle body is concerned, we only need to consider vertical displacement (z in Fig. 2), the rotation around x axis (roll, ϕ), and the rotation around y axis (pitch, θ). At four corners of the body, an electromagnet assembly described above is attached and generates a magnetic force. Using the notation defined in Fig. 3, the kinematics between the coordinates of the mass center and the displacements at four corners can be written as

$\[ \left[\begin{array}{c}{z}_1\\ z_2\\ z_3\\ z_4\end{array}\right]=\left[\begin{array}{ccc}1& \frac{w_v}{2}& -\frac{l_v}{2}\\ 1& \hspace{0.33em}\frac{w_v}{2}& \frac{l_v}{2}\\ 1& -\frac{w_v}{2}& -\frac{l_v}{2}\\ 1& -\frac{w_v}{2}& \frac{l_v}{2}\end{array}\right]\left[\begin{array}{c}z\\ \varphi \\ \theta \end{array}\right] \]$

(4)

or simply as

$\[ \mathrm{z}=\mathrm{W}\mathrm{q} \]$

(5)

Fig. 3

Definition of coordinate system and displacements that are used in the dynamic model

Assuming that electromagnetic forces are acting at the four corners, the dynamic equations in a vector form are

$\[ \mathrm{M}\ddot{\mathrm{q}}={\mathrm{W}}^T\mathrm{f} \]$

(6)

where the mass matrix is defined as M = diag(m, I_xx, I_yy). Using the force model of Eq. (2), the dynamic equations can be revised as

$\[ \mathrm{M}\ddot{\mathrm{q}}={\mathrm{W}}^T{\mathrm{K}}_z\mathrm{c}+{\mathrm{W}}^T{\mathrm{K}}_z\mathrm{h}+{\mathrm{W}}^T{\mathrm{K}}_i\mathrm{i} \]$

(7)

where K_z and K_i are diagonal matrices with their diagonal elements are either K_z or K_i, respectively. Considering only the linear perturbations from the nominal values, Eqs. (3) and (5) can be inserted into Eq. (7):

$\[ \mathrm{M}\ddot{\mathrm{q}}=-{\mathrm{W}}^T{\mathrm{K}}_z\mathrm{W}\mathrm{q}+{\mathrm{W}}^T{\mathrm{K}}_z\mathrm{h}+{\mathrm{W}}^T{\mathrm{K}}_i\mathrm{i} \]$

(8)

Using a state-space vector $$ {\mathrm{x}}_m={\left[\mathrm{q}\mathrm{ }\dot{\mathrm{q}}\right]}^T$$, we can rewrite Eq. (8) into a state-space form as

$\[ \begin{array}{l}{\dot{\mathrm{x}}}_m={\mathrm{A}}_m{\mathrm{x}}_m+{\mathrm{B}}_{m,h}\mathrm{h}+{\mathrm{B}}_{m,i}\mathrm{i}\\ \mathrm{c}={\mathrm{C}}_m{\mathrm{x}}_m\end{array} \]$

(9)

where the matrices are defined as follows:

$\[ \begin{array}{l}{\mathrm{A}}_m=\left[\begin{array}{cc}0& \mathrm{I}\\ -{\mathrm{M}}^{-1}{\mathrm{W}}^T{\mathrm{K}}_z\mathrm{W}& 0\end{array}\right],\\ {\mathrm{B}}_{m,h}=\left[\begin{array}{c}0\\ {\mathrm{M}}^{-1}{\mathrm{W}}^T{\mathrm{K}}_z\end{array}\right],\hspace{1em}{\mathrm{B}}_{m,i}=\left[\begin{array}{c}0\\ {\mathrm{M}}^{-1}{\mathrm{W}}^T{\mathrm{K}}_i\end{array}\right],\\ {\mathrm{C}}_m=\left[\begin{array}{cc}\mathrm{W}& 0\end{array}\right]\end{array} \]$

(10)

2.4 Maglev System Model

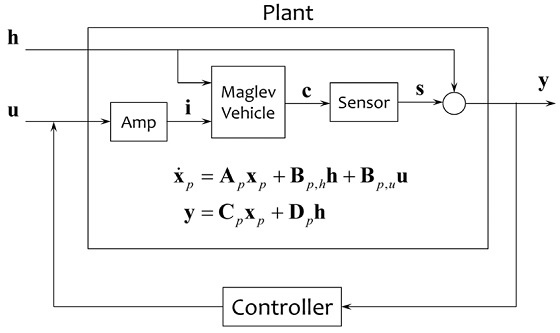
Aforementioned models of the amplifier, the maglev vehicle, and the sensor can be combined into a plant model. In a state-space form, this plant model can be written as

$\[ \begin{array}{l}{\dot{\mathrm{x}}}_p={\mathrm{A}}_p{\mathrm{x}}_p+{\mathrm{B}}_{p,h}\mathrm{h}+{\mathrm{B}}_{p,u}\mathrm{u}\\ \mathrm{y}={\mathrm{C}}_p{\mathrm{x}}_p+{\mathrm{D}}_p\mathrm{h}\end{array} \]$

(15)

where h represents guideway jumps, and u is the control input generated from a feedback controller.

The controller used in this research is a proportional-derivative (PD) type which supplies adequate damping by providing phase lead in the control bandwidth. Ideally, the transfer function of a PD controller is

$\[ G_{PD}\left(s\right)=K_P+K_{D}s \]$

(16)

However, Eq. (16) is not proper and thus unrealizable. The high-frequency gain of the derivative term must be restricted. The transfer function of a realistic PD controller should be

$\[ \frac{-u}{y}=G_{PD}\left(s\right)=K_P+\frac{K_{D}s}{{\tau }_{D}s+1} \]$

(17)

The system model including the controller can then be synthesized. The block diagram showing the signals and the connections are illustrated in Fig. 4.

Fig. 4

Block diagram of the maglev vehicle system including the dynamic model of the vehicle

One advantage of the state-space form model is the capability to access any signals in the model. For example, we can extract acceleration signals from the model. Using Eq. (8), accelerations at the four corners are

$\[ \begin{array}{l}\ddot{\mathrm{z}}=-\mathrm{W}{\mathrm{M}}^{-1}{\mathrm{W}}^T{\mathrm{K}}_z\mathrm{W}\mathrm{q}+\mathrm{W}{\mathrm{M}}^{-1}{\mathrm{W}}^T{\mathrm{K}}_z\mathrm{h}\mathrm{ }\\ +\mathrm{W}{\mathrm{M}}^{-1}{\mathrm{W}}^T{\mathrm{K}}_i\mathrm{i}\end{array} \]$

(18)

Since the amplifier output signal i is determined by the control input signal u using Eq. (11) which is in turn related to the plant output signal y by Eq. (17). Therefore, the acceleration signals can be written as a linear combination of states and guideway jumps.

3. Test Rig for Model Validation

In order to validate the maglev vehicle model, a scaled-down maglev system is utilized. Shown in Fig. 5 is a picture of the test rig. The electromagnets used in the vehicle are biased with permanent magnets. Thus, the coil currents only need to generate control forces. The vertical positions of the vehicle with respect to the guideway are measured by eight commercial eddy-current sensors (PU-20 from AEC Corp., Japan), grouped as a pair for each corner. The sensor signals are fed to a digital controller (MicroBox from Terasoft, Taiwan) through an A/D converter. The controller is run by xPC Target software.¹⁰ The command signals from the controller are sent to the current-mode amplifiers (JSP-180 from Copley Controls, USA). Integrated-chip type current sensors (ACS714 from Allegro, USA) are used for measuring coil currents. The sampling rate of the digital controller is 1.82 kHz. Several notable parameters of the test rig are summarized in Table 1.

Fig. 5

Picture of the test rig for model validation

Table 1

Parameters of maglev vehicle system

In order to simulate a guideway jump, a small piece of silicon-iron sheet (thickness of approximately 1 mm) is slid into the guideway between the guideway and the sensor to eliminate the cross coupling between the suspension and the forward motion. The signals are collected using the xPC Target machine and an auxiliary data acquisition system when the sheet is inserted into the left rear end (number 2 in our notation) of the vehicle.

4. Results and Discussions

Using the same jump input as in the test rig, computer simulations are carried out. Since the diameter of the eddy-current sensors are rather big (20 mm), the gap measurement would contain transitory periods when the sensor head is partially over the edge of the jump. The effect of this transition is approximated as a cosine curve of

where λ is the characteristic length and v is the forward speed of the vehicle. In this paper, it is assumed that the characteristic length is equal to the diameter of the eddy-current sensor.

When a jump disturbance is applied to the sensor number 2 (rear left), the measured clearances of all four actuators are shown in Fig. 6. The figure also displays the simulated clearance for comparison. All of the simulated clearances match well with the experimental data. The actuator number 2 responded a bit larger than the input of approximately 1 mm. Since the silicon-iron sheet is freely sliding on the guideway, the actual jump seen by the sensor might have been larger than the thickness of the sheet.

Fig. 6

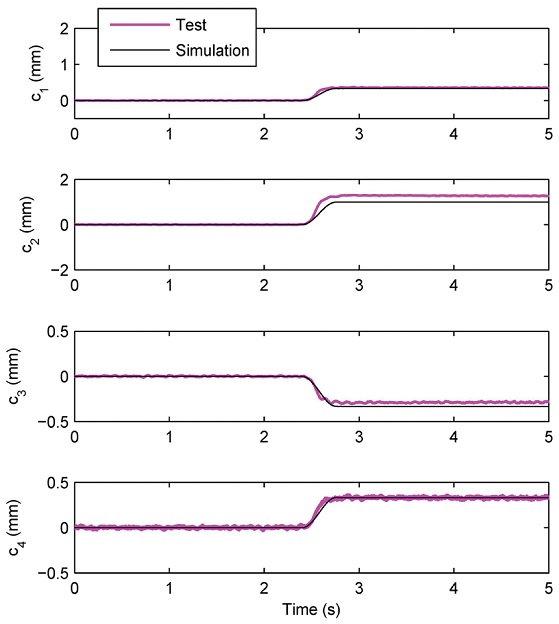
Simulated magnetic clearances at four actuators due to 1 mm guideway jump at sensor number 2. The jump is applied at 2.5 s. The simulated clearances are compared with corresponding test data

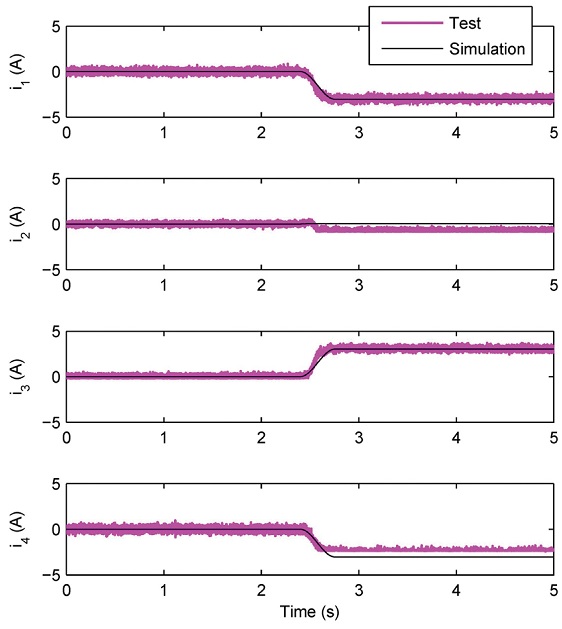
Comparisons of simulated coil currents with the measurements also show excellent agreement as shown in Fig. 7. It can be seen that the jump at c₂ is counteracted by the current jumps at other actuators. Since the amplifiers are a switching type, the current measurements have higher noise components than the gap signal.

Fig. 7

Simulated coil currents compared with measurements

5. Conclusions

In this paper, a dynamic model of a maglev vehicle is proposed. The model contains the effect of amplifier bandwidth, sampling delays, and anti-aliasing filters. The simulation model matches very well the measurements taken from a test rig, which indicates the validity of the model. In the future, this model will be utilized for virtual testing of the algorithms that estimate the irregularities of the guideway.

Acknowledgments

This research was supported by a grant (15RTRP-B070526-03) from Railroad Technology Research Program funded by Ministry of Land, Infrastructure and Transport of Korean government.

REFERENCES

• Han, H.-S. and Kim, D.-S., “Magnetic Levitation: Maglev Technology and Applications,” Springer, Dordrecht, pp. 1-243, 2016. [https://doi.org/10.1007/978-94-017-7524-3_7]
• Sinha, P. K., “Electromagnetic Suspension: Dynamics and Control,” IEE Control Engineering Series, Vol. 30, pp. 1-260, 1987.
• Nieter, W., “Guideway Monitoring during Operational Use on the First Transrapid Line in Shanghai,” Proc. of the 18th International Conference on Magnetically Levitated System and Linear Drives, pp. 480-485, 2004.
• Nieter, W. and Shao, J. C, “Long Wave Guideway Contour Monitoring,” Proc. of the 20th International Conference on Magnetically Levitated Systems and Linear Drives, 2008.
• Lee, J., Jo, J., Han, Y., Lee, C., and Sun, Y., “A Study on the Sensor Applications for Position Detection and Guideway Monitoring in High Speed Maglev,” Modern Mechanical Engineering, Vol. 4, No. 4, pp. 165-174, 2014. [https://doi.org/10.4236/mme.2014.44016]
• Choi, W., Yoo, S., Cha, K., Cho, C., Kim, S., et al., “Methods of Measuring the Vibrations of a Gun Tube under Impulse Loads,” Journal of Mechanical Science and Technology, Vol. 25, No. 12, pp. 2987-2993, 2011. [https://doi.org/10.1007/s12206-011-0821-1]
• Ljung, L., “System Identification: Theory for the User,” Prentice-Hall, Upper Saddle River, pp. 69-105, 1999.
• Yau, J. D., “Response of a Maglev Vehicle Moving on a Series of Guideways with Differential Settlement,” Journal of Sound and Vibration, Vol. 324, No. 3, pp. 816-831, 2009. [https://doi.org/10.1016/j.jsv.2009.02.031]
• Schweitzer, G. and Maslen, E. H., “Magnetic Bearings: Theory, Design, and Application to Rotating Machinery,” Springer, Dordrecht, pp. 333-334, 2009.
• Mathworks, MATLAB & Simulink, “xPC Target User’s Guide,” 2010.