유한요소해석에 기초한 다중 타원구 숏볼의 경사충돌에 의해 생성된 피닝잔류응력해

1. 서론

숏피닝 가공기술은 부품 또는 금속재료 표면에 무수히 많은 작은 구형의 강구들을 연속 다중충돌 시킴으로써 소성변형을 일으키고 압축잔류응력 층을 생성시키는 표면처리 기술 중 하나이다. 숏피닝 기술은 항공기 및 산업용 발전설비 부품, 철도차량, 자동차용 내구부품 등 다양한 산업분야에서 활발히 사용되고 있다.^1,2 따라서 부품 표면에 인가되는 인장응력에 저항하는 압축잔류응력의 크기 및 깊이를 예측하는 것은 매우 중요하다. 잔류응력은 보통 X-선 및 중성자 회절, 홀 드릴링, 식각법, 곡률-변형률 측정법, 빔 굽힘법 등으로 측정된다.^3,4 그러나 대부분 정확성, 민감성, 분해능, 편이성, 재료/기하형상에 따라 많은 제약을 받는다.^5,6 특히 숏피닝 잔류응력은 거의 X-선 회절 (XRD)에 의해 측정되는데 측정 시간이 상당히 길다는 점과 측정자의 숙련도에 따라 측정 값의 오차가 크다는 점이 가장 큰 문제로 대두되고 있다. 이와 같은 실험적 측정에 의한 문제들을 해결하기 위한 방법으로 최근 전산해석 기술의 꾸준한 성장으로 3차원 유한요소해석에 기초한 잔류응력 예측 연구들이 꾸준히 소개되고 있다. 국내외로 수 많은 연구자들에 의해 과거 수직 단일충돌 해석 연구부터 최근 다중충돌 연구에 이르기까지 수 많은 연구들이 수행되고 있다. 특히 최근에는 다중경사충돌 연구들^7,8이 중심을 이루고 있는 가운데 좀 더 사실적인 피닝현상을 구현하기 위해 랜덤충돌을 포함한 해석연구들도 소개되고 있다. 하지만 이들 선행된 숏피닝 잔류응력 해석연구들을 살펴보면 숏볼의 형상을 모두 완전한 구형으로 가정하고 있다. 사실상 숏피닝 공정에 사용되는 주강 숏볼들은 완전한 구형의 형상이 아니며 다양한 형상들로 제조된다.⁹ 또한 경강선을 절단하여 구형화 작업을 거쳐 제조되는 컷와이어 구형 숏볼들도 완전한 구형이라기 보다는 구형에 가까운 타원구 형상이 대부분을 차지한다. 이들 타원구형 숏볼은 장축과 단축이 존재하므로 사실상 충돌 후 재료표면에 다양한 모양의 압흔들을 생성시킨다. 결국 재료에 전이되는 충돌에너지도 각각 다르기 때문에 압축잔류응력의 크기 및 깊이도 달라진다. 이점에 착안하여 본 연구에서는 장축과 단축이 존재하는 타원구 형상의 숏볼을 새로운 해석모델로 구현하고 무작위적으로 다중 경사충돌되는 유한요소 모델을 제안하여 해석 후 완전한 구형의 해석해와 비교한다. 그리고 X-선 회절 (XRD: X-ray Diffraction)에 의한 실험해와 비교하여 해석모델의 유효성을 확인해 본다.

2. 타원구 숏피닝 유한요소모델

2.1 타원구 축비 (a/D)와 유한요소모델

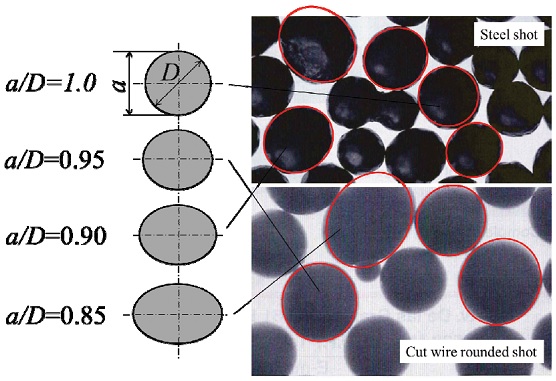
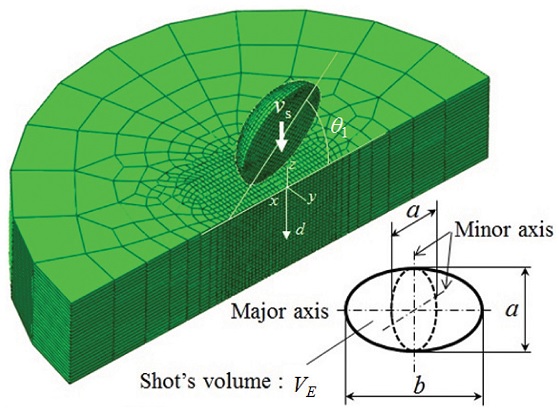
Fig. 1은 일반적으로 숏피닝 공정에 많이 사용되는 평균 지름이 0.8 mm인 주강 및 컷와이어 구형 숏볼 (CWRS: Cut Wire Rounded Shot)들을 보여준다. 대부분 완전한 구형이 아닌 타원구 형상을 가짐을 알 수 있다. 이를 바탕으로 본 연구에서는 랜덤 다중경사충돌 해석에 앞서, Fig. 2와 같이 장축 길이 b와 단축 길이 a를 갖는 3차원 타원구 숏볼이 포함된 유한요소 단일충돌 해석모델을 수립하였다. 이때 완전한 구형의 숏볼 직경 D를 0.8 mm로 하였으며, 이를 기준으로 타원구 숏볼의 단축길이 a와 D의 비가 a/D = 1.0, 0.95, 0.9, 0.85가 되도록 숏볼을 모델링하였다. 또한 완전한 구형 숏볼의 체적 V_S와 타원구 숏볼의 체적 V_E가 동일하도록 하였다. 이는 이들 숏볼들의 질량 변화가 충돌 후 잔류응력에 미치는 영향을 배제하고 숏볼의 형상변화에 대한 영향을 집중적으로 살펴보기 위해서이다. 해석시간의 유효성을 위해 숏볼과 재료를 x-축 기준으로 1/2이 되도록 모델링 하였으며, 대칭조건을 부여하였다. 또한 숏볼의 무게중심이 재료모델의 축 중심으로 충돌되도록 설정하였다. 이때 타원구 장축이 x-축과 일치되도록 배치하고 재료표면과 이루는 각 θ₁을 0°로 하였다.

Fig. 1

Various real shot ball with elliptical and spherical shapes

Fig. 2

The vertical impact FE model with an elliptical shot ball

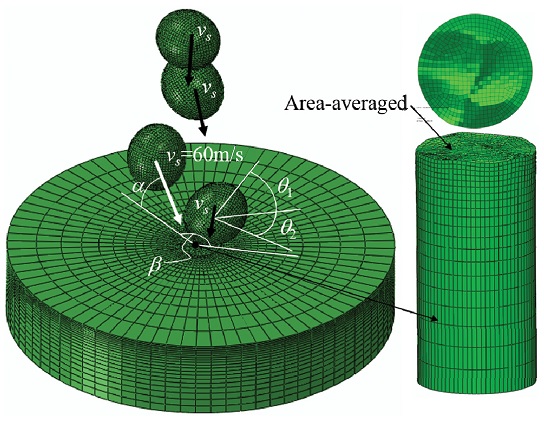
Fig. 3은 다중 타원구형 숏볼의 랜덤 경사충돌해석 모델을 보여준다. 다중 타원구 숏볼들은 숏볼의 질량 중심에서 임의의 회전 각들을 갖도록 설정된다. 먼저 타원구 장축과 x-축이 이루는 각을 θ₁이라 하고, x-축을 0°로 하였을 때 장축이 반시계 방향으로 회전된 각을 θ₂라 정하였다. 그리고 이들 각들은 다중 타원구 숏볼들이 무작위적으로 충돌 되는 현상을 고려하여 임의의 각도들로 배치된다. 재료의 해석모델은 3차원 전체모델로 설정하였으며, 바닥 면은 완전구속 처리를 하였다.

Fig. 3

The random angled-impact FE model with elliptical multi-shots

3. 타원구 단일충돌 예비 해석

3.1 유효 축비 (a/D)의 선정

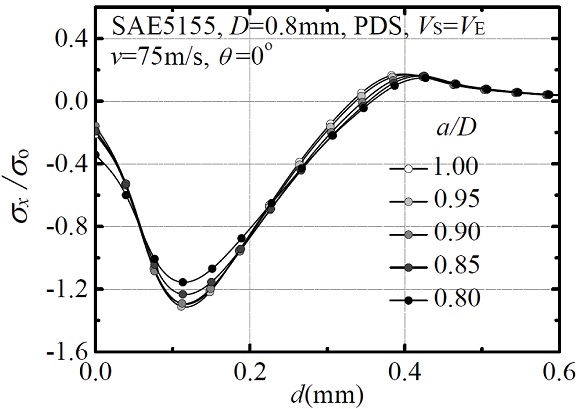
Fig. 4는 Fig. 1에서 정의된 타원구 축비 (a/D)가 1.0, 0.95, 0.9, 0.85일 때 단일충돌 후 재료 표면에 생성된 x-축 방향의 잔류응력 (s_x/s_o)을 보여준다. 이들 잔류응력들은 숏볼이 충돌된 재료모델의 축 중심으로부터 깊이 방향으로 얻어진다. 통상적으로 숏피닝의 효과는 최대압축잔류응력의 크기와 깊이를 통해 예측된다. Fig. 4에서 최대압축잔류응력 해석해는 약 0.12 mm 깊이에서 a/D가 1.0 - 0.9일 때 가장 유용한 피닝잔류응력 해를 주었다. 또한 표면에서는 a/D가 0.8일 때를 제외하고 모두 수렴된 해를 주었다. 이들 표면 및 최대압축잔류응력을 동시에 만족하는 유효 a/D 범위는 1.0 - 0.9이며, 이는 SAE J441 및 SAE J444에 규정된 숏피닝 입자의 기준 범위를 만족한다.^11,12

Fig. 4

Residual stresses with various axis ratio (a/D) of an elliptical shot ball in FE model

3.2 기울임각 (θ)의 효과

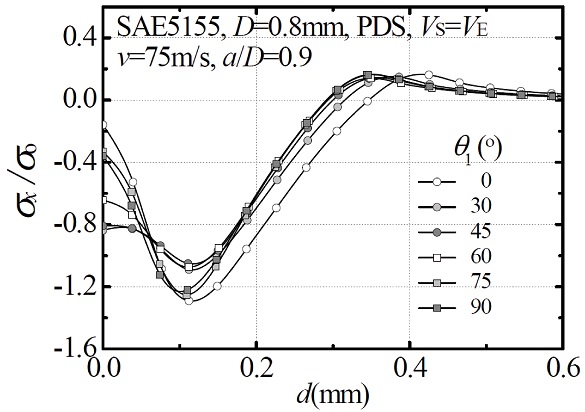
Fig. 5는 타원구 숏볼의 장축이 재료표면과 이루는 각 θ₁의 변화에 따른 유한요소 피닝잔류응력 들을 보여준다. 이때 축비 a/D = 0.9를 반영하였다. 이는 Fig. 4의 해석결과를 바탕으로 완전한 구형 (a/D = 1.0) 보다는 타원구의 영향이 클 것으로 판단 되기 때문이다. θ₁을 0°, 30° - 90°까지 15° 간격으로 해석을 수행하였다. 해석 후 θ₁이 0°, 75° - 90°일 때 최대압축잔류응력 해가 컸으며 유효하였다. 즉 타원구 숏볼의 장축 또는 단축이 재료표면과 수직에 근접할 때이다. 이는 완전구형의 숏볼은 숏볼 질량중심이 충돌위치 축선과 일치하여 충돌에너지가 그대로 전이되나, 타원구 숏볼은 0°와 90°를 제외하면 질량중심이 충돌위치 축선으로부터 떨어져 있어 충돌시 모멘텀으로 인해 운동에너지의 불균형을 초래하기 때문으로 판단된다.

Fig. 5

Residual stresses with turn angle (q1) of an elliptical shot ball in FE model

4. 타원구 다중랜덤 경사충돌 유한요소모델

4.1 축비 (a/D), 기울임각 (θ₁), 회전각 (θ₂) 선정

Fig. 3의 타원구 다중숏 랜덤충돌해석 모델에 Fig. 4에서 얻은 유효 축비 (a/D)를 반영하고 랜덤성을 고려하여 기울임각 (θ₁)과 회전각 (θ₂)을 정했다. 이들 변수 값들은 각각 1.0 ≤ a/D ≤ 0.9, 0° ≤ θ₁ ≤ 90°, 0° ≤ θ₂ ≤ 360°에 포함되며, 타원구 다중 숏볼들의 랜덤한 상태를 구현하기 위해 Table 1과 같이 상용 수치계산 프로그램의 난수발생 명령어를 이용하여 숏볼의 질량중심을 기준으로 임의의 기울임 및 회전 각도들을 정리하였다.

Table 1

Axis ratio and turn angle of the elliptical shots

4.2 충돌위치 및 투사각 (a)의 선정

본 절에서는 다중 경사충돌의 랜덤충돌 특성을 반영하기 위하여 숏볼들이 재료표면에 충돌되는 임의의 충돌위치 좌표 (x, y)들과 숏볼들이 충돌되는 투사각 (a) 및 투사방향 (b)을 선정하였다. Table 2는 이들 랜덤 충돌을 위한 투사위치, 투사각 및 투사방향을 보여주며, 난수발생 함수에 의해 도출되었다.

Table 2

Impact input conditions of elliptical shot ball

4.3 숏피닝 실험에 기초한 투사속도 선정

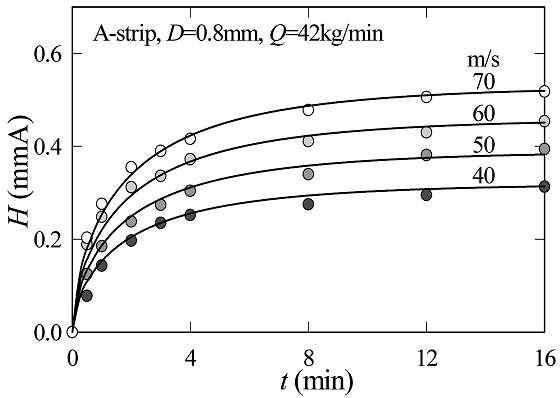
본 연구에서는 실험적 숏피닝 공정조건에 기초하여 XRD 잔류응력 측정해를 얻고 이를 유한요소 해석해와 비교했다. 최대한 사실해에 근접되도록 XRD 실험해를 주는 피닝 조건들을 해석모델에 반영하였다. Tables 3과 4는 각각 해석에 사용된 피닝가공 변수 및 XRD 측정 조건들을 보여준다. 또한 Fig. 6은 숏피닝 가공 정도를 가늠하는 알멘선도를 보여준다. 이는 숏피닝 가공시간에 따른 알멘스트립의 아크하이트 (H)로 표현된다. 본 연구에서는 실험적 피닝커버리지 C = 87%이고, 아크하이트 H = 0.375 mmA이므로, 이를 Fig. 5의 알멘선도에 대응시키면 투사속도 v_s = 60m/s가 얻어진다. 그리고 이 투사속도를 해석모델에 채용하였다.

Table 3

Experimental shot peening conditions

Table 4

The measurement conditions of X-ray diffraction

Fig. 6

The experimental Almen saturation curves

5. 타원구 다중랜덤 경사충돌해석

5.1 완전구형 숏볼의 다중랜덤 수직 및 경사 충돌해석

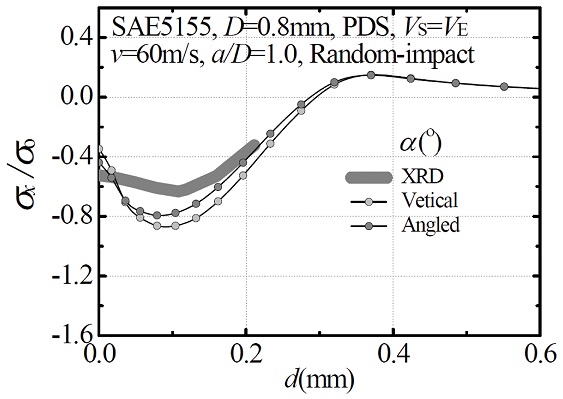
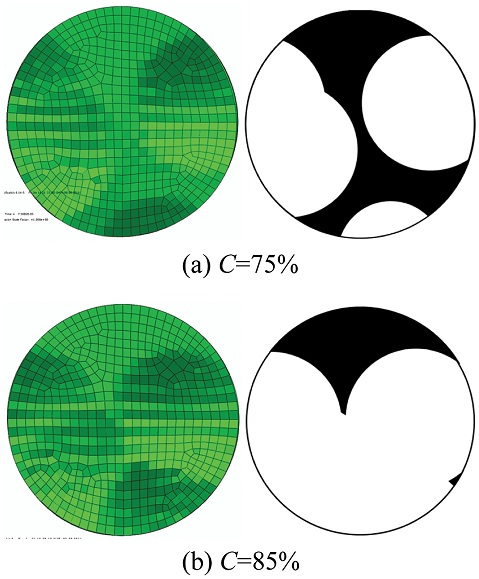
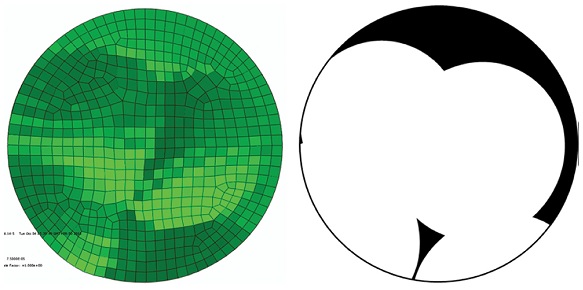
타원구 다중랜덤 경사충돌 해석에 앞서 기존의 구형 숏볼이 포함된 3차원 다중랜덤 수직충돌해석을 수행하였다. 이들 모든 다중충돌 해석해들은 Fig. 3의 해석모델 중심부의 일정 면적에 포함되는 모든 절점들에서의 평균된 면적평균해¹³들로 얻어진다. 이는 통상적으로 XRD 실험해가 X-선이 조사되는 면적에서 평균된 해를 주기 때문이다. 또한 좀 더 사실적이고 근접한 해를 얻기 위해 유한요소 피닝커버리지^7,14를 반영하였다. 실험 커버리지가 87%이므로 이에 근접한 유한요소 피닝커버리지를 주는 숏볼의 개수 4개를 적용하였다. Fig. 7은 Fig. 3 좌측의 유한요소모델 중심부에 완전한 구형 숏볼 4개를 연속 랜덤충돌시켜 해석 후 모델 중심의 일정면적에 해당하는 지정된 단위 셀(우측)의 표면부터 깊이방향의 면적평균 피닝잔류응력해를 보여준다. 충돌위치는 Table 2의 랜덤 특성이 고려된 좌표 값들을 활용하였다. 두 해석해들 모두 실험해와 차이를 보이긴 하나 경사충돌 해석해가 수직충돌 해석해보다 XRD 실험해에 근접함을 알 수 있다. Fig. 8의 좌측은 숏볼 4개가 연속 충돌된 후의 단위 셀 모델에서의 유한요소 피닝커버리지를, 우측은 압흔의 밀집정도를 계산하기 위한 흑백 이미지를 보여준다. 여기서 흰색의 면적비율이 커버리지에 해당된다. Fig. 8(a)의 수직충돌인 경우 약 80%, (b)의 랜덤경사충돌인 경우 약 85%의 커버리지를 주어 랜덤경사충돌이 실험커버리지에 근접하였다. 이들 잔류응력의 수렴 정도와 커버리지의 근접성을 기준으로 경사충돌 해석모델을 타원구형 숏볼의 다중랜덤 경사충돌 해석에 활용하기로 하였다.

Fig. 7

Comparison with FE residual stresses in spherical shot model and XRD experimental one

Fig. 8

The FE peening coverage of (a) Vertical impact and (b) Angled-Impact in spherical shot model

5.2 타원구형 숏볼의 다중랜덤 경사충돌 해석

본 절에서는 Fig. 3의 유한요소 모델에 Tables 1과 2의 조건으로 랜덤 특성이 고려된 타원구 숏볼들의 다중랜덤 경사충돌 해석을 수행하였다. 이때 숏볼들이 경사충돌 되도록 랜덤한 투사각 a와 x-축을 0°로 할 때 투사되는 방향(각) b를 반영하였다. 이때 투사속도를 수평성분과 수직성분으로 분해하여 입력하였으며, 충돌시에는 v_s = 60m/s가 되도록 하였다. 또한 수직충돌 해석과 같이 면적평균해 개념을 도입하였다.

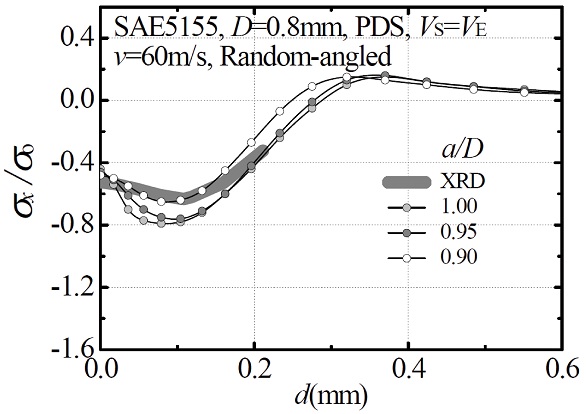
Fig. 9는 타원구형 숏볼의 다중랜덤 경사충돌 해석 후 얻은 x-방향의 잔류응력 분포를 보여준다. 이때 축비 a/D는 1.0, 0.95, 0.9를 반영하였다. 해석 후 축비 a/D가 점차 작아질수록 표면잔류응력은 변화가 거의 없으나, 최대압축잔류응력은 점차 작 은 값을 주어 a/D = 0.9일 때 해석해가 XRD 실험해에 가장 근접한다. 또한 Fig. 10과 같이 유한요소 피닝커버리지가 약 C = 85%로 실험 피닝커버리지 87%에 매우 근접함을 알 수 있다. 이로부터 타원구의 축비가 0.9인 다중랜덤 경사충돌 해석모델이 잔류응력 및 피닝커버리지 모두 실험해를 만족시키며, 기존 해석모델들에 비해 가장 사실적인 숏피닝 공정을 모사할 수 있는 해석모델임을 확인하였다. 이 모델은 향후 여러 산업 군에서 내피로 부품이나 금속 소재들의 피닝잔류응력을 예측할 수 있는 모델로 충분히 활용될 것으로 기대된다.

Fig. 9

Residual stresses with various axis ratio (a/D) of the random angled-impact FE model

Fig. 10

FE peening coverage (C= 85%), when a/D is 0.9

6. 결론

본 연구에서는 타원구형 숏볼을 갖는 다중랜덤경사충돌 유한요소 모델을 제안하였다. 기존 해석연구들 대부분 완전한 구형숏볼들을 사용해 오고 있으나 실제 숏피닝 공정에서는 제조되는 숏볼의 품질검사를 거쳐 일정 기준의 축비 범위에 포함된 숏볼들만 선별하여 공급하고 있다. 이 점에 착안하여 먼저 유효 축비(a/D)를 반영하고 랜덤충돌을 고려하여 숏볼의 질량중심을 기준으로 기울임각 (θ₁)과 회전각 (θ₂)을 각각 1.0 ≤ a/D ≤ 0.9, 0° ≤ θ₁ ≤ 90°, 0° ≤ θ₂≤ 360°와 같이 정리하였다. 랜덤충돌 현상을 반영하고자 상용수치계산 프로그램의 난수발생 명령어를 이용하여 타원구 다중숏볼들이 임의의 위치에 충돌되도록 좌표 값을 반영하였다. 또한 최대한 사실해에 근접되도록 XRD 실험해를 주는 실험적 피닝 조건들을 채용하였다. 이때 실험적 피닝커버리지 C = 87%와 아크하이트 H = 0.375 mmA를 알멘선도에 대응시켜 투사속도 v_s = 60m/s를 얻었다. 타원구형 숏볼의 다중랜덤 경사충돌 해석 후 a/D = 0.9일 때 해석해가 XRD 실험해에 가장 근접하였으며, 유한요소 피닝커버리지도 약 C = 85%로 실험 피닝커버리지에 근접하였다. 이로부터 본 연구에서 제안한 해석모델의 유효성과 기존 해석모델들보다 가장 사실적인 숏피닝 공정을 모사할 수 있어 매우 유용함을 확인하였다. 이는 다양한 산업 현장에서 내피로 부품 및 금속 소재들의 피닝잔류응력을 예측하는데 적극적으로 활용될 것으로 판단된다.

Acknowledgments

이 논문은 2015학년도에 청주대학교 산업과학연구소가 지원한 학술연구조성비(특별연구과제)에 의해 연구되었음.

REFERENCES

• Rhee, H. W. and Park, Y. S., “Distribution Characteristics of Residual Stresses Induced by Shot-Peening in the Aircraft Structural Material,” J. Korean Soc. Precis. Eng., Vol. 21, No. 5, pp. 149-157, 2004.
• Lyu, S. K., Jeon, H. J., and Moon, B. H., “A Study on the Effect of Shot Peening Treatments on the Strength of Carburized Gears,” J. Korean Soc. Precis. Eng., Vol. 14, No. 9, pp. 61-67, 1997.
• Verpoort, C. M. and Gerdes, C., “Influence of Shot Peening on Material Properties of Turbine Blades,” Shot Peening Theory and Application, Institute for Industrial Technology Transfer International, Vol. 1, pp. 11-70, 1989.
• Garibay, R. P. and Terry, S. L., “High Technology Shot Peening for Automotive Industry,” Shot Peening Theory and Application, Institute for Industrial Technology Transfer International, Vol. 1, pp. 227-234, 1991.
• Carlsson, S. and Larsson, P. L., “On the Determination of Residual Stress and Strain Fields by Sharp Indentation Testing. Part I: Theoretical and Numerical Anaysis,” Acta Materialia, Vol. 49, No. 12, pp. 2179-2191, 2001. [https://doi.org/10.1016/S1359-6454(01)00122-7]
• Suresh, S. and Giannakopoulos, A. C., “A New Method for Estimating Residual Stresses by Instrumented Sharp Indentation,” Acta Materialia, Vol. 46, No. 16, pp. 5755-5767, 1998. [https://doi.org/10.1016/S1359-6454(98)00226-2]
• Kim, T., Lee, H., Kim, M., and Jung, S. H., “A 3D FE Model for Evaluation of Peening Residual Stress under Angled Multi-Shot Impacts,” Surface and Coatings Technology, Vol. 206, No. 19, pp. 3981-3988, 2012. [https://doi.org/10.1016/j.surfcoat.2012.03.078]
• Kim, T., Lee, H., Hyun, H. C., and Jung, S. H., “Effects of Rayleigh Damping, Friction and Rate-Dependency on 3D Residual Stress Simulation of Angled Shot Peening,” Materials and Design, Vol. 46, pp. 26-37, 2013. [https://doi.org/10.1016/j.matdes.2012.09.030]
• Gillespie, R. D., “Its Effect on Process Consistency and Resultant Improvement in Fatigue Characteristics,” Proc. of the 5th International Conference on Shot Peening, pp. 81-90, 1993.
• Kim, T., Lee, H., Hyun, H. C., and Jung, S. H., “A Simple but Effective FE Model with Plastic Shot for Evaluation of Peening Residual Stress and Its Experimental Validation,” Materials Science and Engineering A, Vol. 528, No. 18, pp. 5945-5954, 2011. [https://doi.org/10.1016/j.msea.2011.04.012]
• SAE J441, “Cut Wire Shot,” http://standards.sae.org/j441_201310, / (Accessed 17 January 2017)
• SAE J444, “Cast Shot and Grit Size Specifications for Peening and Cleaning,” http://standards.sae.org/j444_201209/, (Accessed 17 January 2017)
• Kim, T., Lee, J. H., Lee, H., and Cheong, S. K., “An Area-Averaged Approach to Peening Residual Stress Under Multi-Impacts Using A Three-Dimensional Symmetry-Cell Finite Element Model with Plastic Shots,” Materials and Design, Vol. 31, No. 1, pp. 50-59, 2010. [https://doi.org/10.1016/j.matdes.2009.07.032]
• Kim, T., Lee, H., Jung, S. H., and Lee, J. H., “A 3D FE Model with Plastic Shot for Evaluation of Equi-Biaxial Peening Residual Stress due to Multi-Impacts,” Surface and Coatings Technology, Vol. 206, No. 13, pp. 3125-3136, 2012. [https://doi.org/10.1016/j.surfcoat.2011.12.042]