롤투롤 시스템에서 플렉시블 소재에 인가된 장력과 분사 높이가 액적 접촉각에 미치는 영향

1. 서론

대량, 고속 생산을 위한 롤투롤 연속공정 시스템(Roll-to-Roll Continuous System)은 최근 주목 받고 있는 공정 중 하나이다. 디스플레이 산업 구조가 웨어러블(Wearable) 기기, 곡면 TV, 곡면 스마트폰 등의 제품으로 재편되고 있으며 그를 생산하는 제조 및 공정 기술의 발전이 주를 이루고 있다. 이러한 시장성, 기술 발전 요인에 의해 플렉시블 소재(Flexible Substrate)가 주목 받고 있는 동시에 수요도 급증하고 있다. 이와 같이 롤투롤 연속공정 시스템은 급증한 수요와 원가 절감의 측면을 만족시키기 위한 시스템으로 대량, 고속 생산이 가능하여 차세대 공정으로서 활용되기에 적합하다. 플렉시블 디스플레이는 복합적 물질이 적층 구조를 이루는 것이 특징이다. 특히, 다층의 적층 공정으로 생산된 제품에서 폭 방향 두께 편차를 최소화하는 것이 제품 성능 결정에 중요한 요소가 된다. 다층적층을 위한 단일 소재간 접합공정(Laminating)에서 소재 사이에 일정 두께의 박막(Thin Layer) 코팅액 도포 공정이 제품의 폭 방향 두께 편차를 결정하게 된다. 이러한 박막 코팅이 가능한 공정에는 스프레이(Spray), 슬롯-다이(Slot-Die) 코팅 등의 방법이 있다.¹ 코팅층의 횡 방향 두께 편차를 최소화하기 위해서는 코팅액의 단일 최적화뿐만 아니라 코팅액과 공정간 발생하는 상호작용을 고려해야 한다.^2-4

Busscher와 Arends⁵ 등에 의해 소재의 표면 거칠기(Surface Roughness)가 고착 액적(Sessile Droplet)의 접촉각(Contact Angle)형성에 미치는 영향을 소재의 다양한 거칠기 환경에서 실험적으로 확인하였다.

Lee⁶ 등은 간섭계(Interferometer)를 사용하여 얻어진 이미지로 플렉시블 소재에 인가된 장력이 소재 표면거칠기에 영향을 미치는 것을 실험적으로 검증하였다.

Good과 Koo⁷에 의해 액적의 크기가 고착 액적의 접촉각 형성에 영향을 미치는 것이 확인되었다. 이 연구를 통해 접촉각 형성에 중력이 중요한 변수로 작용하는 것을 확인할 수 있었다.

기존연구에서 고착 액적의 접촉각 형성에 관한 연구가 많이 진행되었지만, 공정간 상호작용을 고려하지 못하였다. 따라서, 본 연구에서는 코팅액형상과 공정간의 상호작용을 확인하기 위해 플렉시블 소재에 인가된 장력과 액적의 분사 높이가 고착 액적의 접촉각형성에 미치는 영향을 분석함으로써 공정변수간 상호작용을 확인하였다.

2. 고착 액적의 접촉각 형성에 미치는 영향

2.1 장력의 영향

Fig. 1은 롤투롤 장비 개략도를 나타낸다. 롤투롤 시스템에서 이송되는 소재는 장력을 인가 받는다. 소재의 인가된 장력은 수학적 장력모델에서 소재 폭 방향으로 일정하다고 가정된다.⁸ 하지만 실제로 장력은 소재 폭 방향으로 중앙에서 최대, 양 끝단에서 최소로 나타난다.⁹ 장력이 증가할수록 중앙과 양 끝단에서 장력 편차는 가중되기 때문에 장력 편차를 최소화하기 위해서는 저장력 범위에서 소재를 이송해야 한다. 하지만 생산성을 높이기 위한 고속 이송조건에서는 장력 수준을 높이는 것이 필요하다. 왜냐하면 저장력-고속 이송조건에서는 소재와 롤 사이 공기층이 유입되어 미끌림(Slip) 발생 및 감김 공정에서는 소재와 감김롤 층간 공기가 유입되면 텔레스코핑(Telescoping) 등의 결함이 발생되기 때문이다.^10-13 이러한 결함은 소재에 인가된 장력을 높임으로써 발생 빈도를 감소시킬 수 있다. 따라서 롤투롤 공정에서 장력제어는 중요한 이슈 중 하나이다.

Fig. 1

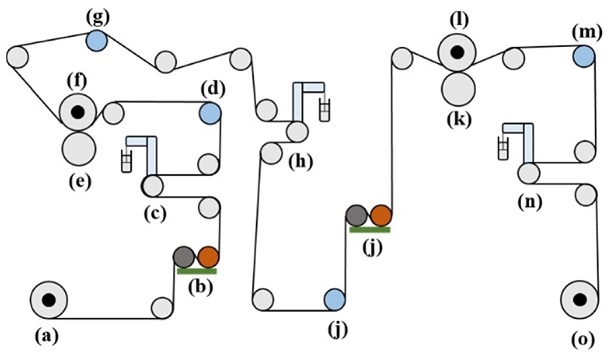
The schematic of roll-to-roll continuous systems: (a) Unwinder, (b), (j) EPC, (c), (h), (n) Dancer, (d), (g), (i), (m) Load cell, (e), (k) Nip roll, (f) Driven roll, (j) Master speed, (o) Rewinder

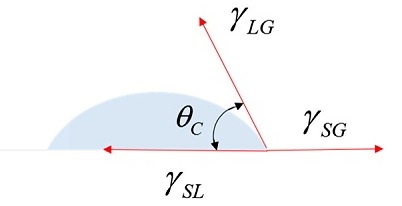
Fig. 2는 고착 액적의 개략도를 나타낸다. 식(1)은 영의 방정식(Young’s Equation)으로, 접촉각과 표면 에너지에 대한 상관관계를 나타낸다.

$\[ {\gamma }_{SG}-{\gamma }_{SL}-{\gamma }_{LG}\cos {\theta }_C=0 \]$

(1)

Fig. 2

The schematic of sessile droplet in Young’s equation

γ_SG는 고체-기체간의 계면 에너지, γ_SL은 고체-액체간의 계면 에너지, γ_LG는 액체-기체간의 계면 에너지를 각각 나타낸다. θ_C는 평형 접촉각(Equilibrium Contact Angle)으로 소재의 표면 에너지에 대한 정보가 주어지면 영의 방정식을 통해 이론적으로 계산 가능하다.

앞서 언급된 Lee⁶ 등의 연구에 의해 소재에 인가된 장력이 소재 표면 거칠기에 영향을 미친다는 것을 확인했다. 식(2)는 후크의 법칙(Hooke’s Law)을 나타내고, 후크의 법칙을 통해 장력이 인가된 플렉시블 소재는 연신됨을 알 수 있다.

$\[ T=AE\epsilon \]$

(2)

T는 장력, A는 소재의 단면적, E는 소재의 탄성계수, ε은 연신률을 나타낸다.

장력에 의해 연신된 소재는 표면 상태 변화로 인하여 표면 에너지가 변하게 된다. 변화된 표면 에너지는 고착 액적의 접촉각 형성에 영향을 미치게 된다. Fig. 3은 소재 인가된 장력이 3 kgf, 5 kgf, 7 kgf일 경우의 고착 액적의 형상이다. 본 연구에서는 소재에 인가된 장력의 변화가 고착 액적의 접촉각 형성에 미치는 영향을 실험적으로 검증한다.

Fig. 3

The images of sessile droplet according to tension levels: (a) 3 kgf, (b) 5 kgf, (c) 7 kgf

2.2 분사 높이의 영향

Good⁷ 등에 의해 액적의 크기에 따른 고착 액적의 접촉각 변화가 확인되었다. 액적의 부피가 클수록 중력의 영향을 받는 액적의 면적이 증가 한다. 따라서 액적의 크기가 증가할수록 크기가 작은 액적에 비해 형상이 퍼지는 경향을 나타난다. 그 결과로 고착 액적의 접촉각 형성에 중력이 중요 변수로 작용함을 알 수 있다. 액적의 분사 높이가 높을수록 액적이 소재에 고착되기까지 걸리는 체공시간이 증가하기 때문에 분사 높이는 접촉각 형성에 영향을 미치게 됨을 알 수 있다. 본 연구에서는 분사 실험을 통해 액적의 분사 높이가 접촉각 형성에 미치는 영향을 확인한다. Fig. 4는 일정 장력 조건에서 분사 높이에 따른 고착 액적의 형상을 나타낸다.

Fig. 4

The images of sessile droplet according to drop height levels (a) 1 mm, (b) 25 mm

3. 실험

3.1 실험 준비

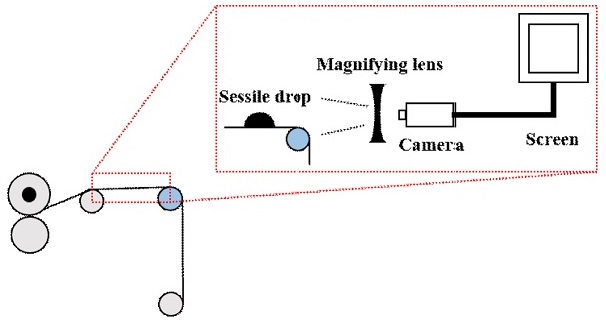
Fig. 5는 실험 장비의 구성도를 나타낸다. 플렉시블 소재로 Polyethylene Terephthalate (PET) 필름을 사용하였고, 액적은 상온의 물을 사용하였다. 물은 수소 결합(Hydrogen Bond)에 의해 다른 액체 물질에 비해 분자간의 응집력이 강하다. 따라서 물은 다른 물질과 접촉하여도 물 분자간에 응집이 강해 접촉각 측정에 용이한 특성을 가진다.

Fig. 5

Experimental setup of the equipment in roll-to-roll systems

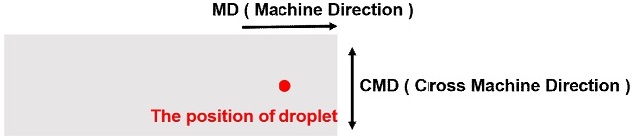
일정량의 액적을 분사하기 위해 마이크로 피펫을 사용하였다. 마이크로 피펫의 사용 범위는 20 - 200 μL이며, 50 μL의 사용범위에서 오차범위는 0.44% 이하이고, 변동계수(Coefficient of Variation)는 0.14% 이하의 성능을 갖는다. 실험에서는 100 μL의 분사조건을 사용하였다. Fig. 6은 액적의 분사 위치를 나타낸다. 고착 액적의 접촉각 형성에 장력의 영향을 확인하기 위하여 장력이 최대로 인가되는 소재 중앙부에 액적을 분사하여 접촉각을 측정하였다.

Fig. 6

The position of droplet on the flexible substrate

3.2 접촉각 측정

고착 액적의 접촉각 측정은 공개 영상 분석 소프트웨어인 ImageJ의 Drop_Analysis를 사용하였다. Drop_Analysis에서는 Drop Snake와 LBADSA 두 가지의 접촉각 측정 방식을 제공한다. LBADSA 법은 Young-Laplace 곡선을 고착 액적 형상에 맞추어 접촉각을 측정하게 된다. 이 방법은 30° 미만의 접촉각에서는 Young-Laplace 곡선이 얻어 지지 않는 단점이 있으나, 좌우 접촉각이 같고 Drop Snake 방식보다 안정적인 장점이 있기 때문에 본 연구에서는 접촉각 측정을 위하여 LBADSA 법을 사용하였다.

Table 1은 접촉각 측정 결과와 분사 높이에 따른 접촉각 형성의 경향을 나타내고, Table 2는 장력에 따른 접촉각 형성의 경향을 나타낸다. 실험은 각 조건 별 10번 수행하였으며, 10개의 실험 데이터 중 최대, 최소 접촉각을 제외한 8개 데이터의 평균값을 사용하였다.

Table 1

The sign of dθ/dh and contact angle of sessile droplet on a flexible substrate

Table 2

The sign of dθ/dT and contact angle of sessile droplet on a flexible substrate

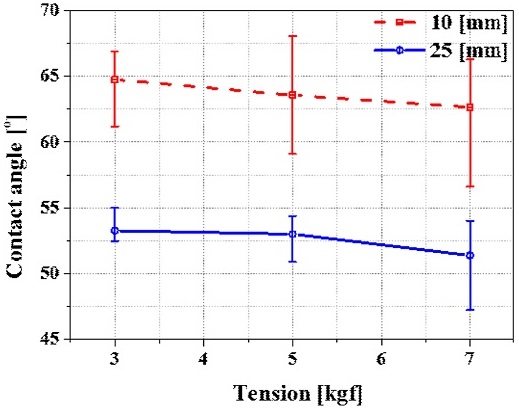
접촉각은 10 mm의 분사 높이에서 장력이 3 kgf일 경우 64.75°, 장력이 5 kgf일 경우 63.57°, 장력이 7 kgf일 경우 62.68°로 측정되었고, 25 mm의 분사 높이에서 장력이 3 kgf일 경우 53.26°, 장력이 5 kgf일 경우 53.00°, 장력이 7 kgf일 경우 52.61°로 측정되었다.

Fig. 7은 장력, 분사 높이에 따른 고착 액적의 접촉각을 나타낸다. Tables 1과 2 및 Fig. 7을 통해 접촉각 형성의 경향을 파악 할 수 있다. 모든 경우에서 분사 높이의 증가는 접촉각 감소를 야기하고, 장력이 증가할수록 평균 접촉각은 감소하는 경향을 나타지만 부분적으로 접촉각 변화가 없거나 접촉각이 증가하는 경우가 발생한다. 따라서 장력의 변화에 의해 형성되는 고착 액적의 접촉각은 분사 높이에 의해 형성되는 접촉각에 비해 외부요인에 민감하게 반응함을 알 수 있다.

Fig. 7

The contact angle of sessile droplet according to tension and drop height

4. 실험계획법

소재에 인가된 장력 및 액적의 분사 높이가 고착 액적의 접촉각 형성에 미치는 영향을 확인하기 위해 실험계획법(Design of Experiment)을 수행하였다. Table 3은 변수 및 변수의 수준을 나타낸다. 장력은 3수준(3, 5, 7 kgf), 분사 높이는 2수준(10, 25 mm)으로 설정하였다.

Table 3

Variables and levels for design of experiment

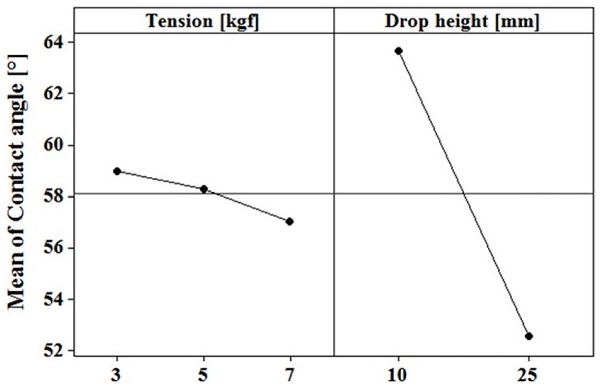
Fig. 8은 주효과도(Main Effects Plot)를 나타내며, 장력과 분사 높이가 고착 액적 접촉각 형성에 미치는 영향을 나타낸다. 주효과도를 통해 고착 액적의 접촉각 형성에 장력변화는 분사 높이 변화에 비해 영향이 미미함을 확인할 수 있다. 그렇지만 장력이 증가함에 따라 접촉각은 감소하는 경향을 나타내므로, 장력의 변화는 접촉각 형성에 영향을 미치는 것을 알 수 있다.

Fig. 8

The main effects plot for contact angle: tension and drop height

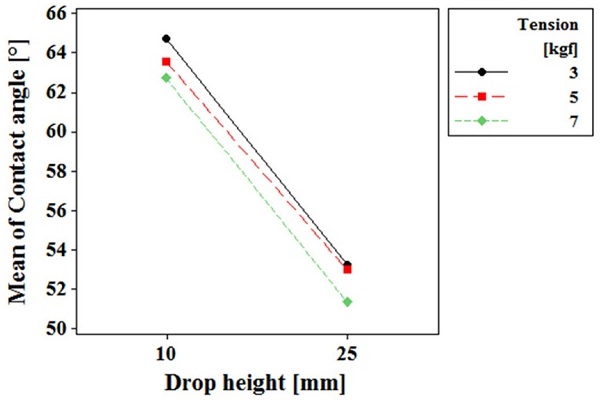
Fig. 9는 교호작용도(Interaction Plot)를 나타낸다. 교호작용도 분석 결과, 장력과 분사 높이 간 교호작용이 유의하지 않음을 확인할 수 있다.

Fig. 9

The interaction plot for contact angle: tension and drop height

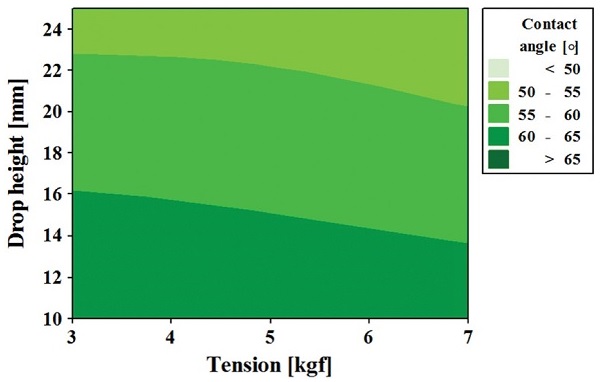
Fig. 10은 등고선도(Contour Plot)를 나타낸다. 등고선도에서는 장력 및 분사 높이의 조건 별 고착 액적의 접촉각을 나타낸다. 등고선도를 통하여 장력과 분사 높이가 증가할수록 접촉각은 감소하는 것을 확인할 수 있다. 또한 장력이 높은 수준(7 kgf)에서는 분사 높이가 접촉각형성에 민감하게 반응함을 확인할 수 있다.

Fig. 10

The contour plot of contact angle versus tension and drop height

5. 결론

본 연구에서는 롤투롤 연속공정 시스템에서 플렉시블 소재에 인가된 장력과 액적의 분사 높이가 고착 액적의 접촉각형성에 미치는 영향을 분석하였다.

(1) 고속 공정에서는 고장력 범위의 소재 이송이 필요하기 때문에 장력 변화가 코팅액 형상의 형성에 미치는 영향을 규명하기 위해 본 연구에서 분사 실험을 통해 확인하였다.

(2) 고착 액적의 접촉각 측정 결과를 통해 접촉각 형성에 미치는 영향은 장력에 비해 분사 높이의 영향이 우세함을 확인하였다. 따라서 연구결과는 스프레이 코팅 등과 같이 분사 높이 조절이 가능한 공정에서 액적 분사 높이 설정의 기초데이터로 사용 가능할 것으로 보인다.

(3) 장력은 분사 높이에 비해 접촉각 형성에 미치는 영향이 미미하지만, 분사 높이는 장비 가동조건에서 고정되는 변수이다. 하지만 장력의 경우 구동롤의 속도 제어나, 외란에 의해 실시간으로 변하는 요소이기 때문에 장력의 변화가 공정상 미치는 영향을 규명하는 것은 중요하다. 본 연구에서는 소재에 인가된 장력의 변화가 고착 액적 접촉각 형성에 미치는 영향을 실험과 분석을 통해 확인하였다.

(4) 액적 분사 실험을 통해 고착 액적의 접촉각 형성에서 장력의 효과를 확인하였고, 플렉시블 소재에 인가된 장력에 의해 소재는 연신되어 소재 표면 에너지가 변하는 것을 실험 결과를 통해 검증하였다.

(5) 본 연구에서는 롤투롤 공정에서 실시간으로 변하는 장력 제어의 중요성을 확인하였고, 연구결과는 장력 제어를 통한 박막 코팅액의 횡방향 두께편차 최소화 기법의 가이드라인으로 사용될 것으로 사료된다.

Acknowledgments

본 연구는 2016년도 한국연구재단(NRF-2014R1A1A1003477)의 지원을 받아 수행된 연구임.

REFERENCES

• Park, J., Shin, K., and Lee, C., “Roll-to-Roll Coating Technology and Its Applications: A Review,” Int. J. Precis. Eng. Manuf., Vol. 17, No. 4, pp. 537-550, 2016. [https://doi.org/10.1007/s12541-016-0067-z]
• Park, J., Shin, K., and Lee, C., “Improvement of Cross-Machine Directional Thickness Deviation for Uniform Pressure-Sensitive Adhesive Layer in Roll-to-Roll Slot-Die Coating Process,” Int. J. Precis. Eng. Manuf., Vol. 16, No. 5, pp. 937-943, 2015. [https://doi.org/10.1007/s12541-015-0122-1]
• Nguyen, H. A. D., Lee, C., and Shin, K.-H., “Approach to Optimizing Printed Conductive Lines in High-Resolution Roll-to-Roll Gravure Printing,” Robotics and Computer-Integrated Manufacturing, Vol. 46, pp. 122-129, 2017. [https://doi.org/10.1016/j.rcim.2017.01.003]
• Nguyen, H. A. D., Shin, K., and Lee, C., “Multi-Response Optimization of R2R Gravure Printing Using Orthogonal Array and Principal Component Analysis as a Weighting Factor,” The International Journal of Advanced Manufacturing Technology, pp.1-12, 2016. [https://doi.org/10.1007/s00170-016-9685-y]
• Busscher, H., Van Pelt, A., De Boer, P., De Jong, H., and Arends, J., “The Effect of Surface Roughening of Polymers on Measured Contact Angles of Liquids,” Colloids and Surfaces, Vol. 9, No. 4, pp. 319-331, 1984. [https://doi.org/10.1016/0166-6622(84)80175-4]
• Lee, C., Kang, H., Kim, C., and Shin, K., “A Novel Method to Guarantee the Specified Thickness and Surface Roughness of the Roll-to-Roll Printed Patterns Using the Tension of a Moving Substrate,” Journal of Microelectromechanical Systems, Vol. 19, No. 5, pp. 1243-1253, 2010. [https://doi.org/10.1109/JMEMS.2010.2067194]
• Good, R. J. and Koo, M., “The Effect of Drop Size on Contact Angle,” Journal of Colloid and Interface Science, Vol. 71, No. 2, pp. 283-292, 1979. [https://doi.org/10.1016/0021-9797(79)90239-X]
• Shin, K.-H., “Tension Control,” Tappi Press, pp. 1-18, 2000.
• Linna, H., Parola, M., and Virtanen, J., “Better Productivity by Measuring Web Tension Profile,” Proc. of 55th Appita Annual Conference, pp. 305-311, 2001.
• Lee, J. and Lee, C., “An Advance Model for the Numerical Analysis of the Radial Stress in Center-Wound Rolls.” International Journal of Mechanical Sciences, Vol. 105, pp. 360-368, 2016. [https://doi.org/10.1016/j.ijmecsci.2015.11.016]
• Shelton, J. J. and Reid, K. N., “Lateral Dynamics of a Real Moving Web,” ASME Journal Dynamics System, Measurement, Control, Vol. 93, No.3, pp. 180-186, 1971. [https://doi.org/10.1115/1.3426494]
• Shin, K.-H. and Kwon, S.-O., “The Effect of Tension on the Lateral Dynamics and Control of a Moving Web,” IEEE Transactions on Industry Applications, Vol. 43, No. 2, pp. 403-412, 2007. [https://doi.org/10.1109/TIA.2006.889742]
• Lee, C., Kang, H., Kim, H., and Shin, K., “Effect of Taper Tension Profile on the Telescoping in a Winding Process of High Speed Roll-to-Roll Printing Systems,” Journal of Mechanical Science and Technology, Vol. 23, No. 11, pp. 3036-3048, 2009. [https://doi.org/10.1007/s12206-009-0906-2]