판재의 소성변형 거동을 동정하기 위한 새로운 응력-변형률 모델

1. 서론

판재 성형의 수치 해석에서 가장 중요한 문제는 재료의 응력-변형률의 관계를 표현하는 근사적인 방정식을 얼마나 정확하게 선택하느냐는 것이다. 이러한 응력-변형률 관계식은 변형률 경화, 변형 속도 민감도, 열적 완화와 같은 다양한 소성현상들을 나타낸다. 현장에서 사용되는 대부분의 상용 금속 재료들에 있어서 변형률 경화는 넥킹에 저항하는 재료의 주된 요소이며, 유동 응력 하에서의 변형률 속도 민감도와 온도에도 부수적으로 관여한다. 이에 본 연구는 판재의 변형률 경화 거동에 대해 논의하고자 한다.

많은 연구에서 변형률 경화는 두 가지의 큰 형태로 나뉠 수 있다. 첫 번째는 대변형 하에서의 포화응력 모델(e.g. Brown-Anand Model, MTS Model, Modified Bodner-Partom Model, Lin-Wagoner Model)이고, 두 번째는 대변형 하에서의 무한 응력 모델(e.g. Zirilli-Armstrong Model, Rusinek-Klepazko Model, Khan-Huang-Liang Model)이다.¹ 첫 번째 형태는 통상적으로 지수법칙(Exponent Law) 또는 Voce 모델이라 칭하고, 두 번째 형태는 멱법칙(Power Law) 또는 Swift 모델이라고 한다. 이들의 일반적인 형태는 다음과 같다.^2,3

여기서 Voce 모델의 재료 상수인 A, b와 Swift 모델의 K, n은 각각 커브 피팅에 의해 구해지고, (ε₀, σ₀)는 재료의 항복점에서의 변형률과 응력이다. 전형적인 멱법칙 모델은 강과 같은 BCC 구조의 재료에 적합하고, 지수법칙 모델은 알루미늄이나 구리 같은 FCC 구조에 잘 적합하다. 앞서 언급한 구성식과 더불어 독립적인 기본 함수들을 조합한 기술적 방법도 있다. 그러나 조합 형태는 더 많은 미결정 파라미터들을 포함하고 있어 판재 성형의 수치적해석에 더 많은 계산을 필요로 한다.

이 연구의 목적은 BCC, FCC, HCP 구조의 재료를 포함하는 모든 미세 구조 금속의 인장 실험 데이터를 완벽하게 모델화할 수 있는 새로운 응력 변형률 모델(Kim-Tuan Hardening Model)을 개발하는 것이다. 이를 위해 먼저 다양한 판재 재료의 단축 인장 시험을 수행하여 응력-변형률 데이터를 획득한다. 본 연구에서는 서로 다른 격자구조를 가지는 Al6016-T4, DP980, CP Ti 판재를 사용하였다. Kim-Tuan 모델로 세가지 재료를 커브 피팅하여 기존의 Swift와 Voce 모델과 비교하여 우수성을 입증한다. 또한 본 연구를 통하여 굽힘 공정에서 CP Ti 판재의 스프링백을 예측할 수 있는 제안된 경화 모델의 응용도 수행한다. 재료의 항복 곡선을 표현하기 위해 Hill의 이방성 항복 조건식을 적용한다.⁴ 등방 운동 경화의 진전은 Armstrong-Frederick의 비선형 운동 경화 이론을 기초로 모델링 한다.^5,6 본 연구에서 제안된 모델의 변형률 경화 예측의 정확도를 평가하기 위해 굽힘 시험을 실시하고 계산된 결과와 비교하였다.

2. 새로운 변형률 경화 모델

Swift나Voce 모델과 같은 변형률 경화 모델이나 이를 조합한 형태는 CP Ti 판재의 응력-변형률 데이터와의 피팅에서 잘 맞지 않는 경향이 있다. 또한 통상적으로 사용되는 다른 형태의 방정식들도 CP Ti 판재의 변형률 증분에서의 응력 평가를 완벽하게 수행하지 못한다. 따라서 새로운 변형률 경화 모델의 필요성이 강조되고 있다. 이에 CP Ti 판재의 응력-변형률 관계를 잘 표현할 수 있는 Kim-Tuan 경화 모델을 제안한다.

여기서 T, m, c는 제안된 방성식의 계수이다. Kim-Tuan 방정식은 σ₀를 생략하고 c를 무한대로 보내면 Swift 방정식으로, m에 0의 값을 넣으면 Voce 방정식으로 간단하게 변환된다.

2.1 Kim-Tuan 모델의 의존변수

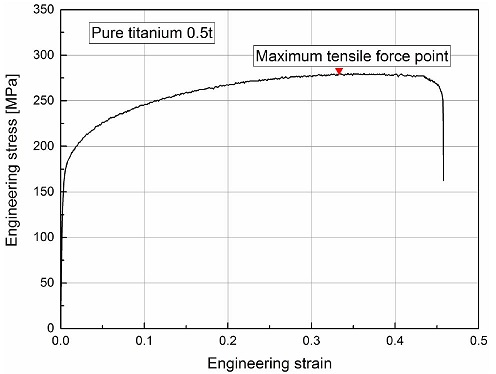
Fig. 1은 CP Ti 판재를 압연방향(0° 방향)으로 단축 인장시험을 실시한 공칭 응력-변형률 선도이다.

Fig. 1

Engineering stress-strain data of CP Ti sheet along rolling direction

재료는 최대 인장 강도에 도달한 후 네킹이 일어나기까지 연속적으로 변형된다. 그러므로 인장 시험에서 균일한 소성 변형률 이후의 신뢰할 수 있는 유동 곡선을 외삽법으로 얻기 위해서는 변형률 경화 모델이 최대 인장 강도 지점(Maximum Tensile Force Point, MTFP), (ε*, σ*)에서 유동 곡선의 기울기를 정확하게 예측하여야 한다.

Swift의 확산넥 이론에 따라 실험 중 최대 인장응력의 상태는 다음과 같이 표현된다.²

$\[ dF=d\left(A\sigma \right)=Ad\sigma +\sigma dA=0 \]$

(5)

$\[ \sigma =-d\sigma \frac{A}{dA}=\frac{d\sigma }{d\epsilon } \]$

(6)

Kim-Tuan 변형률 경화 모델에서 최대 응력 상태는

$\[ \sigma =T{\left(\epsilon +{\epsilon }_0\right)}^{m}c\left({\mathrm{e}\mathrm{x}\mathrm{p}}^{-c\epsilon }\right)+Tm{\left(\epsilon +{\epsilon }_0\right)}^{m-1}\left(1-{\mathrm{e}\mathrm{x}\mathrm{p}}^{-c\epsilon }\right) \]$

(7)

식(7)에 MTFP, (ε*, σ*)을 대입하면

$\[ \sigma \mathrm{*}=T{\left(\epsilon \mathrm{*}+{\epsilon }_0\right)}^{m}c\left({\mathrm{e}\mathrm{x}\mathrm{p}}^{-c\epsilon \mathrm{*}}\right)+Tm{\left(\epsilon \mathrm{*}+{\epsilon }_0\right)}^{m-1}\left(1-{\mathrm{e}\mathrm{x}\mathrm{p}}^{-c\epsilon \mathrm{*}}\right) \]$

(8)

여기서

$\[ R^{\mathrm{*}}={\sigma }^{\mathrm{*}}-{\sigma }_0=T{\left({\epsilon }^{\mathrm{*}}+{\epsilon }_0\right)}^m\left(1-{\mathrm{e}\mathrm{x}\mathrm{p}}^{-c\epsilon \mathrm{*}}\right) \]$

Kim-Tuan 변형률 경화 모델에서 최대 응력 상태는

$\[ \sigma \mathrm{*}=c\left[T\left({\epsilon }_0+\epsilon \mathrm{*}\right)-R\mathrm{*}\right]+\frac{m}{{\epsilon }_0+\epsilon \mathrm{*}}R\mathrm{*} \]$

(9)

$\[ \frac{\sigma \mathrm{*}}{R\mathrm{*}}=c\left(\frac{1}{1-{\mathrm{e}\mathrm{x}\mathrm{p}}^{-c\epsilon \mathrm{*}}}\right)+\frac{m}{{\epsilon }_0+\epsilon \mathrm{*}} \]$

(10)

식(10)을 간단히 표현하면 변수 m과 c의 관계식을 구할 수 있다.

$\[ m=\left(\frac{\sigma \mathrm{*}}{R\mathrm{*}}-\frac{c}{{\exp }^{-\mathit{c\epsilon }\mathrm{*}}-1}\right)\left({\epsilon }_0+\epsilon \mathrm{*}\right) \]$

(11)

여기서 변수 c의 값은 충분히 커서 c/(exp^cε*-1)항은 근사적으로 무시할 수 있다.⁷ 따라서

$\[ m=\frac{\sigma \mathrm{*}}{\sigma \mathrm{*}-{\sigma }_0}\left({\epsilon }_0+\epsilon \mathrm{*}\right) \]$

(12)

식(12)로부터 m은 다른 변수 값에 의존하지 않는 독립 변수 이다. 그러므로 T와 c의 값은 커브 피팅으로 찾을 수 있으며, m의 값은 식(12)로부터 실험적으로 구할 수 있다.

3. 금속 판재의 응력-변형률 관계 묘사

선택된 판재들의 응력-변형률 관계를 얻기 위해서는, 각각의 재료를 KS B0801에 따라 단축 인장 시험을 수행한다. 시편 표면에 커팅 공정 중 발생하는 효과들을 줄일 수 있고 실험의 정확도 향상 시킬 수 있도록 레이저 커팅으로 시편을 준비한다. 통상적으로 판재의 압연 방향으로 단축 인장 시험을 수행한 응력-변형률 데이터를 재료의 유효한 응력-변형률 데이터로 간주한다. 그러므로 단축 소성 변형 과정에서 압연 방향을 따라 측정된 진응력-진변형률 데이터를 사용하여 Swift, Voce, Kim-Tuan 모델에 각각 대입하여 변수 값들을 찾는다.

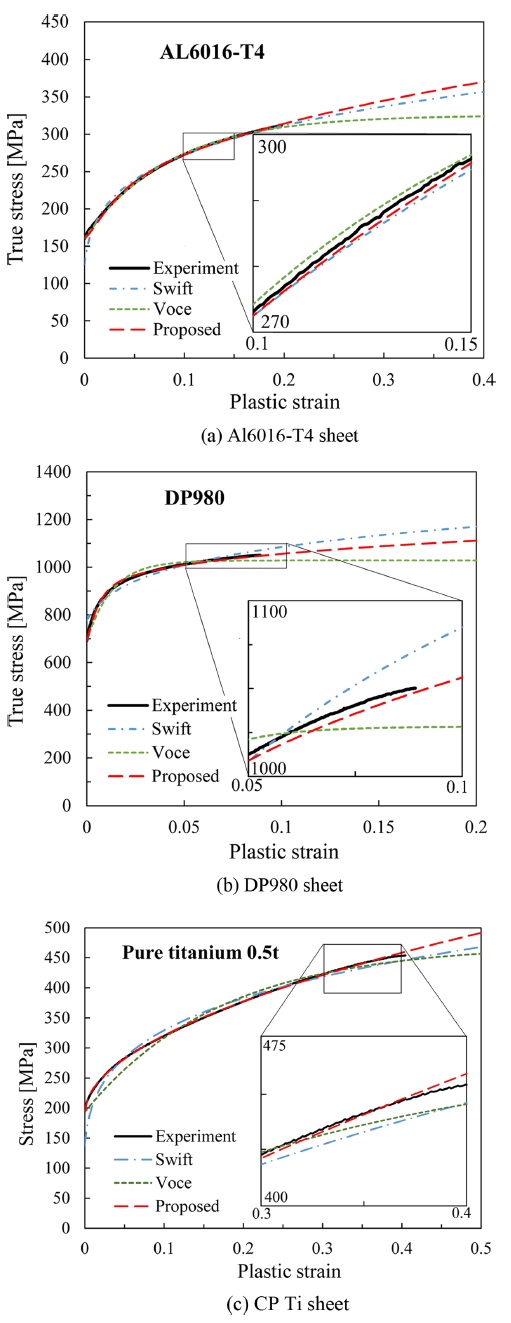
Fig. 2는 본 연구에서 사용된 3가지 재료의 실험 값을 위에서 언급한 Swift, Voce, Kim-Tuan 모델에 각각 대입하여 커브 피팅한 결과이다. 그림에서 알 수 있듯이 Kim-Tuan 모델에서 실험 결과와 커브 피팅한 결과가 잘 일치하는 것을 볼 수 있다. Swift와 Voce 모델에 대한 제안된 모델의 질적 평가를 위해 식(13)을 이용하여 각각의 모델에 대한 평균 오차 평가를 수행하였다.

Fig. 2

Curve fitting results for various sheet material based on three different equations

여기서 σ_i 와 σ_tr은 실험에서 측정된 응력과 변형률 경화 모델로부터 계산된 응력 값들이고, n은 평가에 선택된 데이터 점들의 개수이다. Table 1은 Swift, Voce, Kim-Tuan 모델의 변수 값들과 각각의 모델의 오차 값이다.

Table 1

Curve fitting results and error estimation of three hardening models for studied materials

통상적으로 Swift 모델은 대변형의 범위에서 항복 응력의 변화를 잘 표현하며, Voce 모델은 작은 변형률 범위에서 더 나은 결과를 나타낸다고 알려져 있다. 그럼에도 불구하고, 금속 판재 성형 과정 중에 재료는 파괴가 일어나기 까지 탄성, 소성, 넥킹에 이르는 다양한 변형 거동을 가진다. 성공적인 수치 해석 분석 결과를 얻기 위해서는 하나의 적절한 응력-변형률 모델을 이용하여 재료의 변형 전 범위에 걸쳐 응력-변형률 관계를 완벽하게 모델화할 필요가 있다. 따라서 본 연구에서 제안된 응력-변형률 모델은 실험한 3종류의 재료에 있어서 변형률 전 범위에서 실험 데이터를 잘 표현하고 있다.

Table 1에서 본다면 Swift와 Voce 모델은 이들이 1% 이하의 오차를 가진다면 재료의 응력-변형률 관계를 표현하는데 사용 될 수 있다. 예를 들어 Voce 모델의 경우 Al6061-T4 재료의 응력-변형률 관계를 표현하는데 주로 사용되며,⁸ Swift 모델은 DP980 재료에 적합하다.⁹ 그러나 Fig. 2와 Table 1에서 나타낸 바와 같이 CP Ti 판재에 대해서 응력-변형률 데이터를 피팅하면 신뢰할만한 수치 해석 결과를 얻을 수 없다.

이들 모델은 특히 탄성 변형에서 소성 변형 사이와 소성 변형을 지나 넥킹에 이르는 두 가지 잘 알려진 천이영역에서 CP Ti 재료의 응력을 낮게 평가하는 경향이 있다. 본 연구에서 제안된 모델의 경우 소성 변형 전 범위에 걸쳐 실험 데이터와 잘 일치하는 결과를 얻을 수 있었다. 이것은 제안된 모델은 Swift와 Voce 모델과 비교할 때 확연한 오차의 감소를 나타내기 때문에 모든 종류의 재료(BCC, FCC, HCP)에 대해서 적용될 수 있다. 특히 CP Ti 판재의 경우 Swift와 Voce 모델 모두 큰 오차를 보여주기는 반면에 제안된 모델의 경우 1% 이하의 오차를 가짐으로써 우수한 커브 피팅 결과를 나타내었다.

4. 순 티타늄 판재의 스프링백 예측

제안된 가공경화 모델이 CP Ti 판재의 굽힘 공정에서 발생하는 스프링백을 정확하게 예측하는지를 살펴본다. 스프링백은 프레스 가공 후에 발생하는 탄성 복원 현상으로, 프레스 가공 후 재료의 두께에 따라 불균일한 응력 분포 값을 가지기 때문에 생기는 굽힘의 완화에 의해 발생된다. 그래서 성형 공정 동안 재료에 응력 분포와 관련된 계수들이 프레스 성형된 부품의 스프링백 거동에 영향을 끼친다. 따라서 스프링백에 관한 연구는 점점 활발해지고 있으며, 본 연구의 CP Ti 판재의 스프링백 연구는 재료 성형품의 품질 향상을 위해 필수적이다.

4.1 재료 물성치 확인

본 연구에서는 0.5 mm 두께의 CP Ti 판재를 사용하였다. 단축인장 시험을 수행하여 진응력-진변형률 곡선을 구하고, 압연 방향에서 0°, 45°, 90° 방향의 항복응력 σ₀, σ₄₅, σ₉₀과 소성 변형률비(Lankford Anisotropic Parameters, R-Value), R₀, R₄₅, R₉₀를 측정하였다. 진응력-진변형률 곡선은 Kim-Tuan 모델을 사용하여 피팅하였다. Table 2에는 측정된 재료상수를 나타내었다.

Table 2

Mechanical properties of CP Ti sheets

소성 변형 공정에서 CP Ti 판재의 이동 경화 거동을 보기 위해서 좌굴을 막는 특수한 지그를 가지고 평면 인장-압축 시험을 수행하였다(Fig. 3). Fig. 3에서 반복 하중에서 재료의 항복 응력은 감소한다. 그러므로 이 재료의 가공 경화 거동을 명확하게 알기 위해서는 비선형의 이동 경화 모델의 채택이 필요하다. 따라서 본 연구에서는 CP Ti 재료의 이동 경화 거동을 표현하기 위해Armstrong-Frederick 모델(AF Model)을 적용하였다.⁵

$\[ \mathrm{A}\mathrm{F}\mathrm{ }\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}: d{\alpha }_{ij}=Cd{\epsilon }_{ij}^p-\gamma {\alpha }_{ij}d\overline{\epsilon } \]$

(14)

Fig. 3

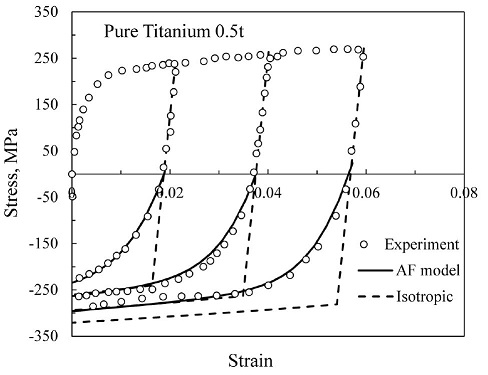
Comparison results of tension-compression test data and amstrong-frederick model for CP Ti sheet in rolling direction

여기서 C와 γ는 재료 상수이다. 본 연구에서는 Fig. 3에서 보여진 바와 같이 C = 15,390 [MPa], γ = 177.57의 값을 사용하여 CP Ti 판재의 실험 결과를 피팅하였다. 더 자세한 AF 모델의 배응력 진전은 참고문헌을 통해 확인할 수 있다.¹⁰

4.2 굽힘 실험

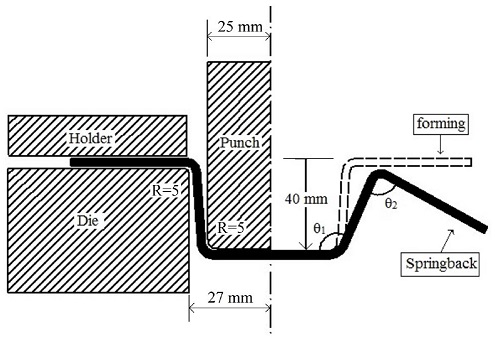
실험적으로 CP Ti 판재의 스프링백을 평가하기 위해 NUMISHEET 1993 Conference를 벤치마킹 하여 굽힘 시험을 실시하였다. 시편의 크기는 0.5 mm × 50 mm × 200 mm이며 실험의 계략도는 Fig. 5와 같다. 펀치와 다이의 어깨 반경은 5 mm이다. 펀치의 스트로크는 40 mm이며 스피드는 40 mm/s로 고정하였다. 먼저 재료를 블랭크 홀딩 포스(BHF)를 가하여 홀더에 고정한다. 다음으로 펀치를 하강시켜 재료를 성형한다. 이때 블랭크 홀딩 포스는 알루미늄 판재의 스프링백을 감소시키기 위해 BHF = 20 kN을 채택하였다.¹¹ 펀치의 변위와 변위에 따른 펀칭력은 실험 동안 모니터링하였다.

Fig. 4

Forming scheme used in bending test

Fig. 5

Punch force-displacement data to determine value of friction

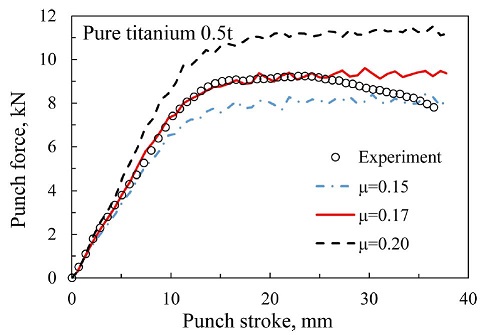
굽힘 시험 동안 모든 접촉 면에는 Coulomb 마찰이 작용하는 것으로 추정한다. 마찰은 스프링백 예측에 매우 중요한 변수이다.¹² 마찰 계수(μ)를 결정하기 위해 다양한 마찰 계수 하에서의 굽힘 시험을 해석적 방법으로 수행하여, 실제 시험에서 얻어진 펀치의 힘-스트로크 결과와 비교를 수행하였다(Fig. 6).

Fig. 6

Experimental results of bending test for CP Ti and Al6016-T4 sheets

Fig. 6의 결과를 토대로 마찰 계수는 CP Ti 판재의 펀치 힘-스트로크 실험 데이터와 잘 맞는 μ = 0.17로 선정하였다.

4.4 결과 및 고찰

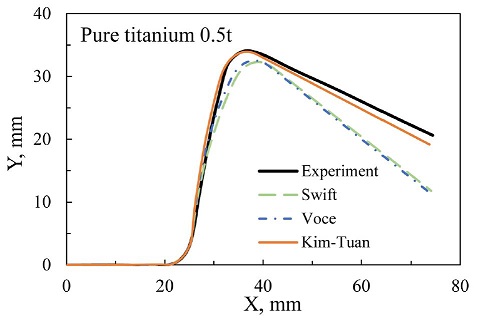
Fig. 7에는CP Ti 판재의 굽힘 실험 후의 변형된 형상을 나타내었다. 또한 CP Ti 판재의 스프링백을 실험적으로 알아보기 위래같은 조건에서 Al6016-T4 판재의 굽힘 시험을 수행하였다. 두 판재 시편의 변형된 형상을 비교하면 CP Ti 판재의 스프링백 양이 더 큰 것을 알 수 있다.

Fig. 7

Effect of strain hardening models on the spring-back prediction for CP Ti sheet

FE 해석은 판재 성형의 스프링백 연구에 매우 효율적인 방법이다.^15,16

CP Ti 판재의 스프링백 예측에서 제안된 Kim-Tuan 경화 모델의 적용을 부각시키기 위해, Fig. 7에서 세가지 다른 경화 모델의 예측 결과를 비교하였다. Fig. 2(c)에서 나타낸 바와 같이 Swift와 Voce 모델은 탄성과 소성의 천이 영역에서 응력-변형률 관계를 과소평가 한다. 게다가 이들 경화 모델은 CP Ti 판재에서 근사적으로 3.5%에 달하는 비슷한 평가 오차를 준다. 그러므로 Swift나 Voce 모델을 이용한 스프링백 예측은 Fig. 7과 같이 비슷한 예측결과를 나타낸다. CP Ti 판재의 응력-변형률 표현에 높은 정확성을 가지는 Kim-Tuan 경화 모델은 재료의 스프링백 예측에 있어서 정확도를 향상시키고 있음을 알 수 있다.

5. 결론

본 연구는 Al6016-T4, DP980, CP Ti 판재의 응력과 변형률 관계를 정확하게 표현할 수 있는 새로운 변형률 경화 모델인 Kim-Tuan 모델을 제안하였다. 부가적으로 CP Ti 판재의 굽힘 시험을 통하여 스프링백을 예측하는데 Kim-Tuan 모델을 적용하였다. 이에 대한 결론은 다음과 같다.

(1) 재료의 응력-변형률 관계를 표현함에 있어서 Swift 모델은 DP980 판재에서, Voce 모델은 Al6016-T4 판재에서 우수한 예측값을 나타내었다. 그러나 CP Ti 판재의 경우 응력-변형률의 관계 표현에 있어 두 가지 모델 모두에서 부정확성을 나타내었다. 본 연구에서 제안한 Kim-Tuan 모델의 경우 수행한 세가지 재료 모두에서 우수한 커브 피팅 결과를 얻을 수 있었다. 그러므로 Kim-Tuan 모델은 다른 금속 판재에서도 응력-변형률 관계의 모델화에 사용될 수 있을 것이다.

(2) CP Ti 판재는 초기 항복 응력과 소성 변형률비(R-Value)에서 알 수 있듯이 큰 이방성을 가지는 재료이다. 인장-압축 시험으로부터 응력 반전 상태에서 재항복 응력이 낮아지는 것도 살펴보았다. 이에 반전 응력 상태를 표현하기 위해서는 AF 모델과 같은 비선형 이동 경화 모델을 적용하였다. 본 연구에서는 AF 모델이 인장-압축 시험의 실험 결과와 잘 맞았다.

(3) Hill의 이방성 항복 조건식, Kim-Tuan 경화 모델, AF이동 경화 모델을 적용한 FE 모델은 CP Ti 판재의 굽힘 시험의 스프링백 예측에서 다른 경화 모델들보다 우수한 정확도를 나타내었다. 그러나 FE 해석 결과와 실험 결과의 차이는 여전히 존재한다. 이에 CP Ti 판재의 스프링백을 밝히고 제어하는 더 많은 연구가 필요할 것으로 사료된다.

Acknowledgments

이 논문은 2016년도 정부(교육부)의 재원으로 한국연구재단의 중점연구소지원사업(2010-0020089)과 기초연구지원사업(NRF-2013R1A1A2058808) 지원에 의해 수행된 연구임.

REFERENCES

• Sung, J. H., Kim, J. H., and Wagoner, R. H, “A Plastic Constitutive Equation Incorporating Strain, Strain-rate and Temperature,” International Journal of Plasticity, Vol. 26, No. 12, pp. 1746-1771, 2010. [https://doi.org/10.1016/j.ijplas.2010.02.005]
• Swift, H. W., “Plastic Instability under Plane Stresses,” Journal of the Mechanics and Physics of Solids, Vol. 1, No. 1, pp. 1-18, 1952. [https://doi.org/10.1016/0022-5096(52)90002-1]
• Voce, E., “The Relationship between Stress and Strain for Homogeneous Deformation,” Journal of Institute of Metals, Vol. 74, pp. 537-562, 1948.
• Hill, R., “The Mathematical Theory of Plasticity,” Clarendon Press, pp. 1-355, 1998.
• Taherizadeh, A., Green, D. E., Ghaei, A., and Yoon, J. W., “A Non-Associated Constitutive Model with Mixed Iso-Kinematic Hardening for Finite Element Simulation of Sheet Metal Forming,” International Journal of Plasticity, Vol. 26, No. 2, pp. 288-309, 2010. [https://doi.org/10.1016/j.ijplas.2009.07.003]
• Frederick, C. O. and Armstrong, P., “A Mathematical Representation of the Multiaxial Bauschinger Effect,” Materials at High Temperatures, Vol. 24, No. 1, pp. 1-26, 2007. [https://doi.org/10.3184/096034007X207589]
• Kim, Y.-S. and In, J.-H., “Evaluation of Press Formability of Pure Titanium Sheet,” Journal of the Korea Academia-Industrial Coorperation Society, Vol. 17, No. 3, pp. 380-388, 2016. [https://doi.org/10.5762/KAIS.2016.17.3.380]
• Santos, A. D., Reis, A., Duarte, J., Teixeira, P., Rocha, A. B., et al., “A Benchmark for Validation of Numerical Results in Sheet Metal Forming,” Journal of Materials Processing Technology, Vol. 155, pp. 1980-1985, 2004. [https://doi.org/10.1016/j.jmatprotec.2004.04.290]
• Choi, S. H., Kim, E. Y., Woo, W., Han, S. H., and Kwak, J. H., “The Effect of Crystallographic Orientation on the Micromechanical Deformation and Failure Behaviors of DP980 Steel during Uniaxial Tension,” International Journal of Plasticity, Vol. 45, pp. 85-102, 2013. [https://doi.org/10.1016/j.ijplas.2012.11.013]
• Chung, K., Lee, M.-G., Kim, D., Kim, C., Wenner, M. L., et al., “Spring-Back Evaluation of Automotive Sheets Based on Isotropic-Kinematic Hardening Laws and Non-Quadratic Anisotropic Yield Functions: Part I: Theory and Formulation,” International Journal of Plasticity, Vol. 21, No. 5, pp. 861-882, 2005. [https://doi.org/10.1016/S0749-6419(04)00088-9]
• Burchitz, I., “Springback: Improvement of Its Predictability: Literature Study Report,” Netherlands Institute for Metals Research, NIMR Project MC1.02121, pp. 1-83. 2005.
• Choi, K. Y., Lee, M. G., and Kim, H. Y., “Sheet Metal Forming Simulation Considering Die Deformation,” International Journal of Automotive Technology, Vol. 14, No. 6, pp. 935-940, 2013. [https://doi.org/10.1007/s12239-013-0103-2]
• Li, K. P., Carden, W. P., and Wagoner, R. H., “Simulation of Springback,” International Journal of Mechanical Sciences, Vol. 44, No. 1, pp. 103-122, 2002. [https://doi.org/10.1016/S0020-7403(01)00083-2]
• Stoughton, T. B., “A Non-Associated Flow Rule for Sheet Metal Forming,” International Journal of Plasticity, Vol. 18, No. 5, pp. 687-714, 2002. [https://doi.org/10.1016/S0749-6419(01)00053-5]
• Yoshida, F. and Uemori, T., “A Model of Large-Strain Cyclic Plasticity and Its Application to Springback Simulation,” International Journal of Mechanical Sciences, Vol. 45, No. 10, pp. 1687-1702, 2003. [https://doi.org/10.1016/j.ijmecsci.2003.10.013]
• Lee, J. W., Lee, M. G., and Barlat, F., “Finite Element Modeling Using Homogeneous Anisotropic Hardening and Application to Spring-Back Prediction,” International Journal of Plasticity, Vol. 29, pp. 13-41, 2012. [https://doi.org/10.1016/j.ijplas.2011.07.007]