스프링조작기 개발을 위한 코일 스프링 설계 프로그램 개발
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Since the performance of the spring operating mechanism for a circuit breaker mainly depends on the dynamic behavior and mass of the coil spring, its dynamic analysis is required to evaluate the performance of the spring operating mechanism. In this study, a coil spring design program is developed for the spring operating mechanism. An experimental approach is used to find the variables satisfying the design constraints’ requirements. The coil spring is formed by using a lumped mass spring model. This program offers reference data for the design of coil springs and for the spring operating mechanism.
Keywords:
Circuit breaker, Spring operating mechanism, Coil spring, Spring design program키워드:
회로 차단기, 스프링 동작 메커니즘, 코일 스프링, 스프링 설계 프로그램1. 서론
회로차단기는 과부하 또는 단락 등에 의한 사고가 발생했을 때 신속하게 전류를 차단시킴으로써 대형화재, 인명피해 등으로 이어지는 사고를 방지해주는 매우 중요한 장치이다. 회로차단기는 용량, 소호방식, 구동 동력원에 따라 구분된다. 용량에 따라 100 kV - 1000 kV는 고압 회로차단기, 1000 kV 이상은 초고압 회로차단기로 분류되고, 아크 소호방식에 따라 유입차단기, 자기차단기, 진공차단기, 공기차단기, 가스차단기 등으로 분류된다. 구동 동력원은 유압, 공압, 스프링을 이용하며 이 중에서 스프링 타입의 회로차단기는 구조가 간단하고 짧은 시간에 큰 부하를 움직이는데 적합하기 때문에 주로 사용된다.
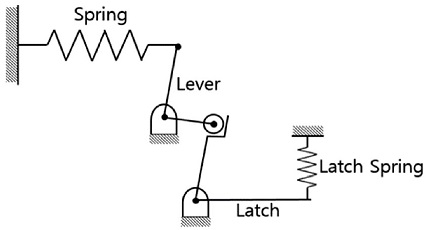
스프링조작기의 구조를 Fig. 1에 간단하게 나타내었다. 스프링은 압축된 상태로 장착되어 구조적으로 평형을 이루고 있으며, 사고 발생시 래치에 외력을 가해 스프링을 방출시키게 된다. 스프링이 방출됨에 따라 차단부의 접점을 움직여 전류가 차단된다. 스프링조작기를 사용하는 회로차단기에서 스프링의 성능이 차단 속도에 직접적인 영향을 미치기 때문에 조작기용 스프링 설계 시 마찰 및 스프링의 질량효과 등에 의한 손실을 고려해야 한다. 특히 스프링의 질량효과에 의한 손실이 지배적으로 작용하는데, 정적수식을 통한 해석으로는 질량에 의한 손실을 고려하기 어렵다. 따라서 스프링 설계 시 스프링의 질량을 고려한 동적 해석을 통해 질량 효과를 고려해야 한다. 스프링의 질량 효과를 모사하기 위해서 스프링을 모델링해야 하지만 자유장, 평균직경 등 스프링 설계에 필요한 변수의 조합에 따라 만들 수 있는 무수히 많은 스프링을 모두 모델링하고 해석을 수행하기에는 어려움이 있다. 따라서 설계변수의 조합을 가지고 조작기와 스프링을 간단히 모델링하여 해석하는 방법이 필요하다.
안길영과 김수현은1,2 집중 매개변수 모델을 적용하여 스프링 구동캠의 마찰에 관한 연구를 수행하였고, 구동 스프링의 최적 설계에 관한 연구를 수행하였다. Sakai와 Kosaki는3 밸브의 운동 해석에 관한 연구에서 스프링을 집중질량과 등가강성으로 표현하는 집중매개변수 모델을 제안하였다. 유완석은4 고압 회로차단기용 코일스프링을 선형모델, 절점모델 및 모드모델로 모델링하여 시뮬레이션과 시험 결과를 비교하였다. 유완석은5 고압 회로차단기용 스프링의 동적 거동을 분석하여 스프링의 질량에 의한 손실 및 에너지 전달 효율을 분석하고, 실험계획법을 이용한 스프링 최적설계 연구를 수행하였다.
앞선 연구에서 조작기용 스프링 설계를 위한 스프링 모델링 방법 및 최적설계 연구를 수행하였으나 스프링의 좌굴을 고려하지 않았고, 최종 속도만을 고려하여 최적설계를 수행하였다. 따라서 본 연구에서는 고압 회로차단기용 스프링의 설계에 참고할 수 있는 데이터를 얻기 위해 실험계획법을 통해 스프링의 유효권수, 평균직경, 소선경, 자유장을 조절하여 스프링 조합을 만들어 내고, 스프링 및 조작기의 안정성을 위해 설정한 제약 조건을 만족하는 모든 설계변수 조합에 대해서 스프링 조작기를 등가질량 및 집중 질량-스프링으로 간단히 모델링하여 동적 해석을 수행하여 에너지 전달 효율, 최종 속도, 응력 등 설계에 참고할 수 있는 전반적인 데이터를 출력해주는 프로그램을 개발하였다.
2. 프로그램 구성
2.1 프로그램 전체 구성도
본 설계 프로그램은 조작기 구동에 필요한 에너지 범위를 만족하기 위해서 비슷한 수준의 에너지 용량을 가지면서 효율이 높은 스프링을 설계하기 위해 사용된다.
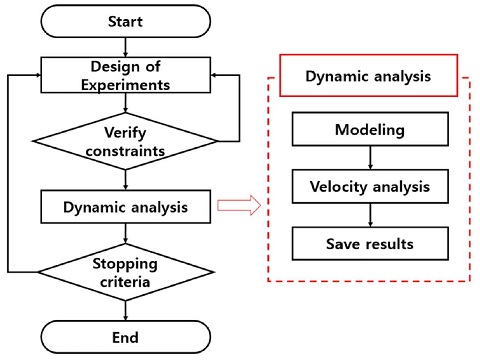
해석 순서는 Fig. 2와 같다. 먼저 실험계획법을 통해 제약 조건만족 여부를 판별하게 되는데, 유완석은5 변수의 민감도 및 교호작용 분석을 통해 어느 하나의 설계변수 변경만으로는 목적함수의 개선을 기대하기 어려우므로 모든 설계변수의 조합을 고려할 필요가 있음을 보였다. 따라서 실험계획법을 통한 제약 조건 만족여부 판별 과정에 혼합수준 요인 배치법(Mixed Level Design)을 적용하였다. 입력 조건에 따라 설계변수의 범위와 수준이 정해지며, 설계 변수를 최소값에서부터 시작하여 제약 조건 만족여부를 판별하고 제약 조건을 만족하지 못할 경우 설계 변수의 수준을 한 단계씩 올려가며 모든 설계 변수에 대한 제약 조건 만족 여부를 판별한다.
제약 조건을 만족할 경우 스프링을 집중 질량 모델로 모델링하여 최대 압축 상태에서 초기 압축 상태로 방출하는 해석을 수행하여 스프링 끝 단의 속도를 계산한다. 설계 변수가 설정한 최댓 값에 도달하면 해석이 종료된다. 결과 테이블에서는 제 약 조건을 만족하는 모든 스프링에 대한 해석 결과를 볼 수 있어 스프링 설계에 참고할 수 있다.
2.2 스프링 설계를 위한 전처리기 개발
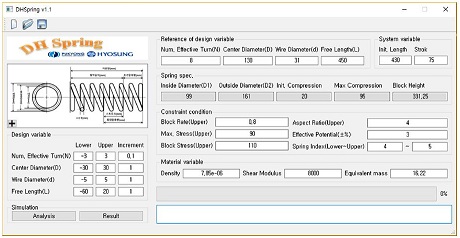
Fig. 3은 전처리기 구성 화면을 보여준다. 스프링 모델링을 위한 설계 변수 기준값 및 범위, 스프링 재질의 물성치와 해석을 위한 스프링 장착 조건, 제약 조건을 입력 받는다. 스프링의 재질, 유효권수(N), 스프링 평균 직경(D), 소선경(d), 자유장(L)을 입력하여 스프링의 특성을 설정하고, 장착 길이(Linst)와 스트로크(δstroke)를 입력하여 장착 조건을 설정한다. 설계 변수 기준값과 장착 조건을 입력하면 기준이 되는 스프링에 대해서 초기 압축량(δpre comp), 최대 압축량(δtotal comp) 등 기본적인 사양이 자동으로 계산된다. 스프링은 초기 압축 상태에서 스트로크 만큼 추가로 압축되며, 이때 스프링의 길이를 최대 압축 변위라 하며, 압축된 양을 최대 압축량, 전단응력을 최대응력(τtotal comp)으로 정한다.
장착 길이는 스프링 조작기에 스프링을 장착했을 때 길이를 말하며 스프링의 자유장 보다 짧아야 한다. 이때 자유장에서 장착 길이를 뺀 값이 초기 압축량이 된다. 스트로크는 스프링 조작기가 움직이는 범위에 따라 결정된다.
2.3 스프링 설계를 위한 주 처리기 개발
밀착고(Lsolid)는 스프링이 완전히 압축되어 소선이 모두 붙은 상태의 길이를 말하며 식(1)과 같이 계산된다.
| (1) |
최대 압축 상태의 스프링의 길이는 밀착고보다 길어야 한다. 스프링을 밀착고까지 압축했을 때의 압축량을 밀착고 변위(δsolid), 전단응력을 밀착고응력(τsolid),으로 정한다. 밀착고 변위와 최대 압축량의 비를 밀착율(rsolid)로 정의하였다. 밀착율은 식(2)와 같이 계산된다.
| (2) |
밀착율이 1이 되면 최대 압축 시 스프링이 완전히 밀착되므로 1이하의 값을 입력해야 한다. 동적 해석 시 조작기의 질량은 스프링 끝에 매달린 등가의 질량으로 고려하며, 이 때의 질량을 등가질량(meq)이라고 한다. 본 연구에서는 회로가 차단되는 시점, 즉 스프링이 초기압축 상태에 도달한 시점에서의 운동에너지를 분석하는 것이 중요하다. 등가질량은 조작기 모델링을 간단히 하여 해석 속도를 향상시키기 위해 사용되며, 유완석은5 특정한 순간에 기구의 각 링크는 일정한 속도비를 가지며, 기구를 스프링 끝 단에 대한 등가질량으로 고려한 해석과 기구 전체를 고려한 해석결과가 유사함을 보였다.
조작기 및 스프링의 파괴를 방지하기 위해서 최대응력, 밀착고 응력 하중이 고려되며 최대응력은 식(3)으로 계산된다.
| (3) |
Ptotal comp는 최대 압축 시 하중을 의미하며 스프링의 강성과 최대 압축량의 곱으로 구해진다. 코일 스프링에서 최대 전단 응력은 안쪽 면에서 발생하며 곡률에 의한 영향을 고려하기 위해 Wahl의 응력 수정 계수(W)를 사용하였다. Wahl의6 응력 수정 계수는 식(4)과 같다.
| (4) |
식(4)의 c는 스프링지수를 의미하며, 스프링의 평균직경과 소선경의 비를 말하며 D/d로 계산된다. 밀착고 응력은 식(5)로 계산된다.
| (5) |
위 식에서 Psolid는 밀착고 하중을 의미한다. 유효포텐셜은 최대 압축 시 스프링의 포텐셜 에너지와 초기 압축 시 스프링의 포텐셜 에너지 차이를 의미하며, 기존의 스프링과 유사한 에너지를 갖도록 유효 포텐셜(PEact) 범위를 입력할 수 있도록 하였다. 유효 포텐셜은 식(6)과 같이 계산된다.
| (6) |
k는 스프링의 강성을 의미한다. 조작기의 요구 성능에 따라서 스프링의 유효 포텐셜 에너지 범위가 결정되므로 초기 압축량, 최대 압축량 및 스프링의 강성을 조절하여 유효 포텐셜 에너지 범위를 만족시켜야 한다.
최대 사용시 하중은 기준 값의 120% 이하를 만족하도록 설정하였고, 스프링의 강성은 300% 이하, 질량은 30 kg 이하를 만족하도록 설정하여 사용자가 변경할 수 없도록 하였다. 스프링의 제작 가능성 및 스프링의 좌굴을 방지하기 위해 종횡비(AR), 스프링지수, 밀착율을 고려하였으며, 종횡비는 스프링의 자유장과 평균직경의 비로 L/D로 계산된다.
해석 버튼을 클릭하면 설정한 설계 변수에 대해서 정적 해석을 수행한 후 제약 조건 만족 여부를 판별하고, 만족하지 않는 경우에는 설계 변수를 변경하여 다시 제약 조건 만족 여부를 판별하게 되고 제약 조건을 만족하는 경우 동적 해석을 수행한다.
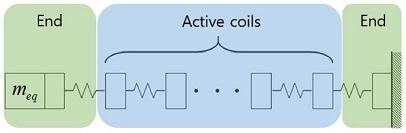
동적 해석 수행 시 스프링 조작기는 집중 질량-스프링과 등가 질량으로 모델링된다. 집중 질량-스프링은 끝단부와 유효권선부로 나누어 모델링하였다. 끝단부는 양 끝에 각각 1개, 유효권선부는 9개의 질량으로 구성되어 총 11개의 질량으로 구성되어 있으며, 최대 압축 상태로 모델링 된다. Fig. 4에는 등가질량 및 집중 질량-스프링 모델을 개략적으로 나타내었다. 스프링의 한 쪽 끝은 고정되어있고, 반대쪽 끝에는 등가질량이 부착되어 있다. 각각의 질량은 10개의 스프링에 의해서 직렬 연결되어있다. 한 쪽 끝이 고정되어있는 스프링-질량-감쇠계의 운동방정식을 행렬 형태로 나타내면 식(7)과 같다.
| (7) |
[M], [c], [k]는 각각 질량 행렬, 감쇠 행렬, 강성 행렬을 의미하며 {x}, {}, {}, {F}는 변위 벡터, 속도 벡터, 가속도 벡터, 힘벡터를 의미한다. 외력이 작용하지 않는 경우를 고려하였으므로 힘 벡터는 0이다.
동적 해석은 스프링을 최대 압축 상태로 모델링하고, 스프링의 복원력에 의해서 방출되는 해석을 수행한다. 스프링이 초기 압축 상태까지 방출되면 해석이 종료된다. 등가질량이 부착된 스프링 끝단부의 위치, 속도, 가속도를 얻기 위해 4차 Runge-Kutta 방법(Runge-Kutta 4th Order Method)을 사용하였다. Runge-Kutta 방법은 식(8)과 같이 미분방정식으로 이루어진 초기값 문제를 해결하기 위해 사용된다.
| (8) |
Runge-Kutta 방법을 이용하면 미분방정식을 반복적으로 미분하지 않아도 되므로 계산이 간단해지며, 그 방법은 식(9)와 식(10)과 같다.
| (9) |
식(9)에서 yn+1은 y(tn+1)의 근사값을 의미하고, h는 시간 간격을 의미한다. 상수 k1, k2, k3, k4는 식(10)과 같이 계산된다.
| (10) |
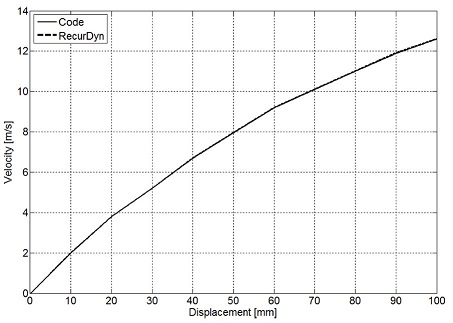
집중 질량-스프링 모델의 해석 정확성을 검증하기 위해 개발 프로그램과 상용 해석 소프트웨어인 RecurDyn의7 해석 결과를 비교하였다. 스프링의 사양이 동일한 Fig. 4와 같은 집중 질량-스프링 모델을 생성하고, 스프링을 100 mm만큼 압축시킨 후 놓았을 때 스프링의 변위에 따른 스프링 끝 단의 속도를 비교하였다. 두 해석 결과의 차이는 0.005% 미만으로 거의 일치하는 결과를 보인다.
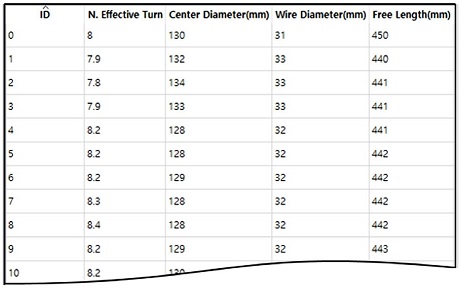
정적, 동적 해석을 통해 제약 조건을 만족하는 모든 설계 변수의 조합이 저장되고 결과 테이블에 나타난다. Fig. 6는 해석 결과 테이블의 일부를 보여준다. 해석 결과로 설계 변수에 따른 강성, 질량, 밀착고, 최대 사용시 하중, 밀착고 하중, 최대 사용시 응력, 밀착고 응력, 유효 포텐셜 에너지, 전달 에너지, 에너지 전달 효율, 스프링 끝 단의 속도를 확인할 수 있다.
3. 스프링 설계 적용
3.1 해석 조건 설정
본 연구에서 개발한 스프링 설계 프로그램을 이용하여 같은 조건에서 가장 높은 효율을 가지는 스프링을 설계하고자 한다. 스프링 설계 시 기준이 되는 스프링은 임의로 설정하였다. 또한 장착 길이는 350 mm, 스트로크는 50 mm, 기구의 등가질량은 임의로 스프링과 비슷한 수준으로 설정하였으며, 예제 스프링의 질량이 약 9 kg이므로 등가질량은 10 kg으로 설정하였다. 설계의 기준이 되는 예제스프링의 사양을 Table 1에 나타내었다.
에너지 및 응력 조건을 동일하게 맞추기 위해서 예제 스프링의 최대응력과 밀착고응력, 유효포텐셜을 제약조건으로 입력하고, 종횡비는 4이하, 스프링지수는 4 - 10이내, 밀착율은 0.8이내가 되도록 하였다.
3.2 해석 결과 분석
해석 결과 제약 조건을 만족하는 조합의 수는 6714가지로 나왔고, Intel i3-3220 (3.3 GHz) CPU와 8GB의 메모리를 가진 PC에서 약 5분의 해석시간이 소요되었다. 해석 결과 에너지 효율은 약 55.3% - 68.3%, 속도는 약 8120 mm/s - 9040 mm/s, 질량은 8.9 kg - 15.2 kg의 범위를 가지는 것을 확인하였다. 결과 테이블에서 효율이 가장 높은 스프링과 질량이 가장 작은 스프링, 동작 완료 시 속도가 가장 빠른 스프링을 선정하여 Table 2에 나타내었다. Case 1은 예제 스프링, Case 2는 효율이 가장 높은 경우, Case 3는 속도가 가장 빠른 경우, Case 4는 질량이 가장 작은 경우를 의미한다.
스프링 설계 예시에서는 예제 스프링의 에너지 및 응력 조건을 제약 조건으로 해석을 수행하였기 때문에 제약 조건 내에서 예제 스프링이 100%에 가까운 성능을 발휘한다고 볼 수 있으므로 각 Case별 성능 차이가 미미하게 나타났다.
효율이 가장 높은 경우 68.33%로 예제 스프링에 비하여 0.53% 상승하였으나 동작 완료 시 스프링의 속도의 변화가 거의 없으므로 성능에 큰 영향이 없을 것으로 보인다. 또한 스프링의 질량이 0.24 kg 증가함에 따라 제작 비용도 증가할 것이므로 최적 스프링으로 선정하기에는 어려움이 있다. 스프링의 속도가 가장 빠른 경우 동작 성능은 우수하지만 효율이 0.24% 낮고 스프링의 질량이 0.36 kg 증가하여 제작 비용이 증가할 것으로 보인다. 스프링의 질량이 가장 작은 경우에는 질량이 0.09 kg 감소하였으며 효율은 0.33% 증가하였다. 하지만 속도가 약 90 mm/s 느려지므로 동작 성능이 저하될 것으로 보인다. 이와 같이 스프링 설계 시 해석 결과를 참고하여 사용자가 원하는 스프링을 선정하는데 도움을 줄 수 있다.
4. 결론
고압 회로차단기용 스프링은 스프링 자체의 질량에 의한 손실이 존재하며, 질량에 의한 영향을 분석하기 위해서는 동적 해석이 필요하다. 하지만 원하는 성능의 스프링을 얻기 위해 제약 조건을 만족하는 스프링을 찾아내고, 모든 경우에 대해서 동적 해석을 수행하기에는 어려움이 있다. 따라서 본 연구에서는 실험계획법을 기반으로 하여 제약 조건을 만족하는 스프링을 찾아내고, 동적 해석을 수행하여 효율을 계산하는 프로그램을 개발하였다. 본 프로그램을 이용하여 같은 에너지 수준을 가지는 고압 회로차단기용 스프링 설계에 참고할만한 데이터를 얻을 수 있다.
Acknowledgments
본 연구는 ‘(주)효성중공업’의 지원을 받아 수행된 연구임(CD-2014-1125).
REFERENCES
-
Ahn, K.-Y. and Kim, S.-H., “Influence of Spring Dynamics and Friction on Dynamic Responses in a Spring-Driven Cam,” Transactions of the Korean Society of Mechanical Engineers A, Vol. 27, No. 2, pp. 247-254, 2003.
[https://doi.org/10.3795/KSME-A.2003.27.2.247]

- Ahn, K. Y. and Jeong K. Y., “Optimization of the Spring Design Parameters of a Circuit Breaker for Satisfying Specified Dynamic Characteristics,” J. Korean Soc. Precis. Eng., Vol 21, No 3, pp. 132-138, 2004.
- Sakai, H. and Kosaki, H., “Analysis of Valve Motion in Overhear Valve Linkage-Roles of Valve Spring Surge in Valve Motion,” Journal of the Faculty Engineering B, Vol. 33, No. 4, pp. 441-446, 1976.
-
Sohn, J.-H., Lee, S.-K., Kim, S.-O., and Yoo, W.-S., “Study of Spring Modeling Techniques for Kinematic and Dynamic Analysis of a Spring Operating Mechanism for the Circuit Breaker,” Transactions of the Korean Society of Mechanical Engineers A, Vol. 31, No. 7, pp. 777-783, 2007.
[https://doi.org/10.3795/KSME-A.2007.31.7.777]

-
Lee, D. W., Sohn, J. H., and Yoo, W. S., “Optimum Design of a Coil Spring for Improving the Performance of a Spring-Operated Mechanism,” Transactions of the Korean Society of Mechanical Engineers A, Vol. 40, No. 3, pp. 275-280, 2016.
[https://doi.org/10.3795/KSME-A.2016.40.3.275]

- Wahl, A. M., “Mechanical Springs,” McGraw-Hill, 1963.
- Functionbay, Inc., “RecurDyn,” http://www.functionbay.co.kr/documentation/onlinehelp/default.htm, (Accessed 9 MAR 2017)