나노유체 극미량 절삭유 윤활 밀링 가공 공정에서의 나노유체 분무 거동에 관한 전산유체역학 분석

1. 서론

최근 산업사회의 급속한 발전으로 인한 환경오염 및 인체 유해물질 배출 문제 등을 해결하기 위해 많은 노력이 이루어지고 있으며, 이러한 추세로 인해 산업 현장에서는 친환경 생산기술 개발이 중요한 이슈로 대두되고 있다.¹ 이러한 관점에서 환경과 관련된 국제 규격인 ISO 14000에서는 작업 환경에 대한 규제를 강화하고 있고, 이로 인해 환경 오염을 최소화하기 위한 절삭유 처리 및 설비 유지 관리 비용이 증가하고 있다. 이러한 절삭유 관리 비용은 총 생산 비용의 7 - 17%로 공구비용의 4배 이상이라는 통계도 발표되었다.² 일반적으로 절삭유는 기계 가공에서 칩의 원활한 배출, 공구와 공작물의 윤활 및 냉각 작용을 목적으로 사용된다.

환경친화적 관점으로 기계 가공에서 부각되고 있는 대표적인 윤활 기술이 극미량 절삭유 윤활(Minimum Quantity Lubrication, MQL)기술이다. MQL기술은 절삭유 미스트를 고압 공기를 통해 가공영역에 공급하는 윤활기술로서 기계가공에 있어서 공구 및 공작물 접촉부의 윤활 작용을 증대시키며, 칩 배출을 원활하게 한다. 또한 최근에는 MQL가공의 상대적으로 미흡한 냉각 작용을 좀 더 향상시키기 위해 절삭유에 나노입자를 추가하여 열전도율을 높인 나노유체(Nanofluid)를 이용한 나노유체 MQL기술이 제안되었으며 연삭, 선삭, 밀링, 드릴링 등의 기계 가공에 적용되고 있다.

공구 및 가공물 접촉부에 절삭유 미스트가 효과적으로 침투되어야만 가공 성능이 향상되므로 이러한 침투를 증가시키기 위한 분사 유량, 압력, 위치 등의 최적값 선정에 관한 연구가 진행되고 있다.^3-5 상기한 연구 중 수치해석 관점에서는 전산유체역학(Computational Fluid Dynamics, CFD)방법을 기반으로 밀링 공구와 노즐을 모델링하여 MQL 적용시 싱글 노즐의 2D 속도해석⁶과 다중 노즐의 3D 속도 해석 결과에⁷ 따른 유동 분석 연구가 진행되고 있고, MQL 노즐 끝에서 공기와 MQL 절삭유가 합쳐지는 영역에서의 유동 분석 연구 또한 진행되고 있다.⁸

그러나 나노유체 MQL을 적용한 기계 가공에 있어서 공구 및 가공물 접촉부에 가해지는 나노유체 미스트의 윤활 효과에 대한 전산유체역학 연구는 구체적으로 이루어지지 않았다. 따라서 본 논문에서는 나노유체 MQL 밀링 가공에 대한 전산유체역학 기반 수치해석 모델을 개발하여 나노유체 MQL 분사 시 분사각도에 따라 회전하는 공구의 표면에 포집되는 액적량을 계산하고 이를 실험으로부터 얻은 밀링 가공력과 연계하여 검증하는 연구를 수행하였다.

2. 나노유체 MQL 밀링 가공 실험

2.1 실험 장치 구성 및 실험 조건

나노유체 분사 조건에 따른 나노유체 MQL밀링 가공 성능 및 윤활 특성을 분석하기 위해 Fig. 1에 보여지는 것처럼 나노유체 분사 모듈을 장착한 밀링 가공 실험 시스템을 구축하였다.

Fig. 1

Photo of the experimental system for nanofluid MQL milling process

밀링 가공 실험은 CNC 머시닝 센터(NVD 4000 DCG, DMG MORI SEIKI)에서 수행되었으며, 공구는 직경이 16 mm인 Sandvik사의 R390-016A16L-11이 사용되었고, 인서트 역시 Sandvik사의 R390-11 T3 08M-KM H13A가 사용되었다.

가공물은 티타늄 합금(Ti-6Al-4V Grade 5)이고, 나노유체 MQL분사 장치는 UNIST Korea사의 UNIMAX 202F이며, 적정압력은 5 - 6 Bar이고 최대유량은 16 ml/min이다. 이 때 MQL 분사에 있어서 압력계와 윤활조절밸브를 통해 공기의 압력 및 오일의 토출량을 조절할 수 있다.

나노유체에 사용된 나노입자는 Hexagonal Boron Nitride (hBN)와 Nanodiamond (ND)이며, 크기는 각각 35 nm, 70 nm 이고, 질량비는 0.5 wt.%가 고려되었다. 나노유체 분사 유량 및 분사 각도가 독립변수로 고려되었으며, 절삭 합력이 관측 인자로 고려되었다. 실험에 있어서 나노유체 종류는 hBN, ND이며, 분사 유량은 2, 3, 4 ml/min, 이송 방향 분사 각도는 0°, 45°, 90°가 고려되었으며 총 18가지 조건으로 6 pass 반복 실험이 수행되었다. Table 1에는 나노유체 MQL밀링 가공 실험 조건이 요약되어 있다.

Table 1

Experimental conditions

2.2 실험 결과

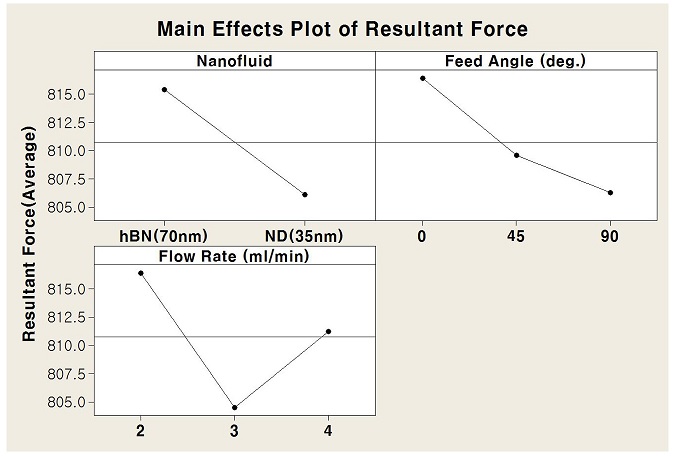
밀링 가공 실험 중 공구동력계를 이용하여 절삭력을 측정하였으며, 실험 결과를 바탕으로 통계적인 분석을 수행하여 주효과 분석도(Main Effect Plot)를 도출하였다. Fig. 2는 나노유체 종류(hBN, ND), 분사 유량(2, 3, 4 ml/min), 분사 각도(0°, 45°, 90°)가 절삭력에 미치는 영향에 대한 주효과 분석도를 보여준다. Fig. 2에서 알 수 있듯이 ND 나노유체, 분사 유량 3 ml/min, 분사 각도 90°인 경우 절삭력의 크기가 최소가 됨을 알 수 있다.

Fig. 2

Main effect plots of the resultant milling forces

Fig. 2에 주어진 분석 결과를 고찰할 때 크기가 작은 구형 나노입자(ND)의 경우 상대적으로 큰 열전도율 및 볼베어링 효과로 인해 크기가 상대적으로 큰 판형 나노입자(hBN)보다 나노유체 MQL 절삭력 감소효과가 더 우수한 것으로 판단되며 분사각도가 90°인 경우 더 많은 액적의 침투가 예상되어 절삭력 감소효과가 증대하는 것으로 판단된다.

유량에 있어서 3 ml/min인 경우에 2 ml/min 및 4 ml/min의 경우와 비교하여 가장 큰 절삭력 감소효과가 나타나는데 이는 나노유체 미스트가 공구 표면에 포집되는데 최적의 유량 조건을 있음을 의미한다고 볼 수 있다.

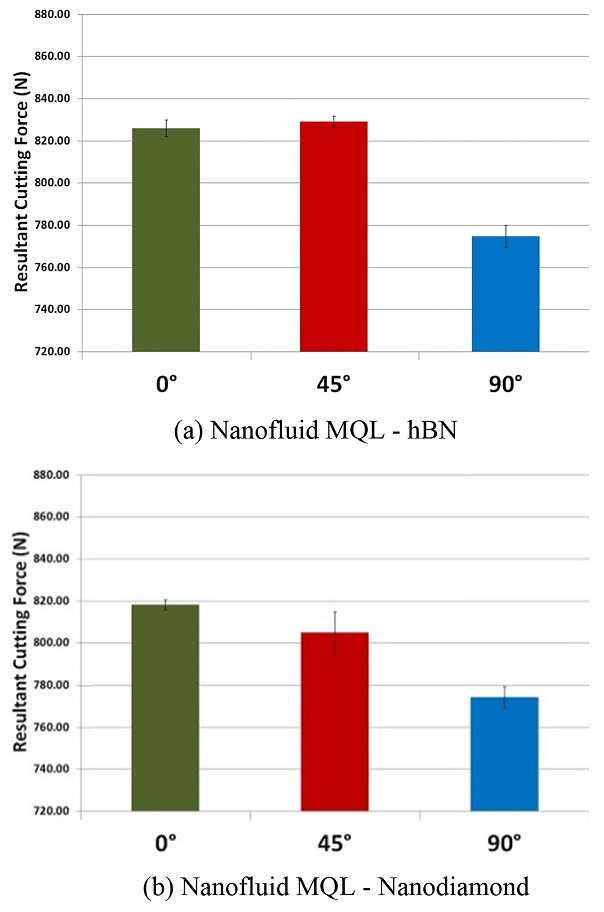
또한 Fig. 3은 유량이 3 ml/min인 경우에 있어서 나노유체 종류별로 분사 각도에 따라 이송방향과 이송 수직 방향으로 측정된 절삭력의 벡터 합을 취한 합력의 크기를 보여준다. Fig. 3에서 재확인할 수 있듯이 분사 각도 90°인 조건에서 가장 작은 절삭력이 측정되었다.

Fig. 3

Measured resultant milling forces (Flow rate: 3 ml/min)

3. 나노유체 극미량 분사 유동 거동 수치해석

3.1 해석 모델 구성

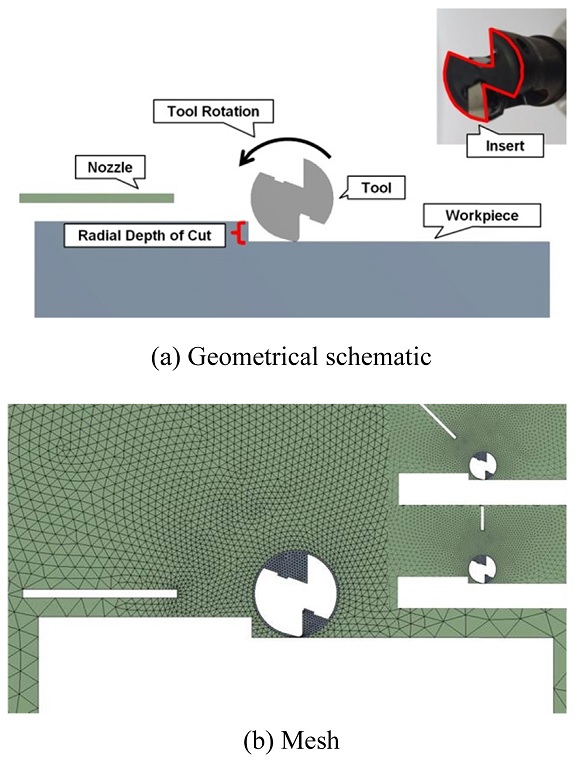
나노유체 극미량 분사 유동 해석을 위해 상용프로그램인 ANSYS FLUENT를 이용하여 2차원 수치해석 모델을 구성하였다. Fig. 4(a)는 해석 모델 구성을 위해 사용된 실제 실험 환경과 유사한 가공 영역의 2차원 기하학적 조건을 도식적으로 보여주며 Fig. 4(b)는 상기한 기하학적 조건을 기반으로 생성된 Mesh 결과를 보여주고 있으며 이송방향을 기준으로 나노유체를 분사하는 노즐의 각도가 0°, 45°, 90°인 경우에 상응하는 각각의 Mesh 모델이 주어져 있다. 또한, 본 해석 모델의 격자 형상은 삼각형(Triangle)이고, 노드 수는 8,269개, 격자 수는 16,035개이다.

Fig. 4

The machining geometry and generated mesh for numerical analysis considering nanofluid MQL flow

유동 해석 모델 생성에 있어서 공구 형상은 분사되는 유체의 흐름에 상당한 영향을 미치므로 도면을 기반으로 실제 공구의 기하학적 형상을 상세히 반영하여 모델링 하였고 노즐 형상은 유체가 분사되는 홀(Hole)의 형상이 영향을 미치므로 외부 구조는 생략하고 홀 부분의 모델링만을 수행하였다. 가공물은 밀링 가공 시 공구가 가공물 너비의 중앙 지점에 위치했을 때 반경 방향 절삭 깊이 4 mm를 고려하여 모델링을 수행하였다.

3.2 해석 방법

나노유체 극미량 분사를 적용한 밀링 가공에 있어서 노즐로부터 분사되는 분무의 액적(Droplet)이 공구 및 가공물 접촉부에 침투되는 양이 많을수록 윤활 작용은 향상되고 이로 인한 절삭력 감소의 효과가 나타난다. 따라서 본 연구에서는 수치해석을 통해 분사 조건에 따른 공구 및 가공물 접촉부에의 나노유체 액적 침투율을 상대적으로 비교하고자 한다.

나노유체 극미량 분사에 있어서 노즐에서 토출되는 분무 액적의 개수는 1,500개로 가정하고 이에 대하여 해석을 수행하여 밀링 공구에 포집되는 액적의 개수를 계산한 후 이를 전체 입수 액적 개수인 1,500개로 나누어 액적 침투율을 계산하였다. 해석에 있어서 액적 분사가 가능한 모델인 다상 유동 모델(Discrete Phase Model)을 사용하였고 지배방정식은 식(1)과 같다.⁹

$\[ m_p\frac{d{u}_p}{dt}=F_{drag}+F_{pressure}+F_{virtualmass}+F_{gravity}+F_{other} \]$

(1)

난류 모델로는 Standard k - ε의 변종으로 회전에 대한 유동을 잘 예측할 수 있는 Realizable k - ε 모델을 적용하였다. 회전하는 공구의 표면에 포집되는 액적의 개수를 계산하기 위해 해석 도메인이 좌표계와 함께 움직이는 Moving Reference Frames (MRF)기법을 적용하였고 공구의 실제 실험 회전 속도인 2387 RPM을 적용하였다. 이 기법은 과도 해석(Transient Analysis)에 사용된다.¹⁰

노즐에서 분사되는 유체는 기본적으로 공기와 나오미테크사의 순정오일이 사용되었고 또한, 나노유체의 경우는 ND 및 hBN 나노입자를 순정오일 첨가하여 제작하였고 질량비는 전술한 바와 같이 0.5 wt.%가 고려되었다. 해석 수행에 있어서 공기와 순정오일의 점도 및 밀도 등의 물성치는 FLUENT에서 제공하는 기본 데이터를 사용하였으며 ND 및 hBN 나노유체의 경우 점도는 Viscometer 장치를 사용하여 측정하였으며 밀도의 경우는 질량비(0.5 wt.%)와 나노입자 및 순정오일의 밀도를 고려하여 계산하였다. Table 2는 공기 및 각 나노유체의 밀도 및 점도 수치를 보여준다.

Table 2

Material properties used in the numerical analysis

밀링 가공 시 공구 표면에 포집되는 액적의 개수는 공구의 회전각도를 10°씩 증가시키면서 계산하였다. 각 회전각도에서 공구의 회전속도가 2387 RPM인 경우 공구가 10°만큼 회전 하는데 0.0007초의 실제 시간이 걸리고 노즐에서 분사되는 유체가 안정화 되는데 30 Time Steps인 0.021 초가 소요된다. 따라서 공구가 한 바퀴인 360°를 회전하는 경우 총 36회의 해석이 필요하며 이때 각 회수에서 유체의 안정화를 위해 30 Time Steps에 해당하는 계산이 필요하다. 수치 해석은 전술한 바와 같이 이송방향 기준 노즐의 분사각도가 각각 0°, 45°, 90°인 경우에 대하여 ND 및 hBN입자가 포함된 2가지 나노유체를 고려하여 총 6번이 수행되었다.

3.3 해석 결과

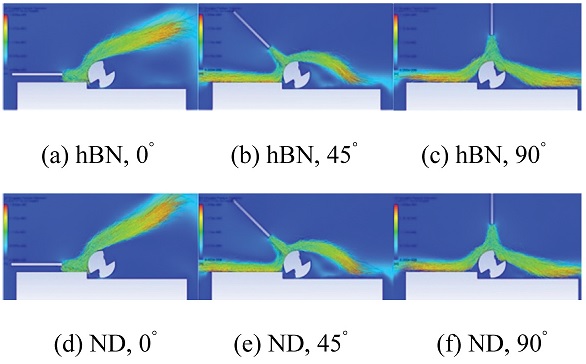
Fig. 5는 수치해석을 통해 도출한 나노유체 유동 거동에 대한 시각적 결과를 보여주며 이 결과는 노즐로부터 공구에 가해지는 나노유체 분무 액적의 크기 분포를 의미한다. 즉, Fig. 5에서 파란색 부분은 작은 액적을 의미하고 붉은색 부분은 큰 액적을 의미한다. Fig. 5 결과에 대한 정성적 분석을 수행했을 때 이송방향기준 분사각도가 0°인 경우에 비하여 분사각도가 45°, 90°인 경우 공구 표면에 좀 더 많은 액적이 분포함을 고찰할 수 있다.

Fig. 5

Visualized mist droplets around the tool according to a nanofluid type and a spray angle

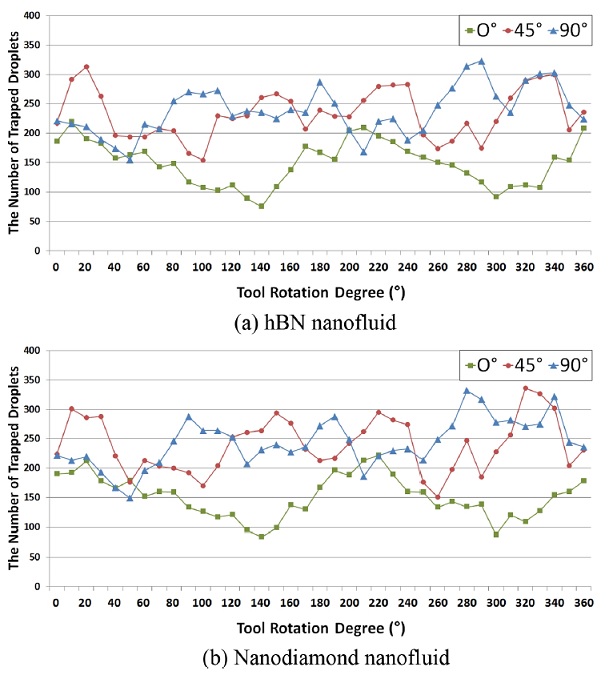
이를 정량적으로 분석하기 위해 Fig. 6는 ND 및 hBN 나노유체 분무가 노즐로부터 밀링 공구 및 가공물 접촉부에 가해질 때 공구가 10°씩 회전할 때마다 각 회전 각도 별로 공구 표면에 포집된 분무 액적의 개수를 계산한 결과를 보여준다. Fig. 6에서 알 수 있듯이 분사 각도가 90°인 경우의 공구 표면에 포집된 액적 개수가 분사 각도가 0°, 45°인 경우의 포집된 액적 개수보다 상대적으로 많음을 알 수 있으며 이는 Fig. 7과 Table 3에서도 재확인되고 있다.

Fig. 6

Calculated numbers of trapped droplets according to a tool rotation angle

Fig. 7

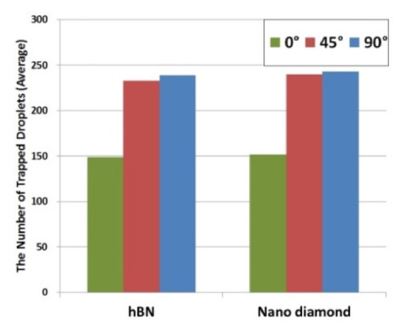
The average numbers of trapped droplets to the tool according to the feed direction angle of the nozzle

Table 3

Ratios of trapped droplets on the tool versus total input droplets

Fig. 7은 Fig. 6에서 보여주는 공구의 회전 각도 별 포집된 액적 개수의 평균값을 의미한다. 또한, Table 3은 노즐로부터 공급된 전체 나노유체 분무 액적 개수에 대하여 노즐 분사 각도 별로 공구 표면에 포집된 액적 개수의 비를 나타낸다. Fig. 7과 Table 3의 결과에서 알 수 있듯이 분사 각도가 90°인 경우 평균적으로 가장 많은 액적이 공구 표면에 포집되며 분사 각도가 0°인 경우는 포집되는 액적이 수가 가장 적다.

수치 해석 결과, 이송방향 기준 대비 나노유체 노즐 분사각도가 90°인 경우 밀링 가공 시 공구 표면에서 포집되는 나노유체 액적 침투비율이 가장 크게 나타나는데 이는 Figs. 2 및 3에서 보여주는 해당 분사각도에서의 가장 낮은 측정 절삭력과 밀접한 관련이 있다. 즉, 상대적으로 많은 개수의 액적이 공구 표면에 포집되는 경우 공구 및 가공물 간 윤활 작용이 향상되어 마찰력이 감소되고 이로 인해 측정되는 절삭력이 감소한다. 또한, 상대적으로 높은 ND 나노유체의 액적 침투비율로 인해 ND 나노유체가 hBN 나노유체의 경우보다 절삭력 감소에 효과적임을 Table 3을 통해 알 수 있고, 이는 Fig. 2에서 보여주는 실험결과에 기인한 주 효과 분석 결과와도 일치한다.

4. 결론

본 논문에서는 티타늄 합금의 나노유체 MQL 밀링 가공에 있어서 전산유체역학적 수치해석 모델을 개발하여 공구 및 가공물 접촉부에의 나노유체 분무 거동을 해석하고 이 해석결과를 실험 결과와 비교하여 모델의 타당성을 검증하는 연구를 수행하였다.

나노유체의 종류, 나노유체의 분사 유량 및 분사 각도가 절삭력에 미치는 영향을 분석하기 위해 나노유체 MQL 밀링 가공 실험을 수행하였다. 실험에서 나노유체에 사용된 입자는 ND 및 hBN이고 고려된 나노유체 분사 유량은 2, 3, 4 ml/min이며 이송방향 기준 분사각도는 0°, 45°, 90°이다. 이 때 절삭력이 가장 작게 측정되는 경우는 나노유체의 종류가 ND 나노유체이고, 유량은 3 ml/min, 각도는 90°인 경우이다.

상기한 실험 결과를 기반으로 공구 및 가공물 접촉부에의 나노유체 분무 거동을 분석하는 수치해석 관점에서의 검증을 위하여 상용 프로그램인 ANSYS FLUENT를 이용하여 2차원 해석 모델을 구성하였다. 본 모델 개발에 있어서 난류 모델로는 Realizable k - ε 모델을적용하였고 해석 도메인이 좌표계와 함께 이동하는 MRF 기법을 적용하여 밀링 공구 및 가공물 접촉부에 포집되는 나노유체 분무 액적의 침투비율을 계산하였다. 즉, 공구 표면에 포집되는 나노유체 분무 액적의 개수를 공구의 회전 각도를 10°씩 증가시키면서 계산하였고, 계산된 각 회전 각도 별 포집 액적개수의 평균값을 노즐로부터 입수되는 전체 액적 개수로 나누어 각 조건 별로 나노유체 액적 침투 비율을 도출하였다.

각 조건 별로 도출된 액적 침투 비율을 비교했을 때 ND 나노유체를 이송 방향 기준 90°로 분사한 경우 액적 침투 비율이 가장 큼을 확인하였다. 이는 해당 조건에서 상대적으로 많은 개수의 액적이 공구 표면에 포집되어 공구 및 가공물 간 윤활 작용이 향상되고 이를 통한 마찰력 감소가 이루어져 절삭력이 감소하게 됨으로 설명할 수 있고 실험 결과와도 일치하여 구축된 수치 해석 모델의 타당성이 검증되었다.

Acknowledgments

이 논문은 2013 년도 정부(교육부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업임(No. 2013R1A1A2012313).

REFERENCES

• Lee, P. H., Nam, T. S., Li, C., and Lee, S. W., “Experimental Study on Meso-Scale Milling Process Using Nanofluid Minimum Quantity Lubrication,” Transfer Korean Society Mechanical Engineering A, Vol. 34, No. 10, pp. 1493-1498, 2010. [https://doi.org/10.3795/KSME-A.2010.34.10.1493]
• Klocke, F. and Eisenblatter, G., “Dry Cutting, Keynote Paper,” Annals of the CIRP, Vol. 46, No. 2, pp. 519-526, 1997. [https://doi.org/10.1016/S0007-8506(07)60877-4]
• De Lacalle, L. L., Angulo, C., Lamikiz, A., and Sanchez, J. A., “Experimental and Numerical Investigation of the Effect of Spray Cutting Fluids in High Speed Milling,” Journal of Materials Processing Technology, Vol. 172, No. 1, pp. 11-15, 2006. [https://doi.org/10.1016/j.jmatprotec.2005.08.014]
• Yan, L., Yuan, S., and Liu, Q., “Influence of Minimum Quantity Lubrication Parameters on Tool Wear and Surface Roughness in Milling of Forged Steel,” Chinese Journal of Mechanical Engineering, Vol. 25, No. 3, pp. 419-429, 2012.
• Liu, Z. Q., Cai, X. J., Chen, M., and An, Q. L., “Investigation of Cutting Force and Temperature of End-Milling Ti-6Al-4V with Different Minimum Quantity Lubrication (MQL) Parameters,” Journal of Engineering Manufacture, Vol. 225, No. 8, pp. 1273-1279, 2011. [https://doi.org/10.1177/2041297510393793]
• Najiha, M. S., Rahman, M. M., Kamal, M., Yusoff, A. R., and Kadirgama, K., “Minimum Quantity Lubrication Flow Analysis End Milling Processes: A Computational Fluid Dynamics Approach,” Journal of Mechanical Engineering and Sciences, Vol. 3, pp. 340-345, 2012. [https://doi.org/10.15282/jmes.3.2012.10.0032]
• Najiha, M. S. and Rahman, M. M., “A Computational Fluid Dynamics Analysis of Single and Three Nozzles Minimum Quantity Lubricant Flow for Milling,” Journal of Mechanical Engineering and Sciences, Vol. 10, pp. 1891-1900, 2014. [https://doi.org/10.15282/ijame.10.2014.6.0157]
• Najiha, M. S., Rahman, M. M., Yusoff, A. R., and Kadirgama, K., “Investigation of Flow Behavior in Minimum Quantity Lubrication Nozzle for End Milling Processes,” International Journal of Automotive and Mechanical Engineering, Vol. 6, pp. 768-776, 2012. [https://doi.org/10.15282/ijame.6.2012.8.0062]
• ANSYS, Inc., “ANSYS Fluent User’s Guide,” 2013.
• ANSYS, Inc., “ANSYS Fluent Tutorial Guide,” 2013.