유성기어박스의 캐리어 핀홀 위치 오차의 위상에 따른 유성기어의 하중 분할 연구
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
The planetary geartrain can be reduced in size and weight, and has excellent durability since the input torque is divided by the number of planet gears when the power is transmitted. In order to improve its durability, the load sharing among planet gears must be even. However, of the various manufacturing errors possible, the carrier pinhole position error has the greatest influence on load sharing. This study compared and analyzed the load sharing and the gear safety of planetary gears, according to the phase of the carrier pinhole position error. We confirmed that load sharing among the planet gears varied, depending on the phase of the carrier pinhole position error. The mesh load factor is inversely related to the gear safety factor for bending and contact, and affects the durability of the planetary geartrain. Also, in the design of the planetary geartrain, the load sharing among planet gears is directly affected by the carrier pinhole position error and its phase. Therefore, the geometric tolerance must be managed efficiently, which needs to be reflected in the production drawings.
Keywords:
Planetary gearbox, Load sharing, Carrier pinhole position error, Mesh load factor키워드:
유성기어박스, 하중 분할, 캐리어 핀홀 위치 오차, 하중 분할 계수1. 서론
유성기어트레인은 여러 개의 유성기어에 의해 입력 토크가 분할되어 동력을 전달함으로 소형화 및 경량화가 가능하고, 내구성이 뛰어나다. 유성기어트레인의 내구성을 향상시키기 위해서는 유성기어간의 하중 분할이 균일하여야 한다. 그러나 유성기어트레인을 구성하는 기어, 베어링, 유성핀, 캐리어 등의 부품들은 오차가 존재하며, 이로 인하여 유성기어간의 하중 분할을 균일하게 하는 것이 쉽지 않다. 기어의 제작 오차는 치형 오차, 피치 오차, 런아웃 오차가 있으며, 베어링 제작에 의한 내륜과 외륜, 전동체의 오차, 유성핀을 캐리어에 억지 끼움시 조립 오차, 캐리어 런아웃 및 핀홀 위치 오차 등에 의해 유성기어간의 하중 분할이 불균일하게 발생한다.1 또한 이러한 오차들은 기어의 미스얼라인먼트를 유발하여 유성기어트레인의 요구 수명을 만족시키지 못하는 결과를 초래할 수 있다.
이전 연구는 유성기어 3 - 6개를 가진 1단 유성기어트레인 시뮬레이션 모델을 해석적으로 입력 토크 증가, 캐리어의 핀홀 위치 오차를 핀홀 여러 개 중에 1개의 핀홀에 원주 방향의 핀홀 위치 오차를 고려하여 유성기어간의 하중 분할을 연구하였다.2,3
본 연구는 유성기어트레인의 하중 분할에 영향을 미치는 여러 제작 오차 중에 캐리어의 핀홀 위치 오차를 산업용 유성기어박스 시뮬레이션 모델에 반영하여 유성기어간의 하중 분할을 해석하고 유성기어트레인의 내구성에 미치는 영향을 연구하였다. 개발된 시뮬레이션 모델은 상용 프로그램4을 이용하였으며, 이 모델은 Kim5의 이전 연구에서 검증되었다. 해석 조건인 캐리어의 핀홀 위치 오차는 핀홀 6개로 구성된 캐리어6의 3차원 측정을 통해 얻은 원주 방향의 핀홀 위치 오차 중에 최대값을 이용하여 핀홀 4개로 구성된 캐리어에 반영하여 해석을 수행하였다.
2. 유성기어트레인의 시뮬레이션 모델
2.1 유성기어트레인의 구조
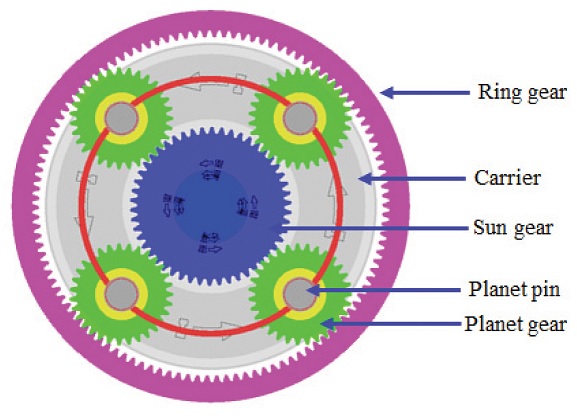
유성기어트레인은 선기어, 유성기어, 링기어, 캐리어로 구성된 1단 유성기어 구조로 유성기어의 개수는 4개이다. 동력은 링기어로 입력되어 선기어로 출력되며, 캐리어는 고정이다.
2.2 유성기어간의 하중 분할
유성기어트레인에서 유성기어간의 하중 분할은 하중 분할 계수, Kγ로 나타낸다.7 하중 분할 계수가 1에 가까울수록 유성기어간의 하중 분할이 균일하며, 여러 개의 유성기어 중에 하중 분할 계수가 1이상인 경우에 유성기어간의 하중 분할이 균일하지 않음을 의미한다. 즉, 유성기어트레인의 입력 토크(Tin)가 유성기어의 개수(NCP)로 나누어질 때, 하중 분할 계수가 1.5인 경우, 토크를 크게 받는 유성기어는 1.5·Tin/NCP가 된다. 유성기어간의 하중 분할 계수는 식(1)과 같이 계산한다.
| (1) |
2.3 기어 강도 평가
기어 강도 평가는 ISO 규격8을 이용하여 기어의 굽힘 강도와 면압 강도를 평가하였다. 유성기어간의 하중 분할은 기어의 굽힘 강도와 면압 강도에 영향을 준다.
기어의 굽힘 강도는 이뿌리 응력 한도, σFG와 이뿌리 응력, σF의 비로 계산한다. 기어 이뿌리부에서 발생하는 응력이 이뿌리 응력 한도보다 크면, 이뿌리부에서 균열이 발생하여 균열이 진전하여 기어 이의 절손을 유발한다.9
기어의 공칭 이뿌리 응력, σF0는 식(2)와 같이 계산한다.
| (2) |
기어의 이뿌리 응력, σF는 식(3)과 같이 계산한다.
| (3) |
기어의 이뿌리 응력 한도, σFG는 식(4)와 같이 계산한다.
| (4) |
기어의 면압 강도는 기어의 접촉 응력 한도, σHG와 접촉 응력, σH의 비로 계산하며, 두 기어 사이에서 발생하는 접촉에 의한 강도이다. 기어 치면에서 발생하는 응력이 접촉 응력 한도보다 크면 기어 치면에서 아주 작은 조각이 떨어져 나와 작은 구멍인 피트(Pits)가 발생한다. 피트가 증가하고 커짐에 따라 피팅이 되며, 이는 기어 치면의 내구성에 영향을 준다.9
기어의 공칭 접촉 응력, σH0는 식(5)와 같이 계산한다.
| (5) |
기어의 접촉 응력, σH는 식(6)과 같이 계산한다.
| (6) |
기어의 접촉 응력 한도, σHG는 식(7)과 같이 계산한다.
| (7) |
2.4 캐리어 핀홀 위치 오차의 위상에 따른 해석 조건
본 연구는 Kim6의 이전 연구에 소개된 캐리어의 핀홀 위치 오차를 시뮬레이션 모델에 반영하여 해석하였다. 이전 연구에서 캐리어는 핀홀 6개로 구성하였으며, 실제 산업 현장에서 제작된 캐리어의 오차를 반영하기 위하여 3차원 측정을 통해 핀홀 위치 오차를 측정하였다. 측정된 캐리어 핀홀 위치 오차는 원주 방향의 최대값이 +80 μm, 최소값이 -80 μm로 나타났다.
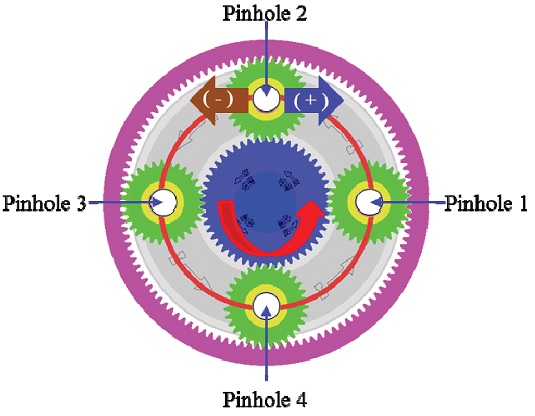
본 연구는 핀홀 4개로 구성된 캐리어에 핀홀 1은 핀홀 위치 오차가 존재하지 않는 것으로 가정하였으며, 핀홀 2 - 4는 측정된 핀홀 위치 오차의 위상을 변화시키면서 해석을 수행하였다.
Fig. 2는 캐리어 핀홀 위치 오차의 위상을 나타낸 것으로, 핀홀을 기준으로 시계 방향은 (+)의 오차를, 반시계 방향은 (-)의 오차를 나타낸 것이다.
Table 2는 시뮬레이션 모델에 반영한 캐리어 핀홀 위치 오차의 위상에 따른 해석 조건이다. Table 2에서 Case A는 캐리어의 핀홀 위치 오차가 존재하지 않는 경우와 핀홀 위치 오차가 핀홀 1개에 존재하는 경우이다. Case B는 캐리어의 핀홀 위치 오차가 핀홀 2개에 존재하는 경우이고, Case C는 캐리어의 핀홀 위치 오차가 핀홀 3개에 존재하는 경우이다.
3. 유성기어트레인의 시뮬레이션 모델 해석
3.1 캐리어 핀홀 위치 오차의 위상에 따른 유성기어간의 하중 분할 해석
유성기어트레인 시뮬레이션 모델을 활용하여 캐리어 핀홀 위치 오차의 위상에 따른 유성기어간의 하중 분할을 해석하였다. 유성기어트레인의 입력 토크 및 속도는 18,238.5 Nm@85.9 RPM이며, 회전 방향은 링기어를 기준으로 반시계 방향이다.
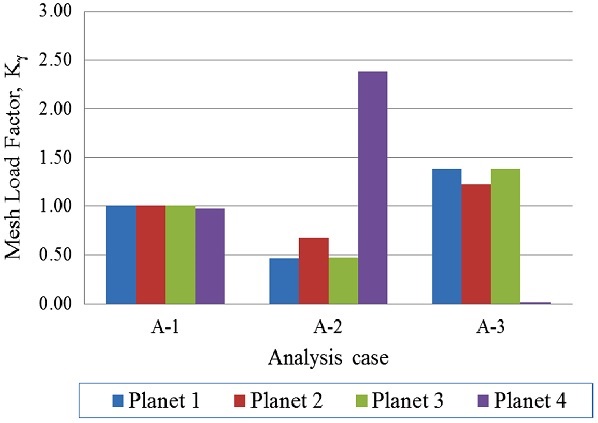
Fig. 3은 핀홀 위치 오차가 존재하지 않는 경우와 핀홀 1개에 핀홀 위치오차가 존재하는 경우에 대한 해석 결과이다. Case A-1모델은 핀홀 위치 오차가 존재하지 않는 조건으로 각 유성기어의 핀홀 위치에 따른 중력의 영향을 제외하면, 유성기어간의 하중 분할 계수는 1로 균일하였다. Case A-2모델은 핀홀 4에 (+) 위상의 핀홀 위치 오차가 존재함으로 유성기어 4에서 가장 먼저 기어 물림이 발생하여 가장 높은 하중이 작용하였다. 유성기어 4의 양쪽 측면에 위치한 유성기어 1과 3은 가장 작은 하중이 작용하며, 유성기어 4의 180°위치에 존재하는 유성기어 2는 유성기어 1과 3보다는 큰 하중이 작용하였다. Case A-3모델은 핀홀 4에 (-) 위상의 핀홀 위치 오차가 존재함으로 유성기어 4에서 기어 물림이 발생하지 않고, 유성기어 4의 양쪽 측면에 위치한 유성기어 1과 3에서 먼저 기어 물림이 발생하여 큰 하중이 작용하고, 유성기어 4의 180° 위치에 존재하는 유성기어 2에 상대적으로 작은 하중이 작용하였다.
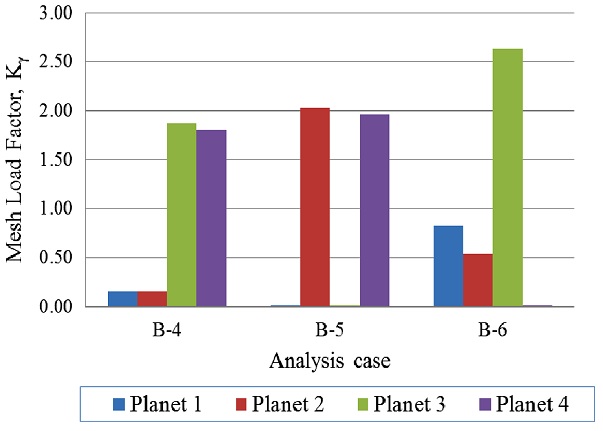
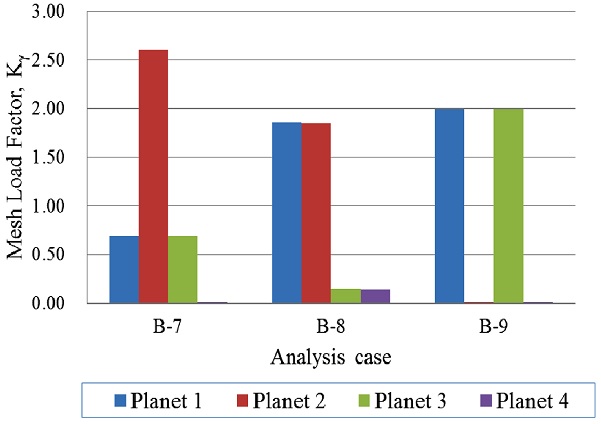
Figs. 4와 5는 캐리어 핀홀 위치 오차가 핀홀 2개에 존재하는 경우에 대한 해석 결과이다. Case B-4와 B-8 모델은 캐리어 핀홀 위치 오차가 2개의 핀홀에 연속적으로(핀홀 3과4) 같은 위상을 갖는 경우로 B-4모델은 유성기어 3과 4에, B-8 모델은 유성기어 1과 2에서 기어 물림이 먼저 발생하여 하중 분할 계수가 1.5보다 큰 경향성을 보였다. Case B-5와 B-9 모델은 캐리어 핀홀 위치 오차가 2개의 핀홀에 180° 위치 간격(핀홀 2와 4 또는 핀홀 1과 3)으로 같은 위상을 갖는 경우로, B-5 모델은 유성기어 2와 4에, B-9모델은 유성기어 1과 3에서 기어 물림이 먼저 발생하는 경향성을 보였다. Case B-6과 B-7 모델은 캐리어 핀홀 위치 오차가 원주 방향을 기준으로 2개의 핀홀에 서로 다른 위상을 갖는 경우로, (+) 위상의 핀홀 위치 오차를 갖는 유성기어는 하중 분할 계수가 2.5보다 큰 경향성을 보이며, (-) 위상의 핀홀 위치 오차를 갖는 유성기어는 기어 물림이 발생하지 않았다.
Case B 모델을 보았을 때, 캐리어 핀홀 위치 오차가 동일한 위상으로 핀홀 4개 중 2개에 존재하는 경우, 2개의 유성기어에 하중 분할이 균일하게 발생하는 경향성을 보였으며, 핀홀 위치 오차가 핀홀 2개에 반대 위상으로 존재하는 경우에는 (+) 위상의 핀홀 위치 오차를 갖는 유성기어에서 먼저 물림이 발생하며, (+) 위상의 양쪽 측면에 존재하는 유성기어에서 그 다음 하중을 분할하는 경향성을 보였다.
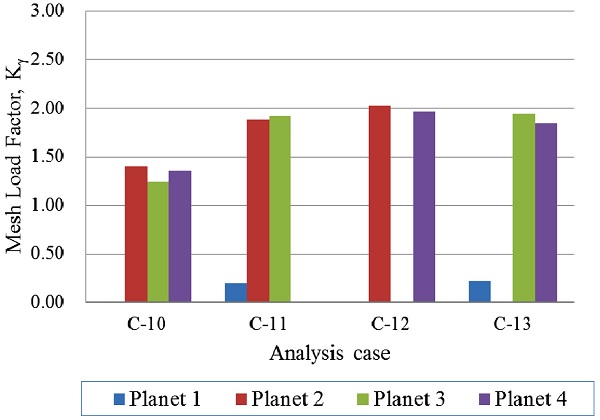
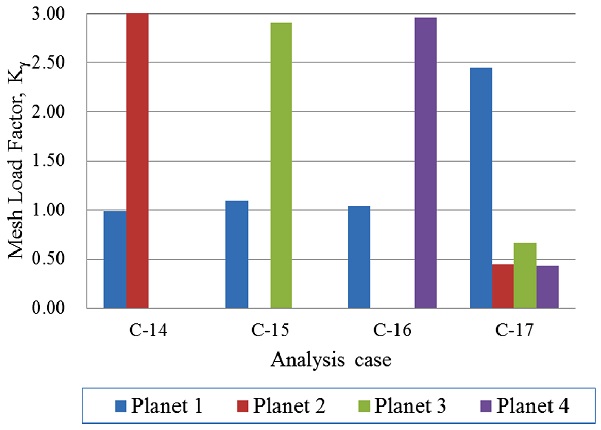
Fig. 6과 7은 캐리어 핀홀 위치 오차가 핀홀 3개에 존재하는 경우로, Case C-10 모델은 캐리어 핀홀 위치 오차가 모두 (+) 위상을 가지므로 유성기어 2, 3, 4에서 기어 물림이 발생하고 유성기어 1은 물림이 발생하지 않았다. 이는 Case A-3 모델과 유사한 경향성을 보이며, 유성기어의 최대 하중 위치만 변경되었다. Case C-11 - C-13 모델은 캐리어 핀홀 위치 오차가 핀홀 2개에 (+) 위상, 핀홀 1개에 (-) 위상을 가지므로, 연속적으로(핀홀 2와 3 또는 핀홀 3과 4) (+) 위상을 갖는 유성기어는 2개의 유성기어에서 하중을 분할하고, 핀홀 위치 오차가 존재하지 않는 유성기어에서 나머지 하중을 분담하였다. 그러나, 불연속적으로(핀홀 2와 4) (+)의 위상을 갖는 유성기어는 2개의 유성기어에서 하중을 약 50%씩 분할하고, 나머지 유성기어는 하중을 분담하지 않았다. Case C-14 - C-16 모델은 캐리어 핀홀 위치 오차가 핀홀 1개에 (+) 위상, 핀홀 2개에 (-) 위상을 가지므로, (+) 위상이 존재하는 유성기어에서 기어 물림이 먼저 발생하고, 기어 이의 변형량이 증가함에 따라 핀홀 위치 오차가 존재하지 않는 유성기어에 하중이 분할되었다. Case C-17 모델은 캐리어 핀홀 위치 오차가 모두 (-) 위상을 가지므로 유성기어 1에서 먼저 기어 물림이 발생하고, 유성기어 3, 2, 4에 기어 물림이 발생하였다. 이는 Case A-2 모델과 유사한 경향성을 보이며, 유성기어의 최대 하중 위치만 변경되었다.
결과적으로 링기어가 반시계 방향으로 회전할 때 1개의 핀홀 위치 오차가 (+) 위상으로 존재하는 경우, 핀홀 위치 오차가 존재하는 유성기어에서 가장 먼저 기어 물림이 발생하며, 그 다음은 가장 먼저 기어 물림이 발생한 유성기어의180° 위치에 존재하는 유성기어에서 하중을 분담하는 경향성을 보였다. 여러 개의 핀홀 위치 오차가 유성기어의 순번에 따라 연속적으로 (+) 위상을 갖는 경우, 핀홀 위치 오차가 존재하는 유성기어에서 기어 물림이 발생한다. 그러나 여러 개의 핀홀 위치 오차가 유성기어의 순번에 따라 (+)와 (-) 위상으로 존재하는 경우에는 (+) 위상으로 핀홀 위치 오차가 존재하는 유성기어에서 기어 물림이 발생하며, 핀홀 위치 오차가 존재하지 않는 유성기어에서 하중이 분할되었다.
링기어가 반시계 방향으로 회전시 핀홀 위치 오차가 (+)의 위상으로 180° 위치에 존재하는 경우에 비해 90°위치에 존재하는 경우에 유성기어간의 하중 분할이 향상되는 경향성을 나타내었다.
4. 결론
본 연구는 유성기어트레인의 하중 분할에 영향을 미치는 여러 제작 오차 중에 캐리어 핀홀 위치 오차를 유성기어박스 시뮬레이션 모델에 반영하여 유성기어의 하중 분할이 유성기어트레인의 내구성에 미치는 영향을 분석하였다. 캐리어 핀홀 위치 오차의 위상에 따라 유성기어의 하중 분할과 기어 강도를 비교 분석하였으며, 이를 통해 얻은 결론은 다음과 같다.
캐리어 핀홀 위치 오차의 위상에 따라 유성기어의 하중 분할이 달라짐을 확인할 수 있었다. 하중 분할 계수는 기어의 굽힘 강도와 면압 강도의 안전계수와 반비례 관계이며, 계수의 증가는 유성기어트레인의 안전계수와 수명을 감소시킴을 확인하였다. 또한, 유성기어트레인 설계 시 캐리어 핀홀 위치 오차 및 위상이 유성기어의 하중 분할에 영향을 미치므로 제작 도면에 이를 반영하여 기하 공차를 효율적으로 관리해야 한다.
NOMENCLATURE
| u : | Gear ratio |
| d1 : | Reference diameter of pinion (mm) |
| Ft : | Nominal transverse tangential load at reference cylinder per mesh (N) |
| KA : | Application factor |
| KFα : | Transverse load factor for root stress |
| KFβ : | Face load factor for root stress |
| KHα : | Transverse load factor for contact stress |
| KHβ : | Face load factor for contact stress |
| KV : | Dynamic factor |
| Kγ : | Mesh load factor |
| mn : | Normal module |
| NCP : | Number of planet gears |
| Tin : | Input torque (Nm) |
| Tbranch : | Torque in branch with heaviest load (Nm) |
| YB : | Rim thickness factor |
| YDT : | Deep tooth factor |
| YF : | Tooth form factor |
| YNT : | Life factor for root stress |
| YRrelT : | Relative surface factor |
| YS : | Stress correction factor |
| YST : | Stress correction factor for reference test gear |
| YX : | Size factor for root stress |
| Yβ : | Helix angle factor for root stress |
| YδrelT : | Relative notch sensitivity factor |
| ZB,D : | Single pair tooth contact factor |
| ZE : | Elasticity factor (N/mm2) |
| ZH : | Zone factor |
| ZL : | Lubricant factor |
| ZNT : | Life factor for contact stress |
| ZR : | Roughness factor |
| ZX : | Size effect factor for contact stress |
| ZV : | Velocity factor |
| ZW : | Work hardening factor |
| Zβ : | Helix angle factor for contact stress |
| Zε : | Contact ratio factor |
| σF : | Tooth root stress (MPa) |
| σF0 : | Nominal tooth root stress (MPa) |
| σFG : | Tooth root stress limit (MPa) |
| σFlim : | Nominal stress number for bending (MPa) |
| σH : | Contact stress (MPa) |
| σH0 : | Nominal contact stress (MPa) |
| σFG : | Pitting stress limit (MPa) |
| σHlim : | Allowable stress number for contact (MPa) |
Acknowledgments
본 논문은 한국생산기술연구원 기관주요사업 “2017년 중소, 중견기업 타킷형 육성 생산기술 개발 사업(1/3) (KITECH JG-17-0010)”의 지원으로 수행한 연구입니다.
REFERENCES
- Kim, J. G., “Effects Analysis of Gear Design Parameter on Load Sharing of Planetary Geartrain,” Ph.D. Thesis, School of Mechanical Design Engineering, Chungnam National University, 2017.
-
Bodas, A. and Kahraman, A., “Influence of Carrier and Gear Manufacturing Errors on the Static Load Sharing Behavior of Planetary Gear Sets,” JSME International Journal Series C, Vol. 47, No. 3, pp. 908-915, 2004.
[https://doi.org/10.1299/jsmec.47.908]

-
Singh, A., “Application of a System Level Model to Study the Planetary Load Sharing Behavior,” Journal of Mechanical Design, Vol. 127, No. 3, pp. 469-476. 2005.
[https://doi.org/10.1115/1.1864115]

- Romax Technology Co., Ltd., “Romax Designer Software Manual,” https://www.romaxtech.com, / (Accessed 22 MAY 2017)
-
Kim, J. G., Park, Y. J., Lee, G. H., Kim, Y. J., Oh, J. Y., et al., “Effect Analysis of Carrier Pinhole Position Error on the Load Sharing and Load Distribution of Planet Gear,” Journal of Korean Society of Manufacturing Process Engineers, Vol. 15, No. 5, pp. 66-72, 2016.
[https://doi.org/10.14775/ksmpe.2016.15.5.066]

-
Kim, J. G., Park, Y. J., Lee, G. H., and Kim, J. H., “An Experimental Study on the Effect of Carrier Pinhole Position Errors on Planet Gear Load Sharing,” Int. J. Precis. Eng. Manuf., Vol. 17, No. 10, pp. 1305-1312, 2016.
[https://doi.org/10.1007/s12541-016-0155-0]

- AGMA 6123-B06, “Design Manual for Enclosed Epicyclic Gear Drives,” 2006.
- ISO 6336-(1:6), “Calculation of Load Capacity of Spur and Helical Gears,” 2003-2007.
-
Kim, J. G., Park, Y. J., Lee, G. H., and Kim, J. H., “Effect Analysis of Carrier Pinhole Position Error on the Load Sharing of Planetary Gear,” Journal of the Korean Society of Manufacturing Process Engineers, Vol. 15, No. 4, pp. 67-72, 2016.
[https://doi.org/10.14775/ksmpe.2016.15.4.067]

-
Kim, J. G., Park, Y. J., Lee, G. H., and Kim, J. H., “Effects of Bearing Characteristic on the Gear Load Distribution in the Slewing Reducer for Excavator,” Journal of the Korean Society of Manufacturing Process Engineers, Vol. 13, No. 5, pp. 8-14, 2014.
[https://doi.org/10.14775/ksmpe.2014.13.5.008]

-
Han, S. G., Shin, Y. I., Yoon, C. H., and Song, C. K., “Strength and Durability Analysis of the Double Planetary Gears,” Journal of the Korean Society of Manufacturing Process Engineers, Vol. 13, No. 5, pp. 28-34, 2014.
[https://doi.org/10.14775/ksmpe.2014.13.5.028]