굴삭기 선회시스템의 관성 내구 시험을 위한 플라이휠의 등가관성 모멘트 결정

2.1 선회감속기 모델

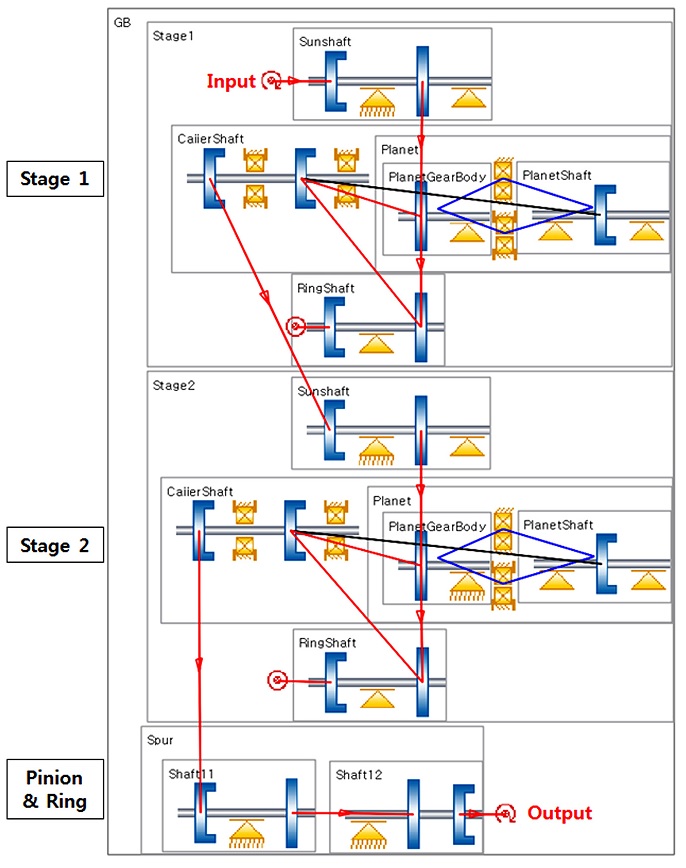
본 연구에서는 H사의 5.5톤 궤도형 굴삭기를이용하여 상부회 전체의 선회 시험을 수행하였다. 선회감속기는 선기어 입력, 캐리어 출력, 링기어 고정의 2단 유성기어트레인으로 구성되며, 굴삭기 선회시스템의 시뮬레이션 모델을 구성하기 위하여 상용 소프트웨어를 사용하여 선회감속기에 대해 3D 모델링을 수행하였고 Fig. 1 및 Table 1과 같다. 이를 이용하여 기어, 축, 베어링, 캐리어 등 각 부품의 질량과 질량관성모멘트를 구하였다.

Fig. 1

Assembly drawing of the slewing reducer

Table 1

Specification of slewing reducer

또한, 기어의 물림 특성을 고려하기 위하여 상용소프트웨어(KISSsoft)를 이용한 선회감속기의 모델링을 수행하였다. Fig. 2와 같이 이 모델을 이용하여 유성 기어의 백래쉬(Gear Backlash), 기어 물림 률(Gear Contact Ratio), 기어 감쇠 비(Gear Damping Ratio), 기어 치 강성(Gear Teeth Stiffness) 등을 도출하였고 시뮬레이션 검증 모델에 반영하였다.

Fig. 2

Power flow of the slewing reducer gearbox

2.2 속도추정 제어기 모델

굴삭기 선회 시험에서 측정한 선회 모터의 속도를 시뮬레이션 모델이 제대로 추정할 수 있도록 Fig. 3과 같이 PID 제어기를 사용하였다.⁴

Fig. 3

Simulation model of PID controller

3.1 시험 장비

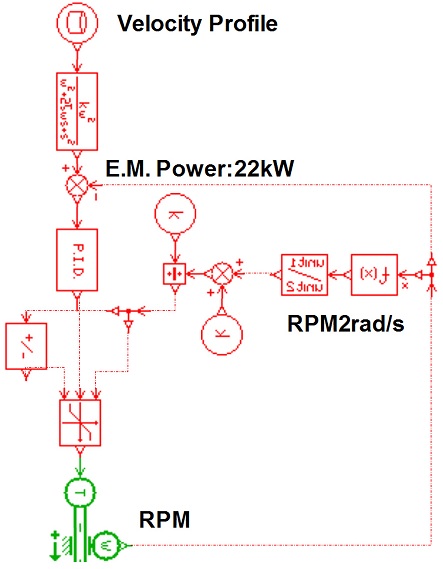
굴삭기 선회 시험에서 선회 속도의 제어 편의성과 재현성을 확보하기 위하여 유압모터 대신 전기모터와 인버터를 이용하였다. 인버터는 PLC 제어를 통하여 선회 시험 시 속도의 변화가 일정하게 유지되도록 구현하였다.

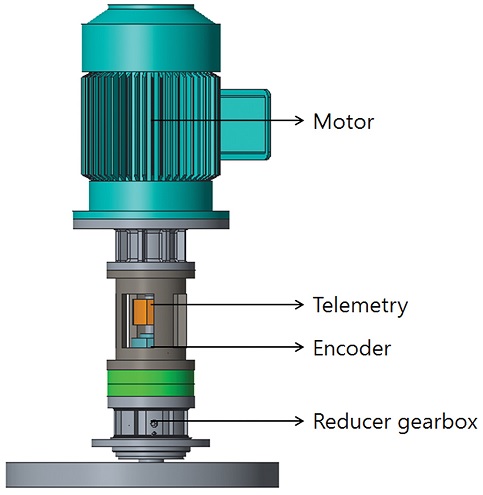
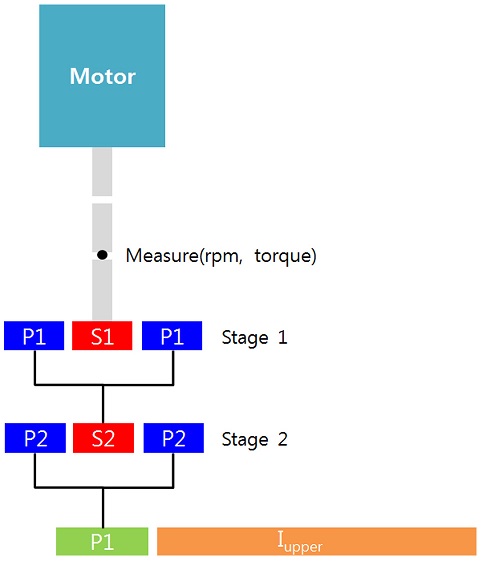
선회감속기의 입력 토크와 속도를 측정하기 위하여 전기모터와 선회감속기 사이에 토크미터(Telemetry Type)와 속도 센서(Encoder)를 설치할 수 있도록 축과 보조구조물을 설치하였다.

Figs. 4와 5는 굴삭기 선회 시험을 수행하는 모습과 시험장비의 구성요소를 나타낸 것이다. 시험장비의 상세사양은 Table 2와 같다.

Fig. 4

A view of test rig of excavator

Fig. 5

Configuration of test rig components

Table 2

Specification of the test equipment

Fig. 6

A view of length of working device of excavator

3.2 시험결과 분석

선회 시험을 통한 굴삭기 상부회전체의 질량관성모멘트를 도출하기 위하여 5개의 시험 조건에서 선회감속기에 작용하는 토크와 회전속도를 측정하였다. 작업장치(붐, 암, 버켓)의 자세는 선회 중심부터 최대 굴삭 반경 6,150 mm의 절반 정도의 3,100 mm로 1가지 자세를 유지하였으며, 가속 시간을 5가지(2초, 3초, 4초, 5초, 6초)로 변경하며 시험을 수행하였다. 측정되는 토크와 속도의 데이터 샘플링은 토크의 순간 피크 변동을 감지할 수 있도록 1,000 Hz로 설정하였고, 동일한 조건을 3회 반복 측정하여 반복성을 확인하였다.

굴삭기 상부회전체 선회 시험 결과, 선회 모터의 정격 속도인 1,200 rpm까지의 가속 시간에 따라 다른 측정 결과가 도출되었다. 가속시간이 2초와 3초인 경우의 시험 결과는 인버터의 제어 속도보다 굴삭기의 가속 시간에서 운동초기 정지마찰저항에 의하여 초기 구동이 늦어져 시간 지연이 발생한 것을 확인하였다. 또한, 가속시간이 매우 짧아 가속 관성부하 구간에서 정지마찰저항 구간을 제외한 관성부하 구간에서의 각가속도를 측정하기 쉽지 않아 시뮬레이션 모델과의 검증을 하기에는 적합하지 않은 것으로 판단하였다.

속도 제어에 따른 응답성 등을 고려하여 선회감속기 입력 속도 측정 결과 중 제어 시간과 유사하고 각가속도 분석이 용이한 가속 시간 4초의 데이터에서 굴삭기 상부회전체의 질량관성모멘트를 도출하였다.

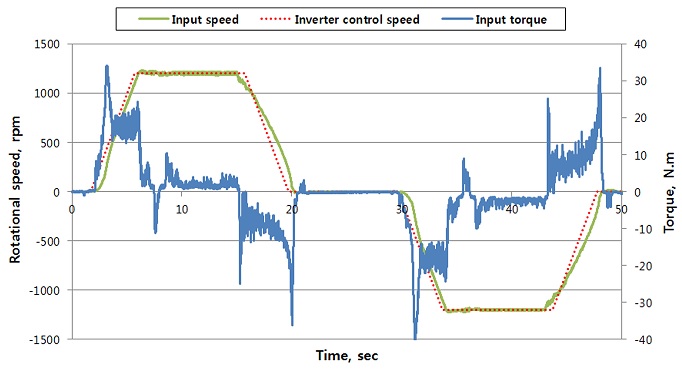
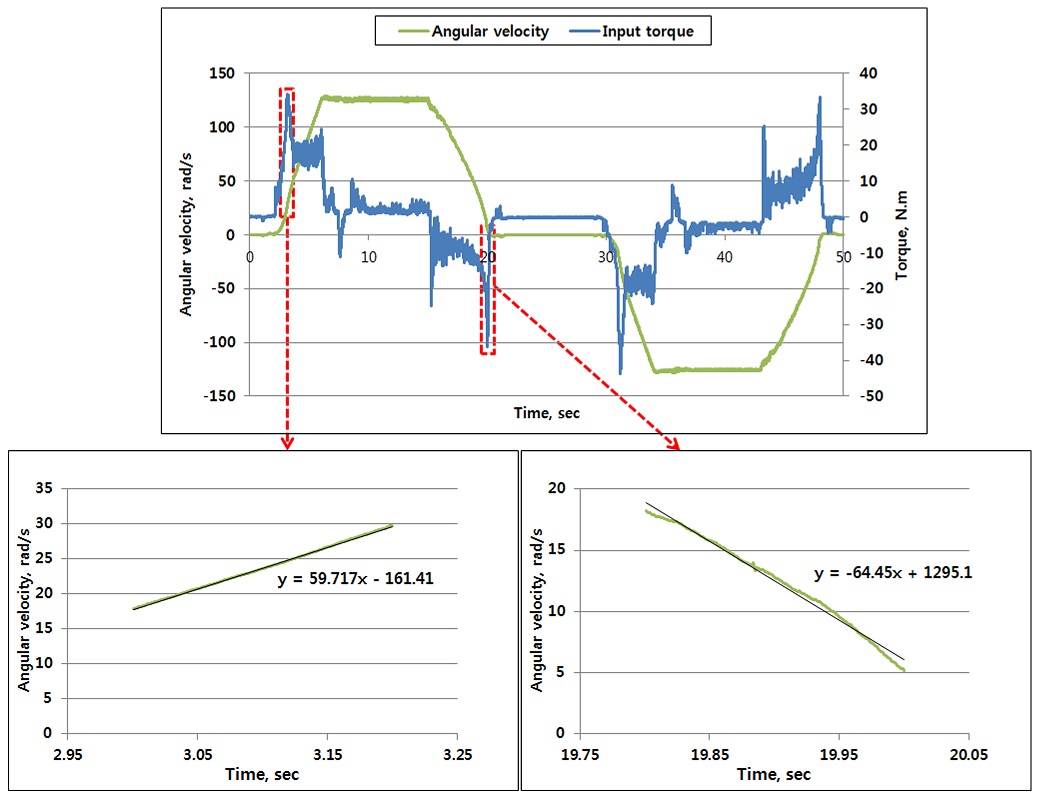
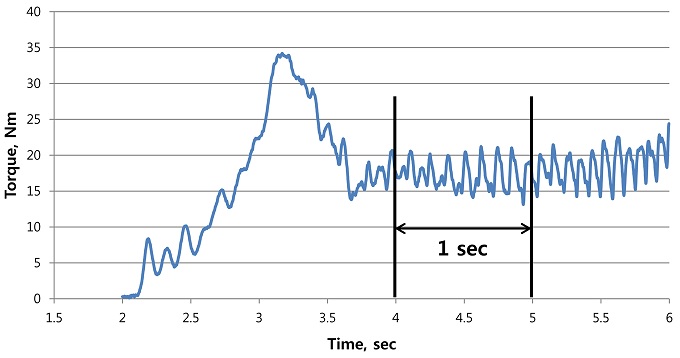
가속시간 4초의 시험 결과는 Fig. 7과 같이 2초에서 6초까지의 4초간의 가속 운동이 시작될 때 초기 마찰저항에 의한 피크 토크(34.19 Nm)가 발생하였고 그 이후 등가속구간에서는 굴삭기 상부회전체의 질량관성모멘트에 의한 토크(14.7 Nm - 21.57 Nm)가 발생하였다. 10초에서 20초까지의 10초간의 등속운동 구간에서는 단지 운동마찰저항에 의한 토크(0.73 Nm - 4.91 Nm)만 작용하였다. 또한, 16초에서 20초까지의 감속 운동 구간에서는 굴삭기 상부회전체의 질량관성모멘트에 의한 토크(-3.01 Nm부터 -13.25 Nm)가 발생하였으며, 정지 시 피크 토크는 -36.45 Nm로 측정되었다.

Fig. 7

Torque and speed measured when acceleration & deceleration time was 4 sec

선회 시험 결과 가속 시 발생한 피크 토크보다 감속 시 발생한 피크 토크가 더 큰 것을 확인하였다. 가속 운동으로 인한 피크 토크는 34.19 N, 정지 운동으로 인한 피크 토크는 -36.45 Nm로 1.1배의 차이가 발생하였다. 그 이유는 Fig. 8에서와 같이 가속 시의 각가속도(59.72 rad/s²)보다 감속 시의 각가속도(-64.45 rad/s²)의 크기가 1.07 배 더 크게 제어되었기 때문이며, 이는 굴삭기 상부회전체의 질량관성모멘트의 크기에 의한 인버터 제어 특성으로 판단된다. 즉, 전기모터를 제어하는 인버터의 특성에 의해 굴삭기 상부회전체를 가속할 때의 작동 모드(Motoring)와 감속할 때의 작동 모드(Braking)에 의한 가속도 편차가 원인이다. 또한, 상승 가속 구간과 하강 감속 구간에서의 토크 차이가 발생하는 이유는 인버터 제어 특성에 의해 상승 가속시의 속도 변화율이 하강 감속시의 속도 변화율보다 크게 제어가 되었기 때문으로 생각된다.

Fig. 8

Comparison of angular velocity during acceleration and deceleration operation

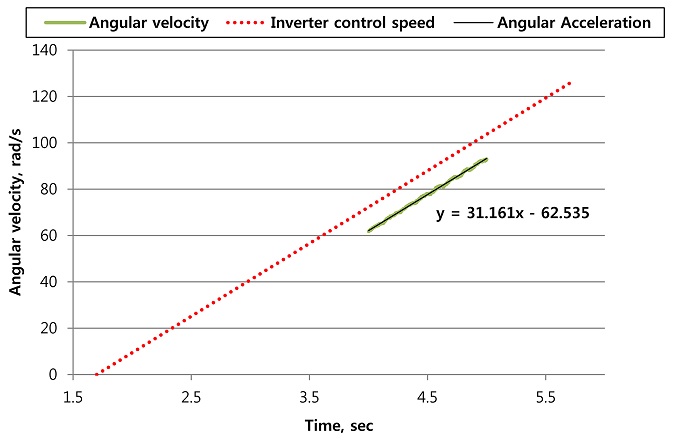
선회 시험을 통해 측정한 데이터를 이용하여 Fig. 9과 같이 등 가속 구간 중 4 - 5초 구간의 각속도의 추세선을 이용하여 각가속도 31.22 rad/s²를 도출하였다. 또한, 같은 구간에서의 평균 토크는 Fig. 10에서와 같이 17.34 Nm로 계산되었다.

Fig. 9

Variation of angular speed measured when acceleration time was 4 - 5 sec

Fig. 10

Variation of torque measured when acceleration time was 4-5 sec

4 - 5초의 가속 구간에서 계산한 각가속도와 평균토크를 이용하여 선회감속기 입력축에 작용하는 질량관성모멘트는 5.55E + 5 kg.mm²로 계산되었다. 이 값은 굴삭기 상부회전체의 질량관성모멘트와 선회감속기와 선회베어링의 구성요소인 기어, 축, 캐리어 등이 모두 고려된 값이다.

굴삭기 상부회전체만의 질량관성모멘트를 계산하기 위하여 Fig. 11과 식(1)부터 식(3)의 스퍼기어와 유성기어의 질량관성모멘트 이론을 적용하여 계산하였다.^5,6 굴삭기 상부회전체의 질량관성모멘트를 미지수로 설정하고 각 지점에서의 등가관성모멘트를 계산하여 선회감속기 입력 위치에서의 관성모멘트 5.55E + 05 kg.mm²가 도출되도록 반복법(Iteration Method)을 사용하여 계산하였다. 계산 결과, 굴삭기 상부회전체의 관성모멘트는 8.68E + 09 kg.mm²로 계산되었다.

Fig. 11

Configuration of slewing system

4.1 시뮬레이션 모델 비교 검증

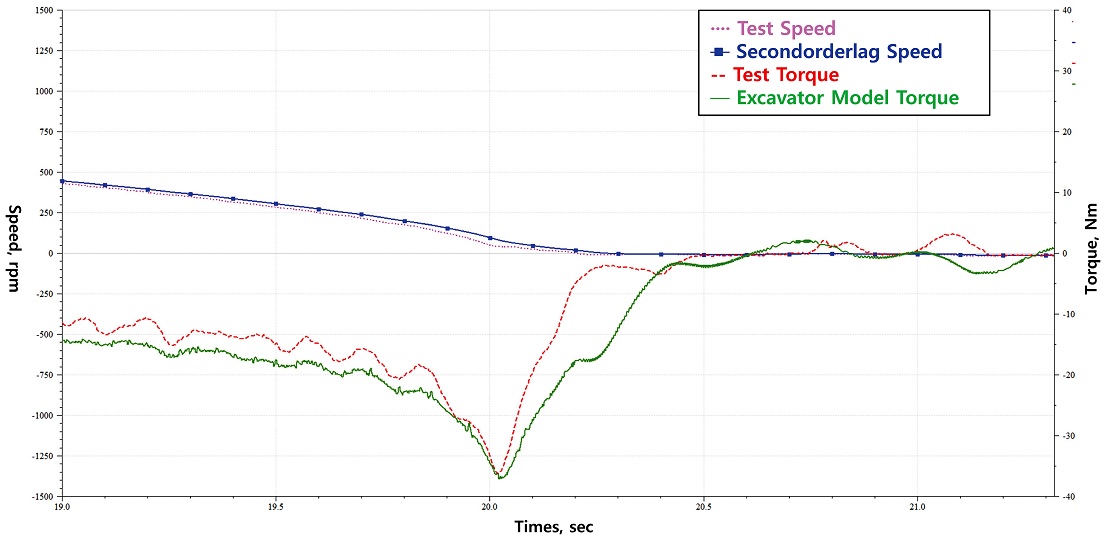
굴삭기 선회시스템의 시뮬레이션 모델 검증을 위하여 굴삭기 상부회전체 선회 시험에서 측정한 선회감속기 입력 속도를 시뮬레이션 입력 속도로 사용하였다. 측정된 속도 데이터에서 고주파 잡음(Noise)을 제거하기 위하여 2차 필터를 추가하였으며, 필터의 특성에 의해 속도 프로파일에 0.05초에서 최대 1초정도의 시간 지연(Time Delay)이 발생하였다. 시뮬레이션 결과, 시간 지연은 관성 부하가 작용하는 가속과 감속 시 토크 변동에는 영향을 미치지만, 내구 수명 평가에서 가장 중요한 피크 토크의 크기에는 영향을 미치지 않았다(Fig. 12).

Fig. 12

Comparison between test torque and simulation torque according to time delay

PID 제어기의 게인(Gain)값은 시행착오법을 통하여 정하였으며, 비례 게인은 0.97, 적분 게인은 0, 미분 게인은 0으로 선정하였다. 또한, 굴삭기 상부회전체의 질량관성모멘트는 선회 시험으로 도출한 8.68E + 09 kg.mm²를 적용하였다.

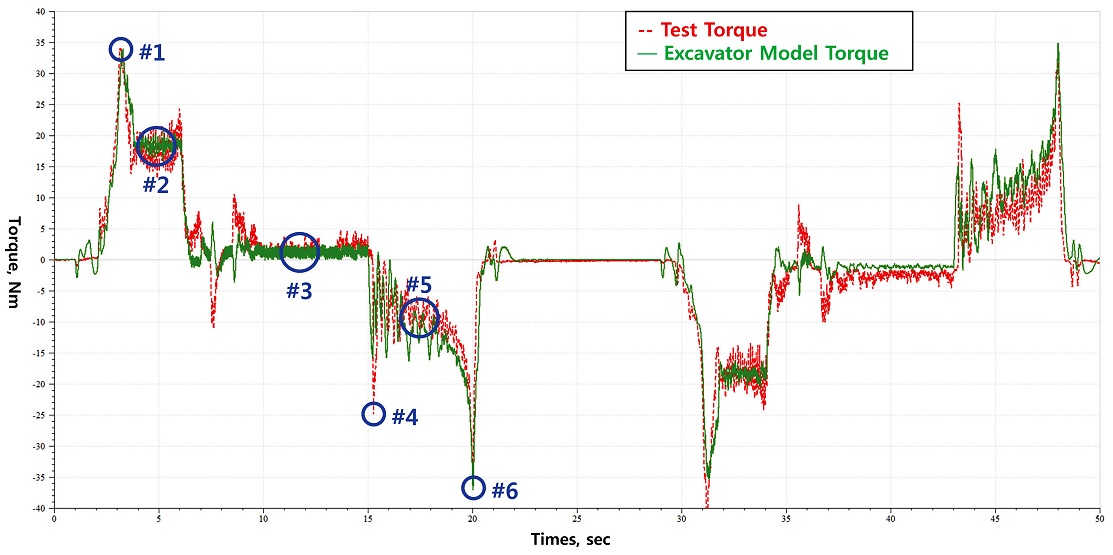
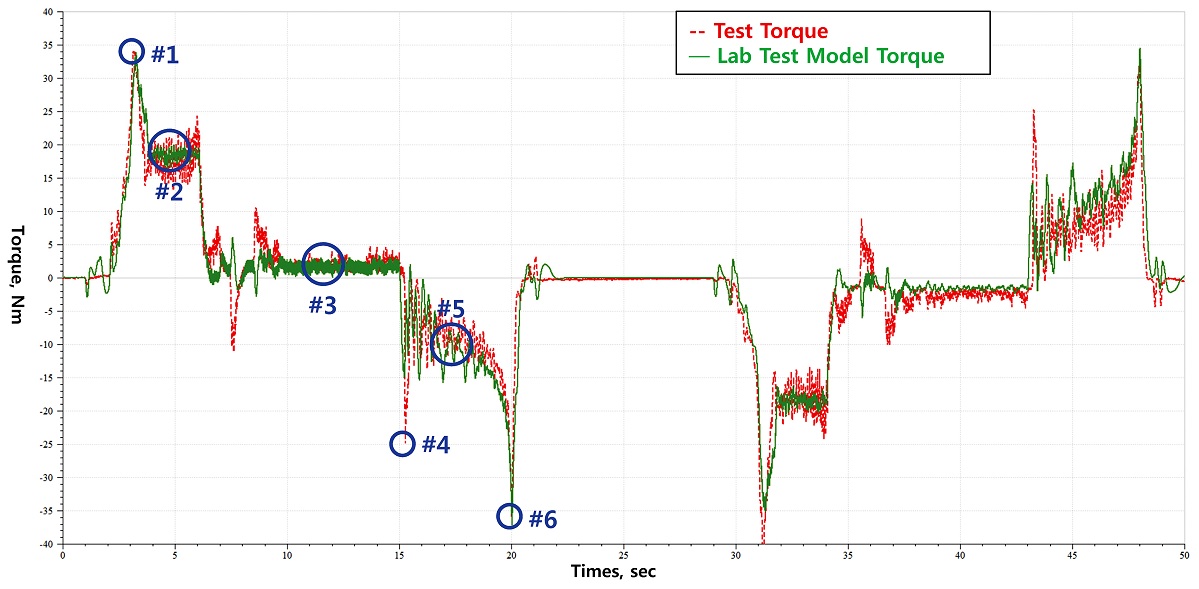
선회감속기 입력 토크에 대한 선회 시험 결과와 시뮬레이션 결과는 Fig. 14과 같이 가속, 등속, 감속 시 총 6 곳에서의 토크 값으로 비교하였다. 각 지점의 오차율은 0.82% - 41.24%로 나타났다. 오차율이 가장 큰 3번 지점(41.24%)의 경우, 오차율이 크게 나타난 이유는 등속 구간의 시험과 시뮬레이션의 토크 크기가 각각 1.77 Nm와 1.06 Nm로 나타났기 때문이며, 이 구간에서의 토크 값이 다른 구간의 토크 값에 비해 상대적으로 매우 작기 때문에 크게 문제가 되지 않는다고 판단하였다. 오차율이 두 번째로 큰 4번 지점(37.42%)의 경우, 2차 필터의 사용으로 인하여 시뮬레이션 구현 속도의 기울기가 시험 속도의 기울기 보다 작아져서 나타난 현상으로 판단되었다. 그로 인한 시험 결과와 시뮬레이션의 편차는 9.33 Nm로 다소 큰 토크 차이를 보였지만 선회감속기의 내구 수명 조건으로 볼 때 1번과 6번 지점에서의 피크 토크보다 작은 결과가 도출되어 내구 수명에는 큰 영향을 끼치지 않을 것으로 판단되었다. 선회감속기의 내구 수명에서 가장 큰 영향을 미치는 1번과 6번 위치에서의 시험 측정 결과와 시뮬레이션 결과의 토크 오차율은 각각 0.82%과 1.73%이며, 편차는 각각 0.28 Nm과 0.63 Nm로 나타났다. 그러므로 개발된 시뮬레이션 모델은 굴삭기 상부회전체의 동적 관성 거동을 근사적으로 모사한다고 생각되며, 이 모델을 확장하여 선회감속기의 실험실 시험 모델 개발이 가능하다고 판단하였다.

Fig. 13

Layout of simulation model for excavator slewing system

Fig. 14

Comparison of torque profile between test and simulation

4.2 실험실 시험 시뮬레이션 모델 개발

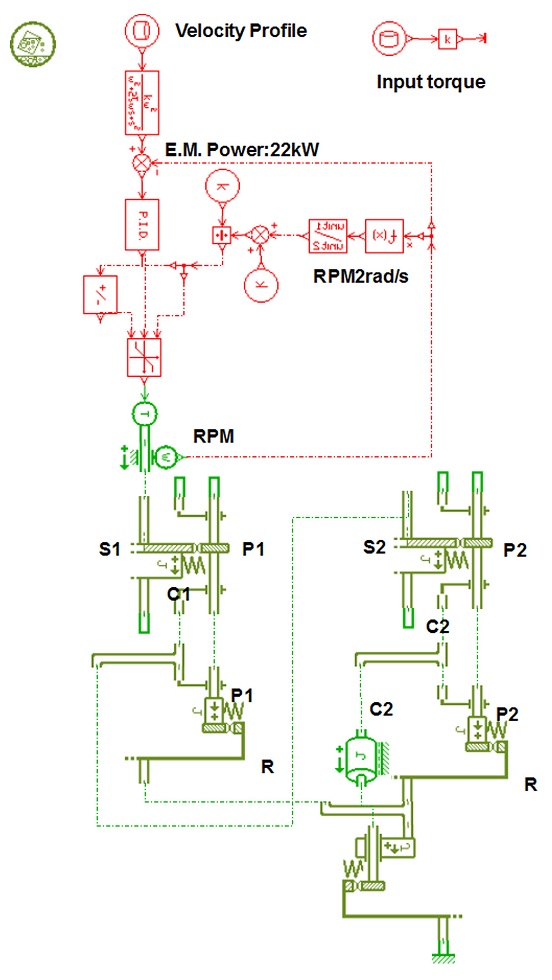
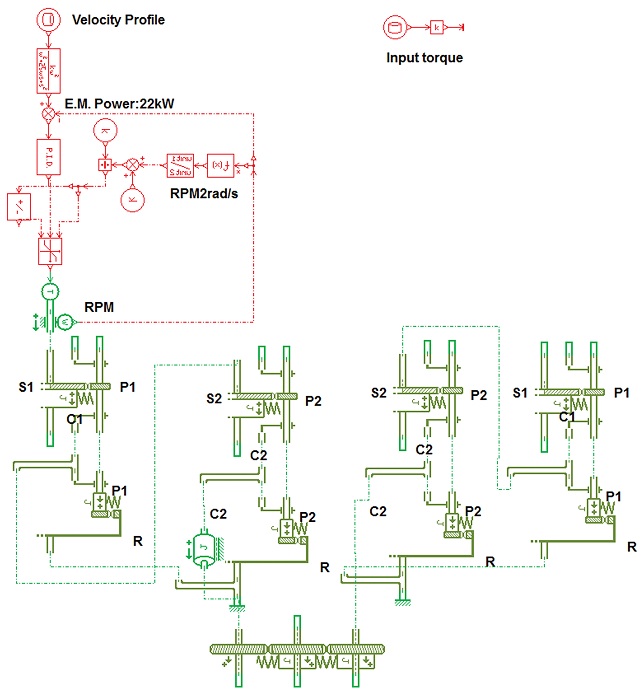
굴삭기 선회시스템에 대한 실험실 내구 수명 시험장비의 경우, 시험 장비의 안정성, 편리성, 시험 비용 등을 고려했을 때 굴삭기 상부회전체의 회전 구동과 동일한 구조로 시험을 수행하기에는 적합하지 않다고 판단되었다. 그래서 검증된 시뮬레이션 모델을 이용하여 굴삭기 상부회전체의 관성모멘트를 반영한 선회시스템 내구 수명 시험 모델을 개발하였다.

Table 3

Comparison of peak torque between test and simulation

굴삭기 선회시스템 시뮬레이션 모델은 선회 링기어가 하부주행체에 고정되어 있고, 선회감속기가 상부회전체에 고정되어 선회 링기어의 회전중심을 기준으로 선회감속기가 공전하는 구조로 구성되어 있다. 실험실 시험 시뮬레이션 모델은 실제 내구 시험 장비와 동일하게 선회감속기가 지면에 고정되고, 선회 링기어가 회전하는 작동 메커니즘을 구현하였다.

실험실 시험 시뮬레이션 모델에서는 굴삭기 상부회전체의 질량관성모멘트를 선회감속기와 플라이휠로 대체하였으며, 플라이 휠의 등가 질량관성모멘트는 선회감속기의 기어비(u = 128.76)를 고려해서 5.24E + 05 kg.mm²로 계산되었다.

선회감속기 입력 토크에 대한 선회 시험 결과와 실험실 시험 시뮬레이션 모델 결과는 Fig. 16와 같이 가속, 등속, 감속 시의 총 6곳에서의 토크 값을 비교하였다. 1번에서 6번까지의 오차율은 0.91% - 71.19%로 나타났으며, 최대 오차율인 3번 지점에서의 편차는 -1.26 Nm, 4번 지점에서의 편차는 -11.4 Nm로 나타났다. 선회감속기의 수명에 가장 연관이 있는 피크 토크가 발생한 1번 지점과 6번 지점의 피크 토크 오차율은 0.91%, 2.22%로 나타났으며, 편차는 0.31 Nm, 0.81 Nm으로 확인되었다.

Fig. 15

Layout of simulation model for lab test equipment

Fig. 16

Comparison of torque profile between test and lab test simulation