Influence of Corrugation Angle and Load Position on the Flexural Characteristics of Lightweight Plastic Sandwich Panel with Corrugated Cores
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
The flexural characteristics of corrugated sandwich panels are anisotropic and depend on its corrugation geometry and load position. The objective of this paper is to examine the influence of corrugation angle and load position on the flexural characteristics of plastic sandwich panels with trapezoidal corrugated cores subjected to ASTM three-point bending via finite element analysis. The stress distributions at mid span have been plotted to determine the stress concentration at different corrugation angle and load position. The specific flexural stiffness and modulus have been estimated from the load-displacement and stress-strain curves, respectively. The failure of the specimen due to stress or strain limit has been examined via maximum limit stroke. Results have shown that the specific flexural stiffness and modulus improve as the corrugation angle decreases. The load position has influenced the flexural characteristics due to the occurrence of local bending and local tension.
Keywords:
Sandwich structure, Lightweight structure, Corrugated cores, Bending, Flexural properties키워드:
샌드위치 구조, 경량 구조, 주름 코어, 굽힘, 굴곡 속성1. Introduction
In line with the need for global sustainability development, lightweight sandwich structures have been well accepted in automotive, maritime and aerospace engineering due to their high strength-to-weight ratio.1-4 Sandwich panels have also been found in building structures such as roofs, walls and floor.5-7 Besides, sandwich panels may serve as thermal insulating and impact absorption structure.8,9
While sandwich panels are common, design of full plastic sandwich panel may be rare compare to other materials such as metals and composites. Currently, full plastic sandwich panels are used mainly for decorative purposes such as roofing sheets and curtain wall facades, where bending load is not critical.10 Schürmann, in 2005, patented the pressed plastic sandwich panels with fiber reinforcement as formwork panels for construction.11 However, recent progress in 3D printing has stimulated a renewed interest in plastic sandwich panel for potential load bearing. Direct fabrication with 3D printer will have great benefit for design and cost, especially for the complex cores and curved geometries such as blades.12,13
Typically, a corrugated sandwich panel comprises of sinusoidal, triangular or trapezoidal corrugation as the inner cores bonded in between two strong and thin faces.14,15 Corrugated cores have the benefit of sustaining not only vertical shear, but the bending and torsion as well.16 The change in corrugation angle of the core will imply different flexural behavior on the sandwich panel.1,16,17
Various works have been conducted to investigate the bending response of corrugated sandwich panels according to their geometry parameters of the corrugated core. Zhang et al. conducted experimental studies on composite trapezoidal corrugated-core sandwich panels and observed that the specific bending strength improved as the corrugation angle and core sheet thickness increased.16 Libove and Hubka derived the flexural stiffness of a corrugated sandwich panel as a function of Young modulus of elasticity, Poisson’s ratio and moment of inertia.17 The model assumed an equivalent homogenous model. Based on Libove and Hubka’s formulation, Djoković et al. reported that the sandwich panels are more resistant with equal face and core sheet thicknesses (tf = tc), core pitch-to-depth ratio between 1 and 1.2 (1 ≤ p/hc ≤ 1.2), and corrugation angle near 60° (θ - 60°).1 Boorle and Mallick modelled the global bending of corrugated sandwich panels and noted that the simultaneous effect of optimized corrugation angle, smaller pitch, larger face distance, and same thickness for face and core sheet has produced smaller deflection.18 Other analytical models on the bending behavior of a corrugated sandwich panel were also using the homogenization theory.15,19-21
Finite element analysis were also conducted by Mohammadi et al. and Xia et al. to validate their analytical models using shell elements.15,21,22 Due to the homogenization, Biancolini noted that the equivalent orthotropic material reduced for the corrugated core is not valid for bending and stretching.22 Instead, he evaluated the equivalent stiffness of sinusoidal and triangular corrugated board by extracting the core stiffness detail from FEM model.22 The effect of the bending load on different position of the panels has not been studied. The effect of the radius of loading nose on the flexural characteristics of the sandwich panel has been neglected, thus the stress concentration throughout the bending is not known.
The objective of this paper is to investigate the influence of the trapezoidal corrugation angle and load position on the flexural behavior of ABS plastic sandwich panel using finite element analysis (FEA). Three-point bending is applied for this study in accordance with ASTM D790 specification.23 The stress distributions at mid span are observed throughout the bending to determine the location of the critical stress concentration. The specific flexural stiffness and modulus are estimated from the slopes of load-displacement and stress-strain curves, respectively. The failure of the specimen due to stress or strain limit is examined via maximum limit stroke. Comparing these results, the influence of the corrugation angle and load position on the flexural characteristics of the sandwich panels with corrugated cores is discussed.
2. Finite Element Analysis
2.1 Design of Specimen
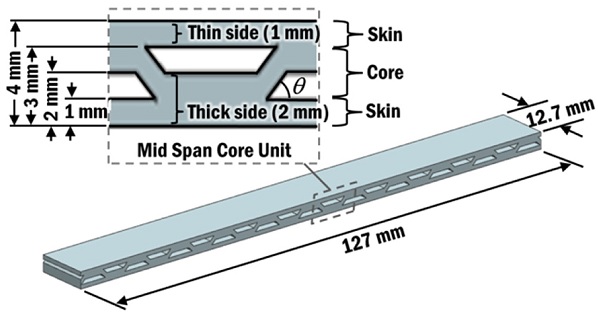
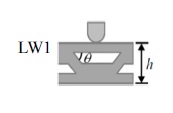
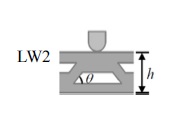
For this investigation, four trapezoidal corrugated core sandwich panels were designed with fixed thickness of 4.0 mm and corrugation pitch of 12 mm as the test specimens. They were modeled as 3D elastic solid as shown in Fig. 1. The thickness of the face sheet and core sheet was set at 1 mm. Therefore, the skins have the thickness of 1 mm each and the core has the thickness of 2 mm. Engineering-grade thermoplastic ABS was chosen for the whole specimens. The type of specimens is tabulated in Table 1. The depth and length of the model were derived based on the ASTM D790 specification.23
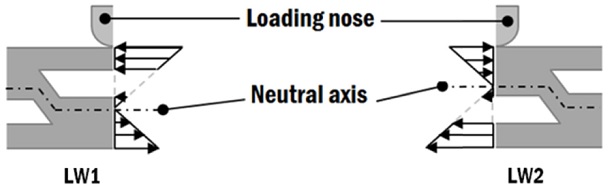
Due to the corrugation construction as in Fig. 1, there are alternating thin and thick sides for each corrugation pitch. Notation LW1 and LW2 are assigned to the specimen where the loading nose is on the thin side and thick side, respectively.
2.2 Model of Analysis
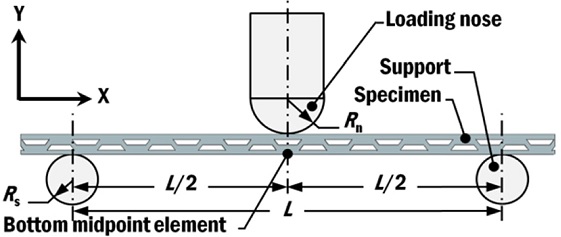
Fig. 2 shows the three-point bending test setup for the study of the flexural characteristic of the panel. The loading nose and support radius parameters for ASTM D790 standardized normal, maximum and minimum test setup are listed in Table 2.
A three-dimensional non-linear FEA was carried out using ABAQUS Explicit V6.11. The test setup was modeled as a quarter model with symmetrical planes normal to X- and Z-axis at the midpoint of the specimen. The specimens were meshed with solid element type of 8-node linear brick reduced integration (C3D8R), which had been applied in studies by Raj et al. and Magnucki et al..7,24 Five layers of elements were chosen for the face sheets and core sheets to simulate the bending behavior appropriately. Therefore, there were at least 68,900 solid elements and 84,600 nodes to represent the sandwich panel specimens. No core debonding was considered.
Table 3 shows the material properties of the ABS that had being assigned as a homogenous isotropic material for the specimens. The loading nose and supports were modeled as 3D discrete rigid shell with quadrilateral elements. The loading nose was set to displace 5 mm against the Y-axis direction for the simulation. The supports were constrained for translation and rotation in all directions. The friction coefficient between the specimen, loading nose and supports is 0.38.
3. Flexural Modulus and Specific Flexural Modulus
Stress-strain curve for bending test is important to determine the flexural modulus of the specimen. It can be obtained from the effective stress and strain information of the bottom midpoint element throughout the FEA simulation.
In order to determine the flexural modulus, chord modulus method is applied at flexural strain ε1 = 0.0005 and ε2 = 0.0025 based on ISO 178 standard.25 The flexural modulus (Ef) is calculated using the Eq. (1).
| (1) |
For comparison between specimens where the weight is concerned, specific flexural modulus (Efs) is calculated as Eq. (2).
| (2) |
4. Results and Discussions
4.1 Bending Patterns of the Mid Span Core Unit
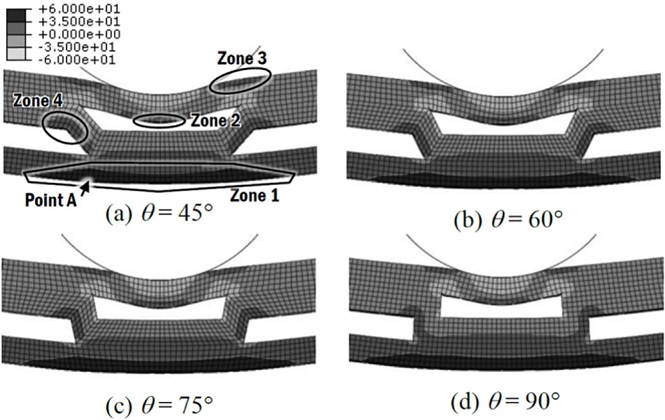
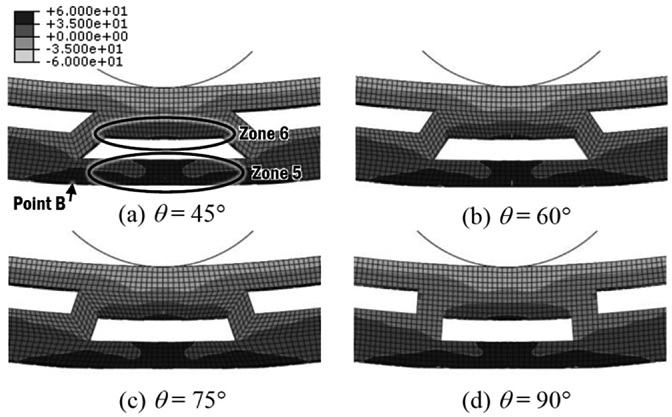
The maximum stress always occurs at the bottom midpoint element for the bending of a homogeneous solid specimen. However, this is not the case for the corrugated sandwich panel due to the existence of stress concentration area at the corrugation core. Therefore, the bending pattern of the core unit at mid span of the corrugated sandwich panels was investigated using the results of the FEM analysis, as shown in Figs. 3-6.
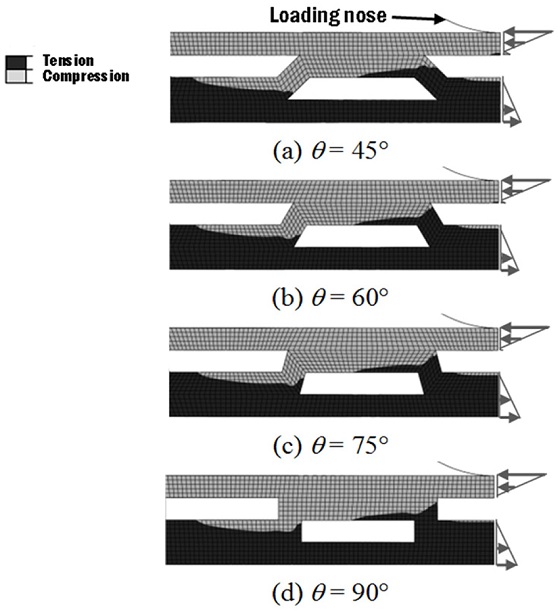
The stress plot in Fig. 3 shows various stress zones in the mid span core unit. The largest tensile stress zone (zone 1) occurs at the bottom surface of the specimen and it indicates the overall bending stress acting on the specimen. The bottom surface of the thin side of LW1 specimens is also in tension (zone 2) and this implies the occurrence of that local bending. High tension near the pin contact area (zone 3) supports the local bending. As the corrugation angle increases, tension at zones 2 and 3 decreases. Based on these observations, it can be concluded that the local bending effect is greater on smaller corrugation angle. This local bending pattern is a result of the bending load not being transferred directly to the lower thick side due to the lack of direct connection at the mid span. This is evidenced by the existence of two neutral axes at the mid span plane, as shown in Fig. 7.
In addition, the result shows that maximum tensile stress changes location as the pin deflection increases. The highest tensile stress point is typically located at Point A. This critical stress point has been identified as the parting point between the thick side and thin side on the bottom face, which has significant difference in strength. This maximum stress point changes position to zone 2 when the effect of local bending becomes severe at higher load. When the displacement is approximately 5 mm, except for LW1-90, stress concentration at corrugation web edge (zone 4) is observed to be dominant.
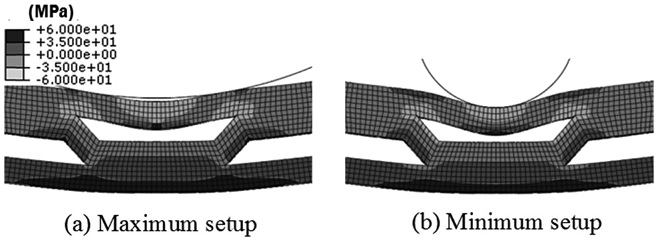
Fig. 4 shows that zones 2 and 3 become smaller as the pin radius increases. Hence, it is deduced that the effect of local bending on the upper face is crucial for LW1 arrangement, particularly when the radius of the loading nose is relatively smaller than the groove width of corrugation. This happens because load from the nose contact is away from the corrugation web, resulting in the increase of local bending moment.
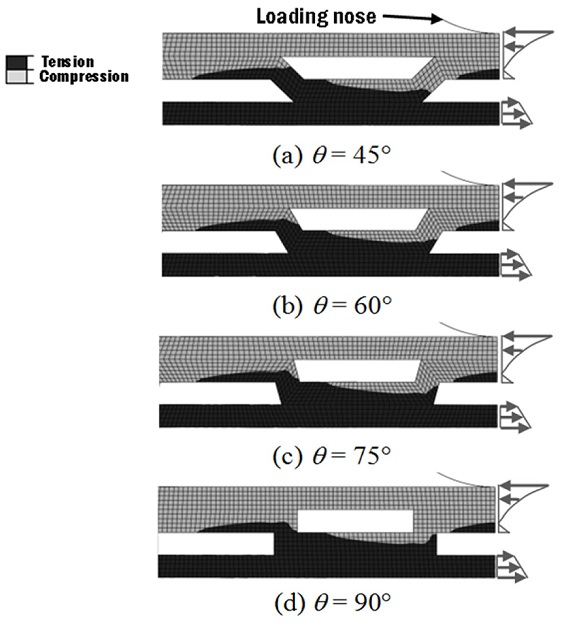
In Fig. 5, the tensile stress zones are uniformly located at the bottom of both thin (zone 5) and thick (zone 6) side faces. It can be observed that the thin side at the mid span is straightened instead of bended, because only tensile stress is acting at zone 5, resembling a tensile case. This is due to the neutral axis location at thick side of LW2, as shown in Fig. 8, and the direction of the corrugation web has diverted the compressive load away from the mid span thin face of LW2.
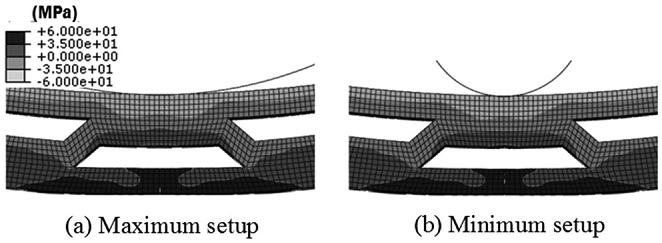
There is no significant difference observed in stress distribution when the corrugation angle changes, except for the stress area at web edge in zone 6, which diminishes as the corrugation angle increases. This happens because the bending load is transferred from the top face to the bottom face through the corrugation web. As the corrugation angle increases from 45° to 90°, the downward shear component acting on the corrugation web edge reduces. Besides, the stress distribution does not vary at different test setup, as shown in Fig. 6. This indicates that the corrugation angle and the test setup have minimal influence on bending behavior of LW2.
Similar to the LW1, the highest tensile stress point is observed at Point B for most of the time throughout the bending. This critical stress point shifts from the bottom face towards the nearest corrugation web edge as the bending continues, forming a locus that represents the parting line between the thick side and thin side of the bottom face. When the local tension becomes greater, the highest tensile stress point is found in the middle of the thin side face of zone 5, where necking is expected.
For the corrugated sandwich panels, the actual neutral axes (as shown in Figs. 7 and 8, which are at the boundary between tension and compression obtained from the FEA analysis, reveal that they cannot be predicted using the theoretical neutral axis based on cross section, as shown in Fig. 9. The compressive shear on the top face is found to be higher for both LW1 and LW2. The bending load at the empty gap in the core is distributed horizontally through the upper face and reaches the bottom face via the corrugation web. Thus, at different corrugation angle and test position (LW1 & LW2), the neutral axes and shear load distribution are different too.
4.2 Flexural Stiffness and Modulus
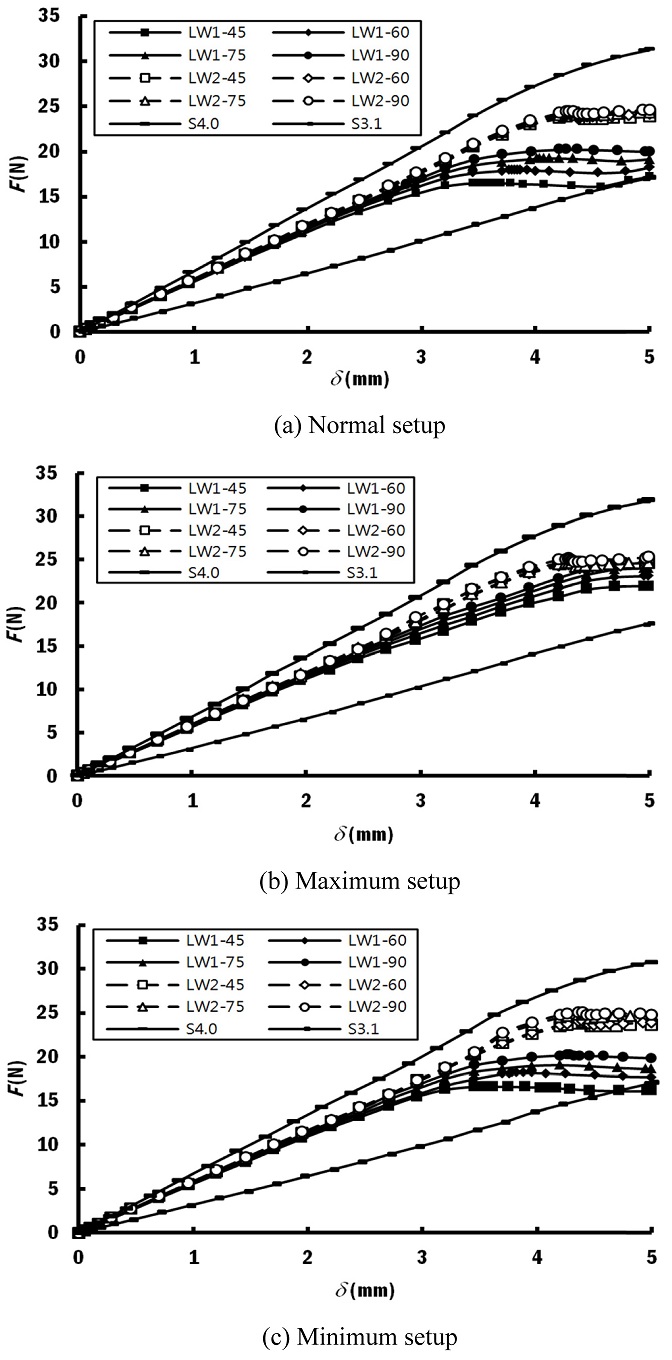
The force-displacement curves for the designed specimens under different test setups were plotted, as shown in Fig. 10. Fig. 10(a) shows that the specimen of different corrugation angle has different maximum load F capability, especially for LW1 specimens. The obvious difference in LW1 is due to the local bending effect, which is greater on smaller corrugation angle. Therefore, the maximum load decreases as the corrugation angle decreases in LW1 specimens. The local bending effect in LW2 is minimal as the corrugation angle changes. This explains the similarities of the bending characteristics between LW2 specimens.
Comparing LW1 specimens in Figs. 10(a)-10(c), it is noticed that the specimen is able to sustain higher bending load at maximum test setup compared to the normal and minimum test setup. The occurrence of local bending causes the bending load distribution from the loading nose to be ineffectively reflected on the overall bending of the specimen, which explains the lower bending load characteristics of LW1 shown in Figs. 10(a) and 10(c). In contrast, the specimens within the LW2 and solid groups show similar force-displacement relationship regardless of the test setup. This is consistent with the observation of similar stress distribution for LW2, as discussed previously.
When comparing the slope of the force-displacement curve in Figs. 10(a)-10(c), it is noticed that the flexural stiffness of the sandwich panels is approximately 13 - 18% lower than solid S4.0, but 74-84% better than solid S3.1. The LW2 group of specimens is 2-4% stiffer than the LW1 group of specimens. Due to the corrugated core, the load is not distributed equally across the cross section of the specimen. The thick side of the load face in LW2 is observed to accommodate more compressive load directly from the bending load, compared to the thin side of the load face of LW1, as shown in Figs. 7 and 8. Hence, LW2 specimens show better flexural stiffness compared to LW1 specimens.
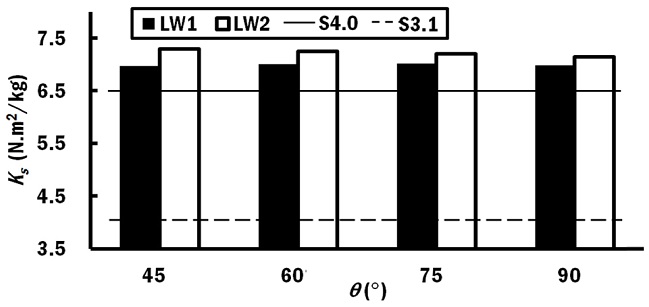
The specific stiffness of the sandwich panels are 7-12% and 74-84% better than the solid S4.0 and S3.1, respectively, as shown in Fig. 11. This advantage is due to the lower apparent density. Specific stiffness for LW1 specimens is near constant. However, LW2 specimens have their specific stiffness reduced as the corrugation angle increases.
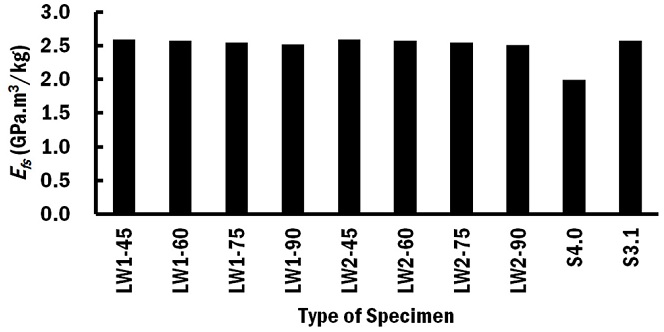
Using Eq. (2), the specific modulus was compared, as shown in Fig. 12. These sandwich panels have higher specific modulus compared to the solid panel S4.0 by 26-30%. The corrugation angle does not have significant influence on the flexural modulus. Hence, this specific modulus improvement is mainly due to their weight reduction of 20-24%. The solid S3.1 specimen, which has apparent density similar to LW1-60 and LW2-60 specimens, has similar specific modulus, but with 76% and 82% lower in stiffness, respectively.
4.3 Limit Stroke
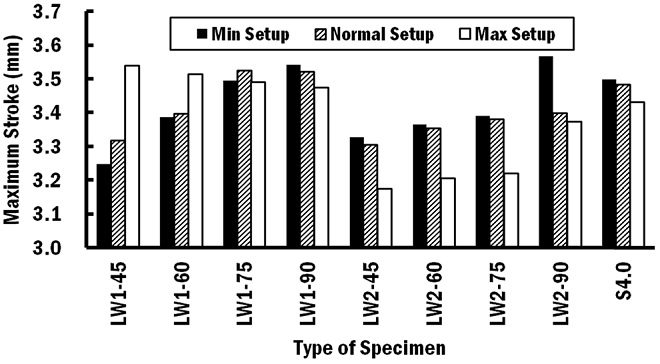
To investigate the maximum stroke that the specimen can sustain before breakage occurs, ABS tensile strength of 40 MPa and 6% elongation at break limit were applied. The maximum stroke is limited by either tensile strength limit or elongation at break limit, whichever lower, as shown in Fig. 13.
From Fig. 13, the maximum stroke increases as the corrugation angle increases, except for the case of LW1 under maximum test setup. When comparing between the LW1 and LW2 specimens, it is observed that the LW2 specimens have lower maximum stroke. This is due to the tension is acting locally on the thin side of LW2 during the bending test, as illustrated in Fig. 8. The tensile stress on the thin side of LW2 becomes dominant at maximum test setup due to the removal of the notch stress concentration effect of the loading nose. Therefore, for LW2 and solid specimens, the maximum strokes are observed to have a decreasing trend when the radius of the loading nose and support increases from minimum to maximum test setup.
Besides, it is also observed that the maximum stroke is limited by the tensile strength of the material, except for all LW1 specimens under minimum test setup and LW1 specimens at 45 to 75° corrugation angles under normal test setup. The local bending at the thin side causes the elongation at break limit to occur first, which explains why the limit stroke due to elongation at break limit happens at all LW1 specimens under minimum test setup and some LW1 specimens under normal test setup.
5. Conclusions
This paper has investigated the flexural characteristics of plastic sandwich panels with corrugated cores subjected to ASTM D790 three-point test conditions using a three-dimensional FEA.
The tensile stress acting at the mid span core unit has been carefully observed to assess the bending pattern of the corrugated sandwich panels at different corrugation angle and loading side. It has been noted that the highest tensile stress location for LW1 and LW2 are typically found at the bottom face, where the alternating thick and thin side is joined.
Besides, the neutral axis and stress distribution at mid span have been plotted from the simulation results to understand the bending pattern of sandwich panels with different corrugation angle and load position. The actual neutral axes are found to be different from the theoretical neutral axes due to the discontinued cross sectional area of the corrugated core. Through the determination of the actual position of neutral axis at the corrugated sandwich panels from the FEA results, it has been shown that the occurrence of local bending and local tension of the specimen can be clearly explained.
In order to compare the flexural characteristics among specimens, specific stiffness and specific modulus has been used. From the results of the analysis, the designed sandwich panels with smaller corrugation angle have been found to possess higher specific stiffness and specific modulus. This is mainly due to the benefit of weight saving has surpassed the decrease in flexural stiffness and flexural modulus as the corrugation angle decreases. Therefore, among the specimens that are being analyzed in this paper, the specimen with corrugation angle 45° has the best flexural characteristics.
From the force-displacement curves analysis, it has been noted that the LW2 specimens are 2-4% stiffer than the LW1 specimens of the same corrugation angle and test setup. The limit stroke analysis has shown that most LW1 specimens fail at the top face. In contrast, LW2 specimens are likely to fail at bottom face. Hence, it can be deduced that the load position has influence on the flexural characteristics of a plastic corrugated sandwich panels. The load position on thick side of face, as shown in LW2 specimens, have the advantage of higher flexural stiffness and is not affected by the notch effect of the loading nose when compare to load position as in LW1 specimens.
To further enhance this work, analytical investigation can be carried out to better approximate the position of the neutral axis. Further experimental studies should be carried out to the validate results, particularly to the LW1 specimens, which show different flexural characteristics in different corrugation angle. Numerical analysis can be performed to investigate various factors such as core pitch-to-depth ratio, face-to-core thickness ratio and pitch-to-nose radius ratio on the bending characteristics based on stress distributions. Fracture analysis should be considered in the future work when the crack front or cohesive joint has been identified.
NOMENCLATURE
| E : | Young’s modulus |
| Ef : | Flexural modulus |
| Efs : | Specific flexural modulus |
| F : | Loading force |
| h : | Panel thickness |
| hc : | Height of core |
| Ks : | Specific flexural stiffness |
| L : | Support span length |
| m : | Mass of specimen |
| p : | Half pitch of core |
| Rn : | Radius of loading nose |
| Rs : | Radius of support |
| tc : | Core sheet thickness |
| tf : | Face sheet thickness |
| v : | Poisson’s ratio |
| θ : | Corrugation angle |
| σ : | Flexural stress |
| σ1 : | Flexural stress at strain 0.0005 |
| σ2 : | Flexural stress at strain 0.0025 |
| ε : | Strain |
| δ : | Displacement |
| ρ : | Density |
| ρa : | Apparent density |
| μ : | Coefficient of friction |
REFERENCES
-
Djoković, J. M., Nikolić, R. R., Bujnak, J., and Živković, K., “Geometrical Parameters Influence on Behavior of the Sandwich Plates with Corrugated Core,” http://www.matec-conferences.org/articles/matecconf/pdf/2016/49/matecconf_ipicse2016_01001.pdf, (Accessed 15 FEB 2017)
[https://doi.org/10.1051/matecconf/20168601001]

-
Xiong, J., Ghosh, R., Ma, L., Ebrahimi, H., Hamouda, A., et al., “Bending Behavior of Lightweight Sandwich-Walled Shells with Pyramidal Truss Cores,” Composite Structures, Vol. 116, pp. 793-804, 2014.
[https://doi.org/10.1016/j.compstruct.2014.06.006]

-
Park, K.-J., Jung, K., and Kim, Y.-W., “Evaluation of Homogenized Effective Properties for Corrugated Composite Panels,” Composite Structures, Vol. 140, pp. 644-654, 2016.
[https://doi.org/10.1016/j.compstruct.2016.01.002]

-
He, W., Liu, J., Tao, B., Xie, D., Liu, J., et al., “Experimental and Numerical Research on the Low Velocity Impact Behavior of Hybrid Corrugated Core Sandwich Structures,” Composite Structures, Vol. 158, pp. 30-43, 2016.
[https://doi.org/10.1016/j.compstruct.2016.09.009]

-
Abdolpour, H., Garzón-Roca, J., Escusa, G., Sena-Cruz, J. M., Barros, J. A., et al., “Development of a Composite Prototype with GFRP Profiles and Sandwich Panels Used as a Floor Module of an Emergency House,” Composite Structures, Vol. 153, pp. 81-95, 2016.
[https://doi.org/10.1016/j.compstruct.2016.05.069]

-
Fernando, P., Jayasinghe, M., and Jayasinghe, C., “Structural Feasibility of Expanded Polystyrene (EPS) Based Lightweight Concrete Sandwich Wall Panels,” Construction and Building Materials, Vol. 139, pp. 45-51, 2017.
[https://doi.org/10.1016/j.conbuildmat.2017.02.027]

-
Raj, S., Kumar, V. R., Kumar, B. B., Gopinath, S., and Iyer, N. R., “Flexural Studies on Basalt Fiber Reinforced Composite Sandwich Panel with Profile Sheet as Core,” Construction and Building Materials, Vol. 82, pp. 391-400, 2015.
[https://doi.org/10.1016/j.conbuildmat.2015.02.087]

-
Lurie, S., Solyaev, Y. O., Volkov-Bogorodskiy, D., Bouznik, V., and Koshurina, A., “Design of the Corrugated-Core Sandwich Panel for the Arctic Rescue Vehicle,” Composite Structures, Vol. 160, pp. 1007-1019, 2017.
[https://doi.org/10.1016/j.compstruct.2016.10.123]

-
Hou, S., Zhao, S., Ren, L., Han, X., and Li, Q., “Crashworthiness Optimization of Corrugated Sandwich Panels,” Materials & Design, Vol. 51, pp. 1071-1084, 2013.
[https://doi.org/10.1016/j.matdes.2013.04.086]

- ArchiExpo, “Building Polycarbonate Panel,” http://www.archiexpo.com/architecture-design-manufacturer/building-polycarbonate-panel-54846.html, (Accessed 26 FEB 2017)
- Schürmann, E. D., “Nagelbare, Gepresste Kunststoffplatte aus Langglasfaserverstärktem Polypropylen Mit Einem Integrierten Kantenschutz ohne Metalleinlage,” GER Patent, DE2005100 30842 A1, 2007.
- Stratasys, “Aviradyne Technology - Sandwich Composite Production Cost Reduced 52% with Direct Digital Manufacturing,” http://www.stratasys.com/resources/case-studies/commercial-products/aviradyne, (Accessed 15 FEB 2017)
-
Yang, K., Park, J., Choi, T., Hwang, J., Yang, D., et al., “Analysis of Mechanical Characteristics of Polymer Sandwich Panels Containing Injection Molded and 3D Printed Pyramidal Kagome Cores,” Journal of Elastomers and Composites, Vol. 41, No. 4, pp. 275-279, 2016.
[https://doi.org/10.7473/EC.2016.51.4.275]

-
Bartolozzi, G., Pierini, M., Orrenius, U., and Baldanzini, N., “An Equivalent Material Formulation for Sinusoidal Corrugated Cores of Structural Sandwich Panels,” Composite Structures, Vol. 100, pp. 173-185, 2013.
[https://doi.org/10.1016/j.compstruct.2012.12.042]

-
Xia, Y., Friswell, M., and Flores, E. S., “Equivalent Models of Corrugated Panels,” International Journal of Solids and Structures, Vol. 49, No. 13, pp. 1453-1462, 2012.
[https://doi.org/10.1016/j.ijsolstr.2012.02.023]

-
Zhang, J., Supernak, P., Mueller-Alander, S., and Wang, C. H., “Improving the Bending Strength and Energy Absorption of Corrugated Sandwich Composite Structure,” Materials & Design, Vol. 52, pp. 767-773, 2013.
[https://doi.org/10.1016/j.matdes.2013.05.018]

- Libove, C. and Hubka, R. E., “Elastic Constants for Corrugated-Core Sandwich Plates,” National Advisory Committee for Aeronautics, No. NACA-TN-2289, 1951.
-
Boorle, R. K. and Mallick, P., “Global Bending Response of Composite Sandwich Plates with Corrugated Core: Part I: Effect of Geometric Parameters,” Composite Structures, Vol. 141, pp. 375-388, 2016.
[https://doi.org/10.1016/j.compstruct.2015.05.068]

-
Chang, W.-S., Ventsel, E., Krauthammer, T., and John, J., “Bending Behavior of Corrugated-Core Sandwich Plates,” Composite Structures, Vol. 70, No. 1, pp. 81-89, 2005.
[https://doi.org/10.1016/j.compstruct.2004.08.014]

-
Buannic, N., Cartraud, P., and Quesnel, T., “Homogenization of Corrugated Core Sandwich Panels,” Composite Structures, Vol. 59, No. 3, pp. 299-312, 2003.
[https://doi.org/10.1016/S0263-8223(02)00246-5]

-
Mohammadi, H., Ziaei-Rad, S., and Dayyani, I., “An Equivalent Model for Trapezoidal Corrugated Cores Based on Homogenization Method,” Composite Structures, Vol. 131, pp. 160-170, 2015.
[https://doi.org/10.1016/j.compstruct.2015.04.048]

-
Biancolini, M., “Evaluation of Equivalent Stiffness Properties of Corrugated Board,” Composite Structures, Vol. 69, No. 3, pp. 322-328, 2005.
[https://doi.org/10.1016/j.compstruct.2004.07.014]

- ASTM D790-03, “Standard Test Methods for Flexural Properties of Unreinforced and Reinforced Plastics and Electrical Insulating Materials,” http://mahshahr.aut.ac.ir/lib/exe/fetch.php?media=labs:astm_d790.pdf, (Accessed 9 JUN 2017)
-
Magnucki, K., Magnucka-Blandzi, E., and Wittenbeck, L., “Elastic Bending and Buckling of a Steel Composite Beam with Corrugated Main Core and Sandwich Faces-Theoretical Study,” Applied Mathematical Modelling, Vol. 40, No. 2, pp. 1276-1286, 2016.
[https://doi.org/10.1016/j.apm.2015.06.035]

- BS EN ISO 178 “Plastics: Determination of Flexural Properties,” http://img42.chem17.com/5/20120529/634738817689531250.pdf, (Accessed 9 JUN 2017).