레이더 시스템의 구동장치 설계를 위한 바람토크 분석 및 실험적 검증에 대한 연구

1. 서론

일반적으로 레이더 시스템은 함정용 탐색 및 추적 레이더부터 항공기 관제, 포탄의 궤적을 분석하여 화포의 위치를 추정하는 대포병탐지 레이더까지 다양한 활용 범위를 갖고 있다. 특히 차량 일체형 레이더는 자체 생존성을 보장하기 위해 기동성을 우선적으로 고려하여 개발되고 있는 추세이다. 또한 운용환경에 있어 레이더를 탑재한 레이더 체계는 좁은 도로 및 비포장, 야지 등이 포함된 비정상인 도로를 신속하고 안전하게 이동해야 되며, 이동간 발생되는 진동/충격 등의 하중조건과 레이더 운용간 최대풍속 등의 가혹한 운용환경 조건을 견딜 수 있도록 개발되고 있다.¹ 특히 레이더의 운용을 위해 개방되어 있으며 지상에서부터 일정 높이 이상인 장소에 설치 운용됨에 따라, 눈과 비 또는 바람과 같은 외부환경적인 영향을 피할 수 없게 되며, 강한 바람은 레이더가 정상적으로 동작하는데 있어 여러 가지의 물리적 영향을 발생시킨다. 특히, 레이더가 회전하는데 있어 속도를 바꿔 놓거나, 지속적으로 레이더 안테나에 영향을 미치게 되면 레이더의 전자파투과면인 레이돔의 변형 및 구동장치의 손상까지도 발생 하게 된다.^2,3 따라서 레이돔이나 구동장치 설계에 있어 풍하중을 반영하여 설계되지 않으면 형상의 구조적 변형으로 인해 전기적 특성에도 영향을 미치게 된다. 특히 레이돔의 경우 전파 통과 위치에 따라 굴절률 차이가 발생되며, 레이더 빔의 왜곡현상이 발생한다.⁴ 이러한 이유로 레이돔에 대한 전산유체 해석을 통한 레이돔의 구조설계뿐만 아니라 레이더의 구조최적화에 대한 연구는 많은 연구자들이 다양하게 수행하고 있다.^5-9 하지만 외력으로 작용하는 풍하중의 영향성에 대한 연구는 제한적으로 이루어지고 있으며, 항력계수를 가정하여 집중하중 혹은 등분포하중으로 치환하여 구조해석을 통해 설계하고 있다. 또한 실제 제작된 레이더 및 대형구조물의 경우 풍동실험 시설이 제한되어 실제 풍속조건하에서 성능검증방법에 대한 연구가 이루어지지 않고 있다. 일반적으로 구동 장치 설계 시 레이더의 단면 형상에 따라 문헌에 나와있는 항력계수를 사용하거나, 해석을 통해 계산하는 경우가 대부분이다. 하지만 박리점이 일정한 사각 단면의 경우에도 폭과 두께비에 따라 항력 계수는 0.9에서 2.4까지 달라질 수 있다.¹⁰ 따라서 대상 레이더 구조물의 형태에 따라 항력계수가 너무 큰 값이 사용되거나 너무 작은 값이 사용 되는 경우가 생길 수 있다.

본 연구에서는 레이더의 구동 장치 설계를 위해 유체역학적 상사 법칙에 따라 모형을 제작 하여 일반적인 운용풍속 조건인 5-26 m/s에서 레이놀즈수 영향을 평가하였다. 또한 레이더 회전각도를 변화시켜 바람입사각에 따른 풍압과 공기력 측정을 통해 공력 계수를 도출하고, 풍속 조건에 따른 토크를 분석하였다. 마지막으로 분석된 토크를 기준으로 실제 구동장치를 설계 및 제작하여 풍동실험을 통해 도출된 풍하중을 인가하였을 때 레이더가 정상적으로 구동되는지 구동성능 실험을 통해 검증하고, 그 결과를 제시하였다.

2. 풍동실험

2.1 구동장치의 구성

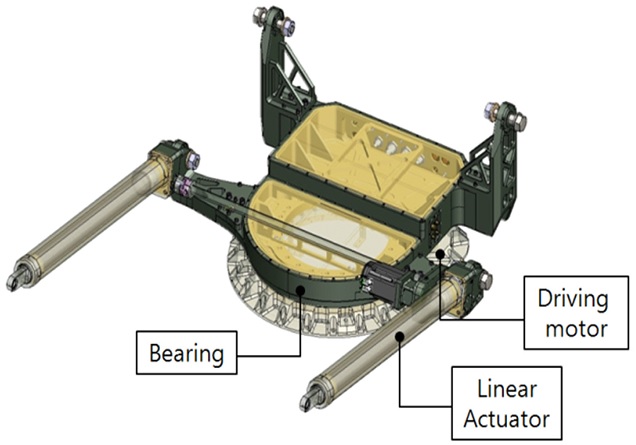
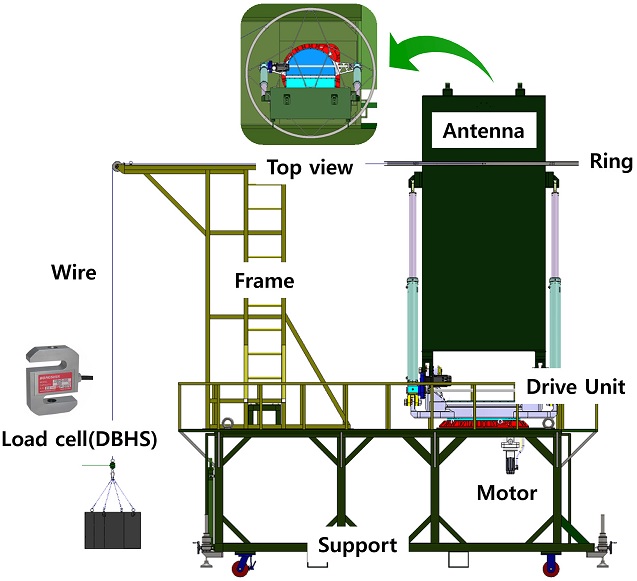
본 연구에 있어 구동장치는 안테나의 방위각 회전을 위해 베어링과 감속기, 구동모터 등으로 구성된다. 구동장치의 개략형상은 Fig. 1과 같다. 구동모터의 선정을 위해서는 관성부하에 의한 회전토크와 바람토크 및 마찰토크가 고려되어야 하며, 회전토크와 바람토크 T_R (Rotating Torque)에 대한 정의는 식(1)과 같다.

$\[ T_R=I\times 2\pi rf/t \]$

(1)

Fig. 1

Schematic view of drive unit

여기서 I, f, t는 회전관성모멘트, 단위 초당 회전 수, 가속시간이다. 일반적으로 관성부하에 의한 회전토크는 바람토크에 비해 매우 작다.

2.2 상사모형의 제작

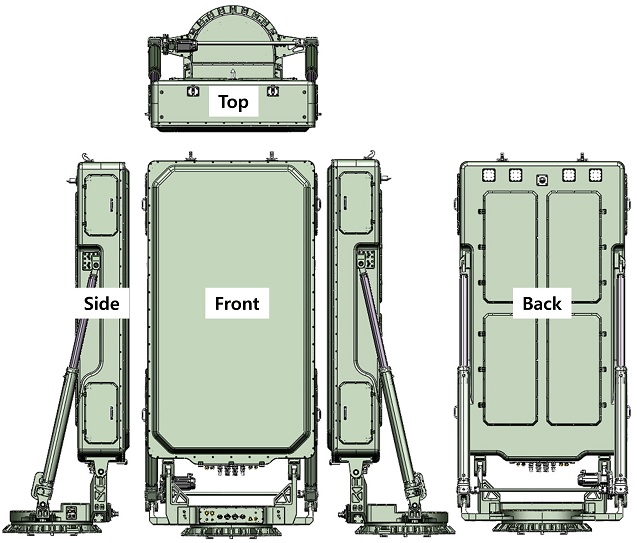
본 연구에 있어 레이더시스템의 풍동실험 모형은 폐쇄율을 고려하여 1 : 8 스케일의 모형으로 제작하였으며, 제작된 모형의 크기는 길이 1131 mm, 높이 434 mm, 폭 360 mm이다. 차량과 레이더까지 모사된 풍동실험 모형의 전체는 아크릴로 제작되었으며, 레이더 하부 구동부와 엑츄에이터는 구조적 강성을 확보하기 위해 두랄루민(Duralumin)으로 제작하였다. 레이더시스템의 구동장치와 안테나형상은 Fig. 2와 같다.

Fig. 2

Test model of antenna and drive unit

2.3 풍동 실험 시설 및 실험 장비

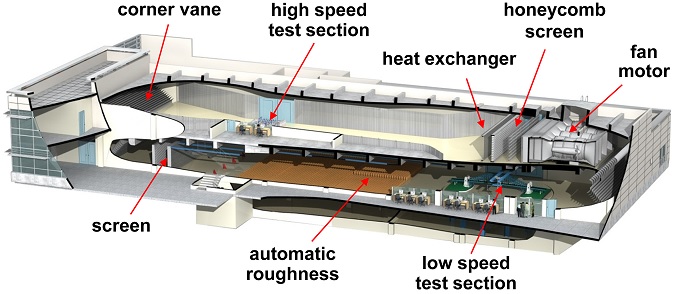
본 연구는 전북대학교 KOCED 대형풍실험센터에서 보유한 경계층 풍동에서 수행하였다. 5개의 송풍기가 수평으로 배치된 수직 순환형 폐회로 방식의 경계층 풍동으로 풍속조건과 시험부 규모에 따라 고속시험부와 저속시험부로 구분되어 있다. 본 연구 대상인 레이더시스템은 풍속조건 26 m/s까지 시험을 수행하기 위해 고속시험부에서 수행하였다. 고속시험부의 크기는 폭 5 m, 높이 2.5 m, 길이 20 m이며, 풍속범위는 0.5-31 m/s 이다. 풍동 내 기류는 난류강도 1.5% 미만의 등류를 형성할 수 있도록 되어있다. 대형풍동 고속시험부의 개략적 내부 단면도는 Fig. 3과 같다.

Fig. 3

Cross section of KOCED wind tunnel center

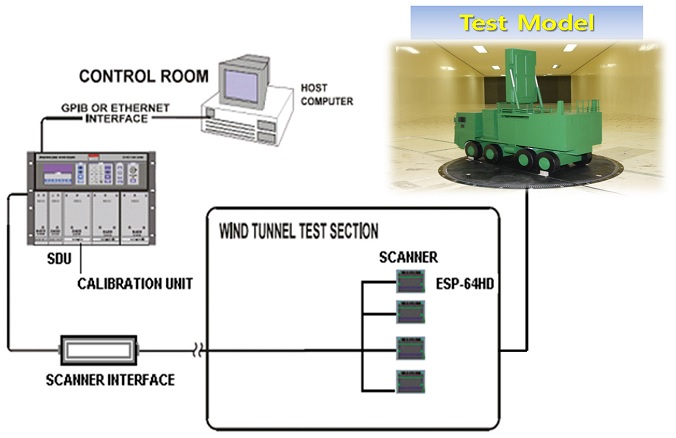
레이더 시스템에 작용하는 풍압을 측정하기 위하여 ± 254 mmAq까지 압력 측정이 가능한 PSI사의 8400 System풍압측정장비를 사용하였다. 실험 시에는 총 3개의 ESP-64HD 모듈이 사용되었고, ESP 모듈은 각각 64개의 채널을 사용할 수 있다. 압력 측정 장치의 구성도는 Fig. 4에 나타나 있다. 또한 레이더 시스템 상사 모형에 작용하는 공기력을 측정하기 위해 Fx, Fy, Fz, Mx, My 및 Mz 방향의 힘과 모멘트를 동시 측정할 수 있는 6 분력계(JR3사, Model: 160M50)를 사용하였다.

Fig. 4

Experimental equipment of pressure measurement

2.4 구동성능시험 장치

본 연구에 있어 상사모형 레이더시스템의 풍동실험을 통해 레이더의 회전에 따른 항력을 측정하였고, 항력계수를 도출하였다. 도출된 항력계수를 통해 실제 레이더시스템의 다양한 풍속조건 및 회전각도에 따른 토크를 계산하였고, 레이더시스템의 최대 운용풍속조건인 26 m/s를 적용하여 회전각도에 따른 토크를 계산하였다. 계산된 바람토크로부터 풍하중을 산정하여 구동장치의 감속기 및 구동모터를 선정하였고, Fig. 5와 같이 설계 및 제작된 구동장치의 구동 성능시험을 풍동실험을 통해 도출된 풍하중이 인가된 상태에서 수행하였다. 풍하중 실험장치는 방위각 회전방향의 하중을 수직하중으로 부여하기 위해 링조립체와 프레임, 와이어와 무게추로 구성되었다. 와이어와 무게추 사이에는 정확한 하중을 측정하기 위해 S-Beam형 로드셀(Model:DBHS)를 설치하였다.

Fig. 5

Schematic view of performance test of drive unit

3. 결과 및 고찰

3.1 공기력 측정

3.1.1 실험 조건

공기력 측정 실험 시 기류는 등류로 한정하였다. 등류는 난류 강도가 낮고 공간적인 변동이 적은 기류를 의미하며, 본 연구에서의 고려한 기류조건은 난류강도가 1.5% 미만이다. 풍동 유로내 턴테이블 하부에 있는 수직축이 관통 할 수 있도록 만들어진 차량 모형을 먼저 턴테이블 바닥에 설치하고 수직축을 안테나 위치까지 올려 수직축 위에 공기력을 측정하기 위한 로드셀과 안테나 모형을 설치하였다. 안테나 구동에 따른 바람 입사각은 차량과 안테나 각각 0-180도까지 45도 간격으로 유체역학적 상사에 따라 9.2 m/s에서 실험을 수행하였다. 풍동 유로 내 실험모형 설치 사진과 공기력 실험조건은 각각 Fig. 6과 Table 1에 나타나 있다.

Fig. 6

Mode of aerostatic force test

Fig. 7

Coordinate of structure

Fig. 8

Coordinate of fluid

Table 1

Test condition of aerodynamic force

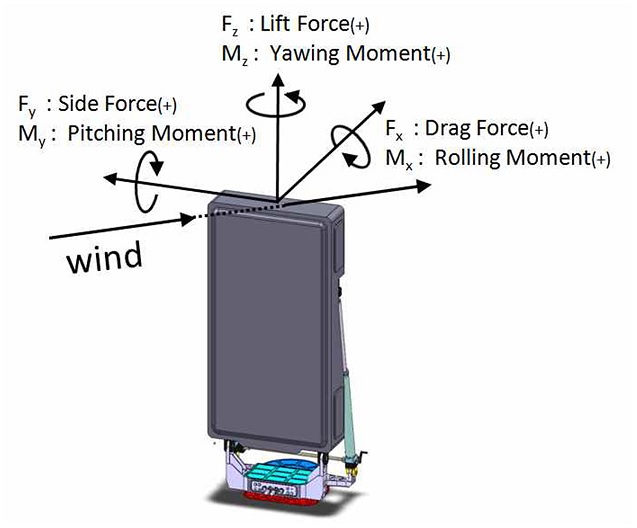
본 연구에서 공기력 실험 시 좌표계는 구조물 좌표계를 적용하여 실험을 진행하였으며, 바람입사각 변화에 대한 좌표계의 변환은 식(2)부터 식(5)와 같다.

$\[ F_d=F_x{cos}\theta +F_y\sin \theta \]$

(2)

$\[ F_s=F_x\sin (\theta +180)+F_y\cos \theta \]$

(3)

$\[ M_R=M_x\cos \theta +F_y\cos \theta \]$

(4)

$\[ M_P=M_x\sin (\theta +180)+M_y\cos \theta \]$

(5)

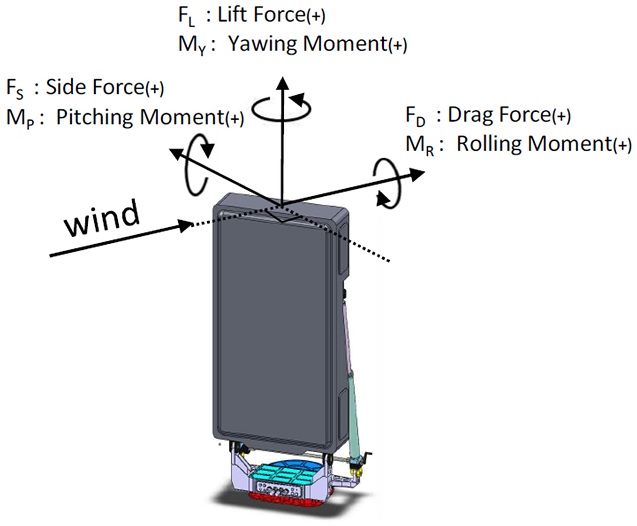
공기력계수는 풍하중을 무차원한 계수로 다양한 공기 밀도 및 풍속에 대해서 하중을 얻어낼 수 있다는 장점이 있다. 또한 비슷한 형상의 단면이면 거의 같은 값을 사용 할 수 있다. 정적 공기력계수 C_D (Drag Force Coefficient), C_S (Side Force Coefficient), C_MR (Rolling Moment Coefficient), C_MP (Pitching Moment Coefficient), C_MY (Yawing Moment Coefficient)에 대한 정의는 식(6)과 같다.

$\[ C_D,\mathrm{ }{C}_S,C_L=\frac{F_D,\mathrm{ }{F}_S,F_L}{\frac{1}{2}\rho U^{2}A},\mathrm{ }{C}_{MR}, C_{MP}, C_{MY}=\mathrm{ }\frac{M_R, M_P,M_Y}{\frac{1}{2}\rho U^{2}AH} \]$

(6)

여기서 F_D, F_S, F_L, M_R, M_P, M_Y는 각각 Drag Force, Side Force, Lift Force, Rolling Moment, Pitching Moment, Yawing Moment이고, ρ는 공기밀도, A는 실험모형의 면적, H는 실험모형의 높이, U는 평균 풍속이다.

3.1.2 레이놀즈수의 영향

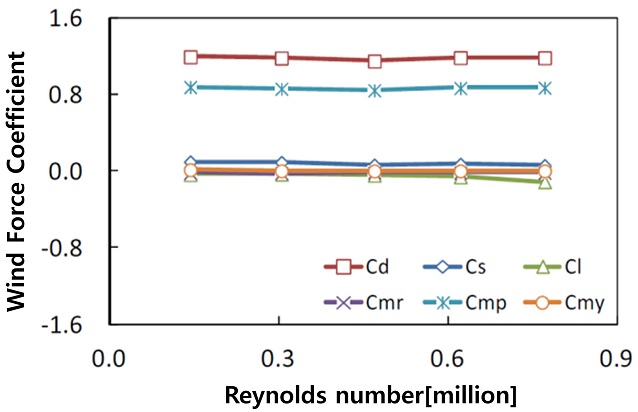
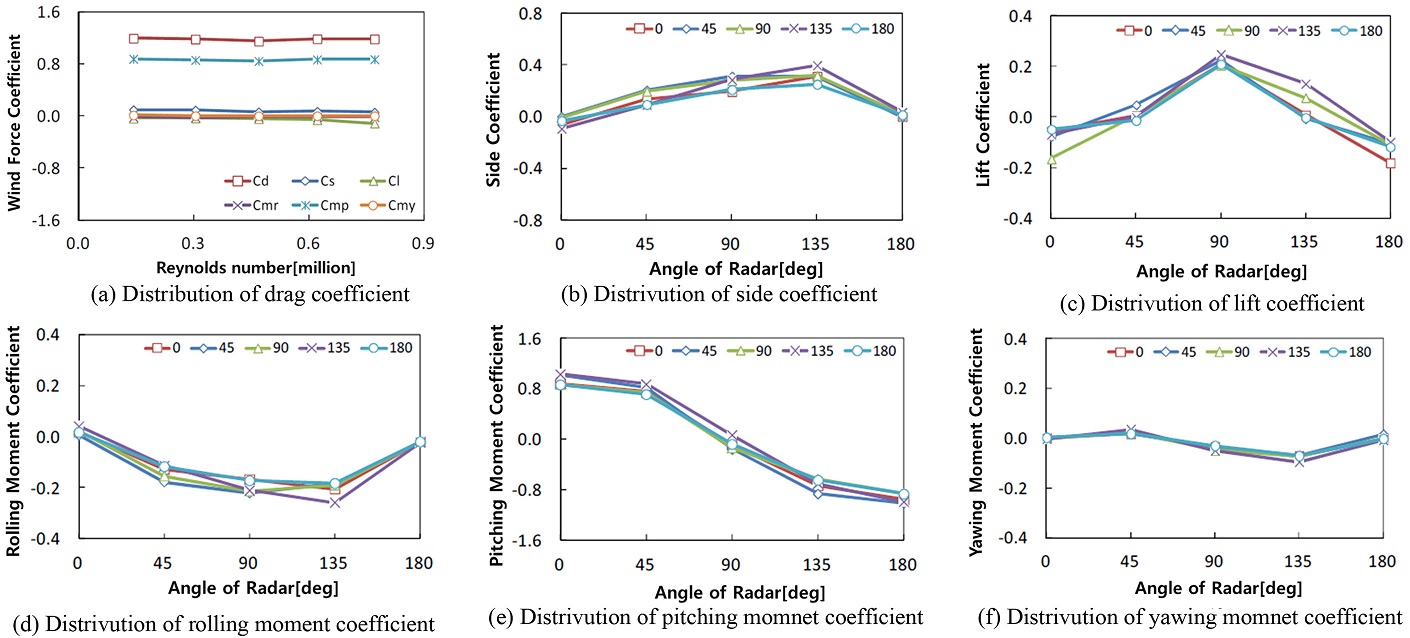
축소 모형 실험이 실제 풍동실험의 결과를 반영하기 위해서는 먼저 레이놀즈수에 따른 풍하중 및 풍압의 변화여부를 확인해야한다. 이때 풍동 실험 결과가 실제 구조물 설계에 유용한 데이터가 되기 위해서는 반드시 레이놀즈수에 독립적인 범위 내에서 수행되어야 한다. 이에 기류 조건은 등류로 한정하고, 레이놀즈수를 1.5 × 10⁵-7.9 × 10⁵으로 달리하여 실험을 수행하였다. 실험 조건은 Table 2와 같고, 레이놀즈수에 따른 공기력의 변화는 Fig. 9와 같다. 실험 결과 레이더시스템은 레이놀즈수의 영향을 받지 않는 것으로 나타났다.

Table 2

Test condition according to reynolds number

Fig. 9

Aerostatic force coefficient according to reynolds numbers

3.1.3 공기력실험 결과

레이더시스템에 작용하는 바람 입사각 변화에 따른 공기력 측정 실험 조건은 풍압 실험과 동일한 조건에서 실험을 수행하였다. 실험 결과는 Fig. 10에 나타나 있다. 공기력계수와 모멘트계수 모두 차량 바람입사각 135도, 안테나 바람입사각 0도에서 가장 크게 나타났으며, 그때의 공기력계수는 C_D (Drag Force Coefficient)로 1.430 ± 0.044(95% 신뢰수준)과 모멘트계수는 C_MR (Pitching Moment)로 1.032 ± 0.043(95% 신뢰수준)로 나타났다. 따라서 특정 바람입사각에서 차량으로 인한 기류의 변화가 공기력계수와 모멘트계수를 증가시킬 수 있음을 확인하였다.

Fig. 10

Distribution of aerostatic force coefficient (U = 9.2 m/s)

3.2 풍압 측정

3.2.1 실험 조건

풍압 측정을 위해 정면, 좌측면, 우측면, 평면 및 후면에 각각 77, 26, 26, 27, 54개 총 210개의 풍압공을 설치하였으며, 정확한 풍압 측정을 위해서 모형 내부에 ESP Module를 내장하였다. 풍압 측정 실험 시 기류는 등류로 한정하였으며, 안테나 구동에 따른 바람입사각은 실험풍속 9.2 m/s에 대해서 공기력실험과 동일하게 실험을 수행하였다.

3.2.2 레이놀즈수의 영향

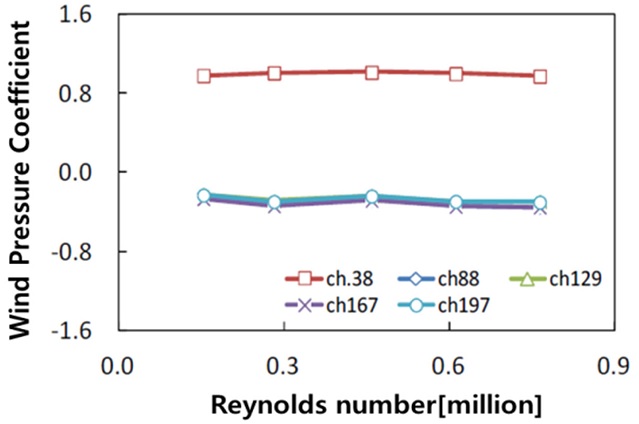
실험 조건은 공기력실험(Table 2)과 동일하며 대표 풍압공의 레이놀즈수 변화에 따른 대표 풍압공의 풍압 변화는 Fig. 11에 나타나 있다. 풍속을 달리하여 레이놀즈수의 영향을 검토해본 결과 공기력 실험결과와 동일하게 레이놀즈수의 영향을 받지 않는 것으로 나타났다.

Fig. 11

Effect on Reynolds number of pressure tap

3.2.2 풍압실험 결과

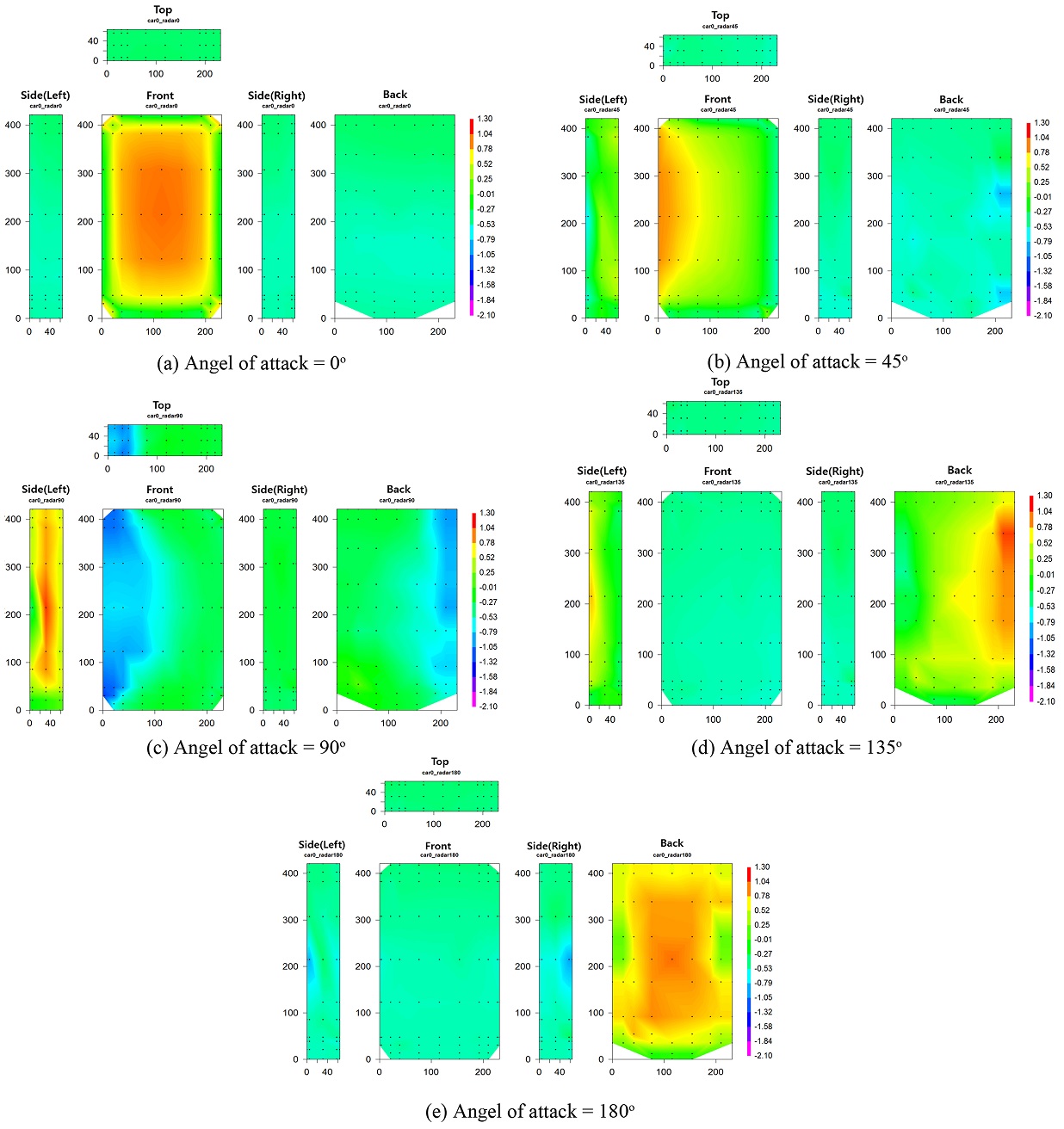
본 연구에서는 다양한 바람입사각 조건에서의 풍압분포를 알아보기 위하여 풍속조건 9.2 m/s에서 실험을 수행하고 결과를 비교하였다. Fig. 12는 차량 바람입사각 0도에서 안테나 바람입사각에 따른 풍압계수 분포를 나타내고 있다. 최대 정압은 차량 바람입사각 0도, 안테나 바람입사각 90도에서 측면도 정중앙 위치에서 1.21로 나타났고, 최대 부압은 차량 바람입사각 0도, 안테나 바람입사각 90도에서 정면도 좌측 하단 위치에서 -2.06으로 나타났다. 최대 정압의 경우 바람 방향과 수직인 면의 정 중앙에서 가장 큰 값이 나타났으며, 최대부압은 안테나의 하단 모서리에 가장 인접한 풍압공들에서 나타났다. 이는 차량으로 인한 기류변화가 안테나에 국부적으로 더 큰 압력을 가할 수 있음을 의미한다. 풍압 실험의 경우 풍압공의 개수 및 위치가 적절하게 배치되지 않으면, 많은 오차를 포함하게 된다.

Fig. 12

Distribution of pressure coefficient according to angle of attack (Angle of vehicle = 0°)

차량 바람입사각0도, 안테나 바람입사각 0도 조건에서 측정된 풍압 분포를 각각의 대표 면적으로 적분하여 얻어진 항력계수는 1.167으로 공기력 실험에서 6 분력계를 사용하여 측정된 값인 1.169와 약 0.2% 오차를 보이며 잘 일치하고 있다. 이는 풍압공의 위치가 대표성을 가지고 있으며, 압력측정을 위한 풍압공의 개수도 충분하다고 할 수 있다.

3.3 구동성능 시험

3.3.1 실험 조건

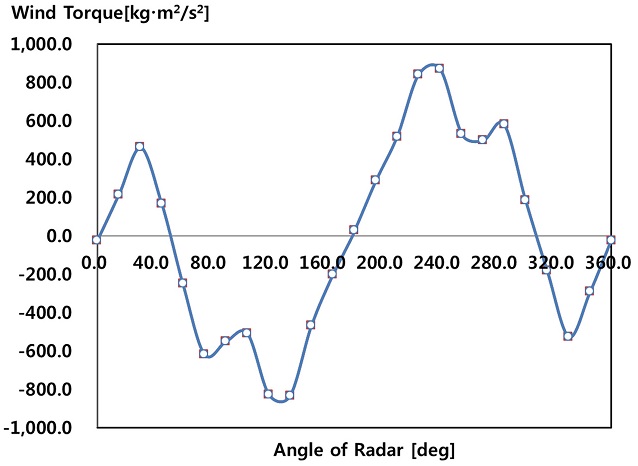
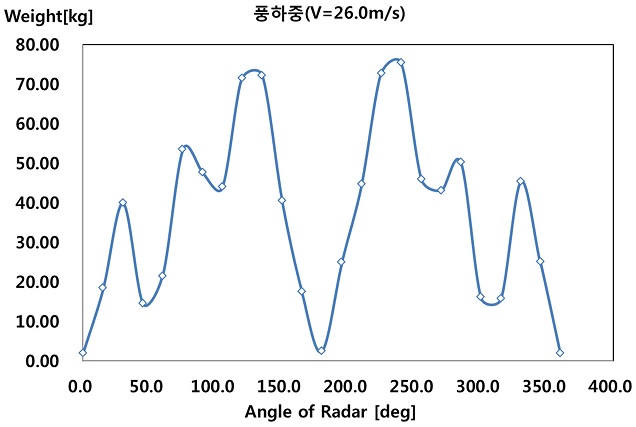
구동성능 시험을 위해 최대 운용풍속조건인 26 m/s 조건에서 풍하중을 인가하여 레이더의 방위각 구동성능시험을 수행하였다. 구동장치에 대한 요구되는 구동성능기준은 Table 3에 나타냈다. 바람토크는 앞서 실험을 통해 측정된 회전관성모멘트 C_MY (Yawing Moment Coefficient)으로 부터 계산되며, Fig. 13은 레이더 회전 각도에 따른 바람토크를 나타내고 있다. 풍하중은 레이더 방위각 회전에 따른 변동에 무관하게 최대 하중을 적용하였다. 이는 실제 레이더가 구동 간 회전에 따른 하중을 가변적으로 부여하는데 제한되기 때문이다. 반면 최대 하중을 부여하여 구조물의 안전율을 확인할 수 있다. 최대 하중은 바람토크로부터 식(7)을 적용하여 풍하중에 상당하는 무게로 변환 가능하다.

Table 3

Specification of drive unit

Fig. 13

Wind torque according to angle of radar

$\[ W_{\mathrm{m}\mathrm{a}\mathrm{s}\mathrm{s}}=\frac{T_w}{Rg} \]$

(7)

여기서 W_mass는 풍하중에 상당하는 무게추의 무게이며, T_W는 바람토크, R은 링조립체와 레이더의 회전중심간의 거리, g는 중력 가속도이다. Fig 14는 변환된 무게를 나타내고 있으며, 본 구동성능시험에 있어서는 최대 무게인 75.8 kg을 적용하여 시험을 수행하였다.

Fig. 14

Wind weight according to angle of radar

3.3.1 실험 결과

최대 풍하중이 인가된 상태에서 레이더의 구동시간과 구동에 대한 각도정확도를 확인하였다. 레이더의 구동시간은 구동장치를 구동할 수 있게 제작된 별도 시험 프로그램을 통해 구동명령 및 구동정지 신호를 받아 측정하였으며, 각도정확도는 구동장치의 설치된 각도검출기 (엔코더 : Zettlex사 INC-3-75)를 통해 확인하였다. Table 4는 구동성능시험 결과를 나타내고 있다. 레이더의 구동시간은 0도에서 +180도 회전 시 최대 31.4초가 걸렸으며, +180도에서 -180도까지 360도 회전 시 최대 69.6초로 요구규격인 40초와 80초를 만족하였다. 회전 시 각도정확도 결과는 최대 0.05도로 요구규격인 ± 0.2도를 만족하였다.

Table 4

Results of drive performance test

4. 결론

본 연구에서는 레이더시스템의 구동장치 설계 및 제작 검증을 위해 1:8로 축소한 상사모델을 이용하여 풍동실험을 수행하였고, 차량과 레이더의 회전각도에 따른 풍압과 공기력을 도출하였다. 또한 최대 운용풍속 조건인 26 m/s에서 토크를 분석하였고, 분석된 토크를 기준으로 실제 제작된 구동장장치에 풍하중을 인가하여 레이더가 정상적으로 구동되는지 구동성능 실험을 통해 검증하였으며 다음과 같은 결론을 얻었다.

(1) 실험모형에 대한 레이놀즈수의 영향성을 검토한 결과 레이놀즈수의 영향을 받지 않는 것으로 나타났다. 따라서 실험모형에 대한 풍압과 공기력 실험의 측정결과는 유효하였다.

(2) 공기력계수와 모멘트계수 모두 차량 바람입사각 135도, 안테나 바람입사각 0도에서 가장 크게 나타났으며, 그때의 공기력계수는 C_D (Drag Force Coefficient)로 1.430 모멘트계수는 C_MR (Pitching Moment)로 1.032로 나타났다. 이는 레이더가 받는 기류가 차량 또는 구조물에 의해 변화가 발생하며 공기력계수와 모멘트계수를 증가시키거나 감소시킬 수 있음을 확인 할 수 있었다.

(3) 풍압측정 실험은 공기력 측정실험의 검증과 레이더의 형상 설계자료로 활용하기 위해 수행하였다. 실험결과 최대 정압은 차량 바람입사각 0도, 안테나 바람입사각 90도에서 측면도 정중앙 위치에서 1.21로 나타났고, 최대 부압은 차량 바람입사각 0도, 안테나 바람입사각 90도에서 정면도 좌측 하단 위치에서 -2.06으로 나타났다. 또한 풍압 분포를 각각의 대표 면적으로 적분하여 얻어진 항력계수를 공기력 실험에서 측정된 값과 비교한 결과 0.2%오차를 보이며 잘 일치하였다.

(4) 최대 운용풍속조건인 26 m/s의 풍하중을 모사하여 레이더가 정상적으로 구동되는지 확인결과 요구규격인 구동시간과 각도 정확도 모두 만족하는 것을 확인하였다.

이와 같은 실험과 검증방법을 통해 실제 풍동실험이 불가능한 대형 레이더시스템과 대형구조물의 회전장치 설계뿐만 아니라 풍동실험에 대한 평가방법으로도 적용이 가능할 것이다.

REFERENCES

• Jung, H. Y., Lee, K. M., Kang, K. H., and Kang, J. G., “The Study on the Vehicle-Mounted Radar System of Structural Design Under Environment,” J. Korean Soc. Precis. Eng., Vol. 33, No. 10, pp. 797-804, 2016. [https://doi.org/10.7736/KSPE.2016.33.10.797]
• Yim, S. H., Kang, K. H., Choi, J. H., Lee, S. H., and Kwon, S. D., “Wind Tunnel Test of Aerodynamic Forces and Wind Tunnel Test of Aerodynamic Force and Wind Pressures Acting on Multi-Layer Radom in Active Phased Array Radar,” Journal of the Korea Institute of Military Science and Technology, Vol. 17, No. 1, pp. 149-157, 2014. [https://doi.org/10.9766/KIMST.2014.17.1.149]
• Simiu, E. and Scanlan, R. H., “Wind Effects on Structures,” John Wiley & Sons, pp. 155-168, 1996.
• Peterson, D., Otto, J., and Douglas, K., “Radome Boresight Error and Compensation Techniques for Electronically Scanned Arrays,” http://www.dtic.mil/get-tr-doc/pdf?AD=ADA344639, (Accessed 23 AUG 2017)
• Shin, D. J., Lee, J. H., Kang, Y. S., and Choi, J. H., “Structural Stability Analysis of the Large Radar for Transport Environment,” Proc. of the Korean Society for Noise and Vibration Engineering Spring Conference, pp. 241-246, 2015.
• Cho, K. D., Kim, K. H., Kwon, M. S., and Hong, S. I., “Outer Shape Design of Rotating Medium Antenna Installed on Ship Mast,” Transactions of the Korean Society of Mechanical Engineers: A, Vol. 36, No. 8, pp. 843-850, 2012. [https://doi.org/10.3795/KSME-A.2012.36.8.843]
• Jeong, D. H., Seo, M, S., Kim, D. H., Choi, H. J., Kang, E, J., et al., “Hydraulic Radome Drive Open-Close Equipment CFD Aerodynamic and Structural Analysis,” The Korean Society of Mechanical Engineers Spring Conference, pp. 352- 356, 2013.
• Zarchan, P. and Gratt, H., “Adaptive Radome Compensation Using Dither,” Journal of Guidance Control and Dynamics, Vol. 22, pp. 51-57, 1999. [https://doi.org/10.2514/2.4370]
• Jeong, D.-H., Seo, M.-S., Kim, D.-H., Choi, H.-J., Kim, E.-J., et al., “Long Rang Tracking Radome CFD Aerodynamic and Structural Analysis,” Proc. of the Korean Society of Mechanical Engineers Spring Conference, pp. 259-260, 2013.
• Courchesne, J. and Laneville, A., “A Comparison of Correction Methods Used in the Evaluation of Drag Coefficient Measurements for Two-Dimensional Rectangular Cylinders,” Journal of Fluids Engineering, Vol. 101, No. 4, pp. 506-510, 1979. [https://doi.org/10.1115/1.3449019]