반응표면분석법 기반 고경도 베어링강의 하드터닝 공정 최적화

1. 서론

하드터닝은 약 45 HRC 이상으로 열처리된 재료를 선삭 가공에 적용한 공정이다. 절삭유를 사용하지 않기 때문에 자연친화적 공정이며, 표면조도가 우수하다는 것이 특징이다. 기존 연삭공정은 복잡한 부품형상에 대해 특수 연삭휠의 제작이 요구되지만, 하드터닝은 유연하게 대처가 가능하다.

하드터닝 공정은 열적 연화(Thermal Softening)에 의해 칩 형성(Chip Formation)이 발생함으로써 기계 가공이 가능하게 한다.¹ 공구 및 재료에 가해지는 절삭온도 및 압력은 일반적인 가공 공정에 비해 높으므로, 적합한 공구를 선정하는 것이 중요하다. 하드터닝 공정은 주로 Cubic Boron Nitride (CBN) 및 세라믹(Alumina Ceramic) 공구를 사용한다. CBN공구의 경우 열적 안정성 및 화학적 안정성, 공구수명, Chipping 등에 대해 우수한 장점을 갖는 반면 제작 공정 및 가격이 대단히 복잡하고, 비싸다는 단점이 있다.² 세라믹 공구의 경우 CBN공구에 비해 가격이 낮은 대신, Chipping 및 공구 파손 등에 취약하다는 단점이 있다.

높은 절삭력 및 절삭온도는 공구 파손 및 낮은 생산성을 야기시키며, 부품의 표면 품질을 악화시킨다. 저품질의 표면조도는 가공 부품의 수명 결정하기 때문에, 이에 대한 영향력 평가가 반드시 필요하다.³ 하드터닝 공정에서는 가공속도 및 이송속도에 따라 표면조도, 절삭력 및 공구마모 등이 서로 긴밀하게 연관된다. 따라서, 생산성 향상을 위해서 가공조건 최적화에 대한 연구가 요구된다.⁴

최적화 연구는 주로 실험적으로 진행되어 왔으며, 통계적 방식을 이용하여 최적 조건을 정의할 수 있다. Davim⁵은 직교배열법을 이용하여 실험조건을 선정하여, 냉간강(60 HRC)에 대해 연삭가공 표면조도(Ra < 0.8 μm)에 준하는 가공 조건을 정의하였다. Yang⁶은 ANOVA 분석 및 다구치 해석(Taguchi Method)을 이용하여 최적 조건을 적용하여, 표면 조도 및 공구수명에 대해서 향상하였다. Nayak⁷은 그레이 관계(Grey Relation) 분석법을 적용하여, 소재제거율(Material Removal Rate, MRR), 절삭력, 표면조도에 대해 최적 조건을 정의하였다. 최근, 머신 러닝이 대한 관심이 커지면서, 신경망(Neural Network)을 기반으로 한 딥러닝 기법을 적용한 연구가 늘고 있다.^8,9 딥러닝은 예측성능은 우수하지만, 많은 예비 데이터와 절대 학습시간이 필요하다. 또한, 가공 인자들 간의 통계적 해석이 불가능하기 때문에 제약이 뒤따른다. 최적화를 위한 통계적 접근방법 중, 반응표면분석법(Response Surface Methodology)은 실험 횟수를 줄이는 것이 가능하며, 요인들에 대한 통계적 분석이 가능하다.

본 논문에서는 반응표면분석기법을 이용하여, 기 개발된 하드터닝 전용 장비의 가공 최적 조건을 정의하는 것이 목적이다. 가공 재료로는 50 HRC로 열처리된 베어링강(AISI 52100)을 선정하였으며, 가공속도(RPM), 이송속도(Feed Rate, mm/rev), 절입량(a_p, mm)에 대해 각 3 level로 정의하였다. 실험 설계는 박스-벤(Box-Behnken) 방법에 의해 실시하였다. 표면조도 및 절삭력이 최소되는 지점을 도출하기 위해 Minitab^®18을 이용하여, 반응표면분석을 실시하였다.

2. 실험 조건 및 장비

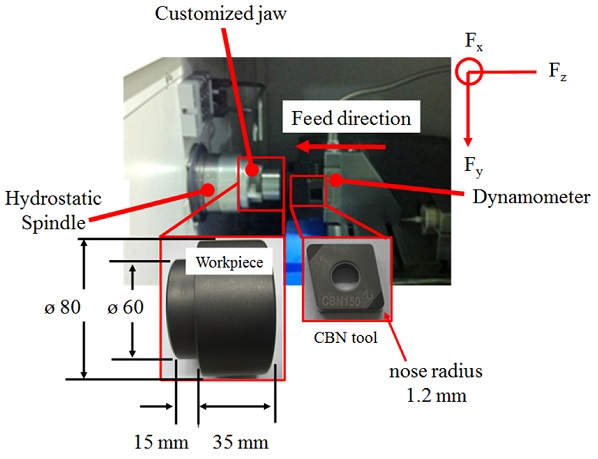
하드터닝 공정을 위해서는 기계 전체의 고강성 설계가 필요하다. 일반적인 CNC머신의 경우 강성 20 N/micron이지만, 기 개발된 하드터닝 전용기는 40 N/micron 강성으로 설계되었다. 재료에 대한 일정한 고정압력을 위해 전면접촉이 가능하도록 특수 제작한 Jaw를 사용하였으며, 채터(Chatter) 방지 및 정밀 가공을 위해 유정압 주축(Hydrostatic Spindle)을 사용하였다(Fig. 1).

Fig. 1

Experimental set-up for the hard turning process

재료는 고주파열처리를 통해 약 50 HRC의 경도를 가지도록 처리하였다. 특수 제작한 Jaw는 반경 30 mm, 길이 15 mm 부분을 고정하며, 반경 40 mm, 길이 35 mm 부분은 실험 공정에 적용하였다. CBN공구는 세코(SECO)社의 CNGA 120412S-01525-L0-B모델을 사용하였으며, 공구 선단 반경(Nose Radius) 1.2 mm, Uncoated CBN 50% 함량을 가진다.

CBN공구 및 AISI 52100재료에 대한 가공속도(RPM), 이송속도(Feed Rate), 절입량(a_p)에 대해 각각 2500-3500 RPM, 0.02-0.08 [mm/rev], 0.03-0.13 [mm] 범위 내에서 설정하였다. 최적 조건에 대한 관심범위를 Table 1과 같이 지정하였다. 반응표면의 근사모형으로는 각 독립변수들이 곡선효과가 고려되어야 하므로 2차 다항 회귀 모형(Regression Model of 2nd Order)이 적합하다고 판단하였다. 박스-벤켄 실험 계획법은 인자의 수가 k개인 경우에 3 k요인배치법보다 실험점의 수가 많지 않으면서도 직교블록을 만들기에 용이하다. 또한, 2차 다항 회귀 모형에 의해 범위 내 최적 조건을 찾을 수 있기 때문에 구석점(Corner Point)에 대한 실험은 고려하지 않았다.

Table 1

Cutting parameters and their levels

실험에 대한 결과인자로는 가공 중 발생하는 절삭력 데이터와 가공 후 표면조도로 설정하였다. 절삭력의 경우 키슬러(Kistler)社의 공구동력계(Dynamometer)를 사용하였으며, 표면조도는 나노시스템즈社의 NV-3000을 이용하여 측정하였다.

3. 공정 결과 및 분석

3.1 표면조도(Ra)에 대한 RSM분석

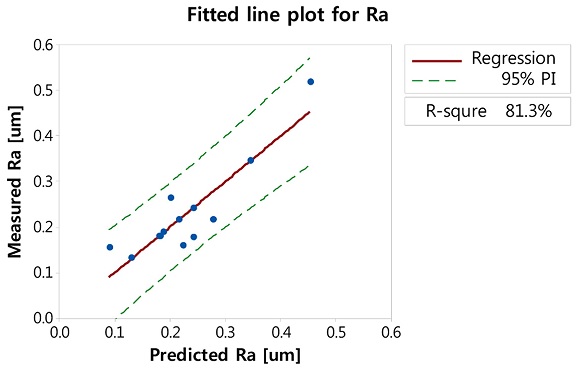
Table 2는 박스-벤켄 실험 계획법에 의해 결정된 실험 조건, 실험 실행 순서, 표면조도 측정 결과를 나타낸다. 표면조도에 대한 회귀모델(Regression Model)은 완전 2차 다항식의 형태로 식(1)과 같이 결정됐다. 표면조도 회귀 모델은 실험 데이터에 대해 약 81.3% (R-Square)의 설명력을 가진다(Fig. 2). 예측 구간(PI) 95% 하한과 상한 내에서 실험치가 존재하므로, 표면조도에 대한 회귀 모델은 실험치에 대해서 잘 예측한다.

$\[ \begin{array}{c}{R}_a=4.07-0.002586\cdot RPM-10.95\cdot f+0.65\cdot a_p\\ +6.3\cdot f^2-12.0\cdot a_p^2+0.00395\cdot RPM\cdot f\\ +0.00055\cdot RPM\cdot a_p+0.20\cdot f\cdot a_p\end{array} \]$

(1)

Table 2

Experiment parameter and results for surface roughness (Ra)

Fig. 2

Comparison between measured and predicted values for surface roughness (Ra)

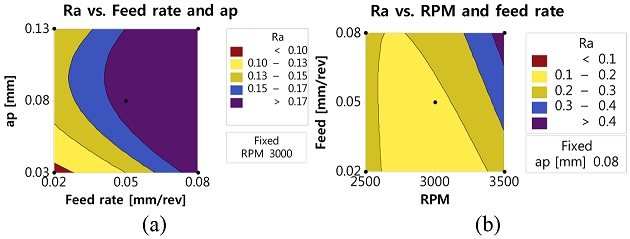
식(1)을 이용하여 반응표면 예측 등고선도를 Fig. 3에 나타내었다. RPM을 3000으로 고정된 조건에서는, 이송속도와 절입량이 낮을 때, Ra값이 낮아지는 것을 확인할 수 있었다(Fig. 3(a)). 이송속도와 절입량이 낮아지게 되면, 표면의 산과 산(Peak-to-Peak Height)의 크기가 작게 생성된다. 이에 따라, 산과 골(Peak-to-Valley Height)의 크기도 작게 되기 때문으로 표면조도가 좋아지는 것으로 분석된다. RPM의 경우 중간 값인 3000 RPM 근처 범위에서 표면조도 값이 가장 좋은 것으로 분석된다(Fig. 3(b)). 저 RPM대에서는 전체 절삭력 기준 마찰에 대한 영향이 커지므로 마찰 온도 및 공구와 표면 접촉 시간의 증가로 인해 표면 품질이 떨어지는 것으로 분석된다. 고RPM에서는 기계의 채터 및 공진(Resonance) 발생 가능성이 높으며, 상대적으로 고온이 발생하기 때문에, 표면조도에 악영향을 미칠 가능성이 매우 크다. 중간 범위 내(2900-3100 RPM)에서 표면조도 가장 좋은 것으로 분석된다.

Fig. 3

Estimated response surface for surface roughness (a) at fixed RPM 3000, (b) at fixed ap 0.08 [mm]

3.2 절삭력에 대한 RSM분석

Table 3은 앞서 표면조도에서 설정한 가공 조건과 같으며, 절삭력 3방향 Fx, Fy, Fz에 대한 측정을 실시했다. 측정 절삭력을 바탕으로 각 방향에 대한 회귀 모델은 식(2)부터 식(4)와 같다.

Table 3

Experiment parameter and results for forces

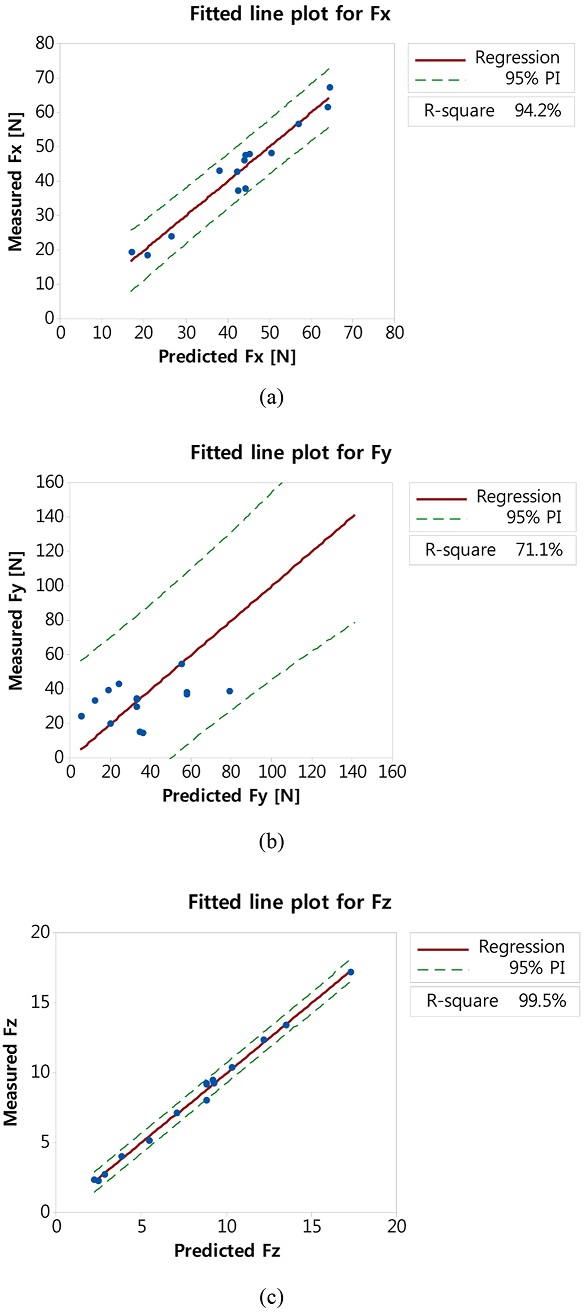
회귀 모델을 기반으로 각 측정한 절삭력에 대한 비교를 실시하였다. Figs. 4(a)-4(c)는 각각 Fx, Fy, Fz에 대한 절삭력과 예측 절삭력에 대한 비교를 나타내었다. 회귀 모델은 Fx는 94.1%, Fy는 71.1%, Fz는 99.5%로 실험치에 대해서 설명을 한다. Fy의 경우 다소 낮은 R-Square값을 갖지만, 예측 상한 및 하한선 내에 모두 결과 값이 위치하므로 유의한 데이터로 판단된다.

$\[ \begin{array}{c}{F}_x=-180+0.1776\cdot RPM-2325\cdot f+417\cdot a_p\\ +0.000033\cdot RP{M}^2+9.774\cdot f-1237\cdot a_p^2\\ +0.315\cdot RPM\cdot f-0.029\cdot RPM\cdot a_p\\ +3030\cdot f\cdot a_p\end{array} \]$

(2)

$\[ \begin{array}{c}Fy=-780+0.537\cdot RPM-155\cdot f+43\cdot a_p\\ +25596\cdot f^2+7204\cdot a_p^2+0.12\cdot RPM\cdot f\\ -0.039\cdot RPM\cdot a_p-24358\cdot f\cdot a_p\end{array} \]$

(3)

$\[ \begin{array}{c}Fz=-30.3+0.02330\cdot RPM-138.3\cdot f+83.5\cdot a_p\\ -48\cdot f^2\cdot 84\cdot a_p^2\cdot 0.0286\cdot \mathrm{R}\mathrm{P}\mathrm{M}\cdot f\\ -0.0107\cdot RPM\cdot a_p+1341\cdot f\cdot a_p\end{array} \]$

(4)

Fig. 4

Comparison between measured and predicted values for (a) Fx, (b) Fy, (c) Fz

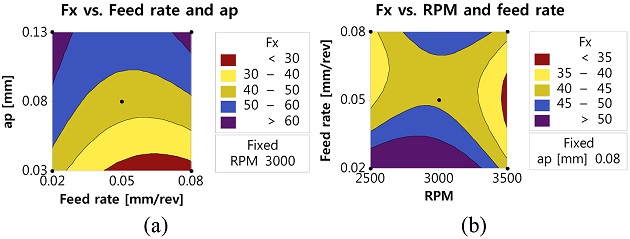
Figs. 5부터 7은 반응표면분석을 통해 추정한 Fx, Fy, Fz 절삭력 데이터이다. Fx의 경우, RPM을 3000으로 고정한 상태에서는 절입량의 증가에 따라 절삭력이 증가하는 것을 알 수 있다 (Fig. 5(a)). 절입량이 최소인 구간에서는, 이송량 낮을 때보다, 0.05-0.08 [mm/rev] 사이에서 오히려 절삭력 Fx가 작아지는 것으로 분석되었다. 그 이유로는 이송 속도 증가에 따라 가공열도 같이 증가하면서 열적 연화에 의한 효과에 대한 영향이 커진다. 따라서, 절삭력이 낮아지는 것으로 판단된다. 고 RPM에서 역시 열적 연화의 효과가 커지면서 절삭력은 낮아진다(Fig. 5(b)).

Fig. 5

Estimated response surface for Fx at fixed RPM 3000, (b) at fixed ap 0.08 [mm]

Fig. 6

Estimated response surface for Fy at fixed RPM 3000, (b) at fixed ap 0.08 [mm]

Fig. 7

Estimated response surface for Fz at fixed RPM 3000, (b) at fixed ap 0.08 [mm]

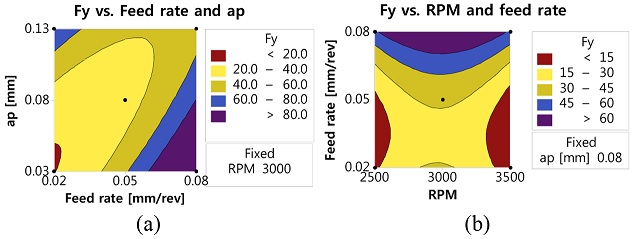
Fy의 경우, 재료의 전단(Shear)에 의해 발생되는 절삭력으로 절입량 및 이송속도가 낮은 범위에서는 변형(Strain) 및 변형율(Strain Rate)의 경화(Hardening) 효과가 작아지면서 절삭력이 낮아지는 것으로 분석된다(Fig. 6). 반면, 고 RPM에서 역시 열적 연화에 의한 효과 및 낮은 이송량 영역대에서의 변형 경화의 복합 효과로 인해 절삭력은 낮아지는 것으로 분석된다.

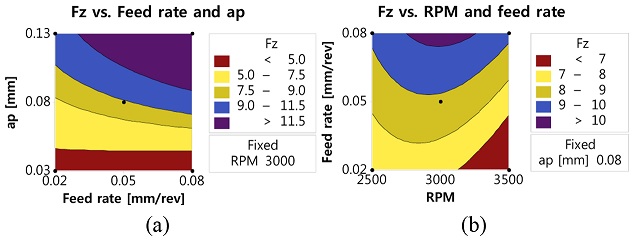
Fz는 이송량과 상관 없이 절입량에 따라 변화하는 것을 확인할 수 있다(Fig. 7(a)). 또한, 열적 연화에 대한 효과에 의해 낮아지는 것은 Fig. 7(b)에서 확인할 수 있다. 그러나, Fz의 값의 범위는 Fx 및 Fy값보다 훨씬 낮기 때문에, 공정에 큰 영향을 미치지는 않을 것으로 판단한다.

3.3 하드터닝 최적 조건

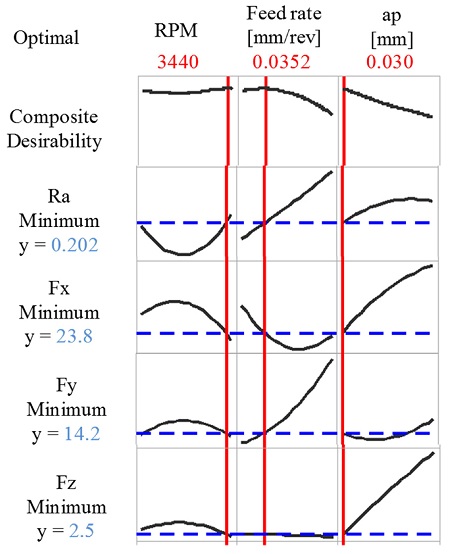
Fig. 8은 Ra 및 절삭력에 대한 주효과 분석도 및 최적 조건 분석 그래프이다. 가공 조건내의 표면조도(Ra)와 절삭력(Fx, Fy, Fz) 모두 최소값을 가지도록 목적함수로 두었다. 표면 조도 및 절삭력에 대해 각각 1의 가중치로 설정하였다.

Fig. 8

The main effects plot and optimal cutting condition for minimized Ra and forces

RPM 변화에 따라 Ra의 값의 변화가 가장 큰 것을 확인할 수 있다. 따라서, 표면조도는 RPM에 대한 의존도가 가장 크며, 저속 이송 및 얇은 절입량을 가질 때 표면조도의 품질이 가장 좋은 것으로 판단된다.

Fx의 경우 3500 RPM, 이송량 0.05 [mm/rev], 절입량 0.03 [mm] 일 때 값이 가장 적게 예측된다. Fy는 2500과 3500 RPM, 이송량 0.05 [mm/rev], 절입량 0.08 [mm]에서 낮은값으로 예측한다. Fz는 RPM과 이송량의 변화에 따라 크게 변화하지 않는 것으로 예측되며, 절입량에 따라 크게 변화하는 것으로 판단된다.

하드터닝 공정에 대한 최적 조건은 Fig. 8과 같다. 표면 조도 및 절삭력을 함께 고려한 종합 만족도(Composite Desirability)가 최대가 되는 지점에 대한 최적 조건 예측을 실시하였다. 그 결과 RPM 3440, 이송량 0.0352 [mm/rev], 절입량 0.30 [mm]의 가공 조건을 가질 때, 표면조도는 0.202 μm를 가지는 것으로 예측된다. 절삭력의 경우, Fx 23.8 N, Fy 14.2 N, Fz 2.5 N으로 기존 실험 조건에 비해 절삭력은 낮아질 수 있는 것으로 판단된다.

4. 결론 및 향후계획

본 논문은 기 개발된 하드터닝 가공기의 최적 조건을 찾기 위해 반응표면분석법을 통해 최적화를 실시하였다. 표면조도(Ra) 및 절삭력(Fx, Fy, Fz)에 대한 회귀 모델을 각각 정의하였으며, 실험값은 예측 구간 내에 존재하므로 데이터는 유의했다. RPM은 표면조도에 가장 큰 영향을 미치며, 이송량 및 절입량은 절삭력에 대해 영향이 가장 컸다. 표면조도 및 절삭력에 대해 최소를 모두 만족 시키는 가공 조건은 RPM 3440, 이송량 0.0352 [mm/rev], 절입량 0.03 [mm]으로 분석된다. 이때의 표면조도는 약 0.202 μm로 예측되었다. 향후, 예측 정확성을 더 높이기 위해 본 데이터를 기반으로 딥러닝 알고리즘과 결합한 모델 연구가 필요하며 실제 현장에 적용하여 검증을 실시할 예정이다.

Acknowledgments

본 연구는 한국생산기술연구원 주관 티타늄/CGI 가공을 위한 액체질소 적용 극저온 가공 공정 및 시스템 개발연구(10048871) 및 고속 고정밀 기계장비의 메카트로닉스 최적화 기술 개발 연구의 일환으로 수행되었음.

REFERENCES

• Tang, L., Yin, J., Sun, Y., Shen, H., and Gao, C., “Chip Formation Mechanism in Dry Hard High-Speed Orthogonal Turning of Hardened AISI D2 Tool Steel with Different Hardness Levels,” The International Journal of Advanced Manufacturing Technology, pp. 1-16, 2017. [https://doi.org/10.1007/s00170-017-0667-5]
• Dogra, M., Sharma, V. S., Sachdeva, A., Suri, N. M., and Dureja, J. S., “Tool Wear, Chip Formation and Workpiece Surface Issues in CBN Hard Turning: A Review,” Int. J. Precis. Eng. Manuf., Vol. 11, No. 2, pp. 341-358, 2010. [https://doi.org/10.1007/s12541-010-0040-1]
• Sharma, V. S., Dhiman, S., Sehgal, R., and Sharma, S., “Estimation of Cutting Forces and Surface Roughness for Hard Turning Using Neural Networks,” Journal of Intelligent Manufacturing, Vol. 19, No. 4, pp. 473-483, 2008. [https://doi.org/10.1007/s10845-008-0097-1]
• Selvaraj, D. P., Chandramohan, P., and Mohanraj, M., “Optimization of Surface Roughness, Cutting Force and Tool Wear of Nitrogen Alloyed Duplex Stainless Steel in a Dry Turning Process Using Taguchi Method,” Measurement, Vol. 49, pp. 205-215, 2014. [https://doi.org/10.1016/j.measurement.2013.11.037]
• Davim, J. P. and Figueira, L., “Machinability Evaluation in Hard Turning of Cold Work Tool Steel (D2) with Ceramic Tools Using Statistical Techniques,” Materials & Design, Vol. 28, No. 4, pp. 1186-1191, 2007. [https://doi.org/10.1016/j.matdes.2006.01.011]
• Yang, W. P. and Tarng, Y., “Design Optimization of Cutting Parameters for Turning Operations Based on the Taguchi Method,” Journal of Materials Processing Technology, Vol. 84, No. 1, pp. 122-129, 1998. [https://doi.org/10.1016/S0924-0136(98)00079-X]
• Nayak, S. K., Patro, J. K., Dewangan, S., and Gangopadhyay, S., “Multi-Objective Optimization of Machining Parameters during Dry Turning of AISI 304 Austenitic Stainless Steel Using Grey Relational Analysis,” Procedia Materials Science, Vol. 6, pp. 701-708, 2014. [https://doi.org/10.1016/j.mspro.2014.07.086]
• Mia, M. and Dhar, N. R., “Prediction of Surface Roughness in Hard Turning under High Pressure Coolant Using Artificial Neural Network,” Measurement, Vol. 92, pp. 464-474, 2016. [https://doi.org/10.1016/j.measurement.2016.06.048]
• Bouacha, K. and Terrab, A., “Hard Turning Behavior Improvement Using NSGA-II and PSO-NN Hybrid Model,” The International Journal of Advanced Manufacturing Technology, Vol. 86, No. 9, pp. 3527-3546, 2016. [https://doi.org/10.1007/s00170-016-8479-6]