[ SPECIAL ]

Journal of the Korean Society for Precision Engineering - Vol. 34, No. 11, pp.771-779

ISSN: 1225-9071 (Print) 2287-8769 (Online)

Print publication date 01 Nov 2017

Received 24 Jul 2017 Revised 06 Sep 2017 Accepted 10 Oct 2017

DOI: https://doi.org/10.7736/KSPE.2017.34.11.771

모터입력전압 변화에 따른 백래시 비율의 영향 변화

백주현¹^{, #}

1LIG넥스원 기계연구소

The Change of the Influence of Backlash Ratio according to the Change of Motor Input Voltage

Joo Hyun Baek¹^{, #}

1Mechanical Engineering R&D Lab, LIG Nex1 Co., Ltd.

Correspondence to: ^#E-mail: drbaek100@naver.com, TEL: +82-31-8026-4840, FAX: +82-31-8026-7084

Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract

This paper investigated the influence of the backlash ratio on frequency response characteristic in servo systems with two-stage gear reducer, according to the change of magnitude of motor input voltage. The backlash ratio is defined as the ratio of the first gear stage backlash magnitude in relation to total backlash magnitude. This paper presents that the maximum anti-resonance and resonance frequency of the system can take place at the maximum backlash ratio if the motor input voltage of the system is large. On the other hand, if the motor input voltage is small, the maximum anti-resonance and resonance frequency of the system will occur at an arbitrary backlash ratio. In order to develop the geared servo system with fast response, it is effective to increase the maximum allowable motor input voltage and to reduce the magnitude of backlash on the second gear reduction stage.

Keywords:

Backlash ratio, Motor input voltage, Servo system, Anti-resonance frequency, Resonance frequency

키워드:

백래시 비율, 모터입력전압, 서보시스템, 반공진주파수, 공진주파수

1. 서론

최근 모터개발기술의 발전으로 기어감속기가 필요없는 직접구동방식의 모터를 사용한 서보시스템들이 많이 개발되고 있다. 그러나, 직접구동모터의 출력토크가 상대적으로 작아 설치공간 및 고토크를 요구하는 곳에는 아직까지 기어감속기를 사용한 서보시스템이 많이 사용되고 있다.

서보시스템의 속도제어 대역폭 및 성능은 모터 토크 입력에 대한 모터 각속도 출력에서 나타나는 시스템의 반공진 및 공진 주파수에 의해 제한을 받게 되며, 특히 반공진주파수는 시스템의 대역폭을 결정하므로 기어감속 서보시스템이 빠른 추종성과 응답성을 갖도록 하기 위해서는 높은 반공진주파수를 갖도록 만드는 것은 중요하다.^1-2 따라서, 설계단계에서 제작될 기어감속 서보시스템의 반공진주파수를 보다 정확히 예측하고, 기어감속 서보시스템의 반공진 및 공진주파수에 영향을 주는 인자들에 대한 연구가 필수적이다.

이와 관련 된 연구로서 Rue³는 기어감속 서보시스템의 구동부 강성과 부하 관성모멘트 등이 시스템 반공진 및 공진주파수에 큰 영향을 미침을 보고하였다. 그러나, 구동부 강성을 키워 반공진 및 공진주파수를 높이는 방법은 시스템 무게증가를 동반하여 무게제한을 받는 시스템에 적용하기 쉽지 않으며 시스템의 무게증가 없이 대역폭을 확장시킬 수 있는 적절한 방법은 시스템 백래시 크기를 줄이는 것이다.⁴

Baek, Hong, Yang, Kim과 Kwak⁴은 2단 기어감속 서보시스템에 있어서 각 단에 존재하는 백래시가 최종단에 만 존재한다는 가정 하에 반공진주파수에 미치는 백래시 영향이 사용하는 모터의 최대입력전압 크기에 따라 크게 달라질 수 있음을 보여주었고 대역폭을 높이기 위해 필요한 백래시 크기 감소량이 사용하는 모터의 최대입력전압에 따라 달라짐을 보여주었다.

Baek, Hong, Yang, Kim과 Kwak⁵는 모터 회전축 고정 시 최종 부하단에서 측정되는 전체백래시 크기가 동일할지라도 각 감속단에 존재하는 백래시 크기 조합이 달라짐에 따라 시스템의 주파수 응답특성에 나타나는 반공진 및 공진주파수가 크게 달라질 수 있음을 보여 주었으며 반공진주파수를 최대로 만들 수 있는 감속단의 최적 백래시 조합이 존재함을 보여주었다.

Baek, Hong, Kwak과 Kim⁶은 Baek, Hong, Yang, Kim과 Kwak⁵의 연구결과를 이용하여 2단 기어감속 서보시스템에서 전체백래시 크기를 아는 경우 각 감속단에 존재하는 기어 백래시 크기를 추정하는 방법을 제안하였다.

Baek⁷은 1단 기어감속 서보시스템에서 모터입력전압 크기를 낮추면 작은 기어 백래시 크기 변화에도 반공진 및 공진주파수가 크게 변화할 수 있음을 보고하였다.

그러나, 앞선 연구^1-7 모두 2단 기어감속 서보시스템에서 전체 백래시 크기가 동일할 때 모터입력전압이 달라짐에 따른 각 단 백래시 비율(Backlash Ratio) 변화가 반공진 및 공진주파수 변화에 미치는 영향에 대해서는 다루지 않았다. 이에 본 연구에서는 각 단 백래시 비율이 모터입력전압크기 변화에 따라 반공진 및 공진주파수에 미치는 영향을 관찰하는데 연구목적이 있다.

참고로 본 연구에서 사용된 전체백래시란 2단 기어감속 서보시스템에서 모터 회전축 고정 시 최종회전단에서 측정된 부하회전각을 의미하며, 백래시 비율이란 첫번째 감속단에 존재하는 백래시 크기가 전체백래시 크기에 차지하는 비율을 의미한다.

2. 모델링

본 연구에서 고려한 기어감속 서보시스템은 Baek, Hong, Kwak과 Kim⁶이 고려한 시스템과 유사한 시스템으로 방위각구동서보시스템(Azimuth Driving Servo System, ADSS)와 고각구동서보시스템(Elevation Driving Servo System, EDSS)의 2종류의 시스템을 각각 다루었다. 본 연구의 EDSS는 Baek, Hong, Kwak과 Kim⁶이 고려한 시스템과 동일하며, ADSS는 부하관성모멘트 J_L과 등가비틀림강성 k₂만 다르고 나머지 파라미터는 Baek, Hong, Kwak과 Kim⁶의 시스템 파라미터와 동일하다. 사용된 시스템의 구성도, 개략도, 모델, 블록선도 및 파라미터를 각각 Figs. 1-4와 Table 1에 나타내었다.

Fig. 1

The constitution diagram

Fig. 2

The structure and model of ADSS with a two-stage gear reducer

Fig. 3

The structure and model of EDSS with a two-stage gear reducer6

Fig. 4

Block diagram6

Table 1

Specifications for considered systems

2.1 ADSS의 모델

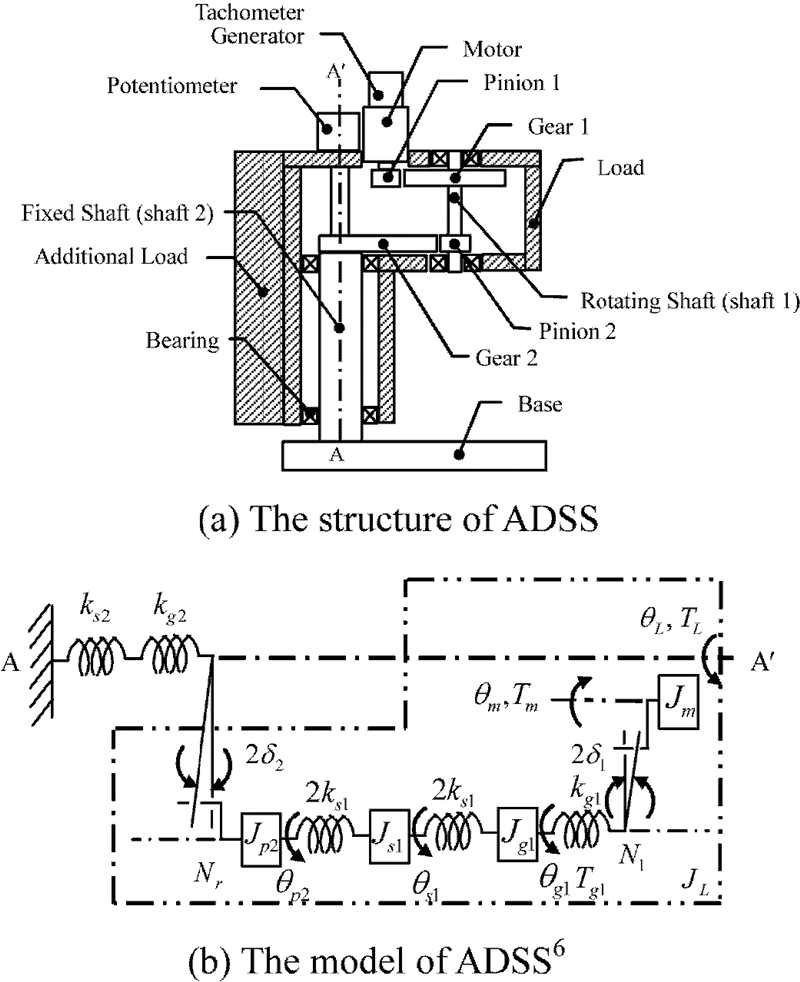
Fig. 2(a)은 본 연구에서 고려한 2단 감속 서보 시스템의 개략도이다. 고정축에 고정된 세그멘트 기어 2는 회전하지 않고, 피니언 2, 회전축, 기어 1, 피니언 1, 모터 및 베어링을 포함한 Fig. 2(a)에서 사선 친 부분이 $A A' ¯$ 축에 대해 회전한다.

각 회전축에 존재하는 베어링은 예압에 의해 간극 없이 각 축을 지지한다고 가정하였으며, 점성마찰 및 감쇠효과는 무시하였다. 이와 같은 가정 하에 얻어진 Fig. 2(a)에 대한 상세 모델은 Fig. 2(b)와 같다. 여기서 피니언 1과 기어 1은 각각의 관성모멘트와 하나의 비틀림스프링으로 모델링하였다.

피니언1의 관성모멘트는 모터 관성모멘트에 포함시켰으며, 기어 1측에 표현된 비틀림스프링은 피니언 1과 기어 1의 이 강성에 의해 생기는 비틀림강성로 표현하였다.⁸ 회전축의 경우 관성모멘트는 기어 1과 피니언 2사이의 회전축 길이 1/2되는 지점에 집중되어 있다고 가정하였으며, 비틀림스프링은 회전축 비틀림강성 값의 2배 인 비틀림스프링이 기어 1과 피니언 2에 각각 연결된 것으로 모델링 하였다.

그리고, 기어 2와 고정축은 회전하지 않으므로, 비틀림스프링만이 존재한다고 가정하였고, 이 물림에서 발생하는 백래시는 피니언 고정 시 회전하는 기어의 회전각으로 각각 표현하였다. 이점쇄선으로 묶은 부분은 Fig. 2(a)의 전체 회전부로 부하를 의미한다.

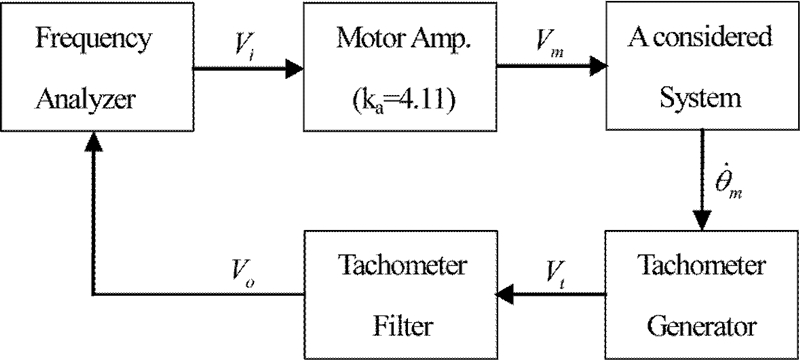
본 연구에서 고려된 서보시스템은 Fig. 1에 나타낸 바와같이 Fig. 2(a)의 세부구조, 모터전압증폭기 및 태코제너레이터 필터로 구성되어 있다.

모터전압증폭기는 모터에 입력되는 전압을 증폭하기 위해 사용되며, 엑추에이터로는 태코제너레이터가 부착된 영구자석 필드형 DC 모터가 사용되었다.

또한, 태코제너레이터의 출력전압을 필터링하기 위하여 2차 저역필터가 사용되었으며, 모터전압증폭기의 특성은 관심있는 주파수영역 전체에 걸쳐 일정하여 모터입력전압과 모터전압증폭기의 입력전압의 관계식은 다음과 같다.

V m = k a V i

(1)

또한, 엑츄에이터인 모터의 전기식 방정식은 다음과 같다.

L a d i a d t + R m i a + k b θ ˙ m = V m

(2-a)

T m = k t i a

(2-b)

그리고, 모터 회전 각속도를 측정하기 위해 사용된 태코제너레이터의 출력전압과 모터 회전각속도와의 관계는 다음과 같다.

V t = k t s θ ˙ m

(3)

테코제너레이더 필터를 통과한 테코제너레이터필터 출력전압은 다음과 같다.

V o (s) = G f (s) V t (s)

(4)

엑츄에이터로 사용된 모터의 운동방정식은 다음과 같다.

J m θ ¨ m + B m θ ˙ m = T m - T g 1 / N 1 - T f, m s i g n (θ ˙ m)

(5)

피니언 1과 기어 1사이의 백래시에 의해 기어 1에 전달된 토크는 다음과 같이 비선형 식으로 표현되며 이때 사용한 백래시 모델은 Nordin, Galic과 Gutman⁹의 연구논문에 수록된 데드존 모델을 사용하였다.

T g 1 = k g 1 (θ d 1 - δ 1), θ d 1 > δ 1 0, θ d 1 < δ 1 k g 1 (θ d 1 + δ 1), θ d 1 < - δ 1

(6)

여기서, ADSS의 첫번째 기어 감속단의 각 전달오차는 다음과 같다.

θ d 1 = θ m / N 1 - θ g 1

(7)

기어 1의 운동방정식은 다음과 같다.

J g 1 θ ¨ g 1 = T g 1 - 2 k s 1 (θ g 1 - θ s 1)

(8)

회전축 1의 운동방정식은 다음과 같다.

J s 1 θ ¨ s 1 = 2 k s 1 (θ g 1 + θ p 2) - 4 k s 1 θ s 1

(9)

피니언 2의 운동방정식은 다음과 같다.

J p 2 θ ¨ p 2 = 2 k s 1 (θ s 1 - θ s 2) - T L / N r

(10)

여기서, 피니언 2와 기어 2사이의 공전 감속비는 다음과 같다.

N r = N 2 + 1

(11)

부하 토크는 식(6)과 같이 피니언 2와 기어 2사이의 백래시에 의해 다음과 같이 표현된다.

T L = k 2 (θ d 2 - δ 2), θ d 2 > δ 2 0, θ d 2 < δ 2 k 2 (θ d 2 + δ 2), θ d 2 < - δ 2

(12)

여기서, 두번째 기어 감속단의 각 전달오차는 다음과 같다.

θ d 2 = θ p 2 / N r - θ L

(13)

또한, 기어 2와 고정축의 등가비틀림강성은 Chubb⁸에 의해 다음과 같이 표현된다.

k 2 = k g 2 k s 2 / k g 2 + k s 2

(14)

마지막으로, ADSS의 최종부하단 운동방정식은 다음과 같다.

J L θ ¨ L = T L - T f, L s i g n (θ ˙ L)

(15)

지금까지 유도한 식들로부터 모터전압증폭기 입력전압 V_i에 대한 태코제너레이터필터의 출력전압 응답 V_o을 얻을 수 있다.

그리고, 백래시 비율이란 정의에 따라 다음과 같다.

B a c k l a s h R a t i o = b 1 / N r / b t × 100 %

(16)

각 단의 백래시 크기와 전체 백래시 크기와의 관계를 살펴보면 다음과 같다.

b t = b 1 / N r + b 2

(17)

끝으로 각도 백래시 b_i와 δ_i와 관계는 다음과 같다.

d i = 36 0 ∘ δ i / π (i = 1,2)

(18)

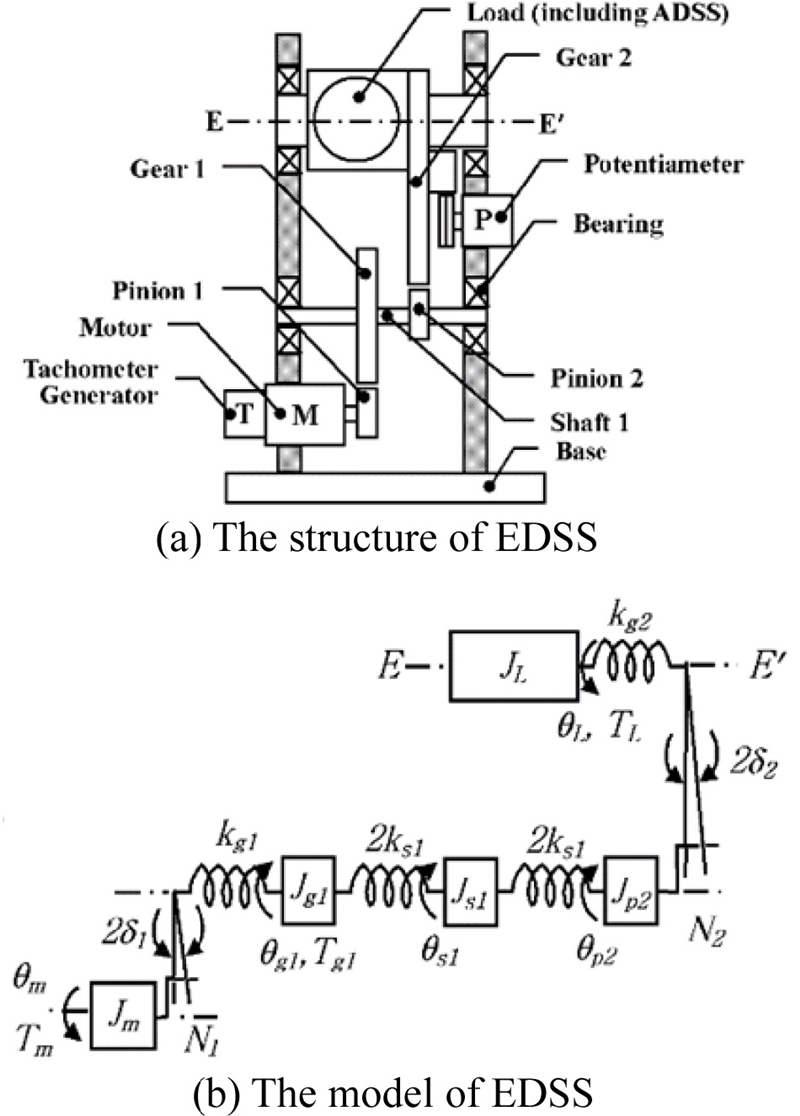
2.2 EDSS의 모델

Fig. 3(a)는 EDSS의 상세구조를 나타내며, 모델은 Fig. 3(b)와 같이 표현된다. 기어 2는 부하에 직접 부착되어 있으므로 기어 2의 관성모멘트는 부하 관성모멘트에 포함시키고 비틀림강성 만을 스프링으로 표현하였다. EDSS는 구조가 다소 다르긴 하나 ADSS와 동일한 모터전압증폭기와 태코제너레이터 필터를 사용하고 있으며 ADSS와 유사한 2단 기어감속구조를 가지므로 2.1절의 식(10)부터 식(14)와 식(16), 식(17)들을 다음 식(19)부터 식(23)들로 대체하면 EDSS의 운동방정식들을 구할 수 있다.

J p 2 θ ¨ p 2 = 2 k s 1 (θ s 1 - θ p 2) - T L / N 2

(19)

T L = k g 2 (θ d 2 - δ 2), θ d 2 > δ 2 0, θ d 2 < δ 2 k g 2 (θ d 2 + δ 2), θ d 2 < - δ 2

(20)

θ d 2 = θ p 2 / N 2 - θ L

(21)

B a c k l a s h R a t i o = b 1 / N 2 / b t × 100 %

(22)

b t = b 1 / N 2 + b 2

(23)

결국, 식(1)부터 식(9), 식(15), 식(19)부터 식(23)으로부터 모터 전압증폭기 입력전압 V_i에 대한 태코제너레이터 필터의 출력전압응답 V_o을 얻을 수 있다.

3. 시뮬레이션

ADSS와 EDSS 두 시스템에 있어 전체 백래시 b_t는 Table 1과 같이 각각 0.066º와 0.276º로 일정하게 두고 모터입력전압 크기 변화에 따른 백래시 비율 변화의 영향을 관찰하고자 한다.

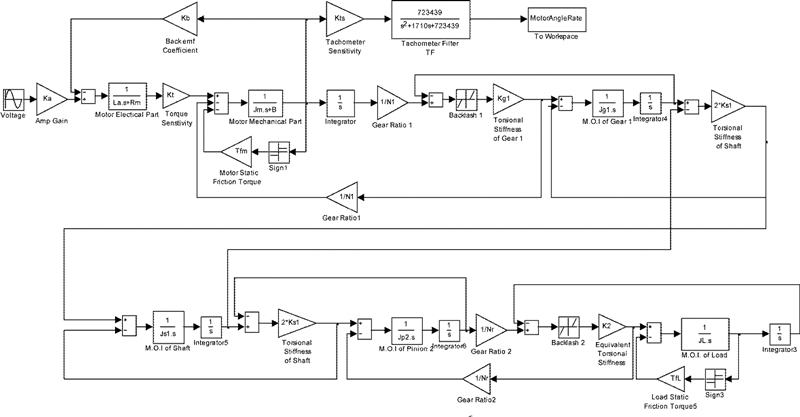
이것을 위해 2장에서 유도한 운동방정식들을 Fig. 4의 블록선도로 변환하였으며 각 가진주파수에 대한 시간영역 응답을 얻기 위하여 MathWorks사의 Matlab Simulink를 이용하였다.

시뮬레이션 조건으론 모터전압증폭기에 입력되는 정현파 전압의 피크 진폭을 증가시키고, 백래시 비율은 0%, 20%, 40%, 60%, 80%, 100%로 변경시켜가며 시뮬레이션 하였고, 샘플링 시간은 10 msec, 솔버로는 Runge-Kutta를 사용하였다.

정상상태응답을 얻기 위하여 각 가진주파수 별로 4초간 시뮬레이션 한 후, 초기 2초간의 데이터는 버리고 나머지 2초간의 데이터만을 취하여 가진 주파수 성분을 추출하는 주파수 분석을 수행하였다.

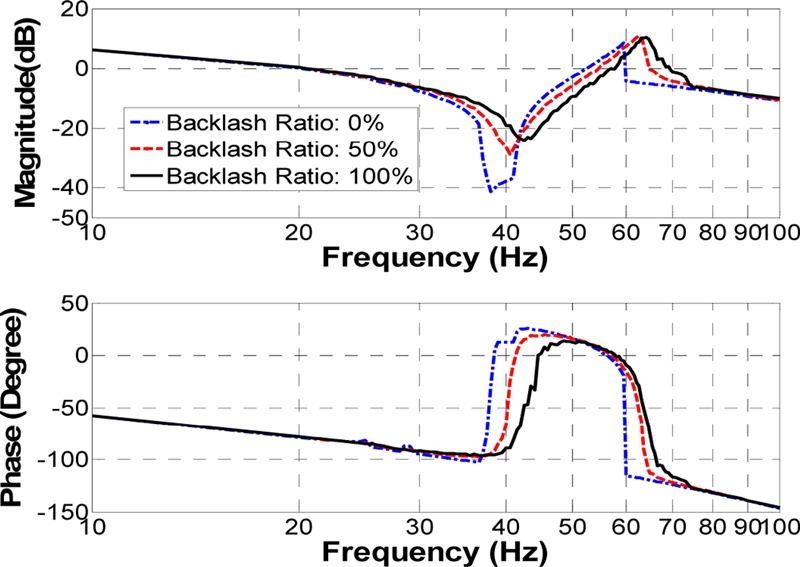
이와 같은 방법으로 얻어진 결과 중 모터전압증폭기 입력전압 V_i이 1.46 V_pk이고 백래시 비율이 0%, 50%, 100% 인 경우의 ADSS 보드선도를 Fig. 5와 Table 2에 나타내었다.

Fig. 5

The Bode diagram (Vo/Vi) of ADSS according to the change of backlash ratio when Vi is 1.46 Vpk

Table 2

Simulation results of ADSS according to the change of backlash ratio when Vi is 1.46 Vpk

Fig. 5와 Table 2을 보면 백래시 비율이 0% 일 때 보다 백래시 비율이 100% 일때 반공진주파수는 약 12%, 공진주파수는 약 8%가 커짐을 알 수 있다.

3.1 방위각구동서보시스템(ADSS)

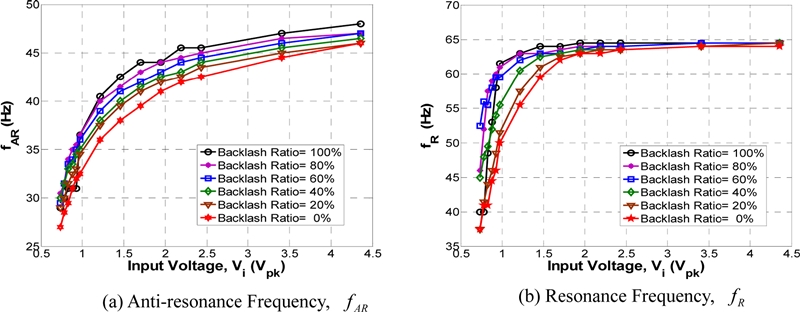
Fig. 6은 입력전압 V_i가 0.97 V_pk, 1.22 V_pk, 1.46 V_pk, 1.95 V_pk, 2.43 V_pk, 3.41 V_pk일때 ADSS의 반공진 및 공진주파수의 크기변화를 나타내며, 백래시 비율이 커질수록 반공진 및 공진주파수 값이 커지며 백래시 비율이 100%일 때 반공진 및 공진주파수가 최대가 됨을 볼 수 있다. 이것은 2단 기어감속 서보시스템에서 최종 부하단에서 측정되는 전체백래시 크기가 동일할지라도 가능하면 2번째 감속단에 존재하는 백래시 크기가 작아야 시스템이 넓은 속도제어대역폭을 가질 수 있음을 의미한다.

Fig. 6

The change of anti-resonance & resonance frequency of ADSS according to the backlash ratio when the input voltage Vi is between 0.97 Vpk and 3.41 Vpk

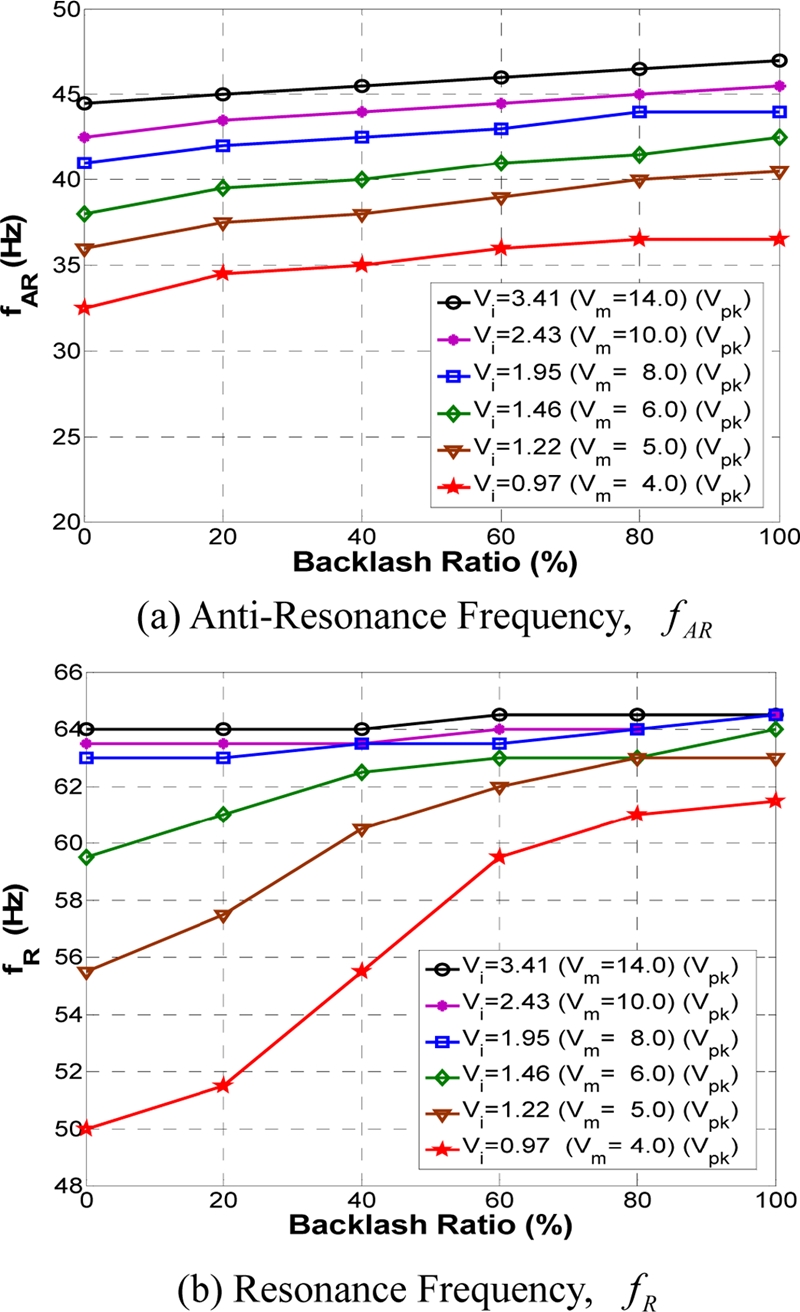
Figs. 7는 6에서 사용한 가장 낮은 전압 0.97 V_pk보다 낮은 입력전압인 0.73 V_pk, 0.78 V_pk, 0.83 V_pk, 0.88 V_pk, 0.93 V_pk일때 백래시 비율 변화에 따른 ADSS의 반공진 및 공진주파수변화를 나타내며 Fig. 6의 결과와 달리 백래시 비율이 100% 일 때 반공진 및 공진주파수가 최대가 되는 것이 아니라 각 입력 전압 별로 서로 다른 백래시 비율에서 반공진 및 공진주파수가 최대가 됨을 볼 수 있다. Figs. 6과 7의 결과를 통해 백래시 비율이 100%일 때 반공진 및 공진주파수가 최대가 되기 위해서는 본 시스템의 경우 모터입력전압 크기가 일정크기(V_i = 0.97 V_pk) 이상이 되어야 함을 알 수 있다.

Fig. 7

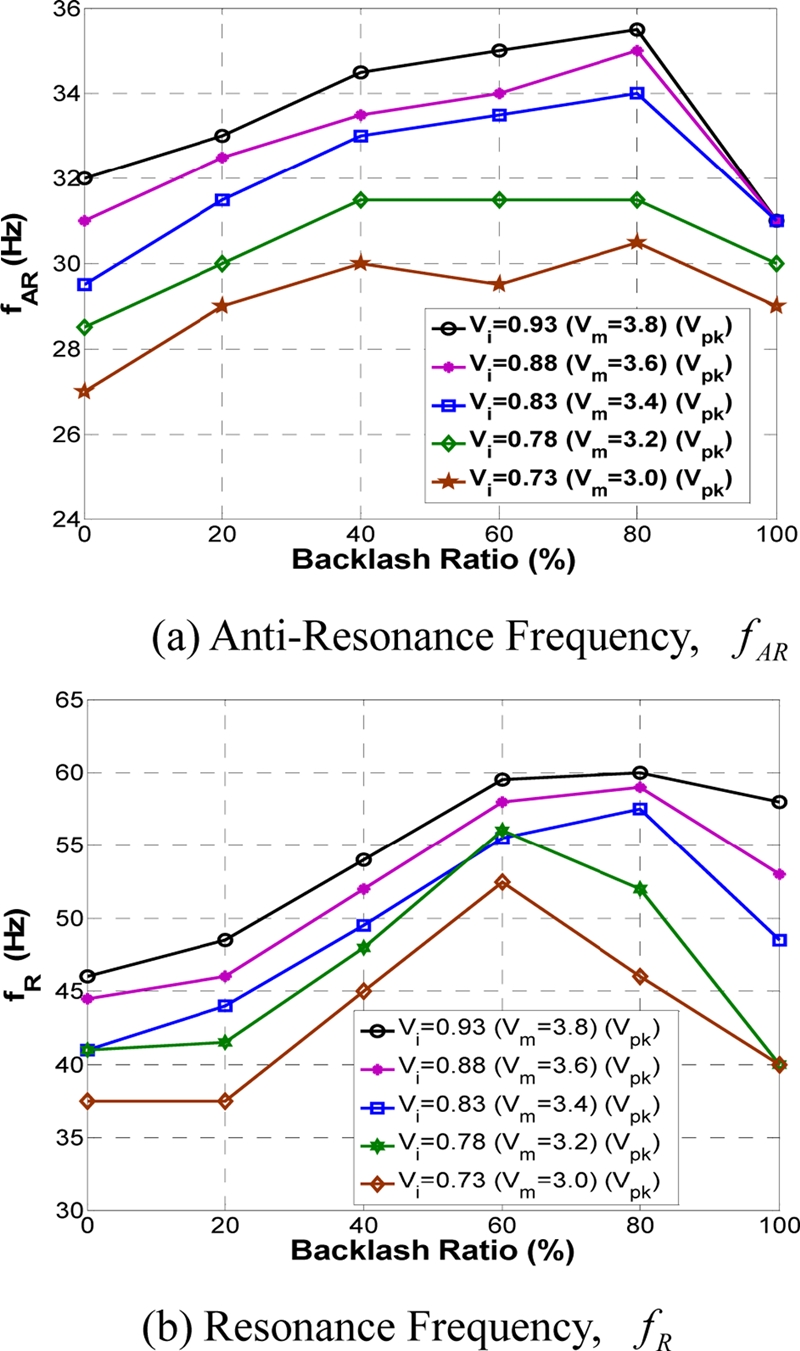
The change of anti-resonance & resonance frequency of ADSS according to the backlash ratio when the input voltage Vi is between 0.73 Vpk and 0.93 Vpk

Fig. 8은 입력전압 V_i 크기가 증가함 따라 ADSS의 반공진 및 공진주파수가 증가하는 모습을 보여주며, 일정크기(0.97 V_pk) 이상의 전압에서는 백래시 비율이 100% 일 때 반공진 및 공진주파수 크기가 최대가 됨을 볼 수 있다.

Fig. 8

The change of anti-resonance & resonance frequency ADSS according to the backlash ratio when the input voltage Vi is between 0. 73 Vpk and 4.36 Vpk

3.2 고각구동서보시스템(EDSS)

Fig. 9은 EDSS의 모터전압증폭기에 입력되는 입력전압과 백래시 비율에 따른 반공진 및 공진주파수 변화 모습으로 Fig. 6과 달리 백래시 비율이 커지더라도 반공진 및 공진주파수가 일정하게 커지는 현상을 관찰되지 않으며 각 입력전압 별로 반공진 및 공진주파수가 최대가 되는 백래시 비율이 서로 다름을 볼 수 있다.

Fig. 9

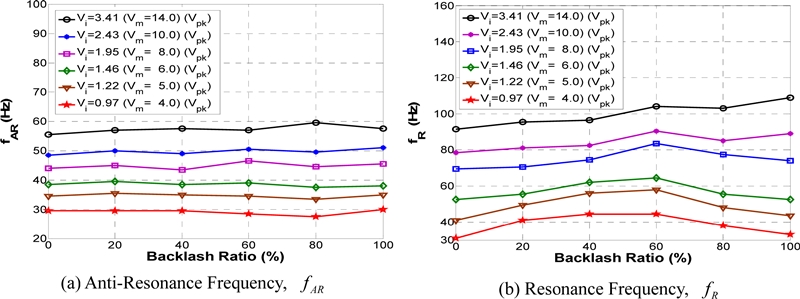
The change of anti-resonance & resonance frequency of EDSS according to the backlash ratio when the input voltage Vi is between 0.97 Vpk and 3.41 Vpk

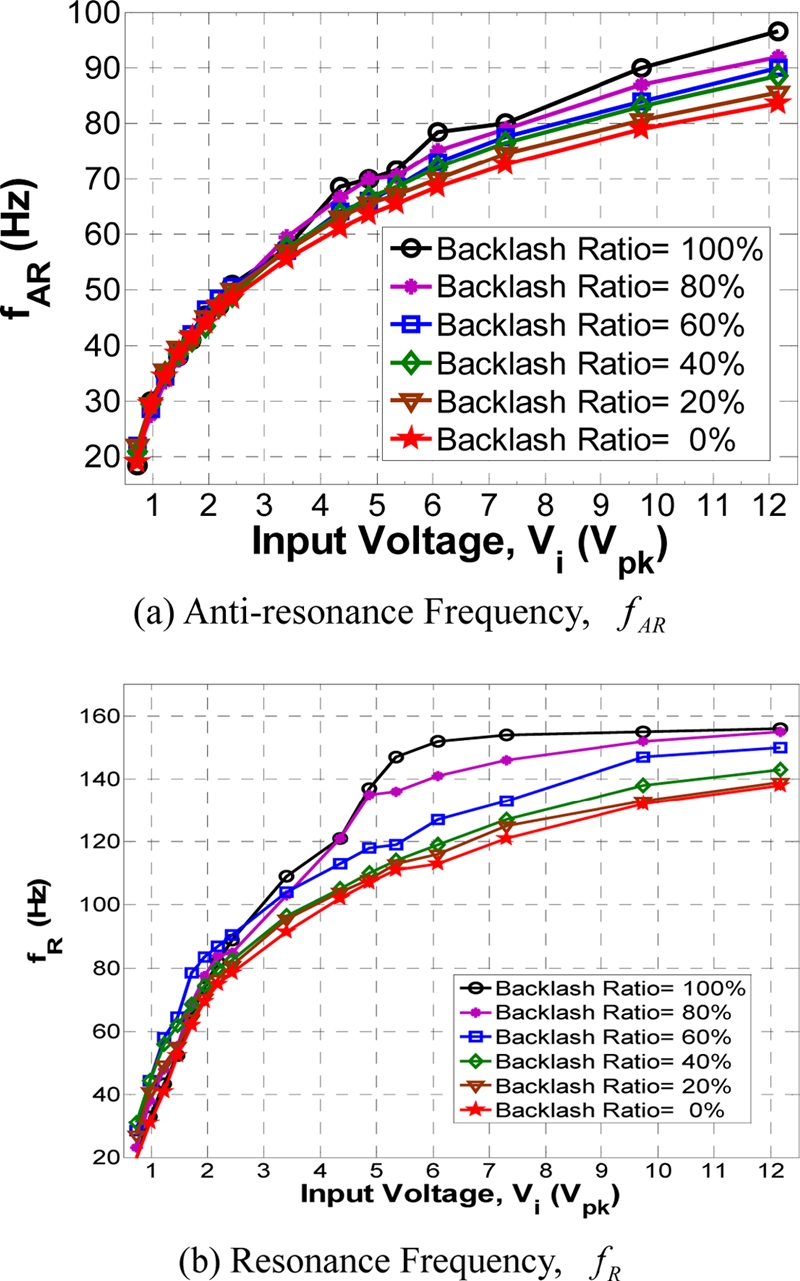
Figs. 9과 6이 서로 다른 현상을 나타내는 원인분석을 위해 ADSS와 EDSS 사용된 모터의 최대입력허용전압은 V_m = 17.9V_pk (V_i = 4.36 V_pk) 이나 EDSS 의 경우 모터에 입력되는 입력전압을 V_m = 20.0 V_pk (V_i = 4.87V_pk), 25.0 V_pk (V_i = 5.35 V_pk), 30.0 V_pk (V_i = 7.3 V_pk), 40.0 V_pk(V_i = 9.73 V_pk), 50.0 V_pk (V_i = 12.17 V_pk)로 증가시켜가며 시뮬레이션하여 그 결과를 Fig. 10에 나타내었다.

Fig. 10

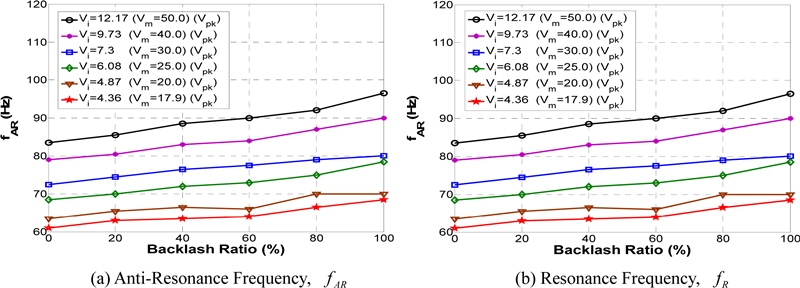
The change of anti-resonance & resonance frequency of EDSS according to the backlash ratio when the input voltage Vi is between 4.36 Vpk and 12.17 Vpk

Fig. 10는 입력전압 V_i가 충분히 커지면 Fig. 6의 결과와 마찬가지로 백래시 비율이 커질수록 시스템의 반공진 및 공진주파수가 커짐을 볼 수 있으며 Fig. 6과 마찬가지로 백래시 비율이 100%일때 반공진 및 공진주파수가최대가 됨을 볼 수 있다.

Fig. 11은 입력전압이 커짐에 따른 EDSS의 반공진 및 공진주파수의 변화이며 입력전압이 커짐에 따라 전체적인 반공진 및 공진주파수가 커짐을 볼 수 있으며, Fig. 8과 마찬가지로 일정크기 (V_i = 4.36 V_pk)이상의 입력전압에서는 백래시 비율이 100%일 때 반공진 및 공진주파수가 최대가 됨을 볼 수 있다.

Fig. 11

The change of anti-resonance & resonance frequency EDSS according to the backlash ratio when the input voltage Vi is between 0.97 Vpk and 12.17 Vpk

3.3 시뮬레이션 결과 고찰

Figs. 6과 10을 통해 전체백래시 크기가 동일한 2단 기어감속 서보시스템에 있어서 모터입력전압이 충분히 큰 경우에는 백래시 비율이 클수록 시스템의 반공진 및 공진주파수가 커진다는 것을 알 수 있었다. 여기서, 백래시 비율이 크다는 의미는 전체 백래시중 첫번째 감속단의 백래시가 크다는 것을 의미하며 다시 말해 2번째 감속단에 존재하는 백래시를 가능한 작게 해야 시스템 반공진 및 공진주파수가 커지며 시스템 응답성능이 향상될 수 있음을 의미한다. 모터입력전압이 큰 경우 첫번째 감속단에 존재하는 백래시가 반공진 및 공진주파수에 미치는 영향이 두번째 감속단에 존재하는 백래시 영향보다 상대적으로 작아지는 이유는 Baek⁷이 설명한 바와같이 모터입력전압이 커짐에 따라 첫번째 감속단의 각 전달오차진폭크기가 커져 첫번째 감속단의 백래시 영향이 두번째 감속단의 백래시 영향 보다 상대적으로 작아지는 것으로 판단된다.

반면에 Figs. 7 과 9와 같이 시스템에 따라 모터입력전압 크기가 작은 경우에는 반공진 및 공진주파수가 최대가 되는 백래시 비율이 별도로 존재하므로 반공진주파수를 최대로 하는 각 단 백래시 크기를 결정하는 것이 시스템 무게증가 없이 보다 빠른 응답성을 갖는 시스템 설계에 유리함을 알 수 있다. 백래시 크기를 조정하는 방법으로는 기어와 피니언의 회전축간 거리를 조정하거나 기어 치형 가공 시 정밀가공을 통해 백래시를 조정하는 방법이 있다.¹⁰

4. 결론

2단 기어감속 서보시스템에서 모터입력전압크기가 충분히 큰 경우에는 백래시 비율이 클수록 시스템 반공진 및 공진주파수가 커지나, 모터입력전압이 충분히 크지 않은 경우에는 반공진 및 공진주파수가 최대가 되는 각각의 백래시 비율이 존재하여 각 단 백래시 크기 결정 시 최적 백래시 비율을 고려할 필요가 있음을 알 수 있었다. 또한, 2단 기어감속 서보시스템 설계 시 시스템이 가능한 큰 모터입력전압을 갖도록 설계하고, 허용되는 전체백래시 크기가 정해진 경우 2번째 감속단에 존재하는 백래시를 가능한 작게 만드는 것이 보다 넓은 대역폭을 갖는 시스템 설계에 효과적임을 알 수 있었다.

NOMENCLATURE


B_m :	Viscous damping coefficient of motor (N·m/(rad/sec))
b₁ :	Angular backlash to be measured at the gear i(º) (i = 1, 2)
b_i :	Total backlash to be measured at the output stage (º)
f_AR :	Anti-Resonance Frequency (Hz)
f_R :	Resonance Frequency (Hz)
G_f(s) :	Transfer function of tachometer filter
i_a :	Motor current (A)
*J_g1, J_L, J_m, J_s1, J_p2 :*	Moment of inertia of gear 1, load, motor, shaft 1, and pinion 2 (kg·m²)
k₂ :	Equivalent torsion stiffness between gear 2 and shaft (N·m/rad)
k_a :	Gain of motor amplifier
k_b :	Back emf constant of motor (V·s/rad)
k_gi :	Torsion stiffness between pinion i and gear i (N·m/rad) (i=1, 2)
k_si :	Torsion stiffness of shaft i (N·m/rad) (i = 1, 2)
k_t :	Torque sensitivity of motor (N·m/A)
k_ts :	Tachometer sensitivity (V·m/rad)
L_a :	Inductance of motor (H)
N_i :	Gear ratio of pinion i and gear i (i = 1, 2)
N_r :	Revolution gear ratio between pinion 2 and gear 2
R_m :	Resistance of motor (Ω)
T_f,L, T_f,m :	Static friction torque of load and motor (N·m)
T_g1 :	Transmitted torque of gear 1 (N·m)
T_m, T_L :	Motor and load torque (N·m)
V_i :	Input voltage of motor amplifier (V)
V_m :	Input voltage of motor (V)
V_t :	Output voltage of tachometer (V)
V_o :	Output voltage of tachometer filter
δ_i :	Half the value of angular backlash to be measured at the side of gear i (rad) (i = 1, 2)
θ_di :	Angular transmission error of i_th stage (rad) (i = 1, 2)
θ_di, θ_L, θ_m, θ_p2, θ_s1 :	Rotation angle of gear 1, load, motor, pinion 2, and shaft 1 (rad)
sign(·) :	Sign of value in the parenthesis

Acknowledgments

본 논문은 2016년도 산업통상자원부 산업기술혁신사업 항공우주부품기술개발사업(과제번호: 10067095)의 연구비 지원으로 수행되었습니다.

REFERENCES

Bigley, W. J., “Wideband Base Motion Isolation Control via the State Equalization Technique,” Optical Engineering, Vol. 32, No. 11, pp. 2805-2811, 1993. [https://doi.org/10.1117/12.148097]
Bigley, W. J. and Rizzo, V. J., “Wideband Linear Quadratic Control of a Gyro-Stabilized Electro-Optical Sight System,” IEEE Control Systems Magazine, Vol. 7, No. 4, pp. 20-24, 1987. [https://doi.org/10.1109/MCS.1987.1105331]
Rue, A. K., “Precision Stabilization Systems,” IEEE Transactions on Aerospace and Electronic Systems, No. 1, pp. 34-42, 1974. [https://doi.org/10.1109/TAES.1974.307961]
Baek, J. H., Hong, S. M., Yang, T. S., Kim, S. H., and Kwak, Y. K., “A Study on the Bandwidth of Gear Reduction Servo System according to Backlash and Motor Supplied Voltage,” J. Korean Soc. Precis. Eng., Vol. 19, No. 6, pp. 119-127, 2002.
Baek, J. H., Hong, S. M., Yang, T. S., Kim, S. H., and Kwak, Y. K., “Frequency Response Characteristics of Two-Staged Gear Reduction Servo System according to the Backlash Contribution Ratio Variation of Each Gear Reduction Stage,” J. Korean Soc. Precis. Eng., Vol. 19, No. 5, pp. 103-109, 2002.
Baek, J. H., Hong, S. M., Kwak, Y. K., and Kim, S. H., “Backlash Estimation of a Seeker Gimbal with Two-Stage Gear Reducers,” Transactions of the Korean Society Mechanical Engineer A, Vol. 26, No. 10, pp. 2130-2141, 2002. [https://doi.org/10.3795/KSME-A.2002.26.10.2130]
Baek, J. H., “The Utilization of Frequency Response Characteristic for the Detection of Change of Backlash Magnitude,” Journal of the Korea Society for Simulation, Vol. 24, No. 3, pp. 45-54, 2015. [https://doi.org/10.9709/JKSS.2015.24.3.045]
Chubb, B. A, “Modern Analytical Design of Instrument Servomechanisms,” Addison-Wesley, 1967.
Nordin, M., Galic, J., and Gutman, P. O., “New Models for Backlash and Gear Play,” International Journal of Adaptive Control and Signal Processing, Vol. 11, No. 1, pp. 49-63, 1997. [https://doi.org/10.1002/(SICI)1099-1115(199702)11:1<49::AID-ACS394>3.0.CO;2-X]
Park, Y. C., “Mechanical Design,” Bosung, 2001.

Backlash ratio (%)	b₁ (°)	b₂ (°)	Anti-Resonance (dB/Hz)	Resonance (dB/Hz)
0	0	0.066	-41.3 / 38.0	8.5 / 59.5
50	0.346	0.033	-28.8 / 40.5	10.7 / 62.5
100	0.693	0	-24.1 / 42.5	10.3 / 64.0

Parameter	Unit	ADSS	EDSS
N₁	-	5.94	6.41
k_g1	(N·m/rad)	3.40E4	4.74E4
J_g1	(kg·m²)	2.34E-5	3.69E-5
k_s1	(N·m/rad)	22.8	1.54E2
J_s1	(kg·m²)	8.30E-8	2.04E-7
J_p2	(kg·m²)	2.21E-7	4.84E-7
N_r, N₂	-	10.5	7.75
k₂	(N·m/rad)	2.59E3	2.54E5
J_L	(kg·m²)	2.46E-2	1.44E-2
T_f,L	(N·m)	7.0E-3	7.1E-3
b_t	(Degree)	0.066	0.276
L_a	(H)	8.50E-4
R_m	(Ω)	4.1
k_b	(V·s/rad)	3.44E-2
k_t	(N·m/A)	3.49E-2
J_m	(kg·m²)	8.60E-6
T_f,m	(N·m)	1.40E-2
k_a	-	4.11
k_ts	(V·s/rad)	8.60E-2
B_m	(N·m/(rad/s))	1.6E-4
G_f(s)	-	$723439 s 2 + 1710 s + 723439$