수치 해석을 통한 비행체 내부 압력 예측과 실험적 검증
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
In this study, a numerical analysis for predicting the internal pressure of the flight vehicle system with relief valve and N2-injection type cooler was conducted to operate the system safely in an unsteady-state condition. By adopting an incompressible ideal gas equation to computational domain at each time step, internal pressure was calculated without iteration. To increase the accuracy of the numerical analysis results, numerical model was correlated by modifying the volume of the computational domain. To modify the volume of computational domain, internal pressure along time was compared with experimental results. It showed good agreement within system operating time. Air mass flow rate at the relief valve is calculated by interpolating the performance curve data. For accurate and rapid calculation of the internal pressure in an unsteady-state condition, time step size convergence study was conducted additionally. By using a correlated numerical model, Pcr of the relief valve is conducted to remain the flight vehicle system within an internal pressure range of 0.6-2.0 atm, in each flight profile. Finally, specific Pcr of relief valve was applied to the system and the experimental results showed that the internal pressure remained in a safe range.
Keywords:
Numerical analysis, Unsteady state, Flight vehicle, Relief valve, Internal pressure, Ideal gas equation키워드:
수치 해석, 비정상 상태, 비행체, 릴리프 밸브, 내부 압력, 이상 기체 상태 방정식1. 서론
다양한 고도 환경에서 운용되는 고기동 비행체는 급격한 대기압 변화를 경험하며, 이로 인해 비행체의 내부 장비 또한 급격한 대기압 변화에 노출될 수 있다. 이러한 대기압 저하는 비행체 시스템을 구성하는 각종 전자 장비, 특히 고전압으로 작동하는 송수신 장비(T/R Module)가 아크 방전(Arcing)을 일으키는 원인으로 작용할 수 있다. 따라서 대기압 조건에 민감한 시스템에는 극단적인 압력 변화로부터 내부 기압의 일정한 유지를 위한 기밀(Hermetic Seal) 설계가 적용되어 왔으며, 이를 통해 시스템은 다양한 고도 환경에서 다양한 운용 조건으로 안정적인 작동이 가능하다. 반면, 전자 장비의 집적화, 고발열 설계 적용으로 인해 전도를 통한 방열 설계뿐만 아니라 강제 냉각 방식의 설계 적용이 불가피해지고 있다. 뿐만 아니라 고기동 비행체는 심각한 운용 진동으로 인한 신뢰성 확보 차원에서 전자 장비에 대한 수냉식 방열 설계가 지양되기 때문에 냉각 가스 분사를 통한 냉각 방식이 종종 사용되고 있다. 지속적인 냉각 가스 분사는 시스템 내부 기압을 상승시키고, 내부 기압 상승은 외부 대기압과의 압력 차이를 증가시킨다. 이는 격벽 구조에 가해지는 하중 증가의 원인이 되며, 상황에 따라 1 atm(100 kPa) 이상의 압력 차이가 발생할 수 있기 때문에 이를 완화시키기 위한 벤트 구조 적용이 일반적인 설계 방법이다.1
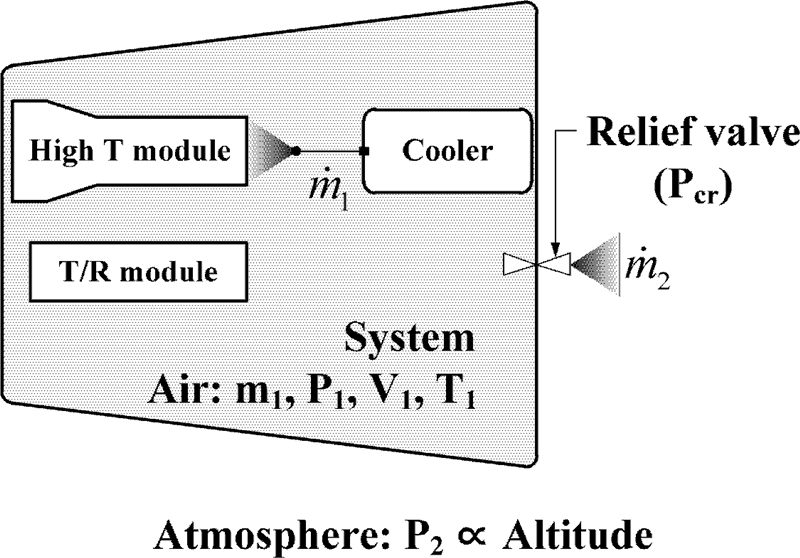
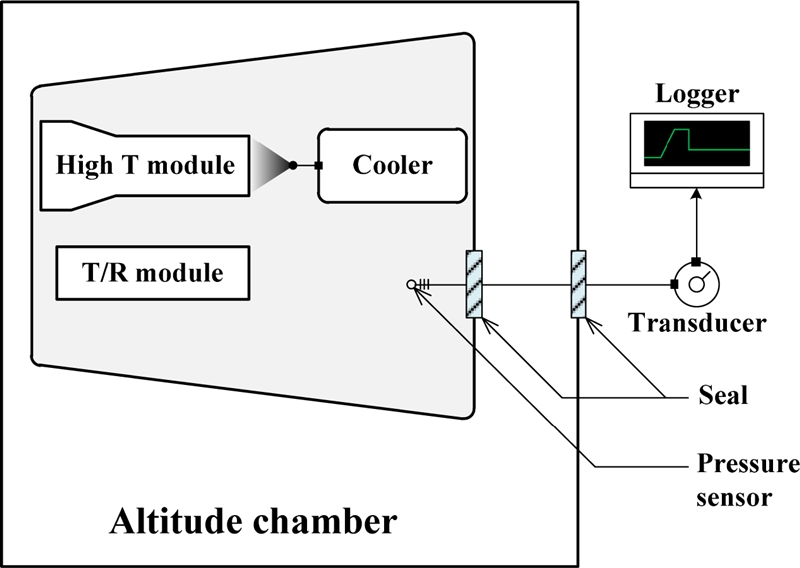
본 시스템에는 송수신 장비와 냉각 가스 분사 방식의 설계가 동시에 장착되어 있으며, 벤트(Vent) 구조가 바로 적용될 경우 압력이 급격하게 감소하는 고고도에서 내/외부의 기압이 동일해져 송수신 모듈의 안정성이 크게 저하될 수 있다. 따라서 릴리프 밸브(Relief Valve) 장착을 통해 시스템 내/외부 압력 차이가 적절한 크래킹 압력(Pcr)으로 유지되도록 하였으며, 그 개략도를 Fig. 1에 나타내었다. 릴리프 밸브를 통해 시스템과 내부 압력은 고고도에서도 크래킹 압력 이하로는 절대 감소하지 않기 때문에 크래킹 압력을 최소 송수신 기압 조건인 0.6 atm(60 kPa) 이상으로만 설정해도 아크 방전 문제는 발생하지 않는다. 하지만, 크래킹 압력이 필요 이상 높은값으로 설정될 경우 시스템 내부 압력이 과하게 높아져도 외부로 빠져 나가지 않아 구조 하중 증가로 인한 안정성 저하가 발생한다. 따라서 릴리프 밸브에 대한 적절한 크래킹 압력 설정이 시스템 안정성 확보를 위한 중요한 설계 변수가 된다.
릴리프 밸브를 적용한 시스템의 압력 예측 및 성능 분석은 항공 시스템, 특히 위성 발사체 연구 분야를 비롯한 자동차 분야에서 실험적, 해석적 방법으로 진행되어 왔다. Kim 등은 주유중 증발 가스의 효율적이고 안정적인 배출을 위한 릴리프 밸브 성능 분석을 해석적으로 진행하였다.2 Hwang 등은 FLUENT를 통한 열유동 해석으로 CNG 충전시 체크 밸브(Check Valve)에서의 결빙 현상을 예측하였고3, Jang 등은 위성 발사체에 적용되는 벤트-릴리프 밸브(Vent-Relief Valve)의 성능 최적화를 위해 FLUENT, AMESim의 해석적인 방법을 통한 분석을 수행하였다. 이를 위해 FLUENT에서는 릴리프 밸브의 실제 형상과 동일한 해석 모델 구축 및 격자 수렴성에 대한 검증을 선행하였으며, AMESim의 Vent-Valve Model 해석 결과와 비교하여 검증하였다4. Ok 등은 PLF 장비의 압력 조건 유지를 위해 상용 벤트 밸브 성능 검증 실험 후 그 결과를 격실의 압력 예측 프로그램에 입력하여 분석하였다.5 Ok 등은 추가로 벤트 밸브의 최적화 설계를 위해 단순화된 실험 용기로 벤트 Hole의 면적, 상대 위치 및 개수가 내부 압력에 미치는 영향을 실험적으로 확인하였다.6 상용 해석 프로그램과 실험을 통한 내압 예측은 형상 변경 시마다 발생하는 비용적, 시간적 비효율성이 증가하며, 암시적(Implicit) 방식으로 계산되는 상용 프로그램 해석은 많은 횟수의 반복 계산을 통한 수렴 과정이 필수적이다. 따라서 압축성 등엔트로피 관계식을 적용하여 지배 방정식을 단순화하고 적은 양의 반복 계산만으로 예측 값을 얻을 수 있는 연구도 진행된 바 있다.7-9 반면, 이러한 등엔트로피 관계식은 각 벤트에서의 유동 유출입을 직접 계산하지 않고 도메인 자체 열량과 온도 변화로부터 압력 변화를 계산하기 때문에 여러 지점의 벤트에서 유동 유출입이 일어나는 경우를 반영하기 어려운 단점이 있다.
본 연구에서는 다수 지점에서 공기 유출입이 동시에 일어날 때(냉각 가스 분사, 릴리프 밸브 배출) 시스템 내부 압력을 이상기체 상태 방정식으로 예측하고자 하였다. 릴리프 밸브 성능 곡선 모사, 실험 결과와의 비교 및 해석 모델 보정을 통해 계산 결과의 신뢰성을 확보하였으며, 보정된 해석 모델을 통한 사례 연구로 시스템 요구 사항을 만족시키는 릴리프 밸브의 운용 조건별 크래킹 압력을 선정하였다.
2. 본론
2.1 실험 및 해석 모델 보정, 검증
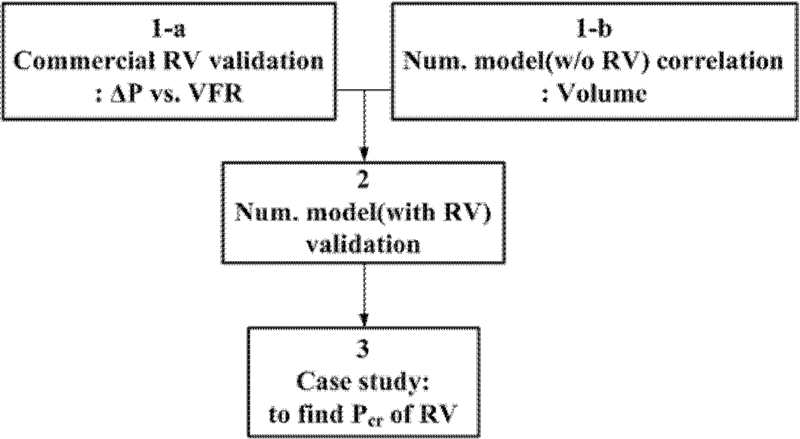
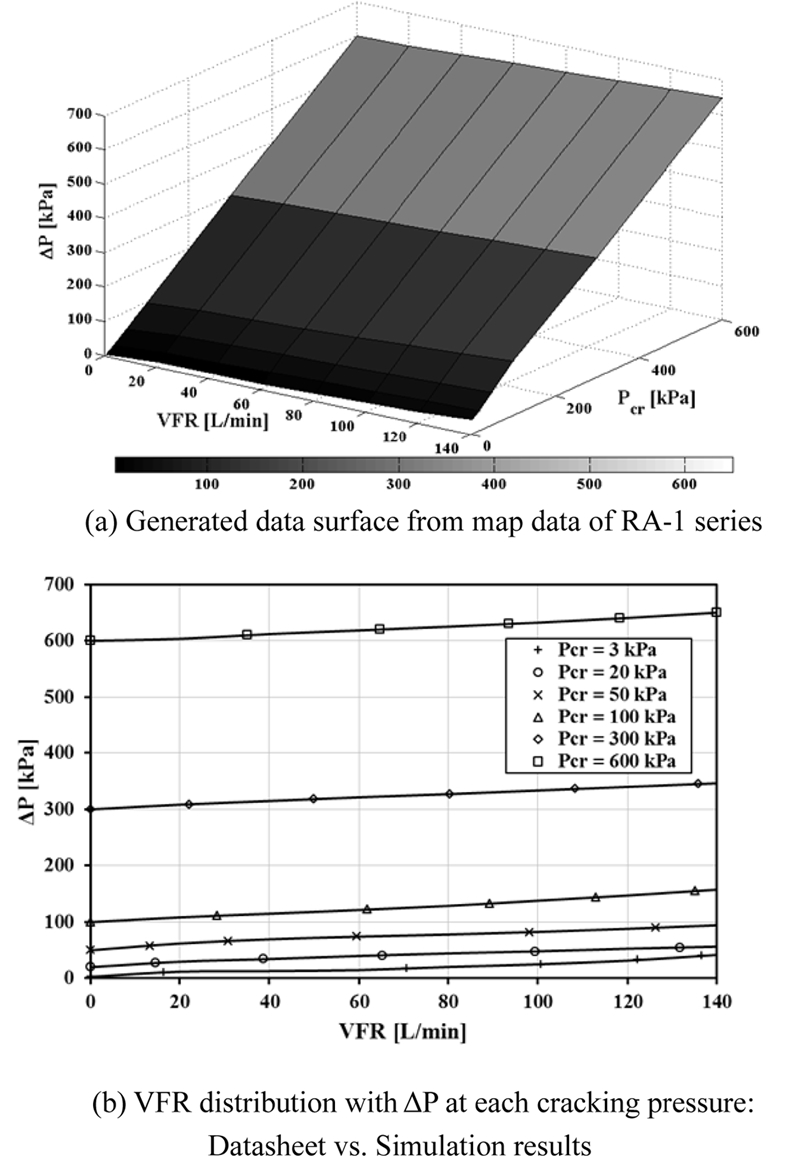
해석 모델의 신뢰성 확보를 통한 사례 연구 수행 프로세스를 Fig. 2에 나타내었다. 상용 릴리프 밸브의 압력 유지 성능을 정확하게 모사하기 위한 해석 모델 정확도 확인 후, 도메인 체적 보정을 통해 해석 신뢰성을 확보하였다. 체적 보정은 실험 결과의 오차 요인을 최소화하기 위해 릴리프 밸브가 장착되지 않은 형상에 대해 수행하였으며, 보정 이후 릴리프 밸브가 장착된 형상에 대한 최종 모델 검증을 실험과 비교하여 수행하였다. 검증된 해석 모델을 통해 다양한 환경에서 안정적인 시스템 운용이 가능하도록 릴리프 밸브 크래킹 압력에 대한 사례 연구를 수행하였다. 해석 모델을 통한 릴리프 밸브 성능 모사 결과를 Fig. 3에 나타내었다. Fig. 3(a)에는 공기를 유동 매질로 삼는 릴리프 밸브(IBS 社 RA-1 계열) 성능 곡선을 제조사 카탈로그10에서 추출 후 선형 보간하여 생성한 데이터 곡면을 나타내었고, 이로부터 임의 크래킹 압력에서의 압력 차이(ΔP)에 의해 계산된 유량(Volume Flow Rate, VFR)을 성능 곡선과 비교하여 Fig. 3(b)에 나타내었다. 릴리프 밸브의 성능 모사는 단순한 함수로부터 선형 보간되어 계산되기 때문에 결정 계수(Coefficient of Determination, R2) 0.99 이상의 정확도를 가지며 해석 모델 상에서 릴리프 밸브 성능은 거의 동일하게 모사됨을 확인할 수 있다. 또한 선형 보간된 데이터 곡면을 통해 카탈로그 에 명시되지 않은 크래킹 압력에서의 차압-유량 관계도 추가로 계산할 수 있음을 확인하였다.
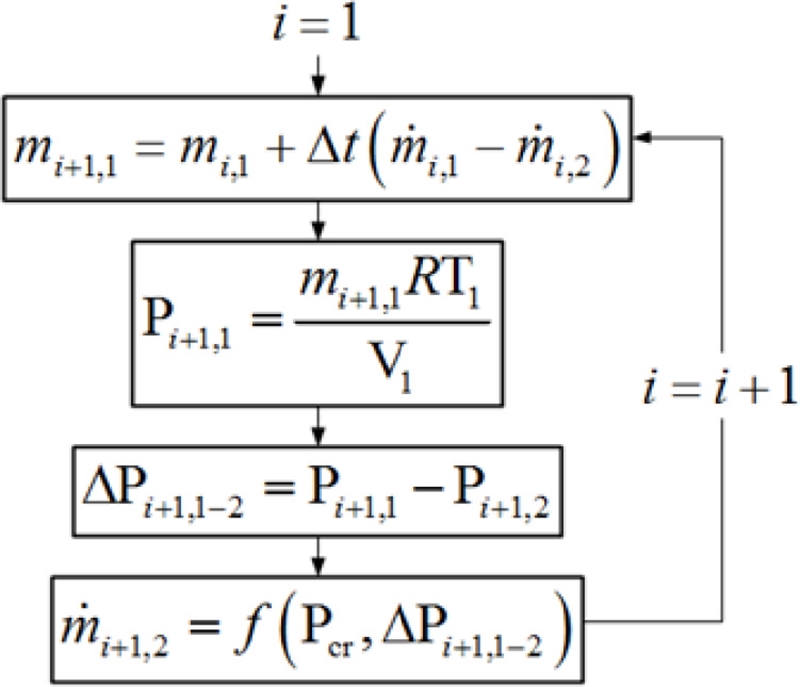
내부 압력의 비정상 상태 계산을 위해 해석 모델의 각 도메인에는 Fig. 4의 알고리즘이 적용되었다. 도메인 내부 공기는 미 군사 규격인 MIL-STD-810G에서 규정하는 고온 규격인 71°C로 유지되고 있으며11, 내부 기압도 최대 200 kPa 내에서 분포하기 때문에 이상 기체로 가정할 수 있다. 따라서 해석 상의 매 시간 도메인(Time Domain, i) 압력은 이상 기체 상태 방정식으로 계산될 수 있으며, 이 결과는 다음 시간 도메인(i+1)에서의 릴리프 밸브 양단의 압력 차이(ΔPi+1,1-2) 계산에 사용된다. 이 알고리즘을 사용하면 반복 계산을 통한 수렴이 필요 없으며 동시에 여러 지점에서의 공기 유출입을 계산할 수 있기 때문에, 등온 조건 가정 하에서 빠르고 안정적인 내부 압력 계산이 가능하다.
냉각 용기(Cooler)로부터 공급되는 질소 가스의 유량()은 운용 조건마다 시간에 따른 설정 값이 적용되며, 릴리프 밸브 양단 압력 차이에 의해 발생하는 유량()은 실제 성능 곡선과 거의 일치함을 확인하였다(Fig. 3). 이 때 내부 온도(T1)가 균일하게 유지되면, 도메인 내부 기압(Pi,1)에 영향을 미치는 유일한 변수는 이상 기체 상태 방정식에 의해 도메인 체적(V1)이 된다. 따라서 해석 도메인의 체적은 계산 신뢰성에 지대한 영향을 미치게 된다. 반면, 밀폐 시스템 내부에서 공기가 차지하는 체적은 실제 일정하지만 그 값을 산술적으로 정확히 계산하기는 불가능하다. CAD 기술의 발전으로 대략적인 값은 추정할 수 있지만, 케이블 및 전자 소자를 포함한 CAD에 반영되지 않는 형상들의 체적 계산이 어렵기 때문이다.
따라서 특정 형상과 환경 조건에서 실험을 통한 내압 측정 결과와 비교하며 해석 결과와의 오차를 최소화 시킬 수 있는 값으로 해석 모델 상의 체적 값을 보정해야 한다.
본 시스템의 내부 압력 측정 실험은 Fig. 5에 나타낸 것과 같이 고도 챔버 내에 구성하였다. 모델 보정 오차 최소화를 위해 릴리프 밸브는 제거하고 시스템을 밀폐시켰으며, 시스템 밀폐로 인해 외부 기압의 영향이 없기 때문에 외부 고도는 변화시키지 않고 대기압 상태에서 실험하였다. 냉각 가스는 두 단계로 나누어 분사되며, 초반 15초간 급속 냉각을 위해 약 0.6 g/s의 유량으로 분사한 후, 저온 유지를 위해 0.05 g/s의 유량으로 분사된다. 냉각 가스의 급속 냉각 구간은 운용 조건에 따라 달라지며, 급속 냉각 구간을 제외한 나머지 구간은 전부 저온 유지 구간에 해당한다.
체적 보정을 통한 해석 결과를 실험 결과와 비교하여 Fig. 6에 나타내었다. 공기 영역의 체적을 CAD로부터 산출(약 31.6 × 10-3 m3)하여 해석 모델에 적용 후 시스템 내압을 계산하면 Fig. 6(a)에 나타낸 것과 같이 실험 결과보다 상대적으로 낮은 증가 경향이 나타난다. 이는 CAD 상에서 생략된 케이블 및 커넥터 등 기타 구성품들의 체적 또한 전부 공기 체적으로 포함되도록 계산되어 동일한 유량의 질소 가스 유입에도 압력이 천천히 증가되었기 때문이다. 이를 피하기 위해 10% 감소한(약 28.7 × 10-3 m3) 공기 체적으로 사례 연구한 결과 Fig. 6(b)에 나타낸 것과 같이 실험 결과와 거의 동일하게 계산되고 있음을 확인하였다.
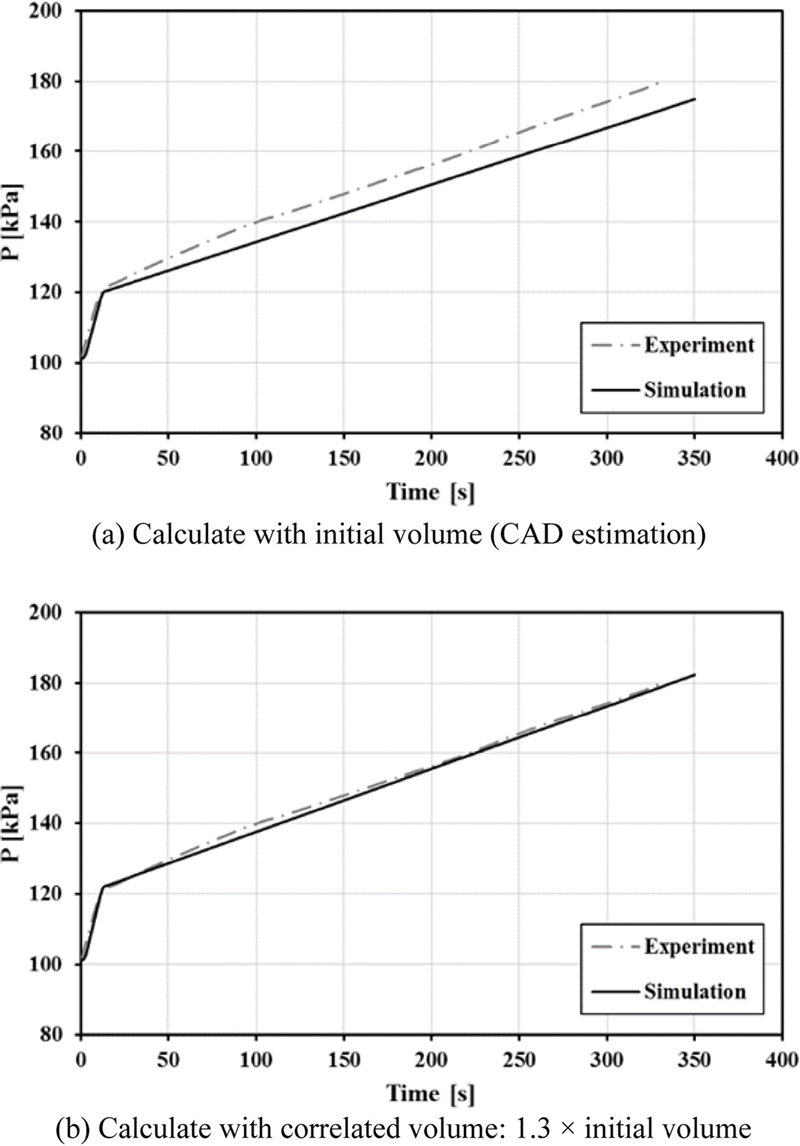
Internal pressure distribution with operating time: Experimental results vs. Simulation results (w/o relief valve)
따라서 해석 모델 상의 공기 체적은 28.7e-03 m3으로 고정하여 이후 해석을 진행하였으며, 최종 검증 단계로 릴리프 밸브가 장착된 형상에 대해 실험 및 해석을 수행한 후 그 오차를 확인하였다. 동일한 실험 구성(Fig. 5)에서 크래킹 압력 25 kPa로 설정된 릴리프 밸브를 시스템에 장착하여 특정 환경에서 수행하였다(Table 1).
고도 상승과 동시에 냉각 가스는 시스템 내부로 분사되며 90초간의 급속 냉각 구간을 지난 후, 운용 종료 시까지 유지 구간을 갖는다. 운용 시간 동안 시스템은 고도 20 km까지 상승하여 일정 시간 유지 후 하강하며, 고도가 변함에 따라 외부 압력도 함께 변한다. 이에 대한 실험 및 해석 결과를 Fig. 7에 나타내었다.
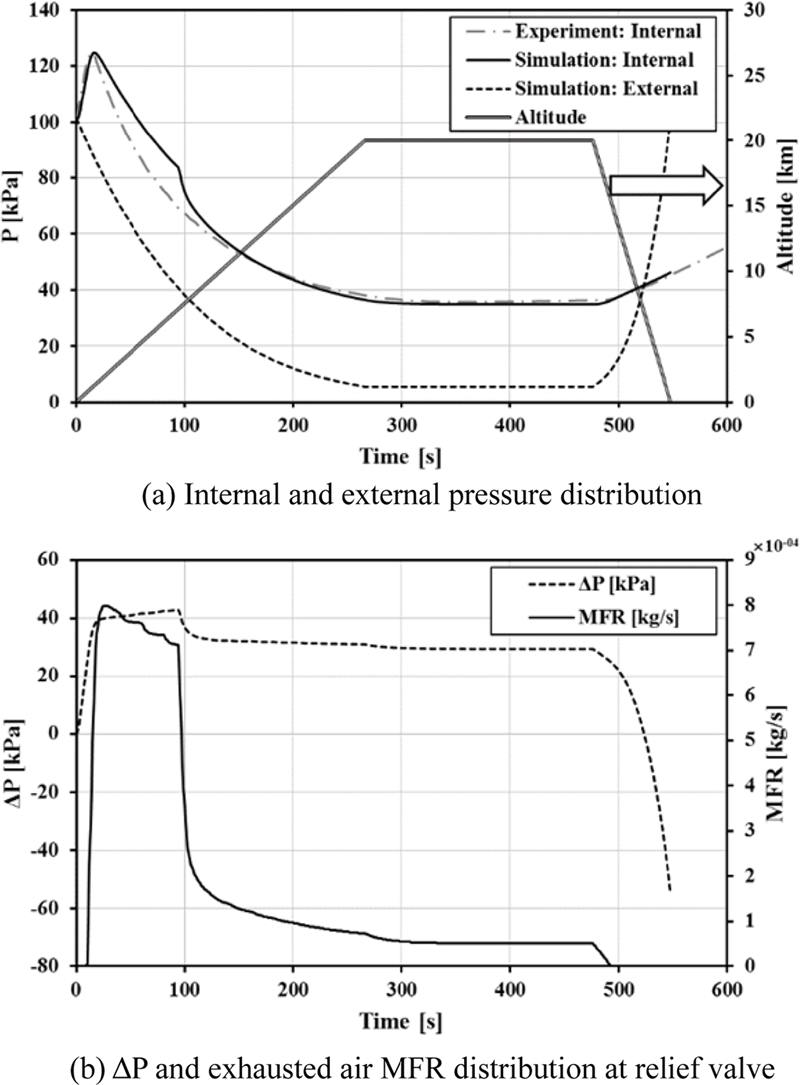
Simulation model validation by comparison of experimental results with simulation results (Pcr = 25 kPa)
Fig. 7(a)에서 해석 결과가 실험 결과를 매우 작은 오차로 모사하고 있음을 확인할 수 있다. 단, 냉각 가스 분사 모드 변경 시점(90초)에서 유량의 급격한 변화가 계단 함수(Step Function)로 반영된 해석 결과는 내부 압력 기울기 변화가 비연속적으로 나타나지만, 실험에서는 유량이 서서히 감소하기 때문에 이러한 현상이 나타나지 않는다. 외부 압력은 실험 시작과 함께 고도 증가로 인해 감소하지만, 내부 압력은 냉각 가스의 급속 냉각 모드(대용량 분사)로 인해 급격하게 증가하기 시작한다. 내/외부 압력 차이가 크래킹 압력인 25 kPa을 넘어서면서 릴리프 밸브가 개방되어 내부 공기가 배출되고 시스템 내부 압력은 조금씩 감소하기 시작한다. Fig. 7(b)에 내/외부 압력 차이 및 그에 따라 릴리프 밸브를 통해 배출되는 공기의 유량을 나타내었다. 급속 냉각 구간에서 냉각 가스 분사량은 매우 크기 때문에 내부 압력 감소율이 매우 더디지만 90초 이후 냉각 가스 분사가 유지 모드로 전환되면서 유량이 급격히 줄어들고 이로 인해 내/외부 압력 차이도 25 kPa에 빠르게 수렴해 간다.
300초 이후부터 냉각 가스 분사량과 릴리프 밸브를 통한 공기 배출량이 동일해지면서 시스템 내부는 평형 상태를 유지하게 된다. 고도 상승 이후 고고도 유지 구간이 지속되면서 내/외부 압력 차이는 크래킹 압력에 수렴하지만, 고도 하강과 함께 외부 압력은 100 kPa로 빠르게 회복되고, 이로 인한 내/외부 압력 차이 감소로 릴리프 밸브가 폐쇄되어 압력 차이는 음압으로 역전된다. 이 결과를 통해 밀폐 시스템에 대한 비정상 상태(Unsteady) 내부 압력이 이상 기체 상태 방정식을 통해 실험과 매우 유사하게 모사될 수 있음을 확인하였다.
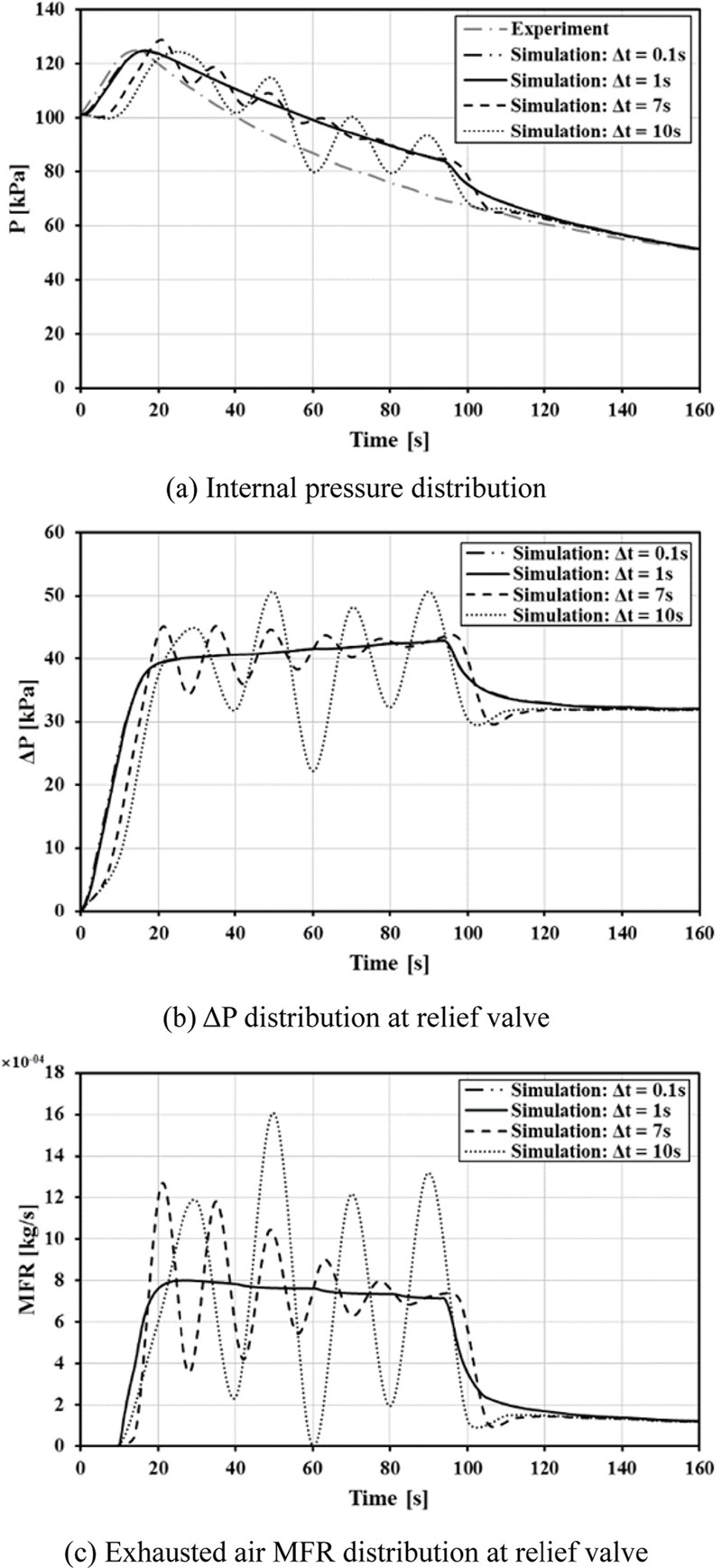
단, 해석 결과의 정확도는 시간 증분(Time Step Size, Δt)에 따라 크게 좌우될 수 있으며, 이를 확인하기 위해 시간 증분에 따른 수렴성 검증을 추가로 수행하였다. 각 시간 도메인에서 시스템에 유출입 되는 공기의 양은 Fig. 4에서 확인할 수 있듯이 시간 증분의 크기에 따라 계산되며, 시간 증분이 매우 큰 값으로 설정될 경우 한 시간 도메인에서 시스템 질량은 과다한 공기 유출입으로 인해 급격하게 증가하거나 감소한다. 이로 인해 시스템 내/외부 압력 차이는 급격하게 증가하며, 릴리프 밸브에서의 유량은 압력 차이로부터 결정되기 때문에 불규칙적인 유동 발생으로 인한 불규칙한 압력 변화가 발생하거나, 혹은 릴리프 밸브 성능 대비 과도 압력 차이가 발생할 경우 해석 자체가 발산하게 될 수 있다. 본 연구에서는 시간 증분 차이에 따른 외부와의 압력 차이, 릴리프 밸브에서의 공기 배출량 및 내부 압력을 계산하여 Fig. 8에 나타내었으며, 냉각 가스 유입량이 특히 큰 시간(0-160 s)에서 확인하였다.
시간 증분이 크게 설정 될수록 실험 시작과 함께 이전 시간 도메인과의 압력 변화가 크게 발생하며, 이로 인해 외부 대기압과의 압력 차이도 커지게 된다. 이는 릴리프 밸브를 통한 공기 배출량이 극단적으로 증가하는 원인이 되며, 이어지는 시간 도메인에서 내부 압력이 크게 감소하는 현상으로 이어진다. 결과적으로, 시간 증분이 크게 설정될 수록 한 시간 도메인에서 유출입 되는 공기의 질량이 크게 변화하며, 이는 큰 폭으로 변화하는 내부 압력, 내/외부 압력 차이 및 공기 배출량의 원인이 된다. 본 연구에서는 급속 냉각 구간에서 이 현상을 확연하게 확인할 수 있으며, 시간 증분이 1초 이하로 작아지면 해석 결과는 완전히 수렴하게 된다. 시간 증분은 해석에 소요되는 해석 시간과 정확도에 밀접한 영향을 주며, 그 효과는 서로 상충되기 때문에 해석 모델 보정시 최적의 시간 증분이 적용되었는지 반드시 확인되어야 한다.
2.2 사례 연구 및 실험
릴리프 밸브 성능 모사 정확도, 도메인 체적 및 시간 증분에 대한 검증이 완료된 해석 모델로 시스템 요구 규격 만족을 위한 사례 연구가 해석적으로 진행되었으며, 이를 위한 시스템 운용 조건, 요구 사항 및 크래킹 압력을 Tables 2와 3에 나타내었다.
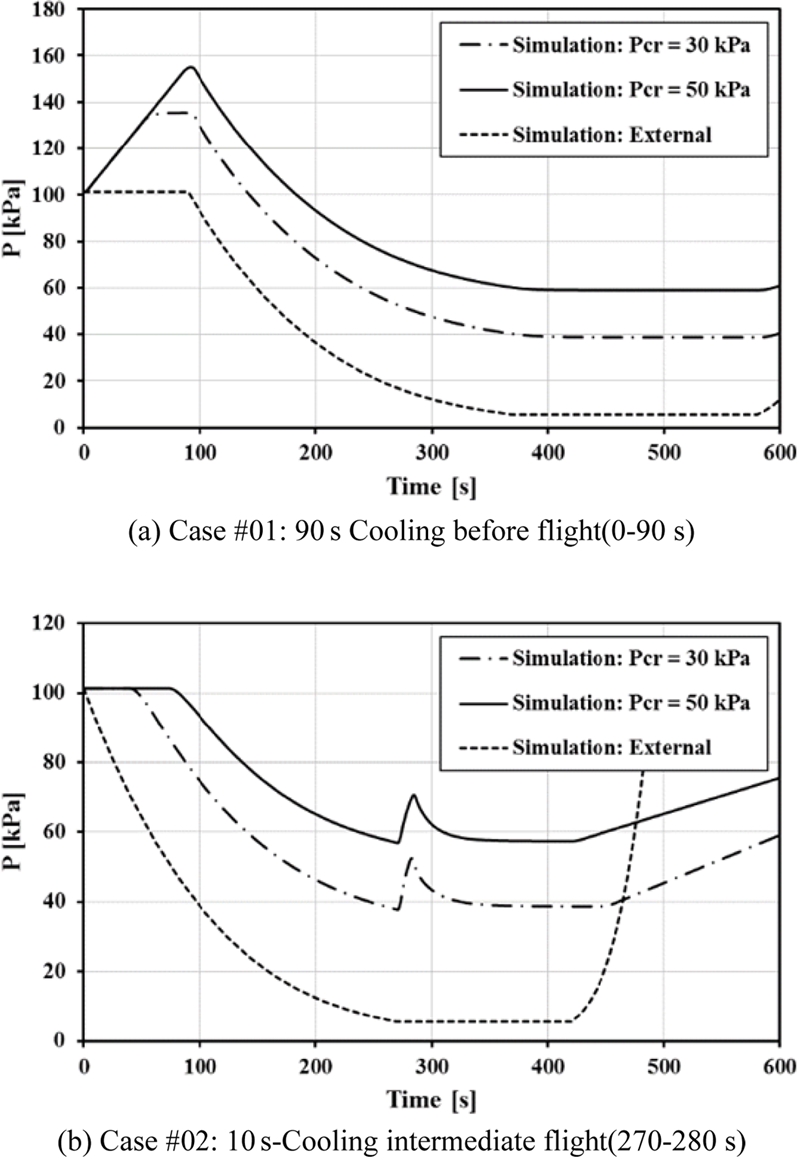
동일한 고도 환경 및 서로 다른 냉각 가스 운용 환경(분사 시점, 집중 냉각 시간)에서 송수신 장비의 운용 안정성(60 kPa 이상) 확보 여부 확인을 위해 릴리프 밸브의 크래킹 압력을 30 kPa과 50 kPa로 변경하며 계산하였고, 그 결과를 Fig. 9에 나타내었다.
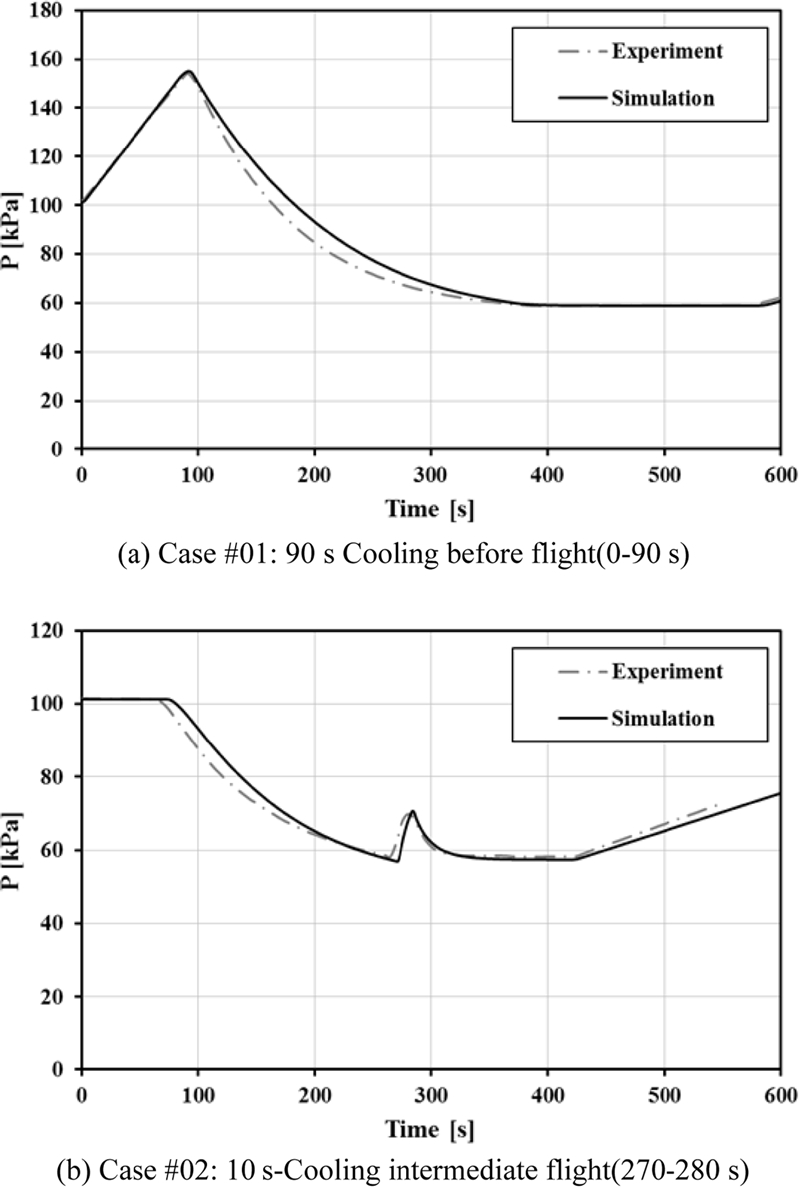
초기 급속 냉각 구간 및 고도 상승 구간에서는 크래킹 압력이 낮을수록 내부 공기 배출이 먼저 시작되며, 그 차이만큼 전 구간에서의 내부 압력이 낮아진게 된다. 고도 유지 구간에서 릴리프 밸브를 통한 공기 배출이 오랜 시간 진행되면서 내부 압력은 외부 대기압과 크래킹 압력의 합에 수렴하며, 이로부터 시스템이 고 고도에서 일정 시간 이상 유지될 경우 시스템 내부 압력 은 크래킹 압력에 절대적인 영향을 받고 있음을 확인할 수 있다. 따라서 외부 대기압이 약 5.5 kPa(고도 20 km, 표준 대기압)로 유지되고 있는 환경에서 크래킹 압력을 30 kPa로 설정할 경우 시스템 내부 압력은 두 운용 조건 모두에서 송수신 시점(600초) 요구 규격인 60 kPa에 도달하지 못하는 반면, 크래킹 압력이 50 kPa로 설정될 경우 60 kPa 이상 유지할 수 있음을 확인할 수 있다. 단, 이러한 성능은 릴리프 밸브의 공기 배출 용량이 충분하여 고도 유지 구간 내에서 평형 상태에 이를 수 있을 때 가능하기 때문에 적절한 성능의 릴리프 밸브 선정이 필수적이다. 본 시스템에는 50 kPa의 크래킹 압력이 설정된 릴리프 밸브를 적용하여 송수신 장비 안정성을 확보하고자 하였으며, 장착 후 실제 운용 실험을 수행하고 그 결과를 Fig. 10에서 해석 결과와 함께 비교하였다. 두 운용 조건 모두 해석 결과가 실험 결과를 유사하게 예측하고 있으며, 수치 해석으로부터 선정된 크래킹 압력을 통해 시스템 요구 규격이 만족되었음을 확인하였다.
3. 결론
본 연구에서는 비행체 전자 장비의 안정적인 운용을 위해 필요한 시스템 내부 압력 조건 확보를 목적으로 릴리프 밸브를 적용하였고, 릴리프 밸브 크래킹 압력에 따른 운용 조건별 내부 압력을 수치 해석적으로 분석하였다.
해석 결과의 신뢰성 확보를 위한 모델 보정은 다음 절차에 따라 수행하였다.
(1) 릴리프 밸브 성능 모사: 릴리프 밸브 성능 모사를 위한 Map Data 및 성능 예측 함수 생성
(2) 해석 도메인 체적 보정: 사전 실험 결과와 가장 유사한 결과를 갖는 도메인의 체적 도출 및 해석 모델 적용
(3) 시간 증분 최적화: 시간 증분에 따른 해석 결과 수렴성 비교 및 계산 시간 대비 정확도를 최대화시킬 수 있는 시간 증분 최적화 및 해석 모델 적용
보정된 해석 모델에 의한 사례 연구 결과 고도 유지 구간의 존재로 인해 내부 압력은 릴리프 밸브 크래킹 압력에 지배적인 영향을 받고 있음을 확인하였다. 모든 운용 조건에서 송신 장비 생존 요구 규격을 만족하는 크래킹 압력을 도출하였으며, 도출된 크래킹 압력이 적용된 릴리프 밸브를 시스템에 장착하여 실험한 결과 해석 결과와의 오차가 매우 작으며, 요구 규격 또한 만족시킬 수 있음을 확인하였다.
NOMENCLATURE
| m : | Mass |
| : | Mass flow rate |
| P : | Static pressure |
| R : | Ideal gas constant of air |
| T : | Static temperature |
| V : | Volume |
| ΔP : | Pressure difference |
| Δt : | time step size |
SUBSCRIPTS
| i : | Time domain |
REFERENCES
- NASA Space Vehicle Design Criteria (Structure), “Compartment Venting,” NASA SP-8060, 1970.
- Kim, S. H. and Lee, J. C., “An Analytical Investigation on Fluid Dynamics of Filler Neck Check Valve for On-Board Refueling Vapor Recovery,” J. Korean Soc. Precis. Eng., Vol. 20, No. 10, pp. 105-111, 2003.
- Hwang, Y. G., Park, T. J., Song, M. G., and Kang, B. R., “Thermal Flow Analysis of Check Valve for Hydrogen Refueling,” Proc. of KSPE Spring Conference, pp. 767-768, 2008.
- Jang, J. S., Koh, H. S., Han, S. Y., and Lee, K. W., “Analysis of Dynamics Characteristics and Performances of Vent-Relief Valve,” Journal of the Korean Society of Propulsion Engineers, Vol. 15, No. 6, pp. 70-77, 2011.
- Ok, H. N., Koh, J. Y., and Kim, I. S., “Prediction of the Pressure Drop in the Payload Fairing of a Launch Vehicle Considering Performance of the Vent Valves,” Proc. of the Korean Society for Aeronautical & Space Sciences Annual Conference, pp. 149-152, 2006.
- Ok, H. N., Ra, S. H., Choi, S. H., and Kim, I. S., “Analysis of Measurement of Pressure Drop in a Compartment through Vent Holes,” Aerospace Engineering and Technology, Vol. 4, No. 1, pp. 150-161, 2005.
- Ok, H. N., Kim, I. S., Ra, S. H., and Oh, B. S., “Design of Vent Holes on the Nose Fairing of a Launch Vehicle,” Proc. of 5th Symposium of Space Launch Vehicle Technology, pp. 305-310, 2004.
- Ok, H. N., Kim, I. S., Ra, S. H., and Oh, B. S., “A Study on the Prediction Methods of Pressure Drop in a Compartment through a Vent Hole,” Proc. of the Korean Society of Mechanical Engineers Annual Conference, pp. 160-160, 2004.
- Ok, H. N. and Kim, I. S., “Development of a Vent Analysis Method for Multiple Compartments Connected through Multiple Ports,” Proc. of the Korean Society for Fluid Machinery Annual Conference, pp. 547-550, 2006.
- IBS Inc., http://www.ask-ibs.jp/english, (Accessed 19 OCT 2017)
- MIL-STD-810G, http://everyspec.com/MIL-STD/MIL-STD-0800-0899/MIL-STD-810G_12306, / (Accessed 19 OCT 2017)