Analysis of the Stiffness and Fatigue Life of Double-Row Angular Contact Ball Bearings
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
This paper presents an analysis of the stiffness and fatigue life of double-row angular contact ball bearings (D-ACBBs). To this end, a comprehensive quasi-static model was developed for D-ACBBs subjected to five degree-of-freedom (DOFs) loading and displacement. The model was verified by a commercial computational program. A rigorous numerical investigation was performed, based on the developed model regarding the effects of external load, rotational speed, axial clearance, bearing arrangement, and angular misalignment on the stiffness and fatigue life of the D-ACBB. The D-ACBB was subjected to negative axial clearance and yielded improved performance in terms of fatigue life and stiffness. The effect of angular misalignment on the bearing fatigue life was found to be significantly dependent on the amount of axial clearance. The moment stiffness of the D-ACBB in a back-to-back arrangement was higher than the face-to-face arrangement owing to the increased effective load center distance, whereas the radial stiffness and fatigue life were almost unchanged for back-to-back and face-to-face arrangements.
Keywords:
Double-row angular contact ball bearing, Stiffness matrix, Contact load, Angular misalignment, Axial clearance, Fatigue life키워드:
복열 각접촉 볼베어링, 강성행렬, 접촉하중, 각 어긋남, 축방향 클리어런스, 피로 수명1. Introduction
Rolling element bearings are extensively used in a variety of industrial machines. Even though single-row rolling bearings can be used in many cases, double-row bearings can also be employed as a comparative solution in the case where space is crucial. A double-row ball/roller bearing often requires lesser assembly space in comparison to a single-row bearing with the same rigidity or load capacity.
High-speed rotating systems, such as spindle systems, employ angular contact ball bearings because of high precision, as well as sustainability against both axial and radial loading.1,2 While single-row angular contact ball bearings (S-ACBB) have attracted increased attention from researchers, prior work on double-row angular contact ball bearing (D-ACBB) has been limited. The D-ACBB consists of solid inner and outer rings, and ball and cage assemblies. The structure of the D-ACBB is similar but narrower than that of a pair of S-ACBBs.3 This means that a smaller space would be required for the D-ACBB with a similar mechanical performance. In addition, owing to the bearing structure with the rows of balls arranged in pairs, the D-ACBB can support loads in both axial directions. It is therefore particularly suitable for applications that require rigid axial guidance, such as pumps, agricultural machinery, conveying equipment, elevators, and compressors.4
Modeling of a D-ACBB has been simply approximated by two equivalent S-ACBBs attached next to each other. However, this approximation may result in several problems. One of the noticeable problems relates to the determination of the exact amount of loads acting on each S-ACBB when they are mounted close to each other. In addition, the stiffness matrix of a D-ACBB may not be obtained by simply superposing the stiffness matrices of two S-ACBBs but may need additional calculations. This study developed a five degree-of-freedom(DOF) model for D-ACBB.
Unlike single-row bearings that have been extensively studied, research studies on double-row bearings have been limited. Bercea et al.5 developed several quasistatic models for the double-row tapered roller, spherical and cylindrical rollers, and angular contact ball bearings. However, they did not formulate the bearing stiffness matrix. Petersen et al.6 proposed a two-DOF quasi-static model for a double-row bearing considering the raceway defect. However, in their model, they only provided formulae for translational stiffness elements, which were determined by superposing the stiffness matrices for each row. Mikkola et al.7 and An et al.8 reported a three-DOF model of double-row spherical roller bearings considering the staggered and aligned arrangements of rollers. Zhou et al.9 also developed a three-DOF model for a double-row self-aligning ball bearing by calculating only the diagonal stiffness elements. Gunduz and Singh10 presented a five-DOF model for D-ACBBs that can provide a fully occupied stiffness matrix. However, in their model, they did not account for several important factors, such as the inertial loading of the rolling element, axial clearance, and angular misalignment. Lostado et al.11 used a finite element method (FEM) to estimate the contact stresses in double-row tapered roller bearings. A fairly comprehensive model for double-row cylindrical roller bearings was recently presented by the authors.12
From the literature review, it is evident that there have been very few studies on the mechanical performance of D-ACBBs, especially regarding angular misalignment and axial clearance. In this study, a quasi-static model is developed for D-ACBBs. The bearing is subjected to five-DOFs loading and displacement. The model verification was made by comparing the calculated stiffness, displacements, and basic reference rating life, under various loading conditions, with those obtained by the commercial computational code.13 An extensive numerical study was then carried out regarding the effect of the external load, rotational speed, axial clearance, row arrangement, and angular misalignment on the stiffness and fatigue life of D-ACBB. The elicited results were comprehensively discussed herein.
2. Modeling of D-ACBB
2.1 Bearing Equilibrium
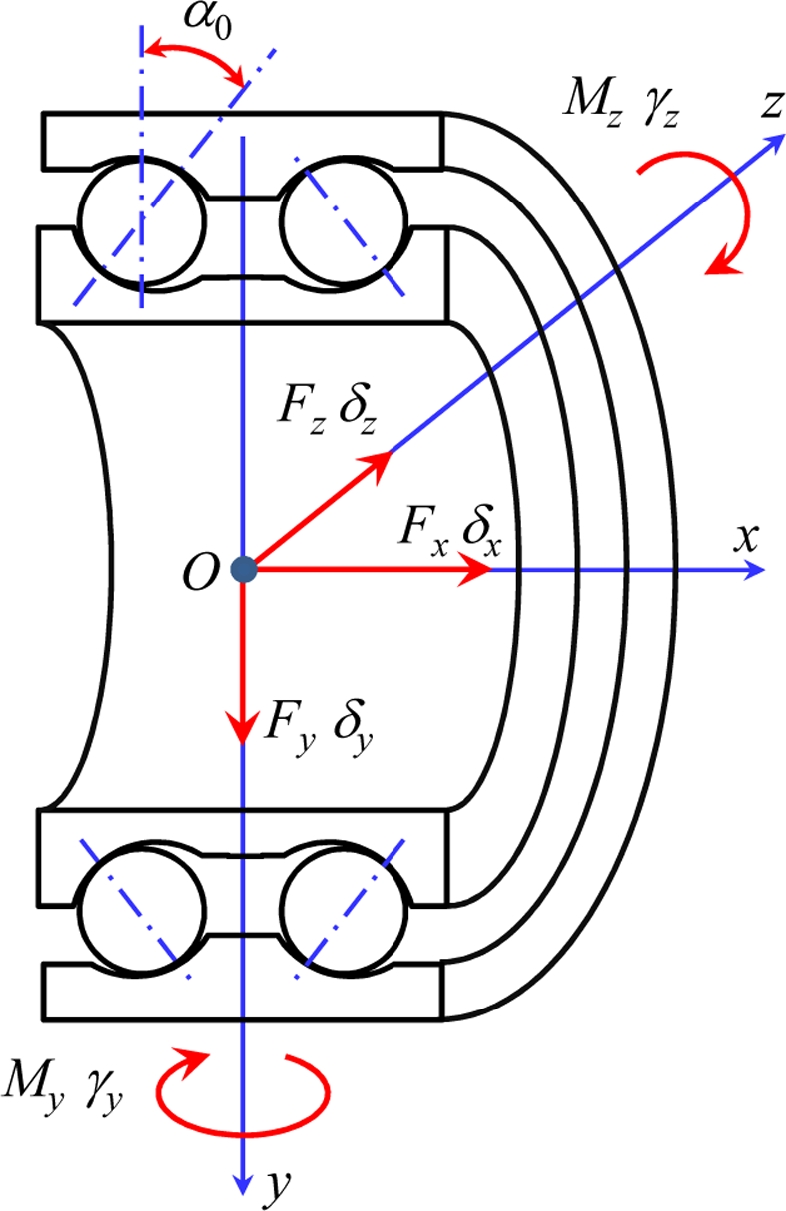
Fig. 1 shows the global coordinate system, loading, and displacements of a D-ACBB. The inner ring load and displacement vectors, {F} and {d}, are respectively represented by
| (1) |
| (2) |
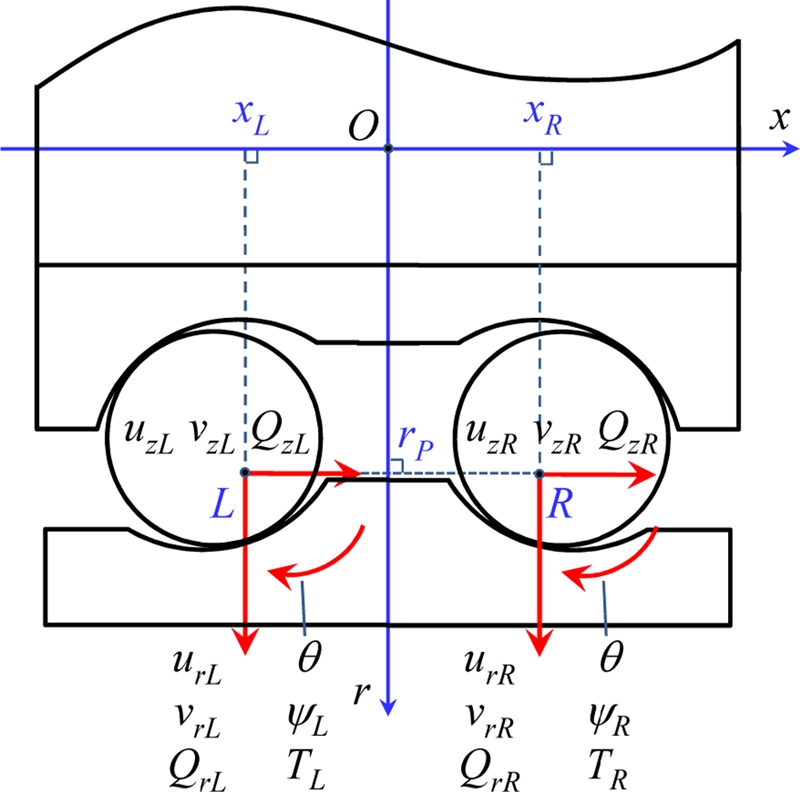
Fig. 2 shows the loads and displacements of the inner ring and ball defined at the inner ring cross-section of a typical ball. Because a bearing consists of two rows, without loss of generality, two local coordinate systems are introduced for a specific ball in accordance to (rm, fm, z), where m = L, and R represent the left and right rows, respectively. The displacement vectors of the inner ring on the left and right cross-sections are defined at the reference points, which coincide with the inner raceway groove centers (L and R), as
| (3) |
The inner ring contact load vectors of left and right rows are written by
| (4) |
The corresponding displacement vectors of balls at the left and right rows are
| (5) |
The relationship between the global and local displacements of the inner ring is described by
| (6) |
where [Rϕm] represents the transformation matrix for the left and right rows, which can be expressed as follows:
| (7) |
| (8) |
where ϕm is the location angle of the ball. xL and xR are the distances from the bearing’s center to the reference points of the left and right rows, respectively.
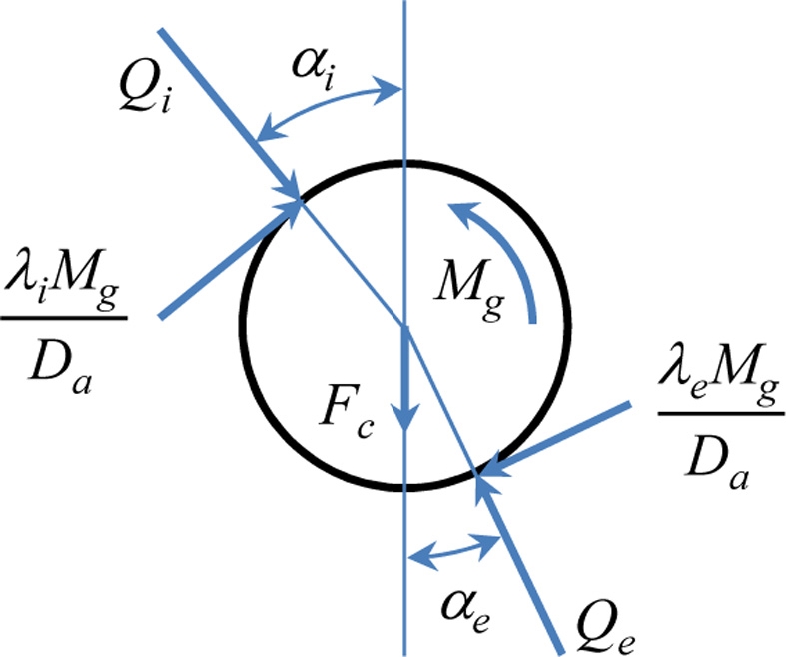
Fig. 3 shows the free-body diagram of a ball, in which the contact forces are represented by Qa. Herein, a = i, e represents the inner and outer rings. Qa can be determined by using the well-known Hertzian contact formula.14 Fc and Mg are the centrifugal force and gyroscopic moment acting on the ball, respectively, which can be determined as described in.14 The equilibrium equations of the ball are then expressed as
| (9) |
where li and le indicate the distribution parameters for the gyroscopic moment, which, in this study, are assumed to be identical on both raceways, li = le = 1. Da and a indicate the ball diameter and contact angle, respectively. The determination of α was described by de Mul et al..15 The above equations are subsequently solved to estimate the ball displacement vector, {vm}, and the ball-ring contact forces. Because these equations are nonlinear, this study uses the iterative Newton–Raphson method as the computational algorithm. The inner ring contact load is found as
| (10) |
Having obtained the inner ring contact loads for all the balls, the global equilibrium equations of the inner ring can be found by taking the summation of the external loads and all inner ring contact loads, as follows:
| (11) |
where j indicates the ball index. Z represents the number of balls for each row. The Newton–Raphson method is employed to solve the global equations of the inner ring required to estimate the global displacements of the bearing, {d}. The bearing stiffness matrix can be derived analytically via the Jacobian matrix of the global equilibrium equations for double-row cylindrical roller bearings, as described in.14
2.2 Bearing Fatigue Life
The fatigue life of a rolling bearing is conventionally defined as the number of revolutions of a bearing until the first appearance of flaking on one of its rings or rolling elements. The bearing’s fatigue life has been predicted statistically based on the theory proposed by Palmgren.16 It is well known that even identical bearings operating under identical conditions may have different fatigue lives.17 The fatigue life of D-ACBBs presented in this study is the basic reference rating life (L10r) that represents an estimated value of fatigue life with a probability of 90%.
To consider more general loading conditions—including the effects of angular misalignment, combined loads, and axial clearance—this study determined the bearing fatigue life based on the ISO16-281 standard.18 In this case, the contact forces of all the rolling elements are required, which are found by using the presented five-DOF quasi-static model. First, the basic dynamic radial load rating of bearing Qc should be determined, which represents the influence of the internal dimensions of the bearing. Details of calculating Qc are presented in.18 Next, the dynamic equivalent rolling element load Qe is determined. Qe reflects the effect of loading conditions on the bearing fatigue life in accordance to
| (12) |
| (13) |
Finally, the basic reference rating life of D-ACBB can be found as follows:
| (14) |
3. Numerical Results
Using the analytical model presented above, this section presents numerical results for a sample bearing. The relevant model parameters are listed in Table 1.
3.1 Model Verification
The calculated stiffness, displacement, and fatigue life of D-ACBB using the proposed model were compared with those elicited using commercially available codes.13 The bearing clearance e and rotational speed n were selected as 0 μm and 1000 rpm, respectively.
Fig. 4(a) shows the displacement of the bearing as a function of the radial load Fy. Subject to the radial loads imposed on the bearing, only radial displacements are induced, which gradually increased as the radial load increased. Fig. 4(a) demonstrates that the calculated radial displacement agrees well with that estimated based on the commercial code. Figs. 4(b)-4(d) depicts the stiffness values of the D-ACBB as a function of radial load. The diagonal stiffness elements are displayed for comparison purposes. Figs. 4(b)-4(d) clearly indicates that the stiffness values of the presented model and commercial code are in a very good agreement for all radial loads.
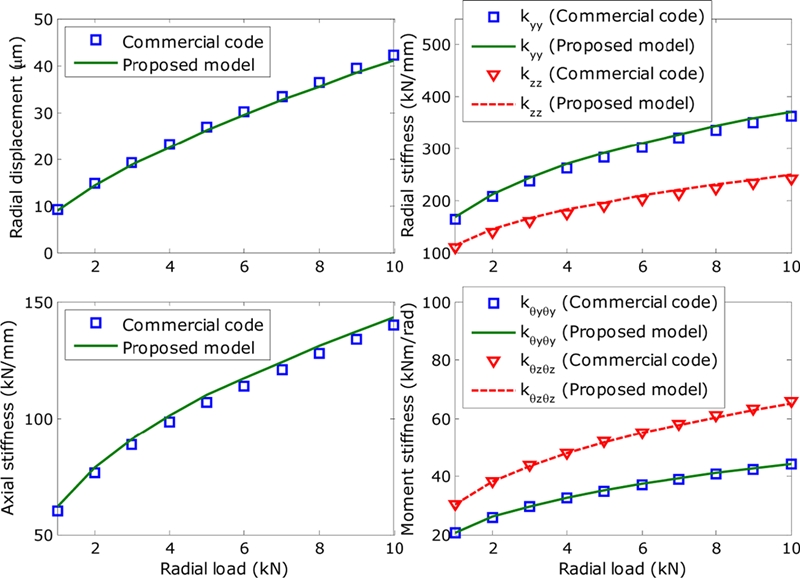
Stiffness and radial displacement of the D-ACBB as a function of radial load Fy (rotational speed n = 1000 rpm)
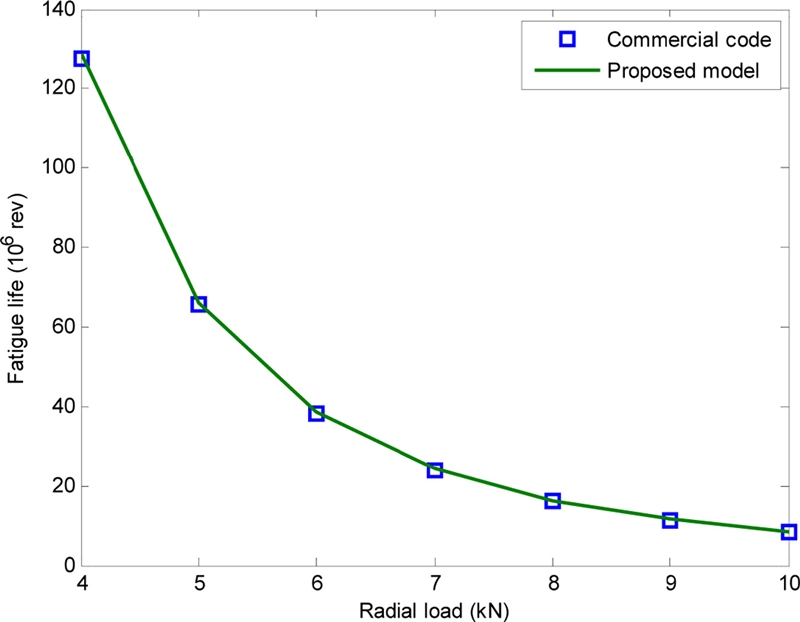
Fig. 5 illustrates the basic reference rating life of the D-ACBB as a function of the radial load. It is shown that the fatigue life of bearings is gradually reduced at increasing radial loads. As expected, the calculated bearing fatigue lives are well matched with those obtained using the commercial code, thus successfully validating the proposed model.
3.2 Effect of Axial Clearance
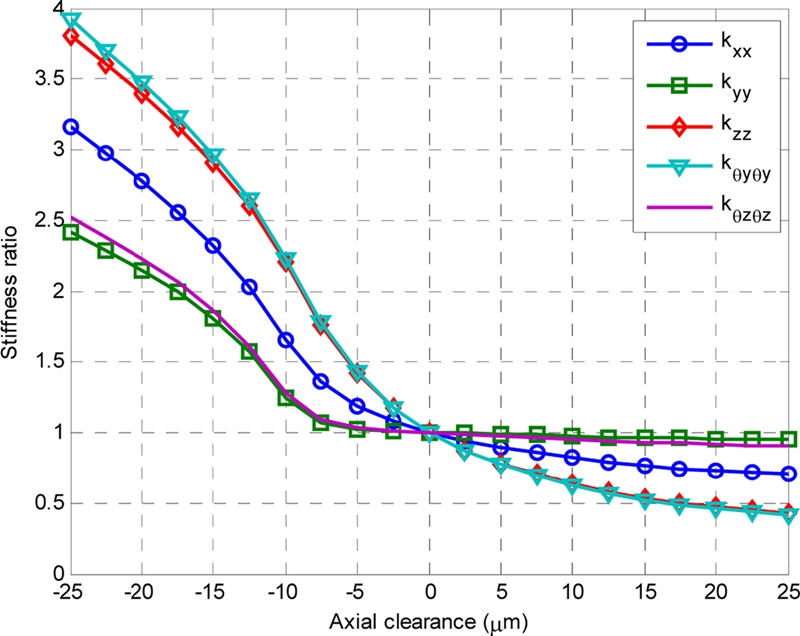
D-ACBBs are often used in the presence of small internal clearance under various operating conditions. Such clearance allows the inner and outer rings to displace axially with respect to each other. Positive axial clearance is mainly assigned for avoiding bearing seizure caused by thermal expansion. However, D-ACBBs may be installed with a negative axial clearance. This implies that the D-ACBBs are initially preloaded before operation. Such a preload leads to the development of constant elastic compressive forces at the contact points between the rolling element and raceway surfaces. This leads to an increase in the bearing rigidity to prevent or suppress shaft run-out, vibration, and noise, as well as to improve the running and locating accuracies. This also reduces smearing, and regulates rolling element rotation.4
This section discusses the effect of axial clearance on the bearing stiffness and fatigue life. The axial clearance was chosen to range from -25 to 25 μm investigation purposes, and the rotational speed was kept constant at 1000 rpm.
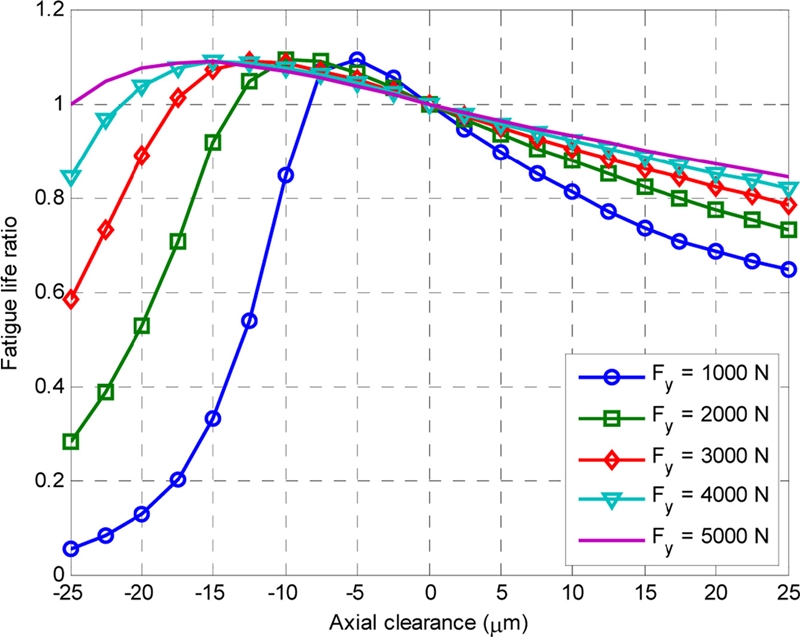
Figs. 6 and 7 show the effect of axial clearance on the stiffness and fatigue life ratios, which are defined as the ratios between the stiffness and fatigue life at an arbitrary axial clearance, and the corresponding values at zero axial clearance. The stiffness values of D-ACBB at negative axial clearance are obviously higher than those of the D-ACBBs with positive clearance because of the increased initial preload. However, as shown in Fig. 7, increasing the magnitude of the negative axial clearance reduces the bearing fatigue life, especially when an increased radial load is applied. This is mainly caused by the increase of the ball and race contact loads, as shown in Fig. 8. It should be noted that the positive axial clearance has a minor effect on the radial stiffness values (kyy and kzz) of the D-ACBB (Fig. 6).
3.3 Effect of Rotational Speed and Radial Load
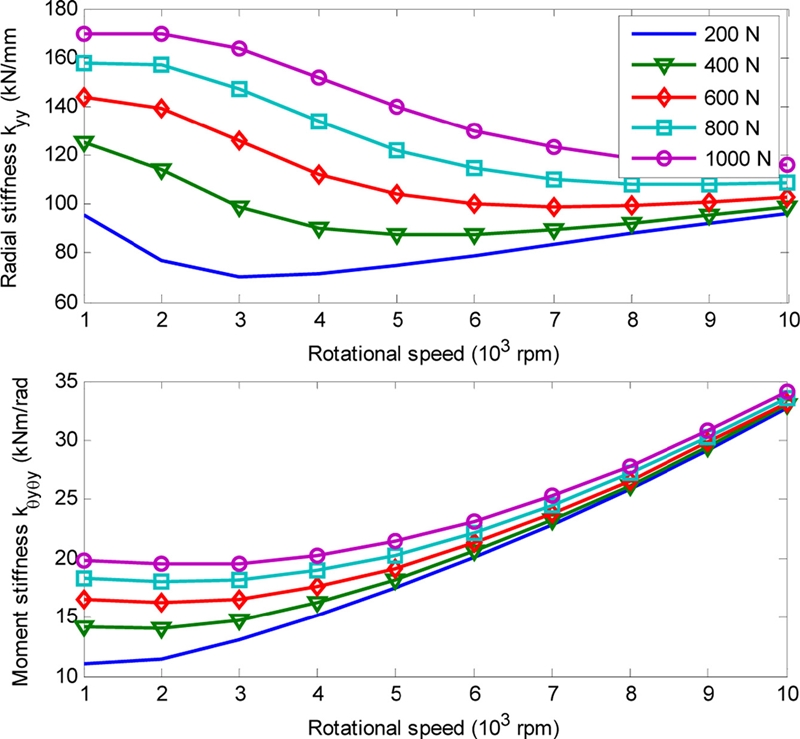
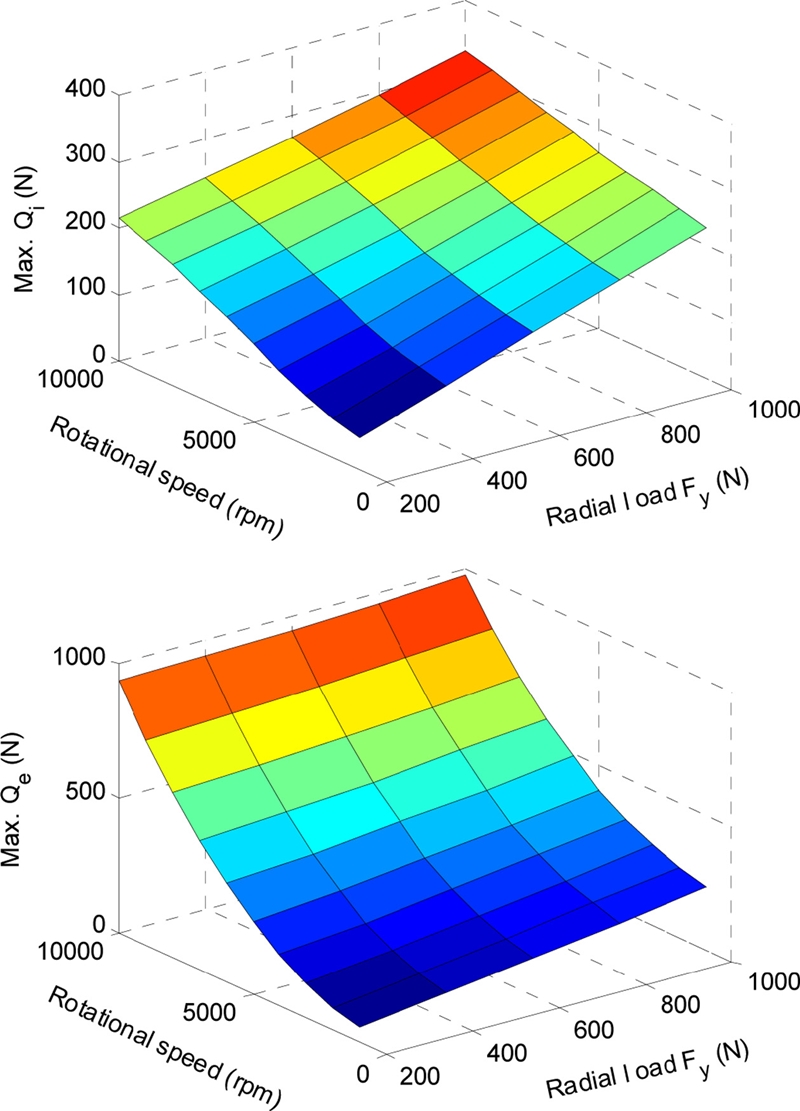
This section presents the effects of rotational speed and radial load on the stiffness and fatigue life of D-ACBB. The axial clearance was set to 0 μm. The radial and moment stiffness values show opposing behavior in the low rotational speed range, as shown in Fig. 9. However, under increased rotational speeds, both stiffness values increase. Additionally, the increase of rotational speed would lessen the effect of radial load on the bearing stiffness values. This could be because the effect of inertial loading under increased speeds prevails over the radial load acting on the bearing.
Fig. 10 shows the fatigue life of the D-ACBB as a function of rotational speed for various radial loads. It is observed that the bearing fatigue life decreases as the rotational speed increases. This means that increasing the rotational speed leads to the increase of the contact load between the ball and bearing races, as demonstrated in Fig. 11. The effect of the rotational speed on the bearing’s fatigue life is significant at low bearing loads.
3.4 Effect of Angular Misalignment
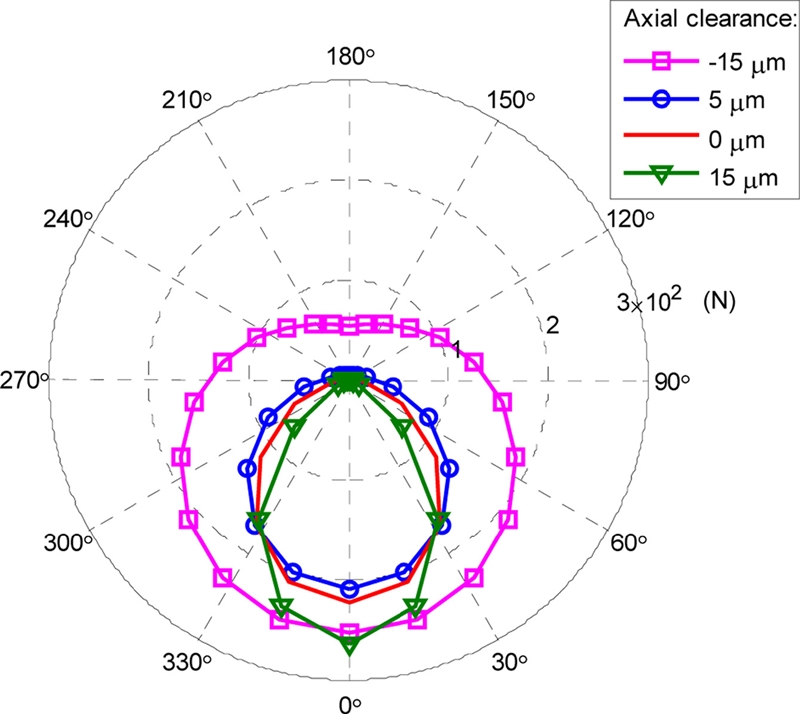
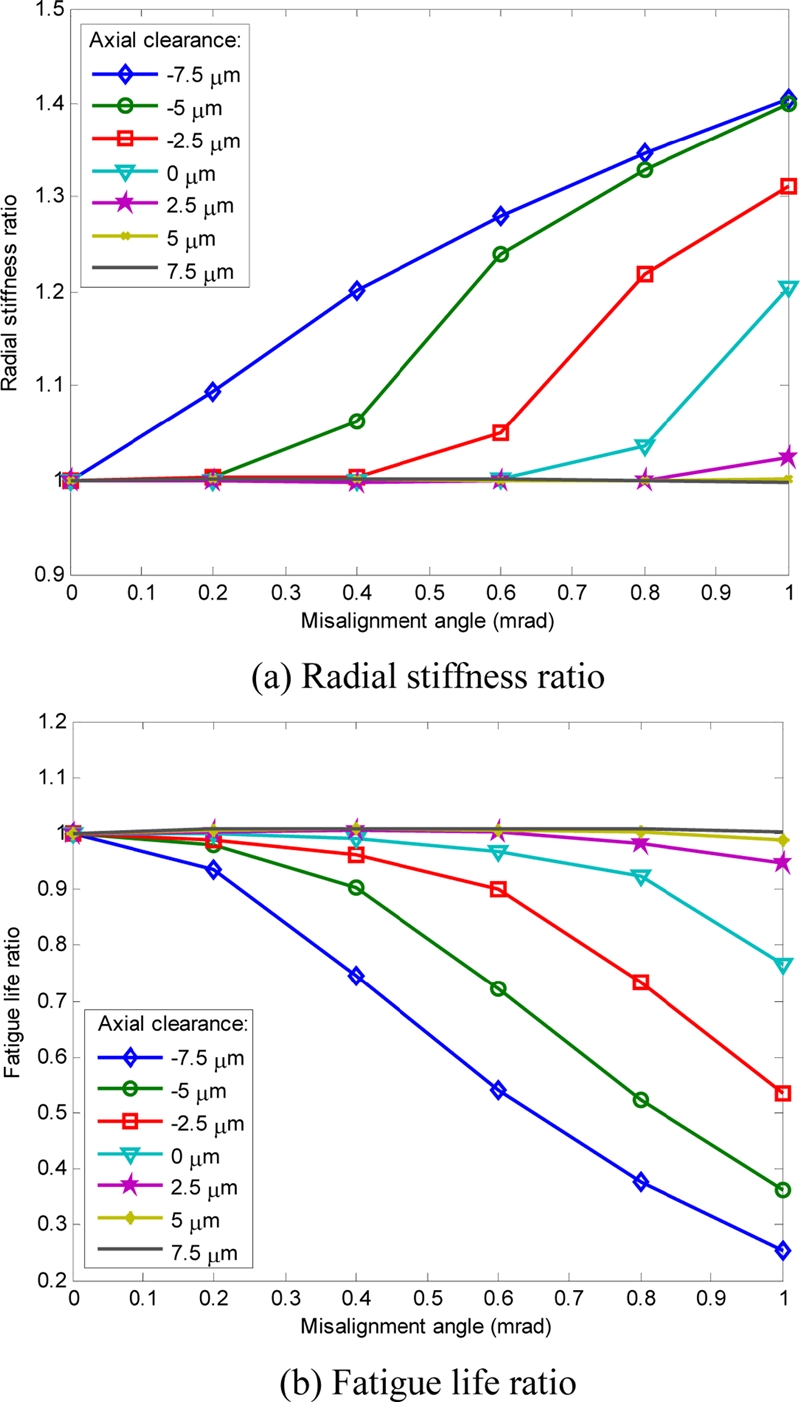
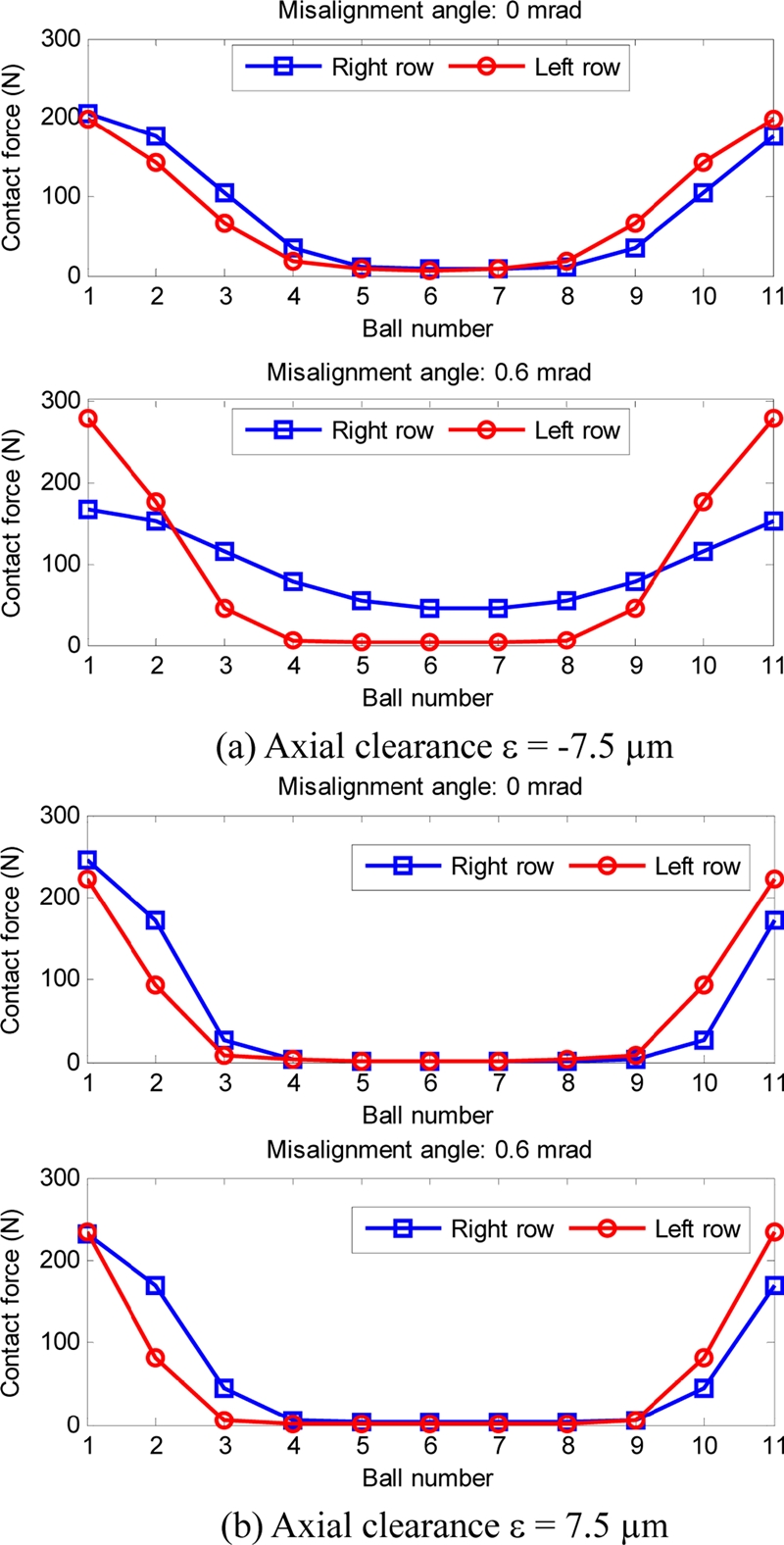
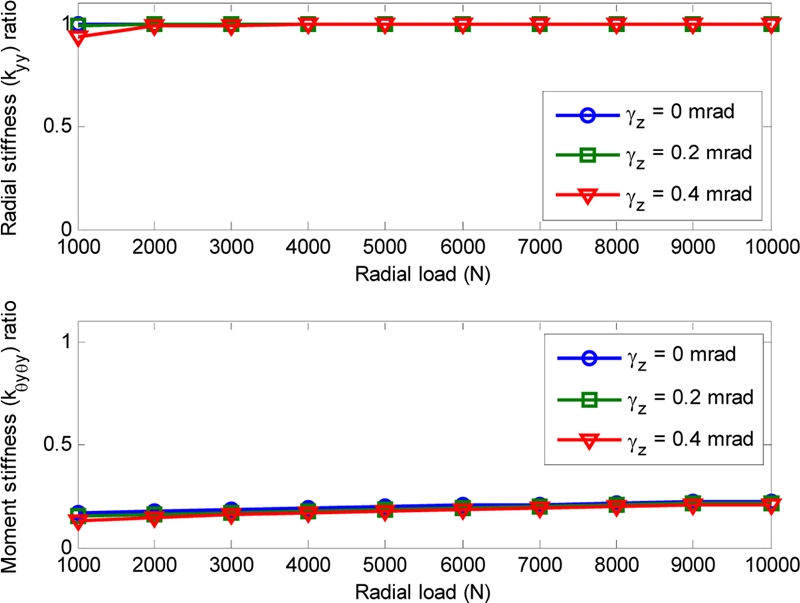
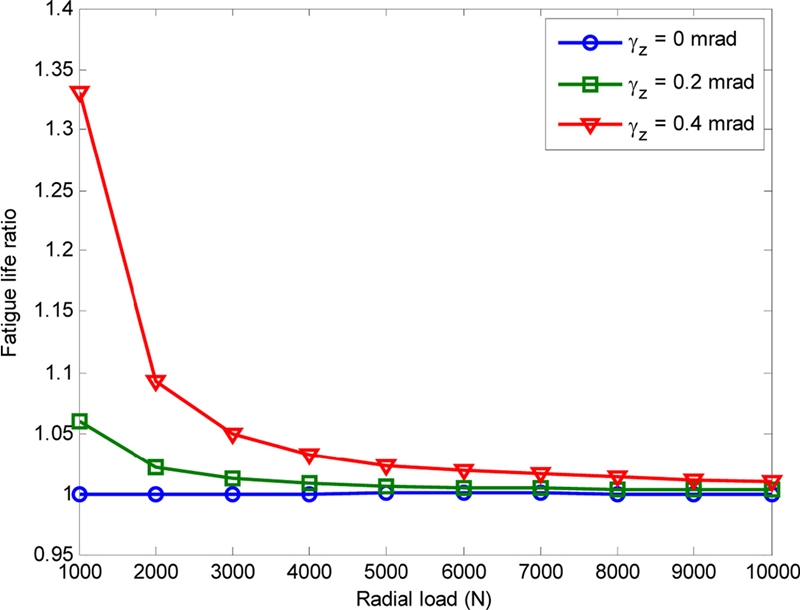
This section presents the effect of angular misalignment on the bearing stiffness and fatigue life of D-ACBBs at different axial clearances. The bearing load and rotational speed are assumed constant at Fy = 1000 N and n = 1000 rpm, respectively. Fig. 12 depicts the bearing radial stiffness and fatigue life ratios for various axial clearances. Only the radial stiffness kyy is shown because the other stiffness elements will have the same behavior. Fig. 13 evaluates the ball and inner race contact load at two values of axial clearance, namely, ε = -7.5 μm and ε = 7.5 μm. Fig. 12 shows that the stiffness of D-ACBB increases with increase in angular misalignment. This behavior may be explained by the increase in the number of balls that sustain the applied load, as shown in Fig. 13(a).
Contrary to the observed variation for the bearing stiffness, the fatigue of the bearing decreases with misalignment increases. This is due to the increase of the contact load in the rolling elements (Fig. 13(a)). However, the variations in both stiffness and fatigue lives are negligible for the D-ACBB that has significantly large axial clearance, as shown in Fig. 12. This is because the internal contact load distribution of the ball and race are unaffected by angular misalignments in the case of sufficiently high axial clearances (such as μ = 7.5 μm), as shown in Fig. 13(b). It is clear from Fig. 13(b) that the internal load distributions are almost identical for both aligned and misaligned bearings.
3.5 Effect of Bearing Arrangement
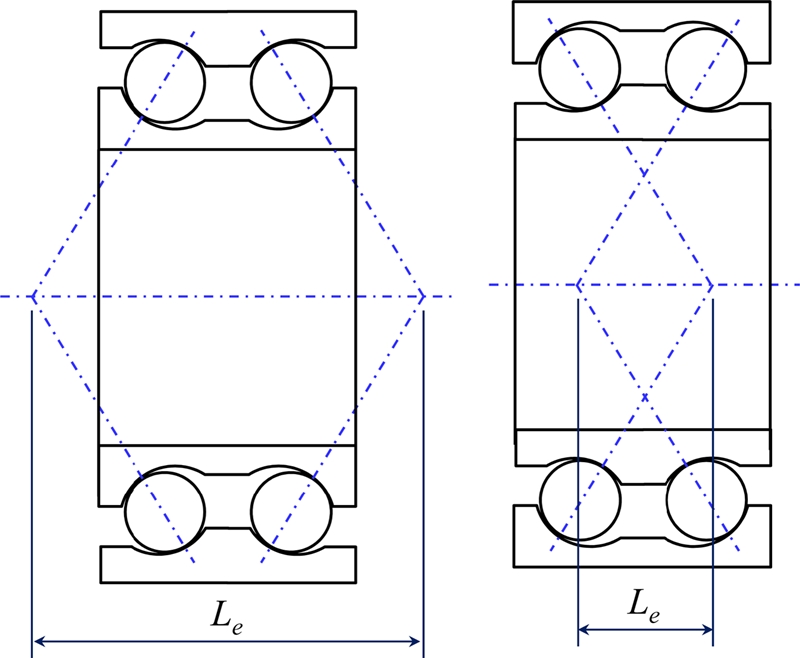
The bearing arrangement is known to affect the characteristics of the implemented bearings.2,19 The effect of the bearing arrangement on the bearing stiffness and fatigue life is discussed in this section. Two types of arrangements are considered: back-to-back, or “O” arrangements, and face-to-face, or “X” arrangements, as shown in Fig. 14. For comparison, the stiffness and fatigue life ratios are introduced, which are defined as the ratios between the stiffness and fatigue lives of the bearings in “X” and “O” arrangement.
Figs. 15 and 16 respectively show the stiffness and fatigue life ratios of D-ACBB as a function of the applied radial load. The axial clearance and rotational speed of the bearing are set to 0 μm and 1000 rpm, respectively. One can see that the bearing in the “O” arrangement is beneficial in terms of moment stiffness. It is obvious that the distance between the effective load centers of the two bearing rows Le is larger when the bearing is in this “O” arrangement, as shown in Fig. 14. Consequently, the capability of the bending resistance for D-ACBB in the “O” arrangement is higher than that of the “X” arrangement. On the other hand, the bearing arrangement does not affect the radial stiffness, or the fatigue life of the bearing. As demonstrated in Figs. 15(a) and 16, the radial stiffness and fatigue life ratios are almost equal to 1.0, regardless of the radial load. It is noted that the D-ACBBs in the “X” arrangement may have a higher fatigue life under low radial load and misalignment conditions compared to that of the bearing in the “O” arrangement, as shown in Fig. 16.
4. Conclusions
A comprehensive quasi-static model for D-ACBBs has been presented to calculate the internal load distribution, fully occupied stiffness matrix, displacements, and the basic reference rating life, subjected to a five-DOF loading. The presented model considers the rotational speed, axial clearance, angular misalignment, and the arrangement of ball rows. The presented model was rigorously verified through comparisons with a commercial code. An extensive analysis on the stiffness and fatigue life of the D-ACBB was conducted, subjected to various practical loading conditions. The presented model is useful for the static and dynamic analyses of rotor-bearing systems containing D-ACBBs.20
NOMENCLATURE
| Da : | Ball diameter |
| {F} : | Bearing load vector |
| F : | External force of bearing |
| Fc : | Centrifugal force |
| k : | Bearing stiffness |
| L10r : | Basic reference rating life |
| M : | External moment of bearing |
| Mg : | Gyroscopic moment |
| n : | Rotational speed |
| {Q} : | Inner ring contact load vector |
| Q : | Ball and race contact force |
| Qc : | Basic dynamic radial load rating of bearing |
| Qe : | Dynamic equivalent rolling element load |
| [Rϕ] : | Transformation matrix |
| r : | Radial coordinate of inner raceway cross-section |
| {u} : | Displacement vector of inner raceway cross-section |
| {v} : | Displacement vector of ball |
| x, y, z : | Cartesian coordinate axes |
| Z : | Number of balls per row |
| α : | Contact angle of bearing |
| γ : | Angular displacement of bearing |
| {δ} : | Bearing displacement vector |
| δ : | Translation displacement of bearing |
| ε : | Axial clearance of bearing |
| λ : | Distribution parameters for the gyroscopic moment |
| ϕ : | Ball location angle |
Acknowledgments
This research was financially supported by the Korea Institute of Machinery and Materials.
REFERENCES
-
Abele, E., Altintas, Y., and Brecher, C., “Machine Tool Spindle Units,” CIRP Annals-Manufacturing Technology, Vol. 59, No. 2, pp. 781-802, 2010.
[https://doi.org/10.1016/j.cirp.2010.05.002]

-
Hong, S.-W., Choi, C.-S., and Lee, C.-H., “Effects of Bearing Arrangement on the Dynamic Characteristics of High-Speed Spindle,” J. Korean Soc. Precis. Eng., Vol. 30, No. 8, pp. 854-863, 2013.
[https://doi.org/10.7736/KSPE.2013.30.8.854]

- Schaeffler Technologies AG & Co. KG, “Double Row Angular Contact Ball Bearings,” https://www.schaeffler.com/remotemedien/media/_shared_media/08_media_library/01_publications/schaeffler_2/brochure/downloads_1/ozs_de_en.pdf, (Accessed 19 OCT 2017)
- SKF, “Double Row Angular Contact Ball Bearings,” http://www.skf.com/group/products/bearings-units-housings/ball-bearings/angular-contact-ball-bearings/double-row-angular-contact-ball-bearings/index.html, (Accessed 10 JUL 2017)
-
Bercea, I., Nelias, D., and Cavallaro, G., “A Unified and Simplified Treatment of the Non-Linear Equilibrium Problem of Double-Row Rolling Bearings. Part I: Rolling Bearing Model,” Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology, Vol. 217, No. 3, pp. 205-212, 2003.
[https://doi.org/10.1243/135065003765714854]

-
Petersen, D., Howard, C., Sawalhi, N., Ahmadi, A. M., and Singh, S., “Analysis of Bearing Stiffness Variations, Contact Forces and Vibrations in Radially Loaded Double Row Rolling Element Bearings with Raceway Defects,” Mechanical Systems and Signal Processing, Vol. 50, pp. 139-160, 2015.
[https://doi.org/10.1016/j.ymssp.2014.04.014]

-
Ghalamchi, B., Sopanen, J., and Mikkola, A., “Simple and Versatile Dynamic Model of Spherical Roller Bearing,” International Journal of Rotating Machinery, Vol. 2013, Article ID: 567542, 2013.
[https://doi.org/10.1155/2013/567542]

-
Ma, F., Ji, P., Li, Z., Wu, B., and An, Q., “Influences of Off-Sized Rollers on Mechanical Performance of Spherical Roller Bearings,” Proceedings of the Institution of Mechanical Engineers, Part K: Journal of Multi-Body Dynamics, Vol. 229, No. 4, pp. 344-356, 2015.
[https://doi.org/10.1177/1464419314566086]

-
Zhuo, Y., Zhou, X., and Yang, C., “Dynamic Analysis of Double-Row Self-Aligning Ball Bearings due to Applied Loads, Internal Clearance, Surface Waviness and Number of Balls,” Journal of Sound and Vibration, Vol. 333, No. 23, pp. 6170-6189, 2014.
[https://doi.org/10.1016/j.jsv.2014.04.054]

-
Gunduz, A. and Singh, R., “Stiffness Matrix Formulation for Double Row Angular Contact Ball Bearings: Analytical Development and Validation,” Journal of Sound and Vibration, Vol. 332, No. 22, pp. 5898-5916, 2013.
[https://doi.org/10.1016/j.jsv.2013.04.049]

-
Lostado, R., Martinez, R. F., and Mac Donald, B. J., “Determination of the Contact Stresses in Double-Row Tapered Roller Bearings Using the Finite Element Method, Experimental Analysis and Analytical Models,” Journal of Mechanical Science and Technology, Vol. 29, No. 11, pp. 4645-4656, 2015.
[https://doi.org/10.1007/s12206-015-1010-4]

-
Tong, V.-C. and Hong, S.-W., “Modeling and Analysis of Double-Row Cylindrical Roller Bearings,” Journal of Mechanical Science and Technology, Vol. 31, No. 7, pp. 3379-3388, 2017.
[https://doi.org/10.1007/s12206-017-0627-x]

- Schaeffler Technologies, “BEARINX®-Online Spindle Calculation,” https://www.ina.de/content.ina.de/en/products_services/calculating/bearinxonlinespindle/bearinx_online_spindle_calculation.jsp (Accessed 22 OCT 2017)
- Harris, T. A., “Rolling Bearing Analysis,” John Wiley and Sons, 4th Ed., 2001.
-
De Mul, J., Vree, J., and Maas, D., “Equilibrium and Associated Load Distribution in Ball and Roller Bearings Loaded in Five Degrees of Freedom while Neglecting Friction—Part II: Application to Roller Bearings and Experimental Verification,” Journal of Tribology, Vol. 111, No. 1, pp. 149-155, 1989.
[https://doi.org/10.1115/1.3261865]

- Palmgren, A., “Ball and Roller Bearing Engineering,” Philadelphia: SKF Industries Inc., 1959.
-
Hong, S.-W. and Tong, V.-C., “Rolling-Element Bearing Modeling: A Review,” Int. J. Precis. Eng. Manuf., Vol. 17, No. 12, pp. 1729-1749, 2016.
[https://doi.org/10.1007/s12541-016-0200-z]

- ISO/TS 16281, “Rolling Bearings-Methods for Calculating the Modified Reference Rating Life for Universally Loaded Bearings,” 2008.
-
Li, H. and Shin, Y. C., “Analysis of Bearing Configuration Effects on High Speed Spindles Using an Integrated Dynamic Thermo-Mechanical Spindle Model,” International Journal of Machine Tools and Manufacture, Vol. 44, No. 4, pp. 347-364, 2004.
[https://doi.org/10.1016/j.ijmachtools.2003.10.011]

-
Tong, V.-C., Bae, G.-H., and Hong, S.-W., “Dynamic Analysis of Spindle Supported by Multiple Bearings of Different Types,” J. Korean Soc. Precis. Eng., Vol. 32, No. 2, pp. 117-125, 2015.
[https://doi.org/10.7736/KSPE.2015.32.2.117]