인공 신경망과 유전 알고리즘을 이용한 관통자 형상의 최적화 설계

2.1 데이터 샘플링

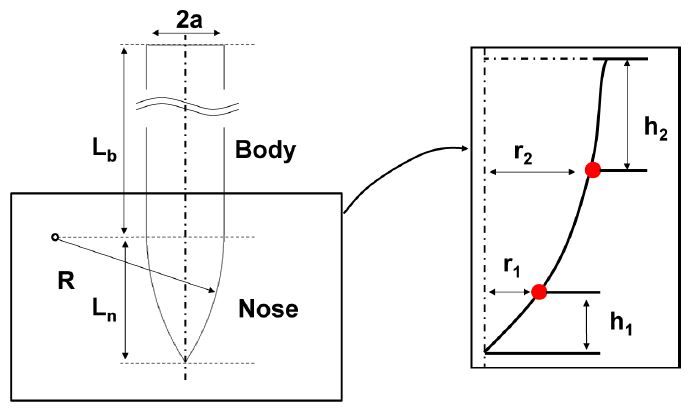
데이터 샘플링을 수행하기에 앞서, 관통자의 형상 파라미터를 정의하였다. 관통자의 형상은 Fig. 1과 같다. 관통자는 몸체(Body)와 탄두(Nose)로 구분된다. 여기에서 관통자의 몸체 길이(L_b)는 59.3 mm, 탄두의 길이(L_n)은 11.8 mm, 탄두의 지름(2a)은 7.1 mm이다.

Fig. 1

Schematic of penetrator geometry

관통자의 형상은 베지어 곡선의 제어점을 이용하여 설계에 필요한 파라미터인 r₁, r₂, h₁, h₂으로 정의하였다. 이는 관통자를 머리와 몸체로 분류하였을 때, 관통자의 머리부인 탄두의 형상을 제어하는 파라미터이다. 여기서 시작점과 끝점을 고정하고 베지어 곡선의 제어점 2개를 사용하여 관통자의 형상을 모사하였다.

데이터 샘플링을 수행하기 위한 형상 파라미터의 조합 범위는 Table 1과 같다. 실제 위의 범위 내의 파라미터 조합으로 표현 가능한 관통자의 형상은 무한이다. 이에 따라 최소의 유한요소해석으로 더 효율적인 결과를 얻기 위해 라틴 방격법을 이용하였다.

Table 1

Range for parameter combination of penetrator geometry

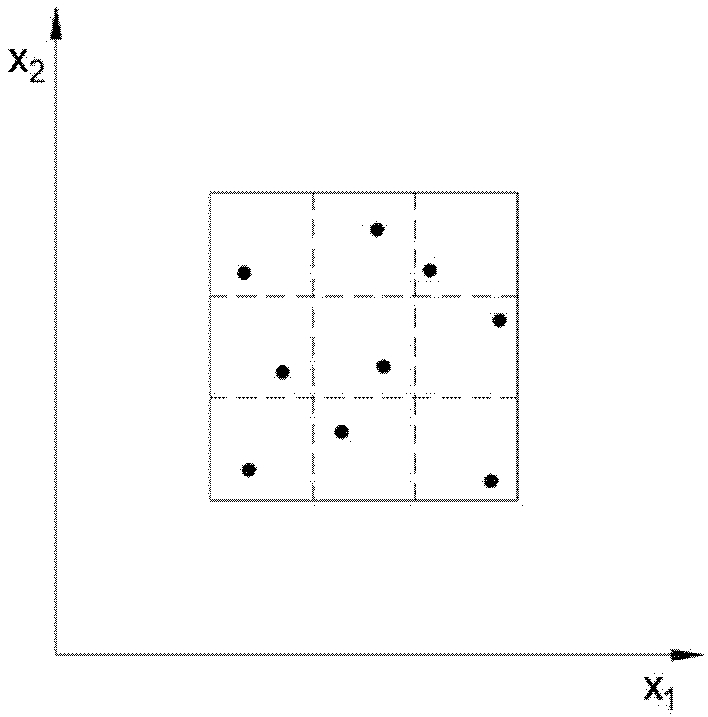
라틴 방격법은 Fig. 2와 같이 표본 공간 전체에서 표본을 추출하는 데이터 샘플링 방법으로 변수의 범위를 일정한 n개의 구역으로 나눈 다음 각 구간에서 하나씩 무작위로 n개의 샘플을 추출하는 방법이다.⁵ 이를 이용하여 본 연구에서는 200개의 학습 데이터와 24개의 검증 데이터를 도출하기 위한 관통자의 형상 파라미터 조합을 샘플링하였다. 일반적으로 전체 데이터 중 80%를 학습 데이터로, 나머지 20%를 성능 평가를 위한 검증 데이터로 이용하지만,⁸ 본 연구에서는 제한된 데이터 개수로 인공 신경망의 성능을 최대화하기 위해 총 데이터 중 약 90%를 학습 데이터로 사용하였다.

Fig. 2

Schematic of Latin hypercube sampling method

2.2 유한요소해석 모델링

관통자의 거동은 Finite Cavity Pressure Method를 사용하여 모사하였다. 이 방법은 관통자의 표면에 작용하는 응력을 유한요소해석을 통해 관통자에 부가하여 관통자의 변형, 투과 깊이 등을 계산하는 방법이다. 이 방법의 장점은 관통자의 형상에 제약이 없으며, 수직은 물론 경사 충돌에 대해서도 투과 깊이를 계산 가능하다. 그리고 관통자의 변형을 고려한 이동 경로 계산, 다층 특성을 고려한 이동 경로, 투과 깊이 계산이 가능하다. 특히 전체를 해석하는 기존 유한요소해석법과 달리 관통자만을 해석하므로 해석이 매우 빠르다.

본 연구에서는 알루미늄 재질의 충돌체에 대하여 충돌 성능을 분석하였다. Warren and Forrestal⁶은 재료의 변형률 속도를 고려하여, 알루미늄 재료의 Cavity Pressure를 식(1)과 같이 2차 식으로 모사하였다. 여기서 $$ {\overrightarrow{V}}_I$$는 질점의 속도, $$ \overrightarrow{n}$$은 해당하는 요소의 수직 벡터, Y₀는 재료의 항복응력, ρ₀는 재료의 밀도이다. 여기에서 식(1)의 3개 변수 A, B, C는 Cavity Pressure Method의 이론식으로부터 2차식으로 피팅한 결과이다. 위의 3가지 변수 A, B, C는 기존 연구 결과를 사용하였으며,⁷ 그 값은 각각 5.0394, 0.9830, 0.9402이다. 또한 재료의 항복응력(Y₀)은 276 MPa, 밀도(ρ₀)는 2710 kg/m³이다.

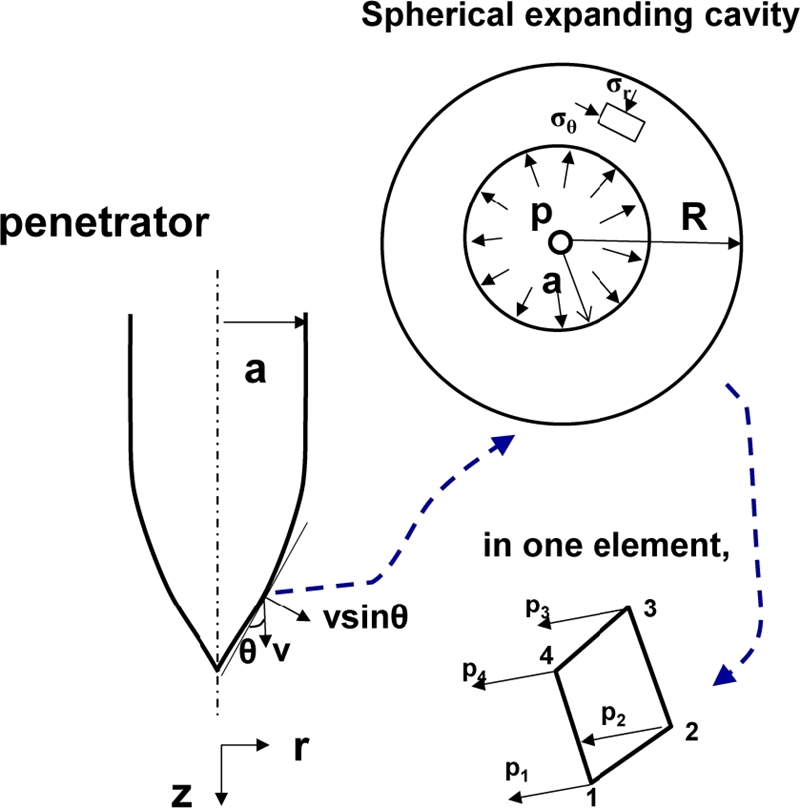
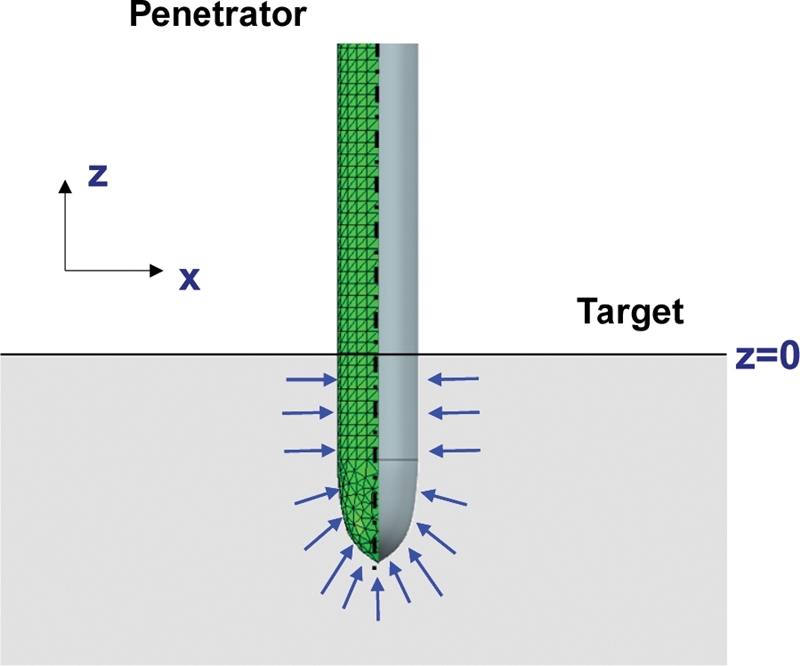
본 연구에서는 관통자의 투과 깊이에 관한 학습 및 검증 데이터를 생성하기 위해 샘플링된 224개의 관통자의 파라미터 조합에 관한 유한요소해석을 수행하였다. 이를 수행하기 위해 ABAQUS v6.13의 User Subroutine 중 하나인 VDLOAD를 이용하여 Finite Cavity Pressure Method를 적용하였다. 위의 방법은 관통자를 다수의 요소로 분할하고 각 요소에서 절점에 작용하는 힘을 계산할 수 있다. 이에 대한 개략도는 Fig. 3과 같다. 이때 하나의 요소가 받는 실제 압력(P_I)는 식(1)과 같다. 여기서 표면 수직 방향과 이동 속도를 계산 후 내적 해준 뒤에 이를 사용하여 표면에 작용하는 압력을 계산할 수 있다. 그리고 Fig. 4와 같이 해당하는 요소의 z 좌표가 0 이하로 내려가는 경우 요소에 Cavity Pressure에 의한 압력이 작용하는 것으로 계산하였다.

Fig. 3

Schematic of the finite cavity pressure method

Fig. 4

Simulation model of the penetrator

전체 유한요소해석을 이용하여 수행하는 경우, 관통자 및 목표물에 대한 요소를 모두 구성해야 한다. 하지만 Finite Cavity Pressure Method를 사용하는 경우, 관통자 형상의 모델링만으로도 유한요소해석이 가능하다. 위의 유한요소해석에서 관통자의 요소 크기는 1 mm이며 ABAQUS/Explicit의 사면체 요소를 사용하였다. 또한 해석 모델 수가 많아 관통자 형상의 제어점을 ABAQUS의 스크립트에 적용하여 자동으로 해석 모델을 구성하였다. 초기 조건으로는 관통자에 충돌 전 속도를 부여하였고, 그 값은 1209 m/s이다.

관통자의 재료는 Vacuum-Arc-Remelted (VAR) 4340 Steel이다. 이 재료의 밀도는 8000 kg/m³이다. 관통자는 음속 이상으로 매우 빠르므로 충돌 시점에서의 변형률 속도가 매우 높다. 따라서 재료의 변형률 속도를 고려한 유효응력을 유한요소해석에 적용해야 한다. Fig. 5는 압축 실험을 통해 얻은 데이터를 기반으로 피팅한 VAR4340의 변형률 속도에 따른 응력-변형률 관계이다.⁶ 변형률 속도가 10^-4인 경우 재료의 항복응력은 1580 MPa이며 ABAQUS/Explicit에 Fig. 5의 유효 변형률 속도에 따른 물성을 사용하였다.

Fig. 5

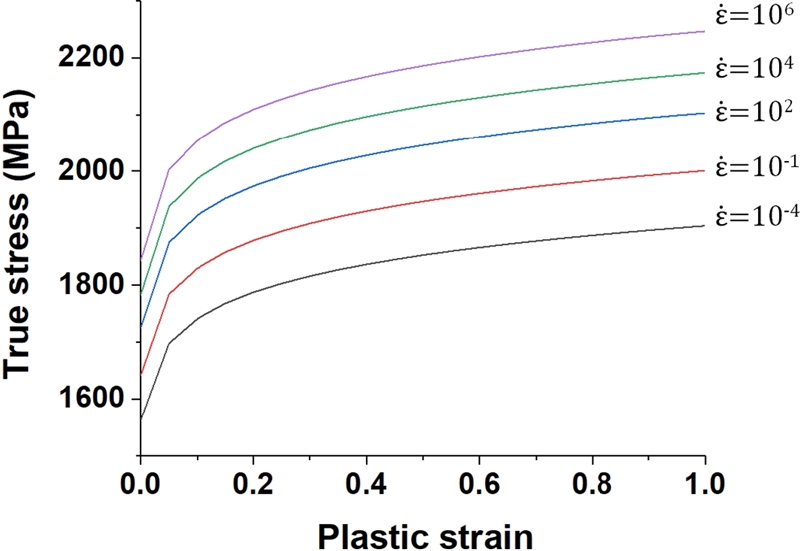
Material properties of VAR4340 with respect to strain rate6 (Adapted from Ref. 6 on the basis of OA)

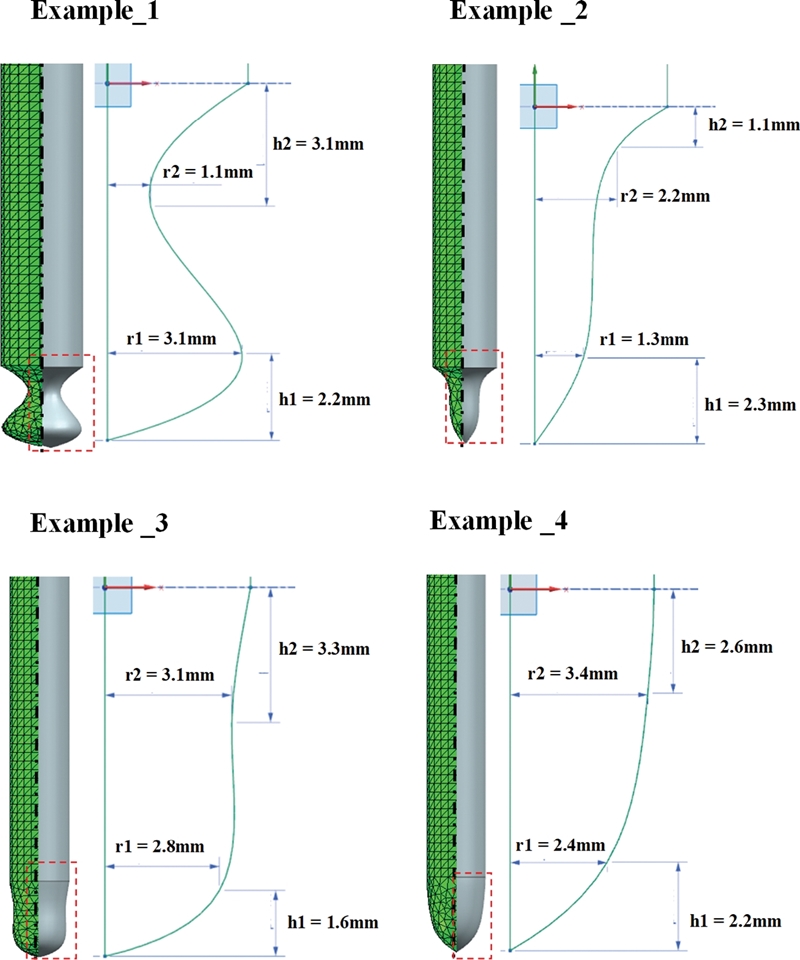
Fig. 6은 학습 데이터를 생성하기 위해 샘플링된 200개의 관통자 형상의 파라미터 조합 중 임의로 선택한 4개 유형의 형상에 대한 해석 모델이다. 학습 데이터를 만들기 위해 다양한 형상의 관통자를 모델링하여 해석을 진행하였다.

Fig. 6

FEA model of penetrator geometry

3.1 하이퍼 파라미터 최적화

인공 신경망의 성능은 학습 데이터의 종류와 양뿐만 아니라 하이퍼 파라미터의 조합에 따라서 크게 결정된다. 인공 신경망의 하이퍼 파라미터는 각 은닉층 내 노드 개수, L2 정규화 계수, 학습률, 학습 횟수, 은닉층 수 등이 있다.⁸ 본 연구에서는 라틴 방격법을 이용하여 샘플링된 100개의 하이퍼 파라미터에서 최소의 RMSE 값을 갖는 하이퍼 파라미터 조합을 최적의 하이퍼 파라미터로 선정하였다. RMSE는 식(2)를 따른다. 또한, 학습 데이터로 도출된 하이퍼 파라미터는 검증 데이터에 관해서 오버 피팅되는 경우가 발생한다. 이에 따라 식(3)을 이용하여 학습 데이터와 검증 데이터에 대한 오차에 가중치를 부여하여 이를 방지하였다. 여기서 W는 가중치, RMSE_train 및 RMSE_valid는 각각 학습 및 검증 데이터에 대한 제곱 평균 제곱근 오차를 나타낸다.

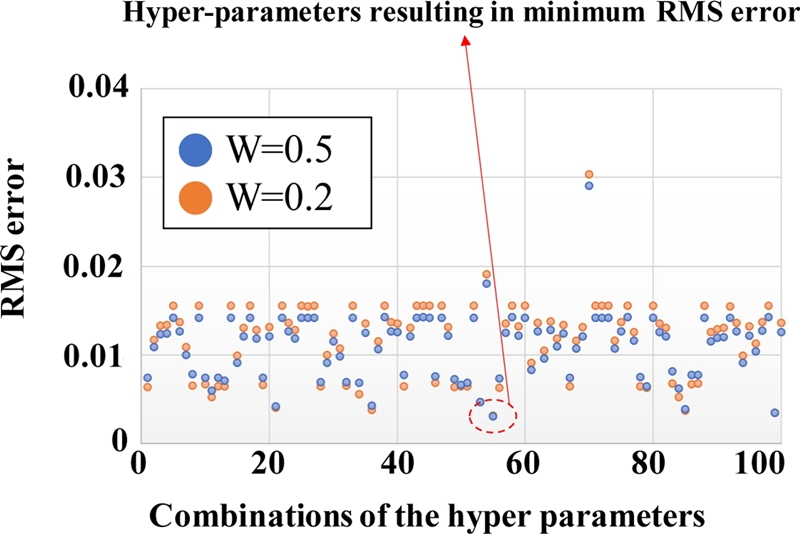
Fig. 7은 샘플링된 하이퍼 파라미터 조합에 따른 RMSE 값이다. 가중치를 각각 0.2와 0.5를 부여하였을 때 공통적인 결과를 도출하는 최소의 RMSE 값을 최적의 하이퍼 파라미터로 선정하였다. 하이퍼 파라미터의 탐색 범위와 탐색할 활성화 함수는 Table 2이다. 활성화 함수는 Sigmoid, Tangent Hyperbolic, ReLU의 조합 중 최적의 조합을 선정하였다. Table 3은 이에 따른 최소 RMSE 값을 갖는 최적의 하이퍼 파라미터 조합과 활성화 함수이다.

Fig. 7

Results of the optimized hyper-parameters

Table 2

Range for the optimization of hyper parameter

Table 3

Results of the optimized hyper-parameter

본 연구에서는 활성화 함수로 식(4)의 Sigmoid 함수와 식(5)의 Tangent Hyperbolic 함수를 사용하였고 최적화 기법으로는 비교적 최근에 제안된 Adam Optimizer를 사용하였다. 학습 속도의 향상과 지역 최적점에 빠지는 것을 피하고자 데이터를 식(6)을 이용하여 정규화하였다. 학습 중 특정 가중치가 상대적으로 커짐에 따라 발생하는 과적합을 방지하기 위해, 식(7)과 같이 손실 함수에 특정 가중치의 증가에 따른 페널티 함수를 적용하는 L₂ Regularization을 사용하였다. 여기서 λ는 정규화 계수로써, 인공 신경망 모델의 하이퍼 파라미터이다. 또한 Gradient Vanishing 현상을 완화하기 위해 가중치 초기화에 Sigmoid, Tangent Hyperbolic 등의 비선형 함수와 함께 사용되는 식(8)에 나타낸 Xavier Initialization 기법을 사용하였다. 여기서 n_in 및 n_out은 각각 각 층의 입력 노드와 출력 노드이다.

3.2 인공 신경망 구성 결과

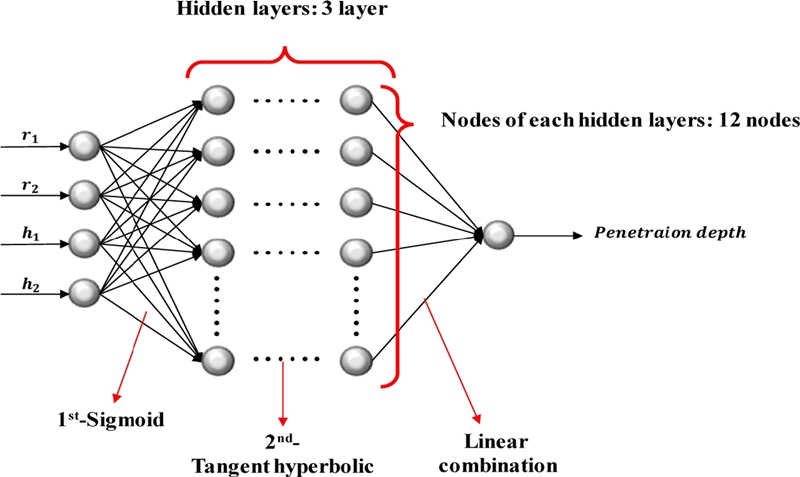
인공 신경망은 크게 입력층, 은닉층, 출력층으로 이루어져 있으며, 각 층은 노드로 구성되어있다. 인공 신경망은 학습하고자 하는 모델의 비선형성, 복잡성, 인자의 개수에 따라 여러 개의 은닉층과 노드로 구성될 수 있다. Fig. 8은 최적의 파라미터와 활성화 함수로 도출된 인공 신경망의 최종 구조이다. 입력 데이터는 관통자의 형상을 제어하는 파라미터이고 출력 데이터는 관통자의 투과 깊이이다. 또한 은닉 층수는 3개, 각 은닉층 내 노드 개수는 12개를 사용한 인공 신경망으로 구성되어있다. 활성화 함수는 Sigmoid와 Tangent Hyperbolic의 조합을 이용하였다.

Fig. 8

Schematic of the final artificial neural network

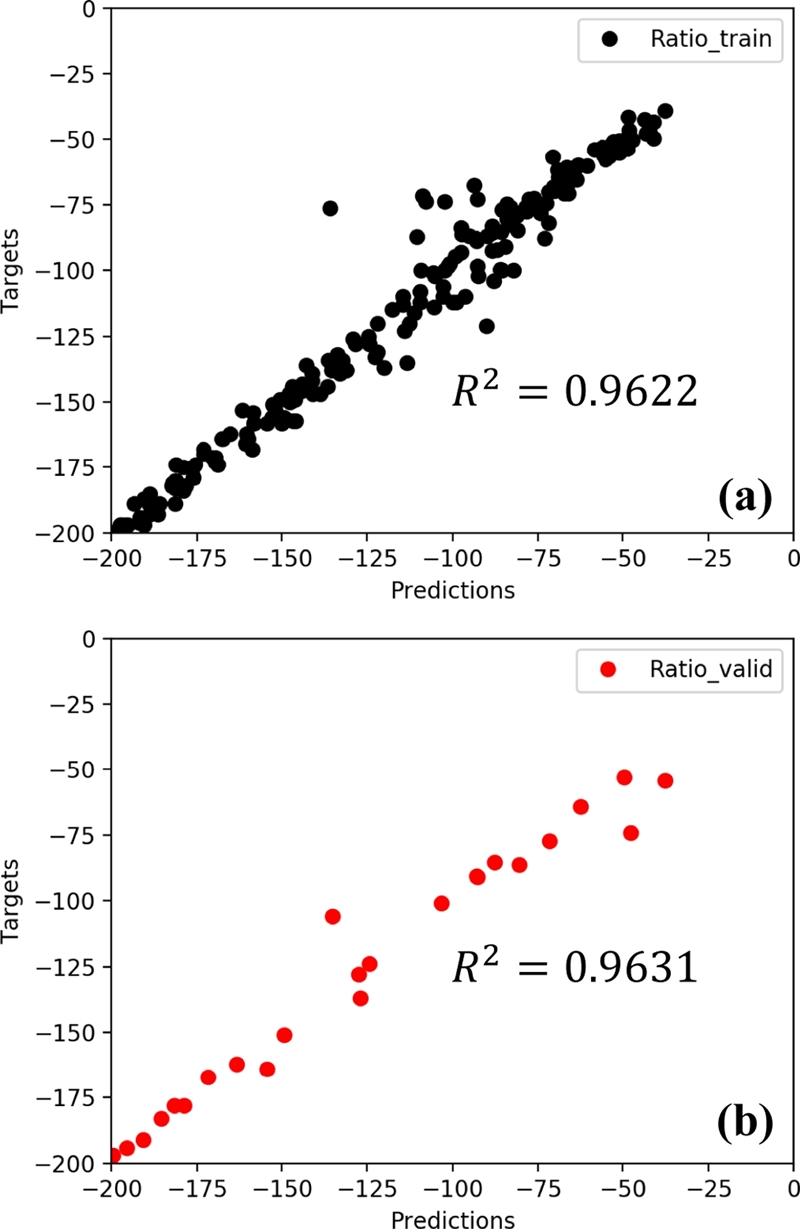
Figs. 9(a)와 9(b)는 각각 학습 데이터와 검증 데이터의 인공 신경망에 관한 학습 결과이다. 인공 신경망을 통해 계산된 예측값과 유한요소해석을 통해 계산된 목표값의 관계를 통해 인공 신경망의 성능을 평가하였다. 학습 및 검증 데이터에 대한 R²는 각각 0.9622와 0.9631로 신경망의 구성이 강건하다는 것을 확인할 수 있다. 하지만 학습 및 검증 결과에서 전체적인 경향을 따르지 않는 데이터가 존재하는데, 이는 유한요소해석에서 탄두의 과도한 변형이 발생하였기 때문이다.

Fig. 9

Learning results of artificial neural network in (a) Training data and (b) Validation data

4.1 최적화 방법

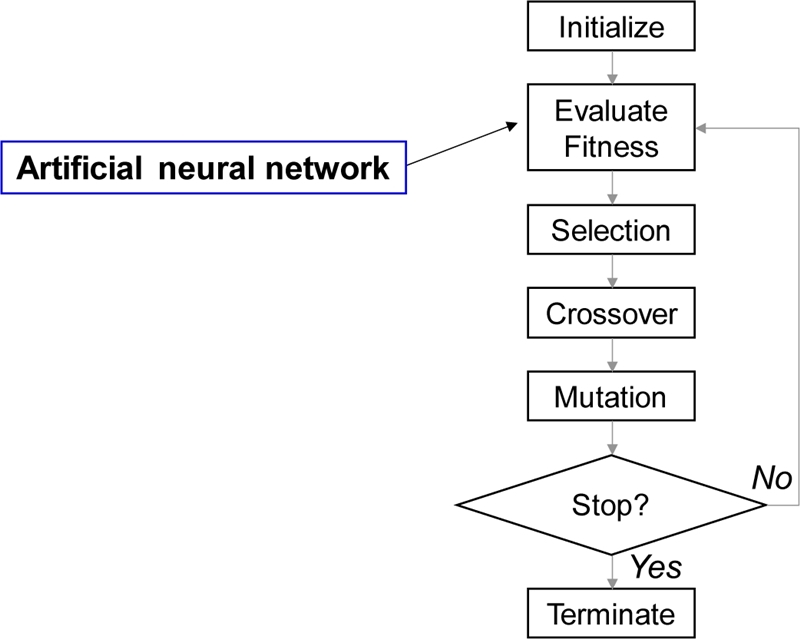
본 연구에서는 인공 신경망을 유전 알고리즘의 적합도 함수로 이용하여 최대 투과 깊이를 예측하는 인자들의 조합을 탐색하였다. 유전 알고리즘은 풀고자 하는 문제에 대한 가능한 해를 정해진 형태의 자료 구조로 표현한 후에 점차 변형함으로 더 적합한 해를 만들어낸다.⁹ Fig. 10은 유전 알고리즘의 연산 순서도이다.

Fig. 10

Flow chart of genetic algorithm

유전 알고리즘의 연산 중 해의 적합도 평가 단계에서 직접적으로 유한요소해석 수행하여 그 결과값을 이용할 수 있지만, 설계 변수의 조합이 너무 많다면 많은 해석 시간이 소요되므로 비효율적이다. 또한 다항식 기반의 모델을 적합도 함수로써 이용하는 경우, 입력과 출력의 비선형성을 잘 모사하지 못하는 단점이 있다. 따라서 본 연구에서는 계산 시간의 감소와 더 많은 형상 파라미터의 탐색을 위해 입력과 출력의 비선형성을 잘 모사할 수 있는 인공 신경망을 이용하여 유한요소해석을 대체할 수 있는 메타 모델을 구성하고, 적합도 함수로서 해의 적합성을 평가하였다.

4.2 형상 최적화 결과

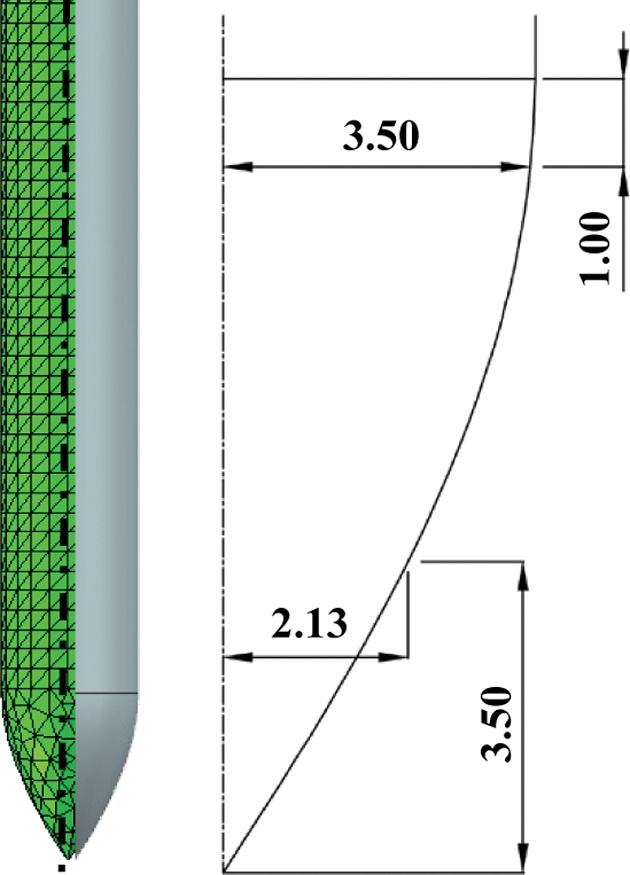
Table 4는 유전 알고리즘을 통해 도출된 관통자의 최적 형상이다. 위의 관통자의 형상 파라미터 조합으로 인공 신경망에서 예측되는 투과 깊이는 -214 mm이며 유한요소해석에서 예측되는 투과 깊이는 -206 mm로 3.88%의 오차율이 발생하였다. Fig. 11은 최대 투과 깊이를 도출할 수 있는 관통자의 최적 형상이다.

Table 4

Optimal parameters of penetrator geometry

Fig. 11

Optimal geometry of penetrator

Fig. 12(a)는 시간에 따른 관통자의 투과 깊이 비교이다. 인공 신경망을 구성하기 위한 200개의 학습 데이터 중 4개 유형의 임의 형상과 최적 형상을 비교하였다. 그 결과, 임의 형상보다 최적 형상의 투과 깊이가 가장 깊다는 것을 확인할 수 있다. Fig. 12(b)는 모든 학습 데이터와 최적 형상의 투과 깊이 비교이다. 탐색한 최적 형상의 투과 깊이가 학습 데이터에서 도출된 최대 투과 깊이보다 우수한 결과값을 도출하였다.

Fig. 12

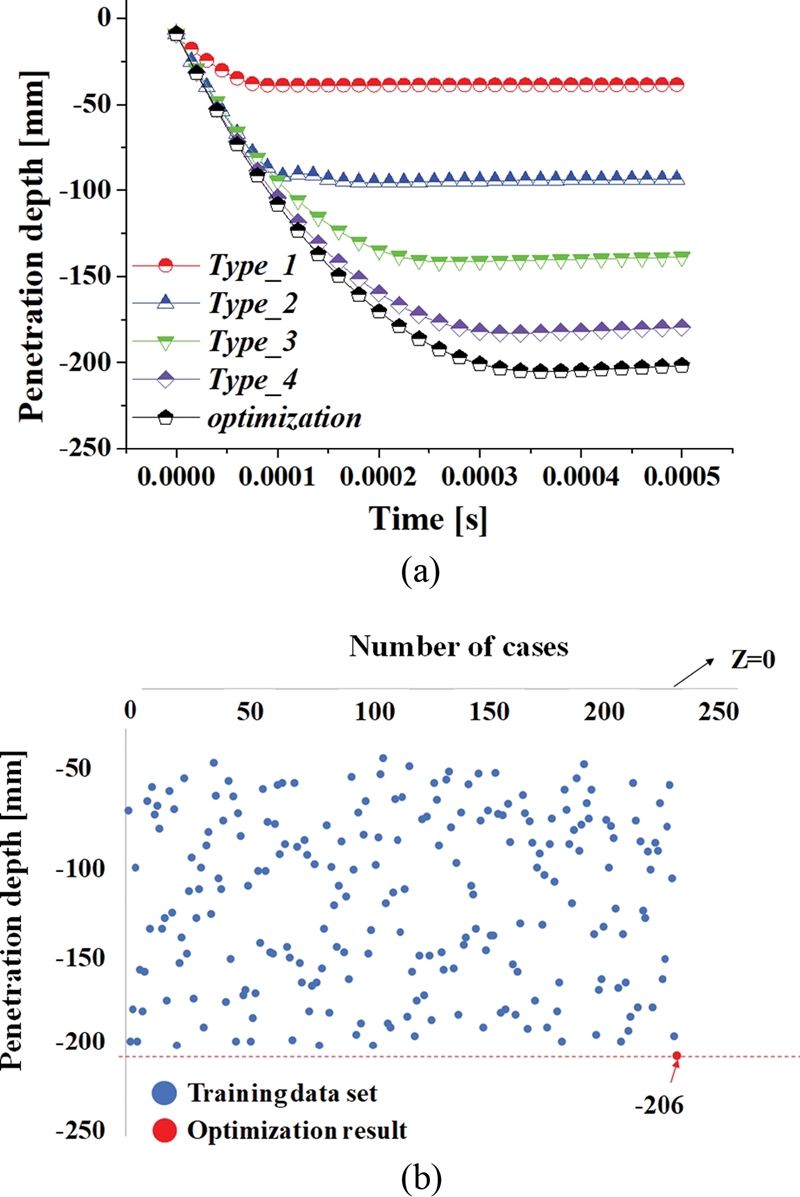
Comparison of penetration depths with the optimum geometry in (a) 5 types and (b) Projectile geometries

Fig. 5의 4가지 임의 형상과 최적 형상에서 투과 깊이와 질량을 비교하였다. Table 5는 200개의 학습 데이터 중 4개 유형의 임의 형상과 최적 형상에 따른 투과 깊이와 질량이다. 본 연구에서 인공 신경망과 유전 알고리즘을 사용한 최적 형상이 투과 깊이가 가장 깊고 질량이 가장 낮았다. 따라서 최적 형상이 투과 성능이 가장 우수하다는 것을 확인하였다.

Table 5

Penetration depth and mass results according to projectile geometries

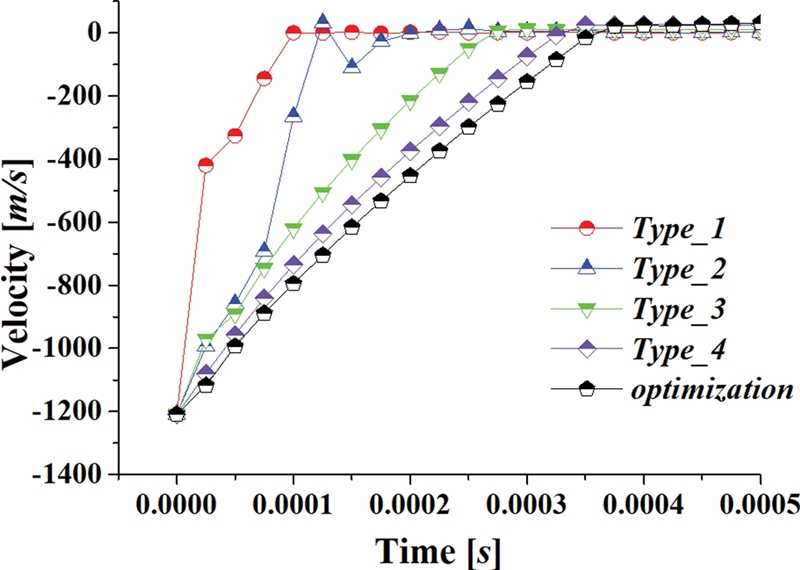
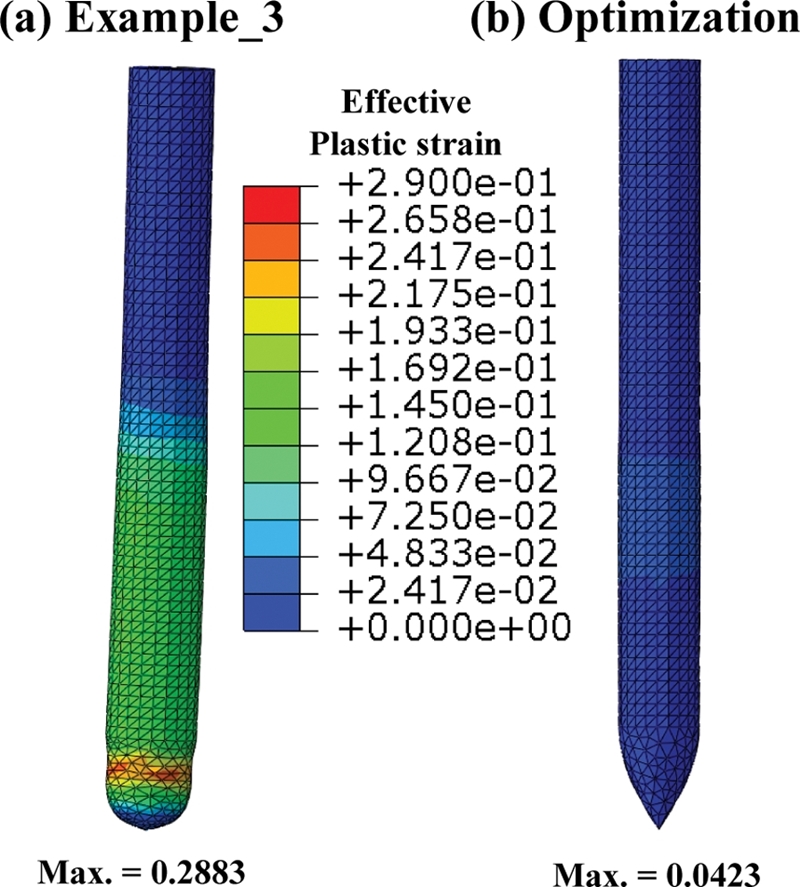
관통자는 충돌 전 모두 동일한 질량 대비 운동에너지를 갖고있다. 충돌 후 운동에너지가 관통자의 소성 변형에너지와 관통 에너지로 전환된다. Fig. 13은 시간에 따른 관통자의 속도 감소를 나타낸 그래프이다. 속도가 적을수록 관통자의 운동에너지가 낮다. 이때 관통자의 초기 운동에너지는 관통자의 변형에너지로 전환된다. 형상에 따른 관통자의 속도가 늦게 감소할수록 상대적으로 관통자의 투과 성능이 우수하고 할 수 있다. 최적 형상이 다른 4개 유형의 임의 형상보다 속도가 가장 느리게 감소하고 있다. Fig. 14는 Fig. 6의 1가지 형상과 본 연구에서 도출한 최적 형상의 정지 후 최종 형상을 비교한 그림이다. Fig. 14(a)는 관통자에서 소성 변형이 발생한 것을 볼 수 있지만, Fig. 14(b)의 최적화 결과에서는 소성 변형이 매우 작으며, 초기 형상을 유지한 것을 확인할 수 있다.

Fig. 13

Comparison of velocities according to time

Fig. 14

Deformation of the projectile after the penetration (a) Example_3 and (b) Optimization result

관통자에 작용하는 압력은 식(1)에 의해 결정된다. 관통자의 탄두 형상이 진행 방향에 수직인 경우 최대 압력이 발생한다. 진행 방향과 동일한 경우 관통자의 끝부분에서는 변형이 크지 않지만, 몸체와 연결부에서 큰 변형이 발생한다. 앞에서 구한 최적화된 형상은 충돌에서 발생하는 소성 변형에너지를 최소화하여 투과 깊이를 최대화할 수 있다.

추가로 수직 충돌이 아닌 경사 충돌의 경우 추가적인 최적화 작업이 필요하다. 또한 실험을 통해 본 해석 내용의 검증이 필요하며 현재 이를 위한 실험을 준비 중이다.